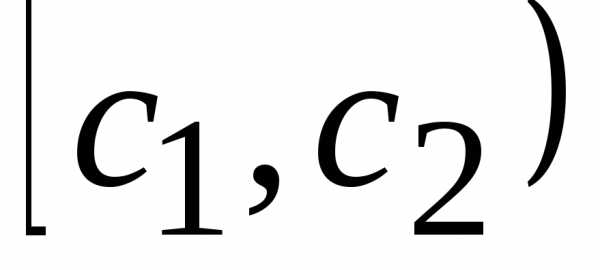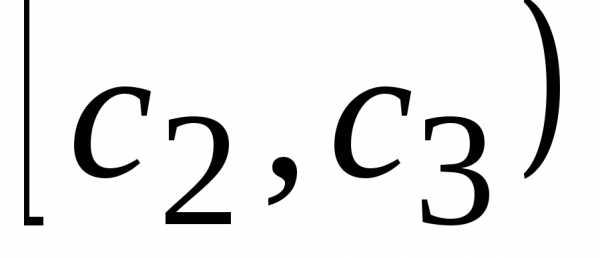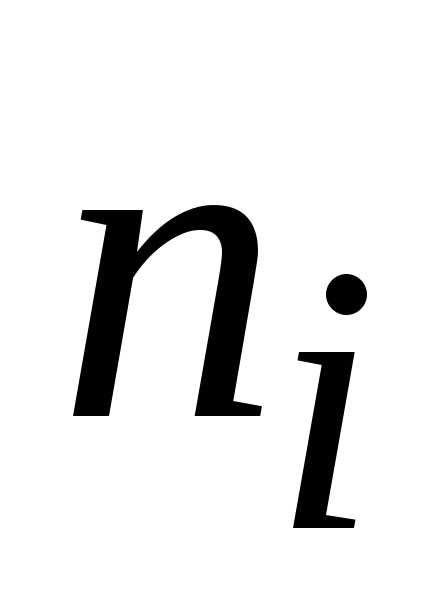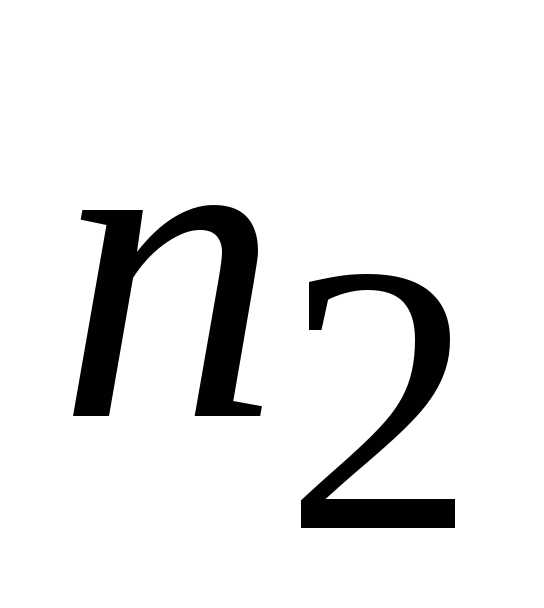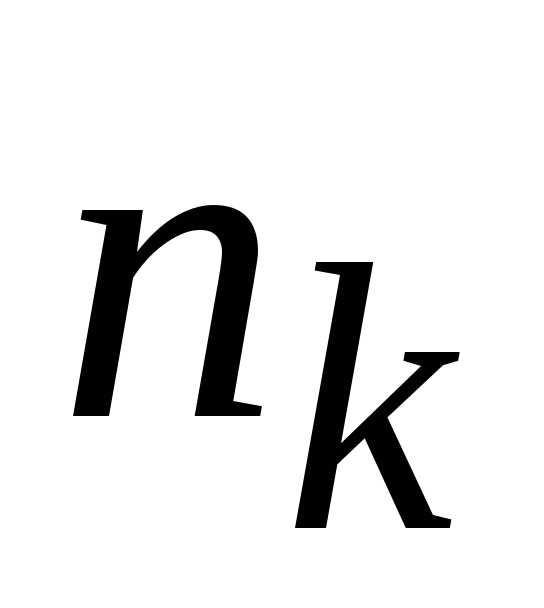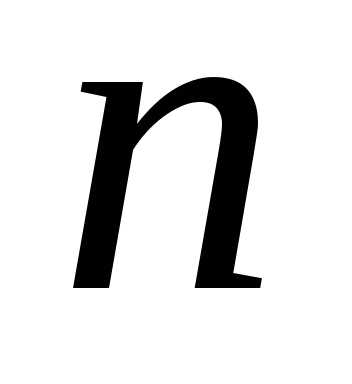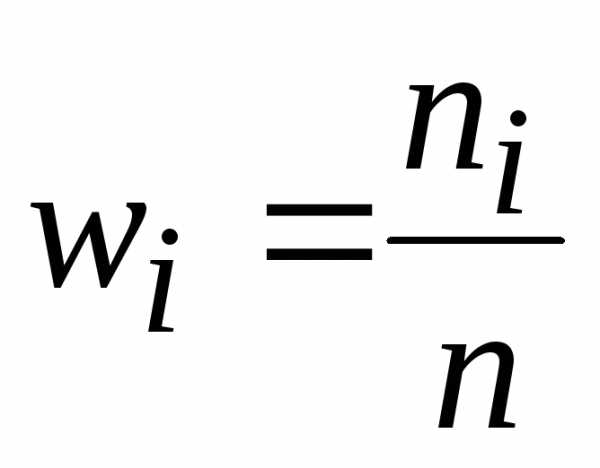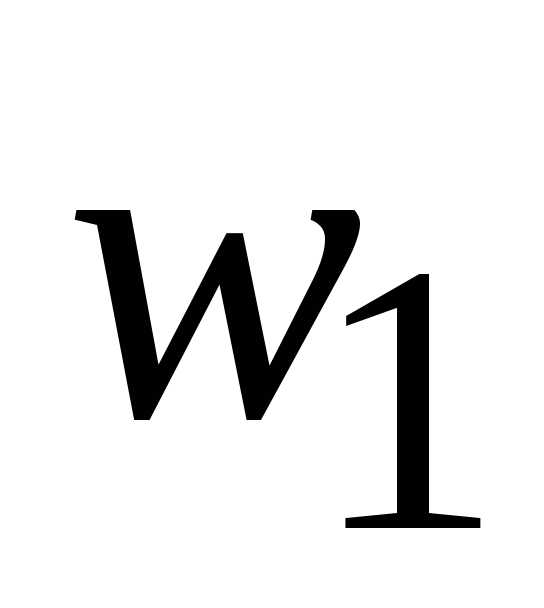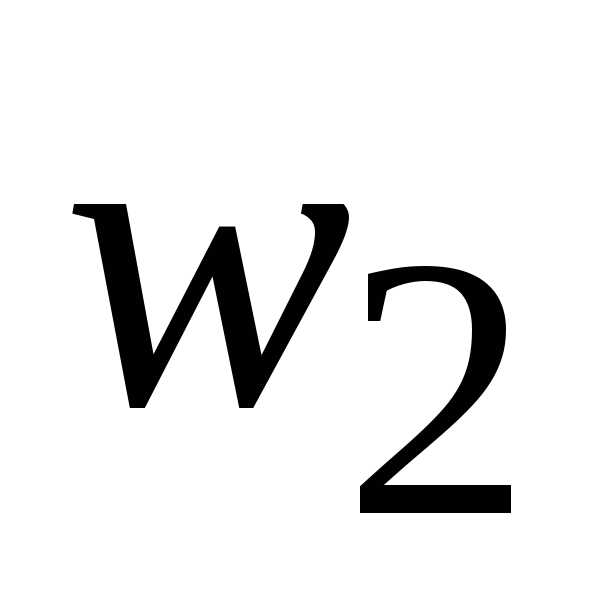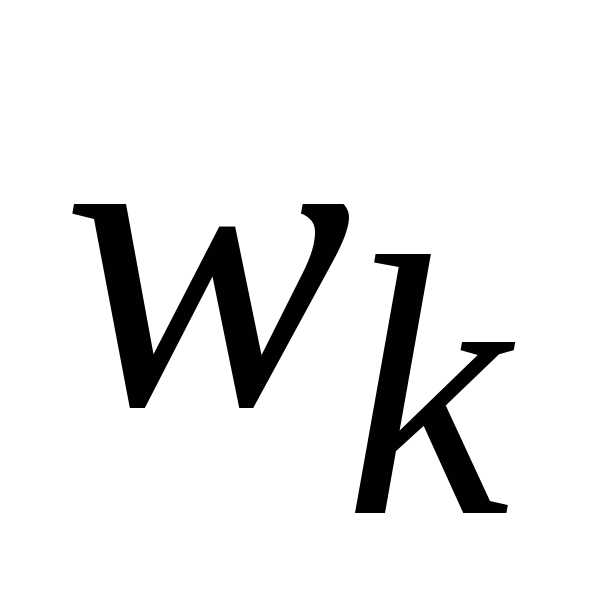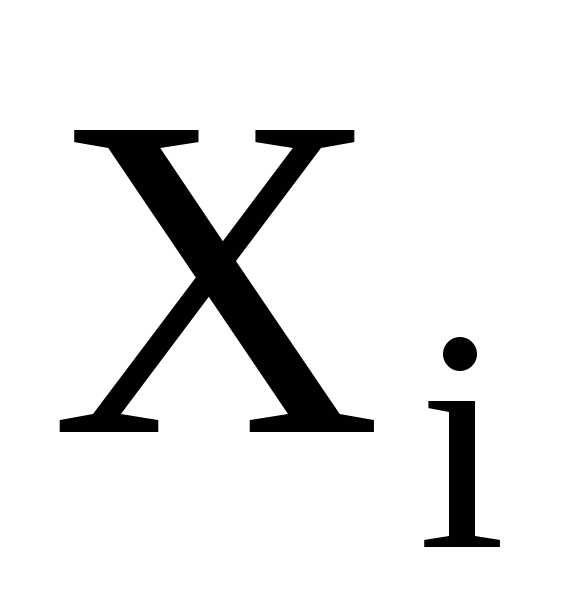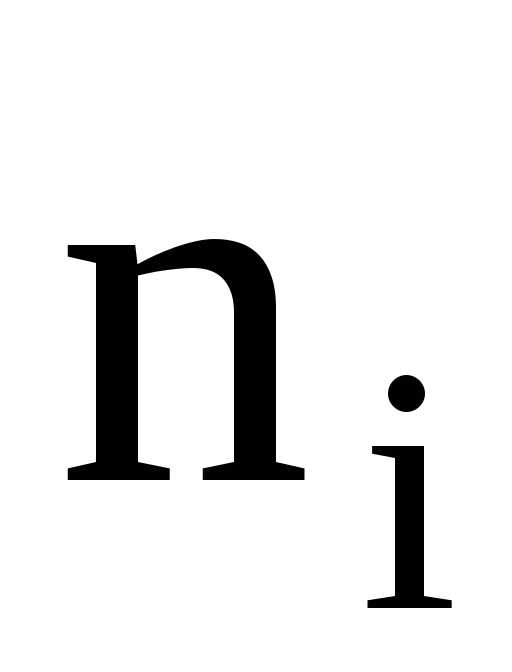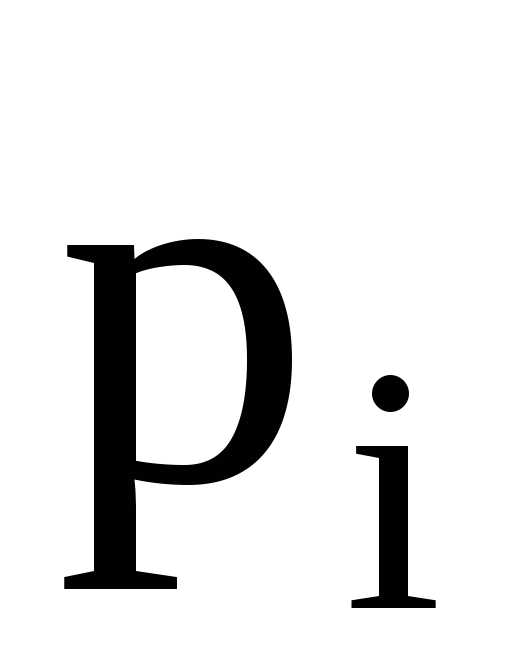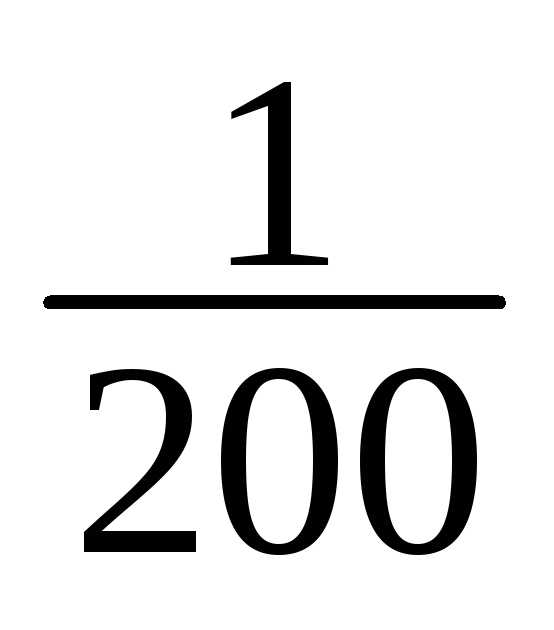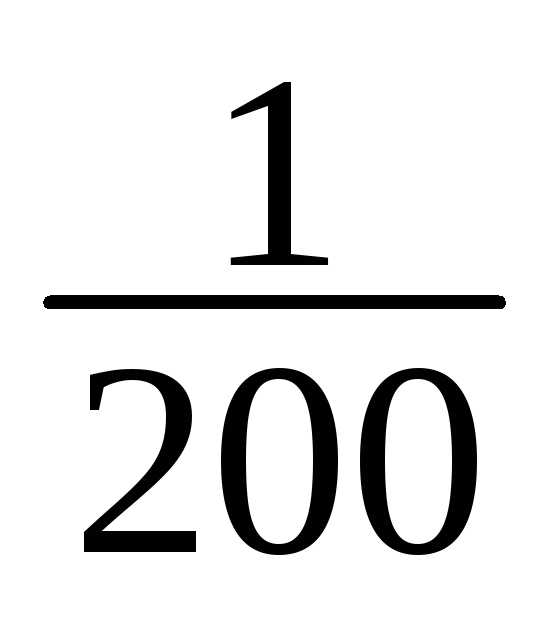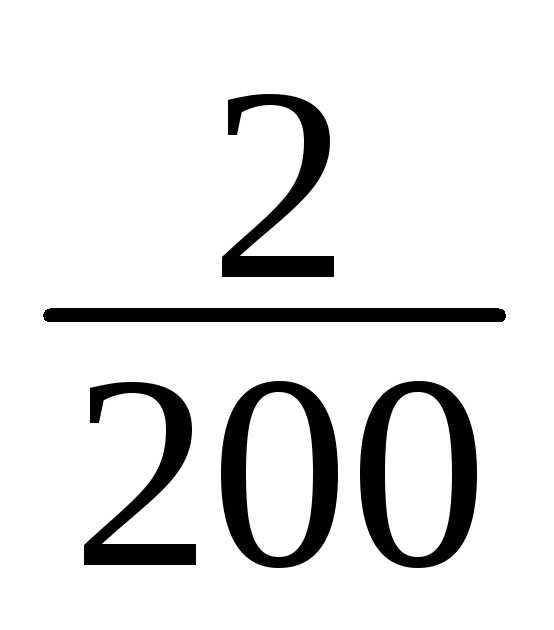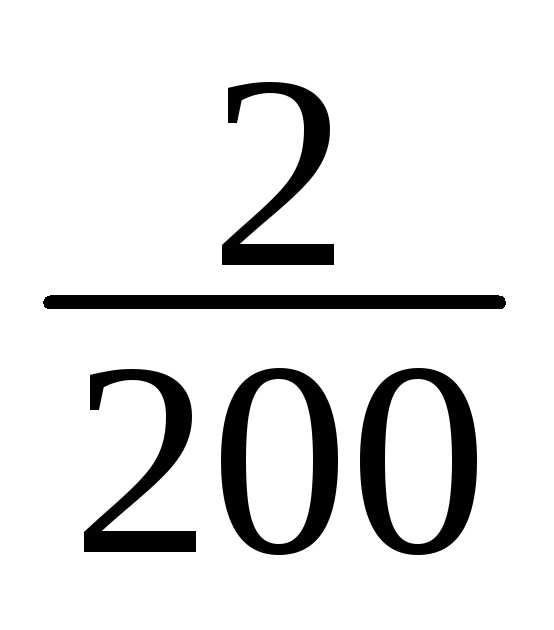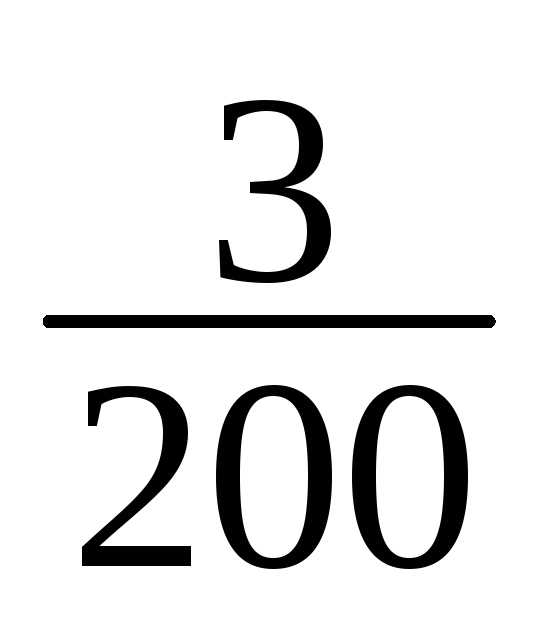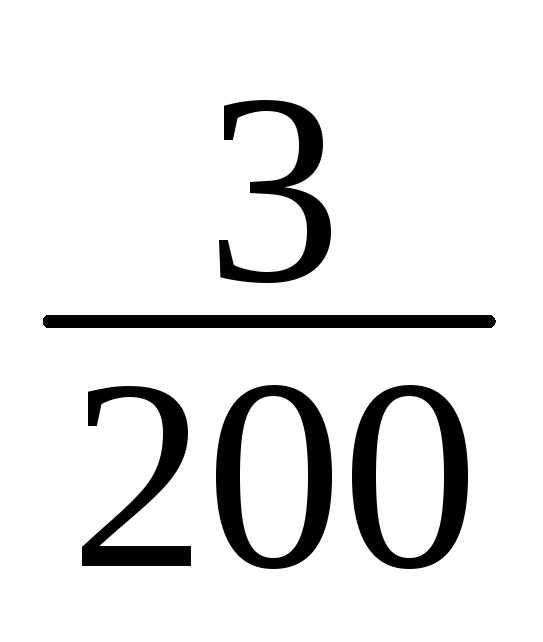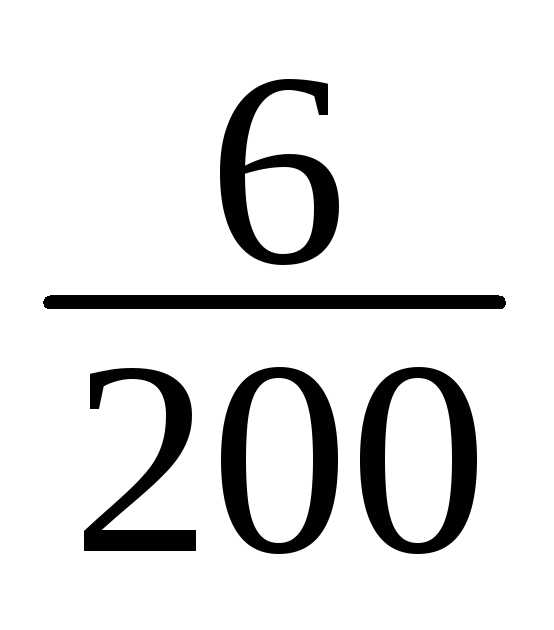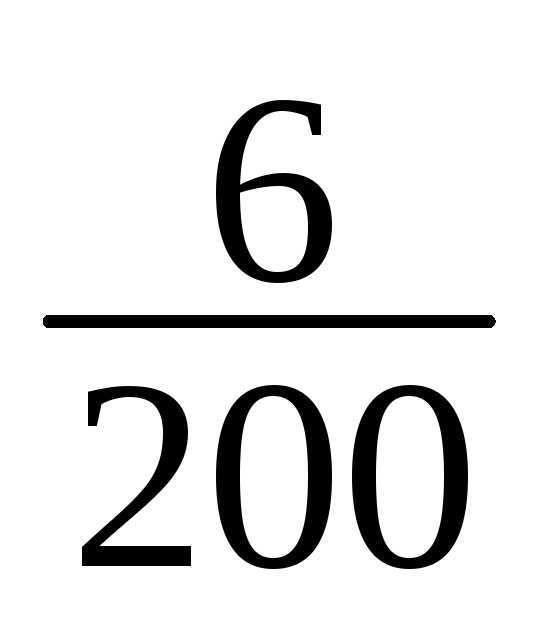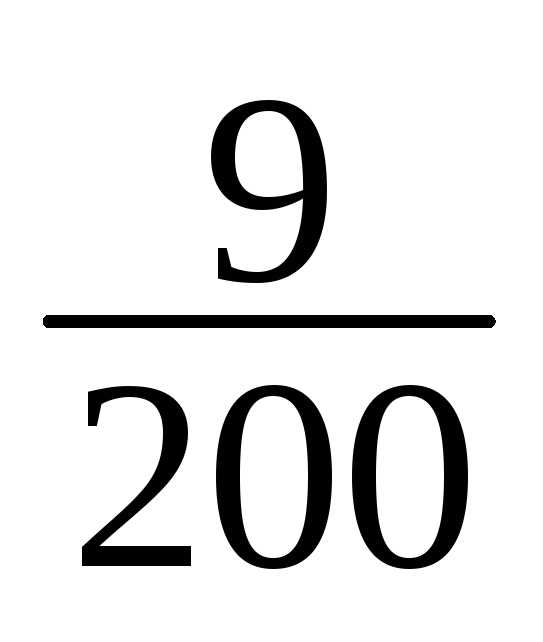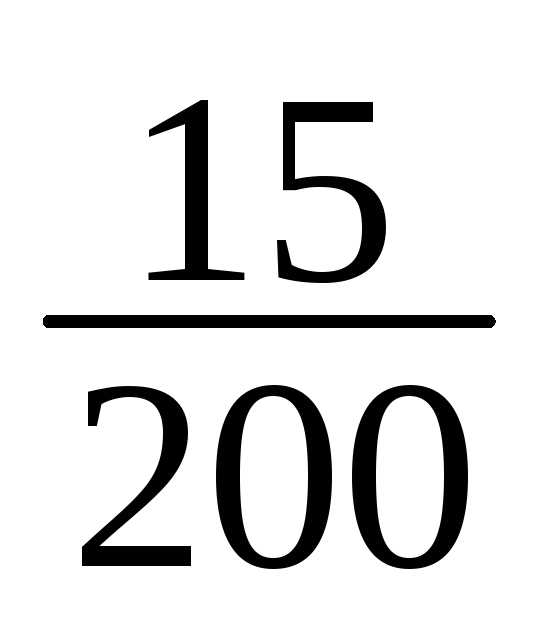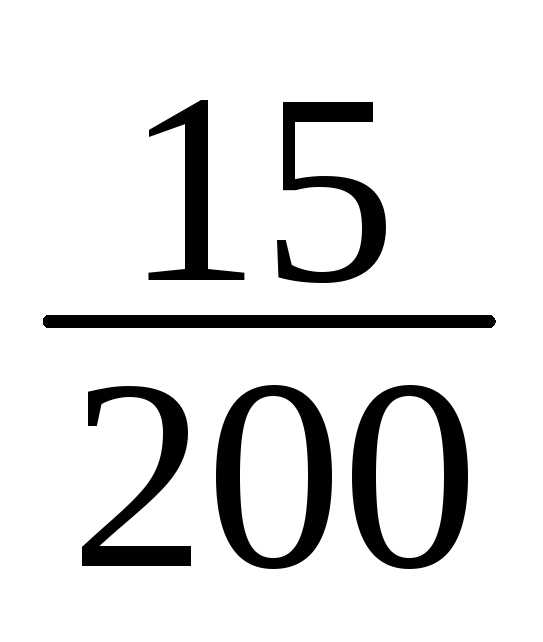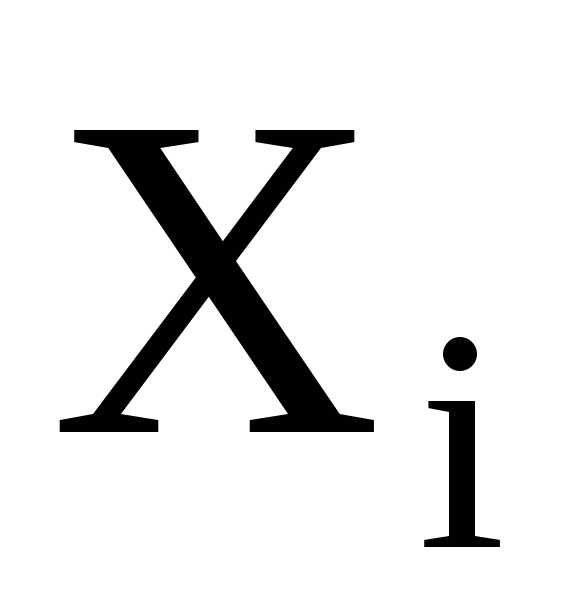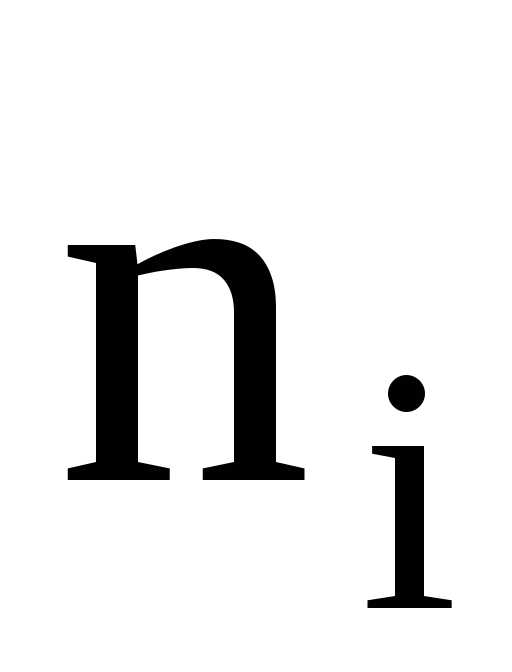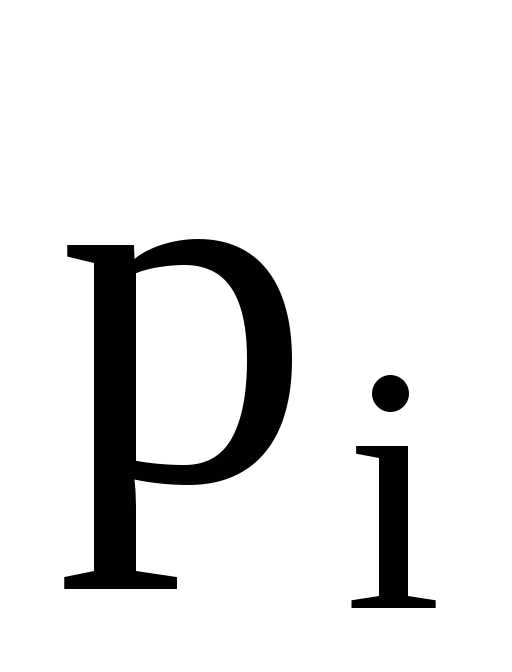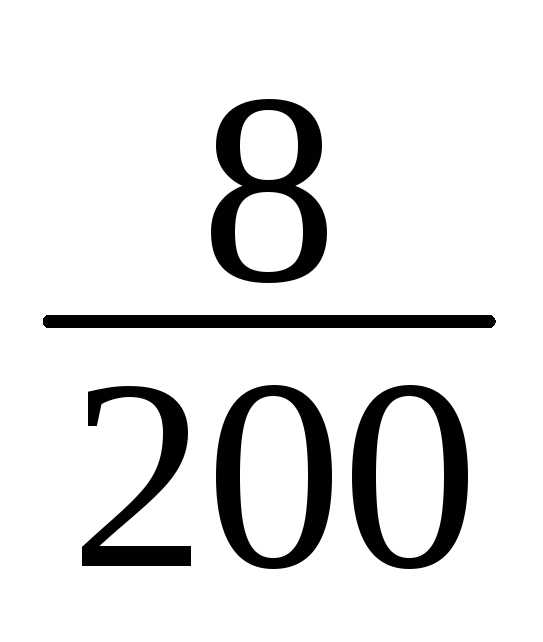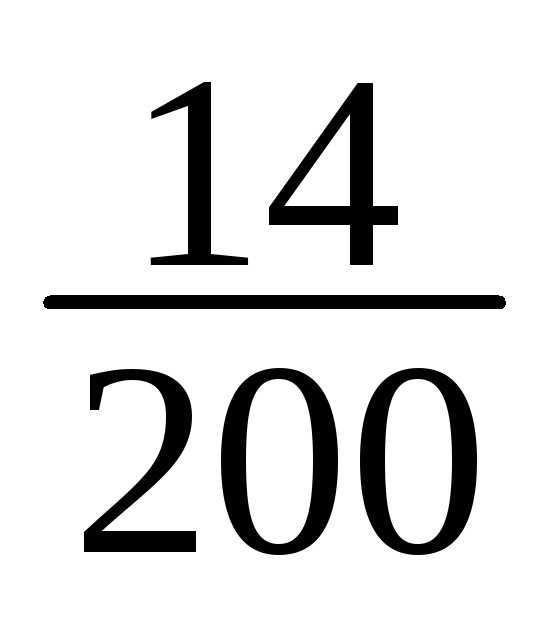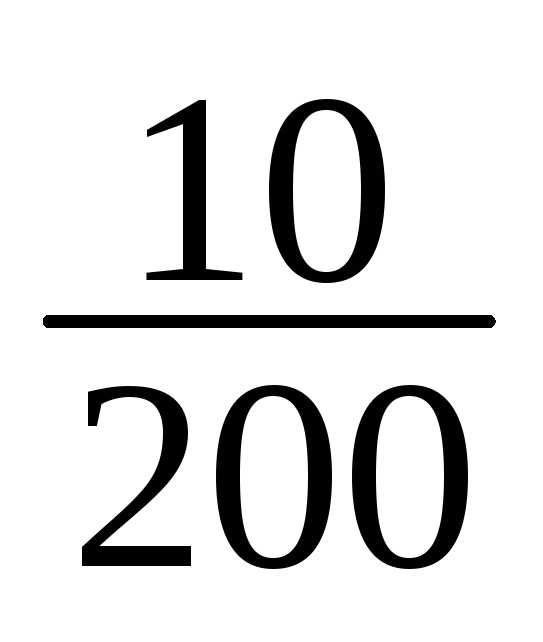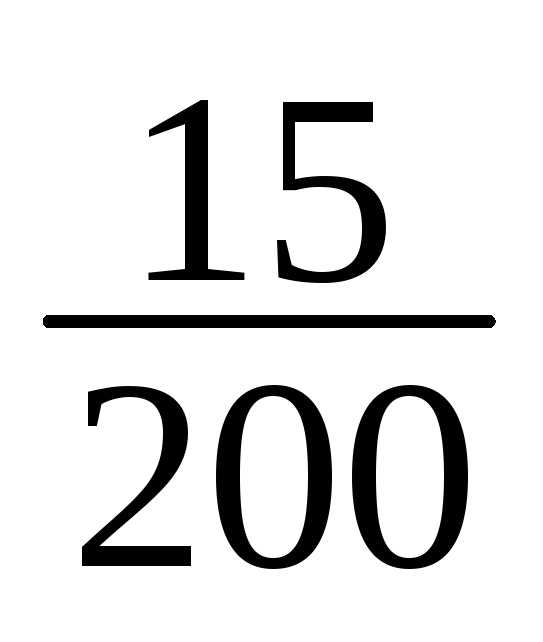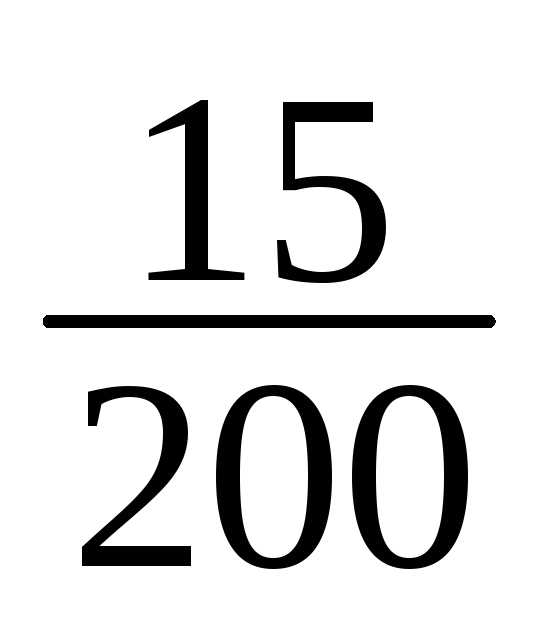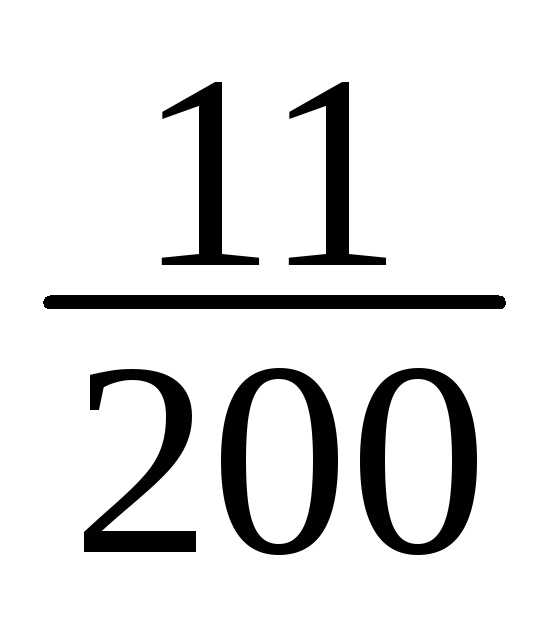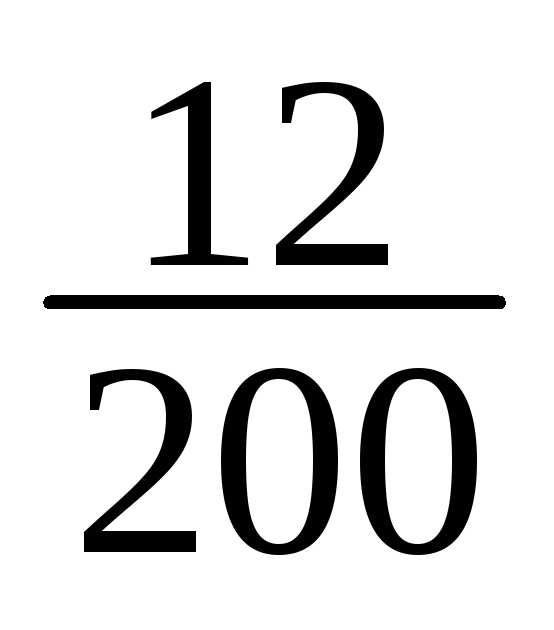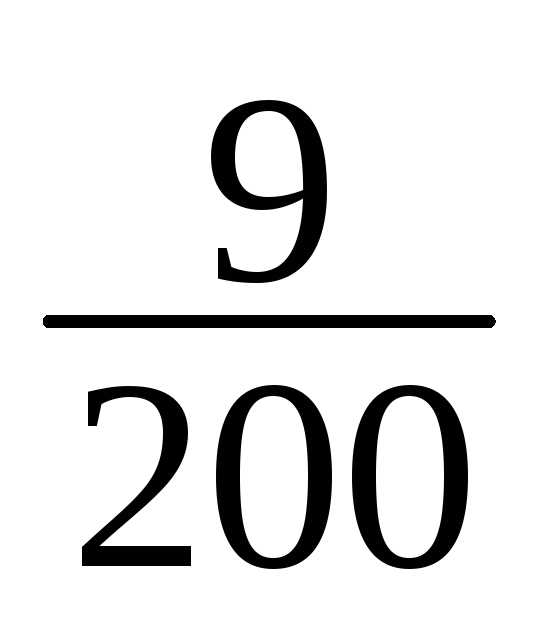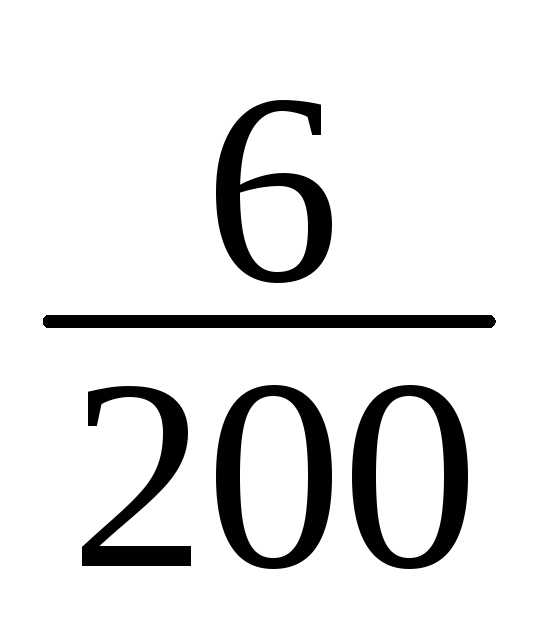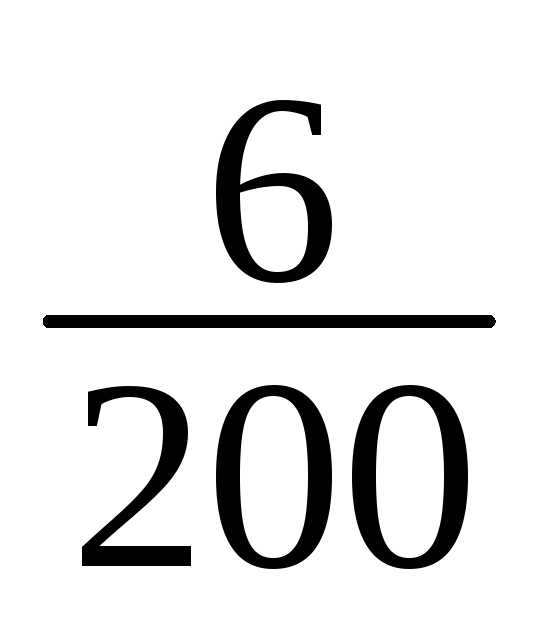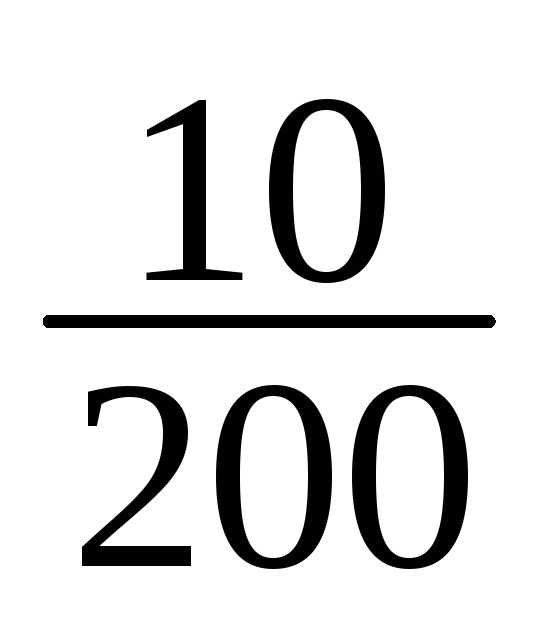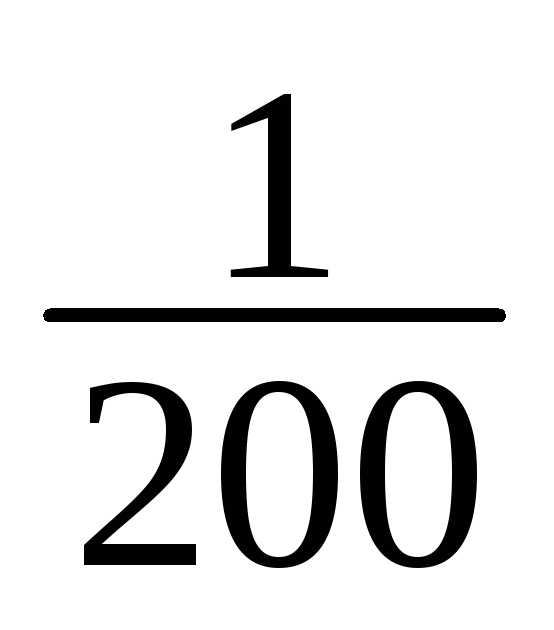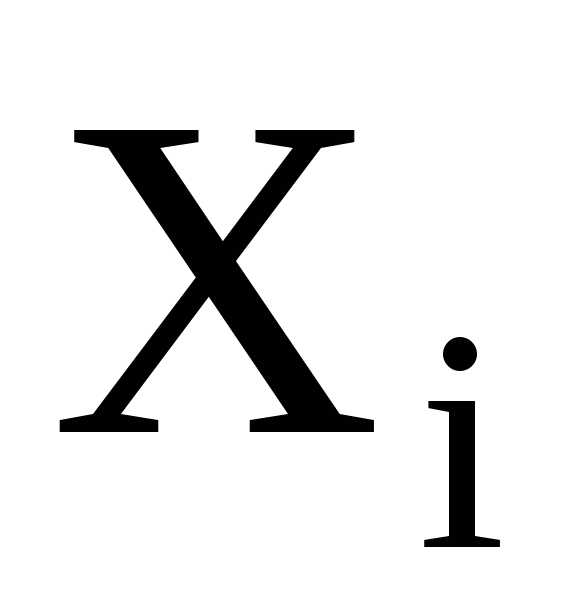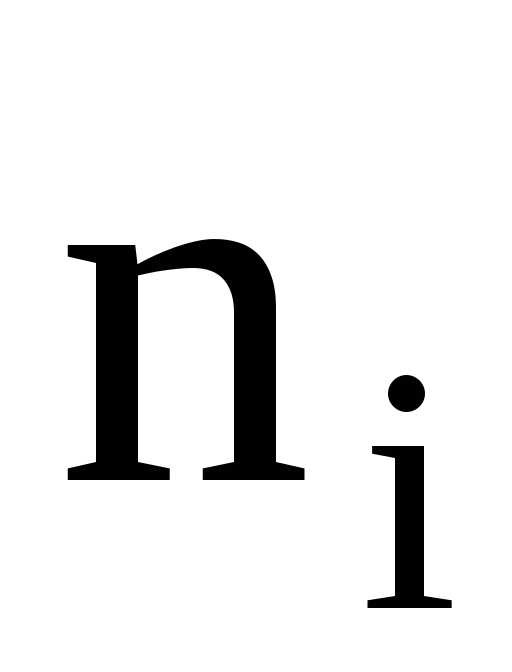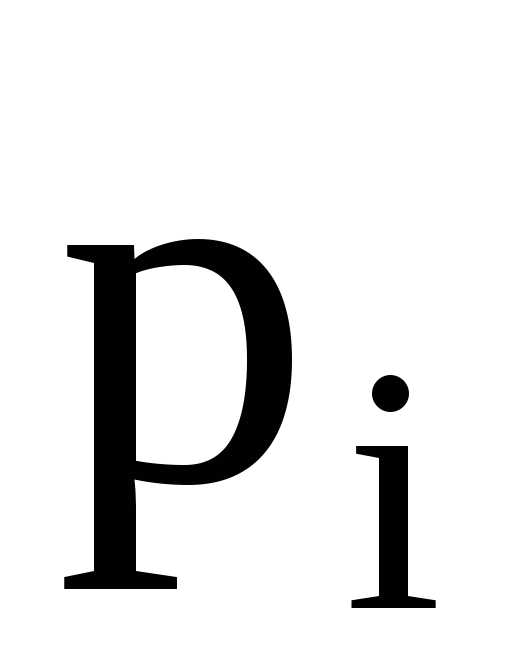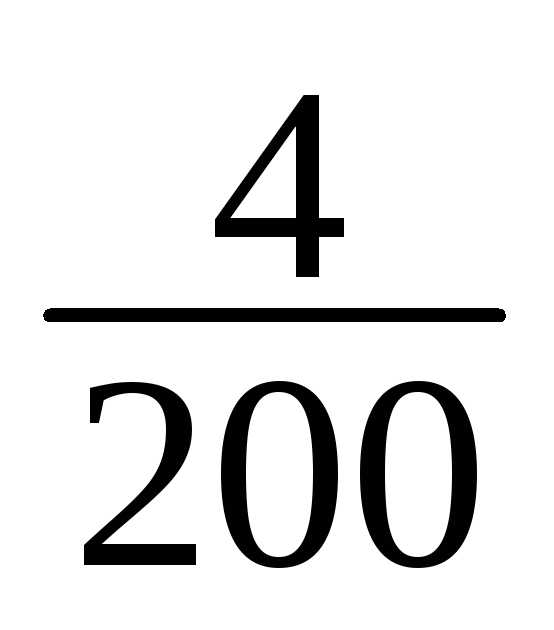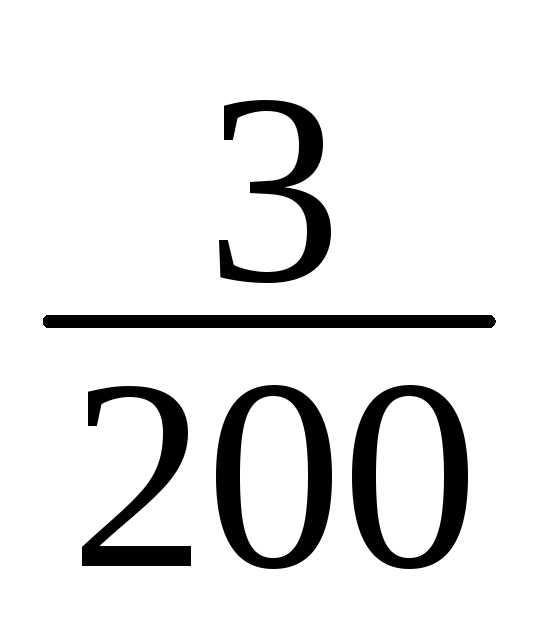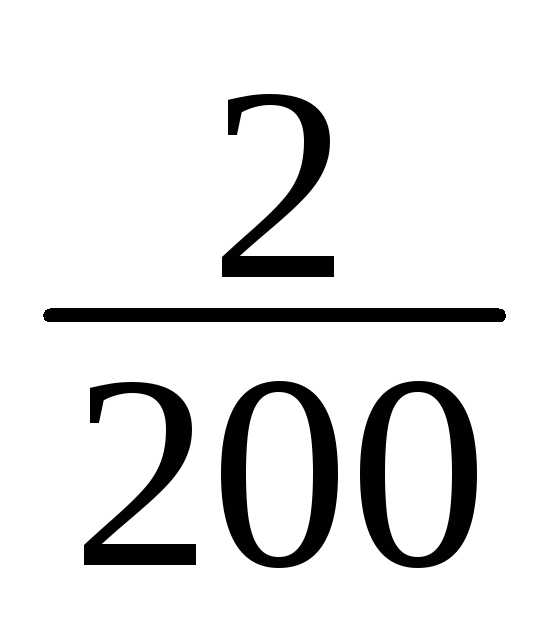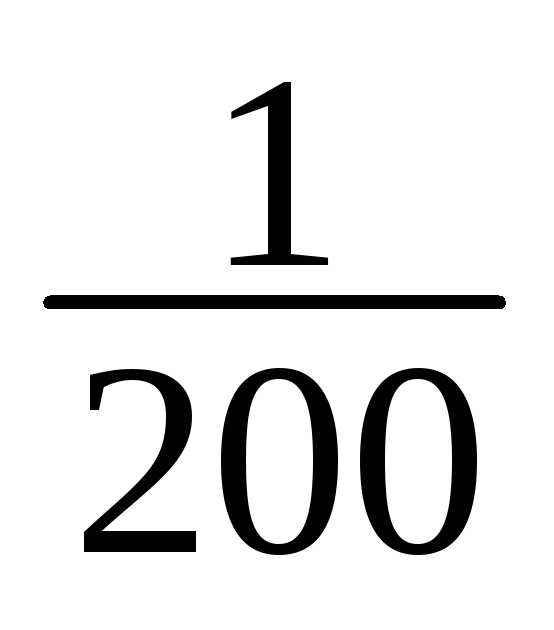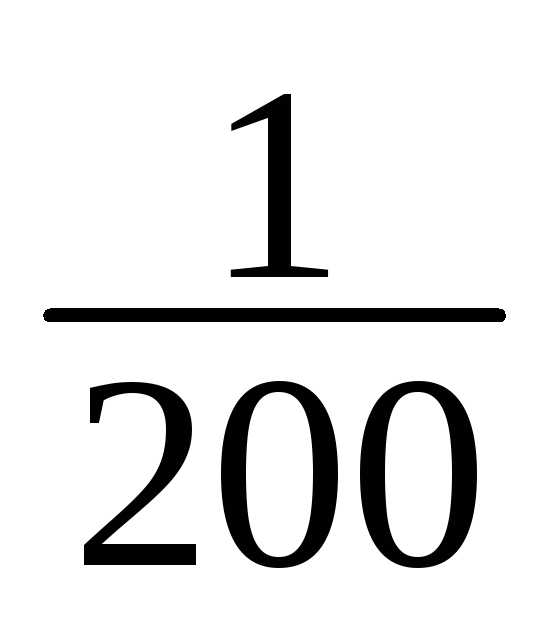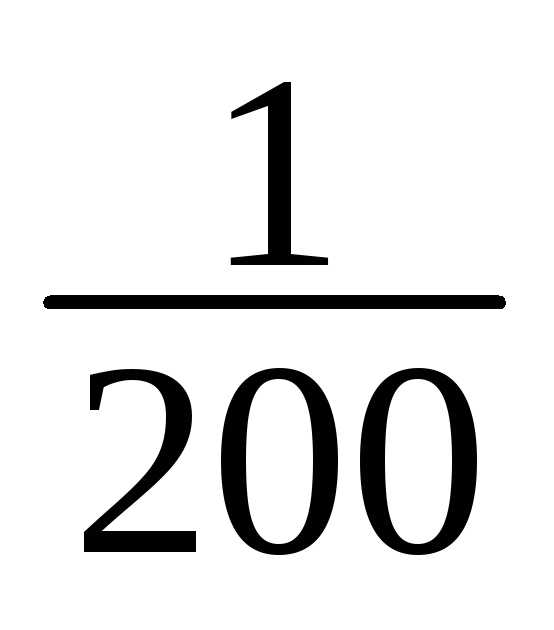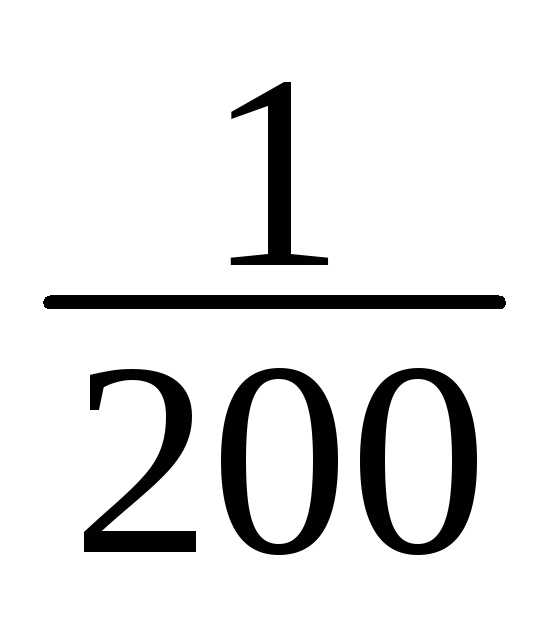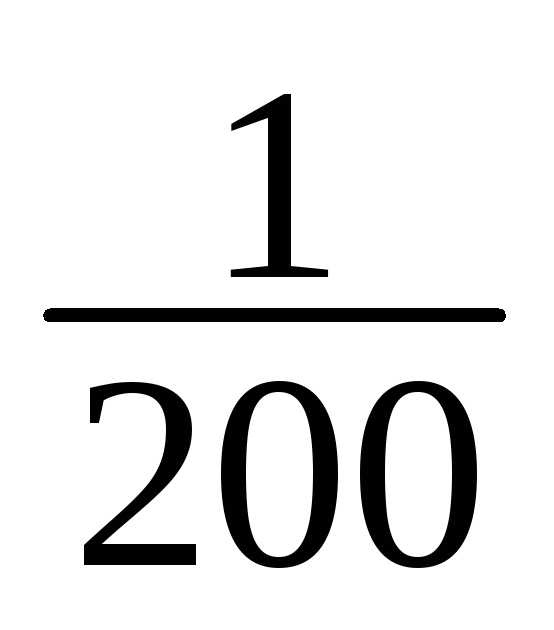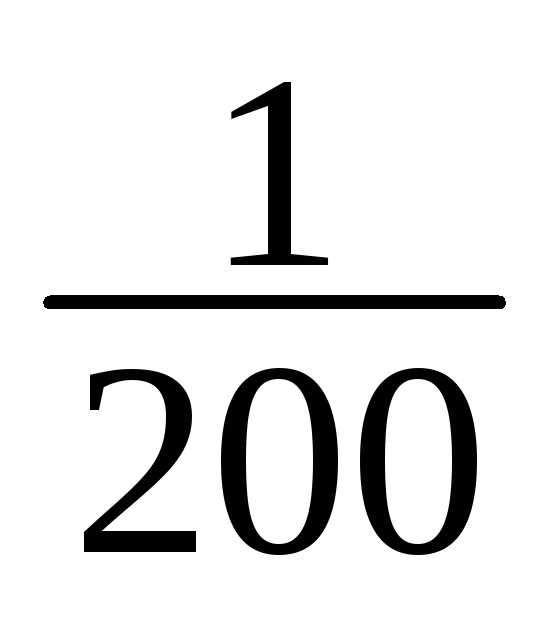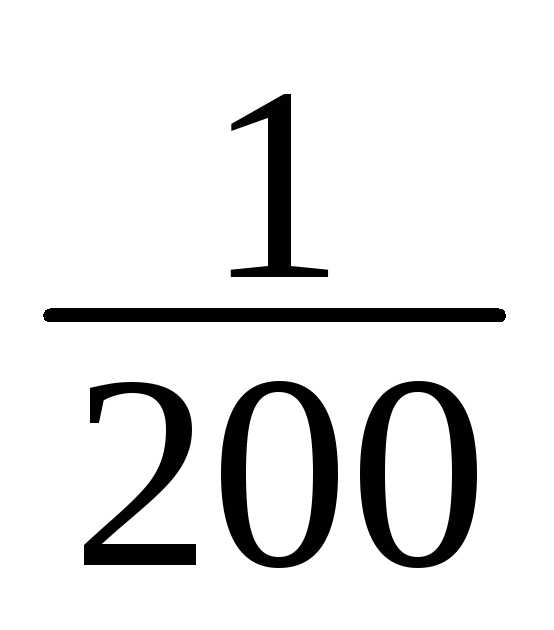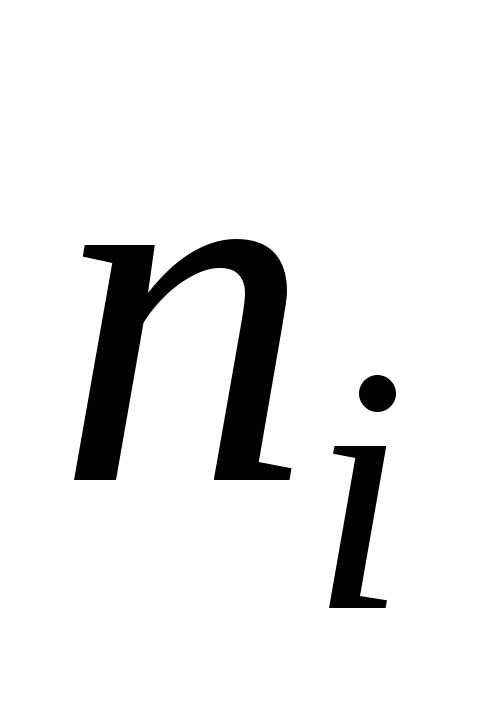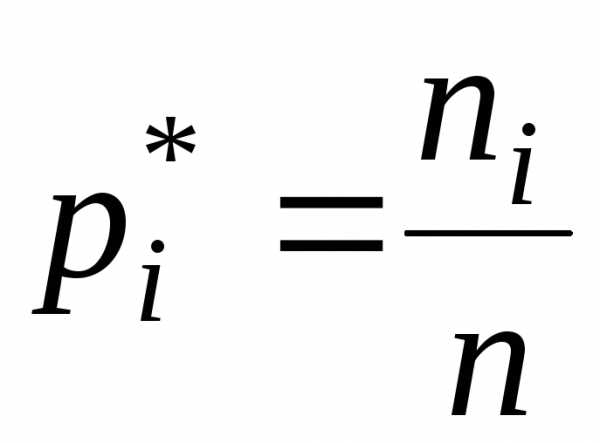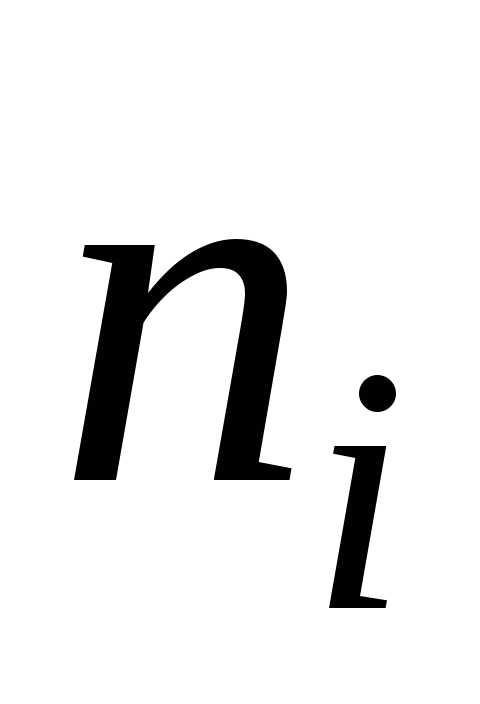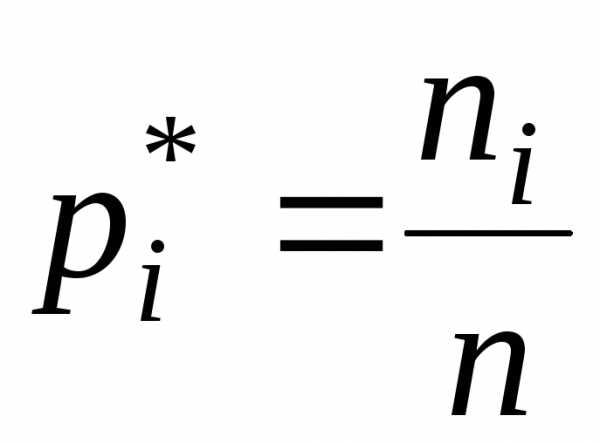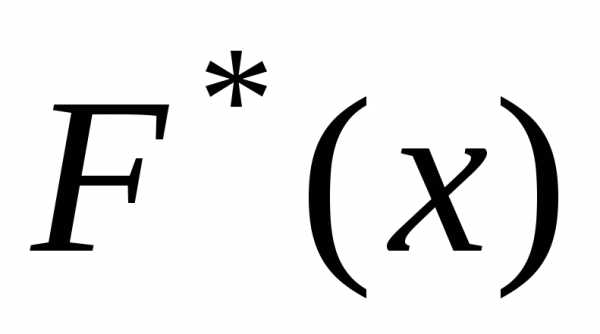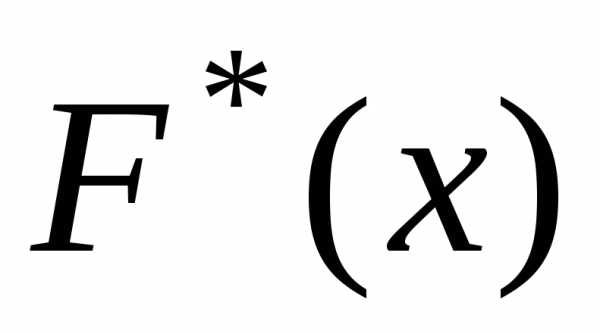Пример построения интервального вариационного ряда
Пусть измерен некоторый экономический показатель в 30 регионах:
23 29 35 7 11 18 23 30 36 18 11 8 13 20 25 27 14 30 20 20 24 19 21 26 22 16 26 25 33 27
Расставим экспериментальные данные в возрастающем порядке:
7 8 11 11 13 14 16 18 18 19 20 20 20 21 22 23 23 24 25 25 26 26 27 27 29 30 30 33 35 36
По таблице 1 определяем число классов
Таблица 1
Объем выборки n | Число классов K |
6-11 | 4 |
12-22 | |
23-46 | 6 |
47-93 | 7 |
94-187 | 8 |
188-377 | 9 |
378-755 | 10 |
756-1515 | 11 |
Для n=30 число классов K=6. Найдем минимальное и максимальное значения вариант: хmin=7, хmax=36. Определим вариационный размах R= хmin-хmax=36-7=29.
Определим величину
классового интервала: =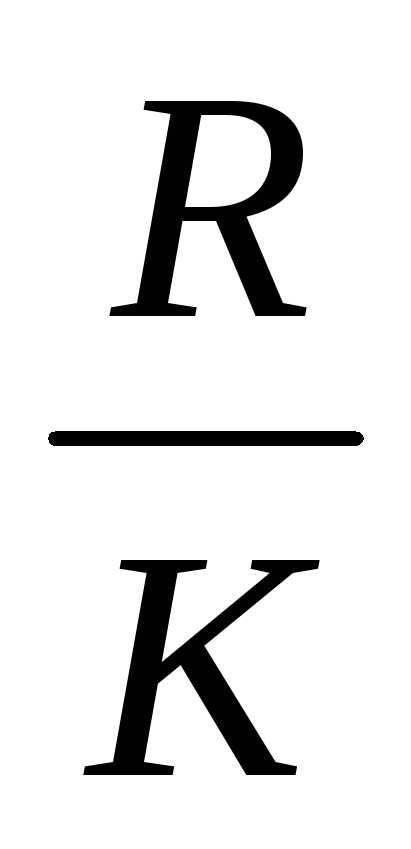
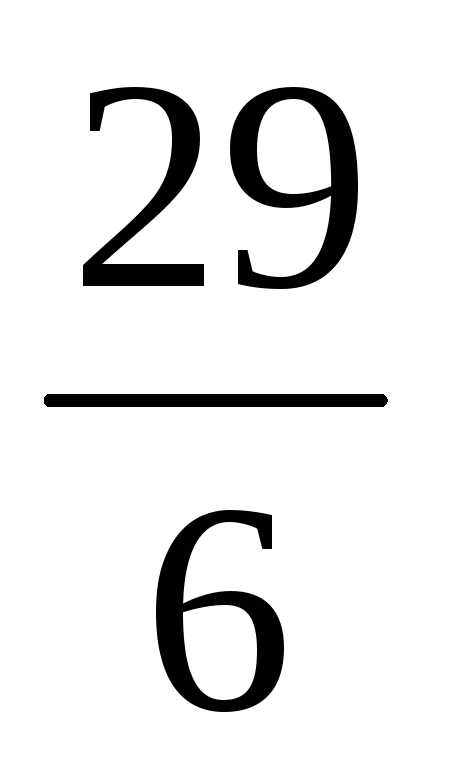=4,8.Хн1= хmin=7; Хв1= хmin+=7+4,8=11,8
Обобщим полученные данные в таблице:
Таблица 2
Номера классов | Классовые интервалы | Серединные значения классов | Частоты | Накопленные частоты |
1 | 7-11,8 | 9,4 | 4 | 4 |
2 | 11,8-16,6 | 14,2 | 3 | 7 |
3 | 16,6-21,4 | 19 | 7 | 14 |
4 | 21,4-26,2 | 23,8 | 9 | 22 |
5 | 26,2-31 | 28,6 | 5 | 27 |
6 | 31-36 | 33,4 | 3 | 30 |
График, называемый гистограммой получается, если в прямоугольной системе координат отложить по оси абсцисс границы классов, а по оси ординат их частоты.
Если серединные точки вершин прямоугольников гистограммы соединить между собой, получится график дискретного варьирования, называемый полигоном распределения.
рис.1. Полигон распределения.
1.2. Мода распределения – это наиболее часто встречающееся значение ряда.
Среднее арифметическое распределения находится по формуле хср= (х1+х2+х3+ …+хn)/n
Дисперсия распределения находится по формуле:
D=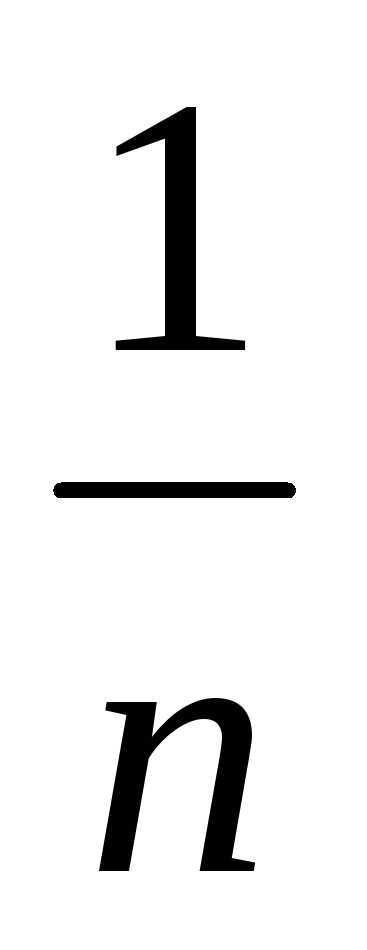
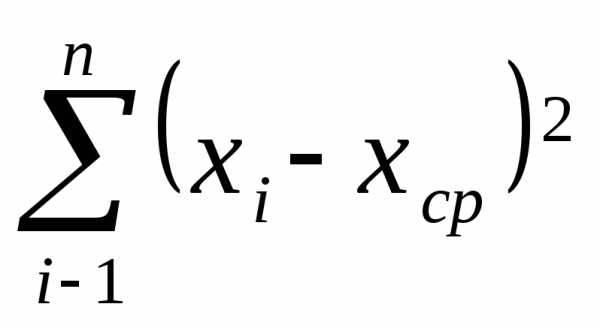
1.5. Стандартное
отклонение S=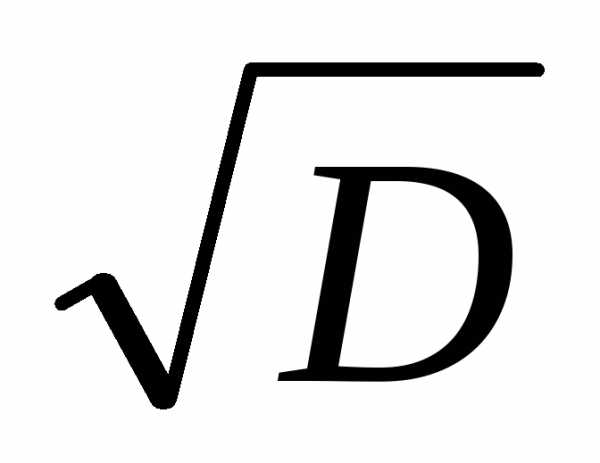
Пример расчета рангового коэффициента корреляции
Пусть при исследовании десяти человек получены следующие показатели Х и Y. Выясним, существует ли между ними связь. Для этого подсчитаем ранговый коэффициент корреляции и дадим его графическую интерпретацию.
Таблица 3
Х | Y |
175 | 2 |
176 | 3 |
179 | 8 |
180 | 9 |
181 | 6 |
184 | 7 |
185 | 13 |
186 | 11 |
191 | 10 |
192 | 12 |
Просуммируем их и подставим в формулу:
rs=1-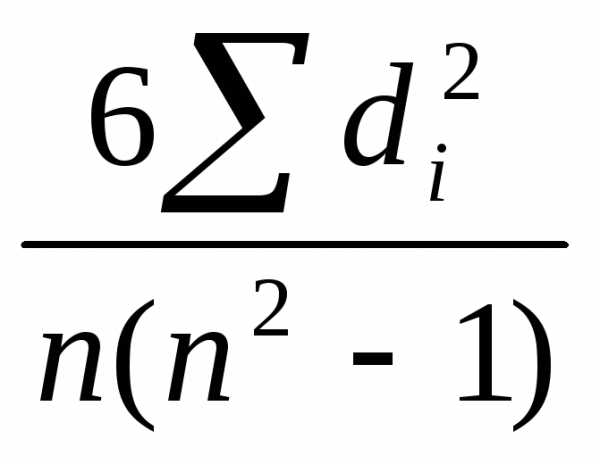
.
Таблица 4
№ | X | Y | Rx | Ry | |d| | d2 |
1 | 175 | 2 | 1 | 1 | 0 | 0 |
2 | 176 | 3 | 2 | 2 | 0 | 0 |
3 | 179 | 8 | 3 | 5 | 2 | 4 |
4 | 180 | 9 | 4 | 6 | 2 | 4 |
5 | 181 | 6 | 5 | 3 | 2 | 4 |
6 | 184 | 7 | 6 | 4 | 2 | 4 |
7 | 185 | 13 | 7 | 10 | 3 | 9 |
8 | 186 | 11 | 8 | 8 | 0 | 0 |
9 | 191 | 10 | 9 | 7 | 2 | 4 |
10 | 192 | 12 | 10 | 9 | 1 | 1 |
Сумма: | 30 | |||||
В нашем случае:
rs=1-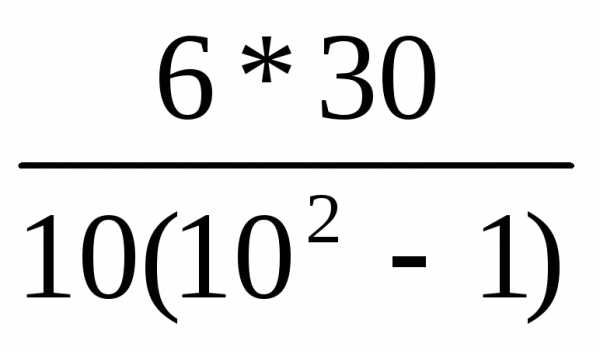
=0,81.
Оценим значимость коэффициента корреляции
tфакт.=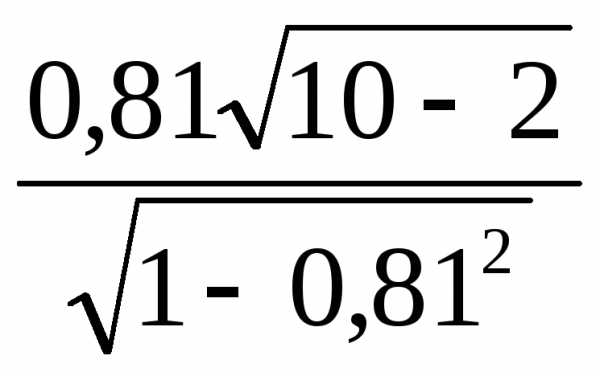
=3,92.
По таблице 5 Приложения 2 определяем, что для уровня значимости р=0,05 tкрит.=2,31. Следовательно, вычисленный коэффициент корреляции значимо отличается от нуля и между показателями х и у наблюдается линейная связь выше среднего.
Для графической интерпретации по оси х откладываются значения признака х, по оси у – значения признака у.
рис.2. Графическая интерпретация коэффициента корреляции.
По значению коэффициента корреляции и графической интерпретации можем сказать, что между признаками х и у есть средняя прямая связь.
studfiles.net
3. Интервальный вариационный ряд
При большом
объеме выборки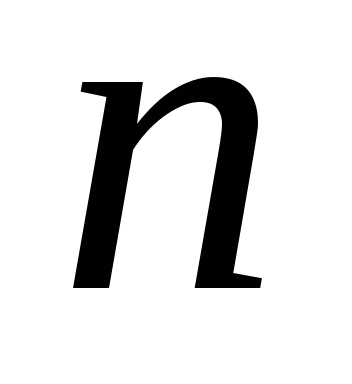 
работа с
вариационными рядами представляет
определенные неудобства, и тогда
наблюдаемые данные группируют.
Группировка должна наиболее полно выявлять существенные свойства распределения. Существуют формулы для определения оптимального количества интервалов, но в психологии считается, что следует брать от 5 до 15 интервалов.
Первый способ построения интервального ряда.
Если
у исследователя нет предварительной
информации о характере распределения
признака, то лучше задавать равные
интервалы,
при этом длина
интервала 
определяется по формуле 
,
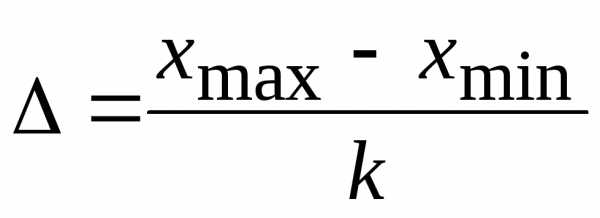где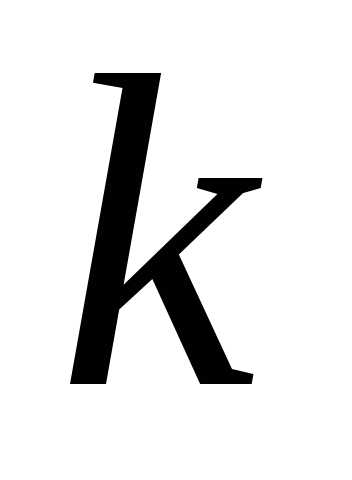
— количество выбранных интервалов (число
округляется до целого значения).
Начало
первого интервала равно
,
а конец(это будет одновременно и началом второго
интервала). Условимся все интервалы
считать соткрытым
правым концом: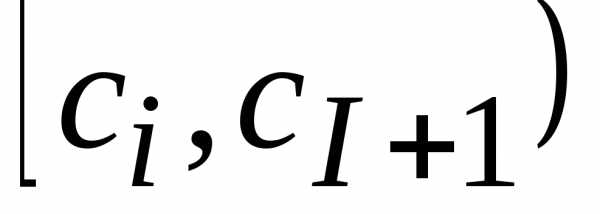 
.
Построение интервалов заканчивается,
если в интервал попало наибольшее
значение признака
.
Далее
подсчитывают число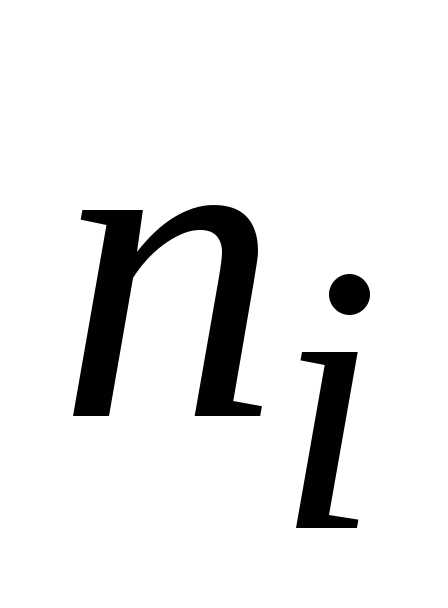 
значений признака, попавших в каждый
интервал (с учетом открытого правого
конца). Получается таблица, называемаяинтервальным
вариационным рядом.
Интервалы
…
Сумма
Частоты,
…
Относительные частоты,
1
Второй способ построения интервального ряда.
Весь
диапазон значений признака от 
до
разбивается на равныеинтервалы,
называемые также классами.
Затем все варианты совокупности распределяются
по этим интервалам.
Порядок действий:
Пример построения интервального вариационного ряда.
Пусть измерен некоторый показатель для 30 испытуемых:
23, 29, 35, 7, 11, 18, 23, 30, 36, 18, 11, 8, 13, 20, 25,
27, 14, 30, 20, 20, 24, 19, 21, 26, 22, 16, 26, 25, 33, 27.
Это статистический ряд.
Расставим экспериментальные данные в возрастающем порядке, то есть построим вариационный ряд:
7, 8, 11, 11, 13, 14, 16, 18, 18, 19, 20, 20, 20, 21, 22,
23, 23, 24, 25, 25, 26, 26, 27, 27, 29, 30, 30, 33, 35, 36.
Число
классов (интервалов) для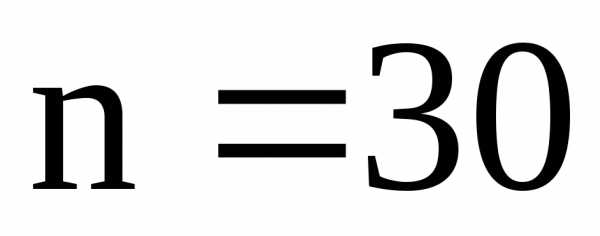 
:
.
Минимальное
и максимальное значения: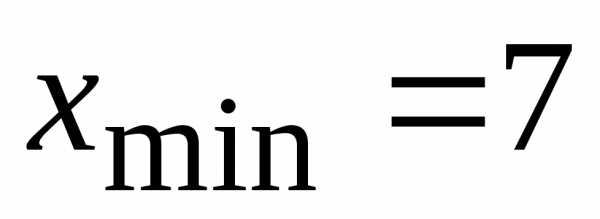 
,.
Вариационный размах: .
Величина интервала: .
Находим границы интервалов:
;
; ;
; ;
; .
Построим интервальный вариационный ряд.
Номера интервалов
Интервалы
Серединные значения интервалов
Частоты
1
4 – 10
7
2
2
10 – 16
13
4
3
16 – 22
19
8
4
22 – 28
25
10
5
28 – 34
31
4
6
34 – 40
37
2
5. Гистограмма
Вариационные ряды изображают графически с помощью полигона и гистограммы.
с1с2с3с4 с5с6с7с8с9
Гистограммой называется графическое изображение интервального вариационного ряда. На оси абсцисс откладываются отрезки, изображающие интервалы значений варьирующего признака, а затем на этих отрезках, как на основаниях, строятся прямоугольники, площади которых пропорциональны частотам (или относительным частотам).
Полигон
частот для
дискретного вариационного ряда — это
ломаная, отрезки которой соединяют
точки с координатами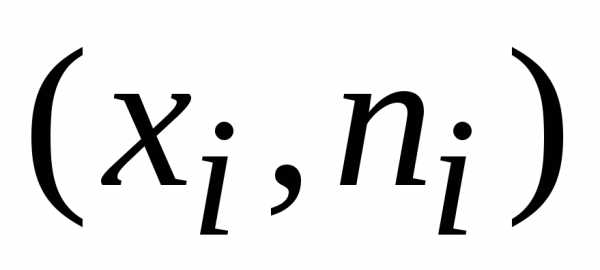 
.
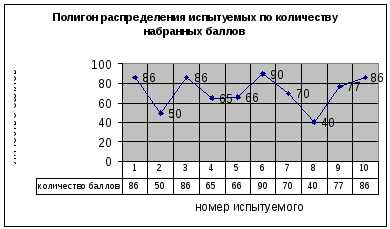
Полигон частот признака
studfiles.net
Алгоритм построения интервального вариационного ряда с равными интервалами
Определяем число интервалов (групп) вариационного ряда
Число групп (интервалов) приближенно определяется по формуле Стерджесса:
m = 1 + 3,322 × lg(n)
где n — общее число единиц наблюдения (общее количество элементов в совокупности и т.д.), lg(n) – десятичный логарифм от n.
Полученную по формуле Стерджесса величину округляют обычно до целого большего числа, поскольку количество групп не может быть дробным числом.
Если ряд интервальный ряд с таким количеством групп по каким-то критериям не устраивает, то можно построить другой интервальный ряд, округлив m до целого меньшего числа и выбрать из двух рядов более подходящий.
Число групп не должно быть больше 15.
Также можно пользоваться следующей таблицей, если совсем нет возможности вычислить десятичный логарифм.
Объем выборки, n | 25-40 | 40-60 | 60-100 | 100-200 | Больше 200 |
Число интервалов, m | 5-6 | 6-8 | 7-10 | 8-12 | 10-15 |
Определяем ширину интервала
Ширина интервала для интервального вариационного ряда с равными интервалами определяется по формуле:
где Xмакс — максимальное из значений xi, Xмин — минимальное из значений xi; m — число групп (интервалов).
Величину интервала (i) обычно округляют до целого числа, исключение составляют лишь случаи, когда изучаются малейшие колебания признака (например, при группировке деталей по величине размера отклонений от номинала, измеряемого в долях миллиметра).
Часто применяется следующее правило:
Количество знаков до запятой | Количество знаков после запятой | Пример ширины интервала по формуле | До какого знака округляем | Пример округленной ширины интервала |
0 | 3 | 0,375 | 0,01 | 0,38 |
0 | 2 | 0,56 | 0,1 | 0,6 |
1 | 3 | 4,658 | 0,01 | 4,66 |
1 | 2 | 2,54 | 0,1 | 2,5 |
2 | любое | 12,54 | 1,0 | 13 |
3 | любое | 672,54 | 10,00 | 670 |
4 | любое | 3472,45 | 100,00 | 3500 |
и т.д. |
Определяем границы интервалов
Нижнюю границу первого интервала принимают равной минимальному значению признака (чаще всего его предварительно округляют до целого меньшего числа с таким же разрядом как ширина интервала). Например, хмин= 15, i=130, хн первого интервала = 10.
хн1 ≈ хмин
Верхняя граница первого интервала соответствует значению (Хmin + i).
Нижняя граница второго интервала всегда равно верхней границе первого интервала. Для последующих групп границы определяются аналогично, т е. последовательно прибавляется величина интервала.
xвi = xнi + i
xнi = xвi-1
Определяем частоты интервалов.
Считаем, сколько значений попало в каждый интервал. При этом помним, что если единица обладает значением признака, равным величине верхней границы интервала, то ее следует относить к следующему интервалу.
Строим интервальный ряд в виде таблицы.
Определяем середины интервалов.
Для дальнейшего анализа интервального ряда понадобится выбрать значение признака для каждого интервала. Это значение признака будет общим для всех единиц наблюдения, попавшим в этот интервал. Т.е. отдельные элементы «теряют» свои индивидуальные значения признака и им присваивается одно общее значение признака. Таким общим значением является середина интервала, которая обозначается x’i .
Рассмотрим на примере с ростом детей, как построить интервальный ряд с равными интервалами.
Имеются первоначальные данные.
90, 91, 92, 93, 94, 95, 96, 97, 98, 99, 92, 93, 94, 95, 96, 98, 100, 101, 102, 103, 104, 105, 106, 107, 108, 109, 100, 101, 102, 103, 104, 105, 106, 107, 108, 109, 100, 101, 102, 104, 110, 112, 114, 116, 117, 120, 122, 123, 124, 129, 110, 111, 113, 115, 116, 117, 121, 125, 126, 127, 110, 111, 112, 113, 114, 115, 116, 117, 118, 119, 120, 121, 122, 123, 124, 125, 126, 127, 128, 129, 111, 113, 116, 127, 123, 122, 130, 131, 132, 133, 134, 136, 137, 138, 139, 140, 141, 142, 143, 144, 145, 146, 147, 148, 149, 150, 131, 133, 135, 136, 138, 139, 140, 141, 142, 143, 145, 146, 147, 148
studfiles.net
Вариационный ряд — 23 Августа 2014 — Примеры решений задач
Вариационный ряд может быть:
— дискретным, когда изучаемый признак характеризуется определенным числом (как правило целым).
— интервальным, когда определены границы «от» и «до» для непрерывно варьируемого признака. Интервальный ряд также строят если множество значений дискретно варьируемого признака велико.
Рассмотрим пример построения дискретного вариационного ряда.
Пример 1. Имеются данные о количественном составе 60 семей.
Построить вариационный ряд и полигон распределения
Решение.
Алгоритм построения вариационного ряда:
1) Откроем таблицы Excel.
2) Введем массив данных в диапазон А1:L5. Если вы изучаете документ в электронной форме (в формате Word, например), для этого достаточно выделить таблицу с данными и скопировать ее в буфер, затем выделить ячейку А1 и вставить данные – они автоматически займут подходящий диапазон.
3) Подсчитаем объем выборки n – число выборочных данных, для этого в ячейку В7 введем формулу =СЧЁТ(А1:L5). Заметим, что для того, чтобы в формулу ввести нужный диапазон, необязательно вводить его обозначение с клавиатуры, достаточно его выделить.
4) Определим минимальное и максимальное значение в выборке, введя в ячейку В8 формулу =МИН(А1:L5), и в ячейку В9: =МАКС(А1:L5).
Рис.1.1 Пример 1. Первичная обработка статистических данных в таблицах Excel
5) Далее, подготовим таблицу для построения вариационного ряда, введя названия для столбца интервалов (значений варианты) и столбца частот. В столбец интервалов введем значения признака от минимального (1) до максимального (6), заняв диапазон В12:В17.
6) Выделим столбец частот, введем формулу =ЧАСТОТА(А1:L5;В12:В17) и нажмем сочетание клавиш CTRL+SHIFT+ENTER
Рис.1.2 Пример 1. Построение вариационного ряда
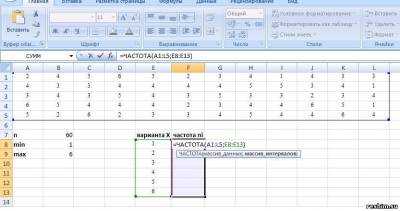
7) Для контроля вычислим сумму частот при помощи функции СУММ (значок функции S в группе «Редактирование» на вкладке «Главная»), вычисленная сумма должна совпасть с ранее вычисленным объемом выборки в ячейке В7.
Построим полигон:
1) выделив полученный диапазон частот, выберем команду «График» на вкладке «Вставка». По умолчанию значениями на горизонтальной оси будут порядковые числа — в нашем случае от 1 до 6, что совпадает со значениями варианты (номерами тарифных разрядов).
2) Название ряда диаграммы «ряд 1» можно либо изменить, воспользовавшись той же опцией «выбрать данные» вкладки «Конструктор», либо просто удалить.
Рис.1.3. Пример 1. Построение полигона частот
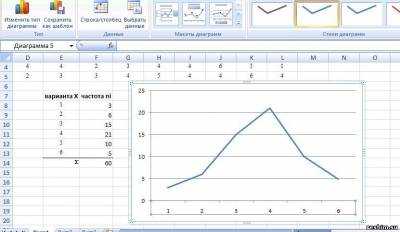
Примечание: можно скачать готовый шаблон построение дискретного вариационного ряда в Excel
Следующая тема: Построение интервального вариационного ряда в Excel.
www.reshim.su
Как построить интервальный вариационный ряд
Интервальный вариационный ряд представляет собой таблицу, состоящую из 2-х столбцов либо строк. В первом указывается промежуток знака, вариация которого рассматривается, во втором – число единиц общности, попадающих в данный промежуток (частот).
Инструкция
1. Для того дабы возвести интервальный вариационный ряд, в первую очередь нужно предпочесть оптимальное число промежутков и установить длину всякого из них. При этом учтите, что длина промежутка должна быть непрерывной, от того что при обзоре вариационного ряда сопоставляют частоты из различных групп. Оптимальное число групп нужно выбирать так, дабы отразить многообразие знаков общности и совместно с тем их закономерное разделение, а также исключить искажение общности случайными колебаниями частот. Учтите, что если групп будет слишком немного, не будет видна обоснованность разделения, а если, напротив, слишком много – случайные прыжки единиц общности исказят ряд разделения.
2. Для определения числа групп в вариационном ряду воспользуйтесь формулой Стерждеса:h = 1 + 3,322 х ln(n), гдеh – число групп в вариационном ряду;n – количество общности.Если полученное значение окажется дробным, то за значение величины шага промежутка, возьмите всякое ближайшее целое число.
3. После этого определите величину промежутка:i = (Хmax – Xmin)/h, гдеХmax – наивысшее значение знака в целом;Xmin – минимальное значение знака в целом.
4. Дальше заполните границы промежутка. Они могут указываться различными методами: верхняя граница предыдущего промежутка может повторять нижнюю рубеж дальнейшего (5-10, 10-15, 15-20) либо не повторять (5-10, 10,1-15, 15,1-20). За предисловие первого промежутка А0 принимается следующее значение:А0 = Хmin – i/2, гдеi – длина промежутка. За конец j-го промежутка принимается значение Аj, представляющее собой верхнюю рубеж j-го промежутка и предисловие (j+1)-го промежутка:Aj = A(j-1) + i.Построение шкалы промежутков продолжается до тех пор, пока величина Аj удовлетворяет соотношению AjСовет 2: Как возвести вариационный ряд
Вариационный ряд представлен определенной последовательностью вариантов (x(1),…,x(n)), которые расположены в порядке убывание либо неубывания. 1-й элемент вариационного ряда x(1) называют минимальным: его обозначают xmin. Конечный элемент этого ряда именуется максимальным и обозначается xmax. На основании данных вариационного ряда строится график.
Вам понадобится
- – линейка;
- – начальная информация;
- – тетрадь;
- – легкой карандаш;
- – ручка.
Инструкция
1. Обратите внимание на то, что существует несколько разновидностей вариационного ряда: дискретный и интервальный. Весь из них имеет свои особенности построения. Дискретной вариацией знака считается та вариация, отдельные значения которой отличаются на определенную величину. Постоянной вариация считается в том случае, если ее отдельные значения разнятся между собой на всякую величину. В интервальном вариационном ряду знаки относятся не к отдельному значению, а к целому промежутку.
2. Раньше чем приступать к построению интервального вариационного ряда верно подберите тезис, на котором основано ранжирование отдельных элементов интервального ряда. Выбор того либо другого знака всецело зависит от однородности анализируемых показателей. К примеру, если представленная общность показателей однородная, то для построения такого вариационного ряда используйте тезис равных промежутков.
3. Впрочем раньше чем определить, однородны показатели либо нет, произведите обстоятельный обзор. Однородность определяется путем построения линейного графика и дальнейшего его обзора с целью обнаружения аномальных (нетипичных для данного вариационного ряда) слежений. Помимо того, правило равных промежутков применяется при построении вариационного ряда со существенными прыжками, повод происхождения которых неведома.
4. Положительно определите величину промежутка, нужную для построения интервального вариационного ряда: она должна быть такой, дабы, во-первых, анализируемый вариационный ряд не казался слишком массивным, и, во-вторых, отчетливо прослеживались постигаемые особенности. Если промежутки равные, то величина промежутка рассчитывается по формуле: h=R/k, в которой R – это размах вариации, а k указывает на число промежутков. При этом R определяется как разность между xmax и xmin.
5. Если выполняется построение дискретного вариационного ряда, то его вариантам можете приписывать не частоты появления какого-то явления, а доли всего варианта в всеобщей анализируемой общности показателей. Эти доли, вычисляемые как отношение определенных частот к всеобщему показателю, называют частостями и обозначают qi. В свою очередь, частости могут быть выражены как в процентах, так и относительных числах.
Обратите внимание!
От правильности обнаружения зависимости между частотами и вариантами вариационного ряда зависит, насколько правильно будет построен график.
Полезный совет
Изредка применяется способ, называемый «расщепление промежутков»: он нужен для сравнения 2-х вариационных рядов, в основе которых находится идентичный знак, но имеющих разные промежутки.
Одно из основных представлений математической статистики – это ряд распределения . Для того дабы было комфортно постигать какое-нибудь явление, данные группируются по определенному варьирующему знаку. На основании ряд а распределения дозволено постигать однородность общности, ее границы и обоснованности становления.
Инструкция
1. Для записи используйте таблицу из 2-х столбцов либо строк. В один из них записывайте группировочный знак, а во 2-й – его частоту либо частость. Частота – это количественное значение знака, скажем, число учащихся с определенной оценкой либо объем продаж за месяц. Дабы рассчитать частость, возьмите всеобщую сумму за 100% и для всей группы укажите долю в всеобщей сумме (скажем, 20%, 30% и 50% – в сумме составляет 100%).
2. В первую очередь обнаружьте знак, метаморфозы которого дозволено будет упорядочить. Скажем, он должен изменяться со временем либо с увеличением объема общности. Дюже комфортно брать в качестве промежутков временные интервалы (месяц, год, день). Рассчитайте значение знака в всяком интервале времени и запишите данные в таблицу.
3. Если вам нужно возвести ряд распределения на основе количественного группировочного знака, поделите его на равные промежутки и посчитайте значение для всякого промежутка отдельно. После этого запишите полученные данные в таблицу. Скажем, если вам нужно составить ряд распределения для учащихся, получивших в итоге ЕГЭ определенное число баллов, поделите группировочный знак – число баллов – на промежутки 0-10, 11-20, 21-30…91-100 и посчитайте, сколько учеников находится в всякой группе. Такие ряд ы будут именоваться интервальными вариационными ряд ами.
4. Если знак, на основе которого вы собираетесь строить ряд , дозволено выразить целым числом, постройте дискретный вариационный ряд . В качестве группирующего знака в этом случае укажите эти числа, скажем, тарифный разряд рабочих, число касс в магазине и т.д.
5. Если численно обозначить знак немыслимо, образуйте ряд распределения по добротному значению. В этом случае обозначьте всякую группу словом, особенно ясно отражающим оглавление. Скажем, дозволено сотворить ряд распределения пород на собачьей экспозиции: болонка, овчарка, терьер, пудель. Наоборот всей породы напишите число собак (4, 5, 5, 6), их процентное соотношение (20%, 25%, 25%, 30%), либо их число в долях (0,2; 0,25; 0,25; 0,3). Такой ряд именуется атрибутивным ряд ом распределения .
Когда ряд разделения теснее дан, дозволено сразу приступать к его изысканию. Но в некоторых задачах в качестве начальных данных представлены легко числа (вес, сумма, число – всякие значения параметра либо знака). В таком случае для того, дабы начать обзор, вначале необходимо возвести интервальный ряд .
Вам понадобится
- – значения параметра.
Инструкция
1. Если значения параметра изменяются с течением времени, используйте в качестве промежутков временные интервалы, скажем, час, день, месяц, год. При выборе малейшего интервала рассматривайте число и разброс данных, усердствуйте, дабы ряд разделения оказался максимально информативным и в то же время суперкомпактным. Скажем, если вам даны данные по месяцам в течение 2-х лет, разбивка на годы ни о чем не сумеет сказать, а применение в качестве промежутка месяц в некоторых случаях приведет к размыванию данных. Оптимальным решением при этом станет разбивка по кварталам.
2. Если время для составления выборки не имеет значения, сформируйте интервальные интервалы в зависимости от значений. Для этого оцените разброс данных, их наивысшее и минимальное значение и выберите величину промежутка. Дозволено применять такой способ: вычтите из максимального значения минимальное и полученную разность поделите на желаемое число промежутков. После этого установите границы, безусловно, отменнее, если это будут целые числа. Скажем, вам даны числа 32, 33, 35, 38, 45, 47, 48, 50, 58, 59, 63. Позже расчетов вы получите (63-32)/5=6,2. Округлите размер промежутка до 7. Таким образом, вы получите промежутки: (32-39), (40-47), (48-55), (56-63).
3. Обратите внимание, отменнее каждого делать границы промежутков не пересекающимися, то есть дальнейший промежуток начинайте не с того же числа, а с большего на единицу. Вследствие этому вы сумеете избежать разногласий и недоразумений.
4. Позже того как вы распределите все промежутки, посчитайте число значений в всем из них. Запишите полученные итоги в таблицу, где в одной строке будут указаны границы, в иной – число значений, лежащих в рамках этого промежутка. В рассмотренном выше примере расчет числа итогов будет выглядеть так: в промежуток (32-39) входят значения 32, 33, 35, 38 – каждого 4 значения. Значит, в первой ячейке таблицы под этим промежутком укажите число 4. Верно так же рассчитайте значения для следующих промежутков: (40-47) – 2, (48-55) – 2, (56-63) – 3.
jprosto.ru
Интервальный ряд | Примеры решений
Условие:
Имеются данные о возрастном составе рабочих (лет): 18, 38, 28, 29, 26, 38, 34, 22, 28, 30, 22, 23, 35, 33, 27, 24, 30, 32, 28, 25, 29, 26, 31, 24, 29, 27, 32, 25, 29, 29.
- Построить интервальный ряд распределения.
- Построить графическое изображение ряда.
- Графически определить моду и медиану.
Решение:
1) По формуле Стерджесса совокупность надо разделить на 1 + 3,322 lg 30 = 6 групп.
Максимальный возраст – 38, минимальный – 18.
Ширина интервала Так как концы интервалов должны быть целыми числами, разделим совокупность на 5 групп. Ширина интервала – 4.
Для облегчения подсчетов расположим данные в порядке возрастания: 18, 22, 22, 23, 24, 24, 25, 25, 26, 26, 27, 27, 28, 28, 28, 29, 29, 29, 29, 29, 30, 30, 31, 32, 32, 33, 34, 35, 38, 38.
Распределение возрастного состава рабочих
Графически ряд можно изобразить в виде гистограммы или полигона. Гистограмма – столбиковая диаграмма. Основание столбика – ширина интервала. Высота столбика равна частоте.
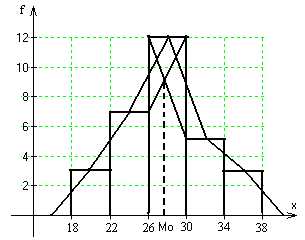
Полигон (или многоугольник распределения) – график частот. Чтобы его построить по гистограмме, соединяем середины верхних сторон прямоугольников. Многоугольник замыкаем на оси Ох на расстояниях, равных половине интервала от крайних значений х.
Мода (Мо) – это величина изучаемого признака, которая в данной совокупности встречается наиболее часто.
Чтобы определить моду по гистограмме, надо выбрать самый высокий прямоугольник, провести линию от правой вершины этого прямоугольника к правому верхнему углу предыдущего прямоугольника, и от левой вершины модального прямоугольника провести линию к левой вершине последующего прямоугольника. От точки пересечения этих линий провести перпендикуляр к оси х. Абсцисса и будет модой. Мо ≈ 27,5. Значит, наиболее часто встречаемый возраст в данной совокупности 27-28 лет.
Медиана (Mе) – это величина изучаемого признака, которая находится в середине упорядоченного вариационного ряда.
Медиану находим по кумуляте. Кумулята – график накопленных частот. Абсциссы – варианты ряда. Ординаты – накопленные частоты.
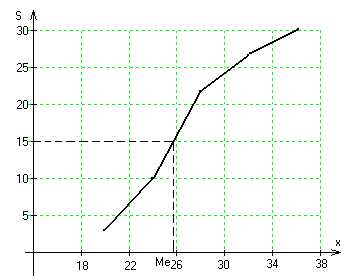
Для определения медианы по кумуляте находим по оси ординат точку, соответствующую 50% накопленных частот (в нашем случае 15), проводим через неё прямую, параллельно оси Ох, и от точки её пересечения с кумулятой проводим перпендикуляр к оси х. Абсцисса является медианой. Ме ≈ 25,9. Это означает, что половина рабочих в данной совокупности имеет возраст менее 26 лет.
mat-reshebnic.ru
Дискретный вариационный ряд
i | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 148 | 155 | 156 | 157 | 158 | 159 | 160 | 161 | 162 | 163 | 164 | 165 |
| 1 | 1 | 2 | 2 | 1 | 3 | 3 | 6 | 6 | 9 | 15 | 15 |
|
|
|
|
|
|
|
|
|
|
|
|
i | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 166 | 167 | 168 | 169 | 170 | 171 | 172 | 173 | 174 | 175 | 176 | 177 |
| 8 | 14 | 10 | 15 | 15 | 11 | 12 | 9 | 6 | 6 | 10 | 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
i | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 |
| 178 | 179 | 180 | 181 | 182 | 183 | 184 | 185 | 186 | 187 | 190 |
| 4 | 3 | 3 | 2 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
|
|
|
|
|
|
|
|
|
|
|
|
В данном примере случайные величины сплошь заполняют промежуток (148;190). Число возможных значений велико. Их нельзя представить в виде случайных величин, принимающих отдельные, изолированные значения, тем самым отделить одно возможное значение от другого промежутком, не содержащим возможных значений случайной величины. Поэтому для построения вариационного ряда будем использовать интервальный ряд распределения. Весь возможный интервал варьирования разобьём на конечное число интервалов и подсчитаем частоту попадания значений величины в каждый интервал. Минимальное и максимальное значения случайной величины: Тогда интервал варьированияR («размах») будет равен R=Длину интервала рассчитывают по формуле:
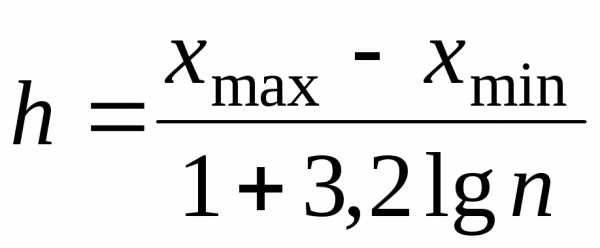(6)
При этом значение признака, находящегося на границе интервалов относят к правой границе интервала.
На практике считают, что правильно составленный ряд распределения содержит от 6 до 15 частичных интервалов. Часто интервальный вариационный ряд заменяют дискретным вариационным рядом, выбирая средние значения интервала (таблица №7).
Для данного примера , округлим до 3, т.е. размер интервалаh=3, а число интервалов будет равно 14. Соответствующий интервальный вариационный ряд приведён в таблице №5.
Таблица 5
Интервальный вариационный ряд
Индекс интервала i | Число покупателей (интервалы) | Частота
| Относительная частота
|
1 | 148-151 | 1 | 1/200 |
2 | 151-154 | 0 | 0 |
3 | 154-157 | 5 | 5/200 |
4 | 157-160 | 7 | 7/200 |
5 | 160-163 | 21 | 21/200 |
6 | 163-166 | 38 | 38/200 |
7 | 166-169 | 39 | 39/200 |
8 | 169-172 | 38 | 38/200 |
9 | 172-175 | 21 | 21/200 |
10 | 175-178 | 15 | 15/200 |
Окончание таблицы 5 | |||
Индекс интервала i | Число покупателей (интервалы) | Частота
| Относительная частота
|
11 | 178-181 | 8 | 8/200 |
12 | 181-184 | 3 | 3/200 |
13 | 184-187 | 3 | 3/200 |
14 | 187-190 | 1 | 1/200 |
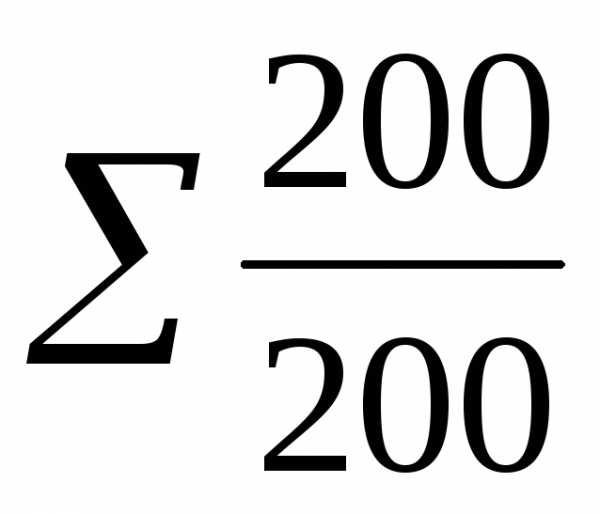=1
2)
После составления вариационного ряда
необходимо построить функцию распределения
выборки или эмпирическую функцию F*(x)=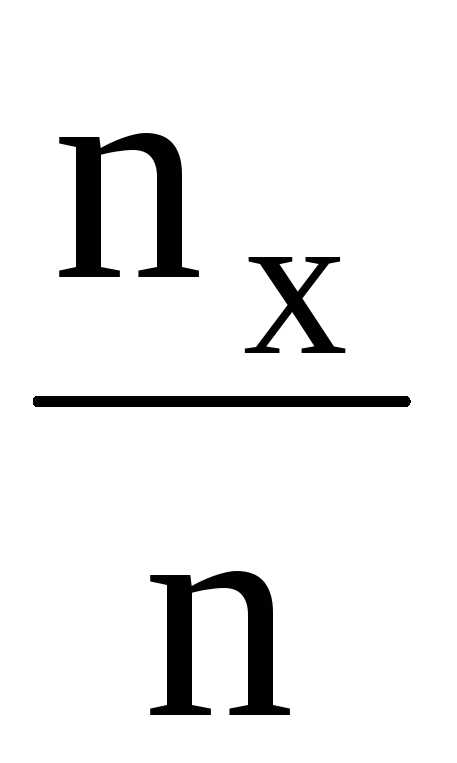
, то есть функцию найденную опытным путём.
Здесь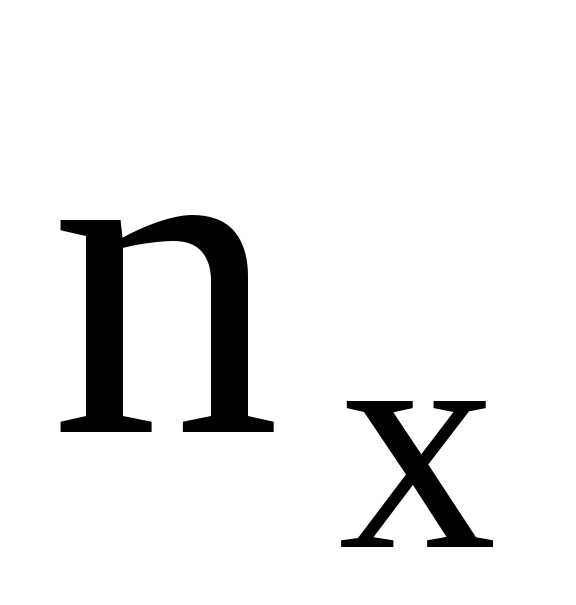 
–
относительная частота события Х< х,n
— общее число значений.
Эмпирическое распределение можно изобразить в виде полигона, гистограммы или ступенчатой кривой.
Построим
выборочную функцию распределения.
Очевидно, что для
функция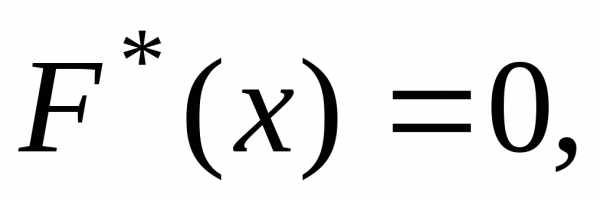
так как
.
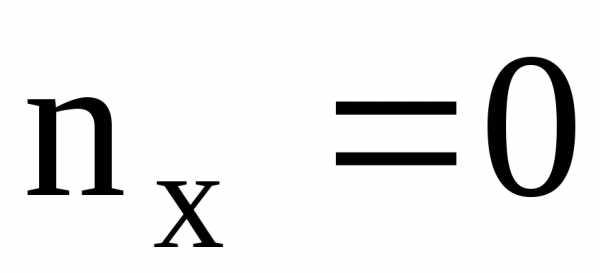На концах интервалов значения функции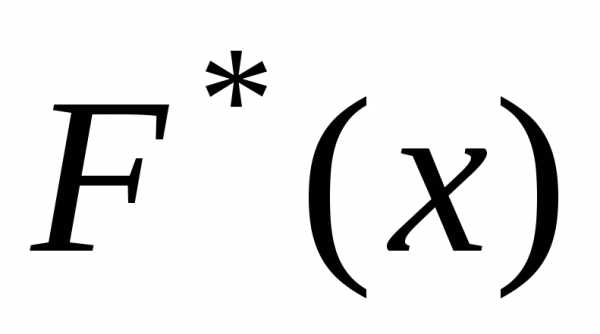
рассчитаем в виде «нарастающей
относительной частоты» (Таблица 6).
Таблица 6
Расчёт эмпирической функции распределения
Индекс интервала i |
|
1 | 1/200 |
2 | 1/200 |
3 | 1/200+5/200=6/200 |
4 | 6/200+7/200=13/200 |
5 | 13/200+21/200=34/200 |
6 | 34/200+38/200=72/200 |
Окончание таблицы 6 | |
Индекс интервала i |
|
7 | 72/200+39/200=111/200 |
8 | 111/200+38/200=149/200 |
9 | 149/200+21/200=170/200 |
10 | 170/200+15/200=185/200 |
11 | 185/200+8/200=193/200 |
12 | 193/200+3/200=196/200 |
13 | 196/200+3/200=199/200 |
14 | 199/200+1/200=200/200 |
Табличные значения не полностью определяют выборочную функцию распределения непрерывной случайной величины, поэтому при графическом изображении её доопределяют, соединив точки графика, соответствующие концам интервала, отрезками прямой (рис.1).
Полученные
данные, представленные в виде вариационного
ряда, изобразим графически в виде
ломаной линии (полигона), связывающей
на плоскости точки с координатами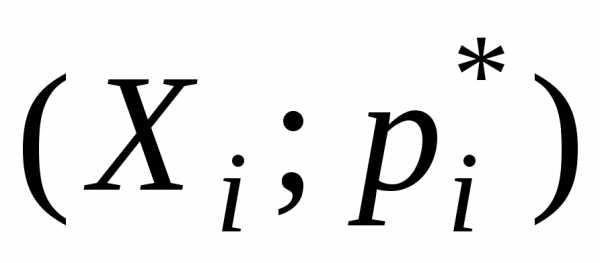 
,
где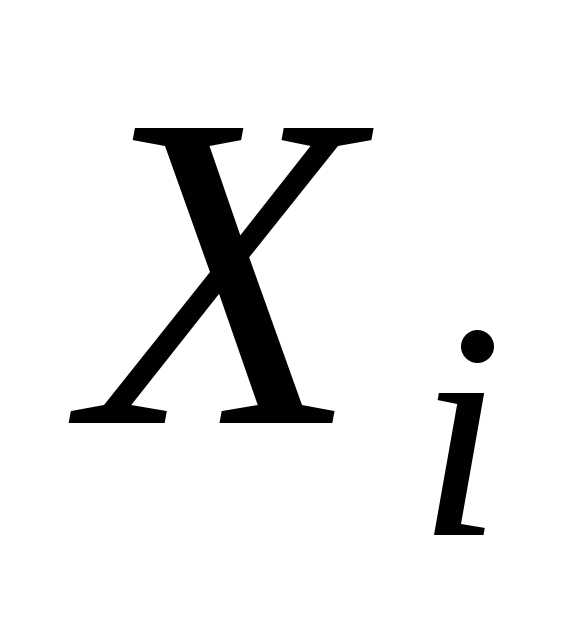
— среднее значение интервала
,
а 
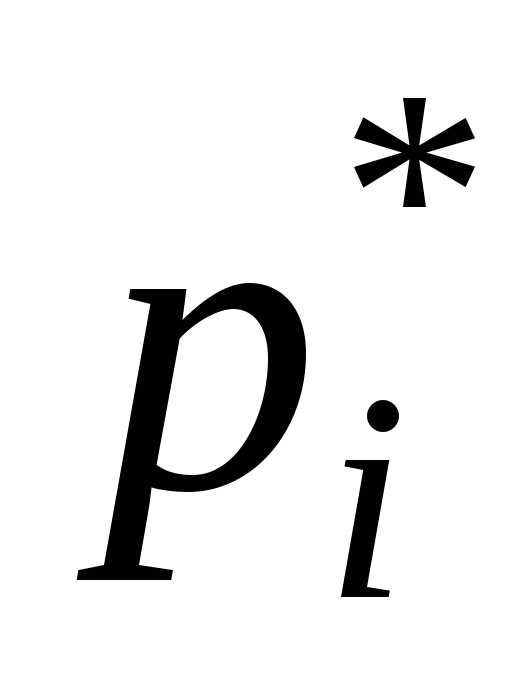— относительная частота.(таблица 7 и
рис.2). На этом же рисунке отобразим
пунктирной линией выравнивающие
(теоретические) частоты.
Таблица 7
studfiles.net