Что такое рациональные выражения – Рациональные выражения это

Рациональные выражения

На этом уроке мы вспомним, какие выражения называют целыми и дробными. Познакомимся с рациональными выражениями. Узнаем, какие значения называют допустимыми. А также научимся находить допустимые значения выражения.

Вы уже знакомы с целыми и дробными выражениями. Давайте вспомним их определения.

Целые выражения – это выражения, составленные из чисел и переменных, содержащие действия сложения, вычитания и умножения, а также деления на число, отличное от нуля.

Например

В отличие от целых выражений, дробные выражения помимо действий сложения, вычитания и умножения, содержат деление на выражение с переменными.

Например

Целые и дробные выражения называют рациональными выражениями.

Определение

Рациональными выражениями

называют выражения, составленные из чисел, переменных, их степеней и знаков арифметических действий.

Например

Напомним, что целые выражения имеют смысл при любых значениях переменных. Чтобы найти значение целого выражения, нужно подставить указанное значение переменной и выполнить все действия.

Дробное выражение при некоторых значениях переменных может не иметь смысла.

Например

Чтобы найти значение рационального выражения, надо:

1)    подставить числовое значение переменной в данное выражение;

2)    выполнить все действия.

Определение

Значения переменных, при которых выражение имеет смысл, называют допустимыми значениями переменных.

Множество всех допустимых значений переменных называется областью допустимых значений

(коротко ОДЗ) или областью определения выражения.

Как вы уже знаете, выражение вида  называется дробью.

Дробь, числитель и знаменатель которой многочлены, называют рациональной дробью.

Например

Задание

Найдите значение дроби.

        

Задание

Найдите допустимые значения переменной в выражениях:

        

Итоги:      

Целые выражения – это выражения, составленные из чисел и переменных, содержащие действия сложения, вычитания и умножения, а также деления на число, отличное от нуля.

В отличие от целых выражений, дробные выражения помимо действий сложения, вычитания и умножения, содержат деление на выражение с переменными.

Рациональными выражениями называют выражения, составленные из чисел, переменных, их степеней и знаков арифметических действий.

Чтобы найти значение рационального выражения, надо:

1)    Подставить числовое значение переменной в данное выражение;

2)    Выполнить все действия.

Значения переменных, при которых выражение имеет смысл, называют допустимыми значениями переменных.

 Множество всех допустимых значений переменных называется областью допустимых значений или областью определения выражения.

videouroki.net

РАЦИОНАЛЬНОЕ ВЫРАЖЕНИЕ — это… Что такое РАЦИОНАЛЬНОЕ ВЫРАЖЕНИЕ?



РАЦИОНАЛЬНОЕ ВЫРАЖЕНИЕ

РАЦИОНАЛЬНОЕ ВЫРАЖЕНИЕ — алгебраическое выражение, не содержащее радикалов и включающее только действия сложения, вычитания, умножения и деления. Напр., a2 + b, x/(y — z2).

Большой Энциклопедический словарь. 2000.

• РАЦИОНАЛЬНАЯ ФУНКЦИЯ
• РАЦИОНАЛЬНОЕ ЧИСЛО

Смотреть что такое «РАЦИОНАЛЬНОЕ ВЫРАЖЕНИЕ» в других словарях:

• Рациональное выражение — Рациональное выражение  алгебраическое выражение, не содержащее радикалов. Другими словам, это одна или несколько алгебраических величин (чисел и букв), соединённых между собой знаками арифметических действий: сложения, вычитания, умножения… …   Википедия

• рациональное выражение — алгебраическое выражение, не содержащее радикалов и включающее только действия сложения, вычитания, умножения и деления. Например, a2 + b, х/(у z2). * * * РАЦИОНАЛЬНОЕ ВЫРАЖЕНИЕ РАЦИОНАЛЬНОЕ ВЫРАЖЕНИЕ, алгебраическое выражение, не содержащее… …   Энциклопедический словарь

• Рациональное выражение —         алгебраическое выражение, не содержащее радикалов, например a2 + b, х/(у z3). Если входящие в Р. в. буквы считать переменными, то Р. в. задаёт рациональную функцию (См. Рациональная функция) от этих переменных …   Большая советская энциклопедия

• РАЦИОНАЛЬНОЕ ВЫРАЖЕНИЕ — алгебрарическое выражение, не содержащее радикалов и включающее только действия сложения, вычитания, умножения и деления. Напр., а2 + b, х/(y z2) …   Естествознание. Энциклопедический словарь

• ВЫРАЖЕНИЕ — первичное математическое понятие, под которым подразумевают запись из букв и чисел, соединённых знаками арифметических действий, при этом могут быть использованы скобки, обозначения функций и т.п.; обычно В формула млн. её часть. Различают В (1)… …   Большая политехническая энциклопедия

• РАЦИОНАЛЬНОЕ — (Rational; Rational) термин, используемый для описания мыслей, чувств и действий, согласуемых с разумом; установка, базирующаяся на объективных ценностях, полученных в результате практического опыта.«Объективные ценности устанавливаются в опыте… …   Словарь по аналитической психологии

• РАЦИОНАЛЬНОЕ ПОЗНАНИЕ — субъективный образ объективного мира,полученный с помощью мышления. Мышление – активный процесс обобщенного и опосредованного  отражения действительности, обеспечивающий открытие на основе чувственных данных ее закономерных связей  и их выражение …   Философия науки и техники: тематический словарь

• УРАВНЕНИЕ, РАЦИОНАЛЬНОЕ — Логическое или математическое выражение, основанное на (рациональных) предположениях о процессах. Такие уравнения отличаются от эмпирических уравнений тем, что их параметры получаются в результате дедуктивных выводов из теоретических… …   Толковый словарь по психологии

• РАЦИОНАЛЬНЫЙ — РАЦИОНАЛЬНЫЙ, рациональная, рациональное; рационален, рациональна, рационально. 1. прил. к рационализм (книжн.). Рациональная философия. 2. Вполне разумный, обоснованный, целесообразный. Он внес рациональное предложение. Рациональное… …   Толковый словарь Ушакова

• РЕЗОЛЬВЕНТА — 1) Р. а л г е б р а и ч е с к о г о у р а в н е н и я f(x)=0степени п алгебраическое уравнение g(y)=0с коэффициентами, рационально зависящими от коэффициентов f(x), такое, что знание корней этого уравнения позволяет найти корни данного уравнения… …   Математическая энциклопедия

dic.academic.ru

рациональное выражение — это… Что такое рациональное выражение?



рациональное выражение

рациона́льное выраже́ние

алгебраическое выражение, не содержащее радикалов и включающее только действия сложения, вычитания, умножения и деления. Например, a² + b, х/(у-z²).

* * *

РАЦИОНАЛЬНОЕ ВЫРАЖЕНИЕ

РАЦИОНА́ЛЬНОЕ ВЫРАЖЕ́НИЕ, алгебраическое выражение, не содержащее радикалов и включающее только действия сложения, вычитания, умножения и деления. Напр.,
a² + b,x/(y — z²).

Энциклопедический словарь. 2009.

• рациональная функция
• рациональное число

Смотреть что такое «рациональное выражение» в других словарях:

• Рациональное выражение — Рациональное выражение  алгебраическое выражение, не содержащее радикалов. Другими словам, это одна или несколько алгебраических величин (чисел и букв), соединённых между собой знаками арифметических действий: сложения, вычитания, умножения… …   Википедия

• РАЦИОНАЛЬНОЕ ВЫРАЖЕНИЕ — алгебраическое выражение, не содержащее радикалов и включающее только действия сложения, вычитания, умножения и деления. Напр., a2 + b, x/(y z2) …   Большой Энциклопедический словарь

• Рациональное выражение —         алгебраическое выражение, не содержащее радикалов, например a2 + b, х/(у z3). Если входящие в Р. в. буквы считать переменными, то Р. в. задаёт рациональную функцию (См. Рациональная функция) от этих переменных …   Большая советская энциклопедия

• РАЦИОНАЛЬНОЕ ВЫРАЖЕНИЕ — алгебрарическое выражение, не содержащее радикалов и включающее только действия сложения, вычитания, умножения и деления. Напр., а2 + b, х/(y z2) …   Естествознание. Энциклопедический словарь

• ВЫРАЖЕНИЕ — первичное математическое понятие, под которым подразумевают запись из букв и чисел, соединённых знаками арифметических действий, при этом могут быть использованы скобки, обозначения функций и т.п.; обычно В формула млн. её часть. Различают В (1)… …   Большая политехническая энциклопедия

• РАЦИОНАЛЬНОЕ

  — (Rational; Rational) термин, используемый для описания мыслей, чувств и действий, согласуемых с разумом; установка, базирующаяся на объективных ценностях, полученных в результате практического опыта.«Объективные ценности устанавливаются в опыте… …   Словарь по аналитической психологии

• РАЦИОНАЛЬНОЕ ПОЗНАНИЕ — субъективный образ объективного мира,полученный с помощью мышления. Мышление – активный процесс обобщенного и опосредованного  отражения действительности, обеспечивающий открытие на основе чувственных данных ее закономерных связей  и их выражение …   Философия науки и техники: тематический словарь

• УРАВНЕНИЕ, РАЦИОНАЛЬНОЕ — Логическое или математическое выражение, основанное на (рациональных) предположениях о процессах. Такие уравнения отличаются от эмпирических уравнений тем, что их параметры получаются в результате дедуктивных выводов из теоретических… …   Толковый словарь по психологии

• РАЦИОНАЛЬНЫЙ

  — РАЦИОНАЛЬНЫЙ, рациональная, рациональное; рационален, рациональна, рационально. 1. прил. к рационализм (книжн.). Рациональная философия. 2. Вполне разумный, обоснованный, целесообразный. Он внес рациональное предложение. Рациональное… …   Толковый словарь Ушакова

• РЕЗОЛЬВЕНТА — 1) Р. а л г е б р а и ч е с к о г о у р а в н е н и я f(x)=0степени п алгебраическое уравнение g(y)=0с коэффициентами, рационально зависящими от коэффициентов f(x), такое, что знание корней этого уравнения позволяет найти корни данного уравнения… …   Математическая энциклопедия

dic.academic.ru

РАЦИОНАЛЬНОЕ ВЫРАЖЕНИЕ — это… Что такое РАЦИОНАЛЬНОЕ ВЫРАЖЕНИЕ?



РАЦИОНАЛЬНОЕ ВЫРАЖЕНИЕ

алгебрарическое выражение, не содержащее радикалов и включающее только действия сложения, вычитания, умножения и деления. Напр., а² + b, х/(y-z²>).

Естествознание. Энциклопедический словарь.

• РАЦИОНАЛЬНАЯ ФУНКЦИЯ
• РАЦИОНАЛЬНОЕ ЧИСЛО

Смотреть что такое «РАЦИОНАЛЬНОЕ ВЫРАЖЕНИЕ» в других словарях:

• Рациональное выражение — Рациональное выражение  алгебраическое выражение, не содержащее радикалов. Другими словам, это одна или несколько алгебраических величин (чисел и букв), соединённых между собой знаками арифметических действий: сложения, вычитания, умножения… …   Википедия

• РАЦИОНАЛЬНОЕ ВЫРАЖЕНИЕ — алгебраическое выражение, не содержащее радикалов и включающее только действия сложения, вычитания, умножения и деления. Напр., a2 + b, x/(y z2) …   Большой Энциклопедический словарь

• рациональное выражение — алгебраическое выражение, не содержащее радикалов и включающее только действия сложения, вычитания, умножения и деления. Например, a2 + b, х/(у z2). * * * РАЦИОНАЛЬНОЕ ВЫРАЖЕНИЕ РАЦИОНАЛЬНОЕ ВЫРАЖЕНИЕ, алгебраическое выражение, не содержащее… …   Энциклопедический словарь

• Рациональное выражение —         алгебраическое выражение, не содержащее радикалов, например a2 + b, х/(у z3). Если входящие в Р. в. буквы считать переменными, то Р. в. задаёт рациональную функцию (См. Рациональная функция) от этих переменных …   Большая советская энциклопедия

• ВЫРАЖЕНИЕ — первичное математическое понятие, под которым подразумевают запись из букв и чисел, соединённых знаками арифметических действий, при этом могут быть использованы скобки, обозначения функций и т.п.; обычно В формула млн. её часть. Различают В (1)… …   Большая политехническая энциклопедия

• РАЦИОНАЛЬНОЕ — (Rational; Rational) термин, используемый для описания мыслей, чувств и действий, согласуемых с разумом; установка, базирующаяся на объективных ценностях, полученных в результате практического опыта.«Объективные ценности устанавливаются в опыте… …   Словарь по аналитической психологии

• РАЦИОНАЛЬНОЕ ПОЗНАНИЕ — субъективный образ объективного мира,полученный с помощью мышления. Мышление – активный процесс обобщенного и опосредованного  отражения действительности, обеспечивающий открытие на основе чувственных данных ее закономерных связей  и их выражение …   Философия науки и техники: тематический словарь

• УРАВНЕНИЕ, РАЦИОНАЛЬНОЕ — Логическое или математическое выражение, основанное на (рациональных) предположениях о процессах. Такие уравнения отличаются от эмпирических уравнений тем, что их параметры получаются в результате дедуктивных выводов из теоретических… …   Толковый словарь по психологии

• РАЦИОНАЛЬНЫЙ — РАЦИОНАЛЬНЫЙ, рациональная, рациональное; рационален, рациональна, рационально. 1. прил. к рационализм (книжн.). Рациональная философия. 2. Вполне разумный, обоснованный, целесообразный. Он внес рациональное предложение. Рациональное… …   Толковый словарь Ушакова

• РЕЗОЛЬВЕНТА — 1) Р. а л г е б р а и ч е с к о г о у р а в н е н и я f(x)=0степени п алгебраическое уравнение g(y)=0с коэффициентами, рационально зависящими от коэффициентов f(x), такое, что знание корней этого уравнения позволяет найти корни данного уравнения… …   Математическая энциклопедия

dic.academic.ru

Рациональное выражение — это… Что такое Рациональное выражение?



Рациональное выражение

        алгебраическое выражение, не содержащее радикалов, например a² + b, х/(у — z³). Если входящие в Р. в. буквы считать переменными, то Р. в. задаёт рациональную функцию (См. Рациональная функция) от этих переменных.

Большая советская энциклопедия. — М.: Советская энциклопедия. 1969—1978.

• Рациональная функция
• Рациональное число

Смотреть что такое «Рациональное выражение» в других словарях:

• Рациональное выражение — Рациональное выражение  алгебраическое выражение, не содержащее радикалов. Другими словам, это одна или несколько алгебраических величин (чисел и букв), соединённых между собой знаками арифметических действий: сложения, вычитания, умножения… …   Википедия

• РАЦИОНАЛЬНОЕ ВЫРАЖЕНИЕ — алгебраическое выражение, не содержащее радикалов и включающее только действия сложения, вычитания, умножения и деления. Напр., a2 + b, x/(y z2) …   Большой Энциклопедический словарь

• рациональное выражение — алгебраическое выражение, не содержащее радикалов и включающее только действия сложения, вычитания, умножения и деления. Например, a2 + b, х/(у z2). * * * РАЦИОНАЛЬНОЕ ВЫРАЖЕНИЕ РАЦИОНАЛЬНОЕ ВЫРАЖЕНИЕ, алгебраическое выражение, не содержащее… …   Энциклопедический словарь

• РАЦИОНАЛЬНОЕ ВЫРАЖЕНИЕ — алгебрарическое выражение, не содержащее радикалов и включающее только действия сложения, вычитания, умножения и деления. Напр., а2 + b, х/(y z2) …   Естествознание. Энциклопедический словарь

• ВЫРАЖЕНИЕ — первичное математическое понятие, под которым подразумевают запись из букв и чисел, соединённых знаками арифметических действий, при этом могут быть использованы скобки, обозначения функций и т.п.; обычно В формула млн. её часть. Различают В (1)… …   Большая политехническая энциклопедия

• РАЦИОНАЛЬНОЕ — (Rational; Rational) термин, используемый для описания мыслей, чувств и действий, согласуемых с разумом; установка, базирующаяся на объективных ценностях, полученных в результате практического опыта.«Объективные ценности устанавливаются в опыте… …   Словарь по аналитической психологии

• РАЦИОНАЛЬНОЕ ПОЗНАНИЕ — субъективный образ объективного мира,полученный с помощью мышления. Мышление – активный процесс обобщенного и опосредованного  отражения действительности, обеспечивающий открытие на основе чувственных данных ее закономерных связей  и их выражение …   Философия науки и техники: тематический словарь

• УРАВНЕНИЕ, РАЦИОНАЛЬНОЕ — Логическое или математическое выражение, основанное на (рациональных) предположениях о процессах. Такие уравнения отличаются от эмпирических уравнений тем, что их параметры получаются в результате дедуктивных выводов из теоретических… …   Толковый словарь по психологии

• РАЦИОНАЛЬНЫЙ — РАЦИОНАЛЬНЫЙ, рациональная, рациональное; рационален, рациональна, рационально. 1. прил. к рационализм (книжн.). Рациональная философия. 2. Вполне разумный, обоснованный, целесообразный. Он внес рациональное предложение. Рациональное… …   Толковый словарь Ушакова

• РЕЗОЛЬВЕНТА — 1) Р. а л г е б р а и ч е с к о г о у р а в н е н и я f(x)=0степени п алгебраическое уравнение g(y)=0с коэффициентами, рационально зависящими от коэффициентов f(x), такое, что знание корней этого уравнения позволяет найти корни данного уравнения… …   Математическая энциклопедия

dic.academic.ru

Рациональные выражения

Вопросы занятия:

·  вспомнить, какие выражения называют рациональными;

·  поговорить об основном свойстве дробей;

· вспомнить, как выполняют действия над рациональными дробями.

Материал урока

Прежде, чем мы начнём говорить о рациональных выражениях, стоит вспомнить такие понятия, как «целые выражения» и «дробные выражения».

Итак, целые выражения – это выражения, составленные из чисел и переменных с помощью действий сложения, вычитания и умножения, а также деления на число, отличное от нуля.

Например, целыми являются выражения:

Любое целое выражение можно представить многочленом.

В отличие от целых выражений, дробные выражения помимо действий сложения, вычитания и умножения, содержат деление на выражение с переменными.

Т.е. дробные выражения – это выражения, составленные из чисел и переменных с помощью действий сложения, вычитания, умножения и деления на выражения с переменными.

Например, дробными будут выражения:

Напомним, что значения переменных, при которых выражение имеет смысл, называют допустимыми значениями переменных.

Множество всех допустимых значений переменных называется областью допустимых значений (коротко ОДЗ) или областью определения выражения.

Область определения целого выражения – любые значения переменных. Чтобы найти значение целого выражения, нужно подставить указанное значение переменной и выполнить все действия.

Например, целое выражение:  имеет смысл при любых действительных , ,  и .

Дробное же выражение при некоторых значениях переменных может не иметь смысла.

Область определения дробного выражения – все значения переменных, при которых делители этого выражения не равны нулю.

Например, дробное выражение  не имеет смысла при . Так как в этом случае в знаменателе получится нуль. А мы помним, что на нуль делить нельзя. При всех же остальных значениях переменных это выражение имеет смысл.

Целые и дробные выражения называют рациональными выражениями.

Определение.

Рациональными выражениями называют выражения, составленные из чисел, переменных, их степеней и знаков арифметических действий.

Например,

Чтобы найти значение рационального выражения, надо:

1)    подставить числовое значение переменной в данное выражение;

2)    выполнить все действия.

Задание.

Найти значение дроби:

а) , при  ;           б) , при ;             в) , при .

Первое выражение: . Подставим указанное значение  в выражение. Выполним действия. В результате получим,

Переходим ко второму дробному выражению . Нужно найти его значение при . Значит, подставим указанное значение вместо а. Выполним все действия по порядку. Получим,

И третье дробное выражение: . Найдём его значение при . Подставим указанное значение. Выполним действия. Получим,

Заметили, в знаменателе получился нуль? Разве мы можем делить на нуль? Правильно! Значит, выражение:  не имеет смысла при , так как на нуль делить нельзя.

Как вы уже знаете, выражение вида  называется дробью.

Определение.

Дробь, числитель и знаменатель которой многочлены, называют рациональной дробью.

Например, выражения:

являются рациональными дробями.

Область определения рациональной дроби – все значения переменных, при которых знаменатель не равен нулю.

Задание.

Указать область определения следующих рациональных дробей:

а) ;                                                б) .

Итак, первый пример: . Область определения данной дроби: все действительные числа, кроме тех, при которых знаменатель , т.е. все числа, кроме  и .

И второй пример: . Область определения данной дроби все действительные числа, так как знаменатель  ни при каких а.

Рассмотрим равенство: .

Это равенство верно при всех допустимых значениях переменной, т.е. при всех , кроме  и .

Такое равенство называют тождеством.

Определение.

Тождество – это равенство, верное при всех допустимых значениях входящих в него переменных.

Два выражения, принимающие равные значения при всех допустимых значениях переменных, называются тождественно равными.

Замену одного такого выражения другим называют тождественным преобразованием выражения.

Справедливо следующее тождество: , если , где  и  – не равные нулю многочлены.

Рассмотрим равенство: .

Это равенство верно при всех допустимых значениях переменной , т.е. при всех  кроме  и . Так как .

Перейдём к основному свойству рациональной дроби.

Итак, основное свойство рациональной дроби сводится к тому, что:

Если числитель и знаменатель рациональной дроби умножить на один и тот же ненулевой многочлен, то получится равная ей дробь.

Если числитель и знаменатель рациональной дроби разделить на один и тот же ненулевой многочлен, то получится равная ей дробь.

Основное свойство рациональной дроби позволяет сокращать дроби и приводить дробь к новому знаменателю.

Чтобы сократить рациональную дробь, нужно предварительно разложить на множители числитель и знаменатель дроби, а затем разделить их на общие множители.

Задание.

Привести дроби к новому знаменателю:

а)  к знаменателю ;              б)  к знаменателю .

Первая рациональная дробь: . Её нужно привести к знаменателю . Не трудно заметить, что  – это произведение . Значит, мы должны умножить дробь на . Напомним, что для того чтобы значение дроби не изменилось, нужно и числитель, и знаменатель умножить на одно и то же число. Тогда получаем дробь:

Множитель:  называют дополнительным множителем к числителю и знаменателю дроби .

Вторая дробь: . Её нужно привести к новому знаменателю . Для этого числитель и знаменатель дроби нужно умножить на выражение: . Выполним умножение. Получим дробь:

Задание.

Сократить дроби:

а) ;                                                              б) .

Рассмотрим первую рациональную дробь. Числитель состоит из произведения ,  и , знаменатель из произведения ,  и . Дробь можно сократить на общий множитель . В итоге получим дробь,

Вторая рациональная дробь: . В числителе вынесем общий множитель  за скобку. Сократим дробь на общий множитель . В результате получим,

Перейдём к действиям над рациональными дробями. Давайте вспомним, какие действия можно выполнять над рациональными дробями и по каким правилам.

Итак, правило сложения рациональных дробей с одинаковыми знаменателями:

Чтобы сложить рациональные дроби с одинаковыми знаменателями, надо сложить их числители, а знаменатель оставить тем же.

В буквенном виде это правило записывают так:

где ,  и  – многочлены, причём  – не равный нулю многочлен. Это правило справедливо при сложении любого числа дробей.

Например, найдём сумму дробей .

Видно, что у первой и второй рациональных дробей один и тот же знаменатель. Воспользуемся правилом сложения рациональных дробей с одинаковыми знаменателями. Сложим их числители, а знаменатель оставим тем же. Получим,

Вычитание рациональных дробей с одинаковыми знаменателями выполняется аналогично сложению.

Вспомним правило вычитания рациональных дробей с одинаковыми знаменателями.

Чтобы выполнить вычитание рациональных дробей с одинаковыми знаменателями, надо из числителя первой дроби вычесть числитель второй дроби, а знаменатель оставить тем же.

В буквенном виде это правило записывают так:

где ,  и  – многочлены, причём  – не равный нулю многочлен.

Рассмотрим пример. Найти разность дробей .

Дроби имеют одинаковые знаменатели. Значит, можем смело воспользоваться правилом вычитания рациональных дробей с одинаковыми знаменателями. Из числителя первой дроби вычтем числитель второй дроби, знаменатель оставим прежним. Сократим числитель и знаменатель дроби на выражение . В итоге получим,

Сложение и вычитание рациональных дробей с разными знаменателями выполняется аналогично сложению и вычитанию дробей с одинаковыми знаменателями, но предварительно нужно дроби привести к общему знаменателю.

где , ,  и  – многочлены, причём ,  – не равные нулю многочлены.

Вспомним алгоритм приведения дробей к наименьшему общему знаменателю:

1) разложить на множители знаменатель каждой дроби;

2) найти дополнительный множитель каждой дроби. Он равен произведению тех множителей знаменателей остальных дробей, которые не содержатся в знаменателе этой дроби;

3) домножить числитель и знаменатель каждой дроби на её дополнительный множитель.

Задание.

Представить в виде дроби:

.

Знаменатели дробей представлены в виде одночленов. Разложим знаменатель последней дроби на множители, применяя формулу разности квадратов. Затем приведём дроби к общему знаменателю. Общим знаменателем трёх дробей является выражение . Значит, дополнительным множителем к первой дроби будет выражение , а дополнительным множителем ко второй дроби: . Тогда получим,

Теперь дроби имеют одинаковые знаменатели. А значит, можем воспользоваться правилом сложения рациональных дробей с одинаковыми знаменателями. Упростим числитель, получившейся дроби. Обратите внимание, в числителе можем вынести общий множитель 2 за скобки. Сократим числитель и знаменатель на выражение . В результате, получим дробь:

Умножение рациональных дробей выполняется аналогично умножению обыкновенных дробей.

Вспомним правило умножения рациональных дробей.

Чтобы умножить дробь на дробь, нужно перемножить их числители и перемножить их знаменатели и первое произведение записать числителем, а второе – знаменателем дроби.

В буквенном виде это правило записывают так:

где , ,  и  – многочлены, причём ,  – не равные нулю многочлены.

Это правило выполняется и когда произведение трёх и более рациональных дробей.

Прежде чем выполнять умножение рациональных дробей, полезно их числители и знаменатели разложить на множители. Это облегчит сокращение той рациональной дроби, которая получится в результате умножения.

Рассмотрим пример. Выполнить умножение рациональных дробей:

.

Воспользуемся правилом и умножим числитель первой дроби на числитель второй дроби, знаменатель первой дроби на знаменатель второй дроби. Сократим дробь. В результате получим:

Теперь вспомним, как выполняется возведение рациональной дроби в степень.

Чтобы возвести дробь в степень, надо возвести в эту степень числитель и знаменатель и первый результат записать в числителе, а второй в знаменателе дроби.

В буквенном виде это правило записывают так:

где 𝒂, 𝒃 – многочлены, причём .

Рассмотрим пример. Возведём в 4-ую степень дробь .

Воспользуемся правилом возведения рациональной дроби в степень. Получим дробь,

Обратите внимание, что и числовой множитель в числителе мы также возводим в степень.

Деление рациональных дробей сводится к делению обыкновенных дробей.

Вспомним правило деления рациональных дробей:

Чтобы разделить одну дробь на другую, нужно первую дробь умножить на дробь, обратную второй.

В буквенном виде это правило записывают так:

где 𝒂, 𝒃, 𝒄 и 𝒅 – многочлены, причём ,  и .

Прежде чем выполнять деление рациональных дробей, полезно их числители и знаменатели разложить на множители. Это облегчит сокращение той рациональной дроби, которая получится в результате деления.

Рассмотрим пример. Выполнить деление рациональных дробей:

.

Воспользуемся правилом деления рациональных дробей. Т.е. первую дробь умножим на дробь обратную второй или, что то же самое числитель первой дроби умножим на знаменатель второй дроби, а знаменатель первой дроби умножим на числитель второй дроби. Заметим, в числителе дроби мы можем вынести  за скобку, а в знаменателе: 3 за скобку. Затем сократим числитель и знаменатель получившейся дроби на  и на выражение . В результате получим дробь:

Итоги урока

На этом уроке мы разобрали тему «рациональные выражения». Вспомнили, какие выражения называют рациональными. Поговорили об основном свойстве дробей. И вспомнили, как выполняют действия над рациональными дробями.

 

 

 

videouroki.net

Знаете ли вы, что значит «рациональный» и какие числа называются рациональными?

В далеком прошлом, когда еще не была придумана система исчисления, люди подсчитывали все на пальцах. С появлением арифметики и основ математики стало гораздо проще и практичнее вести учет товаров, продуктов, а также бытовых предметов. Однако как выглядит современная система исчисления: на какие виды делятся существующие числа и что значит «рациональный вид чисел»? Давайте разберемся.

Сколько разновидностей чисел существует в математике?

Само понятие «число» обозначает некую единицу любого предмета, которая характеризует его количественные, сравнительные или порядковые показатели. Для того чтобы правильно подсчитать количество определенных вещей или провести некие математические операции с числами (сложить, умножить и др.), в первую очередь следует ознакомиться с разновидностями этих самых чисел.

Итак, существующие числа можно разделить по следующим категориям:

1. Натуральные — это те числа, которыми мы подсчитываем количество предметов (самое меньшее натуральное число равно 1, логично, что ряд натуральных чисел бесконечен, т. е. не существует наибольшего натурального числа). Множество натуральных чисел принято обозначать буквой N.
2. Целые числа. К этому множеству относятся все натуральные числа, при этом в него добавляются и отрицательные значения, включая число «ноль». Обозначение множества целых чисел записывают в виде латинской буквы Z.
3. Рациональные числа — это те, которые мы мысленно можем преобразовать в дробь, числитель которой будет принадлежать множеству целых чисел, а знаменатель — натуральных. Чуть ниже мы разберем подробнее, что значит «рациональное число», и приведем несколько примеров.
4. Действительные числа — множество, в которое входят все рациональные и иррациональные числа. Обозначается данное множество буквой R.
5. Комплексные числа содержат в себе часть действительного и часть переменного числа. Используются комплексные числа в решении различных кубических уравнений, которые, в свою очередь, могут иметь в формулах под знаком корня отрицательное выражение (i²= -1).

Что значит «рациональный»: разбираем на примерах

Если рациональными считаются те числа, которые мы можем представить в виде обыкновенной дроби, то получается, что все положительные и отрицательные целые числа также входят в множество рациональных. Ведь любое целое число, например 3 или 15, можно представить в виде дроби, где в знаменателе будет единица.

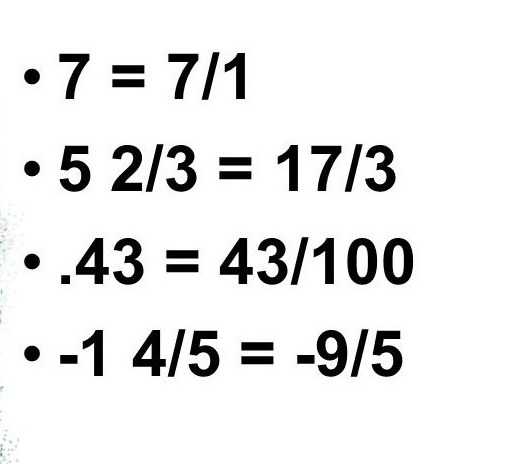
^{_{Дроби: -9/3; 7/5, 6/55 — вот примеры рациональных чисел.}}

Что значит «рациональное выражение»?

Идем дальше. Мы уже разобрали, что значит рациональный вид чисел. Давайте теперь представим себе математическое выражение, которое состоит из суммы, разности, произведения или частного различных чисел и переменных. Вот пример: дробь, в числителе которой сумма двух или нескольких целых чисел, а знаменатель содержит в себе как целое число, так и некую переменную. Именно такое выражение и называют рациональным. Исходя из правила «на ноль делить нельзя» можно догадаться, что значение данной переменной не может быть таковым, чтобы значение знаменателя обращалось в ноль. Поэтому при решении рационального выражения следует сначала определить область значения переменной. Например, если в знаменателе следующее выражение: x+5-2, то получается, что «x» не может быть равен -3. Ведь в таком случает все выражение превращается в ноль, поэтому при решении необходимо исключить целое число -3 для данной переменной.

Как правильно решать рациональные уравнения?

Рациональные выражения могут содержать в себе довольно-таки большое количество чисел и даже 2 переменные, поэтому порой их решение становится затруднительным. Для облегчения решения такого выражения рекомендуется произвести некие операции рациональным путем. Итак, что значит «рациональным способом» и какие правила необходимо применять при решении?

1. Первый вид, когда достаточно всего лишь упростить выражение. Для этого можно прибегнуть к операции сокращения числителя и знаменателя до несокращаемой величины. Например, если в числителе имеется выражение 18x, а в знаменателе 9х, то, сокращая оба показателя на 9x, получаем просто целое число, равное 2.
2. Второй способ практичен тогда, когда в числителе имеем одночлен, а в знаменателе — многочлен. Разберем на примере: в числителе имеем 5x, а в знаменателе — 5x + 20x². В таком случае лучше всего вынести переменную в знаменателе за скобки, получим следующий вид знаменателя: 5x(1+4x). А теперь можно воспользоваться первым правилом и упростить выражение, сократив 5x в числителе и в знаменателе. В итоге получим дробь вида 1/1+4x.

Какие действия можно выполнять с рациональными числами?

Множество рациональных чисел имеет ряд своих особенностей. Многие из них весьма схожи с характеристикой, присутствующей у целых и натуральных чисел, ввиду того что последние всегда входят в множество рациональных. Вот несколько свойств рациональных чисел, зная которые, можно с легкостью решить любое рациональное выражение.

1. Свойство коммутативности позволяет суммировать два или несколько чисел, вне зависимости от их очередности. Проще говоря, от перемены мест слагаемых сумма не меняется.
2. Свойство дистрибутивности позволяет решать задачи с помощью распределительного закона.
3. И, наконец, операции сложения и вычитания.

Даже школьники знают, что значит «рациональный вид чисел» и каким образом решать задачи на основе таких выражений, поэтому взрослому образованному человеку просто необходимо вспомнить хотя бы азы множества рациональных чисел.

fb.ru