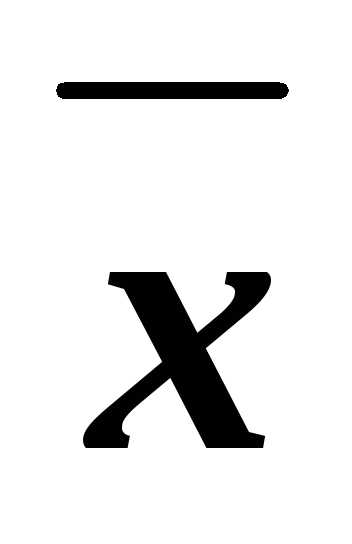Пример составления полинома Жегалкина
Обратная связь
ПОЗНАВАТЕЛЬНОЕ
Сила воли ведет к действию, а позитивные действия формируют позитивное отношение
Как определить диапазон голоса — ваш вокал
Как цель узнает о ваших желаниях прежде, чем вы начнете действовать. Как компании прогнозируют привычки и манипулируют ими
Целительная привычка
Как самому избавиться от обидчивости
Противоречивые взгляды на качества, присущие мужчинам
Тренинг уверенности в себе
Вкуснейший «Салат из свеклы с чесноком»
Натюрморт и его изобразительные возможности
Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д.
Как научиться брать на себя ответственность
Зачем нужны границы в отношениях с детьми?
Световозвращающие элементы на детской одежде
Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия
Как слышать голос Бога
Классификация ожирения по ИМТ (ВОЗ)
Глава 3. Завет мужчины с женщиной
Оси и плоскости тела человека — Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
Отёска стен и прирубка косяков — Когда на доме не достаёт окон и дверей, красивое высокое крыльцо ещё только в воображении, приходится подниматься с улицы в дом по трапу.
Дифференциальные уравнения второго порядка (модель рынка с прогнозируемыми ценами) — В простых моделях рынка спрос и предложение обычно полагают зависящими только от текущей цены на товар.
Совершенная дизъюнктивная нормальная форма
Фиксируем алфавит булевых переменных .
Напомним, что
Определение 1.Элементарной конъюнкцией ранга относительно алфавита назовем форму ,
где . При конъюнкция называется совершенной.
Определение 2. Дизъюнктивной нормальной формой (ДНФ) относительно алфавита называется любая дизъюнкция элементарных конъюнкций. Совершенной дизъюнктивной нормальной формой относительно алфавита называется любая дизъюнкция различных совершенных конъюнкций (СДНФ).
Отметим все важные свойства совершенных конъюнкций:
а) произведение двух различных совершенных конъюнкций равно ;
б) в совершенной дизъюнктивной нормальной форме относительно алфавита при подстановке фиксированного набора либо все совершенные конъюнкции равны нулю, либо равна одна единственная конъюнкция.
Действительно, при произведение
(1)
c одержит для некоторого множители и , отсюда , и поэтому произведение (1) равно . Далее для любого набора уравнение влечет ,…, – единственно возможное решение, т.к. если для некоторого имеем , то и нулю равна вся конъюнкция.
(2)
Дизъюнкция идет по всем наборам, в которых функция равна . Формула (2) следует непосредственно из свойств совершенных конъюнкций.
Вопрос. Чем является функция ?
Ваш ответ :
ДНФ (дизъюнктивная нормальная форма)
Да, правильно. Так как во втором слагаемом нет переменной .
Составление СДНФ
Пример 1. Совершенные ДНФ для элементарных функций (табл. 2):
для конъюнкции: ;
для дизъюнкции: ;
для сложения по mod 2: ;
для импликации: ;
для эквиваленции: ;
для штриха Шеффера: ;
для «стрелки Пирса»: ;
для отрицания : ;
для селекторной функции : ;
для константы : ;
константа не имеет СДНФ.
Пример 2. Написать СДНФ относительно алфавита , , для функции голосования от трех переменных, заданной таблично (см. табл. 3).
СДНФ для содержит четыре совершенные конъ-юнкции (по числу единиц функции)
.
Пример 3. Преобразовать в СДНФ формулу относительно алфавита , , .
Данная формула есть ДНФ, но имеет несовершенные конъюнкции. С помощью преобразований вида доводим конъюнкции до совершенства:
,
раскроем скобки
,
собираем подобные члены по правилу :
.
Это и есть СДНФ.
Замечание. Если функция задана формулой, то можно для функции вычислить таблицу, а затем задача сведется к примеру 2. Однако создание таблицы может оказаться очень трудоемким. Так, например, если алфавит переменных состоит из переменных, то таблица имеет строк, что неприемлемо, так как потребуется много места на доске или бумаге.
Вопрос. Сколько элементарных конъюнкций содержится в СДНФ для функции, заданной своими значениями ?
Ваш ответ :
Три
Да, правильно. Потому что функция равна 1 только на трех наборах.
Полином Жегалкина
Элементарные конъюнкции вида , , …, , (конъюнкция нулевого ранга) называются положительными элементарными конъюнкциями.
Любая сумма по различных положительных конъюнкций называется полиномом Жегалкина. Константу считаем нулевым полиномом Жегалкина. Тогда справедливо утверждение:
Теорема.Всякая функция алгебры логики представима полиномом Жегалкина единственным образом с точностью до перестановки слагаемых.
. (3)
В силу совокупной ортогональности совершенных конъюнкций в (3) знаки дизъюнкции можно заменить на знаки , что приведет к формуле
. (4)
Удаляя в (4) отрицания переменных по формуле , раскрывая скобки и приведя подобные члены по правилу , мы получим полином Жегалкина. Единственность представления функции полиномом следует из того, что полиномов Жегалкина под алфавитом ,…, столько же, сколько и функций от переменных, то есть . ▲
Вопрос. Чем является данная функция ?
Ваш ответ :
Произвольной функцией
Да,правильно.
Пример составления полинома Жегалкина
Пример 1. Пусть задана функция таблицей.
Представим ее СДНФ
.
Отсюда имеем
.
Раскрываем скобки:
.
Приводим подобные члены:
Получили полином Жегалкина.
Пример 2. Пусть задана функция формулой .
ДНФ функции состоит из двух ортогональных конъюнкций ( ), поэтому
.
Получили полином Жегалкина.
Пример 3. Для элементарных функций табл. 2 полиномы Жегалкина имеют вид:
а) для конъюнкции – ;
б) для дизъюнкции – ;
в) для суммы по – ;
г) для импликации – ;
д) для эквиваленции – ;
е) для «штрих Шеффера» – ;
ё) для «стрелки Пирса» – ;
ж) для : ;
з) для , , , – без изменений.
Вопрос. Чему равен полином Жегалкина для функции ?
Ваш ответ :
Да, правильно.
Начало формы
Теорема двойственности
Функция называется двойственной к функции .
Из определения следует, что таблица для двойственной функции может быть получена из таблицы для функции заменой всех нулей на единицы и всех единиц на нули.
Если оказывается, что , то функция называется самодвойственной. Самодвойственная функция на противоположных наборах принимает противоположные значения, т.е. для любого набора .
Отношение двойственности симметрично, .
Пример 1. Двойственные функции к элементарным функциям табл. 2:
, , ,
, , ,
, , , , .
Пример 2. Является ли функция самодвойственной?
Чтобы ответить на этот вопрос, можно составить (вычислить) таблицу и по таблице проверить значения функции на противоположных наборах, и если найдется пара противоположных наборов, на которых функция принимает одинаковые значения, то функция несамодвойственна.
Можно также перейти к двойственной функции
и вычислять одновременно значения двух функций и , и как только обнаружится, что на наборе будем иметь , значит, функция несамодвойственна. В противном случае – самодвойственная, но цена этому выводу высока – ведь вычислены таблицы двух функций. Наконец, если преобразовать и к полиномам Жегалкина, и полиномы оказались разные, то и – несамодвойственна.
Теорема двойственности. Пусть имеется формула (тождество)
,
тогда верно тождество
.
Доказательство.
. ▲
С помощью этой теоремы легко доказываются некоторые тождества. Например,
1) из формулы де Моргана и теоремы двойственности следует другая формула де Моргана, так как влечет ;
2) из формулы (формула сокращения) следует , по теореме двойственности получаем другую формулу сокращения ;
3) из формулы получаем и отсюда .
Замечание. Операция меняет приоритетность операндов, поэтому во избежание ошибок в начальной формуле надо отменить приоритетность, то есть должны быть расставлены все скобки, выделяющие бинарные операции.
Вопрос. Является ли функция , заданная таблично, самодвойственной?
Ваш ответ :
Нет
Правильно, так как таблица не симметрична.
Определение СКНФ
Элементарной дизъюнкцией ранга относительно алфавита назовем форму
,
где . При дизъюнкция называется совершенной.
Любая конъюнкция элементарных дизъюнкций называется конъюнктивной нормальной формой (КНФ). Любая конъюнкция совершенных дизъюнкций называется совершенной конъюнктивной нормальной формой (СКНФ).
Теорема. Всякая функция алгебры логики представима совершенной конъюнктивной нормальной формой
Доказательство. Из условия теоремы запишем СДНФ для функции
,
отсюда и из теоремы двойственности имеем
, что и требовалось доказать. ▲
Вопрос. Чем является функция ?
Ваш ответ :
КНФ
Правильно, так как во второй скобке содержатся не все переменные.
Примеры составления СКНФ
Пример 1. Совершенные КНФ для элементарных функций табл. 1 относительно алфавита переменных , :
для конъюнкции: ;
для дизъюнкции: ;
для суммы по : ;
для импликации: ;
для эквиваленции: ;
для «штрих Шеффера»: ;
для «стрелки Пирса»: ;
для отрицания : ;
для селекторной функции : ;
для константы ;
для константы СКНФ не существует.
Пример 2. Написать СКНФ для функции голосования.
СКНФ для (она содержит четыре нуля и поэтому состоит из четырех совершенных дизъюнкций):
.
Пример 3. Преобразовать в СКНФ формулу относительно алфавита , , .
Данная формула есть ДНФ. Преобразуем ее сначала в КНФ:
.
Преобразуем дизъюнкции в совершенные:
.
Вопрос. Как выглядит СКНФ для функции, заданной таблично?
Ваш ответ :
Правильно.
megapredmet.ru
Об одном методе построения полинома Жегалкина Текст научной статьи по специальности «Общие и комплексные проблемы естественных и точных наук»
Алехина М.А., Пичугина П.Г. ОБ ОДНОМ МЕТОДЕ ПОСТРОЕНИЯ ПОЛИНОМА ЖЕГАЛКИНА
Известно, что любую булеву функцию можно представить полиномом Жегалкина (полиномом по модулю 2), и это представление с точностью до перестановки слагаемых единственно. Приведем некоторые наиболее известные способы построения такого полинома.
Преобразование произвольной формулы алгебры логики: сначала строим дизъюнктивную нормальную форму (ДНФ) или конъюнктивную нормальную форму (КНФ), а затем — полином Жегалкина, используя известные соотношения
x = x ©1, x v y = xy = (x © 1)(y © 1) ©1 = xy © x © y . (1)
Метод неопределенных коэффициентов состоит в следующем: записываем булеву функцию в виде полинома Жегалкина с неопределенными коэффициентами. Приравниваем значения функции к значениям полинома на соответствующих наборах переменных и находим неизвестные коэффициенты.
3) На значениях исходной функции f (x, x2,…, xn) = (f, f2, f,…, fn ) , строим треугольник Паскаля, складывая каждый раз соответствующие значения функции по модулю 2. Тогда числа на левой стороне полученного треугольника определяют коэффициенты полинома Жегалкина при монотонных конъюнкциях, соответствующих наборам переменных. Напомним, что элементарная конъюнкция называется монотонной, если она не содержит отрицаний переменных. Константа 1 (т. е. элементарная конъюнкция нулевого ранга) считается
по определению монотонной конъюнкцией.
Пример 1. Продемонстрируем предложенные методы построения полинома Жегалкина, если
f (x,y,z) = (x v y)(y v xz) .
Преобразуем логическую формулу (xvy)(y v xz) , используя формулы (1):
(x v y)(y v xz) = (xy © x © y)((y ©1)xz © (y ©1) © xz) = (xy © x © yXyZ © xz © y ©1© xz) =
= (xy © x © y)(xyz © y ©1) = xyxyz © xyy © xy © xxyz © xy © x © yxyz © yy © y = xyz © xy © x .
Таким образом, полином Жегалкина P(x, y, z) для данной функции имеет вид P(x, y, z) = xyz © xy © x . Теперь построим его методом неопределенных коэффициентов. Для этого запишем нашу функцию в виде многочлена с неопределенными коэффициентами:
f (x, y, z) = Axyz © Bxy © Cxz © Dyz © Ex © Fy © Gz © H , (2)
где A, B, C, D, E, F, G, H e{0,1}.
Таблица истинности нашей функции выглядит следующим образом:
x У z x V y y xz y V xz f = (x V y)( y V xz)
0 0 0 0 1 0 1 0
0 0 1 0 1 0 1 0
0 1 0 1 0 0 0 0
0 1 1 1 0 0 0 0
1 0 0 1 1 0 1 1
1 0 1 1 1 1 1 1
1 1 0 1 0 0 0 0
1 1 1 1 0 1 1 1
Чтобы определить неизвестные коэффициенты, подставим соответствующие значения переменных в правую и левую части формулы (2) и получим систему:
Н = 0 в 0 Н = 0
Р 0 Н = 0 •
В 0 Р 0 в 0 Н = 0
Е 0 Н = 1
С 0 Е 0 в 0 Н = 1
В 0 Е 0 ^ 0 Н = 0
А 0 В 0 С 0 В 0 Е 0 ^ 0 в 0 Н = 0
Решая систему, находим коэффициенты:
Н = 0 в = 0 Р = 0 •
В = 0 Е = 1 С = 0 В = 1 А = 1
Подставляя найденные значения А, В, С, В, Е, В, О, Н в формулу (2), получим полином Жегалкина того же вида, что и в первом случае: /(х,у,’£) = (хVу)(уVх£) = ху.z©ху©х .
Для реализации третьего метода, зададим исходную функцию набором ее значений /(х,у,г) = (00001101) . На строке значений функции построим треугольник Паскаля, складывая попарно по модулю 2 соседние значения фун кции:
Числа на левой стороне (выделены жирным шрифтом) треугольника определяют коэффициенты полинома при монотонных конъюнкциях, соответствующих наборам значений переменных (значения на левой стороне треугольника дублируют значения найденных неопределенных коэффициентов в предыдущем случае).
Сравнивая предложенные методы построения полинома Жегалкина, студенты (да и преподаватели тоже) отдают предпочтение последнему методу, обосновывая выбор быстротой получения результата и простотой алгоритма построения треугольника Паскаля. Изучая соответствующую данной тематике научную и научнометодическую литературу, мы не нашли строгого доказательства построения полинома Жегалкина с использованием треугольника Паскаля. Поэтому предлагаем свое доказательство для функций двух, трех и четырех переменных (исходя из тех соображений, что на практических занятиях со студентами другие случаи, как правило, не рассматриваются), т. е. п =2, 3, 4.
п=2. Проведем доказательство для булевой функции двух переменных /(х,х2) . Полином Жегалкина для
этой функции в общем виде будет выглядеть следующим образом: / (х, х2) = ахх ® ах ® ах ® аА , (3)
где а1 е {0,1}, I = 1,4 . Таблица истинности данной функции имеет вид:
х1 х2 Л ( x1, х2)
0 0 /1
0 1 /2
1 0 /з
1 1 /4
Значения функции / (1=1,2,3,4) можно определить, подставляя в соотношение (3) всевозможные набо-
Л = а4
ры значений переменных:
Решая систему относительно а,а,а,а, получим:
(4)
а4 = А а3 = /1 0 /2 а2 = /1 0 /3
а1 = Л 0 /20 /30 /4
Покажем, что эти коэффициенты совпадают со значениями на левой стороне треугольника Паскаля, построенного для функции /(х,х2) , заданной набором значений ї= (/,/2,/,/) .
Видим, что числа на левой стороне треугольника в точности определяет коэффициенты полинома Жегалкина, найденные при решении системы (см. соотношения (4)).
п=3. Теперь возьмем функцию трех переменных / (х, х2, х3) и представим ее полином Жегалкина с неопределенными коэффициентами а е {0,1}, I = 1,8 :
/(х, х2, х) = аххх ® ахх ® ахх ® ахх ® ах ® ах ® ах ® а • (5)
Строим таблицу истинности исходной функции:
х1 х2 хз
0 0 0 /1
0 0 1 /2
0 1 0 /з
0 1 1 /4
1 0 0 /5
1 0 1 /б
1 1 0 /7
1 1 1 /8
Используя таблицу истинности и соотношение (5), составим систему:
А = а8
/2 = а7 ® а8
/з = а6 ® а8
/4 = а4 ® аб ® а7 ® а8 .
/5 = а5 ® а8
/ = а ® а ® а ® а8 /7 = а2 а^ аб а8
/8 = а1 ® а2 ® аз ® а4
Решим эту систему и получим
а8 = /1 а7 = /1 0 /2 а6 = /1 0 /3
а4 = / 0 /2 0 /3 0 /4 (6)
а5 = /1 0 /5 а3 = /1 0 /2 0 /5 0 /6 а2 = ./і 0 /3 0 /5 0 /7
, а1 = Л 0 /2 0 /3 0 /4 0 /5 0 /6 0 /7 0 /8
Построим треугольник Паскаля, используя условные обозначения: / = і , /і 0 /, =і+л:
Сравнивая’полученные значения на левой стороне треугольника с найденными выше коэффициентами (б), видим, что они равны.
п=4. Проведем доказательство для функции четырех переменных
/ (х1, х2, Л3, х4) = (/1, /2, /3, /4, /5, /6, /7, /8, /9, /10,/11, /12, /1з, /14, ^5 , /16) * Представим функцию Ї в виде многочлена с неопределенными коэффициентами а Є {0,1}, і = 1,16 .
/(х!, х2, х3, х4 ) = а^хххх^ 0 ах!х2х3 0 ах!х3х4 0 ах!х2х4 0 0ах2х3х4 0 а6х{х2 0 ахх 0 ахіх4 0 а9х2хъ 0 (7)
0ашх2х4 0 апхзх4 0 апх1 0 а1зх2 0 аихз 0 а15х4 0 а16.
Используя таблицу истинности функции Ї и формулу (7), получим систему:
/1 = а16
/2 = а15 0 а16
/з = а14 0 а16
/4 = ап 0 а14 0 а15 0 а16
/5 = а1з 0 а16
/6 = а10 0 а1з 0 а15 0 а16
/7 = а9 0 аи 0 аи 0 а16
/ = а 0 а 0 Оо 0 0і 0 аз 0 а4 0 а15 0 а1б
/9 = а12 0 а16
/10 = а8 0 а12 0 а15 0 а16
/11 = а7 0 а12 0 а14 0 а16
/2 = а 0 а 0 а 0 аі 0 а2 0 0 а 0 а1б
/1з = а6 0 а12 0 а1з 0 а16
/ 4 = а 0 а 0 а 0 ао 0 аг 0 аз 0 а 0 а1б / 5 = а 0 а 0 а 0 а 0 а2 0 а 0 а4 0 а1б
/ б = а 0 а 0 а 0 а 0 а 0 а 0 а 0 а 0 а 0 ао 0 аі 0 аг 0 а 0 а4 0 а 0 аб ■
Решим эту систему относительно коэффициентов а,і = 1,16 , и получим систему (8).
а16 = / а15 = Л 0 /2
а14 = / 0 /з % = / 0 /2 0 /з 0 /4
а1з = /0 /5
а10 = /0 /20 /50 /6
0) = У!0 /з0 /50 /7 (8)
а5 = Л 0 /2 0 /з 0 /4 0 /5 0 /6 0 /7 0 Л
а = / 0 /9
а = / 0 /2 0 /9 0 /10 а7 = Л 0 Л 0 /9 0 /11
а = / 0 /2 0 Л 0 Л 0 /9 0 /10 0 /11 0 /12 а6 = / 0 /2 0 /5 0 /6
а9 = / 0 /5 0 /9 0 /1з
а4 = Л 0 /2 0 /5 0 /6 0 /9 0 Л) 0 /1з 0 /14
а2 = Л 0 Уз 0 /5 0 /7 0 /9 0 /11 0 /1з 0 /15
а = /0 /20 /з0 /40 /50 /60 /70 /80 /90
0/10 0 /11 0 /12 0 /1з 0 /14 0 /15 0 /16.
Нетрудно проверить равенство коэффициентов из системы (8) со значениями на левой стороне треугольника Паскаля, построенного для набора значений данной функции
Щ,/2,/з,/4,/5,/6,/7,/8,/9,Л),/11,/12,/1з,/14,/15,/16) •
Треугольник Паскаля приведен не полностью, выписана лишь интересующая нас левая часть:
2 3 4 5 6 7
1+2 2+3 3+4 4-5 5+6 6+7
1+3 2-4 3+5 4+6 5-7
1+2+3+4 2+3+4+5 3+4+5+6 4+3+6+7
1+5 2+6 3+7 4-8
1+2+5+6 2—3+6+7 3+4+7+8
10 11 12 13 14 15 16
4151819
1+3+5+7 2+4+6+8 3+5+7+9 4+6+8+10
1+2+3+4+5+6+7+8 2+3+4+5+6+7+8+9 3+4+5+6+7+8+9+10
1+9 2-10 3+11
1+2+9+10 2-3+10+11 3+4+11+12
1+3+9+11 2-4+10+12 3+5+11-13
1+2+3+4+9+10+11+12 2+3+4+5+10+11+12+13 3+4+5+6+11+12+13+14
1+5+9+13 2+6+10+14 3+7+11+15
1+2+5+6+9+10+13+14 2+3+6+7+10+11-14+16
1+3+7+9+11+13+15 2+4+6+8+10+12+14+16
1+2+3+4+5+6+7+8+9+10+11+12+13+14+15+16.
Таким образом, для булевой функции / (х1,…, хп) при п =2, 3, 4 нами представлено обоснование (доказательство) возможности использования треугольника Паскаля для построения полинома Жегалкина.
В заключении проиллюстрируем способ построения полинома Жегалкина с использованием треугольника Паскаля на примере.
Пример 2. Представить полиномом Жегалкина функцию f ( х1, х2, х ) = ( 01110 010 ) .
Решение. Запишем наборы значений переменных х1, х2, х3 в лексикографическом порядке для определения монотонных конъюнкций (слева, в скобках, приведены соответствующие монотонные конъюнкции) и построим
треугольник Паскаля на значения:’: функции (справа) .
000 (1) 00 1 (л.)
0 1 О Jx2)
0 11 (Ж2Х3)
1 по ,«
1 0 1 1 1 1
1 (.Tl-Ts)
0..
1 (л-даз)
На левой стороне треугольника Паскаля получены коэффициенты полинома при соответствующих конъюнкциях. Таким образом, f= Х3 Ф Х2 Ф Х2Х3 Ф Х1Х3 .
ЛИТЕРАТУРА
1. Кузнецов О.П., Адельсон-Вельский Г.М. Дискретная математика для инженера. — М.: Энергоатомиз-
дат, 1988.
2. Гаврилов Г.П., Сапоженко А.А. Задачи и упражнения по дискретной математике. — М.: Физматлит,
2004. — 414 с.
cyberleninka.ru
Учебник по дискретной математике. Полиномы Жегалкина
Полиномом (многочленом) Жегалкина от п переменных называется функция
P = a0 + a1x1 +a2x2 + …anxn +an +1x1x2 +…+an +C2nxn-1xn + …+a2n-1x1x2..xn
Всего здесь 2п слагаемых. Напомним, что + сейчас означает сложение по модулю 2, коэффициенты a0, a1,…, a2n-1 являются константами (равными нулю или единице).
Теорема. Любая функция п переменных может быть представлена полиномом Жегалкина и это представление единственно.
Доказательство. Любая функция f(x1, x2, …, xn) имеет свою таблицу истинности. Запишем сначала данную функцию в виде полинома Жегалкина с неопределенными коэффициентами. Затем по очереди подставляем всевозможные наборы переменных и находим коэффициенты. Легко видеть, что за каждую подстановку находим только один коэффициент. Так как число наборов равно числу коэффициентов (и равно 2п), отсюда следует утверждение теоремы.
Доказательство этой теоремы показывает, как по таблице истинности построить полином Жегалкина.
Имеется 2-й способ нахождения полинома Жегалкина для функций, заданных в виде ДНФ. Этот способ основан на том, что х+1 = . Если функция задана в виде ДНФ, то сначала убираем дизъюнкцию, используя при этом правило де Моргана, а все отрицания заменяем прибавлением единицы. После этого раскрываем скобки по обычным правилам, при этом учитываем, что четное число одинаковых слагаемых равно нулю (так как х+ х = 0), а нечетное число одинаковых слагаемых равно одному такому слагаемому.
Пример.
( xy + 1)((x + 1)(y + 1) + 1)((y + 1)z + 1) + 1 = (xy + 1)(xy + x + y)(yz + z + 1) + 1 = (x + y)(yz + z + 1) + 1= xyz + yz + xz +yz + x + y + 1 = xyz + xz + x +y + 1.
Последнее выражение и есть полином Жегалкина данной функции.
Функция f (x1,x2,…,xn) называется линейной, если ее полином Жегалкина содержит только первые степени слагаемых. Более точно функция называется линейной, если ее можно представить в виде
f(x1, x2, …, xn) = a0 + a1 x1 + a2 x2 +…+ an xn.
Класс линейных функций часто обозначают через L. (Заметим, что число линейных функций п переменных равно 2п+1).
Замечание. Если пі 2 то линейная функция в таблице истинности может содержать только четное число единиц. Действительно, если f(x1,x2,…, xn) = x1+ x2+…+xn, то легко видеть что такая функция в таблице истинности содержит одинаковое число нулей и единиц а именно 2п /2 единиц и нулей, т. е. число это четно при пі 2. Столько же нулей и единиц имеет функция . Добавление же фиктивной переменной приводит к увеличению числа единиц (и нулей) в два раза. Разумеется, нелинейная функция может иметь в таблице истинности как четное, так и нечетное число единиц.
www.mini-soft.ru
31. Функционально полные и функционально замкнутые системы булевых функций.
Функционально полной системой булевых функций (ФПСБФ) называется совокупность таких булефых функций (f1, f2, … fk), что произвольная булева функция f может быть записана в виде формулы через функции этой совокупности.
Перечислим предполные классы булевых функций:
булевы функции, сохраняющие константу 0;
булевы функции, сохраняющие константу 1;
самодвойственные булевы функции;
линейные булевы функции;
монотонные булевы функции;
Замкнутый класс в теории булевых функций — такое множество функций алгебры логики, замыкание которого относительно операции суперпозиции совпадает с ним самим: . Другими словами, любая функция, которую можно выразитьформулой с использованием функций множества , снова входит в это же множество.
Особо важны для теории булевых функций следующие замкнутые классы, называемые предполными классами:
32 Полиномы Жегалкина. Метод неопределенных коэффициентов построения полиномов Жегалкина. Примеры.
: Существование полинома доказано вышеприведенным алгоритмом получения полинома из логической формулы. Для доказательства единственности надо показать, что между множеством всех логических функций от n переменных и множеством всех полиномов Жегалкина от n переменных существует взаимно однозначное соответствие. Полином Жегалкина можно найти методом неопределенных коэффициентов. Рассмотрим этот метод на следующим примере.
Пример. Найти полином Жегалкина для функции заданной векторно:
f( x,y ) = ( 0, 1, 1, 0 ).
Составим таблицу 1.14 задания данной функции.
Таблица 1.14
x | y | f |
0 | 0 | 0 |
0 | 1 | 1 |
1 | 0 | 1 |
1 | 1 | 0 |
Полином Жегалкина для функции двух переменных ищем в следующем виде:
f( x, y ) = a0 a1·xa2·ya3·xy (1.6)
Для определения коэффициентов полинома нужно подставить значения неизвестных и соответствующее значение функции в (1.6), согласно таблице 1.14.
Подставляя набор переменных(0,0) в (1.6) получим:
a = 0.
Аналогично для набора (0,1) получим:
. a = 1
34.
Классы и их функциональная замкнутость. Метод определения принадлежности булевой функции классу линейных функций. Примеры.
Замкнутый класс в теории булевых функций — такое множество функций алгебры логики, замыкание которого относительно операции суперпозиции совпадает с ним самим: . Другими словами, любая функция, которую можно выразитьформулой с использованием функций множества , снова входит в это же множество.
Множество всех возможных булевых функций замкнуто.
Особо важны для теории булевых функций следующие замкнутые классы, называемые предполными классами:
Булева функция называется линейной, если существуют такие, где, что для любыхимеет место равенство:
.
studfiles.net
2.2.6. Полиномы Жегалкина | Решение задач по математике и другим предмет
Полином вида , где — элементарные конъюнкции различных переменных без отрицаний (среди может быть константа 1), называется Полиномом Жегалкина.
Например, .
Теорема (Жегалкин). Любая булева функция представляется в виде полинома Жегалкина, причем единственным образом с точностью до порядка следования элементарной конъюнкции (слагаемых) и до порядка следования переменных в элементарных конъюнкциях.
Доказательство. Если функция , то полиномом Жегалкина для данной функции является константа 0. В остальных случаях представим функцию в виде СДНФ: .
Преобразуем СДНФ в полином Жегалкина. Прежде всего, все знаки дизъюнкции можно заменить на знак суммы по модулю 2 :
.
Это можно сделать по следующей причине: дизъюнкция (проверить).
Если и заменить элементарными конъюнкциями из СДНФ, то получим , так как . Действительно и имеют одинаковые наборы переменных, которые отличаются только расстановкой отрицания, поэтому в произведении найдется переменная , которая встречается с отрицанием и без отрицания. А конъюнкция таких переменных: равна нулю: .
Далее в полученной формуле преобразуем отрицания по формуле: (проверить). После этого останется раскрыть скобки, что можно сделать ввиду следующего дистрибутивного закона: (проверить). После раскрытия всех скобок мы получим сумму элементарных конъюнкций без отрицаний. Если среди полученных конъюнкций есть одинаковые, то все их (за исключением, может быть, одной из группы одинаковых) можно убрать по следующему правилу: . В итоге получим полином Жегалкина.
Чтобы убедиться в единственности полинома Жегалкина для данной функции, подсчитаем количество различных полиномов от переменных. Заметим, что можно составить элементарных конъюнкций из переменных без отрицания. (Действительно для каждой из Переменной имеется две возможности: данная переменная входит в данную конъюнкцию или нет). Далее для каждой конъюнкции существует также 2 возможности: она входит в данный полином Жегалкина или нет. Поэтому количество различных полиномов Жегалкина равно , т. е. ровно столько, сколько существует различных булевых функций от переменных. Из данного совпадения вытекает единственность полинома Жегалкина. Действительно, если бы какую-то функцию можно было представить двумя или несколькими полиномами Жегалкина, то некоторые функции нельзя было бы представить полиномом Жегалкина. А уже доказано, что любую функцию можно представить полиномом Жегалкина.
Пример. Пусть функция задана следующей таблицей истинности.
Строим полином Жегалкина сразу Преобразовывая соответствующую СДНФ: | |||||
0 | 0 | 0 | 0 | ||
0 | 0 | 1 | 1 | ||
0 | 1 | 0 | 1 | ||
0 | 1 | 1 | 0 | ||
1 | 0 | 0 | 0 | ||
1 | 0 | 1 | 0 | ||
1 | 1 | 0 | 1 | ||
1 | 1 | 1 | 1 |
| < Предыдущая | Следующая > |
|---|
matica.org.ua
5.3. Полином Жегалкина.
Определение 5. Полиномом Жегалкина называется полином вида
с,
(то есть сумма
произведений вида 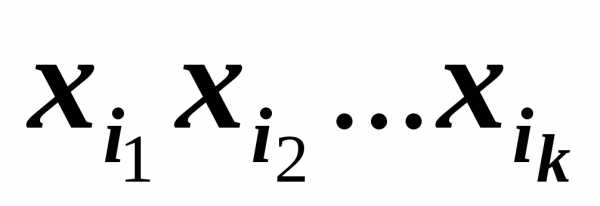 ),
где суммирование ведётся по некоторому
множеству различных наборов (i1, i2,
…, ik),
в которых все ij также различны.
),
где суммирование ведётся по некоторому
множеству различных наборов (i1, i2,
…, ik),
в которых все ij также различны.
Любая булева функция единственным образом (с точностью до следования слагаемых) представима в виде полинома Жегалкина.
Для представления булевой функции в виде полинома Жегалкина достаточно:
1. Привести функцию к ДНФ (КНФ).
2. Выразить операции &, , через операции булева кольца по формулам из п.5.2.
Пример
5.3. Найдём полиномы Жегалкина для функций
из примера 5.2. Для функции (х&у)( &
&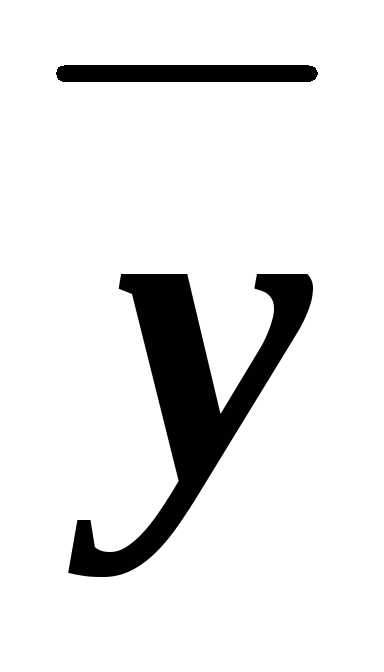 )
имеем
)
имеем
(х&у)( &
&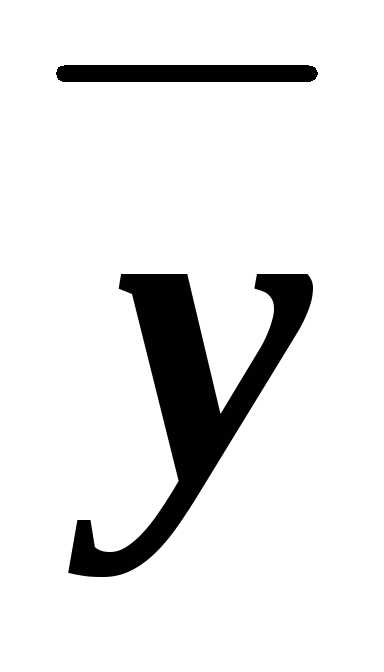 )=ху
)=ху
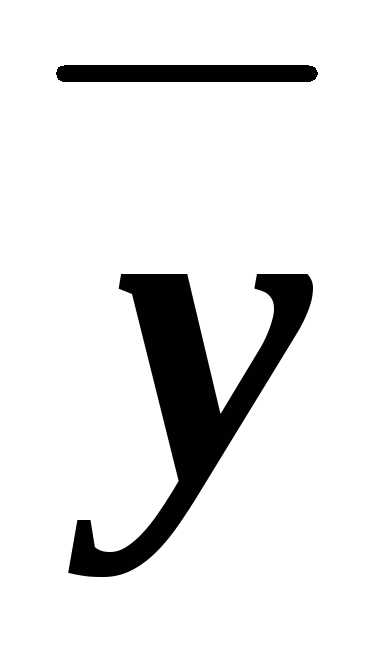 ху
ху
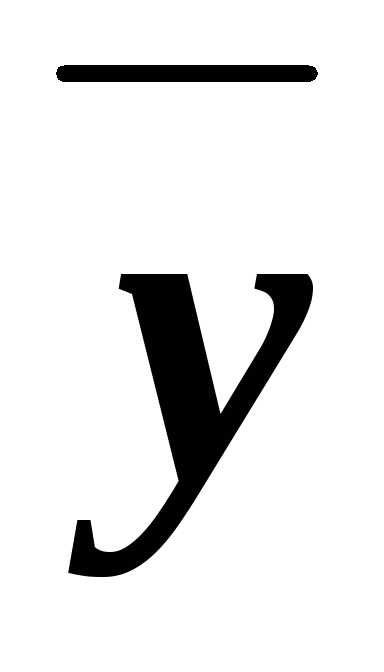 =ху
=ху
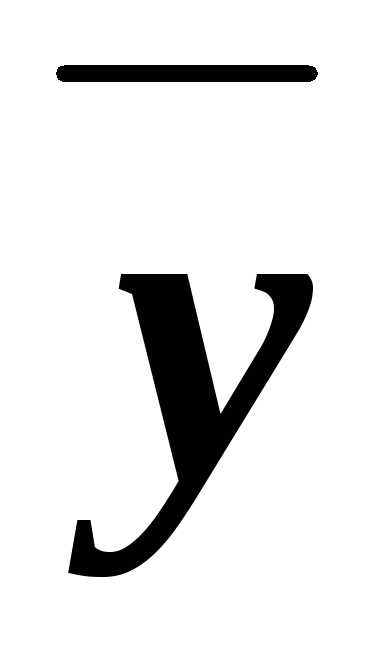 =
=
=ху(1х)(1у)=ху1хуху=1ху,
то есть
(х&у)( &
&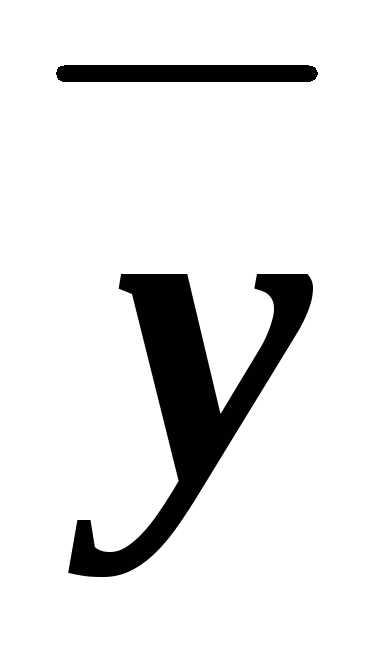 )=1ху (в чём мы уже убеждались). Для функции х
)=1ху (в чём мы уже убеждались). Для функции х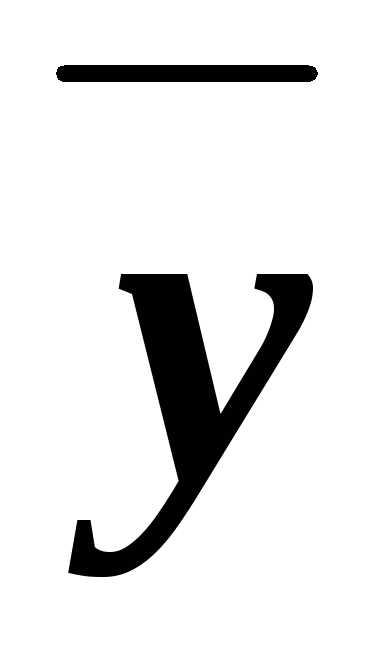 имеемх
имеемх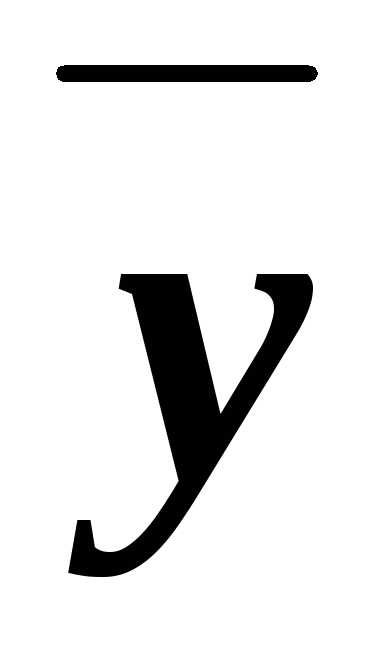 =х(1у)=хху,
то есть х
=х(1у)=хху,
то есть х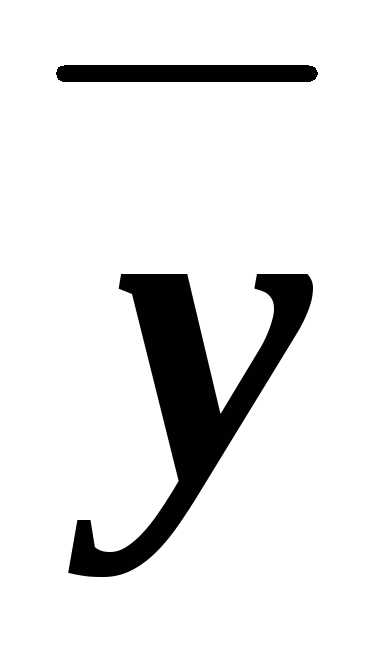 =хху.
=хху.
Как видим, для
функции х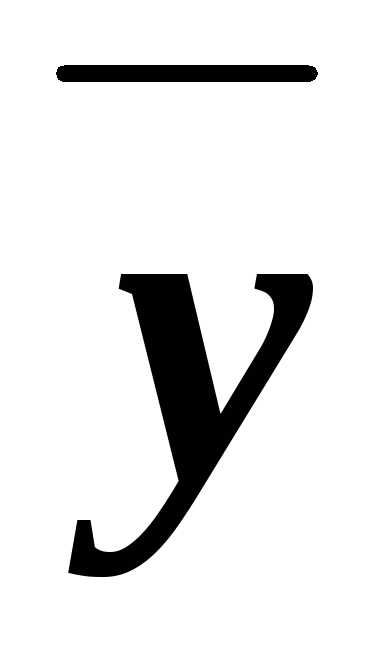 полином Жегалкина содержит произведения
переменных. Такие полиномы называютсянелинейными.
Полиномы Жегалкина вида c0c1x1c2x2…cnxn называются линейными.
Таким образом, линейная функция
представима в виде линейного полинома
Жегалкина.
полином Жегалкина содержит произведения
переменных. Такие полиномы называютсянелинейными.
Полиномы Жегалкина вида c0c1x1c2x2…cnxn называются линейными.
Таким образом, линейная функция
представима в виде линейного полинома
Жегалкина.
Заметим, что если А и В различные конституенты единицы, то они содержат хотя бы одну пару противоположных литер, и тогда АВ=0, АВ=АВ. Поэтому полином Жегалкина удобно получать из СДНФ формулы.
Упражнение 5.4.Построить полиномы Жегалкина для функций упражнения 5.1.
Решение. а) Имеем СДНФf(x,y,z)=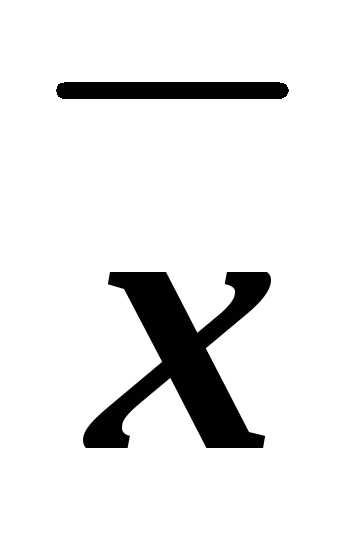
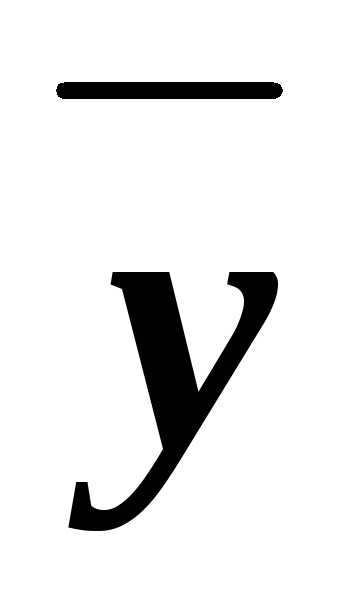 z
z y
y x
x z(см. решение упражнения 5.1, а)). Учитывая,
что
z(см. решение упражнения 5.1, а)). Учитывая,
что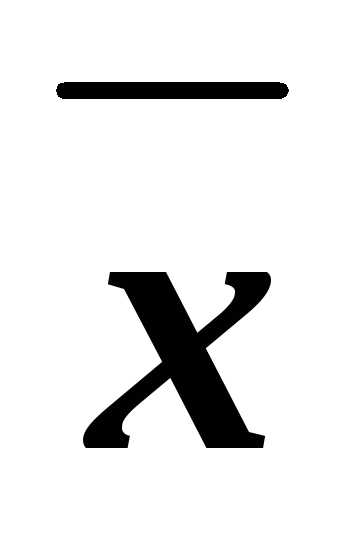 =1х,
=1х, 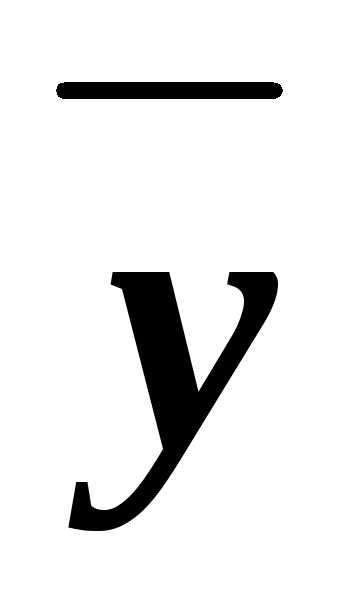 =1у,
=1у, =1 zи раскрывая
скобки, получаем
=1 zи раскрывая
скобки, получаем

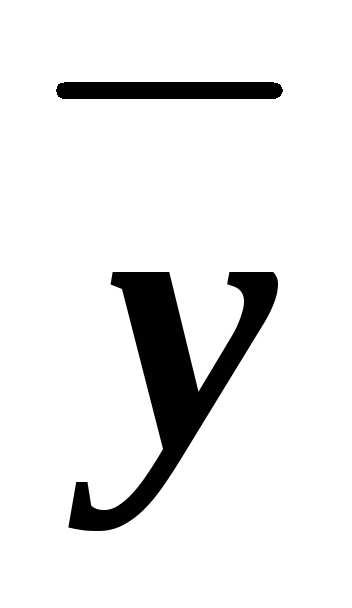 z
z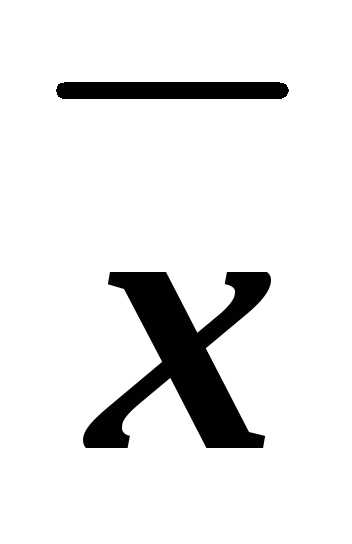 y
y x
x z=
z=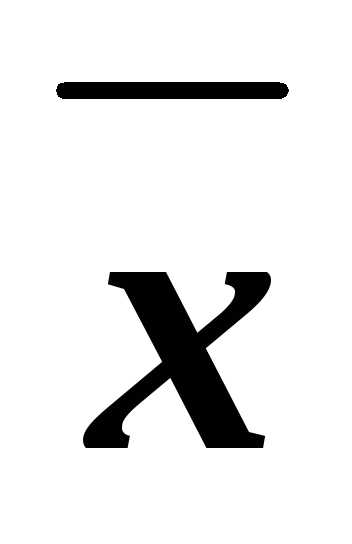
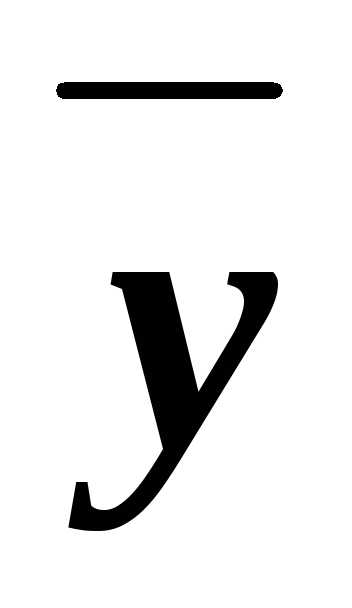 z
z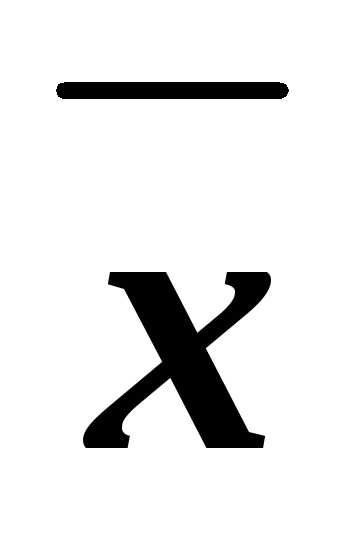 y
y x
x z=(1х)(1у)z(1х)y(1 z)x(1у)z=
z=(1х)(1у)z(1х)y(1 z)x(1у)z=
=zхzуz хyzyхyyzхyzxzxуz=yzxyхyz.
То есть 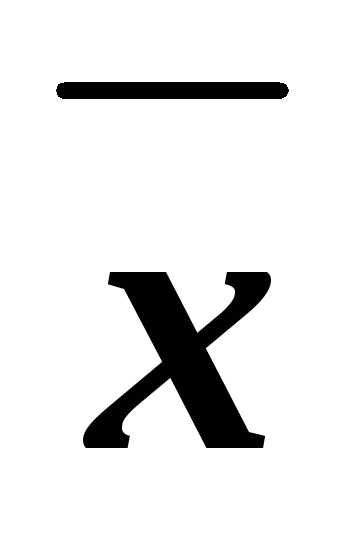
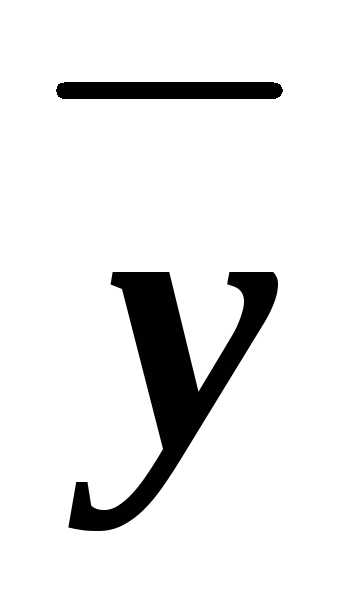 z
z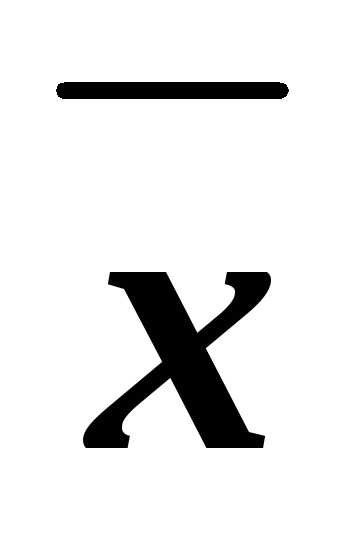 y
y x
x z=yzxyхyz.
В частности, функция не является линейной.
z=yzxyхyz.
В частности, функция не является линейной.
5.4. Функциональная полнота.
Определение 6. Система булевых функций F=f1, f2, …, fn называется полной, если любая булева функция представима в виде суперпозиции функций из F.
Система булевых функций является полной тогда и только тогда, когда для каждого из классов Поста система содержит функцию, не лежащую в данном классе.
Определение 7. Система булевых функций называется базисом, если она полна, и удаление любой функции из этой системы делает её неполной.
Упражнение 5.5.Проверить полноту следующих систем булевых функций:
а) ,; б),; в); г)&,.
Решение. а) Принадлежность данных функций к каждому из классов Поста сведём в таблицу:
P0
P1
S
M
L
xy
+

+
+
В таблице знаком «+» на пересечении строки с указанием функции со столбцом с указанием класса обозначен тот факт, что функция принадлежит соответствующему классу, а знаком «»тот факт, что функция не принадлежит данному классу. В каждом столбце имеется знак «», то есть для любого класса Поста системаF=,содержит функцию, не лежащую в данном классе. Следовательно, система функцийF=,является полной. Она образует базис, так как удаление любой функции из этой системы ведёт к тому, что оставшаяся система является неполной.
§6. Минимизация булевых функций.
6.1. Проблема минимизации булевых функций заключается в том, чтобы для произвольной функции, не являющейся константой 1, получить наиболее простую ДНФ. Прежде, чем приступить к решению проблемы, уточним, что значит «наиболее простая ДНФ».
studfiles.net
Полином Жегалкина — Циклопедия
Мат.Логика. Полином Жегалкина [10:22] Лекция 14: Многочлены Жегалкина // НОУ ИНТУИТ [1:09:58]Полином Жегалкина — это логическая функция, использующая две операции: конъюнкцию и разделительную дизъюнкцию. Полином предложен российским математиком Иваном Ивановичем Жегалкиным в 1927 году.
Назначение полинома Жегалкина — это алгебраическое выражение логических функций.
Введём обозначения:
n – число аргументов функции;
(x1,x2,…,xn) – набор аргументов функции;
P(x1,x2,…,xn) – полином Жегалкина.
- конъюнкция;
- разделительная дизъюнкция.
Конъюнкция — это логическая операция аналогичная арифметическому произведению. Для констант используется обозначение точкой, а для переменных точка опускается.
Разделительная дизъюнкция — это логическая операция аналогичная арифметическому сложению по модулю 2. Используется обозначение знаком плюс в кружке.
Полином Жегалкина имеет следующий вид:
- Заметим, что коэффициенты ai1…ik принимают значения из множества {0,1}, причём если коэффициент равен нулю, то соответствующее слагаемое может быть опущено.
- Полином Жегалкина, состоящий только из слагаемых с единичными коэффициентами (т. е. с опущенными слагаемыми с нулевыми коэффициентами), называется алгебраической нормальной формой (АНФ) соответствующей логической функции.
[править] Примеры полиномов:
[править] С одной переменной
[править] С двумя переменными
- Значения полиномов Жегалкина задаются с помощью таблицы истинности или определяются по формулам.
- Полином Жегалкина является предикатом, определённым на множестве {0,1}.
[править] Другие понятия:
cyclowiki.org