Как решать неравенства 9 класс примеры – Основные правила решения неравенств — урок. Алгебра, 9 класс.

Решение уравнений и неравенств. 9-й класс

Разделы: Математика

---

Тип урока: урок обобщения знаний.

Цели урока:

1. Систематизировать и повторить из курса 8-9 классов способы решения уравнений и неравенств.
2. Развивать аналитическое мышление и эстетическое чувство.
3. Побуждение к самостоятельному выбору методов решения.

Оборудование: проектор, экран.

Ход урока

1. Организационный момент (2-3 минуты).

2. Устный счет.

Решить:

1) Уравнения:		2) Неравенства
а) х2 – 7 = 0		а) х2 – 9 < 0
б) 2х2 + 10х = 0		б) х2 – 25 > 0
в) 3х2 + 300 = 0		в) х2 ≥ 10
г) х2 + 3х – 40 = 0		г) 10х2 ≤ 20
д) х2 – 9х + 20 = 0		д) х2 – 20х > 0
е) х2 + 11х – 12 = 0		е) (х+1)(х – 3) < 0

Как решаются квадратные уравнения и неравенства второй степени?

3. Решение уравнений и неравенств с классом.

Повторим решение дробно-рациональных уравнений, биквадратных/.

№1.

1 – посторонний корень.

Ответ: 2.

№2.

х⁴ – 10х² + 1 = 0

Пусть у = х²

у² – 10у + 1 = 0

№3.

-х² – 2х + 8 < 0 | Ч (-1)

х² + 2х – 8 > 0

1-й способ (методом интервалов).

х² + 2х – 8 = 0

х₁ = -4; х₂ = 2 по теореме Виета.

Ответ: (-∞;-4) U (2;+∞).

2-ой способ (с помощью параболы).

Ответ: (-∞;-4) U (2;+∞).

4. Самостоятельная работа (на экране) с проверкой в классе.

1.

2.

3. х⁶ – 9х³ + 8 = 0

4. 3х² – х + 1 < 0

5. х² – 5х ≤ -4

Сверим ответы:

1	2	3	4	5
		1; 2	Решения нет.	[1;4]

5. Домашнее задание:

1.

2. х⁴ – 4х³ + 5х² – 4х + 1 = 0

3.

19.10.2012

Поделиться страницей:

urok.1sept.ru

Основные понятия, решение линейных неравенств. Видеоурок. Алгебра 9 Класс

Тема: Рациональные неравенства и их системы. Линейные и квадратные неравенства (повторение)

Урок: Основные понятия, решение линейных неравенств

Рациональные неравенства – основные понятия и решения квадратных и линейных неравенств (9 класс)

 

Линейное и квадратное неравенство, повторение, урок 1, основные понятия решения линейных неравенств

 

Неравенство с одной переменной имеет вид: f(x) > 0, вместо (> 0) может быть (≥ 0), (< 0), (≤ 0).

Для определенности будем записывать неравенство в виде f(x) > 0

.

x – переменная,

f – функция, выражение, зависящее от х.

 

В зависимости от f различают разные типы неравенств. Если f – линейная функция, то это линейное неравенство. Если f – квадратичная функция, то это квадратное неравенство.

Итак, линейное неравенство имеет вид ax+b>0, предполагается, что a≠0.

Квадратное неравенство имеет вид .

Значение x_o, при котором неравенство обращается в верное числовое неравенство, является частным решением неравенства. Решить неравенство – найти все решения неравенства. Множество всех решений неравенства называется общим решением неравенства, или просто решением неравенства.

Рассмотрим пример:

1) Решить неравенство 2x – 5 > 9.

Это линейное неравенство, найдем его решение и обсудим основные понятия.

2x – 5 > 9 <=> 2x > 14 (5 перенесли в левую часть с противоположным знаком), далее разделили все на 2 и получили

x > 7. Изобразим множество решений на оси x.

Это положительно направленный луч. Записывается множество решений либо в виде неравенства x > 7, либо в виде интервала  (7; ∞). А что является частным решением этого неравенства? Например, x = 10 – это частное решение этого неравенства, x = 12 – это тоже частное решение этого неравенства.

Частных решений много, но наша цель – найти все решения. А решений, как правило, бесчисленное множество.

Рассмотрим пример 2:

2) Решить неравенство 4a – 11 > a + 13.

Решим его: а перенесем в одну сторону, 11 перенесем в другую сторону, получим 3a > 24, и в результате после деления обеих частей на 3 получим a > 8.

4a – 11 > a + 13 <=> 3a > 24 <=> a > 8.

Тоже изобразим множество

a > 8, но уже на оси а.

Ответ либо записывается в виде неравенства a > 8, либо а  (8; +∞), 8 не включается.

При решении неравенства есть важное отличие его от уравнений, которое состоит в том, что любое решение уравнения можно проверить просто подстановкой в исходное уравнение. В неравенствах такой возможности нет, здесь бесчисленное множество решений подставить в исходное неравенство не представляется возможным. Поэтому есть важное понятие, вот эти стрелочки <=> — это знак эквивалентных, или равносильных, преобразований. Преобразование называются равносильными, или эквивалентными, если они не искажают множества решений. О важности эквивалентных (равносильных) преобразований можно узнать, рассмотрев следующий пример.

3) Решить неравенство  ≤ 1.

Решение будем искать среди x ≠ 0, потому что x стоит в знаменателе. Если x ≠ 0, то обе части неравенства можно умножить на

x: , основное свойство дроби позволяет сократить в левой части , и в результате получим  ≥ 1.

Однако неравенство решено неверно. Почему? Возьмем  =-1, которое не входит в найденный промежуток, подставив его в исходное неравенство, получим -1 ≤ 1, т.е. это еще одно частное решение исходного неравенства: -1.

Что же мы сделали? Мы обе части неравенства  ≤ 1 умножили на , не зная знака этого выражения, ведь  может принимать как положительные значения, так и отрицательные.

Таким образом, мы подтвердили важность эквивалентных, равносильных преобразований. Вспомним, что это за равносильные, эквивалентные преобразования, и продемонстрируем их на конкретном примере.

Решить неравенство 2 – 2 >4.

1. Любой член неравенства можно перенести в другую сторону с противоположным знаком, равносильность, эквивалентность не нарушится.

2 – 2 > 4 <=> -2 > 4 – 2 <=> -2 > 2

Эквивалентность не нарушилась, о чем мы говорим вот таким знаком <=>.

2. Второе правило нам говорит, что обе части неравенства можно умножить или разделить на одно и то же отрицательное число, при этом знак неравенства изменится на противоположный.

3. И еще одно правило: обе части неравенства можно умножить или разделить на одно и то же положительное число, и знак неравенства не изменится.

Теперь исходное неравенство имеет вид: -2x > 2. Давайте обе части неравенства разделим на (-2):

-2 >2 <=>  <-1. Знак неравенства изменится, т.к. мы делим на (-2) и пользуемся соответствующим правилом.

Мы пользовались равносильными, эквивалентными преобразованиями и получили правильный ответ:  < -1.

Еще один пример, решить неравенство a(a – 2) – a² > 5 – 3a. Делаем стандартные преобразования: раскрываем скобки, получаем равносильное неравенство, которое потом упрощаем, т.е. приводим подобные члены – a² уничтожается, -3a

переносим, меняя знак.

a(a – 2) – a² > 5 – 3a <=> a² – 2a — a² > 5 – 3a <=> 3a – 2a > 5 <=> a > 5.

Итак, a(a – 2) – a² > 5 – 3a – исходное неравенство, a > 5 – его решение. Мы пользовались только эквивалентными, равносильными преобразованиями и получили ответ, который не надо проверять.

Следующий пример, решить неравенство 5y² – 5y(y + 4) ≥ 100.

Любые неравенства, в том числе и простейшие, которые мы сейчас рассматриваем, решаются только эквивалентными преобразованиями. Выполняем их:   скобки, приводим подобные члены:

5y² – 5y(y + 4) ≥ 100 <=> 5y² – 5y² – 20y ≥ 100 <=> -20y ≥ 100 <=> 20y ≤ -100 <=> y ≤-5.

Исходное неравенство 5y² – 5y(y + 4) ≥ 100, его ответ y ≤-5.

Таким образом, мы рассмотрели основные понятия, связные с неравенством, вспомнили, что значит «решить неравенство», что такое «общее решение неравенства», вспомнили, что неравенства можно решать только эквивалентными преобразованиями, и выяснили, что же это за эквивалентные преобразования.

Следующий пример. Решить неравенство:

 

Решаем только эквивалентными преобразованиями: перенесем все в одну сторону и приведем все к общему знаменателю, далее обе части можно умножить на знаменатель и получить только числитель. Далее нам приходится разделить на отрицательное число. Это сделать можно, если знак неравенства изменить на противоположный:

 

 

Итак, мы продемонстрировали решение некоторого количества примеров эквивалентными преобразованиями, и только ими можно решать неравенства.

Линейные неравенства – это неравенства вида ax + b > 0. Линейное неравенство тесно связано с линейной функцией. В левой части неравенства стоит линейная функция y = ax + b. Мы знаем график линейной функции, мы знаем, где она положительная, где отрицательная, и поэтому с помощью графика линейной функции мы можем решить неравенство. Например, решить неравенство: 2x + 1 > 0. Рассмотрим линейную функцию y = 2x + 1, составим таблицу:

x	0
y	1	0

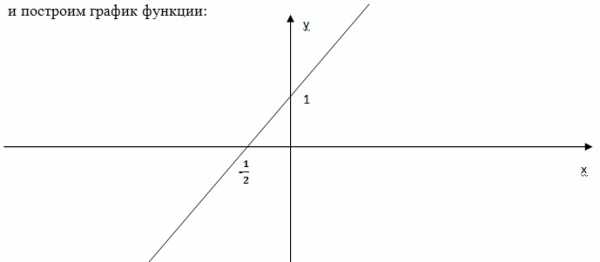
Эта функция положительна при всех значениях x больше . Ответ: x > .

Таким образом, выясняется, что линейная функция разбивает всю область определения на два больших луча. В одном луче она отрицательна, в другом луче она положительна, и, следовательно, решение неравенства очень просто.

Приведем еще один пример. Решить неравенство: -3x + 6 > 0. Снова решаем с помощью линейной функции. Рассмотрим функцию y = -3x + 6 и построим ее график с помощью таблицы:

x	0
y	6	0

 

 

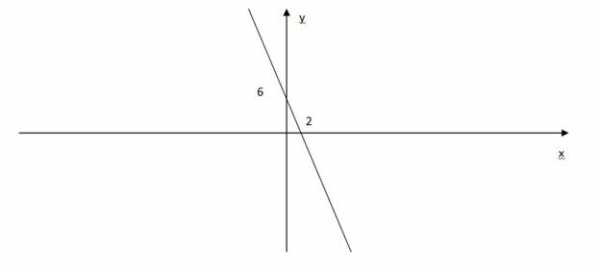
Нулем этой функции является 2. Эта функция сохраняет свой знак при (-∞; 2), и она положительна. И она также сохраняет свой знак при  (2; ∞), и при всех этих значениях функция отрицательна. Нам нужны те x, при которых функция положительна. Получим ответ x , запишем его в виде промежутка (-∞; 2).

 

Итак, мы рассмотрели основные положения, которые нужны для решения неравенств, вспомнили, что такое неравенство, что такое частное решение, что такое общее решение, что такое эквивалентные преобразования, и рассмотрели решение линейных неравенств с помощью эквивалентных преобразований или с помощью графика линейной функции.

 

Список литературы

Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И., Суворова С.Б. Алгебра. 8 класс: учебник д

interneturok.ru

Рациональные неравенства. Алгебра, 9 класс: уроки, тесты, задания.

1.	Рациональное неравенство (знаменатель — число) Сложность: лёгкое	2
2.	Числа, которые являются решением дробного неравенства Сложность: лёгкое	3
3.	Замена рационального неравенства системами неравенств Сложность: лёгкое	1
4.	Рациональное неравенство (линейное уравнение) Сложность: среднее	3
5.	Рациональное неравенство (общий знаменатель) Сложность: среднее	3
6.	Рациональное неравенство (неполный квадратный трёхчлен) Сложность: среднее	4
7.	Рациональное неравенство (три множителя) Сложность: среднее	4
8.	Дробное рациональное неравенство (знаменатель — бином) Сложность: среднее	5
9.	Дробь и единица Сложность: среднее	5
10.	Дробное рациональное неравенство (знаменатель — неполный квадратный трёхчлен) Сложность: среднее	6
11.	Дробное рациональное неравенство (разность квадратов) Сложность: сложное	8
12.	Дробное рациональное неравенство (теорема Виета) Сложность: сложное	7
13.	Значения выражения, переменная x Сложность: сложное	2

www.yaklass.ru

Обобщающий урок по теме «Решение более сложных рациональных неравенств». 9-й класс

Разделы: Математика, Конкурс «Презентация к уроку»

---

Презентация к уроку

Загрузить презентацию (951,1 кБ)

Внимание! Предварительный просмотр слайдов используется исключительно в ознакомительных целях и может не давать представления о всех возможностях презентации. Если вас заинтересовала данная работа, пожалуйста, загрузите полную версию.

---

Цели и задачи:

1. упражнять в решении более сложных квадратных неравенств методом интервалов; закреплять навыки разложения квадратного трёхчлена на множители; развивать логическое мышление;
2. формировать грамотную математическую речь и культуру записи;
3. воспитывать уважительное отношение к товарищам.

Ход урока

I. Актуализация опорных знаний учащихся.

Устно решить неравенства:

А) (х-3)(х+1)(х-8)<0; Б) В)

Учащиеся решают устно координатную прямую чертят на доске

 

II. Решение более сложных рациональных неравенств.

Решить №2.15 в) на доске и в тетрадях Нули функции: -1;; 2; 5. Ответ: (-1; )(2;5)	Учащиеся решают самостоятельно
Решить №2.16 в) в тетрадях Нули числителя: ±13; Нули знаменателя: ±10. Ответ: .	Учащиеся решают самостоятельно с комментированием на месте
Решить №2.17 в) в тетрадях начинает учитель на доске, заканчивают решение учащиеся в тетрадях. Нули функции: 0; ±1. Ответ: ∞).	Учащиеся решают самостоятельно
Решить №2.20 а) в тетрадях и на доске начинает учащийся, продолжает с помощью учителя. Разложим квадратный трёхчлен на линейные множители; D = -23 D< 0 Рассмотрим функцию f(x)= и её график. (слайд) Т.е. квадратный трёхчлен принимает только положительные значения при всех действительных значениях х, следовательно, мы можем разделить обе части неравенства на этот множитель, при этом знак неравенста сохраняется: Значит, данное неравенство равносильно неравенству: Ответ: (- ∞; 1).	Учащиеся решают самостоятельно и с помощью учителя На экране слайд: D<0, a>0 f(x)>0 при x R D<0, a<0 f(x)<0 при x R
Решить №2.28 а) в тетрадях и на доске начинает учащийся, продолжает с помощью учителя Разложим числитель и знаменатель на множители; D = -32 D< 0 Рассмотрим функцию f(x)= и её график (слайд). Т.е. квадратный трёхчлен принимает только положительные значения при всех действительных значениях х, следовательно, мы можем разделить обе части неравенства на этот множитель, при этом знак неравенста сохраняется: Значит, данное неравенство равносильно неравенству: Нули функции: Ответ: (-∞; -3) (3; +∞).	Учащиеся решают самостоятельно и с помощью учителя На экране слайд: D<0, a>0 f(x)>0 при x R D<0, a<0 f(x)<0 при x R
Решить неравенство (заранее написано на доске) в тетрадях и на доске начинает учащийся, продолжает с помощью учителя f(x)= Нули функции: 0; «0» нуль двойной кратности, значит, при переходе через точку х=0 знак функции не меняется. Ответ: (-∞; -3][3; +∞) {0}.	Учащиеся решают самостоятельно и с помощью учителя
Решить уравнение 1.15 в тетрадях и на доске начинает учащийся, продолжает с помощью учителя а) квадратное уравнение имеет два различных корня, если D. Ответ: (-∞; -6)(3; +∞).	Учащиеся решают самостоятельно и с помощью учителя

III. Домашнее задание.

№№ 2.20б, 2.28б, 1.15в.

IV. Итог урока.

1.01.2014

Поделиться страницей:

urok.1sept.ru

Урок алгебры в 9-м классе по теме «Решение квадратных неравенств»

Разделы: Математика

---

Большинство жизненных задач решаются как алгебраические уравнения: приведением их к самому простому виду.

Л. Н. Толстой.

Тип: урок изучения нового материала.

Цели урока:  1. Выработка алгоритма решения квадратных неравенств.
2. Формирование навыков решения квадратных неравенств.
3. Развитие навыков самостоятельной работы.
4. Развитие логического мышления, монологической речи.
5. Воспитание внимания, аккуратности.

Оборудование: «Алгебра 9 учебник» (авторы: Макарычев Ю.Н., Миндюк Н.Г. и др.), памятки с алгоритмом решения неравенств второй степени, компьютер, мультимедийный проектор, экран.

ХОД УРОКА

I этап. Организационный момент (1 мин.).

II этап. Объяснение нового материала (28 мин). (Приложение 1)

Учитель:  Изучение нового материала мы начнем с понятия неравенства второй степени.

Задание 1. Какие из неравенств вы бы назвали неравенствами второй степени:

1) 6х² – 13х>0;                          2) x2 – 3x – 14>0;                      3) (5 + x)(x – 4)>7;

4) ;                               5) ;                      6) ;

7) 8×2>0;                                    8) (x – 5)2 – 25>0;                     9) x(x – 9) – x2>0?

– Теперь давайте сформулируем определение неравенства второй степени:

Определение: Неравенство, левая часть которого есть многочлен второй степени, а правая  –  нуль, называется неравенством второй степени.

Все квадратные неравенства могут быть приведены к одному из следующих видов:

1) ах² + bx + c > 0; 
2) ах² + bx + c < 0;
3) ах² + bx + c > 0;
4) ах² + bx + c < 0.

Задание 2. Какие из чисел являются решениями неравенства ?

1

– 3

0

– 1

5

– 4

– 2

0,5

– К квадратным неравенствам нас приводят следующие задачи.

Задание 3. Планируется разбить прямоугольный цветник, который будет примыкать к дому. Заготовленного штакетника хватит на изгородь длиной 20м. Какими должны быть длина и ширина цветника, чтобы он имел площадь не менее: 1) 48 м²; 2) 50 м².

– Обсудим выполнение этого задания.

Если  за х м принять   длину стороны цветника, примыкающей к дому, то решение задачи сведется к решению неравенств:

1) (20 – 2х)х > 48;
2) (20 – 2х)х > 50.

Используя преобразования, эти неравенства можно привести к таким неравенствам второй степени:

1) х² – 10х + 24 < 0; 2) х² – 10х + 25 < 0.

Попробуем найти способ решения квадратных неравенств, использующий свойства квадратичной функции.

Учащиеся пытаются предложить такой способ. Если идей не возникает, то учитель предлагает выполнить еще одно задание.

Задание 3. На рис. 1 даны графики квадратичных функций. Анализируя эти графики, заполните таблицу. (Приложение 2)

Рис. 1

Учитель: Теперь нам предстоит решить неравенство – х² +  8x – 12 > 0.Какая информация о квадратичной функции может оказаться при этом полезной:

• знак коэффициента а;
• знак дискриминанта D  квадратного трехчлена;
• направление ветвей параболы;
• пересечение параболы с осями координат;
•  координаты вершины параболы;
• примерное расположение параболы?

Обязательно ли для решения неравенства строить график соответствующе квадратичной функции? Если да, то с какой точностью выполнять построение?

Далее рассматриваются различные варианты неравенств с подробным решением и записью в тетради (или справочники). (Приложение 1, слайды 7-13)

Задания:

1) – х² + 8х – 12 > 0.

Решение: Пусть у =  – х² + 8х – 12.

1. а =  – 1, а<0. Ветви параболы направлены вниз.
2. – х² + 8х – 12 = 0; D =  82 – 4(– 1)(– 12) = 16 = 42, D > 0
3. x₁ = 6; x₂ = 2.
4. Схематически строим график функции.

Ответ: х (2; 6).

2) – х² + 8х – 12 ? 0.    Ответ: [2;6].
3) – х² + 8х – 12 < 0.  Ответ: (– ; 2) (6;  + ).
4) – х² + 8х – 12 ? 0.   Ответ: (– ; 2] [6;  + ).
5) x² – 8x + 12 > 0.     Ответ: (– ; 2) (6;  + ).
6) x² – 8x + 12 ? 0.      Ответ: (– ; 2] [6;  + ).
7) х² – 4х + 4 > 0.       Ответ: (– ; 2) (2;  + ).
8) х² – 4х + 4  ? 0.       Ответ: (– ;   + ).
9) х² – 4х + 4  < 0.      Ответ: нет решений.
10) х² – 4х + 4  ? 0.      Ответ: 2
11) х² – 4х + 5> 0.        Ответ: (– ;   + ).
12)  х² – 4х + 5 < 0.      Ответ: нет решений.

Учитель: Теперь давайте попробуем сформулировать алгоритм решения неравенств второй степени, основанный на свойствах квадратичной функции.

После ответов учащихся учитель предлагает сравнить их с готовым алгоритмом, который лежит у каждого на парте (Приложение 3).

III этап. Усвоение новых знаний. (10 мин.)

На этом этапе учащимся предлагается самостоятельно решить несколько неравенств.

1.
2.
3.
4.

Проверка решения проводится по готовым ответам (слайды 14-17).

Для наиболее подготовленных учеников предлагается следующее задание:

Найти область определения функции .

IV этап. Домашнее задание (1 мин.)

§6, п. 14, № 304, 306.

Литература:

Гельфман Э.Г., Бухтяк М.С. и др. Квадратичная функция: учебное пособие по математике для 9 класса. – Томск: Издательство Томского университета, 2004.

21.06.2009

Поделиться страницей:

urok.1sept.ru

9 класс. Алгебра. Рациональные неравенства и их системы. — Как решать рациональное неравенство.

Комментарии преподавателя

 

Мы рас­смот­ре­ли метод ин­тер­ва­лов на при­ме­ре дроб­но-квад­ра­тич­но­го ра­ци­о­наль­но­го нера­вен­ства. Ре­ко­мен­ду­ет­ся са­мо­сто­я­тель­но по­стро­ить эскиз гра­фи­ка функ­ции для дан­но­го при­ме­ра.

2. Ре­шить нера­вен­ство: 

Эк­ви­ва­лент­ны­ми пре­об­ра­зо­ва­ни­я­ми при­ве­дем нера­вен­ство к нуж­но­му виду.

Мно­же­ство ре­ше­ний этого нера­вен­ства сов­па­да­ет со мно­же­ством ре­ше­ний ис­ход­но­го нера­вен­ства

Нера­вен­ство та­ко­го вида мы уже умеем ре­шать ме­то­дом ин­тер­ва­лов.

1. 

2. Об­ласть до­пу­сти­мых зна­че­ний  

3. Нули функ­ции 

4. Опре­де­ля­ем ин­тер­ва­лы зна­ко­по­сто­ян­ства.

4 – вы­ко­ло­тая точка, т.к. при  функ­ция не су­ще­ству­ет, изоб­ра­зим это на гра­фи­ке пунк­тир­ной ли­ни­ей.

5. Рас­ста­вим знаки на про­ме­жут­ках. Са­мо­сто­я­тель­но можно про­ве­рить знаки ме­то­дом проб­ной точки (Рис.2).

Те­перь можно вер­нуть­ся к нера­вен­ству и вы­брать ин­тер­ва­лы, удо­вле­тво­ря­ю­щие за­дан­ным усло­ви­ям.

Ответ: 

Мы при­ве­ли ис­ход­ное нера­вен­ство к дроб­но-ли­ней­но­му виду. Са­мо­сто­я­тель­но можно по­стро­ить эскиз гра­фи­ка функ­ции.

3. Ре­шить нера­вен­ство 

При ре­ше­нии дан­но­го нера­вен­ства может быть до­пу­ще­на гру­бая ошиб­ка. Ре­шать его ме­то­дом умно­же­ния обеих ча­стей на  ка­те­го­ри­че­ски нель­зя, будет по­те­ря­но мно­же­ство ре­ше­ний!

Можно умно­жить обе части нера­вен­ства на по­ло­жи­тель­ное число, тогда знак нера­вен­ства оста­нет­ся преж­ним. Можно умно­жить на от­ри­ца­тель­ное число, тогда знак нера­вен­ства по­ме­ня­ет­ся. Но умно­жать на 

www.kursoteka.ru

«Решение квадратных неравенств». 9-й класс

Разделы: Математика

---

Ход урока

Сегодня на уроке мы научимся решать квадратные неравенства вида ax² + bx + c > 0.

Рассмотрим первый пример: x² + 4x — 5 > 0.

1. Решаем квадратное уравнение вида: x² + 4x - 5 = 0.

Получаем: х₁ = 1;

х₂ = — 5.

2) Создаем функцию: у = x² + 4x – 5 (Слайд №2)

График функции – парабола, ветви которой направлены вверх.

3) Возвращаемся к неравенству

x² + 4x – 5 > 0 (Слайд №3) ответ: (- ; — 5) (1; + )

А теперь рассмотрим неравенство

x² + 4x – 5 >= 0 (Слайд №4) ответ: (- ; — 5] [ 1; + )

А теперь рассмотрим неравенство

x² + 4x – 5 <= 0 (Слайд №5) ответ: [ — 5; + 1]

А теперь рассмотрим неравенство

x² + 4x – 5 < 0 (Слайд №6) ответ: (- 5; + 1)

Рассмотрим второй пример: x² + 4x + 4 > 0.

1)Решаем квадратное уравнение вида: x² + 4x + 4 = 0.

Получаем: х_{1, 2} = — 2

2) Создаем функцию: у = x² + 4x + 4 (Слайд №7)

График функции – парабола, ветви которой направлены вверх.

3) Возвращаемся к неравенству

x² + 4x + 4 > 0 (Слайд №8) ответ: (- ; — 2) (- 2; + )

А теперь рассмотрим неравенство

x² + 4x + 4 >= 0 (Слайд №9) ответ: х  R

А теперь рассмотрим неравенство

x² + 4x + 4 <= 0 (Слайд №10) ответ: х = — 2

А теперь рассмотрим неравенство

x² + 4x + 4 < 0 (Слайд №11) ответ:

Рассмотрим третий пример: x² + 4x + 5 > 0.

1)Решаем квадратное уравнение вида: x² + 4x + 5 = 0.

Получаем: нет корней уравнения

2) Создаем функцию: у = x² + 4x + 5 (Слайд №12)

График функции – парабола, ветви которой направлены вверх.

3) Возвращаемся к неравенству

x² + 4x + 5 > 0 (Слайд №13) ответ: хR

А теперь рассмотрим неравенство

x² + 4x + 5 0 ответ: хR

А теперь рассмотрим неравенство

x² + 4x + 5 0 (Слайд №14) ответ:

А теперь рассмотрим неравенство

x² + 4x + 5 < 0 ответ:

Рассматривая три примера, в которых, в первом случае, дискриминант был больше нуля, во втором – равен нулю, а в третьем – меньше нуля, мы рассмотрели все возможные случаи расположения параболы, ветви которой направлены вверх.

Создадим алгоритм решения квадратных неравенств (Слайд №14):

1. Представить квадратное уравнение в виде аналогичного неравенства и решить его.

2. Создать аналогичную квадратичную функцию.

3. Нанести корни уравнения на ось абсцисс.

4. Нарисовать параболу, ветви которой направлены вверх.

5. Если неравенство имеет вид: ax² + bx + c > 0, то штрихуем ту часть оси абсцисс, где ветви параболы выше нее.

Если неравенство имеет вид: ax² + bx + c < 0, то штрихуем ту часть оси абсцисс, где ветви параболы ниже нее.

Подведем итоги урока (отвечают ученики):

— какую проблему мы сегодня решали?

— чему научились?

— что было самым трудным?

— как вы оцениваете свою работу?

Презентация

20.06.2010

Поделиться страницей:

urok.1sept.ru