Как решать примеры по информатике – 404 Not Found

Содержание

ЕГЭ по информатике задания с пояснением и пробные варианты 2019

поддержать

Решение задач

*** КАНАЛ ЮТЬЮБ ***

Выберите номер задания ЕГЭ с разбором примеров:

Структура заданий ЕГЭ по информатике

Задания ЕГЭ по информатике делятся на два типа:
Задания первого типа (таких заданий 23: с 1 по 23) предусматривают краткий ответ (например, последовательность цифр или букв).
Для решения заданий второго типа (часть 2 ЕГЭ) необходим развернутый ответ (таких заданий 4: с 24 по 27).
По уровню сложности: Базовый – 12, Повышенный – 11, Высокий – 4.
Максимальный первичный балл за работу – 35.
Общее время выполнения работы – 235 мин

Дата проведения (ГИА) ЕГЭ по информатике в 2019 году

Основной период: 13 июня (чт)
Резерв: 20 июня (чт)

Шкала перевода баллов ЕГЭ по информатике

Таблица перевода первичных баллов в отметки по пятибалльной шкале для проведения ЕГЭ в 2019 году:

Первич балл	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20
Тестов балл	7	14	20	27	34	40	42	44	46	48	50	51	53	55	57	59	61	62	64	66

Первич балл	21	22	23	24	25	26	27	28	29	30	31	32	33	34	35
Тестов балл	68	70	72	73	75	77	79	81	83	84	88	91	94	97	100

Объяснения к заданиям ЕГЭ

labs-org.ru

ОГЭ по информатике: Логические операции

Пример 1.

Для какого из приведённых чисел ложно высказывание:

НЕ(число > 50) ИЛИ (число чётное)?
1) 9 2) 56 3) 123 4) 8

Решение. Сначала выполняем сравнения в скобках, затем операция НЕ, в последнюю очередь — операция ИЛИ.

1) Подставим число 9 в выражение:
НЕ (9 > 50) ИЛИ (9 чётное)
НЕ (ложь) ИЛИ (ложь) = истина ИЛИ ложь = истина

9 нам не подходит, так как по условию мы должны получить ложь.

2) Подставим число 56 в выражение:
НЕ (56 > 50)

ИЛИ (56 чётное)
НЕ (истина) ИЛИ (истина) = ложь ИЛИ истина = истина

56 тоже не подходит.

3) Подставим 123:
НЕ (123 > 50) ИЛИ (123 чётное)
НЕ (истина) ИЛИ (ложь) = ложь ИЛИ ложь = ложь

Число 123 подошло.

Эту задачу можно было решить и по-другому:
НЕ(число > 50) ИЛИ (число чётное)

Нам надо получить ложное значение. Мы видим, что операция ИЛИ будет выполняться в последнюю очередь. Операция ИЛИ даст ложь, когда оба выражения НЕ(число) и (число чётное) будут ложны.

Так как условие (число чётное) должно быть равно ложному значению, то сразу отвергаем варианты с числами 56, 8.

Далее, условие НЕ (число > 50) = ложь, соответственно условие (число > 50) = истина. Из двух оставшихся чисел 9 и 123 этому условию подходит число

123.

Итак, можно решать прямой подстановкой, что долго и может дать ошибку при вычислении выражения; или же можно решать задачу быстро, проанализировав все простые условия.

Ответ: 3)

Пример 2

Для какого из приведённых чисел истинно высказывание:

НЕ(Первая цифра чётная) И НЕ(Последняя цифра нечётная)?

1) 6843 2) 4562 3) 3561 4) 1234

Сначала выполняем сравнения в скобках, затем операции НЕ над скобками, в последнюю очередь — операция И. Все это выражение должно принимать истинное значение.

Так как операция НЕ меняет смысл высказывания на противоположный, мы может переписать это сложное выражение так:

(Первая цифра нечётная) И (Последняя цифра чётная) = истина

Как известно, логическое умножение И дает истину только тогда, когда истинны все простые высказывания. Таким образом, оба условия должны быть истинными:

(Первая цифра нечётная) = истина (Последняя цифра чётная) = истина

Как видно, подходит только число 1234

Ответ: 4)

Пример 3

Для какого из приведённых имён истинно высказывание:
НЕ(Первая буква гласная) И (Количество букв > 5)?

1) Иван 2) Николай 3) Семён 4) Илларион

Перепишем выражение:
(Первая буква не гласная) И (Количество букв > 5) = истина
(Первая буква согласная) И (Количество букв > 5) = истина

Оба условия должны выполняться (команда И дает истину когда оба входящих простых условия истинны).

Подходит имя «Николай» (первая буква не гласная и число букв 7>5).

Ответ: 2)

Пример 4

Для какого из приведённых значений числа X истинно высказывание:
НЕ (X > 5) И (X > 4)?

1) 4 2) 5 3) 6 4) 7

Первой выполняется операция НЕ, второй — И.

Перепишем выражение: (X ≤ 5) И (X > 4) = истина

Оба условия должны быть верными. Подходит число 5

Ответ: 2)

ОГЭ по информатике

www.rassyhaev.ru

12.3. Качественные задачи по информатике

По степени трудности задачи делят на: простые, более сложные, повышенной сложности, творческие. Про стые задачи требуют для решения одну формулу и форму лирование одного двух выводов. С простых задач начина ют закрепление нового материала, поэтому их иногда на зывают тренировочными. Более сложные задачи требуют для решения использования нескольких формул, привле чения сведений из других разделов курса информатики, формулировки нескольких выводов.

Творческие задачи различаются большим разнооб разием, но среди них можно выделить исследовательские, которые требуют ответа на вопрос «почему?», и конструк торские, требующие ответа на вопрос «как сделать?».

По используемым для решения программным сред ствам можно выделить задачи, требующие применения: операционной системы, текстового редактора, графиче ского редактора, электронной таблицы, системы управле ния базами данных, других прикладных программ.

По используемым для решения аппаратным сред ствам можно выделить задачи, требующие применения различных средств вычислительной техники и внешних устройств, например, принтера, графопостроителя, скане ра, цифрового фотоаппарата, локальной сети и др.

Комбинированные задачи отличаются большим раз нообразием и предполагают: сочетание учебного мате риала различного содержания, часто из разных разделов курса, формулирования нескольких выводов, использова ния для решения нескольких формул и закономерностей.

Качественной называют такую задачу, в которой главной особенностью является акцент на качественную

305

сторону процесса или явления. Их ещё называют задачи вопросы. Решаются такие задачи путём логических умо заключений, с помощью графиков, рисунков или экспери ментально, обычно без применения математических вы числений.

Качественные задачи по информатике разнообразны по содержанию и используются учителем на большинстве уроков. Они служат средством проверки знаний и умений, способствуют их закреплению и углублению. Умело по ставленные задачи вопросы поддерживают активность учащихся на уроке, повышают интерес к информатике. Ис пользовать качественные задачи особенно необходимо при изучении тех разделов, где нет возможности решать количественные задачи, например, при изучении моде лей, истории информатики, текстового редактора и др. Ка чественные задачи позволяют учителю быстро провести проверку усвоения материала, выявить отсутствие его формального понимания.

Основной способ решения качественных задач – это аналитико синтетический, когда описываемое явление или процесс расчленяется на ряд простых, а затем путём син теза конструируется вывод следствий и получается ответ. С помощью дедукции и индукции строятся логическая це почка рассуждений, умозаключения.

Графический приём решения качественных задач часто подходит при решении задач на построение изобра жений с помощью средств графического редактора, по строения таблицы сложной формы с разновеликими боко виками и головками и др.

Экспериментальный приём решения заключается в получении ответа на основании проведённого опыта. Например:

306

•Что произойдет с выравниванием содержимого ячейки электронной таблицы, если вы введёте в

неё: последовательность чисел и букв; последо вательность букв и чисел?

•В какой из поисковых систем Google, Rambler или Яndex, на запрос по ключевым словам «Информа тика. Базовый курс» будет выдан наибольший список адресов документов?

Впоследней задаче ученикам придется потратить достаточно много времени на подключение к Интернету и проведение поиска в поисковых системах, а затем подсчё та числа выданных адресов.

Следует избегать сложных качественных задач, ре шение которых требует строить длинные цепи умозаклю чений, проследить за которыми по силу лишь немногим учащимся.

12.4. Количественные задачи по информатике

Количественные задачи обычно решаются по сле дующим темам:

•количество и единицы измерения информации; сис темы счисления;

•передача информации по линиям связи, кодирова ние информации;

•хранение информации в памяти компьютера;

•форматы машинных команд;

•представление символьной, числовой, графической и звуковой информации.

Пример решения задачи на количество информации

[6].Условие задачи: Два текста содержат одинаковое количество символов. Первый текст составлен в алфавите

307

мощностью 32 символа, второй – мощностью 64 символа. Во сколько раз отличается количество информации в этих текстах?

Решение: В равновероятном приближении информаци онный объём текста равен произведению числа симво лов на информационный вес одного символа:

I = K x i

Поскольку оба текста имеют одинаковое количество символов (K), то различие информационных объёмов определяется только разницей в информативности сим волов алфавита (i). Найдемi1 для первого алфавита иi2 для второго алфавита:

2 i1 = 32; отсюдаi1 = 5 битов; 2i2 = 64; отсюдаi2 = 6 битов;

Следовательно, информационные объёмы первого и второго текстов:

I1 = Kx 5битов; I2 = Kx 6битов

Отсюда следует, что количество информации во втором тексте больше, чем в первом в 6/5 раз или в 1,2 раза.

Ответ: во втором тексте информации больше в 1,2 раза.

Приведём пример записи условия и решения задачи, способ оформления которого близок к принятому для за дач по физике [41].

Условие задачи: Если сообщение несёт 4 бита информа ции, то во сколько раз была уменьшена неопределён ность?

Дано: Решение

308

i = 4 бита	1.	Неопределённость – это количество воз
Найти:	можных вариантов.
N = ?	2.	2i =N

N= 24 = 16 (вариантов).

3.В данном случае возможно 16 вариан тов. А произошло только одно событие.

16 / 1 = 16 (раз).

Ответ: Неопределённость в результате сообщения уменьшилась в 16 раз.

Такая форма записи условия и решения имеет пре имущество перед свободной записью, так как обладает определённым формализмом, знакома по урокам физики, дисциплинирует учащихся, выстраивает для них чёткий алгоритм решения.

В задачах на подсчёт количества информации можно выделить следующие основные этапы решения [41]:

1)Осмысление условия задачи: определение, однозначно ли сформулирована задача, понимание всех слов и фраз, например «из 256 символьного алфавита», выявление су щественных элементов задачи, определение исходных данных и искомых результатов.

2)Запись краткого условия задачи: записать условное обозначение исходных данных и искомых величин.

3)Поиск пути решения задачи: выявление теоретических положений, связанных с задачей, соотнесение задачи с известным способом решения, разделение задачи на от дельные составляющие части.

4)Осуществление плана решения и получение искомого результата: записать решение словесным способом, по лучить конечную формулу в буквенном выражении и лишь затем подставить в формулу конкретные значения, полу

309

чить правильную единицу измерения искомой величины, записать развёрнутую формулировку ответа на вопрос за дачи после слова «Ответ».

5) Изучение и интерпретация найденного решения: уча щиеся демонстрируют осмысление полученного ответа; верифицируют результат; выполняют проверку путем со ставления и решения задачи, обратной данной, находят другой способ решения.

Как можно заметить, такой порядок во многом соот ветствует тому, что принят при решении задач по физике, поэтому он знаком учащимся и это обстоятельство следует использовать учителю. Приведём образец решения задачи на расчёт объёма памяти для хранения звуковой инфор мации [22, том 1]:

Условие задачи: Определить размер (в байтах) цифрового аудиофайла, время звучания которого со ставляет 10 секунд при частоте дискретизации 22,05 кГц и разрешении 8 бит. Файл сжатию не подвержен.

Решение: Формула для расчёта размера (в бай тах) цифрового аудиофайла (монофоническое звуча ние):(частота дискретизации в Гц) х (время записи в секундах) х (разрешение в битах) / 8.

Таким образом, размер файла вычисляется так: 22050 х 10х 8 / 8 = 220500 байт.

Ответ: 220500 байт.

12.5. Задачи на моделирование явлений и про цессов

Задачи по этой теме занимают важное место в базо вом курсе, так как направлены на формирование умений и навыков владения информационно коммуникационными технологиями. Эти задачи обычно называют практически

310

ми заданиями из за их объёма и длительности решения. Часть задач на моделирование в среде текстового и графи ческого редактора относительно просты для исполнения. Задачи на моделирование в среде электронных таблиц и баз данных могут быть достаточно сложными и громозд кими, потребовать для решения несколько уроков.

Обычно в задачах моделируются физические, хими ческие и биологические явления и процессы, а также ма тематические и экономические расчёты, но есть и приме ры для моделирования литературных произведений. За дачи этого раздела представлены в учебнике Н.Д. Угрино вича по базовому курсу для 9 класса [28], в практикум задачнике под редакцией Н.В. Макаровой [34] и задачни ке практикуме под редакцией И.Г. Семакина и Е.К. Хенне ра [22]. Число имеющихся в них заданий с избытком пере крывает потребности базового курса, а учитель имеет воз можность выбора, исходя из своих предпочтений и вкуса.

Впрактикум задачнике по моделированию под ре дакцией профессора Н.В. Макаровой [34] представлены такие важные и сложные темы курса как:

•моделирование в среде графического редактора;

•моделирование в среде текстового редактора;

•моделирование в электронных таблицах;

•информационные модели в базах данных.

Вэтом практикум задачнике по каждой теме курса дано большое число заданий и приведены подробные указания по их решению, включая выделение таких этапов как: постановка задачи, разработка модели, компьютер ный эксперимент, анализ результатов моделирования. Рассмотрим кратко пример задания по моделированию движения парашютиста. Выполнение задания разбивается на четыре этапа.

311

I этап. Постановка задачи. Описание задачи.

Парашютист при падении к земле испытывает действие силы тяжести и силы сопротивления воздуха. Экспериментально установлено, что сила сопротивле ния зависит от скорости движения: чем больше ско рость, тем больше сила. При движении в воздухе эта сила пропорциональна квадрату скорости с некоторым коэффициентом сопротивления k, который зависит от конструкции парашюта и веса человекаRсопр = k V2 . Каково должно быть значение этого коэффициента, чтобы парашютист приземлился на землю со скоро стью не более 8 м/с, не представляющей опасности для здоровья?

Определите цели моделирования и проведите формализацию задачи.

II этап. Разработка модели.

На этом этапе сначала составляется информаци онная модель, а затем – математическая модель с записью уравнений движения парашютиста и выво дом формул для скорости парашютиста и пройденно го пути. После чего составляется компьютерная мо дель в среде электронной таблицы. Таблица содер жит три области: для исходных данных, для промежу точных расчётов, для результатов.

III этап. Компьютерный эксперимент.

Он включает план эксперимента и собственно проведение исследования.

IV этап. Анализ результатов моделирования.

Анализ состоит в формулировки ответов на по ставленные вопросы.

В учебнике Н.Д. Угриновича по базовому курсу моде лированию и формализации посвящена одна глава, а в

312

компьютерном практикуме моделированию процессов и явлений посвящены 3 практические работы из 23 х. Это проект «Движение Земли», биологическая модель разви тия популяций «Жертва хищник» и модель экспертной системы для лабораторной работы по химии «Распознава ние пластмасс». Причём для выполнения первой и третьей работы применяется система объектно ориентированного программирования Визуал Бейсик.

Моделирование развития биологической популяции проводится с использованием среды электронной табли цы. При этом вначале подробно описывается формальная модель процесса, вводятся коэффициенты роста числа жертв и хищников, коэффициент частоты их встреч. Затем записывается формулы для уменьшения числа жертв и увеличения числа хищников в ходе развития популяции. Потом строится компьютерная модель, которая визуали зируется путём построения графика изменения популяции на несколько лет вперёд.

В задачнике практикуме под редакцией И.Г. Семаки на и Е.К. Хеннера по данной теме в теоретическом введе нии подробно рассмотрено моделирование физических процессов на разнообразных примерах – движение с уче том сопротивления среды, свободное падение, взлёт раке ты, движение заряженных частиц, колебание маятника, теплопроводность в стержне. Моделирование биологиче ских процессов проводится на примере роста популяций, межвидовой конкуренции, системы жертва хищник. Инте рес представляет задание на моделирование случайных процессов – очереди в магазине.

Следует отметить, что подход к моделированию в этом задачнике основан на строгом и точном описании яв ления или процесса, использовании точных физических и

313

studfiles.net

Решение заданий ЕГЭ по информатике с использованим элементов алгебры логики

Разделы: Информатика

В настоящее время на вступительных экзаменах по информатике есть много заданий по теме “алгебра логики”. Цель данного урока – закрепление навыков решения заданий ЕГЭ по информатике с использованием элементов алгебры логики.

Цели урока:

Формирование умения применять полученные знания на практике;
Развитие умения построения таблиц истинности по заданным формулам;
Развитие умения решать текстовые задачи с использованием законов логики.

Задачи урока:

Воспитательная – развитие познавательного интереса, логического мышления.
Образовательная – повторение основ математической логики, выполнение практических заданий.
Развивающая – развитие логического мышления, внимательности.

Ход урока

Повторение логических операций и законов.

Применение логических операций и законов на практике.

Объяснение домашнего задания.

Сегодня мы с вами завершаем тему “Основы логики” и применим основные логические операции, законы преобразования для решения заданий ЕГЭ по информатике.

Урок идет параллельно с презентацией. <Приложение1>

1. Повторение логических операций и законов.

Алгебра логики – раздел математической логики, изучающий строение сложных логических высказываний и способы установления их истинности с помощью алгебраических методов.

Вопросы:

1. Основоположник формальной логики?

Аристотель.

2. Основоположник алгебры логики?

Джордж Буль.

3. Перечислите логические операции:

¬ отрицание (инверсия)
&, /\ конъюнкция (“И”)
V дизъюнкция (“ИЛИ”)
логическое следование (импликация)
равнозначность (эквивалентность)

4. В чем смысл закона двойного отрицания?

Двойное отрицание исключает отрицание.

5. Законы де Моргана (законы общей инверсии).

Отрицание дизъюнкции является конъюнкцией отрицаний:

¬(A V B) = ¬A /\ ¬B

Отрицание конъюнкции является дизъюнкцией отрицаний:

¬(A /\B) = ¬A V ¬B

6. Закон идемпотентности (одинаковости).

A V A = A

A /\ A = A

7. В чём смысл закона исключения третьего?

Из двух противоречащих высказываний об одном и том же одно всегда истинно, второе ложно, третьего не дано:
A V ¬А= 1

8. О чём закон противоречия?

Не могут быть одновременно истинны утверждение и его отрицание:
A /\ ¬А= 0

9. Закон исключения констант.

Для логического сложения:

A V 1 = 1 A V 0 = A

Для логического умножения:

A /\ 1 = A A /\ 0 = 0

10. Как выразить импликацию через дизъюнкцию?

А В = ¬A V В

2. Примение логических операций и законов на практике.

Пример 1. (Задание А11 демоверсии 2004 г.)

Для какого имени истинно высказывание:

¬ (Первая буква имени гласная -> Четвертая буква имени согласная)?

1) ЕЛЕНА

2) ВАДИМ

3) АНТОН

4) ФЕДОР

Решение. Сложное высказывание состоит из двух простых высказываний:

А – первая буква имени гласная,

В – четвертая буква имени согласная.

¬ (А В) = ¬ (¬A V В) = (¬ (¬А) /\ ¬B) = A /\ ¬B

Применяемые формулы:

1. Импликация через дизъюнкцию А ? В = ¬A V В

2. Закон де Моргана ¬(A V B) = ¬A /\ ¬B

3. Закон двойного отрицания.

(Первая буква имени гласная /\ Четвертая буква имени гласная)

Ответ: 3

Пример 2. (Задание А12 демоверсии 2004 г.)

Какое логическое выражение равносильно выражению ¬ (А \/ ¬B)?

1) A \/ B

2) A /\ B

3) ¬A \/ ¬B

4) ¬A /\ B

Решение. ¬ (А \/ ¬B)= ¬ А \/ ¬ (¬B)= ¬ А \/ B

Ответ: 4

Пример 3.

Составить таблицу истинности для формулы

¬ (B /\ C) V (A/\C B)

Порядок выполнения логических операций:

¬ (B /\ C) V (A/\C B)

2 1 5 3 4

Составить таблицу истинности.

Сколько строк будет в вашей таблице? 3 переменных: А, В, С; 2³=8

Сколько столбцов? 5 операций + 3 переменных = 8

Решение:

A B C (B /\ C) ¬ (B /\ C) A/\C (A/\C ? B) ¬ (B /\ C) V (A/\C B)
0 0 0 0 1 0 1 1
0 0 1 0 1 0 1 1
0 1 0 0 1 0 1 1
0 1 1 1 0 0 1 1
1 0 0 0 1 0 0 1
1 0 1 0 1 1 1 1
1 1 0 0 1 0 0 1
1 1 1 1 0 1 1 1

Какие ответы получились в последнем столбце?

Ответ: 1

Логическое выражение называется тождественно-истинным, если оно принимает значения 1 на всех наборах входящих в него простых высказываний. Тождественно-истинные формулы называют тавтологиями.

Решим этот пример аналитическим методом:

упрощаем выражение

¬ (B /\ C) V (A/\C B)= (применим формулу для импликации)

¬ (B /\ C) V ¬ (A /\ C) V B = (применим 1 и 2 законы де Моргана)

(¬B V ¬C) V (¬A V ¬C) V B = (уберём скобки)

¬B V ¬C V ¬A V ¬C V B= (применим переместительный закон)

¬B V B V ¬C V ¬C V ¬A = (закон исключения третьего, закон идемпотентности)

1 V ¬С V ¬A = 1 V ¬A = 1 (закон исключения констант)

Ответ: 1, означает, что формула является тождественно-истинной или тавтологией.

Логическое выражение называется тождественно-ложным, если оно принимает значения 0 на всех наборах входящих в него простых высказываний.

(задание 3 домашнего задания)

Пример 4.

В таблице приведены запросы к поисковому серверу. Расположите обозначения запросов в порядке возрастания количества страниц, которые найдёт поисковый сервер по каждому запросу.

Для обозначения логической операции “ИЛИ” в запросе используется символ I, а для логической операции “И” – символ &.

А Законы & Физика
Б Законы I (Физика & Биология)
В Законы & Физика & Биология & Химия
Г Законы I Физика I Биология

Решение:

Первый способ основан на рассуждении. Рассуждая логически, мы видим, что больше всего будет найдено страниц по запросу Г, так как при его исполнении будут найдены и страницы со словом “законы”, и страницы, со словом “физика”, и страницы со словом “биология”. Меньше всего будет найдено страниц по запросу В, так как в нем присутствие всех четырех слов на искомой странице. Осталось сравнить запросы А и Б. По запросу Б будут найдены все страницы, соответствующие запросу А, (так как в последних обязательно присутствует слово “законы”), а также страницы, содержащие одновременно слова “физика” и “биология”. Следовательно по запросу Б будет найдено больше страниц, чем по запросу А. Итак, упорядочив запросы по возрастанию страниц, получаем ВАБГ.

Ответ: ВАБГ.

Второй способ предполагает использование графического представления операций над множествами. (Смотри презентацию)

Пример 5. (Задание А16 демоверсии 2006 г.)

Ниже в табличной форме представлен фрагмент базы данных о результатах тестирования учащихся (используется стобалльная шкала)

Фамилия Пол Математика Русский язык Химия Информатика Биология
Аганян ж 82 56 46 32 70
Воронин м 43 62 45 74 23
Григорчук м 54 74 68 75 83
Роднина ж 71 63 56 82 79
Сергеенко ж 33 25 74 38 46
Черепанова ж 18 92 83 28 61

Сколько записей в данном фрагменте удовлетворяют условию

“Пол=’м’ ИЛИ Химия>Биология”?

1) 5

2) 2

3) 3

4) 4

Решение:

Выбираем записи: Мальчики (двое) и Химия>Биология (трое, но один мальчик, уже взялся 1 раз). В итоге 4 записи удовлетворяют условию.

Ответ: 4

Задание 6. (Задание В4 демоверсии 2007 г)

В школьном первенстве по настольному теннису в четверку лучших вошли девушки: Наташа, Маша, Люда и Рита. Самые горячие болельщики высказали свои предположения о распределении мест в дальнейших состязаниях.

Один считает, что первой будет Наташа, а Маша будет второй.

Другой болельщик на второе место прочит Люду, а Рита, по его мнению, займет четвертое место.

Третий любитель тенниса с ними не согласился. Он считает, что Рита займет третье место, а Наташа будет второй.

Когда соревнования закончились, оказалось, что каждый из болельщиков был прав только в одном из своих прогнозов.

Какое место на чемпионате заняли Наташа, Маша, Люда, Рита?

(В ответе перечислите подряд без пробелов числа, соответствующие местам девочек в указанном порядке имен.)

Решение:

Обозначим высказывания:

Н1 = “первой будет Наташа”;

М2 = “второй будет Маша”;

Л2 = “второй будет Люда”;

Р4 = “четвертой будет Рита”;

Р3 = “третьей будет Рита”;

Н2 = “второй будет Наташа”.

Согласно условию:

из высказываний 1 болельщика следует, что Н1VМ2 истинно;

из высказываний2 болельщика следует, что Л2VР4 истинно;

из высказываний 3 болельщика следует, что Р3VН2 истинно.

Следовательно, истинна и конъюнкция

(Н1VМ2) /\ (Л2VР4) /\ (Р3VН2) = 1.

Раскрыв скобки получим:

(Н1VМ2) /\ (Л2VР4) /\ (Р3VН2) = (Н1/\Л2V Н1/\Р4 V М2/\Л2 V М2/\Р4) /\ (Р3VН2)=

Н1/\ Л2/\Р3 V Н1/\Р4/\Р3 V М2/\Л2/\Р3 V М2/\Р4/\Р3 V Н1/\Л2/\Н2 V Н1/\Р4/\Н2 V М2/\Л2/\Н2 V М2/\Р4/\Н2 = Н1/\ Л2/\Р3 V 0 V 0 V 0 V 0 V 0 V 0 V= Н1/\ Л2/\Р3

Наташа-1, Люда-2, Рита-3, а Маша-4.

Ответ: 1423

3. Объяснение домашнего задания.

Задание 1. (Задание В8 демоверсии 2007г)

В таблице приведены запросы к поисковому серверу. Расположите обозначения запросов в порядке возрастания количества страниц, которые найдет поисковый сервер по каждому запросу.

Для обозначения логической операции “ИЛИ” в запросе используется символ |, а для логической операции “И” – &.

А волейбол | баскетбол | подача
Б волейбол | баскетбол | подача | блок
В волейбол | баскетбол
Г волейбол & баскетбол & подача

Задание 2 (Задание В4 демоверсии 2008г)

Перед началом Турнира Четырех болельщики высказали следующие предположения по поводу своих кумиров:

A) Макс победит, Билл – второй;

B) Билл – третий. Ник – первый;

C) Макс – последний, а первый – Джон.

Когда соревнования закончились, оказалось, что каждый из болельщиков был прав только в одном из своих прогнозов.

Какое место на турнире заняли Джон, Ник, Билл, Макс?

(В ответе перечислите подряд без пробелов места участников в указанном порядке имен.)

Оценки за урок.
26.02.2008
xn--i1abbnckbmcl9fb.xn--p1ai
Информатика ЕГЭ 5 задание разбор и объяснение
Урок посвящен тому, как решать 5 задание ЕГЭ по информатике

Кодирование информации
5-я тема характеризуется, как задания базового уровня сложности, время выполнения – примерно 2 минуты, максимальный балл — 1
Кодирование — это представление информации в форме, удобной для её хранения, передачи и обработки. Правило преобразования информации к такому представлению называется кодом.
Кодирование бывает равномерным и неравномерным:
при равномерном кодировании всем символам соответствуют коды одинаковой длины;
при неравномерном кодировании разным символам соответствуют коды разной длины, это затрудняет декодирование.
Пример: Зашифруем буквы А, Б, В, Г при помощи двоичного кодирования равномерным кодом и посчитаем количество возможных сообщений:
Таким образом, мы получили равномерный код, т.к. длина каждого кодового слова одинакова для всех кодов (2).
Кодирование и расшифровка сообщений
Декодирование (расшифровка) — это восстановление сообщения из последовательности кодов.
Для решения задач с декодированием, необходимо знать условие Фано:
Условие Фано: ни одно кодовое слово не должно являться началом другого кодового слова (что обеспечивает однозначное декодирование сообщений с начала)
Префиксный код — это код, в котором ни одно кодовое слово не совпадает с началом другого кодового слова. Сообщения при использовании такого кода декодируются однозначно.
если сообщение декодируется с конца, то его можно однозначно декодировать, если выполняется обратное условие Фано:
Обратное условие Фано: никакое кодовое слово не является окончанием другого кодового слова
Постфиксный код — это код, в котором ни одно кодовое слово не совпадает с концом другого кодового слова. Сообщения при использовании такого кода декодируются однозначно и только с конца.

условие Фано – это достаточное, но не необходимое условие однозначного декодирования.
Однозначное декодирование обеспечивается:

Однозначное декодирование

Декодирование
Егифка ©:
Решение 5 заданий ЕГЭ
ЕГЭ 5.1: Для кодирования букв О, В, Д, П, А решили использовать двоичное представление чисел 0, 1, 2, 3 и 4 соответственно (с сохранением одного незначащего нуля в случае одноразрядного представления).
Закодируйте последовательность букв ВОДОПАД таким способом и результат запишите восьмеричным кодом.

✍ Решение:
Переведем числа в двоичные коды и поставим их в соответствие нашим буквам:
О -> 0 -> 00 В -> 1 -> 01 Д -> 2 -> 10 П -> 3 -> 11 А -> 4 -> 100
Теперь закодируем последовательность букв из слова ВОДОПАД:
010010001110010
Разобьем результат на группы из трех символов справа налево, чтобы перевести их в восьмеричную систему счисления:
010 010 001 110 010 ↓ ↓ ↓ ↓ ↓ 2 2 1 6 2
Результат: 22162
Решение ЕГЭ данного задания по информатике, видео:
Рассмотрим еще разбор 5 задания ЕГЭ:

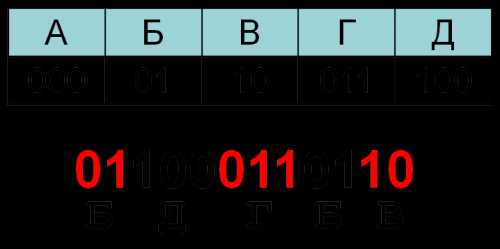
ЕГЭ 5.2: Для 5 букв латинского алфавита заданы их двоичные коды (для некоторых букв — из двух бит, для некоторых — из трех). Эти коды представлены в таблице:
a b c d e
000 110 01 001 10
Какой набор букв закодирован двоичной строкой 1100000100110?

✍ Решение:
110 000 01 001 10 ↓ ↓ ↓ ↓ ↓ b a c d e
Результат: b a c d e.
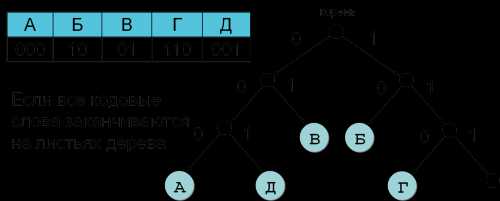
✎ 2 вариант решения:
Этот вариант решения 5 задания ЕГЭ более сложен, но тоже верен.
Сделаем дерево, согласно кодам в таблице:
Сопоставим закодированное сообщение с кодами в дереве:
110 000 01 001 10
Результат: b a c d e.
Кроме того, вы можете посмотреть видео решения этого задания ЕГЭ по информатике:
Решим следующее 5 задание:

ЕГЭ 5.3:
Для передачи чисел по каналу с помехами используется код проверки четности. Каждая его цифра записывается в двоичном представлении, с добавлением ведущих нулей до длины 4, и к получившейся последовательности дописывается сумма её элементов по модулю 2 (например, если передаём 23, то получим последовательность 0010100110).
Определите, какое число передавалось по каналу в виде 01100010100100100110.

✍ Решение:
Рассмотрим пример из условия задачи:
Было 23₁₀ Стало 0010100110₂
Где сами цифры исходного числа (выделим их красным цветом):
0010100110 (0010 - 2, 0011 - 3)
Первая добавленная цифра 1 после двоичной двойки — это проверка четности (1 единица в 0010 — значит нечетное), 0 после двоичной тройки — это также проверка нечетности (2 единицы в 0011, значит — четное).
Исходя из разбора примера решаем нашу задачу так: поскольку «нужные» нам цифры образуются из групп по 4 числа в каждой плюс одно число на проверку четности, то разобьем закодированное сообщение на группы по 5, и отбросим из каждой группы последний символ:
разбиваем по 5:
01100 01010 01001 00110
отбрасываем из каждой группы последний символ:
0110 0101 0100 0011
Результат переводим в десятичную систему:
0110 0101 0100 0011 ↓ ↓ ↓ ↓ 6 5 4 3
Ответ: 6 5 4 3
Вы можете посмотреть видео решения этого задания ЕГЭ по информатике:

ЕГЭ 5.4:
Для кодирования некоторой последовательности, состоящей из букв К, Л, М, Н решили использовать неравномерный двоичный код, удовлетворяющий условию Фано. Для буквы Н использовали кодовое слово 0, для буквы К — кодовое слово 10.
Какова наименьшая возможная суммарная длина всех четырёх кодовых слов?

✍ Решение: ✎ 1 вариант решения основан на логических умозаключениях:
Найдём самые короткие возможные кодовые слова для всех букв.
Кодовые слова 01 и 00 использовать нельзя, так как тогда нарушается условие Фано (начинаются с 0, а 0 — это Н).
Начнем с двухразрядных кодовых слов. Возьмем для буквы Л кодовое слово 11. Тогда для четвёртой буквы нельзя подобрать кодовое слово, не нарушая условие Фано (если потом взять 110 или 111, то они начинаются с 11).
Значит, надо использовать трёхзначные кодовые слова. Закодируем буквы Л и М кодовыми словами 110 и 111. Условие Фано соблюдается.
Суммарная длина всех четырёх кодовых слов равна:
(Н)1 + (К)2 + (Л)3 + (М)3 = 9
✎ 2 вариант решения:
Будем использовать дерево. Влево откладываем 0, вправо — 1:
Теперь выпишем соответствие каждой буквы ее кодового слова согласно дереву:
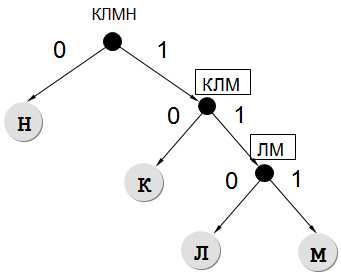
(Н) -> 0 -> 1 символ (К) -> 10 -> 2 символа (Л) -> 110 -> 3 символа (М) -> 111 -> 3 символа
Суммарная длина всех четырёх кодовых слов равна:
(Н)1 + (К)2 + (Л)3 + (М)3 = 9
Ответ: 9
ЕГЭ по информатике 5 задание 2017 ФИПИ вариант 2 (под редакцией Крылова С.С., Чуркиной Т.Е.):
По каналу связи передаются сообщения, содержащие только 4 буквы: А, Б, В, Г; для передачи используется двоичный код, допускающий однозначное декодирование. Для букв А, Б, В используются такие кодовые слова: А: 101010, Б: 011011, В: 01000.
Укажите кратчайшее кодовое слово для буквы Г, при котором код будет допускать однозначное декодирование. Если таких кодов несколько, укажите код с наименьшим числовым значением.

✍ Решение:
Наименьшие коды могли бы выглядеть, как 0 и 1 (одноразрядные). Но это не удовлетворяло бы условию Фано (А начинается с единицы — 101010, Б начинается с нуля — 011011).
Следующим наименьшим кодом было бы двухбуквенное слово 00. Так как оно не является префиксом ни одного из представленных кодовых слов, то Г = 00.
Результат: 00
ЕГЭ по информатике 5 задание 2017 ФИПИ вариант 16 (под редакцией Крылова С.С., Чуркиной Т.Е.):
Для кодирования некоторой последовательности, состоящей из букв А, Б, В, Г и Д, решили использовать неравномерный двоичный код, позволяющий однозначно декодировать двоичную последовательность, появляющуюся на приемной стороне канала связи. Использовали код: А — 01, Б — 00, В — 11, Г — 100.
Укажите, каким кодовым словом должна быть закодирована буква Д. Длина этого кодового слова должна быть наименьшей из всех возможных. Код должен удовлетворять свойству однозначного декодирования. Если таких кодов несколько, укажите код с наименьшим числовым значением.

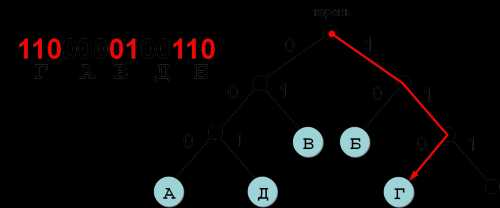
✍ Решение:
Так как необходимо найти кодовое слово наименьшей длины, воспользуемся деревом. Влево будем откладывать нули, а вправо — единицы:
Поскольку у нас все ветви завершены листьями, т.е. буквами, кроме одной ветви, то остается единственный вариант, куда можно поставить букву Д:
Перепишем сверху вниз получившееся кодовое слово для Д: 101
Результат: 101
Подробней разбор урока можно посмотреть на видео ЕГЭ по информатике 2017:
ЕГЭ по информатике 5 задание 2017 ФИПИ вариант 17 (Крылов С.С., Чуркина Т.Е.):
Для кодирования некоторой последовательности, состоящей из букв А, Б, В, Г, Д и Е, решили использовать неравномерный двоичный код, позволяющий однозначно декодировать двоичную последовательность, появляющуюся на приемной стороне канала связи. Использовали код: А — 0, Б — 111, В — 11001, Г — 11000, Д — 10.
Укажите, каким кодовым словом должна быть закодирована буква Е. Длина этого кодового слова должна быть наименьшей из всех возможных. Код должен удовлетворять свойству однозначного декодирования. Если таких кодов несколько, укажите код с наименьшим числовым значением.

✍ Решение:
Для того, чтобы выполнялось условие Фано, необходимо, чтобы код буквы Е не совпадал с началом кода любого кодового слова.
Поскольку кодовые слова достаточно длинные, то использовать для решения дерево не совсем удобно. Воспользуемся таблицей:
Теперь, начиная с однобитных кодов, и, двигаясь сверху вниз, подбираем такой код, который бы удовлетворял условию Фано. С 0 можно не начинать, так как уже есть код 0 для буквы А:
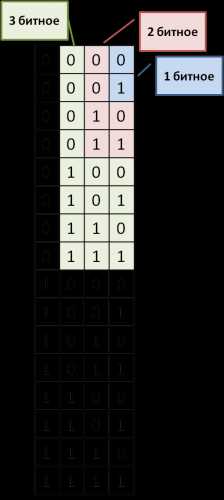
1 - не подходит (все буквы кроме А начинаются с 1) 10 - не подходит (соответствует коду Д) 11 - не подходит (начало кодов Б, В и Г) 100 - не подходит (код Д - 10 - является началом данного кода) 101 - не подходит (код Д - 10 - является началом данного кода) 110 - не подходит (начало кода В и Г) 111 - не подходит (соответствует коду Б) 1000 - не подходит (код Д - 10 - является началом данного кода) 1001 - не подходит (код Д - 10 - является началом данного кода) 1010 - не подходит (код Д - 10 - является началом данного кода) 1011 - не подходит (код Д - 10 - является началом данного кода) 1100 - не подходит (начало кода В и Г) 1101 - подходит
Результат: 1101
Более подробное решение данного задания представлено в видеоуроке:
5 задание. Демоверсия ЕГЭ 2018 информатика (ФИПИ):
По каналу связи передаются шифрованные сообщения, содержащие только десять букв: А, Б, Е, И, К, Л, Р, С, Т, У. Для передачи используется неравномерный двоичный код. Для девяти букв используются кодовые слова.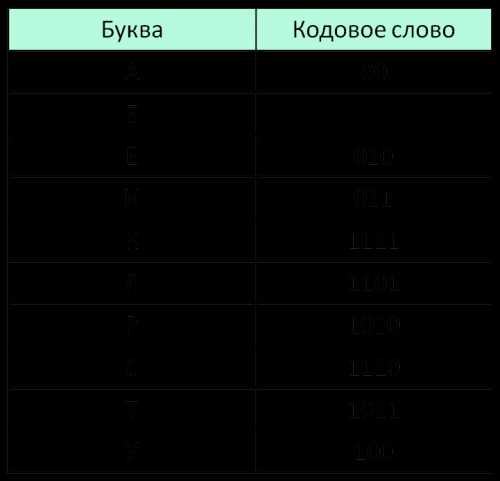
Укажите кратчайшее кодовое слово для буквы Б, при котором код будет удовлетворять условию Фано. Если таких кодов несколько, укажите код с наименьшим числовым значением.
Похожие задания для тренировки

✍ Решение:
Для решения будем использовать дерево. Ветви, соответствующие нулю, будем откладывать влево, единице — вправо.
При рассмотрении дерева видим, что все ветви «закрыты» листьями, кроме одной ветви — 1100:
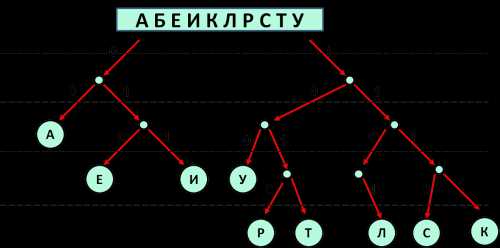
Результат: 1100
Подробное решение данного 5 задания из демоверсии ЕГЭ 2018 года смотрите на видео:
Задание 5_9. Типовые экзаменационные варианты 2017. Вариант 4 (Крылов С.С., Чуркина Т.Е.):
По каналу связи передаются шифрованные сообщения, содержащие только четыре букв: А, Б, В, Г; для передачи используется двоичный код, допускающий однозначное декодирование. Для букв А, Б, В используются кодовые слова:
А: 00011 Б: 111 В: 1010
Укажите кратчайшее кодовое слово для буквы Г, при котором код будет допускать однозначное декодирование. Если таких кодов несколько, укажите код с наименьшим числовым значением.

✍ Решение:
Для решения будем использовать дерево. Ветви, соответствующие нулю, будем откладывать влево, единице — вправо.
Поскольку в задании явно не указано о том, что код должен удовлетворять условию Фано, то дерево нужно построить как с начала (по условию Фано), так и с конца (обратное условие Фано).
Дерево по условию Фано (однозначно декодируется с начала):
Получившееся числовое значение кодового слова для буквы Г — 01.
Дерево по обратному условию Фано (однозначно декодируется с конца):
Получившееся числовое значение кодового слова для буквы Г — 00.
После сравнения двух кодовых слов (01 и 00), код с наименьшим числовым значением — это 00.
Результат: 00
Задание 5_10. Тренировочный вариант №3 от 01.10.2018 (ФИПИ):
По каналу связи передаются сообщения, содержащие только буквы: А, Е, Д, К, М, Р; для передачи используется двоичный код, удовлетворяющий условию Фано. Известно, что используются следующие коды:
Е – 000 Д – 10 К – 111
Укажите наименьшую возможную длину закодированного сообщения ДЕДМАКАР.
В ответе напишите число – количество бит.

✍ Решение:
С помощью дерева отобразим известные коды для букв:
В результирующем слове — ДЕДМАКАР — вде буквы А. Значит, для получения наименьшей длины необходимо для буквы А выбрать наименьший код в дереве. Учтем это и достроим дерево для остальных трех букв А, М и Р:
Расположим буквы в порядке их следования в слове и подставим их кодовые слова:
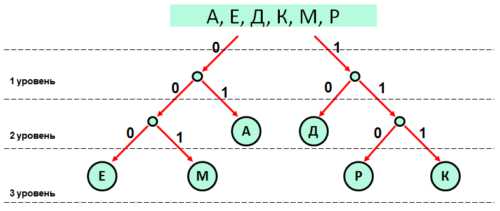
Д Е Д М А К А Р 10 000 10 001 01 111 01 110
Посчитаем количество цифр в итоговом коде и получим 20.
Результат: 20
Смотрите виде решения задания:
labs-org.ru
Решение задач и примеров по информатике

Вы решаете задачи по информатике онлайн?
Тогда добавьте объявление, чтобы найти заказы для решения задач по информатике и заработать на этом.
Добавить решателя
Вам нужна помощь в решении задач по информатике?
Тогда оставьте заявку для поиска решателя и ждите, когда решатель свяжется с вами, чтобы предложить свои услуги.
Найти решателя
Услуги решателя по информатике
Информатика — это одна из самых молодых и наиболее востребованных в современном обществе наук. Огромное количество компьютерных систем на производстве, в офисах и квартирах требует от юношей и девушек соответствующей подготовки. Пользователи должны не просто знать, когда какую кнопку нажать, а понимать то, что они делают. Кроме того, успешное освоение дисциплины открывает дорогу к получению престижной и высокооплачиваемой профессии программиста.
Однако, на пути к вершинам всегда возникают непредвиденные трудности. Одна из них заключается в том, что процесс решения задач для многих школьников становится непреодолимым препятствием по причине отсутствия должных навыков по практическому применению полученных знаний. Веб-сервис «КтоРешит?» предлагает один из лучших вариантов устранения проблемы. Любой школьник получает возможность заказать решение задачи по информатике профильному специалисту, не сомневаясь в том, что получит пошагово выполненное задание со всеми необходимыми пояснениями.
В организационном плане сделать это можно двумя способами. Если надо побыстрее, то лучше всего — ознакомиться с объявлениями решателей, которые опубликованы на нашем сайте. Затем следует выбрать из них то, которое больше всего подходит. После чего останется только связаться со специалистом, изложить условие задачи и оговорить технические детали.
Если задание не слишком срочное, то ученик может опубликовать на страницах веб-ресурса заявку на выполнение услуг. В ней надо кратко описать условие задачи и дать свой контактный номер телефона. У этого варианта тоже есть преимущество. В данном случае со школьником будут связываться только те учителя, которые уже определили, что данный заказ им, безусловно, подходит.
Преподаватели средних и высших учебных заведений также могут воспользоваться услугами сайта «КтоРешит?». С нашей помощью появляется возможность более полно, притом, за дополнительную плату, реализовать свои умственные способности и высокий уровень профессиональной подготовки. В этом нет никакого противоречия с общественной моралью, поскольку в рыночном обществе любой труд должен быть достойно оплачен.
Чтобы мы могли найти дополнительных клиентов для любого преподавателя, который желает принимать заказы на решение задач, достаточно подать объявление. В нем желательно указать следующую информацию: фамилия, имя, отчество, образование, педагогический стаж и расценки за решение одной задачи. В заключение необходимо указать контактные данные. Это может быть не только телефон, но также электронная почта, скайп и т.д. При наличии опыта работы по решению задач на заказ, об этом можно сообщить отдельной строкой.

ktoreshit.ru
Задания ЕГЭ по информатике / Habr
В России все больше внедряется практика оценивания выпускников школ методом сдачи единого государственного экзамена (ЕГЭ).
Уже несколько лет в экспериментах по всей стране сдавали ЕГЭ по самым разным предметам. В этом году впервые массово будет сдаваться ЕГЭ по информатике.
Что же внутри?

ЕГЭ сдается 4 часа, содержит довольно много вопросов (в данной версии 32) и требует приличного уровня знаний для сдачи его на высокую оценку.
Перед рассказом собственно о заданиях хочу поделиться двумя соображениями.
1. У ЕГЭ есть недостатки, однако главный положительный момент в том, что вводится почти объективная оценка реальных знаний ученика. Раньше в пределах школы учитель/директор имел возможность нарисовать любые оценки почти без ответственности за реальный уровень знаний. Случаи непоступления в ВУЗы были редки (ну в крайнем случае – другой ВУЗ/факультет) и мало кого волновали. Теперь же для учителя страшно поставить 5 и столкнуться с ЕГЭ, сданным на 3. Это резко изменило саму атмосферу подготовки.
Впрочем, есть и недостатки. Пример: по утверждениям многих экспертов, в школах почти перестали преподавать геометрию, т.к. в ЕГЭ она представлена только тремя заданиями.
2. Основная цель ЕГЭ – проранжировать учеников по уровню знаний. Дополнительная – поставить оценку по школьной 4-хбалльной системе.
Для ранжирования большого числа учеников НЕ ВАЖНО, какого уровня в среднем будет экзамен. Надо лишь, чтобы самые слабые решили хоть что-то, а самые сильные решили почти все. Допустим, экзамен слишком сложен, и подавляющее большинство решат лишь половину заданий. Что ж, лучшие 20% из них смогут попасть в ВУЗ на соответствующий факультет.
ЕГЭ не столько оценивает (абсолютная оценка), сколько ранжирует (относительная оценка).
Задания
Далее приведены с моими комментариями некоторые примерные задания, предлагаемые Федеральным институтом педагогических измерений (ФИПИ).
Ссылка на полный вариант заданий 2009 года: fipi.ru/binaries/731/infZIP%20-%20WinRAR.zip и 2008 года: fipi.ru/binaries/518/inform.rar (там mime-type неправильно указан, сохраните как rar и откройте).
На мой взгляд, задания сложные (напомню, в среднем выделяется по 7,5 минут на задание). Предлагаю оценить и вам.
I. В велокроссе участвуют 119 спортсменов. Специальное устройство регистрирует прохождение каждым из участников промежуточного финиша, записывая его номер с использованием минимально возможного количества бит, одинакового для каждого спортсмена. Каков информационный объем сообщения, записанного устройством, после того как промежуточный финиш прошли 70 велосипедистов?
1) 70 бит 2) 70 байт 3) 490 бит 4) 119 байт
Требует понимания информационной емкости последовательности нескольких бит, умения оперировать степенями двойки, просто понимания сути термина «информация» и принципов его измерения.
Средний школьник, как мне кажется, его решит, только если занимался информатикой сверх школьного минимума.
II. Световое табло состоит из лампочек. Каждая лампочка может находиться в одном из трех состояний («включено», «выключено» или «мигает». Какое наименьшее количество лампочек должно находиться на табло, чтобы с его помощью можно было передать 18 различных сигналов?

Требует понимания существования систем счисления с любыми основаниями и принципов кодирования такими сигналами. В данном случае — троичной системы.
Средний школьник, как мне кажется, его не решит. Можно решать и перебором все вариантов и их подсчетом, но это долго и велик риск ошибиться.
III. Каково наибольшее целое число X, при котором истинно высказывание
(50<X•X) → (50>(X+1) •(X+1))?

Требует знания логических операций (функции алгебры логики) и неплохих аналитических способностей (проверьте, сколько времени вы будете его решать сами и дайте любому школьнику или студенту младших курсов).
IV. Укажите через запятую в порядке возрастания все основания систем счисления, в которых запись числа 23 оканчивается на 2.

Задание на первый взгляд не особо сложное, но решать его приходится или перебором (то есть сделать множество переводов в системы счисления типа семеричной или одиннадцатеричной, что крайне утомительно), или выработать систему и понять, что
23 mod X = 2, где mod – остаток от деления, а Х – ответ.
Догадались из моих знакомых ИТ-шников далеко не все.
V. Классный руководитель пожаловался директору, что у него в классе появилась компания из 3-х учеников, один из которых всегда говорит правду, другой всегда лжет, а третий говорит через раз то ложь, то правду. Директор знает, что их зовут Коля, Саша и Миша, но не знает, кто из них правдив, а кто – нет. Однажды все трое прогуляли урок астрономии. Директор знает, что никогда раньше никто из них не прогуливал астрономию. Он вызвал всех троих в кабинет и поговорил с мальчиками. Коля сказал: «Я всегда прогуливаю астрономию. Не верьте тому, что скажет Саша». Саша сказал: «Это был мой первый прогул этого предмета». Миша сказал: «Все, что говорит Коля, – правда». Директор понял, кто из них кто. Расположите первые буквы имен мальчиков в порядке: «говорит всегда правду», «всегда лжет», «говорит правду через раз». (Пример: если бы имена мальчиков были Рома, Толя и Вася, ответ мог бы быть: РТВ)

Напоминает задачи на смекалку, не правда ли?
Можно решать с помощью логического аппарата, который школьникам заведомо неизвестен (например, исчисления высказываний/предикатов) или логикой.
Мне, честно говоря, непонятно, какое отношение это задание имеет к информатике.
VI. Два игрока играют в следующую игру. На координатной плоскости стоит фишка. Игроки ходят по очереди. В начале игры фишка находится в точке с координатами (5,2). Ход состоит в том, что игрок перемещает фишку из точки с координатами (x,y) в одну из трех точек: или в точку с координатами (x+3,y), или в точку с координатами (x,y+3), или в точку с координатами (x,y+4). Выигрывает игрок, после хода которого расстояние по прямой от фишки до точки с координатами (0,0) не меньше 13 единиц. Кто выигрывает при безошибочной игре обоих игроков – игрок, делающий первый ход, или игрок, делающий второй ход? Каким должен быть первый ход выигрывающего игрока? Ответ обоснуйте.

Задание интересное. Предлагаю вам его решить. В решениях авторов его предлагается решать перебором всех возможных ходов каждого игрока.
Опять же вопрос, какое отношение это непростое задание имеет к информатике? Проверяем логическое мышление?
VII.
Парадокс, но многие не понимают, что именно делает программа и считают все квадраты 2х2, не содержащие линий.
VIII.

Задание требует внимательности и опыта. Например, далеко не все видят, что тут 2 ошибки, обе из которых надо исправить.
Эти примерные задания обнародованы и активно изучаются всеми, кому предстоит сдавать ЕГЭ.
Многие учителя информатики в шоке от заданий. Напомню, что сейчас во многих школах изучают Word, Paint, набирают тексты или слушают рассказы про машину Чарльза Беббиджа и первую программистку-дочь Байрона. Все это хорошо и полезно, но никак не поможет сдаче этого экзамена.
Многие школьники, кому сдавать этот ЕГЭ, бросились искать репетитора.
Но на мой взгляд, средней сообразительности школьнику, учившему информатику просто как школьный предмет (я так учил географию, что даже примерно не представлял себе карту Европы к 11 классу – так учили), практически нереально подготовиться за жаркие 3 месяца к сдаче этого экзамена на приличную оценку.
Ваше мнение, ИТ-шники? Сколько заданий вы бы решили из расчета 7,5 минут в среднем на каждое?
habr.com
No related posts.