Как решать тригонометрические уравнения сложные – . .

Проект «Методы решения тригонометрических уравнений!

Областное государственное автономное

образовательное учреждение

дополнительного профессионального образования

 «Белгородский институт развития образования»

 

 

 

 

 

 

 

 

 

 

 

 

Методы решения тригонометрических уравнений

(проектное задание)

 

 

 

 

 

 

 

Выполнила:

Остапенко Татьяна Ивановна,

учитель математики и физики

МБОУ «Бехтеевская СОШ

Корочанского района

Белгородскойобласти

Руководитель курса:

Вертелецкая О.В.,

старший преподаватель

кафедры естественно-

математического образования

 

 

 

 

 

 

Белгород

 

СОДЕРЖАНИЕ

                                                                                                 стр.

Введение…………………………………………………………………….3

Теоретическая часть……………………………………………………….4-6

Практическая часть………………………………………………………7-18

Заключение………………………………………………………………19-20

Библиография……………………………………………………………….21

Приложение

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Введение

Тригонометрические уравнения возникают при решении задач по планиметрии, стереометрии, астрономии, физики и в других областях. Еще древнегреческие математики, используя элементы тригонометрии для решения прямоугольных треугольников, фактически составляли и решали простейшие тригонометрические уравнения. Исторически учение о решении тригонометрических уравнений формировалось с развитием теории тригонометрических функций, а также черпало из алгебры общие методы их решения.

Цель работы: изучить методы решения тригонометрических уравнений, исследовать применение их к решению уравнений повышенной сложности и задач различного содержания.

Теоретическая часть

Уравнение, содержащее неизвестную величину под знаком триго­нометрической функции, называется тригонометрическим.

Часть тригонометрических уравнений непосредственно решается сведением их к простейшему виду, иногда – с предварительным разложением левой части уравнения на множители, когда правая часть равна нулю. В некоторых случаях удается произвести замену неизвестных таким образом, что тригонометрическое уравнение преобразуется в «удобное» для решения алгебраическое уравнение.                                                                                                                

Простейшие тригонометрические уравнения — это уравнения вида

sin x = a,       cos x= a,        tq x = a,        ctq x = a

Каждое из таких уравнений решается по формулам, которые следует знать.

sinx = a,   x = (-1)karcsin a + πk,  kЄZ,

arcsin a — угол, содержащийся в промежутке от — π/2 до π/2, синус которого равен a.

cosx= a,  x=arccos a +2πk,  kЄZ,

arccos a — угол, содержащийся в промежутке от 0 до π, косинус которого равен a.

tq x = a, x = arctq a + πk,  kЄZ,

arctg a — угол, содержащийся в промежутке от — π/2 до π/2, тангенс которого равен a.

ctq x = a, x = arcctq a + πk,  kЄZ,

arcctg a — угол, содержащийся в промежутке от 0 до π, котангенс которого равен a.

Поскольку каждому значению тригонометрической функции соответствует неограниченное множество углов, то тригонометрическое уравнение, если не сделано каких-либо оговорок, имеет бесчисленное множество решений.

Особо используются частные случаи элементарных тригонометрических уравнений, когда тригонометрические функции равны -1, 0, 1, в которых решение записывается без применения общих формул.

Частные случаи

 

 

 

При решении тригонометрических уравнений важную роль играет период тригонометрических функций.

Рекомендации по решению тригонометрических уравнений

1.              Если аргументы функций одинаковые, попробовать получить одинаковые функции, использовав формулы без изменения аргументов.

2.              Если аргументы функций отличаются в два раза, попробовать получить одинаковые аргументы, использовав формулы двойного аргумента.

3.              Если аргументы функций отличаются в четыре раза, попробовать их привести к промежуточному двойному аргументу.

4.              Если есть функции одного аргумента, степени свыше первой, попробовать понизить степень, используя формулы понижения степени или формулы сокращенного умножения.

5.              Если есть сумма одноименных функций первой степени с разными аргументами (вне случаев 2,3), попробовать преобразовать сумму в произведение для появления общего множителя.

6.              Если есть сумма разноимённых функций первой степени с разными аргументами (вне случаев 2, 3), попробовать использовать формулы приведения, получить затем случай 5.

7.              Если в уравнении есть произведение косинусов (синусов) различных аргументов, попробовать свести его к формуле синус двойного аргумента, умножив и разделив это выражение на синус (косинус) подходящего аргумента:

8.              Если в уравнении есть числовое слагаемое (множитель), то его можно представить в виде значений функции угла. Например:

 

 

Практическая часть

Методы решения тригонометрических уравнений.

При решении тригонометрических уравнений все задачи сводятся к тому, чтобы привести к такому виду, чтобы слева стояла элементарная тригонометрическая функция, а справа – число. После того, как это будет достигнуто, следует найти значение аргумента функции, используя одну из основных формул выражения аргумента через обратные тригонометрические функции.

1.    Алгебраические уравнения относительно одной из тригонометри­ческих функций.

Необходимо произвести замену неизвестных таким образом, чтобы тригонометрическое уравнение преобразовалось в «удобное» для решения алгебраическое уравнение.

Примеры

1)Решить уравнение 2sin2 + 3sin —2 = 0.

Это уравнение является квадратным относительно sin.

Его корни: sin = , sin =—2. Второе из полученных простейших уравнений не имеет решений, так как Isinl1, решения первого можно записать так:

 +2k,π+ 2k

Если в уравнении встречаются разные тригонометрические функции, то надо заменить их все на какую-нибудь одну, используя три­гонометрические тождества.

2) Решить уравнение 2sin + cos = 2.

Если в этом уравнении заменим косинус на синус (по аналогии с предыдущими примерами) или наоборот, то по­лучим уравнение с радикалами. Чтобы избежать этого, ис­пользуем формулы, выражающие синус и косинус через тангенс половинного угла:

 и .

Делая замену, получаем уравнение относительно:   .

Квадратное уравнение  имеет корни    откуда

Это же уравнение можно решить другим способом, вводя вспомогательный угол:

                                                                                                  

Пусть. Тогда можно продолжить преобразование: . Получаем простей­шее   уравнение  т. е.  , откуда , или

Ответ получился в другом виде, однако можно проверить, что решения на самом деле совпадают.

2.      Понижение порядка уравнения.

Формулы   удвоения позволяют квадраты синуса, косинуса и их произведения заме­нять линейными функциями от синуса и косинуса двойного угла. Такие замены делать выгодно, так как они понижают порядок уравнения.

Примеры

1)Решить уравнение.

Можно заменить cos2 на 2cos2—1 и получить квадратное уравнение относительно cos, но проще заменитьна и получить линейное уравнение относительно.

2) Решить уравнение

Подставляя вместо,  их выражения через, получаем:

,

2

3.     Использование тригонометрических формул сложения и след­ствий из них.

Иногда в уравнениях встречаются тригонометрические функции кратных углов. В таких случаях нужно использовать формулы сложения.                                                                                                             

Примеры

1) Решить уравнение.

Сложим два крайних слагаемых:, откуда,. Тогда, .

2) Решить уравнение.

Преобразуем произведение синусов в сумму:,

откуда. Полученное уравнение можно ре­шить разными способами: 1) воспользоваться формулами сложения; 2) преобразовать в произведение. Удобнее  воспользоваться  условием  равенства  косинусов двух углов  и:.

Получаем два уравнения:  .

Здесь решения второй серии содержат в себе все решения первой серии. Учитывая это, ответ можно записать короче:.

4.    Однородные уравнения.

Уравнение, в котором каждое слагаемое имеет одну и ту же степень, называется однородным. Его можно решить, выполнив деление на старшую степень синуса (или косинуса).

Так как, то постоянные слагаемые можно счи­тать членами второй степени.

Пример:   .

Заменяя 4  на ,получаем:   

5.                  Переход к половинному углу

Рассмотрим этот метод на примере:

Пример 6. Решить уравнение: 3 sin x – 5 cos x = 7.

Решение.

6 sin( x / 2 ) · cos ( x / 2 ) – 5 cos ² ( x / 2 ) + 5 sin ² ( x / 2 ) =

= 7 sin ² ( x / 2 ) + 7 cos ² ( x / 2 ) ,

2 sin ² ( x / 2 ) – 6 sin ( x / 2 ) · cos ( x / 2 ) + 12 cos ² ( x / 2 ) = 0 ,

tg² ( x / 2 ) – 3 tg ( x / 2 ) + 6 = 0 ,

6.                  Введение вспомогательного угла

Рассмотрим уравнение вида:

asinx + bcosx = c,

где a, b, c – коэффициенты; x – неизвестное.

Теперь коэффициенты уравнения обладают свойствами синуса и косинуса, а именно: модуль (абсолютное значение ) каждого из них не больше 1, а сумма их квадратов равна 1. Тогда можно обозначить их соответственно как cos и sin ( здесь — так называемый вспомогательный угол ), и наше уравнение принимает вид:

Пример.  Решить уравнение:

Приемы решения тригонометрических уравнений, требующих искусственных преобразований.

1.    Умножение обеих частей уравнения на одну и ту же тригонометрическую функцию.

Пример. Решите уравнение    

Решение. Раскроем скобки и преобразуем про­изведение

в сумму:                                     

Умножим обе части уравнения на. Заме­тим, что ,  не является решением данного уравнения.   . Преобразуем левую часть уравнения:

;    или тогда

 или, т.е.

Исключим из найденных серий корни вида , :

а).  Ясно, что — четное число, т.е. , а потому .

б).Tax как , то ,но тогда ,.

Ответ:

2.    Прибавление к обеим частям уравнения одного и того же числа, одной и той же     тригонометрической функции.

Пример. Решите уравнение.

Решение. Область определения уравнения задается неравенствами:

При6авим к обеим частям уравнения по единице.  ;

Разделим обе части уравнения на и после преобразований получим.

   

Тогда или .

Из первой серии корней области определения принадлежит только , но это серия корней содержится в серии. Нетрудно убедиться, что  входит в область определения. Например:что верно, поскольку левая часть — число четное, а правая — нечетное.

Ответ:.

3.    Тождественные преобразования одной из частей уравнения.

Пример. Решите уравнение .

Решение. Преобразуем левую часть уравнения:

                                                                                                

Откуда , тогда  или

 Легко видеть, что

Ответ:

4.     Использование свойств пропорции.

Необходимо помнить, что применение равенств

 и т. д. приводит к изменению области определения урав­нения. Так, у пропорции существует ограничение: , а у пропорции  место другое ограничение:.

Пример. Решите уравнение

Решение. Применяя формулу тангенса разности, получим уравнение: . Используем свойство пропорции: ;

Область определения исходного уравнения:

В ходе решения произошло сужение области определения, добавились новые, ограничения: откуда

Проверим, удовлетворяют ли исходному уравне­нию значения

а) -верное равенство,

 — решение исходного уравнения.    

б) верное равенство.

в)-1  -1 — верное равенство, Ответ:

5.     Решение тригонометрических уравнений методом экстремальных значений.

При решении некоторых тригонометрических уравнений бывает удобно использовать ограничен­ность функций,  и. Покажем это на конкретных примерах.

Пример 1. Решите уравнение .

Решение. Так как , то ,, откуда и возможные корни данного уравнения  Подставив эти значения в левую часть уравне­ния, получим а последнее равенство возможно только при .

Следовательно, — решение дан­ного уравнения.

Ответ:

Пример 2. Решите уравнение .

Решение. Легко видеть, что и . Следовательно, , но тогда , , откуда , — возможные корни данного

уравнения. Подстановка  в данное урав­нение показывает, что эти числа действительно являются его корнями.

Ответ:.

6.    Уравнения, содержащие модуль функции и корень четной степени

Пример 1.

 

При отборе корней нет надобности решать неравенство, достаточно вынести корни на тригонометрический круг и выбрать нужные.

Ответ:

Пример 2.

Решение: Учитывая ОДЗ функций, получим:

Ответ:

Уравнения повышенной сложности

1.    (Сканави М.И.8.022)

 2sin3 x +2sin2x cos x – sin x cos2x – cos3x = 0 | : cos3x ≠ 0;

т.к. уравнение однородное тригонометрическое 3-ей степени

 2tg3x + 2tg2x – tgx – 1 = 0;

Разложим левую часть на множители, сгруппировав члены, получим

 (tg x + 1)(2tg2x – 1) = 0;

   tgx = -1                              х= —  + n , n ͼ Z

   tgx=  ;                          х= arctg + k, k ͼ Z.

Ответ: —  + n , n ͼ Z ;arctg + k, k ͼ Z.

2.    ( СканавиМ.И.8.081)

6sin2x + sin x cos x – cos2x = 2;

 4sin2x + sin x cos x – 3 cos2x = 0; | : cos2x ≠ 0;

т. к. уравнение однородное тригонометрическое 2-ой степени

 4tg2x + tg x – 3 = 0;

   tgx = -1,                           х= —  + n , n ͼ Z

   tgx=  ;                             х= arctg  + k, k ͼ Z.

Ответ:  —  + n , n ͼ Z;

              arctg  + k, k ͼ Z.

3.    ( Сканави М.И. 8.076)

sinx – sin 2x + sin 5x + sin 8x = 0;

сгруппировав первое с третьим, второе с четвертым слагаемые левой части и применив формулы суммы и разности синусов, получим

2sin 3x cos 2x + 2sin 3x cos 5x = 0;

вынесем в левой части общий множитель за скобки и применим формулу суммы косинусов

2sin 3x ∙ 2 cos  cos  = 0;

   sin 3x = 0,                  x = , n ͼ Z

   cos  = 0,                  x =  +  , k ͼ Z

   cos  = 0;                  x = + , m ͼ Z.

Произведем отбор корней, воспользовавшись тригонометрической окружностью

                                                                                   Ответ:    , nͼZ;

                                                                                  +  , kͼZ \ { 7m+3| mͼZ }.

 

 

 

4.     ( Сканави  М.И. 8.076)

 = 2;

воспользуемся формулой косинуса двойного угла

 = 2;

sin = 1,

sin  ≠ 0;

sin  = 1;

х= + 4, kͼZ.

Ответ: + 4, kͼZ.

5.    (Сканави М.И.  8.120)

 +  —  —  =0

;понизим степень, воспользовавшись формулами косинуса двойного угла

1 +cos x +1 + cos 3x -1 +cos 4x -1 +cos 8x =0;

сгруппируем слагаемые и воспользуемся формулой суммы косинусов

2cos 2x cos x + 2cos 2x cos 6x =0;

2cos 2x 2cos 3,5x cos 2,5x=0;

произведение всюду определенных множителей равно нулю тогда и только тогда, когда хотя бы один из этих множителей равен нулю

     cos 2x=0                 2x= + , n ͼ Z

    cos 3,5x=0               3,5x= + , m ͼ Z

    cos 2,5x=0;              2,5x= + , k ͼ Z;

x= +, n ͼ Z

x= +, m ͼ Z

x= +, k ͼ Z .

Ответ: +, nͼZ;

             +, mͼZ;

             +, kͼZ .

Заключение.

Изучение тригонометрических уравнений позволяет учащимся овладеть конкретными математическими знаниями, необходимыми для применения в практической деятельности, для изучения смежных дисциплин, развития умственных способностей, умение извлекать учебную информацию на основе сопоставительного анализа графиков, самостоятельно выполнять различные творческие работы.

В данной работе рассмотрены основные методы решения тригонометрических уравнений, причем, как специфические, характерные только для тригонометрических уравнений, так и общие функциональные методы решения уравнений, применительно к тригонометрическим уравнениям.

Для успешного решения уравнений необходимо знать формулы корней простейших тригонометрических уравнений, значение тригонометрических функций для основных углов и значение обратных тригонометрических функций, универсальные правила решения уравнений.  Рассмотрено решение элементарных тригонометрических уравнений, метод разложения на множители, методы сведения тригонометрических уравнений к алгебраическим. Указано, что при решении тригонометрических уравнений широко используются тождества, выражающие соотношение между тригонометрическими функциями одного и разных аргументов.

Приведенные методы не исчерпывают все многообразие способов решений тригонометрических уравнений. Однако рассмотренные типы уравнений встречаются наиболее часто и важно уметь распознавать в данном уравнении тот или иной тип.

Результаты данной работы могут быть использованы в качестве учебного материала при подготовке творческих работ, при составлении факультативных курсов для школьников, так же работа может применяться при подготовке учащихся к Единому государственному экзамену, вступительным экзаменам.

                                                    Библиография

1.    Алексеев А. Тригонометрические подстановки. // Квант. – 1995. — №2. –с. 40 – 42.

2.    Выгодский М. Я. «Справочник по элементарной математике».   М., «Наука», 1982 г.

3.    Г. И. Глейзер История математики в школе. – М.: «Просвещение» 1983г.

4.    Карасев В.А., Лёвшина Г.Д. «12 уроков по тригонометрии» — М.: Илекса, 2013.- 200 с.:ил.

5.              Крамор В.С. Тригонометрические функции. – М.: Просвещение, 1979.

6.    Сост. Гряда Н. Н. и др. Обобщающее повторение в системе подготовки к ЕГЭ по теме «Тригонометрические уравнения»,    Армавир, 2005г.

7.              Цукарь А.Я. Упражнения практического характера по тригонометрии //Математика в школе. 1993-№3- с 12-15.

8.              Шаталов В.Ф. Методические рекомендации для работы с опорными сигналами по тригонометрии. — М.: Новая школа, 1993.

 

 

 

 

 

 

 

 

 

 

infourok.ru

Основные виды тригонометрических уравнений

Рассмотрим некоторые наиболее часто встречающиеся виды тригонометрических уравнений и способы их решения.

\(\blacktriangleright\) Квадратные тригонометрические уравнения
Если после преобразования уравнение приняло следующий вид: \[{\Large{af^2(x)+bf(x)+c=0}}\] где \(a\ne 0, \ f(x)\) — одна из функций \(\sin x, \cos x, \mathrm{tg}\,x, \mathrm{ctg}\, x\),
то такое уравнение с помощью замены \(f(x)=t\) сводится к квадратному уравнению.

 

Часто при решении таких уравнений используются
основные тождества: \[\begin{array}{|ccc|} \hline \sin^2 \alpha+\cos^2 \alpha =1&& \mathrm{tg}\, \alpha \cdot \mathrm{ctg}\, \alpha =1\\ &&\\ \mathrm{tg}\, \alpha=\dfrac{\sin \alpha}{\cos \alpha}&&\mathrm{ctg}\, \alpha =\dfrac{\cos \alpha}{\sin \alpha}\\&&\\ 1+\mathrm{tg}^2\, \alpha =\dfrac1{\cos^2 \alpha} && 1+\mathrm{ctg}^2\, \alpha=\dfrac1{\sin^2 \alpha}\\&&\\ \hline \end{array}\]
формулы двойного угла: \[\begin{array}{|lc|cr|} \hline \sin {2\alpha}=2\sin \alpha\cos \alpha & \qquad &\qquad & \cos{2\alpha}=\cos^2\alpha -\sin^2\alpha\\ \sin \alpha\cos \alpha =\dfrac12\sin {2\alpha} && & \cos{2\alpha}=2\cos^2\alpha -1\\ & & & \cos{2\alpha}=1-2\sin^2 \alpha\\ \hline &&&\\ \mathrm{tg}\, 2\alpha = \dfrac{2\mathrm{tg}\, \alpha}{1-\mathrm{tg}^2\, \alpha} && & \mathrm{ctg}\, 2\alpha = \dfrac{\mathrm{ctg}^2\, \alpha-1}{2\mathrm{ctg}\, \alpha}\\&&&\\ \hline \end{array}\]

Пример 1. Решить уравнение \(6\cos^2x-13\sin x-13=0\)

 

С помощью формулы \(\cos^2\alpha=1-\sin^2\alpha\) уравнение сводится к виду:
\(6\sin^2x+13\sin x+7=0\). Сделаем замену \(t=\sin x\). Т.к. область значений синуса \(\sin x\in [-1;1]\), то \(t\in[-1;1]\). Получим уравнение:

 

\(6t^2+13t+7=0\). Корни данного уравнения \(t_1=-\dfrac76, \ t_2=-1\).

 

Таким образом, корень \(t_1\) не подходит. Сделаем обратную замену:
\(\sin x=-1 \Rightarrow x=-\dfrac{\pi}2+2\pi n, n\in\mathbb{Z}\).

 

Пример 2. Решить уравнение \(5\sin 2x=\cos 4x-3\)

 

С помощью формулы двойного угла для косинуса \(\cos 2\alpha=1-2\sin^2\alpha\) имеем:
\(\cos4x=1-2\sin^22x\). Сделаем эту подстановку и получим:

 

\(2\sin^22x+5\sin 2x+2=0\). Сделаем замену \(t=\sin 2x\). Т.к. область значений синуса \(\sin 2x\in [-1;1]\), то \(t\in[-1;1]\). Получим уравнение:

 

\(2t^2+5t+2=0\). Корни данного уравнения \(t_1=-2, \ t_2=-\dfrac12\).

 

Таким образом, корень \(t_1\) не подходит. Сделаем обратную замену:   \(\sin 2x=-\dfrac12 \Rightarrow x_1=-\dfrac{\pi}{12}+\pi n, \ x_2=-\dfrac{5\pi}{12}+\pi n, n\in\mathbb{Z}\).

 

Пример 3. Решить уравнение \(\mathrm{tg}\, x+3\mathrm{ctg}\,x+4=0\)

 

Т.к. \(\mathrm{tg}\,x\cdot \mathrm{ctg}\,x=1\), то \(\mathrm{ctg}\,x=\dfrac1{\mathrm{tg}\,x}\). Сделаем замену \(\mathrm{tg}\,x=t\). Т.к. область значений тангенса \(\mathrm{tg}\,x\in\mathbb{R}\), то \(t\in\mathbb{R}\). Получим уравнение:

 

\(t+\dfrac3t+4=0 \Rightarrow \dfrac{t^2+4t+3}{t}=0\). Дробь равна нулю, когда числитель равен нулю, а знаменатель отличен от нуля. Таким образом:

 

\(\begin{cases} t^2+4t+3=0\\t\ne 0 \end{cases} \Rightarrow \left[\begin{gathered} \begin{aligned} &t_1=-3\\&t_2=-1 \end{aligned}\end{gathered}\right.\)

 

Сделаем обратную замену:

 

\(\left[\begin{gathered} \begin{aligned} &\mathrm{tg}\,x=-3\\ &\mathrm{tg}\,x=-1 \end{aligned}\end{gathered}\right. \Rightarrow \left[\begin{gathered} \begin{aligned} &x=-\mathrm{arctg}\,3+\pi n\\ &x=-\dfrac{\pi}4+\pi n \end{aligned}\end{gathered}\right. \ \ n\in\mathbb{Z}\)

 

\(\blacktriangleright\) Кубические тригонометрические уравнения
Если после преобразования уравнение приняло следующий вид: \[{\Large{af^3(x)+bf^2(x)+cf(x)+d=0}}\] где \(a\ne 0, \ f(x)\) — одна из функций \(\sin x, \cos x, \mathrm{tg}\,x, \mathrm{ctg}\, x\),
то такое уравнение с помощью замены \(f(x)=t\) сводится к кубическому уравнению.

 

Часто при решении таких уравнений в дополнение к предыдущим формулам используются
формулы тройного угла: \[\begin{array}{|lc|cr|} \hline &&&\\ \sin {3\alpha}=3\sin \alpha -4\sin^3\alpha &&& \cos{3\alpha}=4\cos^3\alpha -3\cos \alpha\\&&&\\ \hline \end{array}\]

Пример 4. Решить уравнение \(11\cos 2x-3=3\sin 3x-11\sin x\)

 

При помощи формул \(\sin 3x=3\sin x-4\sin^3x\) и \(\cos2x=1-2\sin^2x\) можно свести уравнение к уравнению только с \(\sin x\):

 

\(12\sin^3x-9\sin x+11\sin x-3+11-22\sin^2 x=0\). Сделаем замену \(\sin x=t, \ t\in[-1;1]\):

 

\(6t^3-11t^2+t+4=0\). Подбором находим, что один из корней равен \(t_1=1\). Выполнив деление в столбик многочлена \(6t^3-11t^2+t+4\) на \(t-1\), получим:

 

\((t-1)(2t+1)(3t-4)=0 \Rightarrow\) корнями являются \(t_1=1, \ t_2=-\dfrac12, \ t_3=\dfrac43\).

 

Таким образом, корень \(t_3\) не подходит. Сделаем обратную замену:

 

\(\left[\begin{gathered} \begin{aligned} &\sin x=1\\&\sin x=-\dfrac12 \end{aligned}\end{gathered}\right. \Rightarrow \left[\begin{gathered} \begin{aligned} &x=\dfrac{\pi}2+2\pi n\\[1ex]&x=-\dfrac{\pi}6+2\pi n\\[1ex] &x=-\dfrac{5\pi}6+2\pi n \end{aligned}\end{gathered}\right. \ \ n\in\mathbb{Z}\)

 

\(\blacktriangleright\) Однородные тригонометрические уравнения второй степени: \[I. \quad {\Large{a\sin^2x+b\sin x\cos x+c\cos^2x=0}}, \quad a\ne 0,c\ne 0\]

Заметим, что в данном уравнении никогда не являются решениями те значения \(x\), при которых \(\cos x=0\) или \(\sin x=0\). Действительно, если \(\cos x=0\), то, подставив вместо косинуса ноль в уравнение, получим: \(a\sin^2 x=0\), откуда следует, что и \(\sin x=0\). Но это противоречит основному тригонометрическому тождеству, т.к. оно говорит о том, что если \(\cos x=0\), то \(\sin x=\pm 1\).

 

Аналогично и \(\sin x=0\) не является решением такого уравнения.

 

Значит, данное уравнение можно делить на \(\cos^2 x\) или на \(\sin^2 x\). Разделим, например, на \(\cos^2 x\):

 

\(a \ \dfrac{\sin^2x}{\cos^2x}+b \ \dfrac{\sin x\cos x}{\cos^2x}+c \ \dfrac{\cos^2x}{\cos^2x}=0 \Leftrightarrow a\mathrm{tg}^2\,x+b\mathrm{tg}\,x+c=0\)

Таким образом, данное уравнение при помощи деления на \(\cos^2x\) и замены \(t=\mathrm{tg}\,x\) сводится к квадратному уравнению:

 

\(at^2+bt+c=0\), способ решения которого вам известен.

 

Уравнения вида \[I’. \quad {\Large{a\sin^2x+b\sin x\cos x+c\cos^2x=d}}, \quad a\ne0,c\ne 0\] с легкостью сводятся к уравнению вида \(I\) с помощью использования основного тригонометрического тождества: \[d=d\cdot 1=d\cdot (\sin^2x+\cos^2x)\]

Заметим, что благодаря формуле \(\sin2x=2\sin x\cos x\) однородное уравнение можно записать в виде

 

\(a\sin^2 x+b\sin 2x+c\cos^2x=0\)

 

Пример 5. Решить уравнение \(2\sin^2x+3\sin x\cos x=3\cos^2x+1\)

 

Подставим вместо \(1=\sin^2x+\cos^2x\) и получим:

\(\sin^2x+3\sin x\cos x-4\cos^2x=0\). Разделим данное уравнение на \(\cos^2x\):

 

\(\mathrm{tg}^2\,x+3\mathrm{tg}\,x-4=0\) и сделаем замену \(t=\mathrm{tg}\,x, \ t\in\mathbb{R}\). Уравнение примет вид:

 

\(t^2+3t-4=0\). Корнями являются \(t_1=-4, \ t_2=1\). Сделаем обратную замену:

 

\(\left[\begin{gathered} \begin{aligned} &\mathrm{tg}\,x=1\\&\mathrm{tg}\,x=-4 \end{aligned}\end{gathered}\right. \Rightarrow \left[\begin{gathered} \begin{aligned} &x=\dfrac{\pi}4+\pi n\\[1ex]&x=-\mathrm{arctg}\,4+\pi n \end{aligned}\end{gathered}\right. \ \ n\in\mathbb{Z}\)

 

\(\blacktriangleright\) Однородные тригонометрические уравнения первой степени: \[II.\quad {\Large{a\sin x+b\cos x=0}}, a\ne0, b\ne 0\]

Заметим, что в данном уравнении никогда не являются решениями те значения \(x\), при которых \(\cos x=0\) или \(\sin x=0\). Действительно, если \(\cos x=0\), то, подставив вместо косинуса ноль в уравнение, получим: \(a\sin x=0\), откуда следует, что и \(\sin x=0\). Но это противоречит основному тригонометрическому тождеству, т.к. оно говорит о том, что если \(\cos x=0\), то \(\sin x=\pm 1\).

 

Аналогично и \(\sin x=0\) не является решением такого уравнения.

 

Значит, данное уравнение можно делить на \(\cos x\) или на \(\sin x\). Разделим, например, на \(\cos x\):

 

\(a \ \dfrac{\sin x}{\cos x}+b \ \dfrac{\cos x}{\cos x}=0\), откуда имеем \(a\mathrm{tg}\, x+b=0 \Rightarrow \mathrm{tg}\, x=-\dfrac ba\)

 

Пример 6. Решить уравнение \(\sin x+\cos x=0\)

 

Разделим правую и левую части уравнения на \(\sin x\):

 

\(1+\mathrm{ctg}\, x=0 \Rightarrow \mathrm{ctg}\, x=-1 \Rightarrow x=-\dfrac{\pi}4+\pi n, n\in\mathbb{Z}\)

 

\(\blacktriangleright\) Неоднородные тригонометрические уравнения первой степени: \[II.\quad {\Large{a\sin x+b\cos x=c}}, a\ne0, b\ne 0, c\ne 0\]

Существует несколько способов решения подобных уравнений. Рассмотрим те из них, которые можно использовать для любого такого уравнения:

 

1 СПОСОБ: при помощи формул двойного угла для синуса и косинуса и основного тригонометрического тождества:   \({\large{\sin x=2\sin{\dfrac x2}\cos{\dfrac x2}, \qquad \cos x=\cos^2 {\dfrac x2}-\sin^2 {\dfrac x2},\qquad c=c\cdot \Big(\sin^2 {\dfrac x2}+\cos^2 {\dfrac x2}\Big)}}\)   данное уравнение сведется к уравнению \(I\):

 

Пример 7. Решить уравнение \(\sin 2x-\sqrt3 \cos 2x=-1\)

 

Распишем \(\sin 2x=2\sin x\cos x, \ \cos 2x=\cos^2x-\sin^2 x, \ -1=-\sin^2 x-\cos^2x\). Тогда уравнение примет вид:

 

\((1+\sqrt3)\sin^2x+2\sin x\cos x+(1-\sqrt3)\cos^2x=0\). Данное уравнение с помощью деления на \(\cos^2x\) и замены \(\mathrm{tg}\,x=t\) сводится к:

 

\((1+\sqrt3)t^2+2t+1-\sqrt3=0\). Корнями этого уравнения являются \(t_1=-1, \ t_2=\dfrac{\sqrt3-1}{\sqrt3+1}=2-\sqrt3\). Сделаем обратную замену:

 

\(\left[ \begin{gathered} \begin{aligned}&\mathrm{tg}\,x=-1\\ &\mathrm{tg}\,x=2-\sqrt3 \end{aligned}\end{gathered}\right. \Rightarrow \left[ \begin{gathered} \begin{aligned} &x=-\dfrac{\pi}4+\pi n\\[1ex] &x=\mathrm{arctg}\,(2-\sqrt3)+\pi n \end{aligned}\end{gathered}\right. \ \ n\in\mathbb{Z}\)

 

2 СПОСОБ: при помощи формул выражения функций через тангенс половинного угла: \[\begin{array}{|lc|cr|} \hline &&&\\ \sin{\alpha}=\dfrac{2\mathrm{tg}\, \dfrac{\alpha}2}{1+\mathrm{tg}^2\, \dfrac{\alpha}2} &&& \cos{\alpha}=\dfrac{1-\mathrm{tg}^2\, \dfrac{\alpha}2}{1+\mathrm{tg}^2\, \dfrac{\alpha}2}\\&&&\\ \hline \end{array}\] уравнение сведется к квадратному уравнению относительно \(\mathrm{tg}\, \dfrac x2\)

 

Пример 8. Решить то же уравнение \(\sin 2x-\sqrt3 \cos 2x=-1\)

 

Сделаем подстановку \(\sin 2x=\dfrac{2\mathrm{tg}\,x}{1+\mathrm{tg}^2\,x}, \ \cos2x=\dfrac{1-\mathrm{tg}^2\,x}{1+\mathrm{tg}^2\,x}\) и замену \(\mathrm{tg}\,x=t\):

 

\(\dfrac{(\sqrt3+1)t^2+2t+1-\sqrt3}{1+t^2}=0 \Rightarrow (\sqrt3+1)t^2+2t+1-\sqrt3=0\) (т.к. \(1+t^2\geqslant 1\) при всех \(t\), то есть всегда \(\ne 0\))

 

Таким образом, мы получили то же уравнение, что и, решая первым способом.

 

3 СПОСОБ: при помощи формулы вспомогательного угла.
\[{\large{a\sin x+b\cos x=\sqrt{a^2+b^2}\,\sin (x+\phi),}} \quad \text{где } \cos \phi=\dfrac a{\sqrt{a^2+b^2}}\]

Для использования данной формулы нам понадобятся формулы сложения углов: \[\begin{array}{|lc|cr|} \hline &&&\\ \sin{(\alpha\pm \beta)}=\sin\alpha\cdot \cos\beta\pm \sin\beta\cdot \cos\alpha &&& \cos{(\alpha\pm \beta)}=\cos\alpha\cdot \cos\beta \mp \sin\alpha\cdot \sin\beta\\ &&&\\ \hline \end{array}\]

Пример 9. Решить то же уравнение \(\sin 2x-\sqrt3 \cos 2x=-1\)

 

Т.к. мы решаем уравнение, то можно не преобразовывать левую часть, а просто разделить обе части уравнения на \(\sqrt{1^2+(-\sqrt3)^2}=2\):

 

\(\dfrac12\sin 2x-\dfrac{\sqrt3}2\cos 2x=-\dfrac12\)

 

Заметим, что числа \(\dfrac12\) и \(\dfrac{\sqrt3}2\) получились табличные. Можно, например, взять за \(\dfrac12=\cos \dfrac{\pi}3, \ \dfrac{\sqrt3}2=\sin \dfrac{\pi}3\). Тогда уравнение примет вид:

 

\(\sin 2x\cos \dfrac{\pi}3-\sin \dfrac{\pi}3\cos 2x=-\dfrac12 \Rightarrow \sin\left(2x-\dfrac{\pi}3\right)=-\dfrac12\)

 

Решениями данного уравнения являются:

 

\(\left[ \begin{gathered} \begin{aligned} &2x-\dfrac{\pi}3=-\dfrac{\pi}6+2\pi n\\[1.5ex] &2x-\dfrac{\pi}3=-\dfrac{5\pi}6+2\pi n \end{aligned} \end{gathered} \right. \Rightarrow \left[ \begin{gathered} \begin{aligned} &x=\dfrac{\pi}{12}+\pi n\\[1.5ex] &x=-\dfrac{\pi}4+\pi n \end{aligned} \end{gathered} \right. \ \ n\in\mathbb{Z}\)

 

Заметим, что при решении уравнения третьим способом мы добились “более красивого” ответа (хотя ответы, естественно, одинаковы), чем при решении первым или вторым способом (которые, по сути, приводят уравнение к одному и тому же виду).
Таким образом, не стоит пренебрегать третьим способом решения данного уравнения.

 

\(\blacktriangleright\) Если тригонометрическое уравнение можно свести к виду \[{\Large{a(\sin x\pm \cos x)+b\sin x\cos x+c=0}}, \text{где } a\ne 0, b\ne 0,\] то с помощью формулы \[{\large{(\sin x\pm\cos x)^2=1\pm2\sin x\cos x}} \ \ (*)\] данное уравнение можно свести к квадратному.

 

Для этого необходимо сделать замену \(t=\sin x\pm \cos x\), тогда \(\sin x\cos x=\pm \dfrac{t^2-1}2\).

 

Заметим, что формула \((*)\) есть не что иное, как формула сокращенного умножения \((A\pm B)^2=A^2\pm 2AB+B^2\) при подстановке в нее \(A=\sin x, B=\cos x\).

 

Пример 10. Решить уравнение \(3\sin 2x+3\cos 2x=16\sin x\cos^3x-8\sin x\cos x\).

 

Вынесем общий множитель за скобки в правой части: \(3\sin 2x+3\cos 2x=8\sin x\cos x(2\cos^2 x-1)\).
По формулам двойного угла \(2\sin x\cos x=\sin 2x, 2\cos^2x-1=\cos 2x\) имеем: \[3(\sin 2x+\cos 2x)=4\sin 2x\cos 2x\] Заметим, что полученное уравнение как раз записано в необходимом нам виде. Сделаем замену \(t=\sin 2x+\cos 2x\), тогда \(\sin 2x\cos 2x=\dfrac{t^2-1}2\). Тогда уравнение примет вид: \[3t=2t^2-2 \Rightarrow 2t^2-3t-2=0\] Корнями данного уравнения являются \(t_1=2, t_2=-\dfrac12\).

 

По формулам вспомогательного аргумента \(\sin2x+\cos 2x=\sqrt2\sin\left(2x+\dfrac{\pi}4\right)\), следовательно, сделав обратную замену: \[\left[ \begin{gathered} \begin{aligned} &\sqrt2\sin\left(2x+\dfrac{\pi}4\right)=2\\[1ex] &\sqrt2\sin\left(2x+\dfrac{\pi}4\right)=-\dfrac12 \end{aligned} \end{gathered} \right. \Rightarrow \left[ \begin{gathered} \begin{aligned} &\sin\left(2x+\dfrac{\pi}4\right)=\sqrt2\\[1ex] &\sin\left(2x+\dfrac{\pi}4\right)=-\dfrac1{2\sqrt2} \end{aligned} \end{gathered} \right.\] Первое уравнение корней не имеет, т.к. область значений синуса находится в пределах от \(-1\) до \(1\). Значит: \(\sin\left(2x+\dfrac{\pi}4\right)=-\dfrac1{2\sqrt2} \Rightarrow \left[ \begin{gathered} \begin{aligned} &2x+\dfrac{\pi}4=-\arcsin {\dfrac1{2\sqrt2}}+2\pi n\\[1ex] &2x+\dfrac{\pi}4=\pi+\arcsin {\dfrac1{2\sqrt2}}+2\pi n \end{aligned} \end{gathered} \right. \Rightarrow \)  
\(\Rightarrow \left[ \begin{gathered} \begin{aligned} &x=-\dfrac12\arcsin {\dfrac1{2\sqrt2}}-\dfrac{\pi}8+\pi n\\[1ex] &x=\dfrac{3\pi}8+\dfrac12\arcsin {\dfrac1{2\sqrt2}}+\pi n \end{aligned} \end{gathered} \right. \ \ n\in\mathbb{Z}\)

 

\(\blacktriangleright\) Формулы сокращенного умножения в тригонометрическом варианте:

 

\(I\) Квадрат суммы или разности \((A\pm B)^2=A^2\pm 2AB+B^2\):

\((\sin x\pm \cos x)^2=\sin^2 x\pm 2\sin x\cos x+\cos^2x=(\sin^2 x+\cos^2 x)\pm 2\sin x\cos x=1\pm \sin 2x\)

 

\(II\) Разность квадратов \(A^2-B^2=(A-B)(A+B)\):

\((\cos x-\sin x)(\cos x+\sin x)=\cos^2x-\sin^2x=\cos 2x\)

 

\(\sin^2x-\cos^2x=-\cos2x\)

 

\(III\) Сумма или разность кубов \(A^3\pm B^3=(A\pm B)(A^2\mp AB+B^2)\):

\(\sin^3x\pm \cos^3x=(\sin x\pm \cos x)(\sin^2x\mp \sin x\cos x+\cos^2x)=(\sin x\pm \cos x)(1\mp \sin x\cos x)=\)

\(=(\sin x\pm \cos x)(1\mp \frac12\sin 2x)\)

 

\(IV\) Куб суммы или разности \((A\pm B)^3=A^3\pm B^3\pm 3AB(A\pm B)\):

\((\sin x\pm \cos x)^3=(\sin x\pm \cos x)(\sin x\pm \cos x)^2=(\sin x\pm \cos x)(1\pm \sin 2x)\)   (по первой формуле)

 

shkolkovo.net

Решение сложных тригонометрических уравнений — математика, прочее

Сейджанова А.А.,І санатты математика пән мұғалімі,

Новеньский ОЖББМ, Новенький ауылы, Зеленов ауданы, Батыс-Қазақстан облысы.

Бүгінгі кезде оқушы үшін математикалық білім сапасының көрсеткіші ҰБТ-ның есептері негізінде аңықталады. Мұғалім сабақтың әрбір сатысында, әртүрлі бақылау кезеңдерінде ҰБТ тапсырмаларын қолданады. Соның ішінде тригонометриялық теңдеулер оқушыларға қиындық келтіреді . Ол үшін тригонометриялық формулаларын толық білу қажет керек. ҰБТ-ке дайындау барысында көмегі тиіп қалар деген оймен мына есептердің шешу жолдарын ұсынып отырмын .

1. Теңдеу сos2x-3cosx=4cos²

Дәреже төмендету және қосбұрышты формуласын қолданамыз: cos² =

соs2x=2cos²x-1

Сонда шығады: 2cos²x-1-3cosx=4( )

2cos²x-1-3cosx-2-2cosx=0

2cos²x-5cosx-3=0, cosx=y, 2y²-5y-3=0, D=49, y₁=3,y₂=

3 саны косинустың мәндер облысына кірмейді, сондықтан cosx==

x=±+2πn, nZ Жауабы: x=±+2πn, nZ

2. Теңдеу Теңдеуді шешіңіз: ctgx+=2,

ctgx= өрнектеп, теңдеуді шешеміз: +=2

cosx+cos²x+sin²x=2sinx(1+cosx)

(cosx+1)- 2sinx(1+cosx)=0

(cosx+1)*(1-2sinx)=0

cosx=-1 sinx=

x= π+2πn, x=(-1)ⁿ +πk nZ. Жауабы: x= π+2πn, x=(-1)ⁿ +πk nZ

3. Теңдеу sinx+cosx=1 [270⁰; 450⁰] кесіндісіне тиісті түбірлерінің қосындысын табыңыз:

Біріншіден, теңдеуді ге көбейтеміз

sinx+cosx=1 /*

sinx+cosx=

sinsinx+coscosx=

мұнда косинустың қосу формуласын қолданамыз, сонда

cos(x-)=

x-=±+2πn

x=±++2πn, nZ n=0,1,2,3…

n=0, x= += 90⁰[270⁰; 450⁰]

n=1, x=++2π=60⁰+30⁰+360⁰=450⁰, 450⁰[270⁰; 450⁰]

n=1, x=-60⁰+30⁰+360⁰=330⁰, 330⁰[270⁰; 450⁰]

n=2, x=60⁰+30⁰+720⁰= 810⁰, 810⁰[270⁰; 450⁰]

n=2, x=-60⁰+30⁰+720⁰=690⁰, 690⁰[270⁰; 450⁰]

мұнда берілген кесіндіде екі түбір бар екен, олардың қосындысын табайық x=330⁰+450⁰=780⁰

Жауабы: 780⁰

4. Теңдеу:tg²x-3tgx+4= 3ctgx-ctg²x

(tg²x+ ctg²x)-3(tgx+ctgx)+4=0, негізгі тепе-теңдік бойынша ctgx=

(tgx+)²— 3(tgx+)+2=0, tgx+=y

y²-3y+2=0, y= 2;1

tgx+=2, tgx+=1 ортақ бөліміне келтіреміз,

tg²x-tgx+2=0 tg²x-tgx+1=0

D²=0, осыдан tgx=1 x=+πn, nZ Жауабы: x=+πn, nZ

5. Теңдеу 4sin⁴x+cos4x=1+12cos⁴x, cos4x=1-2sin²2x формуланы қолданамыз

. 4sin⁴x+1-2sin²2x=1+12cos⁴x, sin²2x=4 sin²xcos²x

4sin⁴x-8 sin²xcos²x =12cos⁴x

4sin²x(sin²x-2 cos²x)- 12cos⁴x=0, cos²x=1- sin²x

4sin²x(3sin²x-2)- 12cos⁴x=0, жақшаларды ашып, түрлендіреміз

12sin⁴x-8sin²x-12cos⁴x=0

12sin⁴x-12cos⁴x-8sin²x=0, 12-ні жақша сыртына шығарып, қысқаша көбейту формулаларын қолданып, жіктейміз.

12(sin²x- cos²x)( cos²x+ sin²x)- 8sin²x=0, cos²x+ sin²x=1

12 sin²x- 12cos²x -8 sin²x=0

4sin²x-12 cos²x=0 /4 cos²x

tg²x=3, дәреже төмендету формаласын колданамыз tg²x=

= 3, 1-cos2x=3+3cos2x,

-4cos2x=2

cos2x= -, 2x=(π-)+2πn, nZ

x=+ πn , немесе x=+ πn. Жауабы: x=+ πn, nZ

6. Теңдеу: 1+cosx=ctgтеңдеуді шешеміз, мұнда ctg==формуламен алмастырамыз

1+cosx= /* (1-cosx) көбейтіп, теңдеуді түрлендіреміз

1-cos²x-sinx=0

sin²x-sinx=0

sinx(sinx-1)=0

sinx=0, sinx-1=0

x=πn, sinx=1

x=πn , x=+2πk. Жауабы: x=πn; x=+2πk, nZ

7. Теңдеу:. sin²2x+sin²3x+sin²4x+sin²5x=2, дәреже төмендету формулаларын қолданамыз sin²x=

(1-cos4x)+(1-cos6x)+(1-cos8x)+(1-cos10x)=2

(1-cos4x-cos6x –cos8x-cos10x+3)=2

cos4x+cos6x+cos8x+cos10x=0, қосылғыштарды топтап, соsx+cosy= 2coscos формуласын қолданамыз. Сонда

(cos4x+cos10)+(cos6x+cos8x)=0

2coscos+2coscos=0

2cos7xcos3x+2cos7xcosx=0

2cos7x(cos3x+cosx)=0

2cos7x=0, cos3x+cosx=0

7x=+πn 2coscos

x=+n 2cos2xcosx=0

cos2x=0, cosx=0

2x=+πk, x=+πm

х=+k

Жауабы: x=+n, х=+k, x=+πm мұнда nZ

kopilkaurokov.ru

Тригонометрические уравнения 1

В этой статье будут рассмотрены тригонометрические уравнения с корнями. Прежде чем приступить к решению, вспомним, когда появляется опасность потерять корни или приобрести посторонние. Итак:

При решении тригонометрических уравнений могут появиться посторонние корни, если:

1)      Уравнение содержит тангенс или котангенс;

2)      Обе части уравнения умножаются или делятся на выражение, содержащее неизвестное;

3)      Обе части уравнения возводятся в квадрат.

При решении тригонометрических уравнений могут быть потеряны корни, если:

1)      Обе части уравнения умножаются или делятся на выражение, содержащее неизвестное;

2)      Используются тригонометрические формулы, которые справедливы не при всех значениях неизвестного;

3)      При решении системы тригонометрических уравнений для обозначения целого числа в найденных значениях x и y используется только одна буква.

Теперь можно начать решение.

Задача 1. Решить уравнение:

Возводим обе части уравнения в квадрат:

Разложим формулу , и представим единицу как сумму квадрата синуса и квадрата косинуса:

Сгруппируем слагаемые:

Видим, что в первой скобке – квадрат суммы:

Приравниваем к нулю каждый множитель и решаем два получившихся уравнения:

Первое:

При возведении в квадрат:

Заметим, что по решению синус и косинус равны по модулю, но разные по знаку. В этом варианте решения в исходном уравнении слева под корнем окажется величина отрицательная, значит, это – посторонние корни, поэтому мы даже не будем их записывать. Приобрели мы посторонние корни в результате возведения уравнения  квадрат.

Второе:

Возводим в квадрат:

Снова уравнение распалось на два:

– это посторонний корень, который приведет к появлению в исходном уравнении корня из отрицательного числа в правой части.

или  – данный корень тоже содержит посторонние корни, которые также приобретены в результате возведения уравнения в квадрат. При синусе, равном нулю, косинус может быть равен как 1, так и (-1). Второе – недопустимо: в этом случае в правой части исходного уравнения – отрицательное число под корнем. Поэтому решение у уравнения всего одно: .

 

Задача 2. Решить уравнение:

Возводим обе части уравнения в квадрат:

Косинус двойного аргумента заменяем, также от синуса переходим к косинусу с помощью основного тригонометрического тождества:

Вводим замену:

 

Корни:

Обратная замена:

или

Решения:

Проверка показывает, что все корни удовлетворяют исходному уравнению.

 

Задача 3. Решить уравнение:

Чтобы избавиться от корня, возведем в квадрат:

Домножим на 2 для удобства:

Произведем перегруппировку:

или

Первое:

При возведении в квадрат:

Так как правая часть уравнения должна быть неотрицательной, и, кроме того, синус и косинус – разных знаков, то решение одно:

Второе:

Так как решения уравнения не являются решениями исходного уравнения, то деление на не приведет к потере корней, тогда разделим на :

Решением этого уравнения является угол, синус и косинус которого имеют разные знаки. При этом угол в четвертом квадранте нам не подойдет: у такого угла отрицательный синус и положительный косинус, а это противоречит исходному уравнению: приведет к отрицательному значению операции извлечения корня. Угол во втором квадранте нас устроит.

Ответ: ,

 

Задача 4. Решить уравнение:

Сразу делаем вывод, что полученный нами далее в ходе решения должен быть неположительным , иначе результат извлечения корня не будет положительным.

Возводим все уравнение в квадрат, чтобы избавиться от корня:

Раскрываем формулу двойного аргумента и заменяем синусы на косинусы:

Получили квадратное уравнение относительно косинусов:

или   – очевидно, что решение второго – пустое множество.

С учетом того, что синус должен быть отрицателен (или равен нулю), решение единственное:

Ответ: .

 

Задача 5. Решить уравнение:

Полученный в ходе решения косинус может быть или отрицательным числом, или нулем.

Возводим уравнение в квадрат:

Формулу тройного аргумента раскроем:

или – сумма коэффициентов уравнения равна 0, поэтому первый корень – 1, а второй – с/a – (-1/2)

Итак, имеем: , или , или

Решения первого уравнения:

Решения второго уравнения:

– не являются решениями исходного уравнения, так как косинус должен быть отрицателен.

Решения третьего:

Ответ: ,

 

Задача 6. Решить уравнение:

Замечаем, что синус должен быть неотрицательным числом, так как слева – корень.

Возводим в квадрат:

Раскроем формулу тройного аргумента:

Домножим на 3 для удобства:

Приравняем к нулю оба множителя:

или 

Решаем теперь второе, квадратное, уравнение:

Корни получаются такие: 2/3 и (-3/4) – последний корень не подходит по ОДЗ, так как результат извлечения корня не может быть отрицательным.

Второму корню будет соответствовать решение:

и , эти два решения можно объединить в одно и записать:

Ответ: , .

easy-physic.ru

Формулы для решения простейших тригонометрических уравнений

Прежде чем решать тригонометрические уравнения, вы должны хорошо разбираться  в тригонометрическом круге.

Все тригонометрические уравнения, какими они не были  – простыми или сложными, в итоге сводятся к решению четырех типов простейших тригонометрических уравнений.

Вы просто обязаны уметь решать уравнения вида

Формулы–алгоритмы  будут  разбросаны  по  трем статьям,

здесь же они собраны все вместе =>

+ показать

Давайте разбираться. В этой статье мы рассмотрим решение уравнения вида . Решение остальных типов простейших уравнений смотрим здесь: часть 2 (), часть 3 (,  )

 Уравнение вида 

 

Решим уравнение

Мы должны подобрать такие значения аргумента , то есть такие значения углов, косинус которых равнялся бы .

Смотрим на тригонометрический круг, на оси косинусов находим :

Выстраиваем через эту точку вертикаль, получаем две точки на круге:

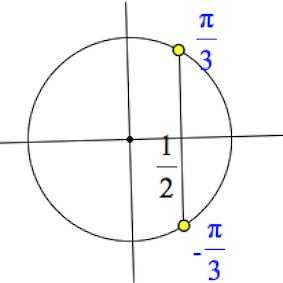
Но надо понимать, что за этими точками скрывается бесконечно много других точек, – таких, косинус в которых также равен . Мы об этом подробно говорили в предыдущей статье, когда знакомились с тригонометрическим кругом.

На координатной прямой подходящие нам точки располагаются  так:

А с графической точки зрения решение уравнения   выглядело бы так:

Как все точки взять в ответ?

Нам поможет счетчик . Возьмем , то есть

Решением уравнения будет

Возьмите, поперебирайте различные значения подставьте в вышеуказанную формулу.

Вы получите как раз точки  при ,

при ,

при и т.д.

То что нам нужно!

Если бы мы решали, например,  уравнение , то решением бы было

.

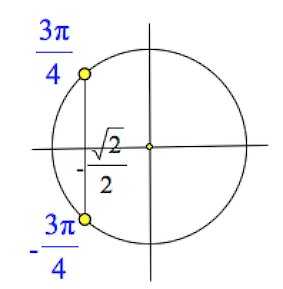
Я думаю, вы уже увидели общий принцип формирования  ответа.

Давайте дадим  формулу, которой можно руководствоваться, решая уравнения

, где – из

(в противном случае, когда – не из – решений нет)

Но вам формула будет понятна, если вы уже знакомы с понятием «арккосинус».

 

Если нам попадается уравнение с нетабличным значением косинуса, вроде этого , то решение будет следующее:

 

 

Частные случаи решения уравнения

1)

 Мы должны бы записать так:

.

Но можно записать решение иначе (ведь в данном случае между точками расстояние – полкруга, значит нам можно использовать полукруговой счетчик ):

2)

У нас только одна серия корней:

то есть 

3) 

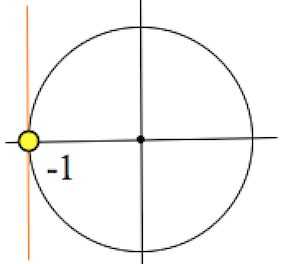
Аналогично решению примера 2, решение такое:

egemaximum.ru

Нестандартные способы решения тригонометрических уравнений

Для решения тригонометрических уравнений используется несколько основных формул, около 20 дополнительных, и всего 8 методов решения. Все эти методы по-своему хороши и применимы для разных видов тригонометрических уравнений. Главная задача при решении тригонометрического уравнения состоит в том, чтобы правильно преобразовать его, свести к какому-нибудь более стандартному варианту подобрать наилучших способ решения для конкретного случая. То есть, в большинстве своём, главная проблема заключается в том, что уравнения надо непременно сначала привести к какому-то виду, прежде чем применить нужный метод решения.

Итак. как я уже сказала, основным методов решения тригонометрических уравнений 8:

1)Разложение одной из частей уравнения на множители.

В данном случае мы все слагаемые переносим в левую часть, раскладываем её на множители и приравниваем каждый множитель к нулю.

Недостаток метода: может быть применён только к узкому кругу уравнений.

2)Замена переменной.

В данном случае уравнение приводят к такому виду, чтобы остался только один вид тригонометрической функции, а затем заменяют её на новую переменную. После решения уравнения относительно введённой переменной, остаётся только решить получившиеся простейшие тригонометрические уравнения согласно базовым формулам.

Преимущество метода: может быть применён к любому тригонометрическому уравнению (если только это целесообразно), так как все тригонометрические функции можно выразить друг через друга. Может также применяться совместно с другими методами.

Недостаток метода: Иногда, пытаясь свести всё уравнение к одному типу тригонометрической функции, мы получаем слишком сложное уравнение, так как не все функции связаны простыми зависимостями. К тому же метод нецелесообразен, когда в уравнении много разных тригонометрических функций.

3)метод решения однородных тригонометрических уравнений. В данном случае мы сначала приводим уравнения к однородному тригонометрическому уравнению. Затем делим обе части на cos x/cos2x/cos3x в зависимости от степени уравнения. Затем производим замену переменной и решаем методом замены переменной.

Преимущество метода: очень прост в применении. Одинаков для всех тригонометрических уравнений одной степени.

Недостаток метода: Далеко не все тригонометрические уравнения можно привести к виду однородных.

4) Решение уравнений вида a*cos x + b*sin x = c с помощью введения вспомогательного угла.

Недостаток метода: можно решить только уравнения определённого вида или сводимые к ним уравнения.

5) Метод подстановки.

В этом случае вместо часто повторяющейся разности или суммы двух функций подставляют переменную, решают уравнение относительно неё, а затем возвращаются к сумме или разности функций, которая была заменена.

Преимущество метода6 даёт большие результаты в комплексном использовании вместе с другими методами.

Недостаток метода: редко применим к сложным уравнениям.

6)Решение тригонометрических уравнении, содержащих обратные тригонометрические функции.

7)Метод универсальной подстановки.

Преимущество: применим для большинства уравнений. В сопряжении с другими методами едва ли не уникален.

Недостаток: после применения подстановки сужается область определения уравнения, поэтому все значения необходимо проверять.

8) ограниченность функций(графический способ). Каждая часть уравнения рассматривается как отдельная функция, причём первая из них – тригонометрическая, а вторая – алгебраическая, строятся графики этих функций, находятся их пересечения.

Преимущество метода: Наглядность, отсутствие сложных преобразований.

Недостатки: Невозможность построения некоторых графиков. Возможность неточностей в определении координат точек пересечения. Возможность ошибки в построении.

*9) Решение тригонометрических уравнений с параметрами.

также существуют общие правила решения тригонометрических уравнений. Во время решения необходимо решать задачи:

1) отсева посторонних корней,

2) потери корней,

3) пересечения решений.

Основная часть.

Общие правила решения тригонометрических уравнений:I.

Решение тригонометрических уравнений сводится, как правило, к решению простейших уравнений: a) sin x = a.

Все решения можно описать формулой: x = (-1)k arcsin a + k, где k – число целое.

b) cos x = a.

Все решения можно описать формулой: x = arccos a + 2k, где k – число целое.

c) tg x = a.

Все решения можно описать формулой: x = arctg a + k, где k – число целое.

d) ctg x = a.

Все решения можно описать формулой: x = arcсtg a + k, где k – число целое.

Если a = 0, то для решения уравнений используются следующие частные формулы: sin x = 0, x = k, где k – число целое.

sin x = 1, x = +2k, где k – число целое.

sin x = -1, x = — + 2k, где k – число целое.

cos x = 0, x = +k, где k – число целое.

cos x = 1, x = 2k, где k – число целое.

cos x = -1, x = +k, где k – число целое.

tg x = 0, x = k, где k – число целое.

ctg x = 0, x = +k, где k – число целое.

1 метод: Разложение одной из частей уравнения на множители.

При данном методе решения всё переносится в левую часть уравнения так, чтобы в правой при этом оставался 0. Затем левая часть уравнения раскладывается на множители и далее уравнение решается согласно известному правилу: если произведение равно нулю, значит хотя бы один из множителей равен нулю. Так мы получаем из сложного уравнения совокупность простых уравнений вида cos t = a, sin t = a, tg t = a, ctg t = a, для решения которых используются вышеприведённые формулы

Примеры применения данного метода:

1) 4sin tcos t – 2cos t + 2sin t — 1 = 0

(2sin t – 1)(2cos t + 1) = 0

2sin t – 1 = 0 или 2cos t + 1 = 0 sin t = или cos t = —

Тогда: t = (-1)karcsin + k, k – число целое или t = arcos(-) a + 2k, где k – число целое.

Иначе: t = (-1)k + k, k – число целое или t = + 2k, где k – число целое.

2) 3tg2 t – 2tg t = 0 tg t (3tg t – 2) = 0 tg t = 0 или 3 tg t – 2 = 0 tg t = 0 или tg t =

Тогда: t = arctg 0 + k = k, где k – число целое или t = arctg + k, где k – число целое.

3) ctg t = ctg3 t ctg t – ctg3 t = 0 ctg t( – ctg2 t) = 0 ctg t( – ctg t)( + ctg t) = 0 ctg t = 0 или – ctg t = 0 или + ctg t = 0

Тогда: t = + k, k – число целое.

t = arcctg + k, где k– число целое t = ( – arcctg ) + k, где k – число целое.

4) 1 – sin xcos x = sin x – cos x

1 – sin xcos x – sin x + cos x = 0

(sin x -1) + cos x (sin x – 1) = 0

(cos x + 1)(sin x – 1) = 0 cos x + 1 = 0 или sin x – 1 = 0 cos x = -1 или sin x = 1 x1 = + k, где k– число целое.

x2 = + 2n, где n – число целое.

2 метод: Замена переменной.

При данном методе решения также все слагаемые переносятся в левую часть, в правой остаётся 0, а тригонометрическая функция в уравнении заменяется переменной. Далее уравнение решается как обычное квадратное уравнение относительно этой переменной. После нахождения значений необходимо заменить переменную соответствующей тригонометрической функцией и найти корни исходного уравнения по формулам.

Примеры применения данного метода:

1) 3cos2 x = 7(sin x +1)

3 – 3sin2 x – 7sin x – 7 = 0

3sin2 x + 7sin x + 4 = 0

Пусть sin x = a, тогда:

3a2 + 7a + 4 = 0

D = 49 – 4*12 = 1 a1 = = -1 a2 = = = , посторонний корень.

Т. к. a = sin x, то: sin x = -1 x = (-1)k+1 * arcsin1 + k, k – число целое.

x = (-1)k+1 * + k, k – число целое.

2) tg2 x + 2tg x – 3 = 0

Пусть tg x = a, тогда: a2 + 2a – 3 = 0

D = 4 + 12 = 16 = 42 a1 = = 1 a2 = = -3

Т. к a = tg x, то: tg x = -3 или tg x = 1 x = -arctg 3 + k или x = + k, где k – число целое.

3) + 10 = + 7

2ctg2 x + 10 + 5ctg x – 7 = 0

2ctg2 x + 5 ctg x + 3 = 0

Пусть ctg x = a, тогда:

2a2 + 5a + 3 = 0

D = 25 – 423 = 1 a1 = = -1 a2 = = -1. 5

Т. к. a = ctg x, то: ctg x = -1 или ctg x = — 1. 5 x = – arcctg1 + k или x = – arcctg1. 5 + k, где k – число целое.

x = + k или x = – arcctg1. 5 + k, где k – число целое.

4)Перепишем уравнение в виде получили уравнение, однородное относительно и Рассмотрим два случая:

1)тогдаоткудачто невозможно, поскольку в этом случае корней нет.

2)тогда разделим обе части уравнения на Пусть Получим откуда Осталось решить уравнения и

Ответ: где

3 метод: Применяется к однородным тригонометрическим уравнениям.

Определение однородных тригонометрических уравнений:

Уравнение вида asin x + bcos x = 0 называют однородным тригонометрическим уравнением первой степени.

Уравнение вида asin2 x + bsin xcos x+ ccos2 x = 0 называют однородным тригонометрическим уравнением второй степени.

Уравнение вида asin3 x + bsin2 xcos x+ csin xcos2 x + dcos3 x = 0 называют однородным тригонометрическим уравнением третей степени.

А вообще тригонометрическое уравнение называют однородным, если после некоторой замены полученный многочлен от двух переменных составлен из одночленов одинаковой степени.

1)Итак, однородные тригонометрические уравнения первой степени решают так:

Сначала обе части уравнения делим почленно на cos x, получим: asin x + bcos x = 0

Выполнив преобразования, получим: atg x + b = 0 tg x =

Отсюда по формуле находим x.

2)Однородные тригонометрические уравнения второй степени решают так: asin2 x + bsin xcos x+ ccos2 x = 0 cos2 x

+ + =

Выполнив преобразования, получим: atg2 x + btg x + c = 0

Далее решаем уравнение методом замены переменной. (см. пример 4) к этому методу).

3)Однородные тригонометрические уравнения третей степени решают так: asin3 x + bsin2 xcos x+ csin xcos2 x + dcos3 x = 0 cos3 x

+ + + = 0

Выполнив преобразования, получим: atg3 x + btg2 x + ctg + d = 0

Далее производим замену переменной и решаем получившееся кубическое уравнение относительно новой переменной. Затем возвращаемся к замене и вычисляем по формуле корни уравнения.

Примеры применения данного метода:

1) sin2 x + 2sin( – x) cos x – 3cos2 (2 – x) = 0

Выполнив преобразования, получим: sin2x + 2sin xcos x – 3cos2 x = 0 cos2 x

+ — = tg2x + 2tg x – 3 = 0

Получаем уравнение, уже решённое нами как пример 2 ко второму методу решения тригонометрических уравнений.

2) 3sin2 3x -2 3 sin3xcos3x + 5cos2 3x = 2

Данное уравнение не является однородным уравнением, поэтому сначала его необходимо привести к виду asin2 x + bsinxcos x+ ccos2 x = 0.

sin2t + cos2t = 1

Тогда 2sin2t + 2cos2t = 2. Заменим t на 3x. Получим равенство:

2sin23x + 2cos23x= 2

Подставим выражение из левой части в правую часть исходного уравнения. Получим:

3sin2 3x — 2sin3xcos3x + 5cos2 3x = 2sin23x + 2cos23x

3sin2 3x — 2sin3xcos3x + 5cos2 3x – 2sin23x – 2cos23x = 0 sin2 3x — 2sin3xcos3x + 3cos2 3x = 0 cos2 3x

— + = tg2 3x – 2tg3x + 3 = 0

Пусть z = tg3x, тогда: z2 – 2z + 3 = 0

(z-)2 = 0 z =, т. е. tg 3x =

Тогда по формуле 3x = arctg + k

3x = П/3 + k x = П/9 + Пk/3, где k – число целое

3) 2sin x – 3cos x = 0

2tg x – 3 = 0 tg x = 1. 5 x = arctg 1. 5 + k, где k – число целое.

4 метод: Решение уравнений вида a*cos x + b*sin x = c с помощью введения вспомогательного угла.

a*cos x + b*sin x = c

Разделим обе части уравнения на = 0.

Легко проверить, что

+ = 1 этому существует такой угол, что cos =, sin =

Если c2 a2 + b2, то найдётся такой угол n,что = cos. В этом случае получим уравнение coscos x + sinsin x = cos cos(x –) = cos, равносильное данному. Решая это уравнение, находим множество решений x = ++ , k – число целое. Если же условие c2 a2 + b2 не выполняется, то уравнение решений уравнение решений не имеет.

Примеры применения данного метода:

1) sin 2x + cos 2x + 1 = 0

+ = sin 2xcos + cos 2xsin = sin(2x + ) =

Откуда x = (-1)k+1 – + , где k – число целое.

2) 12cos x – 5sin x + 13 = 0

Разделив обе части уравнения на = 13, получим cos x – sin x = -1

Полагая cos= и sin=, записываем cos(x +) = -1, где = arccos = arcsin. Решая это уравнение, находим x + = +2k, где k – число целое x = -+ +2k, где k – число целое, откуда x = -arccos + (2k = 1), где k – число целое.

5 метод: Метод подстановки.

Иногда методом введения вспомогательного угла = решаются уравнения, содержащие одно из выражений sin x + cos x, sin x – cos x или sin xcos x. При этом вводят подстановку t = sin x + cos x или t = sin x – cos x и, учитывая, что sin 2x = 2sin xcos x = (sin x + cos x)2 – 1 = t2 – 1 или sin 2x = 1 — (sin x — cos x)2 = 1 – t2, приходят к уравнению относительно переменной t.

Примеры применения данного метода:

1) sin x + cos x = 1 – sin 2x

Обозначим t = sin x + cos x, тогда sin 2x = t2 – 1, поэтому t = 1 – (t2 – 1) t2 + t – 2 = 0,t1 = 1,t2 = -2, откуда: 1) sin x + cos x = 1, x1 = (-1)k – + k, где k – число целое

2) уравнение sin x + cos x = -2 решений не имеет, так как

= cos

Заметим, что при решении тригонометрических уравнений часто произведения разноимённых или одноимённых тригонометрических функций вида sinx* cosx, sinx*sinx, cosx*cosx следует записать в виде суммы или разности этих функций.

6 метод: Решение тригонометрических уравнений, содержащих обратные тригонометрические функции, проводя аналогии с решением подобных уравнений с прямыми тригонометрическими функциями на основе определения зависимости между этими функциями.

Примеры применения данного метода:

1) arcsin x = —

Так как –

2) arcsin2 x – П/2 arcsin x + П2/18 = 0

Воспользуемся методом замены: t = arcsin x, тогда t2 – П/2 t + П2/18 = 0

Решив это уравнение. получим: t1 = , t2 =.

Т. е. arcsin x = или arcsin x =.

Отсюда x1 = , x2 =.

7 метод: Метод универсальной подстановки.

При решении тригонометрических уравнений можно использовать и так называемую универсальную тригонометрическую подстановку на основе формул:

Если теперь ввести обозначение то

С помощью универсальной подстановки мы можем любое уравнение вида свести к алгебраическому уравнению. Важно при этом помнить, что, делая замену, мы можем потерять те корни исходного уравнения, для которых не определён, то есть значения их мы должны проверять отдельно.

В общем о решении тригонометрических уравнений.

При решении тригонометрических уравнений следует соблюдать общие правила: следить за равносильностью преобразований, не допускать потери корней, отбрасывать посторонние корни.

1) Отсев посторонних корней.

При решении уравнений вида возникает проблема отсеивания посторонних корней. Напомним, что

Примеры:

Далее из соотношения получаем , но тогда и

Замечание1.

Найдя корни уравнения, необходимо выбрать те значения m, которые удовлетворяют неравенству Так как период функций, входящих в уравнение, равен , то достаточно выполнить проверку на любом отрезке длины , например, на отрезке На этом отрезке необходимо проверить значения и. Только во второй точкеЭто значение с периодичностью и будет давать ответ.

Замечание2.

Можно заметить, что при Неравенство системы оставляет только один из возможных вариантов —

Область определения уравнения

Выполняя очевидные преобразовании, получим и В результате получаем систему

Ясно, что тогда, когда т. е. Легко видеть, что при но тогда

Находим область определения уравнения:

Решаем уравнение:

Если ,то

Если то

Но область определения даёт тогда но поэтому корни уравнения содержатся среди корней уравнения

В результате получаем систему

Попарная проверка соотношений приводит к соотношения которые всегда выполняются, так как в левой части этих неравенств чётные числа, а в правой – нечётные.

Покажем, что область определения уравнения есть все значения x, удовлетворяющие двойному неравенству

2) Потеря корней.

При решении некоторых тригонометрических равнений может произойти потеря корней. Это связано с применением формул, у которых левая и правая части имеют различные области определения, причём правая часть имеет более узкую область определения, чем левая. Это, например, формулы и т. д.

Замена при решении тригонометрических уравнений левой части указанных формул правой части может привести к потере корней, так как происходит сужение области определения уравнения. Поэтому после применения формул с различными областями определений необходимо выполнить проверку для тех значений неизвестного, при которых не определена правая часть формул. но определена их левая часть.

Примеры:

Для данного уравнения Заменяем исходное уравнение на уравнение

В первоначальном уравнении числа вида принадлежат области определения уравнения, а в полученном уравнении – нет, поэтому проверяем, не являются ли числа вида корнями данного уравнения:

— равенство верное.

Значит, — решение данного уравнения.

Продолжим решение уравнения

Ответ: ;

Область допустимых значений определяется системой неравенств: откуда Применяя формулы с и приходим к уравнению при этом произошло сужение области определения – добавилось ограничение

Для простоты дальнейшего решения положим где тогда уравнение принимает вид Так как то, сократив обе части уравнения на получим

Поскольку то Последнее уравнение положительных корней не имеет, так как при и непосредственная проверка показывает, что числа вида являются корнями данного уравнения.

Находим область определения уравнения. Очевидно, что Замечая, что приходим к уравнению Произошло сужение области определения – к ранее полученным ограничениям на x добавляется новое: Так как равенство верное, то — решение данного уравнения. Введём обозначение тогда последнее уравнение примет вид При и оно равносильно уравнению

или откуда или Но тогда

3) Пересечение решений.

Запись решения тригонометрического уравнения часто связана с понятиями «объединение» и «пересечение» множеств». Обычно при решении уравнений получаются серии корней и ответ записывается в виде объединения этих серий. Но иногда эти серии пересекаются. В этом случае следует исключить повторяющиеся решения. Кроме того, в ответе не должно быть значений неизвестных, при которых выражения в левой и правой частях уравнения не определены. Такие значения, если они появились в процессе решения, надо исключить. Для этого также следует найти пересечения различных серий. При решении некоторых тригонометрических уравнений их заменяют эквивалентной совокупностью уравнений и находят объединение множеств решений этих уравнений.

Пример:

Допустимые значения неизвестного x определяются условиями откуда Эти три условия можно заменить одним: Увидеть это можно, например, на тригонометрическом круге: множество всех чисел вида содержит в себе числа видов Умножив обе части уравнения на получим уравнение равносильное данному на множестве допустимых значений Заметив, что получим

Но поэтому последнее уравнение равносильно совокупности уравнений и которые дают соответственно следующие серии корней: и Поскольку а при получается серия исключается. Рассмотрим серию исключим такие целые k, при которых найдётся такое n, что выполнится равенство или решим это уравнение в целых числах. Левая часть уравнения делится на 4, поэтому и откуда Числа — нечётные, поэтому и Значит, Отсюда следует, что в серии нужно исключить все корни, соответствующие значениям Значит, где — все решения исходного уравнения.

Решение тригонометрических уравнений с параметрами.

1) В зависимости от значений параметра a решить уравнение и определить число его корней на отрезке

Допустимые значения переменной х задаются системой

Исходное уравнение равносильно уравнению которое равносильно совокупности двух уравнений

Так как то второе уравнение системы решений не имеет. Рассмотрим первое уравнение системы. Так как здесь числитель должен равняться нулю, т. е. то При таких значениях х с учётом области допустимых значений находим, что. Итак, при из неравенств следует, что Этим неравенствам удовлетворяют девять целых значений k и, следовательно, исходное уравнение имеет девять решений на заданном промежутке.

Пустьтогда первое уравнение системы запишется в виде Исключая из множества решения уравнений и получим А тогда решая неравенство находим, что и, таким образом, существует пять целых решений рассматриваемого неравенства. Рассмотрим случай При таком значении параметра а имеем уравнение Здесь уже надо из множества решений исключить решения уравнений и Сделав это, получим решая же неравенство окончательно находим, что при исходное неравенство имеет четыре решения.

Ответ: если , то девять корней если то пять корней если то четыре корня

2) При каких значениях параметров a и b уравнение имеет единственное решение? решение задачи основывается на том факте, что если функция f задана равенством то условия А=В, С=0 являются необходимыми и достаточными условиями того, чтобы уравнение имело единственное решение. Таким образом, решение задачи сводится к решению относительно параметров a и b системы

Из первого уравнения этой системы находим, что А так как то приходим к рассмотрению систем и

Как легко видеть, решениями второй системы являются все значения параметра а, определяемые равенством что же касается первой системы, то она оказывается несовместной. Отсюда, с учётом второго уравнения системы поиск требуемых параметров a и b сводится к поиску решений системы ответ здесь очевиден.

Ответ: любое.

3) В зависимости от значений параметров a и b решить уравнение

Обозначив получим систему откуда находим Но так как то и значит

Ответ: если то при других значениях a и b решений нет.

4) В зависимости от значений параметра а решить уравнение

Допустимыми значениями переменной х являются все При таких значениях х полагая перепишем уравнение в виде Если то При записанное уравнение равносильно совокупности Дискриминанты обоих уравнений совокупности совпадают и имеют вид: Поэтому, если то решений у уравнения нет.

Пусть В этом случае решая уравнения совокупности, находим, что

При имеем В остальных случаях все корни определяются формулами.

Ответ: если то решений нет; если то если , то при остальных значениях параметра а

Вывод по работе:

Я провела исследования по способам решения тригонометрических уравнений, выявила 9 основных методов решения тригонометрических уравнений, положительные и отрицательные черты этих методов, решила уравнения, которые не подлежат решению стандартными способами, выявила другие методы решения тригонометрических уравнений. Узнала. что особое внимание следует обратить на решение тригонометрических уравнений с параметрами, поскольку их решение наименее стандартно. При решении нестандартных тригонометрических уравнений следует умело анализировать зависимости между различными тригонометрическими функциями и уметь творчески подходить к работе.

Данная работа имеет большое практическое значение, т. к. тригонометрические уравнения часто содержатся в материалах ЕГЭ и экзаменов для поступления в вузы, а в школьном курсе математике недостаточно изучаются. Исследование может быть употреблено как материал для проведения предметных факультативов по алгебре или при подготовке к ЕГЭ.

www.hintfox.com

Решение тригонометрических уравнений, сводящихся к квадратным уравнениям

Я начинаю цикл статей, посвященных решению тригонометрических уравнений. Решение простейших тригонометрических уравнений и неравенств мы уже рассматривали, и теперь пора заняться более сложными вещами. Чтобы научиться решать более сложные тригонометрические уравнения, нужно хорошо знать типы тригонометрических уравнений и способы их решения.

Начнем с тригонометрических уравнений, сводящихся к квадратным.

Отличительные признаки тригонометрических уравнений, сводящихся к квадратным:

1. В уравнении присутствуют тригонометрические функции от одного аргумента, или они легко сводятся к одному аргументу.

2. В уравнении присутствует только одна тригонометрическая функция, или все функции можно свести к одной.

Заметим, что легко сводится к  или  по формуле косинуса двойного аргумента :

.

легко сводится к  с помощью основного тригонометрического тождества.

Пример 1. Решим уравнение:

1. Воспользуемся формулой приведения:

Получим уравнение:

2. Теперь   нам удобно выразить через , поскольку в уравнении присутствует :

, где 

Ответ: , где 

Пример 2. Решим уравнение.

Упростим выражение  — разложим его на множители по формуле разности квадратов :

Получим:

Введем замену переменной: , 

Получим квадратное уравнение:

По теореме Виета находим корни: ,  . Оба корня нас устраивают.

Теперь можем вернуться к исходной переменной, получим:

или 

, или ,  где 

Ответ: , ,  где 

И.В. Фельдман, репетитор по математике.

Купить видеокурс «ВСЯ ТРИГОНОМЕТРИЯ. Часть В и С1»

ege-ok.ru