Два уравнения с тремя неизвестными
63. Два уравнения с тремя неизвестными. Пусть имеем уравнения:
3x + 4y – 2z = 11
5x + 4y + 2z = 19,
которые надо решить совместно. Мы умеем решать совместно 2 уравнения с двумя неизвестными, почему прежде всего приходит мысль, что здесь одно неизвестное является лишним и что его, вероятно, можно заменить любым числом. И действительно. Если дадим x произвольное значение, например, возьмем x = 7, то получим
21 + 4y – 2z = 11
35 + 4y + 2z = 19,
т. е. 2 уравнения с двумя неизвестными, которые мы умеем решить.
Упростив эти уравнения, получим:
4y – 2z = –10
4y + 2z = –16.
Сложив из по частям, получим:
8y = –26 и y = –3 ¼.
Вычитая из 2-го первое, получим:
4z = –6 и z = –1 ½.
Взяв x = 0, получим:
4y – 2z = 11
4y + 2z = 19.
Решив (так же, как и выше) эти уравнения, получим:
y = 3 ¾; z = 2
Так же для x = 1, получим y = 2 ¾; z = 1 ½ и т. д.
Эти решения можно записать в таблице, причем, как видим, здесь одно неизвестное (у нас x) является независимым переменным, а два других являются зависимыми переменными.
Вот эта таблица:
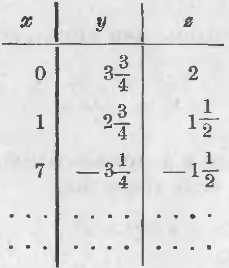
Итак,
два уравнения с тремя неизвестными имеют бесконечно много решений, причем для получения их надо одному из неизвестных давать произвольные значения.
Чтобы удобнее получать эти решения, можно заранее из данных уравнений определить зависимые переменные через независимое.
Для этой цели перенесем члены 3x и 5x, имеющиеся в наших уравнениях, в правую часть (эти члены, ведь, приходится считать известными), — получим:
4y – 2z = 11 – 3x
4y + 2z = 19 – 5x.
Сложив эти уравнения по частям, получим:
8y = 30 – 8x и y = (30 – 8x) / 8 = (15 – 4x) / 4.
Вычитая по частям из 2-го уравнения первое, получим:
4z = 8 – 2x и z = (8 – 2x) / 4 = (4 – x) / 2.
Теперь, взяв для x какое-нибудь значение, например, x = 2, легко в уме найдем: y = 1 ¾ и z = 1.
Вот еще пример. Пусть даны уравнения:
2x + y – z = 7
3x + 2y + 4z = 11.
Определим из них x и y через z. Для этого сначала перенесем члены с z в правую часть уравнения:
2x + y = 7 + z и 3x + 2y = 11 – 4z (1).
Обе части первого уравнения умножим на 2:
4x + 2y = 14 + 2z
3x + 2y = 11 – 4z.
Вычтем по частям из 1-го уравнения второе:
x = 3 + 6z (2)
Таким образом мы определили x через z. Затем умножим обе части 1-го уравнения из системы (1) на 3 и обе части 2-го на 2 (чтобы уравнять коэффициенты при x). Получим:
6x + 3y = 21 + 3z
6x + 4y = 22 – 8z.
Вычитая по частям из 2-го уравнения первое, получим:
y = 1 – 11z (3)
Таким образом определили y через z.
Пользуясь равенствами (2) и (3), легко найти сколько угодно решений данных двух уравнений, причем надо неизвестному z давать произвольные значения. Вот несколько решений:

maths-public.ru
Как решать систему уравнений с двумя неизвестными | ЧтоКак.ру

Уравнение – это тождество, где среди известных членов скрывается одно число, которое необходимо поставить вместо латинской буквы, для того чтобы с левой и правой стороны получилось одинаковое числовое выражение. Чтобы его найти, нужно перенести в одну сторону все известные члены, в другую — все неизвестные члены уравнения. А как решать систему из двух таких уравнений? По отдельности – нельзя, следует связать искомые величины из системы друг с другом. Сделать это можно тремя способами: методом подстановки, методом сложения и методом построения графиков.
Инструкция
1
Способ сложения.Нужно записать два уравнения строго друг под другом: 2 –5у=61-9х+5у=-40.Далее, сложить каждое слагаемое уравнений соответственно, учитывая их знаки:2х+(-9х)=-7х, -5у+5у=0, 61+(-40)=21. Как правило, одна из сумм, содержащая неизвестную величину, будет равна нулю. Составить уравнение из полученных членов:-7х+0=21.Найти неизвестное: -7х=21, ч=21:(-7)=-3.Подставить уже найденное значение в любое из исходных уравнений и получить второе неизвестное, решив линейное уравнение:2х–5у=61, 2(-3)–5у=61, -6-5у=61, -5у=61+6, -5у=67, у=-13,4.Ответ системы уравнений: х=-3, у=-13,4.
2
Способ подстановки.Из одного уравнения следует выразить любое из искомых членов:х–5у=61-9х+4у=-7.х=61+5у, х=61+5у.Подставить получившееся уравнение во второе вместо числа «икс» (в данном случае):-9(61+5у)+4у=-7.Далее решивлинейное уравнение, найти число «игрек»:-549+45у+4у=-7, 45у+4у=549-7, 49у=542, у=542:49, у?11.В произвольно выбранное (из системы) уравнение вставить вместо уже найденного «игрека» число 11 и вычислить второе неизвестное:Х=61+5*11, х=61+55, х=116.Ответ данной системы уравнений: х=116, у=11.
3
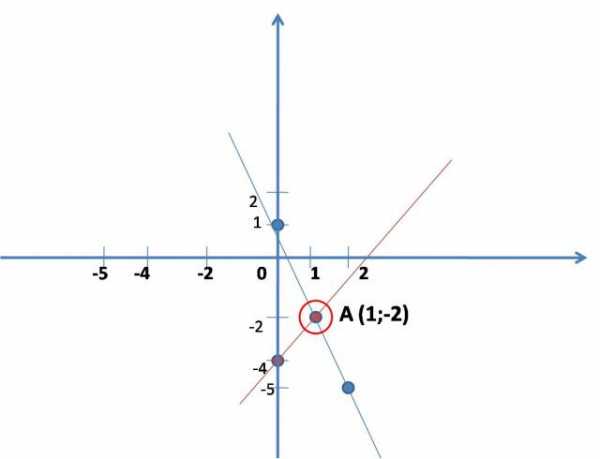
Графический способ.Заключается в практическом нахождении координаты точки, в которой пересекаются прямые, математически записанные в системе уравнений. Следует начертить графики обоих прямых по отдельности в одной системе координат. Общий вид уравнения прямой: – у=kх+b. Чтобы построить прямую, достаточно найти координаты двух точек, причем, х выбирается произвольно.Пусть дана система: 2х – у=4 у=-3х+1.Строится прямая по первому уравнению, для удобства его нужно записать: у=2х-4. Придумать (полегче) значения для икс, подставляя его в уравнение, решив его, найти игрек. Получаются две точки, по которым строится прямая. (см рис.)х 0 1у -4 -2Строится прямая по второму уравнению: у=-3х+1.Так же построить прямую. (см рис.)х 0 2у 1 -5Найти координаты точки пересечения двух построенных прямых на графике (если прямые не пересекаются, то система уравнений не имеет решения – так бывает).
chtokak.ru
Подготовка школьников к ЕГЭ и ОГЭ в учебном центре «Резольвента» (Справочник по математике — Алгебра
Линейные уравнения (уравнения первой степени) с двумя неизвестными
Определение 1. Линейным уравнением (уравнением первой степени) с двумя неизвестными x и y называют уравнение, имеющее вид
где a , b , c – заданные числа.
Определение 2. Решением уравнения (1) называют пару чисел (x ; y) , для которых формула (1) является верным равенством.
Пример 1. Найти решение уравнения
Решение. Выразим из равенства (2) переменную y через переменную x :
| (3) |
Из формулы (3) следует, что решениями уравнения (2) служат все пары чисел вида
где x – любое число.
Замечание. Как видно из решения примера 1, уравнение (2) имеет бесконечно много решений. Однако важно отметить, что не любая пара чисел (x ; y) является решением этого уравнения. Для того, чтобы получить какое-нибудь решение уравнения (2), число x можно взять любым, а число y после этого вычислить по формуле (3).
Системы из двух линейных уравнений с двумя неизвестными
Определение 3. Системой из двух линейных уравнений с двумя неизвестными x и y называют систему уравнений, имеющую вид
| (4) |
где a1 , b1 , c1 , a2 , b2 , c2 – заданные числа.
Определение 4. В системе уравнений (4) числа a1 , b1 , a2 , b2 называют коэффициентами при неизвестных, а числа c1 , c2 – свободными членами.
Определение 5. Решением системы уравнений (4) называют пару чисел (x ; y) , являющуюся решением как одного, так и другого уравнения системы (4).
Определение 6. Две системы уравнений называют равносильными (эквивалентными), если все решения первой системы уравнений являются решениями второй системы, и все решения второй системы являются решениями первой системы.
Равносильность систем уравнений обозначают, используя символ «»
Системы линейных уравнений решают с помощью метода последовательного исключения неизвестных, который мы проиллюстрируем на примерах.
Пример 2 . Решить систему уравнений
| (5) |
Решение. Для того, чтобы решить систему (5) исключим из второго уравнения системы неизвестное х.
С этой целью сначала преобразуем систему (5) к виду, в котором коэффициенты при неизвестном x в первом и втором уравнениях системы станут одинаковыми.
Если первое уравнение системы (5) умножить на коэффициент, стоящий при x во втором уравнении (число 7 ), а второе уравнение умножить на коэффициент, стоящий при x в первом уравнении (число 2 ), то система (5) примет вид
| (6) |
Теперь совершим над системой (6) следующие преобразования:
- первое уравнение системы оставим без изменений;
- из второго уравнения вычтем первое уравнение и заменим второе уравнение системы на полученную разность.
В результате система (6) преобразуется в равносильную ей систему
Из второго уравнения находим y = 3 , и, подставив это значение в первое уравнение, получаем
Ответ. (–2 ; 3) .
Пример 3. Найти все значения параметра p , при которых система уравнений
| (7) |
а) имеет единственное решение;
б) имеет бесконечно много решений;
в) не имеет решений.
Решение. Выражая x через y из второго уравнения системы (7) и подставляя полученное выражение вместо x в первое уравнение системы (7), получим
Следовательно, система (7) равносильна системе
| (8) |
Исследуем решения системы (8) в зависимости от значений параметра p . Для этого сначала рассмотрим первое уравнение системы (8):
| y (2 – p) (2 + p) = 2 + p | (9) |
Если , то уравнение (9) имеет единственное решение
Следовательно, система (8) равносильна системе
Таким образом, в случае, когда , система (7) имеет единственное решение
Если p = – 2 , то уравнение (9) принимает вид
,
и его решением является любое число . Поэтому решением системы (7) служит бесконечное множество всех пар чисел
,
где y – любое число.
Если p = 2 , то уравнение (9) принимает вид
и решений не имеет, откуда вытекает, что и система (7) решений не имеет.
Системы из трех линейных уравнений с тремя неизвестными
Определение 7. Системой из трех линейных уравнений с тремя неизвестными x , y и z называют систему уравнений, имеющую вид
| (10) |
где a1 , b1 , c1 , d1 , a2 , b2 , c2 , d2 , a3 , b3 , c3 , d3 – заданные числа.
Определение 8. В системе уравнений (10) числа a1 , b1 , c1 , a2 , b2 , c2 , a3 , b3 , c3 называют коэффициентами при неизвестных, а числа d1 , d2 , d3 – свободными членами.
Определение 9. Решением системы уравнений (10) называют тройку чисел (x ; y ; z) , при подстановке которых в каждое из трех уравнений системы (10) получается верное равенство.
Пример 4 . Решить систему уравнений
| (11) |
Решение. Будем решать систему (11) при помощи метода последовательного исключения неизвестных.
Для этого сначала исключим из второго и третьего уравнений системы неизвестное y , совершив над системой (11) следующие преобразования:
- первое уравнение системы оставим без изменений;
- ко второму уравнению прибавим первое уравнение и заменим второе уравнение системы на полученную сумму;
- из третьего уравнения вычтем первое уравнение и заменим третье уравнение системы на полученную разность.
В результате система (11) преобразуется в равносильную ей систему
| (12) |
Теперь исключим из третьего уравнения системы неизвестное x , совершив над системой (12) следующие преобразования:
- первое и второе уравнения системы оставим без изменений;
- из третьего уравнения вычтем второе уравнение и заменим третье уравнение системы на полученную разность.
В результате система (12) преобразуется в равносильную ей систему
| (13) |
Из системы (13) последовательно находим
z = – 2 ; x = 1 ; y = 2 .
Ответ. (1 ; 2 ; –2) .
Пример 5. Решить систему уравнений
| (14) |
Решение. Заметим, что из данной системы можно получить удобное следствие, сложив все три уравнения системы:
Если числа (x ; y ; z) являются решением системы (14), то они должны удовлетворять и уравнению (15). Однако в таком случае числа (x ; y ; z) должны также быть решением системы, которая получается, если из каждого уравнения системы (14) вычесть уравнение (15):
Поскольку мы использовали следствие из системы (14), не задумываясь о том, являются ли сделанные преобразования системы (14) равносильными, то полученный результат нужно проверить. Подставив тройку чисел (3 ; 0 ; –1) в исходную систему (14), убеждаемся, что числа (3 ; 0 ; –1) действительно являются ее решением.
Ответ: (3 ; 0 ; –1) .
Замечание. Рекомендуем посетителю нашего сайта, интересующемуся методами решения систем уравнений, ознакомиться также c разделом справочника «Системы с нелинейными уравнениями» и нашим учебным пособием «Системы уравнений».
На нашем сайте можно также ознакомиться с разработанными преподавателями учебного центра «Резольвента» учебными материалами для подготовки к ЕГЭ и ОГЭ по математике.
Приглашаем школьников (можно вместе с родителями) на бесплатное тестирование по математике, позволяющее выяснить, какие разделы математики и навыки в решении задач являются для ученика «проблемными». Запись по телефону (495) 509-28-10 |
Для школьников, желающих хорошо подготовиться и сдать ЕГЭ или ОГЭ по математике или русскому языку на высокий балл, учебный центр «Резольвента» проводит
У нас также для школьников организованы
МОСКВА, СВАО, Учебный центр «РЕЗОЛЬВЕНТА»
www.resolventa.ru
Содержание
Инструкция
|
completerepair.ru