как найти синус через тангенс??
Для упрощения аргумент писать не буду, надеюсь и так понятно. Решается так: ctg^2+1=1/sin^2, отсюда sin^2=1/(1+ctg^2)=1/(1+1/tg^2)=1/((tg^2+1)/tg^2)=tg^2/(tg^2+1), |sin|=tg/sqrt(tg^2+1). В конечной формуле получается абсолютное значение синуса. Для определения знака нужны дополнительные условия. Например ( в примерах аргумент приведен в градусах) : tg(60)=sqrt(3), sin(60)=sqrt(3)/2, tg(30)/sqrt((tg(30))^2+1=sqrt(3)/sqrt(3+1)=sqrt(3)/sqrt(4)=sqrt(3)/2, НО!! ! tg(240)=sqrt(3), tg(240)/sqrt((tg(240))^2+1=sqrt(3)/sqrt(3+1)=sqrt(3)/sqrt(4)=sqrt(3)/2, НО sin(240)=-sqrt(3).
Тангенс умножить на косинус
есть формула 1 + тангенс^2 = 1/синус^2
1.Тангенс альфа=синус/косинус альфа. Эта формула чтобы найти тангенс через косинус. 2.1+тангенс квадрат альфа=1/синус квадрат альфа. Эта чтобы найти синус через косинус. По моему эта формула (2),но на все 100% не уверен.
Как найти косинус через тангенс? Спасибо)))
косинус = синус / тангенс еще косинус = (1-tg^2 x/2) / *(1+tg^2 x/2)
<img src=»//content.foto.my.mail.ru/mail/sveta-matskevich/_answers/i-298.jpg» >
раздели синус на тангенс) удачи) если есть еще вопросы из этой серии задавай)
<img src=»//otvet.imgsmail.ru/download/2c1c68c80a013486f2ef431e0475b634_i-12.jpg» > <a rel=»nofollow» href=»http://ru.wikipedia.org/wiki/Тангенс» target=»_blank» >Смотреть здесь</a>
косинус в квадрате = 1 + 1/(тангенс в квадрате)touch.otvet.mail.ru
Как находить синус угла :: SYL.ru
Синус является одной из основных тригонометрических функций, применение которой не ограничено одной лишь геометрией. Таблицы вычисления тригонометрических функций, как и инженерные калькуляторы, не всегда под рукой, а вычисление синуса порой нужно для решения различных задач. Вообще, вычисление синуса поможет закрепить чертёжные навыки и знание тригонометрических тождеств.
Игры с линейкой и карандашом
Простая задача: как найти синус угла, нарисованного на бумаге? Для решения понадобится обычная линейка, треугольник (или циркуль) и карандаш. Простейшим способом вычислить синус угла можно, разделив дальний катет треугольника с прямым углом на длинную сторону — гипотенузу. Таким образом, сначала нужно дополнить острый угол до фигуры прямоугольного треугольника, прочертив перпендикулярную одному из лучей линию на произвольном расстоянии от вершины угла. Потребуется соблюсти угол именно 90°, для чего нам и понадобится канцелярский треугольник.
Использование циркуля немного точнее, но займёт больше времени. На одном из лучей нужно отметить 2 точки на некотором расстоянии, настроить на циркуле радиус, примерно равный расстоянию между точками, и прочертить полуокружности с центрами в этих точках до получения пересечений этих линий. Соединив точки пересечения наших окружностей между собой, мы получим строгий перпендикуляр к лучу нашего угла, остаётся лишь продлить линию до пересечения с другим лучом.
В полученном треугольнике нужно линейкой измерить сторону напротив угла и длинную сторону на одном из лучей. Отношение первого измерения ко второму и будет искомой величиной синуса острого угла.
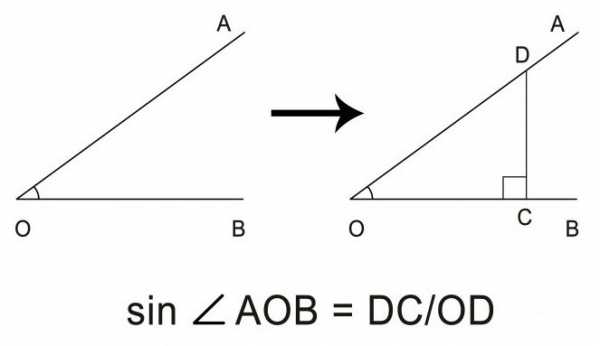
Найти синус для угла больше 90°
Для тупого угла задача не намного сложнее. Нужно прочертить луч из вершины в противоположную сторону с помощью линейки для образования прямой с одним из лучей интересующего нас угла. С полученным острым углом следует поступать как описано выше, синусы смежных углов, образующих вместе развёрнутый угол 180°, равны.
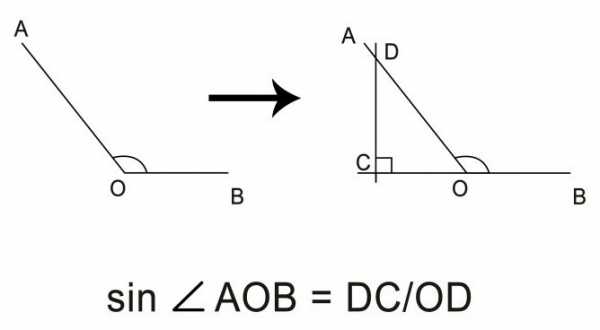
Вычисление синуса по другим тригонометрическим функциям
Также вычисление синуса возможно, если известны значения других тригонометрических функций угла или хотя бы длины сторон треугольника. В этом нам помогут тригонометрические тождества. Разберём распространённые примеры.
Как находить синус при известном косинусе угла? Первое тригонометрическое тождество, исходящее из теоремы Пифагора, гласит, что сумма квадратов синуса и косинуса одного и того же угла равна единице.
Как находить синус при известном тангенсе угла? Тангенс получают делением дальнего катета на ближний или делением синуса на косинус. Таким образом, синусом будет произведение косинуса на тангенс, а квадратом синуса будет квадрат этого произведения. Заменяем косинус в квадрате на разность между единицей и квадратным синусом согласно первому тригонометрическому тождеству и путём нехитрых манипуляций приводим уравнение к вычислению квадратного синуса через тангенс, соответственно, для вычисления синуса придётся извлечь корень из полученного результата.
Как находить синус при известном котангенсе угла? Значение котангенса можно вычислить, разделив длину ближнего от угла катета на длину дальнего, а также поделив косинус на синус, то есть котангенс — функция, обратная тангенсу относительно числа 1. Для расчёта синуса можно вычислить тангенс по формуле tg α = 1 / ctg α и воспользоваться формулой во втором варианте. Также можно вывести прямую формулу по аналогии с тангенсом, которая будет выглядеть следующим образом.
Как находить синус по трём сторонам треугольника
Существует формула для нахождения длины неизвестной стороны любого треугольника, не только прямоугольного, по двум известным сторонам с использованием тригонометрической функции косинуса противолежащего угла. Выглядит она так.
Ну, а синус можно далее рассчитать по косинусу согласно формулам выше.
