Как у треугольника найти высоту – «Как найти в треугольнике высоту?» – Яндекс.Знатоки

Содержание

Как найти высоту треугольника если известно только 3 стороны? СРОЧНО!!!

Через Полупериметр — Площадь, все стороны известны. Затем Высоту из обычной формулы Площади треугольника<img src=»//otvet.imgsmail.ru/download/79ce538a2bb30e3b775e9de15b0dab2f_i-260.jpg» >

Нужно разделить его на два. И получится что его высота, это есть гипотенуза половины. А так как стороны известны, теорема пифагора в помощь.

Такие задания называются «решение треугольника» — нахождение всех сторон и всех углов треугольника. Треугольник можно «решить», если известны три стороны, две стороны и один угол, два угла и одна сторона. Для произвольных треугольников используеься теорема косинусов: Квадрат стороны треугольника равен сумме квадратов двух других сторон без удвоенного произведения этих сторон на косинус угла между ними. и теорема синусов Стороны треугольника пропорционально синусам противоположных углов В твоем случае — находим по сторонам углы, высота делит исходный треугольник на два прямоугольных треугольника, один из которых нужно «решить».

touch.otvet.mail.ru

Как найти высоту треугольника

Давайте разберемся как найти высоту треугольника.
Но прежде вспомним — что же такое высота треугольника?
Высотой называют перпендикуляр, который выходит из любой вершины треугольника и заканчивается на противоположной его стороне.
Если один из углов треугольника является тупым, то перпендикуляр из двух вершин проводится на продолжение сторон такого треугольника.
Высот у треугольника можно провести три (по количеству его вершин). А пересекаются все высоты треугольника в одной точке, которую называют ортоцентром.
Для нахождения длины высоты треугольника существует несколько формул, которые мы и рассмотрим.

Формула 1.
Высоту можно найти через длины сторон треугольника:

Здесь p — полупериметр, который находят по формуле:

По большому счету основанием в этой формуле считается третья сторона треугольника, к которой проведена высота.

Формула 2.
Формула применяется, если известны одна боковая сторона и угол при основании, который прилегает к этой стороне:

Формула 3.
Формулу удобно использовать, если известно основание треугольника и его площадь:

Формула 4.
При известных боковых сторонах треугольника и радиусе описанной окружности:

ru.solverbook.com

как найти высоту треугольника равнобедренного если известны все стороны?

Если высота проведена из вершины В в равнобедренном триугольнике АВС, то пусть она будет ВF, тогда AF=FC= 8/2=4 Т. к. провили высоту то у нас получились 2 равных ПРЯМОУГОЛЬНЫХ триугольника. Рассмотрим триугольник ABF, по теореме Пифагора АВ2=AF2+BF2 ( 2- Квадрат) BF2= AB2-AF2 BF2=9 BF=3 см Ответ: 3 см

по теореме пифагора

Н = корень из (5^2-4^2)=корень из 9=3

У равнобедренного треугольника 3 высоты, (как впрочем у любого треугольника) . Какую ищем?

touch.otvet.mail.ru

Как найти высоту треугольника?

Для решения многих геометрических задач требуется найти высоту заданной фигуры. Эти задачи имеют прикладное значение. При проведении строительных работ определение высоты помогает вычислить необходимое количество материалов, а также определить, насколько точно сделаны откосы и проемы. Часто для построения выкроек требуется иметь представление о свойствах геометрических фигур.

У многих людей, несмотря на хорошие оценки в школе, при построении обычных геометрических фигур возникает вопрос о том, как найти высоту треугольника или параллелограмма. Причем определение высоты треугольника является самым сложным. Это происходит потому, что треугольник может быть острым, тупым, равнобедренным или прямоугольным. Для каждого из видов треугольников существуют свои правила построения и расчета.

Как найти высоту треугольника, в котором все углы острые, графическим способом

Если все углы у треугольника острые (каждый угол в треугольнике меньше 90 градусов), то для нахождения высоты необходимо сделать следующее.

По заданным параметрам выполняем построение треугольника.
Введем обозначения. А, В и С будут вершинами фигуры. Углы, соответствующие каждой вершине – α, β, γ. Противолежащие этим углам стороны – a, b, c.
Высотой называется перпендикуляр, опущенный из вершины угла к противоположной стороне треугольника. Для нахождения высот треугольника проводим построение перпендикуляров: из вершины угла α к стороне a, из вершины угла β к стороне b и так далее.
Точку пересечения высоты и стороны a обозначим h2, а саму высоту h2. Точка пересечения высоты и стороны b будет h3, высота соответственно h3. Для стороны c высота будет h4, а точка пересечения h4.

Далее для каждого вида треугольника будем использовать те же обозначения сторон, углов, высот и вершин треугольников.

Высота в треугольнике с тупым углом

Теперь рассмотрим, как найти высоту треугольника, если один угол тупой (больше 90 градусов). В этом случае высота, проведенная из тупого угла, будет внутри треугольника. Остальные две высоты будут находиться за пределами треугольника.

Пусть в нашем треугольнике углы α и β будут острыми, а угол γ – тупой. Тогда для построения высот, выходящих из углов α и β, надо продолжить противоположные им стороны треугольника, чтобы провести перпендикуляры.

Как найти высоту равнобедренного треугольника

У такой фигуры есть две равные стороны и основание, при этом углы, находящиеся при основании, также являются равными между собой. Это равенство сторон и углов облегчает построение высот и их вычисление.

Сначала нарисуем сам треугольник. Пусть стороны b и c, а также углы β, γ будут соответственно равными.

Теперь проведем высоту из вершины угла α, обозначим ее h2. Для равнобедренного треугольника эта высота будет одновременно биссектрисой и медианой.

Далее построим две другие высоты: h3 для стороны b и угла β, h4 для стороны c и угла γ. Эти высоты будут равными по длине.

Для основания можно сделать только одно построение. Например, провести медиану – отрезок, соединяющий вершину равнобедренного треугольника и противоположную сторону, основание, для нахождения высоты и биссектрисы. А для вычисления длины высоты для двух других сторон можно построить только одну высоту. Таким образом, чтобы графически определить, как вычислить высоту равнобедренного треугольника, достаточно найти две высоты из трех.

Как найти высоту прямоугольного треугольника

У прямоугольного треугольника определить высоты намного проще, чем у других. Это происходит потому, что сами катеты составляют прямой угол, а значит, являются высотами.

Для построения третьей высоты, как обычно, проводится перпендикуляр, соединяющий вершину прямого угла и противоположную сторону. В итоге для того, чтобы узнать, как найти высоту треугольника в данном случае, требуется только одно построение.

fb.ru

Как найти высоту треугольника Как? Так!

Содержимое:

3 метода:

Для вычисления площади треугольника вам необходимо знать его высоту. Если она не дана, вы можете вычислить ее по известным вам величинам! В этой статье мы расскажем о нескольких способах найти высоту треугольника по известным значениям других величин.

Шаги

Метод 1 Как найти высоту по основанию и площади

1 Напомним формулу для вычисления площади треугольника. Площадь треугольника вычисляется по формуле: A = 1/2bh.^{А — площадь треугольника
b — сторона треугольника, на которую опущена высота.
h — высота треугольника}
2 Посмотрите на треугольник и подумайте, какие величины вам уже известны. Если вам дана площадь, обозначьте ее буквой «А» или «S». Вам также должно быть дано значение стороны, обозначьте ее буквой «b». Если вам не дана площадь и не дана сторона, воспользуйтесь другим методом.
- Имейте в виду, что основанием треугольника может быть любая его сторона, на которую опущена высота (независимо от того, как расположен треугольник). Чтобы лучше понять это, представьте, что вы можете повернуть этот треугольник. Поверните его так, чтобы известная вам сторона была обращена вниз.
- Например, площадь треугольника равна 20, а одна из его сторон равна 4. В этом случае «»А = 20″», «»b = 4″».
3 Подставьте данные вам значения в формулу для вычисления площади (А = 1/2bh) и найдите высоту. Сначала умножьте сторону (b) на 1/2, а затем разделите площадь (А) на полученное значение. Таким образом, вы найдете высоту треугольника.
- В нашем примере: 20 = 1/2(4)h
- 20 = 2h
- 10 = h

Метод 2 Как найти высоту в равностороннем треугольнике

1 Вспомните свойства равностороннего треугольника. В равностороннем треугольнике все стороны и все углы равны (каждый угол равен 60˚). Если в таком треугольнике провести высоту, вы получите два равных прямоугольных треугольника. ^{Например, рассмотрим равносторонний треугольник со стороной 8.}
2 Вспомните теорему Пифагора. Теорема Пифагора гласит, что в любом прямоугольном треугольнике с катетами «а» и «b» гипотенуза «с» равна: a²+b²=c². Эту теорему можно использовать, чтобы найти высоту равностороннего треугольника!
3 Разделите равносторонний треугольник на два прямоугольных треугольника (для этого проведите высоту). Затем обозначьте стороны одного из прямоугольных треугольников. Боковая сторона равностороннего треугольника – это гипотенуза «с» прямоугольного треугольника. Катет «а» равен 1/2 стороне равностороннего треугольника, а катет «b» – это искомая высота равностороннего треугольника.
- Итак, в нашем примере с равносторонним треугольником с известной стороной, равной 8: c = 8 и a = 4.
4 Подставьте эти значения в теорему Пифагора и вычислите b². Сначала возведите в квадрат «с» и «а» (умножьте каждое значение само на себя). Затем вычтите a² из c².
- 4² + b² = 8²
- 16 + b² = 64
- b² = 48
5 Извлеките квадратный корень из b², чтобы найти высоту треугольника. Для этого воспользуйтесь калькулятором. Полученное значение и будет высотой вашего равностороннего треугольника!

Метод 3 Как найти высоту с помощью углов и сторон

1 Подумайте, какие значения вам известны. Вы можете найти высоту треугольника, если вам известны значения сторон и углов. Например, если известен угол между основанием и боковой стороной. Или если известны значения всех трех сторон. Итак, обозначим стороны треугольника: «a», «b», «c», углы треугольника: «А», «В», «С», а площадь — буквой «S».
- Если вам известны все три стороны, вам понадобится значение площади треугольника и формула Герона.
- Если вам известны две стороны и угол между ними, можете использовать следующую формулу для нахождения площади: S=1/2ab(sinC).
2 Если вам даны значения всех трех сторон, используйте формулу Герона. По этой формуле придется выполнить несколько действий. Сначала нужно найти переменную «s» (мы обозначим этой буквой половину периметра треугольника). Для этого подставьте известные значения в эту формулу: s = (a+b+c)/2.^{Для треугольника со сторонами а = 4, b = 3, c = 5, s = (4+3+5)/2. В результате получается: s=12/2, где s=6.
Затем вторым действием мы находим площадь (вторая часть формулы Герона). Площадь = √(s(s-a)(s-b)(s-c)). Вместо слова «площадь» вставьте эквивалентную формулу для поиска площади: 1/2bh (или 1/2ah, или 1/2ch).
Теперь найдите эквивалентное выражение для высоты (h). Для нашего треугольника будет справедливо следующее уравнение: 1/2(3)h = (6(6-4)(6-3)(6-5)). Где 3/2h=√(6(2(3(1))). Получается, 3/2h = √(36). С помощью калькулятора вычислите квадратный корень. В нашем примере: 3/2h = 6. Получается, что высота (h) равна 4, сторона b – основание.}
3 Если по условию задачи известны две стороны и угол, вы можете использовать другую формулу. Замените площадь в формуле эквивалентным выражением: 1/2bh. Таким образом, у вас получится следующая формула: 1/2bh = 1/2ab(sinC). Ее можно упростить до следующего вида: h = a(sin C), чтобы убрать одну неизвестную переменную.^{Теперь осталось решить полученное уравнение. Например, пусть «а» = 3, «С» = 40 градусов. Тогда уравнение будет выглядеть так: «h» = 3(sin 40). С помощью калькулятора и таблицы синусов подсчитайте значение «h». В нашем примере h = 1,928.}

Прислал: DarK_Knigt . 2017-11-06 17:18:57

kak-otvet.imysite.ru

Найти наибольшую высоту треугольника | Треугольники

Как найти наибольшую или наименьшую высоту треугольника? Чем меньше высота треугольника, тем больше проведенная к ней высота. То есть наибольшая из высот треугольника — та, которая проведена к его наименьшей стороне. Наименьшая высота — та, которая проведена к наибольшей из сторон треугольника.

Чтобы найти наибольшую высоту треугольника, можно площадь треугольника разделить на длину стороны, к которой проведена эта высота (то есть на длину наименьшей из сторон треугольника).

Соответственно, для нахождения наименьшей высоты треугольника можно площадь треугольника разделить на длину его наибольшей стороны.

Задача 1.

Найти наименьшую высоту треугольника, стороны которого равны 7 см, 8 см и 9 см.

Дано:

∆ ABC,

AC=7 см, AB=8 см, BC=9 см.

Найти: наименьшую высоту треугольника.

Решение:

Наименьшая из высот треугольника — та, которая проведена к его наибольшей стороне. Значит, нужно найти высоту AF, проведенную к стороне BC.

Для удобства записи введем обозначения

BC=a, AC=b, AB=c, AF=ha.

Высота треугольника равна частному от деления удвоенной площади треугольника на сторону, к которой эта высота проведена. Площадь треугольника по сторонам можно найти с помощью формулы Герона. Поэтому

где

Вычисляем:

Ответ:

Задача 2.

Найти наибольшую сторону треугольника со сторонами 1 см, 25 см и 30 см.

Дано:

∆ ABC,

AC=25 см, AB=11 см, BC=30 см.

Найти:

наибольшую высоту треугольника ABC.

Решение:

Наибольшая высота треугольника проведена к его наименьшей стороне.

Значит, нужно найти высоту CD, проведенную к стороне AB.

Для удобства обозначим

BC=a,

AC=b,

AB=c,

CD=hc.

Вычисляем:

Ответ: 24 см.

www.treugolniki.ru

Как найти высоту треугольника 🚩 как отключить всё услуги в Мегафон 🚩 Математика

15 апреля 2011

Автор КакПросто!

Под высотой треугольника понимается отрезок, проведенный перпендикулярно из вершины треугольника к противоположной стороне. Высота треугольника вполне может совпадать со стороной треугольника, если он прямоугольный, а также находиться вне треугольника, если треугольник остроугольный. Расчет длины высоты зависит от типа треугольника.

Статьи по теме:

Вам понадобится

Знать стороны треугольника, а также его площадь.

Инструкция

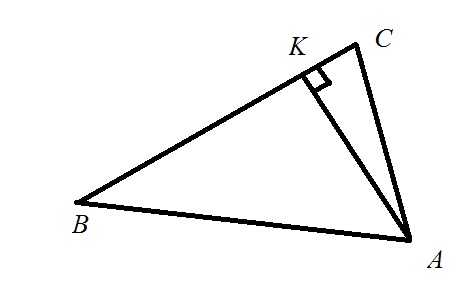
Способ 1. Для всех треугольников.
Пусть в треугольнике ABC AK — высота, опущенная на сторону BC (рис.2), а S — площадь треугольника. Тогда высота AK будет высчитана по формуле:
AK = (2*S)/BC.

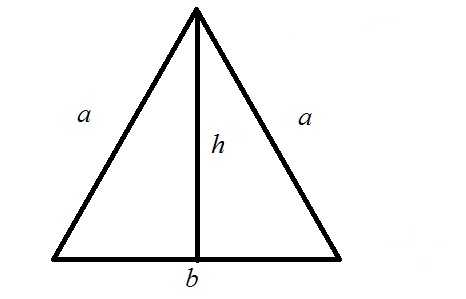
Способ 2. Если перед нами равнобедренный треугольник со равными сторонами a, основанием b. Тогда высоту h, опущенную на основание равнобедренного треугольника, можно рассчитать по следующей формуле(она получается из теоремы Пифагора):
h = v(a2?(b2)/4)).

Способ 3. Пусть дан равносторонний треугольник со стороной a. В таком случае высоту h можно вычислить, использую такую формулу:
h = (a*v3)/2

Видео по теме

<center><ins class="lazy lazy-hidden adsbygoogle" style="display:block;height:250px" data-ad-client="ca-pub-5948177564140711" data-ad-slot="7192702265" data-ad-format="link" data-full-width-responsive="true"></ins> <script>(adsbygoogle=window.adsbygoogle||[]).push({});</script></center>

Обратите внимание

Высота треугольника — перпендикуляр, проведённый из вершины треугольника к прямой, содержащей противоположную сторону. В зависимости от типа треугольника высота может содержаться внутри треугольника.

Полезный совет

Прежде, чем выяснить, как найти высоту треугольника, выясним, что же такое высота треугольника. Высота треугольника это прямая линия, опущеная из его вершины перпендикулярно основанию. Для того, чтобы найти высоту треугольника, необходимо знать величину одной из его сторон и величину угла между этой стороной и основанием треугольника.

Источники:

как находить высоту

Совет полезен?