Двоичная арифметика
Выполнение арифметических действий в любых позиционных системах счисления производится по тем же правилам, которые используются в десятичной системе счисления.
Так же, как и в десятичной системе счисления, для выполнения арифметических действий необходимо знать таблицы сложения (вычитания) и умножения.
Таблица сложения, вычитания и умножения для двоичной системы счисления
| Сложение | Вычитание | Умножение |
| 0 + 0 = 0 | 0 — 0 = 0 | 0 ∙ 0 = 0 |
| 0 + 1= 1 | 1 — 0 = 1 | 0 ∙ 1 = 0 |
| 1 + 0 = 1 | 1 — 1 = 0 | 1 ∙ 0 = 0 |
| 1 + 1 = 10 | 10 — 1 = 1 | 1 ∙ 1 = 1 |
Сложение двоичных чисел
Сложение в двоичной системе счисления выполняется по тем же правилам, что и в десятичной. Два числа записываются в столбик с выравниванием по разделителю целой и дробной части и при необходимости дополняются справа незначащими нулями. Сложение начинается с крайнего правого разряда. Две единицы младшего разряда объединяются в единицу старшего.
Пример: 1011,12 + 1010,112
Интересна также ситуация, когда складываются больше двух чисел. В этом случае возможен перенос через несколько разрядов.
Пример: 111,12 + 1112 + 101,12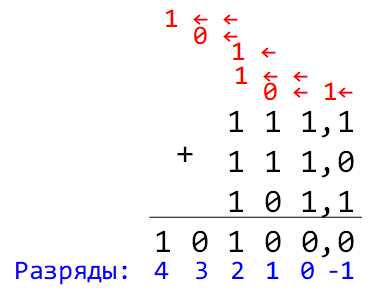
При сложении в разряде единиц (разряд 0) оказывается 4 единицы, которые, объединившись, дают 1002. Поэтому из нулевого разряда в первый разряд переносится 0, а во второй — 1.
Аналогичная ситуация возникает во втором разряде, где с учетом двух перенесенных единиц получается число 5 = 1012. 1 остается во втором разряде, 0 переносится в третий и 1 переносится в четвёртый.
Вычитание двоичных чисел
В случаях, когда занимается единица старшего разряда, она дает две единицы младшего разряда. Если занимается единица через несколько разрядов, то она дает по одной единице во всех промежуточных нулевых разрядах и две единицы в том разряде, для которого занималась.
Пример: 10110,012 — 1001,12
Умножение и деление двоичных чисел
Зная операции двоичной арифметики, можно переводить числа из двоичной системы счисления в любую другую.
Пример: Перевести число 1011110112 в десятичную систему счисления.
Поскольку 1010 = 10102, запишем
Полученные остатки, 10012 = 910, =1112 = 710, 112 = 310. Искомое число 1011110112 = 37910.
Назад: Представление данных и архитектура ЭВМ
Двоичная арифметика
Арифметические действия в двоичной системе производятся по обычным для позиционных систем правилам, которые нам известны из десятичной арифметики, но при этом используются таблицы сложения и умножения двоичной системы:
Таблица сложения
Таблица сложения в двоичной системе очень проста. Надо только помнить, что прибавление нуля не меняет число, а один плюс один, будет два.
Таблица умножения
Таблица умножения ещё проще. Здесь нужно твёрдо знать, что любое число, умноженное на нуль, есть нуль и что умножение на единицу не меняет числа.
Сложение многозначных чисел производится точно так же, как и в десятичной системе, то есть поразрядно, начиная с младшего. Например:
Вычитание в двоичной системе выполняется по таким правилам:
Пример:
Точки, поставленные над некоторыми разрядами уменьшаемого, показывают, что в двоичной системе единица помеченного разряда раздробляется на две единицы низшего разряда.
Умножение и деление двоичных чисел практически не отличается от умножения и деления чисел, записанных в десятичной системе счисления. Единственным отличием является то, что при умножении в столбик не приходится находить произведение первого множителя на значения последовательных разрядов второго множителя, так как значение этих разрядов 1 или 0. А при делении в столбик не нужно подбирать неполное делимое, так как учитывая специфику двоичных чисел, неполное делимое можно определить просто посмотрев на делимое.
Примеры: 1101111 · 101101 = ?, 111100 : 1010 = ?
2. Правила двоичной арифметики
В любой позиционной системе счисления операции сложения и вычитания двух чисел A B=С осуществляются поразрядно, начиная с младших разрядов.
При сложении переполнение из младшего разряда переносится в старший разряд, т. е. код суммы каждого i-ого разряда сi получается в результате сложения ai + bi + 1, где 1 соответствует переносу из младшего (i -1)-разряда в i-ый, если в младшем разряде код суммы получился больше или равным основанию системы счисления.
При вычитании требуемый заем производится из старшего разряда, т. е. код разности каждого i-ого разряда сi получается в результате вычитания ai — bi – 1, где 1 соответствует заему, если он был, в младшие разряды величины, равной основанию системы счисления.
2.1. Правила сложения двоичных чисел.
В каждом разряде выполняется сложение двух цифр слагаемых и единицы переноса из соседнего младшего разряда, если она есть.
Поразрядная сумма формируется по следующим правилам:
0 + 0 = 0
0 + 1 = 1
1 + 0 = 1
1 + 1 = 0 – осуществляется перенос 1 в старший разряд
Например, сложение 510 + 310 = 810
1012 = 510
+ 0112 = 310
Суммирование двоичных чисел в компьютерах осуществляется при помощи устройств, называемых двоичными сумматорами.
2.2. Правила вычитания двоичных чисел.
В каждом разряде выполняется вычитание из цифры числа цифры вычитаемого, при вычитании из нуля единицы происходит заем единицы из соседнего старшего разряда, которая равна 2 единицам данного разряда.
Поразрядная разность формируется по следующим правилам:
0 — 0 = 0
1 — 0 = 1
1 — 1 = 0
0 — 1 = 1 – после заема 1 из старшего разряда
Например, вычитание 610 – 310 = 310
01102 = 610
–00112 = 310
00112 = 310
Как правило, вычитание двоичных чисел в компьютерах осуществляется при помощи двоичных сумматоров: при представлении вычитаемого в дополнительном или обратном коде операцию вычитания можно заменить операцией сложения.2.3. Правила умножения двоичных чисел.
Умножение двоичных чисел производится путем образования промежуточных произведений и последующего их суммирования.
Поразрядные произведения формируются по следующим правилам:
0 x 0 = 0
0 x 1 = 0
1 x 0 = 0
1 x 1 = 1
Например, умножение 510 x 310 = 1510
101
11
101
+101
1111
2.4. Правила деления двоичных чисел.
Деление двоичных чисел производится по правилам умножения и вычитания.
Например, деление 610 : 310 = 210
110 : 11 = 10
110 11
–11 10
00
3. Операция сдвига по разрядной сетке
В компьютерах, кроме операции алгебраического суммирования двоичных чисел, к которой относятся операции сложения и вычитания, выполняется операция сдвига числа по разрядной сетке влево и вправо, осуществляющая, фактически, умножение и деление двоичных чисел.
В случае сдвига влево осуществляется умножение двоичного числа на 2j, а при сдвиге вправо – деление на 2j, где j – количество разрядов, на которое сдвигается двоичное число.
Например, осуществить сдвиг на 2 разряда
1) 0000112 = 310 влево
0011002 = 1210
т. е. 3 х 4(22) = 1210
2) 0010002 = 810 вправо
0000102 = 210
т. е. 8 : 4(22) = 210
В компьютерах часто используется циклический сдвиг, при выполнении которого разрядная сетка, отведенная для операнда (числа, над которым производится действие), представляется замкнутой в кольцо. Тогда при сдвиге влево содержимое старшего разряда попадает в младший разряд операнда, а при сдвиге вправо содержимое младшего разряда попадает в старший разряд операнда.
Умножение в двоичной системе счисления
Для того чтобы умножить двоичное число на 2 (десятичная двойка это 10 в двоичной системе) достаточно к умножаемому числу слева приписать один ноль.
Пример: 10101 * 10 = 101010
Проверка.
10101 = 1*24 + 0*23 + 1*22 + 0*21 +1*20 = 16 + 4 + 1 = 21
101010 =1*25 + 0*24 + 1*23 + 0*22 +1*21 +0*20 = 32 + 8 + 2 = 42
21 * 2 = 42
умножение в двоичной системе счисления сводится к умножению на 10 (то есть на десятичную 2), а стало быть, умножение это ряд последовательных сдвигов. Общее правило таково: как и для десятичных чисел, умножение двоичных выполняется поразрядно. И для каждого разряда второго множителя к первому множителю добавляется один ноль справа.
Пример: 1011 * 101
Это умножение можно свести к сумме трёх порязрядных умножений:
1011 * 1 + 1011 * 0 + 1011 * 100 = 1011 +101100 = 110111
В столбик это же самое можно записать так:
| * | |||||
Проверка:
101 = 5 (десятичное)
1011 = 11 (десятичное)
110111 = 55 (десятичное)
5*11 = 55 верное равенство.
Деление в двоичной системе счисления
Пример: 10010111 / 101
Ищем число, от старшего разряда которое первое было бы больше чем делитель. Это четырехразрядное число 1001. Оно выделено жирным шрифтом. Теперь необходимо подобрать делитель выделенному числу. И здесь мы опять выигрываем в сравнении в десятичной системой. Дело в том, что подбираемый делитель это обязательно цифра, а цифры у нас только две. Так как 1001 явно больше 101, то с делителем всё понятно это 1. Выполним шаг операции.
| - | |||||||||||
Итак, остаток от выполненной операции 100. Это меньше чем 101, поэтому чтобы выполнить второй шаг деления, необходимо добавить к 100 следующую цифру, это цифра 0. Теперь имеем следующее число:
| - | |||||||||||
1000 больше 101 поэтому на втором шаге мы опять допишем в частное цифру 1 и получим следующий результат:
| - | |||||||||||
| - | |||||||||||
Полученное число 110 больше 101, поэтому и на этом шаге мы запишем в частное 1. Получиться так:
| - | |||||||||||
| - | |||||||||||
| - | |||||||||||
Полученное число 11 меньше 101, поэтому записываем в частное цифру 0 и опускаем вниз следующую цифру. Получается так:
| - | ||||||||||||
| - | ||||||||||||
| - | ||||||||||||
Полученное число больше 101, поэтому в частное записываем цифру 1 и опять выполняем действия. Получается такая картина:
| - | ||||||||||||
| - | ||||||||||||
| - | ||||||||||||
| - | ||||||||||||
Полученный остаток 10 меньше 101, но у нас закончились цифры в делимом, поэтому 10 это окончательный остаток, а 1110 это искомое частное.
Проверим в десятичных числах
10010011 = 147
101 = 5
10 = 2
11101 = 29
Составьте таблицу эквивалентов чисел в разных системах счисления ( 10-я 2-я 8-я 16-я системы счисления)
Системой счисления называется совокупность правил для обозначения (записи) действительных чисел с помощью цифровых знаков.
Существуют позиционные и непозиционные системы счисления.
В непозиционных системах вес цифры (т. е. тот вклад, который она вносит в значение числа)не зависит от ее позиции в записи числа.
Примером непозиционной системы счисления является римская, в которой для записи чисел используются буквы латинского алфавита. При этом буква I всегда означает единицу, буква V – пять, X – десять, L – пятьдесят, С – сто, D – пятьсот, М – тысячу и т.д. Например, число 267 записывается в виде ССLХVII (100+100+50+10+7).
В позиционных системах счисления значение каждой цифры числа зависит от ее положения (позиции) в последовательности цифр, изображающих число. Например, в десятичном числе 757,7 первая семерка означает 7 сотен, вторая — 7 единиц, а третья — 7 десятых долей единицы.
Любая позиционная система счисления характеризуется своим основанием.
Основание позиционной системы счисления — это количество различных символов, используемых для изображения цифр в данной системе.
Запись чисел в каждой из систем счисления с основанием q означает сокращенную запись выражения
где – цифры системы счисления; — цифры системы счислен п и т — число целых и дробных разрядов соответственно.
Например, десятичное число 125,4 можно представить так:
Или, если обозначить число как А, основание системы счисление – p, номер старшего разряда – n, номер младшего разряда – m, номер текущего разряда – k, тогда
При работе с ЭВМ используют двоичную, восьмеричную и шестнадцатеричную системы счисления
| Десятичная | Двоичная | Восьмеричная | Шестнадцатеричная |
| A | |||
| B | |||
| C | |||
| D | |||
| E | |||
| F | |||
Переводвосьмеричных и шестнадцатеричных чисел вдвоичнуюочень прост.
В дальнейшем, чтобы отличить в какой системе счисления (СС) записано число, будем указывать основание СС в виде индекса в десятичной СС, например, .
Пример использования редактора формул в WORD. Стр. 91 в методичке
Существует несколько способов создания формул в текстовом документе.
Первый способ применяется для несложных математических выражений, в которых используется возведение в степень или перечисление. Выражение оформляется с использованием параметров оформления символов (верхний и нижний индекс).
Пример: х3-4х2+56х-23=0.
Второй способ позволяет записывать математические выражения, используя символы стандартных шрифтов ОС Windows. Таким образом, можно записать выражение в любом текстовом редакторе с различными возможностями. В MS Word 2007 для этого используется вкладка Вставка\Символ. В диалоговом окне Символ можно выбрать шрифт, просмотреть набор входящих в него символов и выбрать нужный. Это диалоговое окно знакомо нам по работе с маркированными списками.
Третий способ создания математических выражений связан с использованием дополнительных возможностей пакета MS Office – Редактора формул. Этот модуль позволяет набирать в тексте выражения любой сложности и использовать любые математические операторы и конструкции.
Добавление формулы происходит с помощью вкладки Вставка\Формула. Вы можете выбрать готовую формулу из списка предложенных или создать новую. При создании новой формулы открывается дополнительная вкладка Работа с формулами, которая и позволяет создавать нужные математические выражения.
Прежде чем приступить к набору формулы, необходимо подумать, из каких операций и функций она строится, то есть определить структуру формулы.
Возьмем, например, следующее выражение:
Перед нами система, посмотрим, как такое выражение можно создать, используя редактор формул.
Первоначально ставиться системная скобка (используем кнопку Скобка на вкладке). Переходим к первому выражению. Задаём структуру Индекс и заполняем значениями, ставим оператор разности и задаём структуру Скобки, Индекс. Далее указываем значение если.
Переходим ко второму выражению, задаём структуру Индекс и заполняем значениями. Ставим оператор разности и задаем структуру Радикал, заполняем подкоренное выражение. Далее указываем значение Если.
Таким образом, используя редактор формул можно создать математический текст любой сложности, затратив на это оптимальное количество времени.
Переход между различными уровнями структур осуществляется с помощью клавиш управления курсором влево и вправо или с помощью «мыши».
Отдельно выделен блок Символы, с помощью которых можно добавлять математические операторы, символы, греческие буквы и др.
Таким образом, используя редактор формул можно создать математический текст любой сложности, затратив на это оптимальное количество времени.
Средства рисования в Word
Стр.107. в методичке по Word.
Работа с рисунками в Word
Стр.127 в методичке по Word, задание 4.2., стр.115 пункт 4.7.
62. Создание многоколонного текста. Создание составных документов. Колонтитулы, колонцифры, оглавление.
Рекомендуемые страницы:
lektsia.com
1.14 Математические операции с двоичными числами » Try Objective-c
Быстрая навигация:
1.31 Списки — массивы. Первое знакомство.1.30 Функции которые возвращают результат — return1.29 Подпрограммы: функции и процедуры в Питоне1.28 Преобразование типов данных — int()1.27 Ввод данных с клавиатуры — input()1.26 Типы и размеры данных1.25 Цикл с предусловием — while. Числа Фибоначчи1.24 Измерение длины строки, списки1.23 Срезы строк — вывод определенного количества символов из имеющегося текста1.22 Строки и управляющие символы1.21 Системные ошибки в процессе отладки программы1.20 Оператор ветвления — if, комментарии1.19 Вывод на печать — print(), быстрый ввод данных, округление, комментарии1.18 Типы программирования. Часть 2. Объектно-ориентированное программирование1.17 Типы программирования. Часть 1. Структурное программирование. Циклы1.16 Представление символьной информации — ASCII1.15 Деление двоичных чисел1.14 Математические операции с двоичными числами1.13 Как хранится и записывается информация. Биты и байты1.12 Перевод целых чисел десятичной системы счисления в другую систему1.11 Перевод целых чисел из шестнадцатеричной системы счисления в десятичную1.10 Перевод целого двоичного числа в шестнадцатеричное1.9 Перевод целого двоичного числа в другую систему счисления1.8 Системы счисления1.7 Булевая алгебра. Логические выражения1.6 Базовые понятия. Часть 3 — Числа, выражения, операнды, знаки операций1.5 Базовые понятия. Часть 2 — Программа, данные1.4 Базовые понятия. Часть 1 — Задача и алгоритм1.3 Среда разработки СИ1.2 История языков программирования1.1 Введение
1 — сложение двоичных чисел «столбиком» (поразрядное сложение двоичных чисел с переносом)
2 — умножение «столбиком»
3 — умножение посредством сдвига (влево)
4 — отрицательное число
5 — перевод положительного числа в отрицательное.
6 — вычитание двоичных чисел (столбиком)
1
Поразрядное сложение двоичных чисел с переносом
В данном случае сложение производится как и обычные десятичные числа в столбик.
Если складываем 0 и 1 — получается 1
Если складываем 1 и 1 — получается 0 и единица переходит в старший разряд (влево) где складывается со следующим значением.
Примеры показаны для беззнаковых чисел, в которых старший разряд (крайний левый) не является показателем знака.
| + | 0 | 0 | 1 | 0 | ( 210 ) | |
|---|---|---|---|---|---|---|
| 1 | 0 | 1 | 1 | ( 1110 ) | ||
| 1 | 1 | 0 | 1 | ( 1310 ) |
Переполнение
Здесь в качестве примера показано сложение двух двоичных чисел ( в десятичном эквиваленте 15 + 1 )в результате которого происходит «переполнение» ячейки памяти в результате которого результат будет не таким, как ожидалось.
| + | 1 | 1 | 1 | 1 | ( 1510 ) | ||
|---|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 1 | ( 110 ) | |||
| 1 | 0 | 0 | 0 | 0 | 0 |
Другой пример переполнения памяти, когда результатом сложения двух чисел будет 3, а не 19.
Это происходит потому что в четырех битах максимальное число равно 1510 = 11112.
Число 19 не помещается туда физически, как и в примере выше.
| + | 1 | 1 | 1 | 0 | ( 1410 ) | ||
|---|---|---|---|---|---|---|---|
| 1 | 0 | 1 | ( 510 ) | ||||
| 1 | 0 | 0 | 1 | 1 | ( 310 ) |
2
Умножение «столбиком»
Показан просто пример исполнения — без учета знака числа.
Умножение производится по тому же принципу что и для обычных десятичных чисел.
Умножение на ноль дает единицу, а умножение единицы на единицу дает, естественно, тоже единицу.
После перемножения производится сложение для получения общего результата.
Пример умножения «столбиком» 1110 x 101 — в десятичном представлении — 14 x 5 = 70:
| 64 | 32 | 16 | 8 | 4 | 2 | 1 | |
|---|---|---|---|---|---|---|---|
| 26 | 25 | 24 | 23 | 22 | 21 | 20 | |
| × | 1 | 1 | 1 | 0 | |||
| 1 | 0 | 1 | |||||
| + | 1 | 1 | 1 | 0 | |||
| 1 | 1 | 1 | 0 | ||||
| 1 | 0 | 0 | 0 | 1 | 1 | 0 | |
3
Умножение посредством сдвига (влево)
Сдвиг — простыми словами это перенос числа влево (в сторону старшего разряда). При этом в младший разряд записывается 0.
Пример:
имеем число 00112 (это у нас 310)
Сдвигаем его влево и получаем такое число:
Это уже число 610
Что произошло при сдвиге?
Произошло обычное УМНОЖЕНИЕ на 2!
Было 3 — стало 6
Давайте сдвинем это число еще раз:
Имеем:
Сдвигаем его влево и получаем:
Если перевести это число в десятичную систему, то получим число 1210
Если это число снова подвергнуть сдвигу, то результатом будет переполнение.
Следует заметить, что операция сдвига осуществляется намного быстрее, чем операция умножения (или деления)
Следует запомнить, что:
— производя сдвиг влево на ОДИН РАЗРЯД мы производим умножение на 2
— производя сдвиг влево на ДВА РАЗРЯДА мы производим умножение на 4
— производя сдвиг влево на ТРИ РАЗРЯДА мы производим умножение на 8 и т.д.
Сдвиг можно осуществлять и вправо
— в этом случае при сдвиге на 1 разряд будет производиться деление на 2,
— сдвигая вправо на 2 разряда будет производиться деление на 4 и т.д…
Что самое интересное, сдвиг можно производить и с десятичными числами!
Взять то же число 1010 и сдвинуть его влево — т.е. мы присоединяем дополнительный 0 со стороны младшего разряда. Получается 10010
В основе сдвига операция производится с основой системы счисления к которой относится число, над которым проводятся операции сдвига.
В Терминале при помощи Python’а можно также производить операцию сдвига применительно к числам.
Производится эта операция посредством оператора:
— «<<» для сдвига влево
— «>>» для сдвига вправо
Если применять сдвиг к десятичным числам в Питоне, то операция производится путем битового сдвига, т.е. происходит преобразование десятичного числа в двоичное, далее применяется сдвиг и полученное число снова преобразуется в десятичное.
Т.е. если мы наберем в Терминале:
6 << 1 # сдвигаем 6 влево на один разрядТо получим 12, т.е. произошло умножение на 2
Если полученное число 12 сдвинуть влево на один разряд еще раз
12 << 1Получим 24
Соответственно при сдвиге вправо происходит деление:
Сдвинем десятичное число 24 вправо на один разряд
24 >> 1Получим — 12
Чтобы применить сдвиг к другой системе счисления, необходимо использовать соответствующую запись.
Например для двоичного числа:
0b0011 << 1В результате получаем 6
Двоичная форма записи после сдвига преобразовывается в десятичное.
4
Отрицательное число
Это числа меньше нуля, записываются с приставкой «-» перед числом…
Определение отрицательного числа: при наличии положительного числа «a» при сложении такого же отрицательного числа дает в результате НОЛЬ, т.е. при взаимном сложении они «уничтожаются»
Для двоичного формата это утверждение также справедливо
Естественно данные примеры производятся над ЗНАКОВЫМИ числами, в которых старший разряд отведен под указание того, какой знак у числа.
При программировании мы как правило всегда знаем с какого типа данными мы работаем — со знаковыми или беззнаковыми…
В основном, в языках программирования производится так называемое «объявление» переменной, когда мы явным образом указываем с каким типом чисел (в данном случае) мы будем работать.
При объявлении числа типом int — мы будем работать со знаковыми числами, а если число объявить как unsigned int — тогда число будет восприниматься беззнаковым (без какого либо указания на знак в старшем бите).
По умолчанию — числа используются со знаком. Если нам необходимо работать с беззнаковими числами, то мы это должны указать явно.
Если знаковое число +1 в двоичном формате прибавить к -1, то должен получиться ноль (результат будет с переполнением)
| + | +/- знак числа | |||||
|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 1 | 110 | ||
| 1 | 1 | 1 | 1 | -110 | ||
| 1 | 0 | 0 | 0 | 0 | 010 | |
Еще пример
| + | +/- знак числа | |||||
|---|---|---|---|---|---|---|
| 0 | 0 | 1 | 1 | 310 | ||
| 1 | 1 | 0 | 1 | -310 | ||
| 1 | 0 | 0 | 0 | 0 | 010 | |
И еще один пример
| + | +/- знак числа | |||||
|---|---|---|---|---|---|---|
| 0 | 1 | 0 | 1 | 510 | ||
| 1 | 0 | 1 | 1 | -510 | ||
| 1 | 0 | 0 | 0 | 0 | 010 | |
5
Перевод положительного числа в отрицательное
Для того, чтобы произвести перевод положительного двоичного числа в отрицательно надо сделать следующее:
— к младшему байту прибавляем 1 Например возьмем положительное двоичное число 01012 (510) и сделаем из него отрицательное
— меняем единицы на нули и нули на единицы: 10102
— прибавляем единицу к младшему разряду: 10112
Если мы говорим о двоичном числе СО ЗНАКОМ (у которого старший разряд является показателем знака: 0 — положительное число, 1 — отрицательное) то полученный результат будет соответствовать -5 в десятичной системе счисления
Возьмем 01102 (610) и тоже поменяем ему знак:
— меняем единицы на нули и нули на единицы: 10012
— прибавляем единицу к младшему разряду: 10102 (-610)
6
Вычитание двоичных чисел (столбиком)
Помните как мы производим вычитание чисел столбиком в нашей привычной десятичной системе счисления?
Вычитание десятичных чисел
Вычтем из десятичного числа 10080 число 1901
10080 — 1901 = 8179
Красным цветом выделены разряды числа
| — | 5 | 4 | 3 | 2 | 1 | |
|---|---|---|---|---|---|---|
| 1 | 0 | 0 | 8 | 0 | ||
| 1 | 9 | 0 | 1 | |||
10080 — 1901 = 8179
Вы можете посмотреть разбор пошагового вычитания под катом:
Мы не можем из 0 вычесть 1, по этому из соседнего старшего разряда (из 8) мы занимаем разряд — число ДЕСЯТЬ
А почему мы занимаем 10?
Занятое нами число десять является основой десятичной системы счисления, в которой мы производим вычисление.
Это надо запомнить!!!
Вот теперь из занятого числа 10 мы и вычитаем 1 = 9
Во втором разряде (десятки)
Вместо числа 8 у нас осталось число 7
Из него вычитаем 0 = 7
В третьем разряде (сотни)
Мы должны из 0 вычесть 9
Для этого мы должны занять разряд из старшего знака
Занимаем его у единицы находящейся в 5-й позиции
В результате этой операции в 4-й позиции оказывается число ДЕВЯТЬ (число основания системы счисления минус один), а в 3-й позиции — число ДЕСЯТЬ
Из него мы и вычитаем 9 = 1
В четвертом разряде (тысячи)
Здесь остается число 9 и из него мы вычитаем 1
9 — 1 = 8
В пятом разряде (десятки тысяч)
После заема остается 0
В результате у нас получается число равное — 8179
Вычитание двоичных чисел
Для вычитания столбиком двоичных чисел действуют те же самые правила, только в качестве заемного числа выступает число 2, а не 10, поскольку мы оперируем значением двоичной системы счисления — 2
Правила вычитания те же:
0 — 0 = 0
0 — 1 = 1 и занимает разряд из старшего бита
1 — 0 = 1
1 — 1 = 0
Вычитаем:
1101110 (десятичное 110)
- 10111 (десятичное 23)
=1010111 (десятичное 87)
Принцип вычитания следующий:
| — | 8 | 7 | 6 | 5 | 4 | 3 | 2 | 1 | |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 0 | 1 | 1 | 1 | 0 | ( 11010 ) | ||
| 1 | 0 | 1 | 1 | 1 | ( 2310 ) |
Разберем процесс вычитания подробнее
Номера битов указаны красным цветом для наглядности
Разбор находится под катом…
0 — 1 — занимаем из второго бита старший разряд (помните, что мы заняли цифру 2?) и из него производим вычитание.
В результате в первом бите получается 1 (2 — 1 = 1)
2-й бит
В результате предыдущего заема в верхнем числе второго бита получился ноль.
Производим заем старшего разряда из 3-го бита и из него вычитаем 1.
Получаем 1 (2 — 1 = 1)
3-бит
Как и в предыдущем шаге в 3-м бите верхнего числа образовался ноль, по этому занимаем старший разряд из 4-го бита и из него производим вычитание. Получаем снова 1 (2 — 1 = 1)
4-й бит
После выполнения 3-го шага в 4-м бите верхнего числа находится ноль. Т.к. мы занимали из него старший разряд.
По этому производим операцию 0 — 0. Получаем ноль.
5-й бит
В 5-м бите мы снова сталкиваемся с ситуацией, когда необходимо вычесть 1 из 0.
Производим заем разряда из старшего бита. В данном случае из 6-го и из него производим вычитание. Получаем 1 (2 — 1 = 1)
6-й бит
В результате 5-го шага в ячейке 6-го бита верхнего числа находится 0
0 — 0 = 0
7-й бит
Здесь все просто — 1 — 0 = 1
в результате вычисления получаем число 110111
Проверьте в Терминале его десятичное значение:
0b110111Еще несколько примеров вычитания двоичных чисел:
В круглых скобках даны эквиваленты в десятичном формате
456 - 112 = 344
111001000 (456)
- 1110000 (112)
=101011000 (344)234 - 12 = 222
11101010 (234)
- 1100 (12)
=11011110 (222)345 - 232 = 113
101011001 (345)
- 11101000 (232)
=001110001 (113)16 - 3 = 13
10000 (16)
- 11 (3)
= 1101 (13)Метки к статье: арифметические операции, система счисления
www.tryobj.com
Двоичная арифметика
Лабораторная работа №122. Двоичная арифметика.
Цель работы. Научиться выполнять арифметические операции (сложение, вычитание, умножение и деления) с двоичными числами.
Правила выполнения арифметических действий над двоичными числами задаются таблицами двоичных сложения, вычитания и умножения.
Таблица двоичного сложения | Таблица двоичного вычитания | Таблица двоичного умножения |
0+0=0 0+1=1 1+0=1 1+1=10 | 0–0=0 1–0=1 1–1=0 10–1=1 | 0 0 1 1 |
Задание 1. Выполните сложение чисел в двоичной системе счисления 100100111,0012+100111010,1012
Методические указания.
При сложении двоичных чисел в каждом разряде производится сложение цифр слагаемых и цифры, переносимой из соседнего младшего разряда, если она имеется При этом необходимо учитывать, что 1+1 дают нуль в данном разряде и единицу переноса в следующий разряд.
Примеры.
1) Выполнить сложение двоичных чисел X=1101, Y=111.
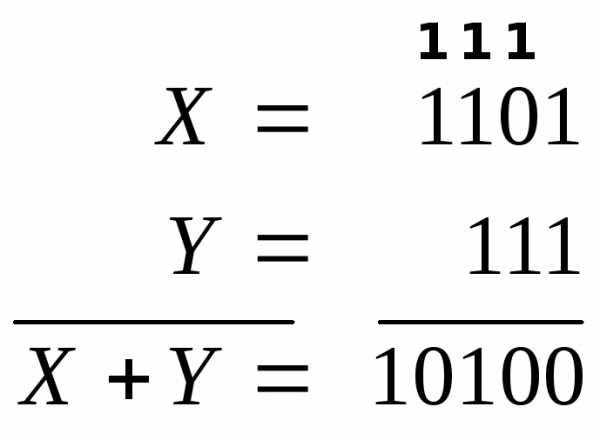
В приведенном примере в младшем нулевом разряде две единицы: 1+1=10 дают нуль в данном разряде и единицу переноса в следующий. В первом разряде: 0+1+1=10 (крайняя единица перенесена из нулевого разряда) дают 0 и единицу переноса в следующий. Во втором разряде 1+1+1=11(крайняя единицы перенесена из первого разряда) дают 1 и единицу переноса в следующий. В старшем третьем разряде 1 и единица переноса из предыдущего разряда дают 1+1=10.
Результат: 1101+111=10100.
2) Сложить три двоичных числа X=1101, Y=101, Z=111.
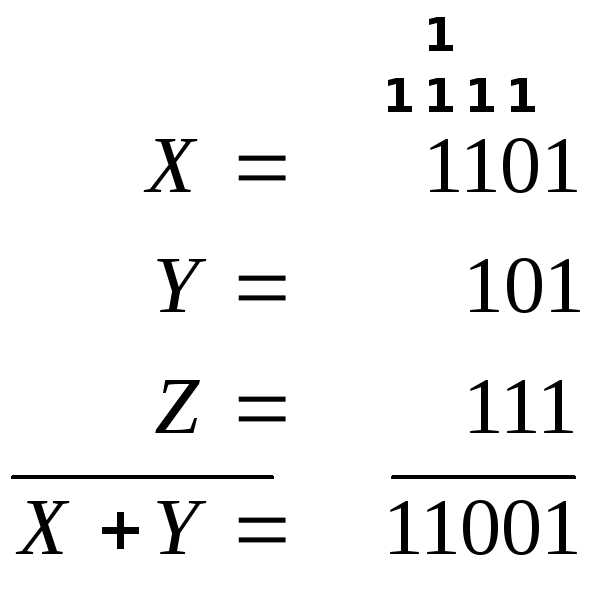
Результат: 1101+101+111=11001.
Задание 2. Выполните вычитание чисел в двоичной системе счисления: 1100110110,00112– 11111110,012.
Методические указания.
При вычитании двоичных чисел в данном разряде при необходимости занимается 1 из старшего разряда. Эта занимаемая 1 равна двум единицам данного разряда, так как 10=1+1.
Примеры.
1) Заданы двоичные числа X=10010 и Y=101. Вычислить X–Y.
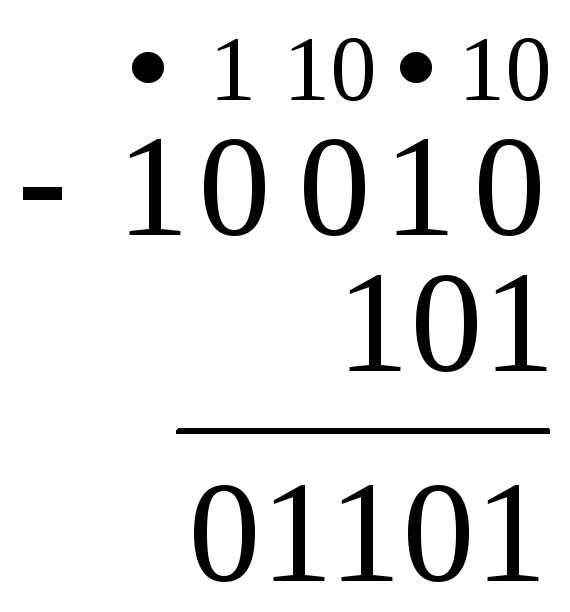
Результат: 100102 – 1012 = 11012.
Замечание. Число 100…002 можно представить в виде суммы
Данное разложение на слагаемые объясняет правило вычитания в столбик. Если вы занимаете 1 из ближайшего старшего разряда, тогда над всеми следующими за единицей нулями следует дописывать 1, а над крайним нулем, для которого произведен заем, 1+1 или 10.
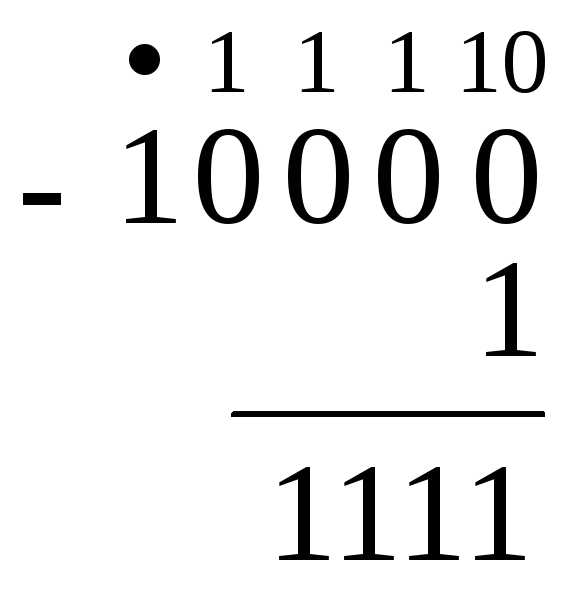
2) Выполнить вычитание: 1100000011,0112 – 101010111,12
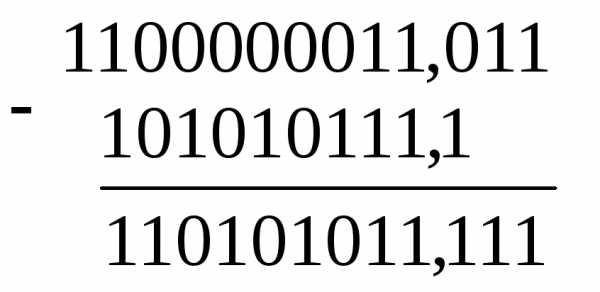
Результат: 1100000011,0112 – 101010111,12 = 110101011,1112.
Задание 3. Выполните умножение чисел 110012 и 10111002 в двоичной системе счисления.
Методические указания.
Правила умножения двоичных чисел такие же, как и для умножения десятичных чисел в столбик, с использованием двоичного умножения и сложения.
Пример.
Найти
произведение 10012 1012
1012
1001
 101
101
1001
+1001
101101
Результат: 10012 1012=1011012.
1012=1011012.Задание 4. Выполните деление чисел 1111012 и 11102 в двоичной системе счисления.
Методические указания.
Деление двоичных чисел производится так же, как и десятичных чисел, при этом используется двоичное умножение и вычитание.
Пример. Найти частное от деления 1100,0112: 10,012
_110001,1 | 1001 |
1001 | 101,1 |
_1101 | |
1001 | |
_1001 1001 | |
0 |
Результат: 1100,0112:10,012=101,12.
Задания для самостоятельной работы
Вариант | Заданы двоичные числа X и Y. Вычислить X+Y и X–Y , если: | Заданы двоичные числа X и Y. Вычислить X*Y и X/Y , если: |
Х=100101,1012 Y=11101,112 | X=100101,0112 Y=110,12 | |
Х=101101,1012 Y=1101,1112 | X=110000,112 Y= | |
Х=110101,1012 Y=11101,112 | X=111001,00012 Y=1010,0112 | |
Х=1101111,1012 Y=10101,112 | X=111011,00012 Y=101,012 | |
Х=1000111,112 Y=11101,1112 | X=111100,0112 Y=101,112 | |
Х=1110001,1012 Y=10011,112 | X=110110,1012 Y=100,112 | |
Х=1010001,1012 Y=10011,112 | X=100110,00012 Y=111,012 | |
Х=1000011,1012 Y=10011,0112 | X=101011,1112 Y=110,112 | |
Х=1101001, 1012 Y=10111,112 | X=1010110,1012 Y=1000,012 | |
Х=1010001,1012 Y=1111,0112 | X=111111,012 Y=101,12 | |
Х=101001, 1012 Y=10111,1112 | X=1011010,1012, Y=111,012 | |
Х=1010111, 1012 Y=11100,1112 | X=1000101,00112, Y=110,112 | |
Х=110101,1012 Y=1111,112 | X=100101,0112, Y=110,12 | |
Х=101111,1012 Y=1101,1112 | X=100000,11012, Y=101,012 | |
Х=110101,0112 Y=10011,112 | Х=110111,112 Y=101,112 | |
Х=1001011,112 Y=10101,1012 | Х=100101,112 Y=111,012 | |
Х=100011,0112 Y=10011,1112 | Х=100011,012 Y=1011,12 | |
Х=1010001,1012 Y=1011,0112 | Х=100001,1012 Y=1001,012 | |
Х=110001,1012 Y=10111,112 | Х=111001,1012 Y=1101,112 | |
Х=1000111,0112 Y=11111,112 | Х=1010111,0112 Y=111,112 | |
Х=111001, 1012 Y=1110,1112 | Х=11100001, 1012 Y=110,112 | |
Х=100001,1012 Y=1111,1112 | Х=1000001,1012 Y=1111,012 | |
Х=1011101, 1012 Y=10111,0112 | Х=1010101, 1012 Y=100,0112 | |
Х=1111000, 1012 Y=101111,112 | Х=1111001, 0112 Y=1011,112 | |
Х=1100000, 1012 Y=1111,1112 | Х=1100011, 012 Y=11,1112 |
Контрольные вопросы.
1. Каковы правила сложения двоичных чисел?
2. Каковы правила вычитания двоичных чисел?
3. Каковы правила умножения двоичных чисел?
4. Каковы правила вычитания двоичных чисел?
studfiles.net
Двоичное счисление: вычитание, сложение, умножение, деление
Двоичное счисление
Двоичное счисление это
Двоичное счисление имеет в своей основе только две цифры: 0 и 1. Все числа записывают с помощью этих двух цифр. Основание двоичной системы счисления равно двум.
Двоичная система счисления применяется в компьютерной технике. Бит — это наименьшая единица информации. Слово «бит», по-английски bit, происходит от «binary digit», что значит «двоичная цифра». Бит может быть единицей или нулём, ведь в двоичной системе счисления имеются только две цифры: 0 и 1.
Двоичное счисление относится к позиционным системам счисления. Это значит, что значение двоичного числа связано с позициями цифр в нём. Пример: двоичные числа 1101 и 1011 составлены из одинакового количества единиц и нулей, но позиции их различны, значит и числа различны.
Вот таблица позиций числа 1101:
| цифра | 1 | 1 | 0 | 1 |
| позиция | 3 | 2 | 1 | 0 |
Теперь таблица позиций числа 1011:
| цифра | 1 | 0 | 1 | 1 |
| позиция | 3 | 2 | 1 | 0 |
Номера позиций начинаются с нуля.
Двоичные дроби
Дроби в двоичной системе счисления записывают как и в десятичной:
1101,1101
Таблица позиций числа 1101,1101
| цифра | 1 | 1 | 0 | 1 | . | 1 | 1 | 0 | 1 |
| позиция | 3 | 2 | 1 | 0 | -1 | -2 | -3 | -4 |
Позиции дробной части начинаются с -1.
Перевод дробного двоичного числа в десятичное
Переведём двоичное дробное число 1101,1101 в десятичную дробь.
Таблица позиций числа 1101,1101
| цифра | 1 | 1 | 0 | 1 | . | 1 | 1 | 0 | 1 |
| позиция | 3 | 2 | 1 | 0 | -1 | -2 | -3 | -4 |
1 * 23 + 1 * 22 + 0 * 21 + 1 * 20 + 1 * 2-1 + 1 * 2-2 + 0 * 2-3 + 1 * 2-4 = 8 + 4 + 0 + 1 + 0.5 + 0.25 + 0 + 0.0625 = 13.8125
Степени 2 равны номеру позиции.
Итак, двоичное число 1101,1101 равно 13,8125 в десятичной системе счисления.
Двоичная система счисления: как сравнить два числа?
Двоичные числа сравнивают также, как и в десятичной системе счисления, примеры:
100 > 10
100 < 110
111 < 1111
111 < 1000
www.sbp-program.ru

 0=0
0=0 1=0
1=0 0=0
0=0 1=1
1=1 2
2