Упрощение тригонометрических выражений. Задание 9
Упрощение тригонометрических выражений. Задание 9.
При упрощении тригонометрических выражений полезно придерживаться такой последовательности действий:
1. С помощью формул приведения привести все тригонометрические функции к углам первой четверти.
2. Посмотреть, как соотносятся между собой полученные углы, чтобы определить, какие формулы использовать для преобразования выражения. В большинстве задач это формулы двойного аргумента или соотношение
3. Воспользоваться основными тригонометрическими формулами.
Прежде чем читать дальше, очень рекомендую перечитать статью, как пользоваться формулами приведения и не заучивать их.
Рассмотрим несколько примеров решения задач на упрощение тригонометрических выражений из Открытого банка заданий для подготовки к ЕГЭ по математике.
1. Задание B10 (№ 26756) Найдите значение выражения
Мы видим, что , поэтому либо разложим знаменатель по формуле косинуса двойного аргумента, либо, наоброт свернем числитель по той же формуле:
Ответ: -24.
2. Задание B10 (№ 26757) Найдите значение выражения
Заметим, что
Воспользеумся фомулой приведения:
Ответ: 5.
3. Задание B10(№ 26757) Найдите значение выражения
Преобразуем аргументы тригонометрических функций в знаменателе дроби:
Вспомним, что синус — нечетная функция, а косинус — четная:
А также периодичность синуса и косинуса. Получим:
С помощью тригонометрического круга определим значение
и :
Получим:
Ответ: — 16.
4. Задание B10 (№ 26770) Найдите значение выражения
Воспользуемся формулой приведения:
Ответ: — 5.
5. Задание B10 (№ 26774) Найдите значение выражения
Снова воспользуемся формулой приведения:
Ответ: 12.
6. Задание B10 (№ 26776) Найдите , если и
По основному тригонометрическому тождеству:
Косинус в третьей четверти отрицателен, поэтому
Отсюда
Ответ: 5.
7. Задание B10 (№ 26781) Найдите значение выражения
Воспользуемся формулами приведения:
Получим:
Ответ: 2
Вероятно, Ваш браузер не поддерживается. Попробуйте скачатьFirefox
И.В. Фельдман, репетитор по математике.
Купить видеокурс «ВСЯ ТРИГОНОМЕТРИЯ. Часть В и 13»
ege-ok.ru
Урок по тригонометрии для 10 класса «Применение основных тригонометрических формул к преобразованию выражений»
Цели:
Повторить основные формулы тригонометрии и закрепить их знания в ходе выполнения упражнений;
Развивать навыки самоконтроля.
Воспитание ответственного отношения к учебному труду, воли и настойчивости для достижения конечных результатов.
Оборудование: Компьютерная презентация, свитки с заданиями, карточки с тестами.
Ожидаемый результат:
Каждый ученик должен знать формулы тригонометрии и уметь применять их для преобразования тригонометрических выражений на уровне обязательных результатов.
Знать формулы тригонометрии, уметь выводить эти формулы и применять их для более сложных тригонометрических выражений.
Основные этапы урока:
Сообщение темы, цели, задач урока и мотивация учебной деятельности.
Устный счёт
Сообщение из истории математики
Применение тригонометрических формул к преобразованию выражений
Выполнение теста
Подведение итогов урока
Постановка задания на дом
Ход урока.
Организационный момент.
— Дорогие ребята, сегодня мы с вами повторим основные формулы тригонометрии и закрепим их знания в ходе выполнения упражнений на преобразования тригонометрических выражений.
— Но урок у нас сегодня не обычный. Вы не просто ученики, а группа специалистов, которая нашла и изучает храмовый комплекс древней цивилизации. Мы прибыли с вами в пустыню и разбили лагерь. Нам необходимо открыть Пирамиду знаний и пройдя все испытания, найти древний свиток, который содержит истинные знания. Что касается данной цивилизации, то мы знаем только то, что храмы построены на тригонометрических расчетах. Поэтому, прежде чем мы войдем в это здание, необходимо освежить наши познания в области тригонометрии. Для начала поработаем устно.
II. Устная работа: (Презентация).
Радианная мера двух углов треугольника равна
 и
и  . Найдите градусную меру каждого из углов треугольника. Ответ: 60, 30, 90
. Найдите градусную меру каждого из углов треугольника. Ответ: 60, 30, 90
Может ли косинус быть равным: а)
, г) , б)
, б)  , в)
, в)
 , д)
, д)  -2 ?
-2 ?
Ответ: а) да; б) нет; в) нет; г) да; д) да.
Может ли синус быть равным: а) –3,7; б)
 , в)
, в)  ?
?
Ответ: а) нет; б) да; в) нет.
Сообщение из истории тригонометрии (краткая историческая справка):
Тригонометрия возникла и развивалась в древности как один из разделов астрономии, как её вычислительный аппарат, отвечающий практическим нуждам человека.
Некоторые тригонометрические сведения были известны древним вавилонянам и египтянам, но основы этой науки заложены в Древней Греции.
Греческий астроном Гиппарх во II в. до н. э. составил таблицу числовых значений хорд в зависимости от величин стягиваемых ими дуг. Более полные сведения из тригонометрии содержатся в известном “Альмагесте” Птолемея. Сделанные расчёты позволили Птолемею составить таблицу, которая содержала хорды от 0 до 180º.
Название линий синуса и косинуса впервые были введены индийскими учёными. Они же составили первые таблицы синусов, хотя и менее точные, чем птолемеевы.
В Индии начинается по существу учение о тригонометрических величинах, названное позже гониометрией (от “гониа” — угол и “метрио” — измеряю).
На пороге XVII в. в развитии тригонометрии начинается новое направление – аналитическое.
Тригонометрия даёт необходимый метод развития многих понятий и методы решения реальных задач, возникающих в физике, механике, астрономии, геодезии, картографии и других науках. Кроме этого, тригонометрия является большим помощником в решении стереометрических задач.
IV. Применение тригонометрических формул к преобразованию выражений.
(Презентация 2)
Итак, мы теоретически подготовились и теперь можем идти внутрь храма. И первый переход не заставил нас ждать. Переход закрыт защитным полем. Что же делать? Мы внимательно изучаем все стены и ниши в надежде обнаружить тайную кнопку или что-то вроде этого. И вдруг в углу находим свиток с первым заданием. А находит его:………..
Один учащийся выполняет задание на доске, остальные решают на местах и проверяют решение.
Упростить выражение: 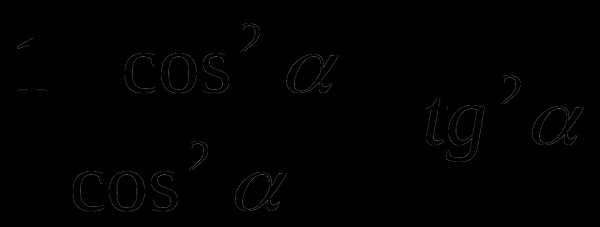
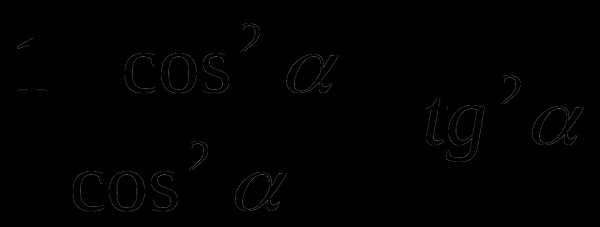
Хорошо, мы благополучно пересекли первый проход! Но что нас ждет дальше? Мы понемногу двигаемся вперед. Изучаем иероглифы, делаем фотографии, записи. И вот незаметно добираемся до следующего прохода. Мы хорошо знаем, что находимся внутри закрытого здания, но здесь настолько светло, что кажется проникает солнечный свет. ……. осторожно заходит на освещенную площадку и вдруг в воздухе снова появляется свиток.
Один учащийся выполняет задание на доске, остальные решают на местах и проверяют решение.
Упростить выражение: cos4x + sin2x · cos2x
cos4x + sin2x · cos2x =
Итак, двери открыты. Мы продолжаем исследования. Такое впечатление, что люди, жившие в то время, обладали большими знаниями, чем мы. Нам нужно дойти до конца и мы с интересом продвигаемся вперед. Новый переход неожиданно появился за следующим поворотом. Его яркие огни приглашали, но как только мы вступили на площадку, заиграла красивая и тихая мелодия. Мы постепенно стали погружаться в сон, нам было очень хорошо, но мелодия быстро закончилась и ловушка захлопнулась. А над нами в воздухе завис свиток. ….. аккуратно взял его и прочел.
Один учащийся выполняет задание на доске, остальные решают на местах и проверяют решение.
Тренировочные упражнения (по учебнику)
Решить № 11 (г):
= =
= = = 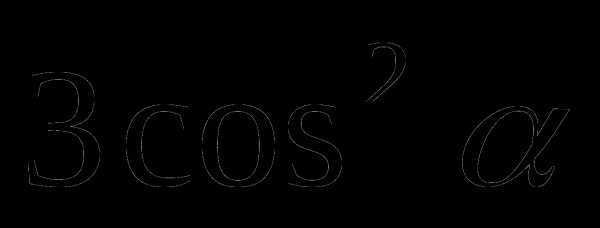 .
.
V. Выполнение теста по теме “Тригонометрические формулы”
И с этим мы быстро справились. И вот мы на пороге самой заветной комнаты. Ее охраняют два сфинкса с чашами. На двери этой комнаты кодовый замок. И нам необходимо подобрать к нему цифры. А чтобы это сделать, мы должны разделиться и каждый будет выполнять персональную миссию. На это нам отведено всего 7 минут.
Ученики выполняют задания на индивидуальных карточках. Задания подобраны разного уровня сложности. Задания теста выбраны из сборников для подготовки к ЕГЭ.
Карточка 1.
Упростить выражение:
а) 4; б) 1; в) 0.
Упростите выражение: .
а) 2; б) 3; в) 1.
Карточка 2.
Преобразовать выражение и найти его значение при
 : .
: .
а) 1; б) 2; в) 0,5
Упростите выражение: .
а) – 0,5; б) 4; в) 0.
Карточка 3.
Преобразовать выражение и найти его значение при
 :
: 
а) 6; б) 0,75; в) 3.
Преобразовать выражение и найти его значение при : .
а) 1; б) 0; в)  .
.
Карточка 4.
Преобразовать выражение и найти его значение при
 :
:
а) 2; б) 4; в) 0.
Упростите выражение:
а) 3; б) 1; в) 4.
Карточка 5.
Упростите выражение:
 .
.
а) -1; б) 1; в) 3.
Преобразовать выражение и найти его значение при
 :
:
а) 2; б) 0; в) 1.
Карточка 6.
Преобразовать выражение и найти его значение при
 : .
: .
а) 1; б) 2; в) 0.
Преобразовать выражение и найти его значение при
 :
:  .
.
а) 0; б) 4; в) 3.
Итак, расчеты окончены и мы с замиранием сердца набираем цифры на кодовом замке. Пожалуйста называйте по порядку получившиеся результаты вашего решения. (Учитель вносит результаты в презентацию на компьютере и выдается соответствующий ответ, который комментируется учителем). И двери открыты. Мы входим в последний зал и видим горы золота, драгоценностей и на невысокой колонне лежит запечатанный свиток. Нам предстоит еще много потрудиться, чтобы вскрыть и прочитать его. Но на сегодня работа окончена.
VI. Подведение итогов, рефлексия.
Продолжите фразу:
“ Сегодня на уроке я узнал…”; “Сегодня на уроке я научился…”; “Сегодня на уроке я познакомился…” “Сегодня на уроке я повторил…” “Сегодня на уроке я закрепил…”.
Все на уроке работали очень хорошо. Особенно мне понравилось решение …… И отметки за сегодняшний урок:
VII. Домашнее задание: (презентация)
§1, п. 1. № 22, № 24, № 25
infourok.ru
Тригонометрические выражения
Тригонометрические выражения. Друзья! Для вас очередная статья с примерами на вычисление тригонометрических выражений. Примеры довольно простые, большинство из них, при определённом навыке, можно решить устно. Если вы основательно изучили тригонометрию и уяснили все важные и необходимые основы, то с решением не будет никаких трудностей.
Что используется в ходе решения данных выражений: формулы приведения, свойства периодичности тригонометрических функций, свойство чётности нечётности, формулы – синуса и косинуса двойного аргумента и, конечно же, основное тригонометрическое тождество.
Рекомендации:
— если в выражении видите, что один угол больше другого в два раза, то смело используйте соответствующую тригонометрическую формулу двойного аргумента;
— если вы видите, что сумма данных углов (или их разность) составляет 90, 180, 270, 360 градусов, то применяйте формулы приведения.
Последнюю статью с выражениями можно посмотреть здесь (там также использовались формулы функций двойного аргумента).
Формулы периодичности, чётности-нечётности здесь.
Основное тригонометрическое тождество здесь.
Рассмотрим задачи:
17289. Найдите значение выражения
Используем формулу синуса двойного аргумента:
Выражение в числителе «сворачиваем»:
*Второй путь: можно было использовать эту же формулу преобразовав знаменатель.
Ответ: 18
63139. Найдите значение выражения
Для решения этого примера достаточно знать формулу косинуса двойного аргумента:
Преобразуем знаменатель:
Ответ: –22
63229. Найдите значение выражения
В данном случае 63 градуса представляем как разность 900 – 270
Ответ: 33
63763. Найдите значение выражения
Представим 1000 как разность 3600 – 2600, применим свойство периодичности нечётности синуса:
Ответ: –34
63819. Найдите значение выражения
Используем формулу приведения косинуса. Представим 1530 как разность 1800 – 270:
Ответ: –38
63875. Найдите значение выражения
Используем формулу приведения для тангенса. Представим 1480 как разность 1800 – 320:
Ответ: 22
63929. Найдите значение выражения
Представим 3730 как сумму 3600 + 130, используем свойство периодичности:
Ответ: –20
63985. Найдите значение выражения
Используем формулы приведения:
*Применили формулу тригонометрии:
Ответ: –5
97369. Найдите значение выражения
Применяем формулу синуса двойного аргумента в числителе, и формулу приведения в знаменателе:
Ответ: –40
97967. Найдите значение выражения
Применяем формулу синуса двойного аргумента:
Ответ: –7
64097. Найдите значение выражения
Используем формулы приведения и основное тригонометрическое тождество:
Ответ: 37
64149. Найдите значение выражения
Используем формулы приведения и основное тригонометрическое тождество:
*Подробнее:
Ответ: –30
64205. Найдите значение выражения
Используем формулу приведения и основное тригонометрическое тождество:
Ответ: 21
63519. Найдите значение выражения
Косинус функция чётная, то есть
Её период равен 2Пn, то есть
Значит
Используем формулу приведения для косинуса:
Ответ: 6
63587. Найдите значение выражения
Период тангенса равен 180 градусам (Пи радиан), функция тангенса нечётная:
Ответ: 132
63651. Найдите значение выражения
Применяем свойство нечётности синуса, выделяем период и используем формулу приведения:
Ответ: 6
26755. Найдите значение выражения
Посмотреть решение
26756. Найдите значение выражения
Посмотреть решение
26757. Найдите значение выражения
Посмотреть решение
26765. Найдите значение выражения
Посмотреть решение
26766. Найдите значение выражения
Посмотреть решение
26767. Найдите значение выражения
Посмотреть решение
27769. Найдите значение выражения
Посмотреть решение
26770. Найдите значение выражения
Посмотреть решение
77412. Найдите значение выражения
Посмотреть решение
77414. Найдите значение выражения
Посмотреть решение
26772. Найдите значение выражения
Посмотреть решение
26773. Найдите значение выражения
Посмотреть решение
26774. Найдите значение выражения
Посмотреть решение
26761. Найдите значение выражения
Посмотреть решение
26762. Найдите значение выражения
Посмотреть решение
26763. Найдите значение выражения
Посмотреть решение
На этом всё! Успеха Вам!
С уважением, Александр Крутицких
P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.
matematikalegko.ru
Задания В11. Числовые тригонометрические выражения
Начало здесь.
Разбор заданий из открытого банка заданий ЕГЭ по математике
Вы можете получить доступ к видеокурсу «Тригонометрия» для подготовки к ЕГЭ по математике.
Числовые тригонометрические выражения
Задача 1.
Найдите значение выражения
Решение: + показать Воспользуемся формулами приведения, для чего прежде представим иначе : на круге располагаются здесь: Отбрасываем согласно формулам приведения , название функции не меняем, знак ставим «–», так как косинус угла III четверти отрицателен: (При необходимости пользуемся тригонометрическим кругом). Ответ: -16. 
Задача 2.
Найдите значение выражения .
Решение: + показать
Задача 3.
Найдите значение выражения
Решение: + показать
Задача 4.
Найдите значение выражения
Решение: + показать
Задача 5.
Найдите значение выражения
Решение: + показать
Задача 6.
Найдите значение выражения
Решение: + показать
Задача 7.
Найдите значение выражения
Решение: + показать В силу нечетности функции , получаем: Далее применяем формулы приведения: Ответ: -13.
Задача 8.
Найдите значение выражения
Решение: + показать Ответ: -8.
Задача 9.
Найдите значение выражения
Решение: + показать
Задача 10.
Найдите значение выражения
Решение: + показать Если мы в формуле двойного угла для косинуса выразим синус через косинус (), то получим: Тогда Далее, так как , то, применяя формулы приведения, получаем: Ответ: 7,5.
Задача 11.
Найдите значение выражения
Решение: + показать Если мы в формуле двойного угла для косинуса выразим косинус через синус (), то получим: Тогда Ответ: 4.
Задача 12.
Найдите , если .
Решение: + показать Воспользуемся следующей формулой двойного угла для косинуса: Ответ: 22.
Задача 13.
Найдите значение выражения
Решение: + показать
Домножим и числитель и знаменатель на 2, чтобы явно увидеть в знаменателе формулу двойного угла для синуса: Ответ: 12.
Задача 14.
Найдите значение выражения
Решение: + показать Ответ: 80.
🙂 Отдохните немного… –> + показать

Вы можете пройти тест по теме «Задания №9. Числовые тригонометрические выражения».
egemaximum.ru
упрощение тригонометрических выражений — Математика
Просмотр содержимого документа
«упрощение тригонометрических выражений»
Тригонометрия
1
3
2
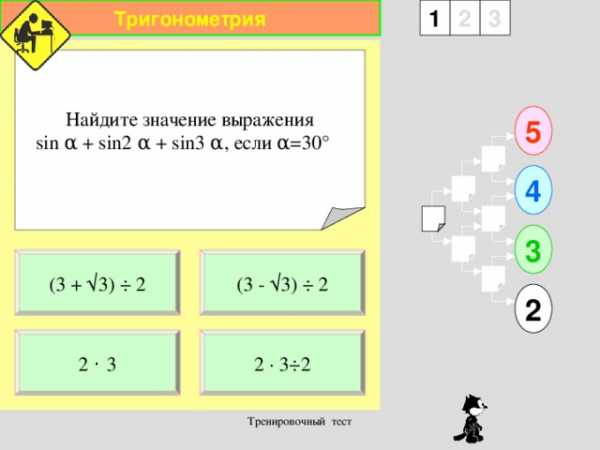
Найдите значение выражения
sin α + sin2 α + sin3 α , если α =30 °
5
4
3
(3 + √ 3) ÷ 2
(3 — √3) ÷ 2
2
2 · 3 ÷ 2
2 · 3
Тренировочный тест
Тригонометрия
1
3
2
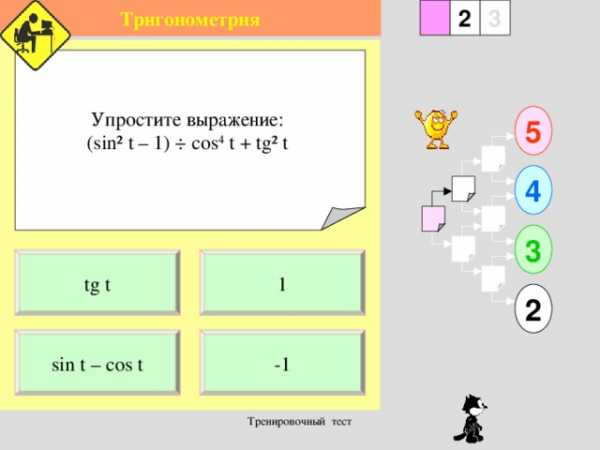
Упростите выражение:
(sin² t – 1) ÷ cos 4 t + tg ² t
5
4
3
1
tg t
2
-1
sin t – cos t
Тренировочный тест

Тригонометрия
3
1
2
Какая четверть, если α = 4200° .
5
4
3
3 четверть
1 четверть
2
4 четверть
2 четверть
Тренировочный тест
Тригонометрия
1
3
2
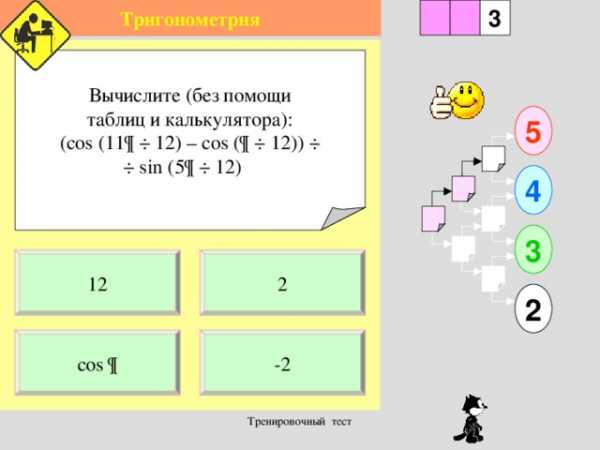
Вычислите (без помощи
таблиц и калькулятора):
(cos (11 ¶ ÷ 12) – cos (¶ ÷ 12)) ÷
÷ sin (5¶ ÷ 12)
5
4
3
2
12
2
-2
cos ¶
Тренировочный тест
Тригонометрия
1
3
2
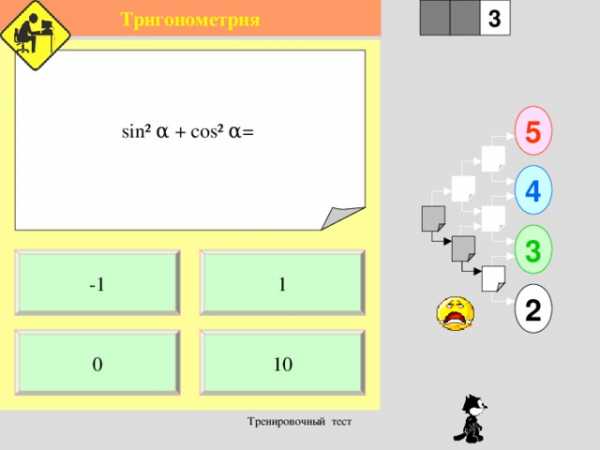
sin ² α + cos ² α =
5
4
3
1
-1
2
10
0
Тренировочный тест
2
1
3
Тригонометрия
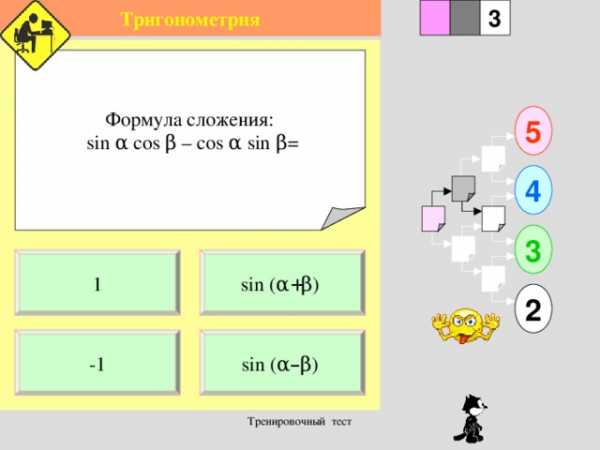
Формула сложения:
sin α cos β – cos α sin β =
5
4
3
sin ( α + β )
1
2
sin ( α – β )
-1
Тренировочный тест
Тригонометрия
1
3
2
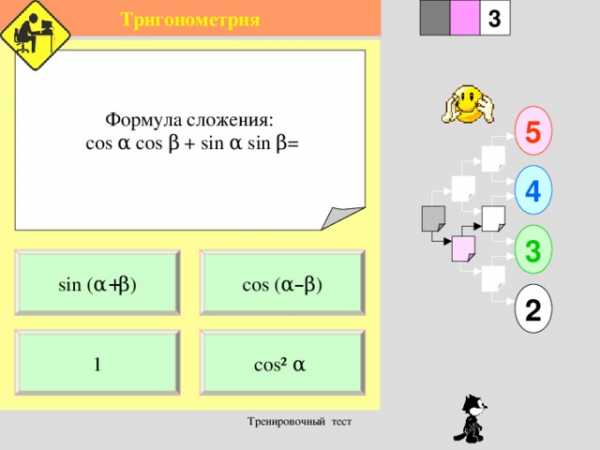
Формула сложения:
cos α cos β + sin α sin β =
5
4
3
cos ( α – β )
sin ( α + β )
2
cos ² α
1
Тренировочный тест

1
Тригонометрия
3
2
5
4
3
2
Тренировочный тест

1
Тригонометрия
3
2
5
4
3
2
Тренировочный тест

1
Тригонометрия
3
2
5
4
3
2
Тренировочный тест

1
Тригонометрия
3
2
5
4
3
2
Тренировочный тест

1
Тригонометрия
3
2
5
4
3
2
Тренировочный тест

1
Тригонометрия
3
2
5
4
3
2
Тренировочный тест
1
Тригонометрия
3
2
5
4
3
2
Тренировочный тест

1
Тригонометрия
3
2
5
4
3
2
Тренировочный тест

Тренировочный тест
multiurok.ru
Упрощение тригонометрических выражений — математика, уроки

Тема урока. Упрощение тригонометрических выражений.
Цели урока.
Дидактические:
обобщить и систематизировать знания учащихся по теме;
продолжить формирование умений и навыков по применению тригонометрических формул;
проконтролировать степень усвоения знаний, умений и навыков по теме.
Развивающие:
совершенствовать, развивать умения и навыки по решению задач на применение тригонометрических формул;
развивать умения и навыки в работе с тестами;
продолжить работу по развитию логического мышления, математической речи и памяти.
Воспитательные:
продолжить формирование навыков эстетического оформления записей в тетради;
приучать к умению общаться и выслушивать других;
воспитание сознательной дисциплины;
развитие творческой самостоятельности и инициативы;
стимулировать мотивацию и интерес к изучению тригонометрии.
Задачи урока:
повторить определение синуса, косинуса, тангенса, котангенса числа ;
повторить формулы приведения, формулы двойного угла, формулы сложения;
повторить основное тригонометрическое тождество и формулы, выражающие связь между тангенсом и косинусом, между котангенсом и синусом.
научить применять полученные знания при решении задач.
Тип урока: урок обобщения и систематизации знаний.
Оборудование: учебники, компьютер, мультимедийный проектор.
Ход урока:
Организационный момент, вступительная беседа.
Блиц-опрос.
Закрепление знаний и умений.
Самостоятельная работа (тест) .
Проверка самостоятельной работы.
Это интересно.
Подведение итогов урока.
Домашнее задание.
1. Организационный момент.
Для успешного решения задач по тригонометрии необходимо уверенное владение многочисленными формулами. Тригонометрические формулы надо помнить. Но это не значит, что их надо заучивать все наизусть, главное запоминать не сами формулы, а алгоритмы их вывода. Любую тригонометрическую формулу можно довольно быстро получить, если твердо знать определения и основные свойства функций sin, cos, tg, ctg,соотношение sin2+ cos2=1 и формулы сложения. Каждый раз выводить нужную формулу, например, для преобразования тригонометрического уравнения время уйдет достаточно много. Поэтому круг формул, которые необходимо знать, должен быть достаточно широким.
Разучивание тригонометрических формул в школе не для того чтобы вы всю оставшуюся жизнь вычисляли синусы и косинусы, а для того чтобы ваш мозг приобрел способность работать. “Дороги не те знания, которые отлагаются в мозгу, как жир; дороги те, которые превращаются в умственные мышцы” писал Г. Спесер, английский философ и социолог.
Так вот, давайте сегодня на уроке работать активно, внимательно, будем поглощать знания с большим желанием, ведь они вам пригодятся.
Тема нашего урока: “Тригонометрические формулы”- последний урок по данной теме, следующий – контрольная работа.
2. Блиц-опрос (по формулам в форме математического диктанта).
Проверка проводится на уроке с выставлением оценок.
“5” — 12; “4” — 10 – 11; “3” — 7 – 9; “2” — 0 – 6
3. Закрепление знаний и умений.
4. Самостоятельная работа обучающего характера в форме теста, с последующей проверкой на уроке.
5. Проверка самостоятельной работы (проверка теста проводится на уроке, оценки выставляются выборочно).
6. Это интересно. Зарождение тригонометрии относится к глубокой древности. Еще задолго до новой эры вавилонские ученые умели предсказывать солнечные и лунные затмения. Это позволяет сделать вывод о том, что им были известны простейшие сведения из тригонометрии. Само название “тригонометрия” греческого происхождения, обозначающее “измерение треугольников”. Одним из основоположников тригонометрии считается древнегреческий астроном Гиппарх, живший во 2 веке до нашей эры. Гиппарх является автором первых тригонометрических таблиц.
Тригонометрия в ладони
Значения синусов и косинусов углов “находятся” на вашей ладони. Протяните руку и разведите как можно сильнее пальцы, так как показано на слайде. Сейчас мы измерим углы между вашими пальцами. (Возьмем два прямоугольных треугольника с углами 30°и 45° и приложим вершину нужного угла к бугру Луны на ладони. Бугор Луны находится на пересечении продолжений мизинца и большого пальца. Одну сторону угла совмещаем с мизинцем, а другую сторону — с одним из остальных пальцев)
Смотрите, я прикладываю угол в 30°; оказывается, это угол
— между мизинцем и безымянным пальцем;
— между мизинцем и средним пальцем — 45°;
— между мизинцем и указательным пальцем — 60°;
— между мизинцем и большим пальцем — 90°;
И это у всех людей без исключения.
Если пальцы считать лучами, исходящими из бугра Луны на ладони, то, если совместить (сжать) пальцы с мизинцем, угол между лучами будет равен 0°, то есть можно считать, что направление мизинца соответствует началу отсчета углов, то есть 0°, а поэтому введем нумерацию пальцев:
№0 — Мизинец
№1 — Безымянный
№2 — Средний
№3 -Указательный
№4 — Большой
| №0 Мизинец 0° №1 Безымянный 30° №2 Средний 45° №3 Указательный 60° №4 Большой 90° n — номер пальца |
Значения синуса и косинуса угла по “ладони” приведено в таблице.
Примечание. Для определения косинуса угла отсчет пальцев происходит от большого пальца руки. [6]
Значения синуса
№ пальца | Угол |
|
0 | 0 |
|
1 | 30° | |
2 | 45° | |
3 | 60° | |
4 | 90° |
Значения косинуса
№ пальца | Угол |
|
4 | 0° | |
3 | 30° | |
2 | 45° | |
1 | 60° | |
0 | 90° |
7. Итоги урока.
8. Домашнее задание.
“Проверь себя”, стр. 166 учебник Никольского С.М.
Спасибо, урок окончен!
kopilkaurokov.ru
Урок в 10 классе по теме «Преобразование тригонометрических выражений»
Урок в 10 классе по алгебре и началам анализа
Тема: Преобразование тригонометрических выражений.
Цели: Обобщить и закрепить основные теоретические знания по данной теме. Проверить уровень знаний, умений и навыков учащихся применять тригонометрические тождества для упрощения выражений. Развивать у учащихся навыки самоконтроля, умения выделять главное. Развивать внимание. Воспитывать у учащихся культуру математической речи. Прививать интерес к математике.
Тип урока: Урок контроля и коррекции знаний, умений и навыков учащихся.
Ход урока.
“Гимнастика для ума”
?
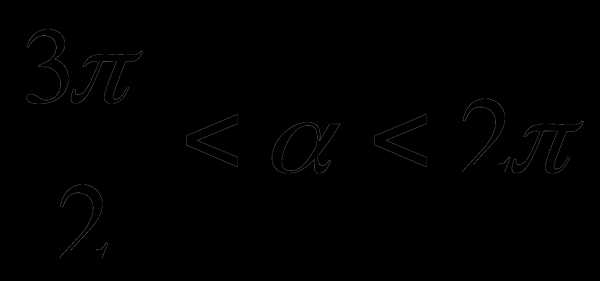
Ответ: .

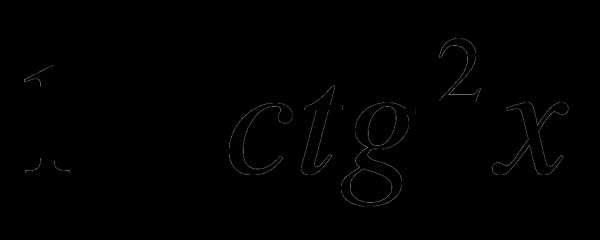
? 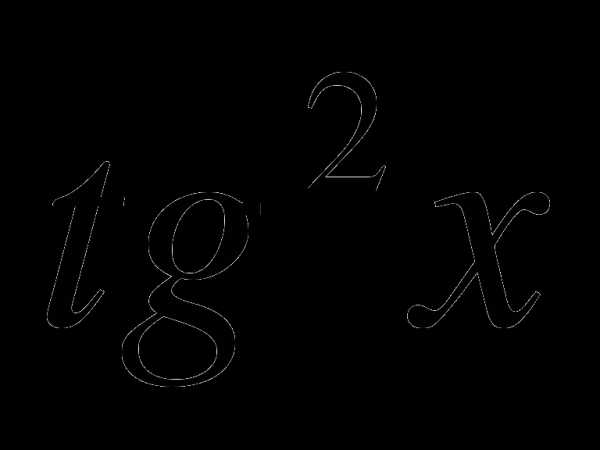
Ответ: sin x
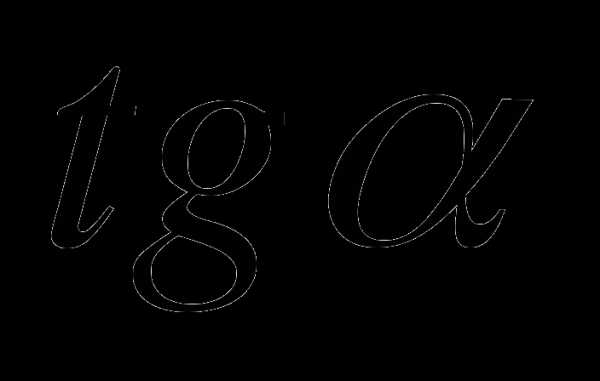



?
Ответ:  .
.
Актуализация опорных знаний учащихся.
/ Игра “Спешите видеть”. Найти и исправить, где это необходимо ошибки. /
1)
— +

+ —
2) 
3) 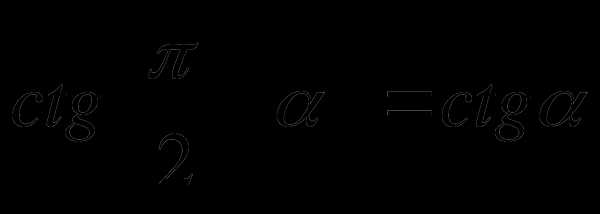
4)
5)
6)
+ +
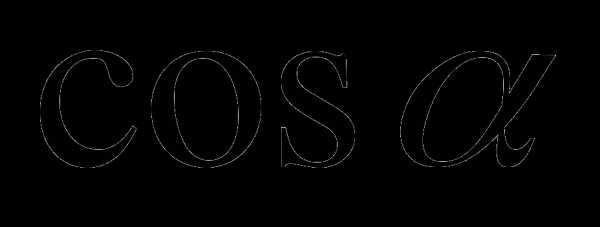
7)
Устные упражнения.
1)
2)
3)
4)
Самостоятельная работа №1 /5 минут/
/ 12 заданий по 0,5 баллов/
Вариант 1 Вариант 2
№1 Выразить в радианной мере угол . Выразить в радианной мере угол
.
№2 Знак косинуса во II четверти. Знак синуса в III четверти.
№3 В какой четверти , а . В какой четверти , а .
№4 

№5 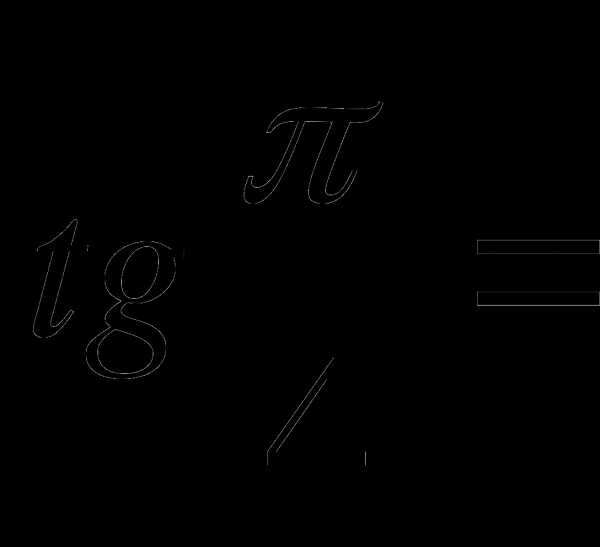
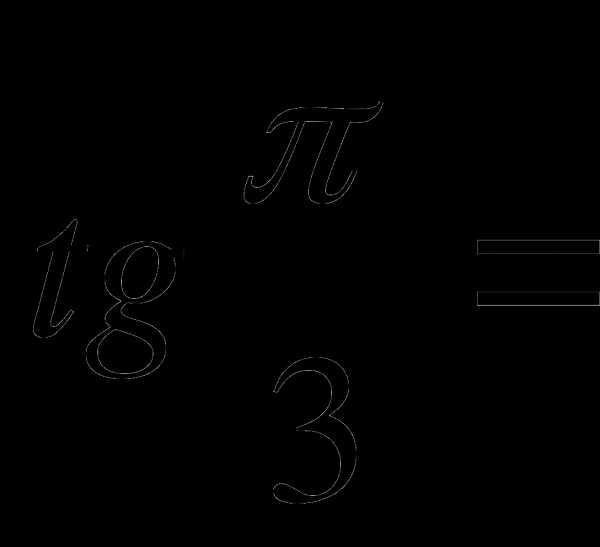
№6
№7 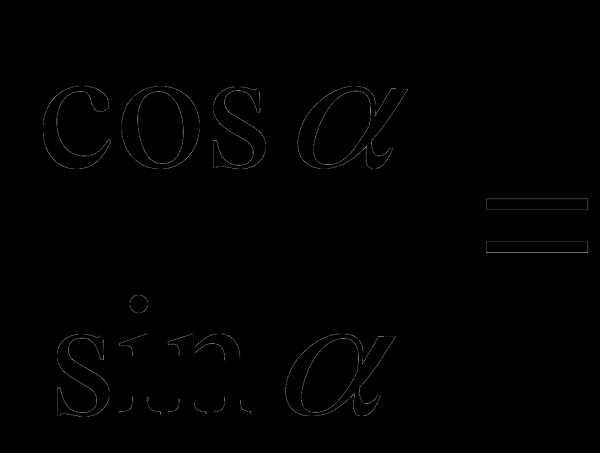
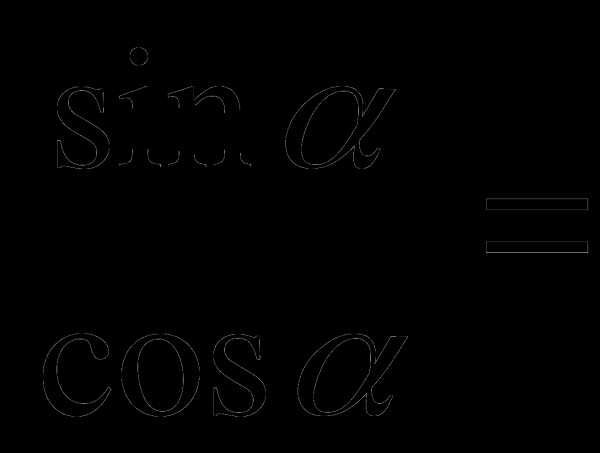
№8 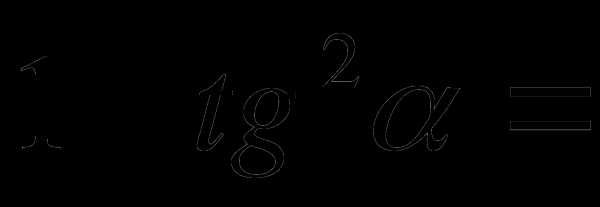
№9 
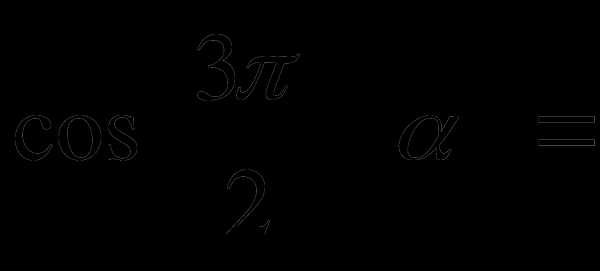
№10 Период функции  равен… Период функции
равен… Период функции  равен…
равен…
№11 
№12
Решение упражнений.
Упростить выражения:
А) ;
Б)
В) ;
Г) .
Самостоятельная работа №2. /15-20 мин/
/ 3 задания по 2 балла/
Вариант 1
№1. Упростить выражение:
а) ;
б) .
№2. Вычислить.
а) ;
б) .
№3. Доказать тождество:
.
Вариант 2.
№1. Упростить выражение:
а) ;
б) .
№2. Вычислить:
а) ;
б) .
№3. Доказать тождество:
а) .
Вариант 3
№1. Упростить выражение:
а) ;
б) .
№2. Вычислить:
а);
б) .
№3. Доказать тождество:
.
Вариант 4
№1. Упростить выражение:
а) ;
б) .
№2. Вычислить:
а) ;
б) .
№3. Доказать тождество:
.
Итог урока.
VIII. Домашнее задание.
Повторить свойства тригонометрических функций, значения тригонометрических функций углов , основные тригонометрические тождества. Решить №49(9,20), №51(16,18).
infourok.ru

 и
и  . Найдите градусную меру каждого из углов треугольника. Ответ: 60, 30, 90
. Найдите градусную меру каждого из углов треугольника. Ответ: 60, 30, 90 , б)
, б) 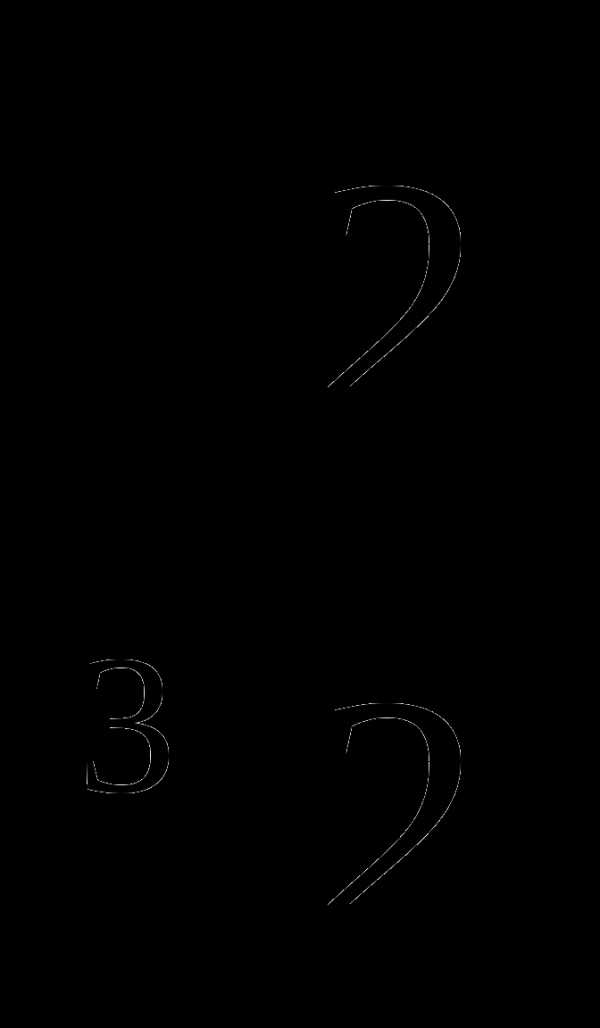
 , д)
, д) 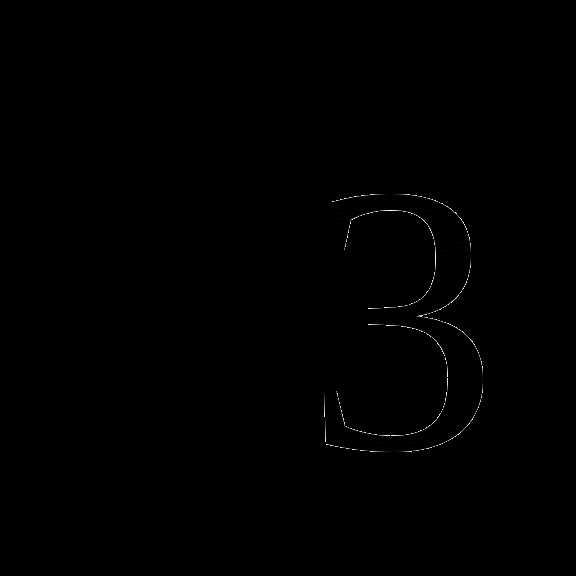 -2 ?
-2 ?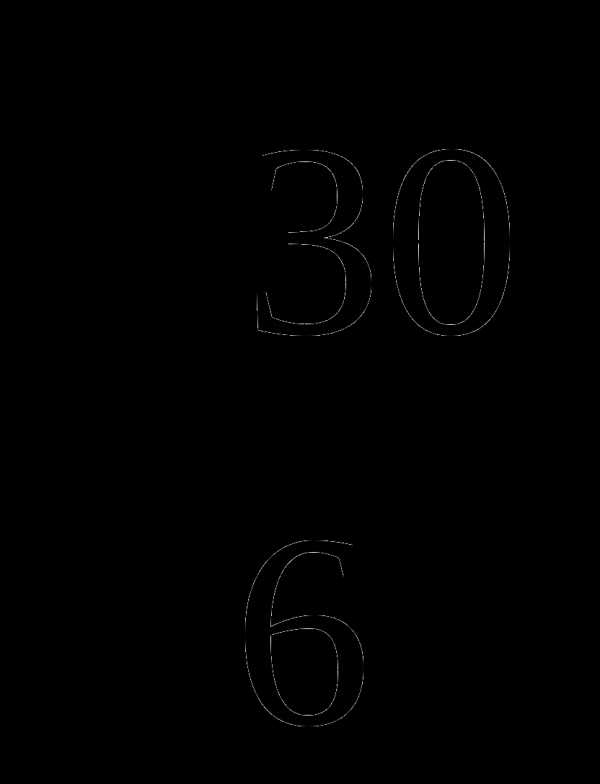 , в)
, в)  ?
? : .
: . :
: 
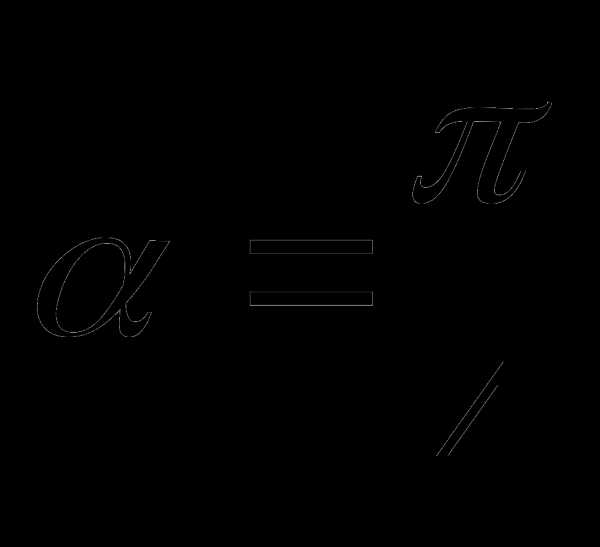 :
: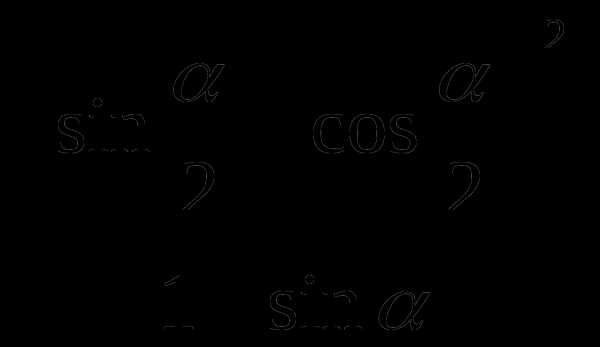 .
. : .
: . .
.