Интеграл от xlnx — Формула, Доказательство, Примеры, Определенный интеграл от xlnx
Интеграл от xlnx равен (x 2 /2) lnx — x 2 /4 + C, где C равно постоянная интегрирования. Этот интеграл можно вычислить методом интегрирования по частям. Воспользуемся методом интегрирования по частям, чтобы найти интеграл от произведения двух функций. Чтобы найти интеграл от xlnx, мы можем рассматривать xlnx как произведение двух функций x и lnx. Математически мы можем записать формулу для интеграла xlnx как ∫xlnx dx = (x 2 /2) lnx — x 2 /4 + C. Мы знаем, что интегрирование является процессом, обратным дифференцированию, и по формуле интегрирования по частям можно найти интеграл от xlnx.
Далее в этой статье мы найдем интеграл от xlnx и выведем его формулу. Мы также найдем интеграл функций с участием xlnx и решим несколько примеров, используя интеграл от xlnx для лучшего понимания концепции.
| 1. | Что такое интеграл xlnx? |
| 2. | Интеграл xlnx Формула |
| 3. | Интеграл xlnx Доказательство |
| 4. | Интеграл от x ln x на √(x 2 — 1) |
| 5. | Часто задаваемые вопросы по интегралу xlnx |
Что такое интеграл xlnx?
Интеграл от xlnx равен (x 2 /2) lnx — x 2 /4 + C, где C — постоянная интегрирования. Мы можем рассчитать интегрирование xlnx, используя интегрирование по частям, которое является одним из наиболее часто используемых и важных методов интегрирования. Мы можем записать интеграл xlnx с символами как ∫xlnx dx = (x 2 /2) lnx — x 2 /4 + C, где ∫ — символ интегрирования, dx указывает, что интегрирование xlnx относительно переменной x, а C — постоянная интегрирования.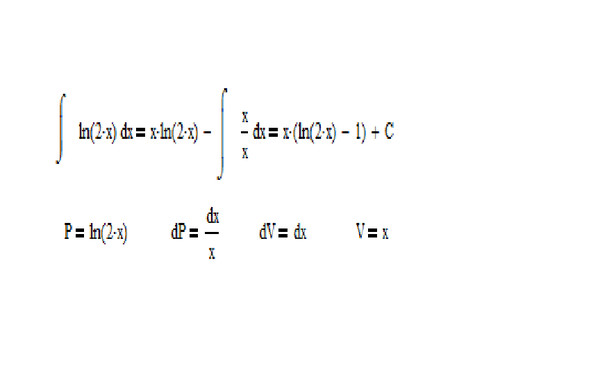
Интеграл xlnx Формула
Формула для интеграла от xlnx имеет вид ∫xlnx dx = (x 2 /2) lnx — x 2 /4 + C, где C – константа интегрирования. Эта формула может быть получена с использованием метода интегрирования по частям. На изображении ниже показана формула интеграла xlnx:
Интеграл xlnx Доказательство
Теперь, когда мы знаем, что интеграл от xlnx равен x 2 lnx/2 — x 2 /4 + C, докажем методом интегрирования по частям. Для интеграла от f(x) g(x) формула имеет вид (х) дх] дх. Для интеграла xlnx мы выберем первую функцию и вторую функцию, используя последовательность ILATE (I — обратная, L — логарифмическая, A — алгебраическая, T — тригонометрическая, E — экспоненциальная), поэтому мы имеем f(x) = lnx и г(х) = х.
∫xlnx dx = ln(x) ∫x dx — ∫[(lnx)’ ∫x dx] dx
= lnx × x 2 /2 — ∫[(1/x) × x 2 / 2] dx
= (x 2 /2) lnx — (1/2) ∫x dx
= (x 2 /2) lnx — (1/2)(x 2 /2) + C
= (x 2 /2) lnx — x 2 /4 + C
Таким образом, мы получили формулу интеграла от xlnx методом интегрирования по частям.
Интеграл от x ln x на √(x
2 — 1) Чтобы найти интеграл от x ln x по √(x 2 — 1), воспользуемся приведенной выше формулой интегрирования по частям. Формула интегрирования по частям имеет вид ∫f(x) g(x) dx = f(x) ∫g(x) dx — ∫[f'(x) ∫g(x) dx] dx. Предположим, что f(x) = ln x и g(x) = x/√(x 2 — 1). Прежде чем вычислять интеграл от x lnx / √(x 2 — 1), вычислим интеграл от x/√(x 2 — 1). Чтобы найти это, предположим, что u 2 = (x 2 — 1). Теперь, дифференцируя обе части, мы имеем 2u du = 2x dx, откуда следует, что xdx = udu. Итак, мы имеем
Чтобы найти это, предположим, что u 2 = (x 2 — 1). Теперь, дифференцируя обе части, мы имеем 2u du = 2x dx, откуда следует, что xdx = udu. Итак, мы имеем
∫[x/√(x 2 — 1)] dx = ∫(u/u) du
= ∫du
= u + K
= √(x 25 2
5 2
5 2
5 1) + K — (1)
Далее вычислим интеграл от √(x 2 — 1)/x. Чтобы найти это, предположим, что v = √(x 2 — 1), тогда dv/dx = x/√(x 2 — 1), откуда следует, что dx = √(x 2 — 1) dv/x = v/√(v 2 + 1) dv и √(x 2 — 1)/x = v/√(v 2 + 1). Следовательно, имеем
∫[√(x 2 — 1)/x] dx = ∫ [v/√(v 2 + 1)] [v/√(v 2 + 1) dv]
= ∫[v 2 /(v
= ∫[(v 2 + 1 — 1)/(v 2 + 1)] 1 dv 900 (v 2 + 1)/(v 2 + 1) dv — ∫1/(v 2 + 1) dv
= ∫dv — ∫1/(v 2 + 1) 1 dv 9000
= v — arctan(v) + M, где M — постоянная интегрирования.
= √(x 2 — 1) — arctg(√(x 2 — 1)) — (2)
Теперь вычислим интеграл от xlnx как
∫x lnx/√ (x 2 — 1) dx = ∫[x/√(x 2 — 1)] lnx dx
= lnx ∫[x/√(x 2 — 1)] dx — ∫[(lnx )’ ∫[x/√(x 2 — 1)] dx] dx
= ln x × (√(x 2 — 1)) — ∫[(1/x) √(x 2 — 1)] dx — [Из (1)]
= √(x 2 — 1) ln x — [√(x 2 — 1) — arctg(√(x 2 — 1))] — [Из (2)]
= √(x 2 — 1) ln x — √(x 2 — 1) + arctg(√(x 2 — 1)) + C, где C — интегрирование постоянной.
Следовательно, интеграл от x lnx / √(x 2 — 1) равен √(x 2 — 1) ln x — √(x 2 — 1) + arctg(√(x 2 — 1)) + C.
Важные замечания по интегралу от xlnx
- Интеграл от xlnx равен (x 2 /2) lnx — x 2 /4 + К.
- Мы можем найти интегрирование xlnx, используя метод интегрирования по частям.

☛ Похожие темы:
- Интеграл от 2sinx
- Интеграция root x
- Интеграл secx tanx
Часто задаваемые вопросы по интегралу xlnx
Что такое интеграл xlnx в исчислении?
Интеграл xlnx равен (x 2 /2) lnx — x 2 /4 + C, где C — постоянная интегрирования. Этот интеграл можно вычислить методом интегрирования по частям.
Какая формула для интеграла xlnx?
Формула для интеграла от xlnx имеет вид ∫xlnx dx = (x 2 /2) lnx — x 2 /4 + C, где C – константа интегрирования.
Какой определенный интеграл xlnx от 0 до 1?
Определенный интеграл xlnx от 0 до 1 равен -1/4. Мы можем вычислить этот интеграл, подставив пределы 0 и 1 в формулу интеграла от xlnx, определяемую выражением (x 2 /2) lnx — x 2 /4 + C.
Как найти интеграл от xlnx?
Интеграл от xlnx можно вычислить методом интегрирования по частям. Можно считать f(x) = lnx и g(x) = x и подставить в формулу ∫f(x) g(x) dx = f(x) ∫g(x) dx — ∫[f'(x) ∫g(x) dx] dx, чтобы найти интеграл от xlnx.
Можно считать f(x) = lnx и g(x) = x и подставить в формулу ∫f(x) g(x) dx = f(x) ∫g(x) dx — ∫[f'(x) ∫g(x) dx] dx, чтобы найти интеграл от xlnx.
Как вычислить интеграл xlnx — 1?
Интеграл от xlnx — 1 можно вычислить по формуле ∫[f(x) — g(x)] dx = ∫f(x) dx — ∫g(x) dx. Интеграл можно записать в виде ∫(xlnx — 1) dx = ∫xlnx dx — ∫dx = (x 2 /2) lnx — x 2 /4 — x + C.
исчисление — Чему равен интеграл от x/ln(x)?
Задавать вопрос
спросил
Изменено 5 лет, 8 месяцев назад
Просмотрено 13 тысяч раз 9{-z}}{z}\,dz$$, что, как указано на странице Википедии, не является элементарной функцией.
$\endgroup$
$\begingroup$
Неопределенный интеграл не может быть выражен через элементарные функции.