Как упрощать выражения 8 класс – Упрощение рациональных выражений — урок. Алгебра, 8 класс.

Алгебра, 8 класс: уроки, тесты, задания

Алгебраические дроби. Арифметические операции над алгебраическими дробями

1. Основные понятия

2. Основное свойство алгебраической дроби

3. Сложение и вычитание алгебраических дробей с равными знаменателями

4. Сложение и вычитание алгебраических дробей с разными знаменателями

5. Умножение, деление и возведение в степень алгебраических дробей

6. Преобразование рациональных выражений

7. Первые представления о решении рациональных уравнений

Квадратичная функция. Функция y = k/x

1. Функция y = kx², её свойства и график

2. Функция y = k/x, её свойства и график

3. Как построить график функции у = f(x + l), если известен график функции у = f(x)

4. Как построить график функции у = f(x) + m, если известен график функции у = f(x)

5. Как построить график функции y = f(x + l) + m, если известен график функции y = f(x)

6. Функция y = ax² + bx + c, её свойства и график

7. Графическое решение квадратных уравнений

Функция квадратного корня. Свойства квадратного корня

1. Понятие квадратного корня из неотрицательного числа

2. Функция квадратного корня, его свойства и график

3. Рациональные числа

4. Свойства квадратных корней

5. Преобразование выражений, содержащих операцию извлечения квадратного корня

Квадратные уравнения

1. Основные понятия

2. Формулы корней квадратного уравнения

3. Рациональные уравнения

4. Рациональные уравнения как математические модели реальных ситуаций

5. Ещё одна формула корней квадратного уравнения

6. Теорема Виета

7. Иррациональные уравнения

Действительные числа

1. Основные понятия

2. Иррациональные числа

3. Множество действительных чисел

4. Модуль действительного числа

5. Приближённые значения действительных чисел

6. Степень с отрицательным целым показателем

7. Стандартный вид числа

Неравенства

1. Числовые промежутки

2. Свойства числовых неравенств

3. Решение линейных неравенств

4. Решение квадратных неравенств

5. Исследование функций на монотонность

Международная оценка образовательных достижений учащихся (PISA)

www.yaklass.ru

Упрощение выражений. Алгебра 8 класс. ИДЗ 2 ЗАДАНИЕ 7

Просмотр содержимого документа
«Упрощение выражений. Алгебра 8 класс. ИДЗ 2 ЗАДАНИЕ 7»

8 класс Алгебра ИДЗ 2

Задание 7

Вариант 1

Упростите выражение: a) , если 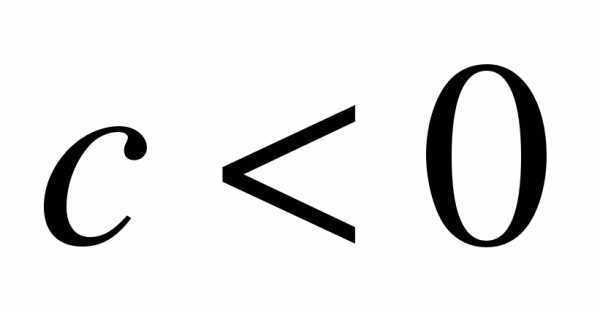б)

в)

Вариант 2

Упростите выражение: a) , если 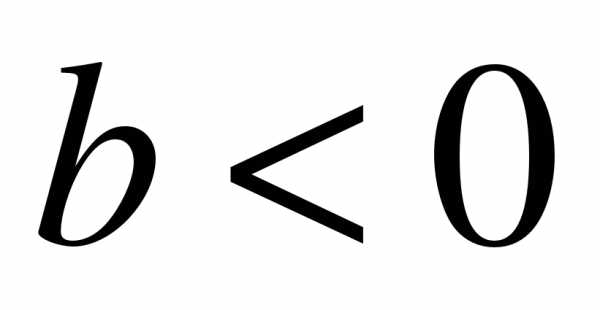б)

в)

Вариант 3

Упростите выражение: a), если 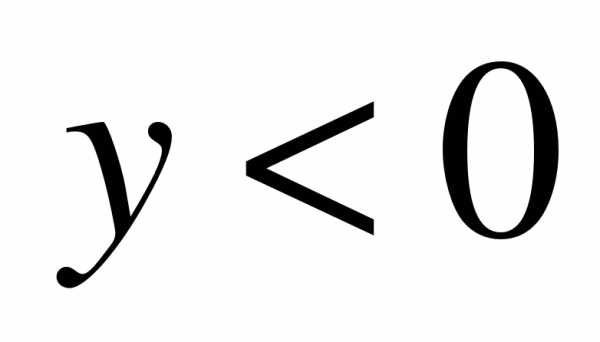б)

в)

Вариант 4

Упростите выражение: a) , если 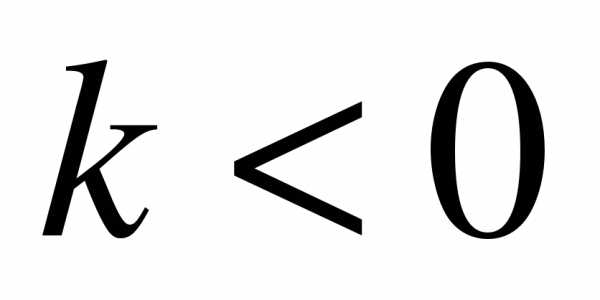б)

в)

Вариант 5

Упростите выражение: a) , если 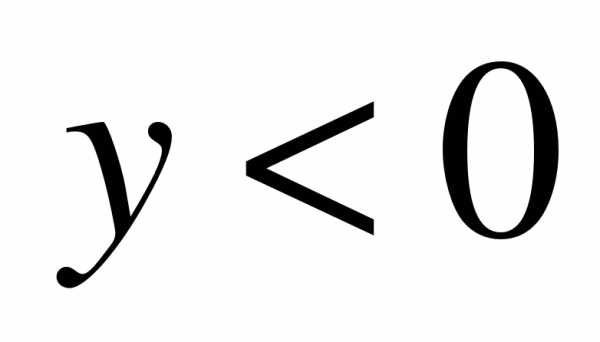б)

в)

Вариант 6

Упростите выражение: a) , если 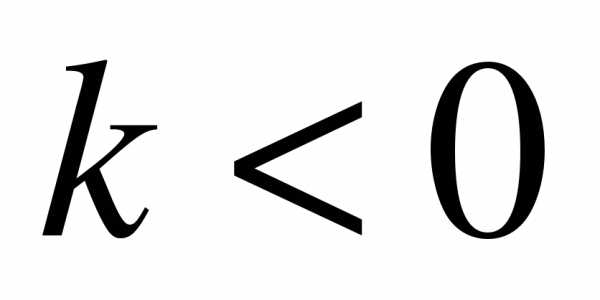б)

в)

Вариант 7

Упростите выражение: а) 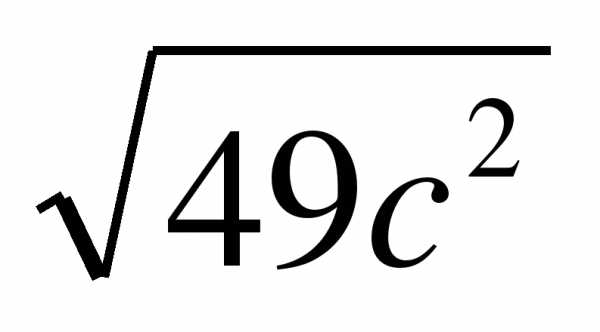, если б)

в)

Вариант 8

Упростите выражение: a) , если б)

в)

Вариант 9

Упростите выражение: a) , если б)

в)

Вариант 10

Упростите выражение: a), если б)

в)

Вариант 11

Упростите выражение: a) где б)

в)

Вариант 12

Упростите выражение: a) , где a б)

в)

Вариант 13

Упростите выражение: a) , где б)

в)

Вариант 14

Упростите выражение: a) _{, где б)}

в)

Вариант 15

Упростите выражение: a) , где б)

в)

Вариант 16

Упростите выражение: a) , где б)

в)

Вариант 17

Упростите выражение: a) , где б)

в)

Вариант 18

Упростите выражение: a) _{, где б)}

в)

Вариант 19

Упростите выражение: a) , если 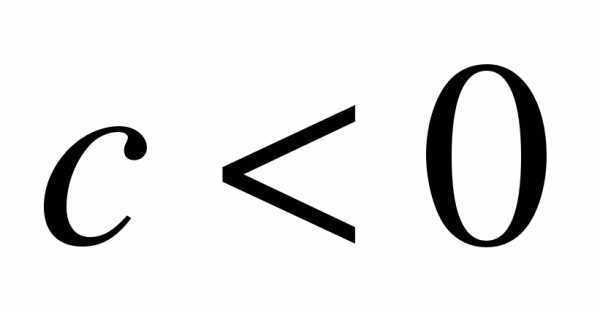б)

в)

Вариант 20

Упростите выражение: a) 14 _б)

в)

Вариант 21

Упростите выражение: a) 3, a, b б)

в)

Вариант 22

Упростите выражение: a) _{, б)}

в)

Вариант 23

Упростите выражение: a) 5, x б)

в)

Вариант 24

Упростите выражение: a) 0,25 , z б)

в)

Вариант 25

Упростите выражение: a) 0,125 , y б)

в)

multiurok.ru

АЛГЕБРА 8 КЛАСС Упростить выражение:

у данного выражения нет начала и конца, идеальное у_прощение — есть вечный идеал.

1. Разложить знаменатели на множители 2. Привести к одному знаменателю 3. Разложить на множители числитель 4. Выполнить сокращения, если будут 5. Если первые четыре пункта не понятны, выпить яду и с разбега головой об стенку удариться.

Надо учить формулы!! ! (а-4)(а-4)+12а-а^2-4а-16=а^2-8а+16+12а-а^2-4а-16=0 -это числитель, в знаменателе а^3-64 Значит, ответ 0

ноль и бесконечность — вечные союзники вселенной

touch.otvet.mail.ru

Преобразование и упрощение более сложных выражений с корнями (алгебра 8 класс)

Дополнительные сочинения

В начале урока мы повторим основные свойства квадратных корней, а затем рассмотрим несколько сложных примеров на упрощение выражений, содержащих квадратные корни.

Тема: Функция . Свойства квадратного корня

Урок: Преобразование и упрощение более сложных выражений с корнями

1. Повторение свойств квадратных корней

Вкратце повторим теорию и напомним основные свойства квадратных корней.

Свойства квадратных корней:

1. , следовательно, ;

2. ;

3. ;

4. .

2. Примеры на упрощение выражений с корнями

Перейдем к примерам использования этих свойств.

Пример 1. Упростить выражение .

Решение. Для упрощения число 120 необходимо разложить на простые множители:

. Квадрат суммы раскроем по соответствующей формуле:

.

Ответ. 11.

Пример 2. Упростить выражение .

Решение. Учтем, что данное выражение имеет смысл не при всех возможных значениях переменной, т. к. в данном выражении присутствуют квадратные корни и дроби, что приводит к «сужению» области допустимых значений. ОДЗ: ().

Приведем выражение в скобках к общему знаменателю и распишем числитель последней дроби как разность квадратов:

при.

Ответ. при.

Пример 3. Упростить выражение .

Решение. Видно, что вторая скобка числителя имеет неудобный вид и нуждается в упрощении, попробуем разложить ее на множители с помощью метода группировки.

. Для возможности выносить общий множитель мы упростили корни путем их разложения на множители. Подставим полученное выражение в исходную дробь:

. После сокращения дроби применяем формулу разности квадратов.

Ответ. 13.

3. Пример на избавление от иррациональности

Пример 4. Освободиться от иррациональности (корней) в знаменателе: а) ; б) .

Решение. а) Для того чтобы избавиться от иррациональности в знаменателе, применяется стандартный метод домножения и числителя и знаменателя дроби на сопряженный к знаменателю множитель (такое же выражение, но с обратным знаком). Это делается для дополнения знаменателя дроби до разности квадратов, что позволяет избавиться от корней в знаменателе. Выполним этот прием в нашем случае:

.

б) выполним аналогичные действия:

       

.

Ответ.; .

4. Пример на доказательство и на выделение полного квадрата в сложном радикале

Пример 5. Докажите равенство .

Доказательство. Воспользуемся определением квадратного корня, из которого следует, что квадрат правого выражения должен быть равен подкоренному выражению:

. Раскроем скобки по формуле квадрата суммы:

, получили верное равенство.

Доказано.

Пример 6. Упростить выражение .

Решение. Указанное выражение принято называть сложным радикалом (корень под корнем). В данном примере необходимо догадаться выделить полный квадрат из подкоренного выражения. Для этого заметим, что из двух слагаемых является претендентом на роль удвоенного произведения в формуле квадрата разности (разности, т. к. присутствует минус). Распишем его в виде такого произведения: , тогда на роль одного из слагаемых полного квадрата претендует , а на роль второго – 1.

. Подставим это выражение под корень:

. Модуль раскрывается в таком виде, т. к. .

Ответ..

На этом занятии мы заканчиваем тему «Функция . Свойства квадратного корня», а на следующем уроке начинаем новую тему «Действительные числа».

Список литературы

1. Башмаков М. И. Алгебра 8 класс. – М.: Просвещение, 2004.

2. Дорофеев Г. В., Суворова С. Б., Бунимович Е. А. и др. Алгебра 8. – 5-е изд. – М.: Просвещение, 2010.

3. Никольский С. М., Потапов М. А., Решетников Н. Н., Шевкин А. В. Алгебра 8 класс. Учебник для общеобразовательных учреждений. – М.: Просвещение, 2006.

Дополнительные рекомендованные ссылки на ресурсы сети Интернет

1. Интернет-портал xenoid. ru .

2. Математическая школа .

3. Интернет-портал XReferat. Ru .

Домашнее задание

1. №357, 360, 372, 373, 382. Дорофеев Г. В., Суворова С. Б., Бунимович Е. А. и др. Алгебра 8. – 5-е изд. – М.: Просвещение, 2010.

2. Избавьтесь от иррациональности в знаменателе: а) , б) .

3. Упростите выражение: а) , б) .

4. Докажите тождество .

dp-adilet.kz

No related posts.