Как упростить дроби – Сокращение обыкновенных дробей.

alexxlab / / Школьная жизнь

Сокращение обыкновенных дробей.

Деление и числителя и знаменателя дроби на их общий делитель, отличный от единицы, называют сокращением дроби.

Чтобы сократить обыкновенную дробь, нужно разделить ее числитель и знаменатель на одно и то же натуральное число.

Это число является наибольшим общим делителем числителя и знаменателя данной дроби.

Возможны следующие формы записи решения примеров на сокращение обыкновенных дробей.

Учащийся вправе выбрать любую форму записи.

 

Примеры. Упростить дроби.

Сократим дробь на 3 (делим числитель на 3;

делим знаменатель на 3).

 

 

Сокращаем дробь на 7.

 

 

 

Выполняем указанные действия в числителе и знаменателе дроби.

Полученную дробь сокращаем на 5.

 

 

Сократим данную дробь 4) на 5·7³ — наибольший общий делитель (НОД) числителя и знаменателя, который состоит из общих множителей числителя и знаменателя, взятых в степени с наименьшим показателем.

 

 

Разложим числитель и знаменатель этой дроби на простые множители.

 

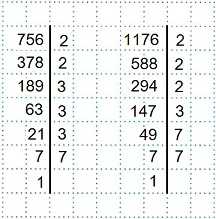Получаем: 756=2²·3³·7 и 1176=2³·3·7².

Определяем НОД (наибольший общий делитель) числителя и знаменателя дроби 5).

Это произведение общих множителей, взятых с наименьшими показателями.

НОД(756; 1176)=2²·3·7.

 

 

Делим числитель и знаменатель данной дроби на их НОД, т. е. на 2²·3·7 получаем несократимую дробь 9/14.

А можно было записать разложения числителя и знаменателя  в виде произведения простых множителей, не применяя понятие степени, а затем произвести сокращение дроби, зачеркивая одинаковые множители в числителе и знаменателе. Когда одинаковых множителей не останется — перемножаем оставшиеся множители отдельно в числителе и отдельно в знаменателе и выписываем получившуюся дробь

9/14.

И, наконец, можно было сокращать данную дробь 5) постепенно, применяя признаки деления чисел и к числителю и к знаменателю дроби. Рассуждаем так: числа 756 и 1176 оканчиваются четной цифрой, значит, оба делятся на 2. Сокращаем дробь на 2. Числитель и знаменатель новой дроби — числа 378 и 588 также делятся на 2. Сокращаем дробь на 2. Замечаем, что число 294 — четное, а 189 — нечетное, и сокращение на 2 уже невозможно. Проверим признак делимости чисел 189 и 294 на

3.

(1+8+9)=18 делится на 3 и (2+9+4)=15 делится на 3, следовательно, и сами числа 189 и 294 делятся на 3. Сокращаем дробь на 3.  Далее, 63 делится на 3, а 98 — нет. Перебираем другие простые множители. Оба числа делятся на 7. Сокращаем дробь на 7 и получаем несократимую дробь 9/14.

 

Запись имеет метки: сокращение обыкновенной дроби

www.mathematics-repetition.com

Как упрощать составные дроби Как? Так!

Содержимое:

2 метода:

Составная дробь – это дробь, у которой в числителе или в знаменателе или и в числителе, и в знаменателе находится дробь. По этой причине составные дроби еще называют многоэтажными дробями. Процесс упрощения составных дробей варьируется от простого к сложному — в зависимости от числа членов выражений, находящихся в числителе и в знаменателе, или от наличия переменных в числителе и в знаменателе.

Шаги

Метод 1 Упрощение составных дробей через умножение на обратную величину

  1. 1 При необходимости упростите и числитель, и знаменатель до одной обыкновенной дроби. Легко упростить составную дробь, у которой и в числителе, и в знаменателе находится одна обыкновенная дробь. Поэтому, если в числителе или в знаменателе данной вам составной дроби находятся несколько дробей или дроби и целые числа, упростите их, чтобы получить по одной дроби и в числителе, и в знаменателе. Для этого потребуется найти наименьший общий знаменатель (НОЗ).
    • Например, дана составная дробь: (3/5 + 2/15)/(5/7 — 3/10). Во-первых, упростим и числитель, и знаменатель этой дроби до одной дроби.
      • Для дробей, находящихся в числителе, НОЗ=15. Поэтому приведем дробь 3/5 к общему знаменателю: 3/5 * 3/3 = 9/15. Перепишем числитель как: 9/15 + 2/15 = 11/15.
      • Для дробей, находящихся в знаменателе, НОЗ=70. Поэтому приведем обе дроби к общему знаменателю: 5/7 * 10/10 = 50/70 и 3/10 * 7/7 = 21/70. Перепишем знаменатель как: 50/70 — 21/70 = 29/70.
      • Таким образом, перепишем составную дробь как: (11/15)/(29/70).
  2. 2 Для получения обратной дроби поменяйте местами числитель и знаменатель. Правило: деление первого числа на второе равно умножению первого числа на обратную величину второго числа. Теперь, когда и в числителе, и в знаменателе составной дроби находится по одной дроби, можно воспользоваться этим правилом для упрощения составной дроби. Во-первых, найдите обратную дробь для дроби, находящейся в знаменателе сложной дроби. Для этого поменяйте местами числитель и знаменатель дроби.
    • В нашем примере дробь в знаменателе — это 29/70. Обратная ей дробь – это 70/29.
      • Обратите внимание, что если в знаменателе составной дроби находится целое число, то его обратная величина находится по тем же правилам. Например, если дана составная дробь (11/15)/(29), то обратная величина целого числа 29 (его можно записать как дробь 29/1) есть дробь 1/29.
  3. 3 Перемножьте две дроби. Умножьте дробь, находящуюся в числителе составной дроби, на полученную обратную дробь. Для этого отдельно перемножьте их числители и отдельно – знаменатели.
    • В нашем примере: 11/15*70/29. 11*70=770 и 15*29= 435. Итак, результат умножения: 770/435.
  4. 4 Упростите полученную дробь, найдя наибольший общий делитель (НОД). НОД – это наибольшее число, на которое делятся и числитель, и знаменатель. Найдите НОД и разделите на него и числитель, и знаменатель.
    • В нашем примере НОД= 5. Таким образом, 770/5=154 и 435/5=87. Упрощенная дробь (и окончательный ответ): 154/87.

Метод 2 Упрощение составных дробей, содержащих переменную

  1. 1 По возможности используйте правило умножения на обратную величину (приведенное выше). Числитель и знаменатель практически любой составной дроби может быть упрощен до одной дроби. Составные дроби, содержащие переменную, не являются исключением; однако, чем сложнее выражение с переменной, тем сложнее его упростить. В случае сложных выражений с переменной (содержащих несколько членов) воспользуйтесь методами упрощения, описанными ниже.
    • Например, составную дробь (1/х)/(х/6) легко упростить через умножение на обратную величину: (1/х)*(6/х)=6/х2.
    • Другой пример: дробь (((1)/(x+3)) + x — 10)/(x +4 +((1)/(x — 5))) трудно упростить через умножение на обратную величину. То есть выражения в числителе и в знаменателе будет сложно упростить до одной дроби. Поэтому воспользуйтесь методами упрощения, описанными ниже.
  2. 2 Начните с поиска наименьшего общего знаменателя дробей, находящихся и в числителе, и в знаменателе составной дроби. Для этого, как правило, просто перемножьте знаменатели этих дробей.
    • Это легче понять на примере. Попробуем упростить составную дробь: (((1)/(x+3)) + x — 10)/(x +4 +((1)/(x — 5))). В этой составной дроби есть дроби (1)/(х +3) и (1)/(х-5). Их наименьший общий знаменатель (НОЗ) равен (х +3)(х-5).
  3. 3 Умножьте и числитель, и знаменатель составной дроби на найденный НОЗ. Другими словами, вы умножите составную дробь на НОЗ/НОЗ (то есть на 1, что не влияет на исходное значение дроби).
    • В нашем примере вы умножите составную дробь (((1)/(х +3)) + х — 10)/(х +4 + ((1)/(х — 5))) на ((х +3)(х-5))/((х +3)(х-5)).
    • Умножьте числитель: (((1)/(x+3)) + x — 10) × (x+3)(x-5)
      • = (((x+3)(x-5)/(x+3)) + x((x+3)(x-5)) — 10((x+3)(x-5))
      • = (x-5) + (x(x2 — 2x — 15)) — (10(x2 — 2x — 15))
      • = (x-5) + (x3 — 2x2 — 15x) — (10x2 — 20x — 150)
      • = (x-5) + x3 — 12x2 + 5x + 150
      • = x3 — 12x2 + 6x + 145
  4. 4 Умножьте знаменатель так же, как вы умножили числитель.
    • Умножьте знаменатель: (x +4 +((1)/(x — 5))) × (x+3)(x-5)
      • = x((x+3)(x-5)) + 4((x+3)(x-5)) + (1/(x-5))(x+3)(x-5).
      • = x(x2 — 2x — 15) + 4(x2 — 2x — 15) + ((x+3)(x-5))/(x-5)
      • = x3 — 2x2 — 15x + 4x2 — 8x — 60 + (x+3)
      • = x3 + 2x2 — 23x — 60 + (x+3)
      • = x3 + 2x2 — 22x — 57
  5. 5 Запишите новую упрощенную дробь. После умножения исходной составной дроби на НОЗ/НОЗ и приведения подобных членов вы получите обыкновенную дробь. Таким образом, умножив на НОЗ исходную составную дробь, вы избавились от дробей и в числителе, и знаменателе, в которых теперь находятся только целые числа и переменные.
    • Итак, в числитель запишите выражение: x3 — 12x2 + 6x + 145, а в знаменатель — выражение: x3 + 2x2 — 22x — 57. Упрощенная дробь: (x3 — 12x2 + 6x + 145)/(x3 + 2x2 — 22x — 57)

Советы

  • Записывайте каждый шаг вычислений. Вы можете легко запутаться в дробях, если не записываете каждый шаг вычислений или делаете их в голове.
  • В интернете или в учебнике найдите составные дроби и попрактикуйтесь в их упрощении.

Прислал: Волкова Александра . 2017-11-12 13:15:01

kak-otvet.imysite.ru

Ответы@Mail.Ru: Упростите смешанную дробь — 5 26/39

26 и 39 сократи на 13

Сокращаем дробную часть на 13 и получим 5 2/3

и числитель и знаменатель делим на 13 => получаем 2/3 всё)

сократить на 13 — 5 2/3

touch.otvet.mail.ru

Как упростить неправильную дробь Как? Так!

Содержимое:

2 метода:

Дробь – это число, которое представляет собой часть целого числа (целой величины). Если числитель дроби больше знаменателя, она называется неправильной дробью и может быть упрощена до смешанного числа, которое включает целую и дробную части. Нет ничего необычного в неправильной дроби, а в некоторых случаях с такой дробью легче работать, чем со смешанным числом. Но в повседневной жизни смешанными числами мы пользуемся чаще, чем неправильными дробями, поэтому полезно знать, как превратить неправильную дробь в смешанное число.

Шаги

Метод 1 С помощью диаграммы

  1. 1 Выясните, является ли дробь неправильной. У неправильной дроби числитель больше знаменателя.
    • Например, дробь 104 2 Найдите знаменатель. Знаменатель – это число, которое находится под дробной чертой. Он указывает, на сколько равных частей поделена целая величина.
      • Например, в дроби 104 3 Найдите числитель. Числитель – это число, которое находится над дробной чертой. Он указывает, сколько дано частей целой величины.
        • Например, в дроби 104 4 Нарисуйте круги, которые будут символизировать целую величину. Каждый круг разделите на одинаковые части (сектора), количество которых равно знаменателю дроби.
          • Например, если знаменатель равен 4, каждый круг разделите на четыре равные части.
        • 5 Заштрихуйте сектора. Количество заштрихованных секторов должно быть равно числителю дроби.
          • Например, если дана дробь 104 6 Посчитайте, сколько полных кругов вы заштриховали. Чтобы упростить неправильную дробь, необходимо превратить ее в смешанное число, которое включает как целое число, так и дробь. Количество полных заштрихованных кругов представляет собой целую часть смешанного числа.
            • Например, в случае дроби 104 7 Посчитайте количество оставшихся заштрихованных частей круга. Оно будет представлять дробную часть смешанного числа. Дробная часть записывается непосредственно после целой части смешанного числа.
              • В случае дроби 104 8 Упростите ответ, если необходимо. Иногда дробную часть смешанного числа можно упростить, чтобы получить окончательный ответ.
                • В нашем примере смешанное число 224

                  Метод 2 С помощью деления

                  1. 1 Выясните, является ли дробь неправильной. У неправильной дроби числитель больше знаменателя.
                    • Например, дробь 104 2 Разделите числитель на знаменатель. Помните, что дробная черта обозначает операцию деления. Чтобы упростить неправильную дробь, нужно превратить ее в смешанное число, которое включает целое число и дробь. Целое количество раз, на которое числитель делится на знаменатель, представляет собой целую часть смешанного числа. Запишите это число и обратите внимание на остаток.
                      • Знаменатель не будет делиться на числитель без остатка, который представляет собой дробную часть смешанного числа.
                      • Например, в случае дроби 104 3 Превратите остаток в дробь. Для этого остаток запишите в числителе новой дроби, а в знаменателе напишите число, стоящее в знаменателе исходной неправильной дроби. Запишите полученную дробь после найденной целой части. Так вы получите смешанное число.
                        • Например, 10÷4=2R2 4 Упростите ответ, если необходимо. Иногда дробную часть смешанного числа можно упростить, чтобы получить окончательный ответ.
                          • В нашем примере смешанное число 224{displaystyle 2{frac {2}{4}}} упрощается до 212{displaystyle 2{frac {1}{2}}}.

                  Советы

                  • Чтобы преобразовать смешанное число в неправильную дробь, умножьте целую часть на знаменатель дробной части, а затем полученный результат прибавьте к числителю дробной части.
                  • Знаменатель не меняйте. Например, 212{displaystyle 2{frac {1}{2}}} можно преобразовать в 52{displaystyle {frac {5}{2}}}, потому что 2×2+1=5{displaystyle 2 imes 2+1=5}.
                  • Некоторые неправильные дроби можно преобразовать в целые числа. Например, 243{displaystyle {frac {24}{3}}} = 8.

Прислал: Васильева Светлана . 2017-11-12 13:14:56

kak-otvet.imysite.ru

Как упростить неправильную дробь

2 методика:Основные понятияУпрощение неправильной дроби

Дробь – это число, состоящее из одной или нескольких частей единицы. Дробь состоит из двух чисел – делимого, которое записывается в числителе (сверху) и делителя, который записывается в знаменателе (снизу). Между этими числами ставится горизонтальная или косая черта, обозначающая знак деления. Если числитель дроби больше ее знаменателя, то такая дробь называется неправильной дробью.

Шаги

Метод 1 из 2: Основные понятия

  1. 1 Дробь состоит из трех частей: числителя, знаменателя и дробной черты.
    • Числитель — это верхнее число. Оно определяет делимое (число, которое делят).
    • Знаменатель – это нижнее число. Оно определяет делитель (число, на которое делят).
    • Дробная черта — горизонтальная или косая черта, обозначающая знак деления (поэтому дробь можно рассматривать как процесс деления).
  2. 2 Правильная дробь – это дробь, числитель которой меньше знаменателя (значение такой дроби всегда меньше 1). Например, дробь 1/2 является правильной дробью.
  3. 3 Неправильная дробь – это дробь, числитель которой больше знаменателя (значение такой дроби всегда больше 1). Например, дробь 3/2 является неправильной дробью.
  4. 4 Смешанное число – это неправильная дробь, записанная в виде целого числа и правильной дроби. Например, неправильную дробь 3/2 можно переписать в виде 1½. Запись неправильной дроби в виде смешанного числа относится к процессу упрощения неправильной дроби.

Метод 2 из 2: Упрощение неправильной дроби

  1. 1 Определите, является ли данная вам дробь неправильной. Если ее числитель больше знаменателя, то дробь неправильная, и вы можете перейти к следующему шагу.
    • Например, дана дробь 9/2. Ее числитель (9) больше знаменателя (2), поэтому это неправильная дробь.
  2. 2 Разделите числитель на знаменатель. Запомните: дробная черта обозначает знак деления, что особенно полезно при работе с неправильными дробями. Разделив числитель на знаменатель, вы сможете выразить неправильную дробь в виде комбинации целого числа и правильной дроби.
    • В приведенном выше примере разделите 9 на 2. Вы получите 4 (целый результат деления) плюс некоторый остаток.
  3. 3 Вычислите остаток. Для этого вычтите из числителя произведение целого результата деления и знаменателя.
    • В приведенном выше примере вычтите из числителя (9) произведение целого результата деления (4) и знаменателя (2): 9 – 4*2 = 1.
  4. 4 Запишите целый результат деления как целую часть смешанного числа, остаток запишите в числителе дробной части смешанного числа, а в знаменателе дробной части смешанного числа запишите знаменатель неправильной дроби.
    • В приведенном выше примере, 4 – целый результат деления, 1 – остаток, 2 – знаменатель неправильной дроби. Таким образом, дробь 9/2 упрощается до смешанного числа 4½.
    • 9/2 = 4½.

Советы

  • Представьте себе пиццу, разрезанную на 8 кусочков. Дробь 9/8 эквивалентна 1 целой пицце и 1 кусочку разрезанной пиццы.
  • Чтобы преобразовать смешанное число в неправильную дробь, умножьте целую часть смешанного числа на знаменатель дробной части и прибавьте сюда числитель. Результат запишите в числителе неправильной дроби, а знаменатель оставьте прежним. Например, 2½ можно переписать в виде 5/2 (2*2 + 1 = 5).

ves-mir.3dn.ru

No related posts.

Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *