Как найти угол между векторами
Угол между векторами
Для того, чтобы мы могли ввести формулу для вычисления угла между векторами через координаты, нужно сначала разобраться с самим понятием угла между этими векторами.
Определение 1
Пусть нам даны два вектора $\overline{α}$ и $\overline{β}$. Возьмем в пространстве какую-либо точку $O$ и отложим от нее векторы $\overline{α}=\overline{OA}$ и $\overline{β}=\overline{OB}$, тогда угол $AOB$ будет носить название угол между двумя векторами. (рис. 1).
Рисунок 1. Угол между векторами. Автор24 — интернет-биржа студенческих работ
Причем мы будем считать, что если векторы $\overline{α}$ и $\overline{β}$ будут сонаправленными, или один или оба из них будет нулевым вектором, то угол между этими векторами будет равняться $0^\circ$.
Обозначение: $∠(\overline{α},\overline{β})$
Нахождение угла между векторами в пространстве с помощью скалярного произведения
Вспомним сначала, что называется скалярным произведением и каким образом его можно находить.
Определение 2
Скалярным произведением двух векторов будем называть такой скаляр (или число), который равняется произведению длин двух этих векторов с косинусом угла между данными векторами.
Математически это может выглядеть следующим образом:
$\overline{δ}\overline{β}=|\overline{δ}||\overline{β}|cos∠(\overline{δ},\overline{β})$
Также, помимо того, как из самого определения 1, для нахождения скалярного произведения можно пользоваться следующей теоремой.
Теорема 1
Скалярное произведение двух данных векторов $\overline{δ}$ и $\overline{β}$ с координатами $(δ_1,β_1,γ_1)$ и $(δ_2,β_2,γ_2)$, равняется сумме произведений их соответствующих координат.
Математически выглядит следующим образом
$\overline{δ}\cdot \overline{β}=δ_1 δ_2+β_1 β_2+γ_1 γ_2$
С помощью скалярного произведения мы можем найти косинус угла между векторами. Пусть нам даны векторы $\overline{δ}$ и $\overline{β}$ с координатами $(δ_1,β_1,γ_1)$ и $(δ_2,β_2,γ_2)$, соответственно. Из определения 2 получим, что
$cos∠(\overline{δ},\overline{β})=\frac{\overline{δ}\cdot \overline{β}}{|\overline{δ}||\overline{β}|}$
Из теоремы 1 мы знаем, что $\overline{δ}\cdot \overline{β}=δ_1 δ_2+β_1 β_2+γ_1 γ_2$, следовательно
$cos∠(\overline{δ},\overline{β})=\frac{δ_1 δ_2+β_1 β_2+γ_1 γ_2}{|\overline{δ}||\overline{β}|}$
Расписывая по формуле длины вектора значения $|\overline{δ}|$ и $|\overline{β}|$, окончательно получим
$cos∠(\overline{δ},\overline{β})=\frac{δ_1 δ_2+β_1 β_2+γ_1 γ_2}{\sqrt{δ_1^2+β_1^2+γ_1^2 } \sqrt{δ_2^2+β_2^2+γ_2^2}}$
Найдя значение косинуса, мы легко найдем и значение самого угла.
Пример 1
Найти косинус угла между векторами $\overline{δ}$ и $\overline{β}$, имеющими координаты $(1,-2,2)$ и $(3,0,4)$, соответственно.
Решение.
Найдем скалярное произведение между данными векторами через координаты:
$\overline{δ}\cdot \overline{β}=1\cdot 3+(-2)\cdot 0+2\cdot 4=11$
Найдем длины этих векторов:
$|\overline{δ}|=\sqrt{1^2+(-2)^2+2^2}=\sqrt{9}=3$
$|\overline{β}|=\sqrt{3^2+0^2+4^2}=\sqrt{25}=5$
В результате, получим
$cos∠(\overline{δ},\overline{β})=\frac{11}{3\cdot 5}=\frac{11}{15}$
Ответ: $\frac{11}{15}$.
Нахождение угла между векторами с помощью векторного произведения
Вспомним сначала, определение векторного произведения и каким образом его можно находить.
Определение 3
Векторным произведением двух векторов называется такой вектор, который будет перпендикулярен обоим данным векторам, и его длина равна произведению длин этих векторов с синусом угла между данными векторами, а также этот вектор с двумя начальными имеют ту же ориентацию, как и декартова система координат.
Обозначение: $\overline{δ}х\overline{β}$.
Математически это выглядит следующим образом:
- $|\overline{δ}х\overline{β}|=|\overline{δ}||\overline{β}|sin∠(\overline{δ},\overline{β})$
- $\overline{δ}х\overline{β}⊥\overline{δ}$, $\overline{δ}х\overline{β}⊥\overline{β}$
- $(\overline{δ}х\overline{β},\overline{δ},\overline{β})$ и $(\overline{i},\overline{j},\overline{k})$ одинаково ориентированы (рис. 2)

Рисунок 2. Векторное произведение. Автор24 — интернет-биржа студенческих работ
Для нахождения вектора векторного произведения можно пользоваться следующей формулой:
$\overline{δ}х\overline{β}=\begin{vmatrix}\overline{i}&\overline{j}&\overline{k}\\δ_1&δ_2&δ_3\\β_1&β_2&β_3\end{vmatrix}$
С помощью векторного произведения мы можем найти синус угла между данными векторами. Пусть нам даны векторы $\overline{δ}$ и $\overline{β}$ с координатами $(δ_1,δ_2,δ_3)$ и $(β_1,β_2,β_3)$, соответственно. Из определения 3 получим, что
${\sin \angle \left(\overrightarrow{\delta },\overrightarrow{\beta }\right)\ }=\frac{\left|\overrightarrow{\delta }х\overrightarrow{\beta }\right|}{\left|\overrightarrow{\delta }\right||\overrightarrow{\beta }|}$
Найдем вектор векторного произведения по формуле:
$\overline{δ}х\overline{β}=\begin{vmatrix}\overline{i}&\overline{j}&\overline{k}\\δ_1&δ_2&δ_3\\β_1&β_2&β_3\end{vmatrix}=(δ_2 β_3-δ_3 β_2,δ_3 β_1-δ_1 β_3,δ_1 β_2-δ_2 β_1)$
Расписывая по формуле длины вектора значения $|\overline{δ}|$, $|\overline{β}|$ и $|\overline{δ}х\overline{β}|$, окончательно получим
$sin∠(\overline{δ},\overline{β})=\frac{\sqrt{(δ_2 β_3-δ_3 β_2)^2+(δ_3 β_1-δ_1 β_3)^2+(δ_1 β_2-δ_2 β_1)^2}}{\sqrt{δ_1^2+δ_2^2+δ_3^2}\sqrt{β_1^2+β_2^2+β_3^2}}$
Найдя значение синуса, мы легко найдем и значение самого угла между векторами через координаты через формулу.
Пример 2
Найти синус угла между векторами $\overline{δ}$ и $\overline{β}$, имеющими координаты $(1,-2,2)$ и $(3,0,4)$, соответственно.
Решение.
Найдем вектор векторного произведения между данными векторами по формуле:
$\overline{δ}х\overline{β}=\begin{vmatrix}\overline{i}&\overline{j}&\overline{k}\\1&-2&2\\3&0&4\end{vmatrix}=-8\overline{i}+2\overline{j}+6\overline{k}=(-8,1,6)$
Найдем длины этих векторов:
$|\overline{δ}х\overline{β}|=\sqrt{(-8)^2+2^2+6^2}=\sqrt{104}=2\sqrt{26}$
$|\overline{δ}|=\sqrt{1^2+(-2)^2+2^2}=\sqrt{9}=3$
$|\overline{β}|=\sqrt{3^2+0^2+4^2}=\sqrt{25}=5$
В результате, получим
$sin∠(\overline{δ},\overline{β})=\frac{2\sqrt{26}}{3\cdot 5}=\frac{2\sqrt{26}}{15}$
Ответ: $\frac{2\sqrt{26}}{15}$.
spravochnick.ru
Угол между векторами, формулы и примеры
Определение и формула угла между векторами
ОПРЕДЕЛЕНИЕ Угол между двумя векторами и , имеющими общее начало, – это наименьший угол, на который нужно повернуть один из векторов вокруг точки приложения до положения, когда он станет сонаправленным с другим вектором (рис. 1).Косинус угла между векторами и равен скалярному произведению векторов , деленному на произведение модулей (длин) этих векторов, то есть
Если векторы сонаправлены, то величина угла между ними равна (на рисунке 2 угол между векторами и ). Угол между противоположно направленными векторами равен (если совместить начала векторов и , изображенных на рисунке 2, то они будут сторонами развернутого угла).
Примеры нахождения углов между векторами
ПРИМЕР| Задание | Найти угол между векторами и |
| Решение |
Вначале вычислим скалярное произведение заданных векторов, оно равно сумме произведений соответствующих координат векторов-сомножителей:
Модули заданных векторов равны корню квадратному из суммы квадратов координат:
Тогда косинус искомого угла
А тогда сам угол
|
| Ответ |
| Понравился сайт? Расскажи друзьям! | |||
ru.solverbook.com
Как вычислить углы между векторами? :: SYL.ru
При изучении геометрии немало вопросов возникает по теме векторов. Особенные трудности обучающийся испытывает при необходимости найти углы между векторами.
Основные термины
Перед тем как рассматривать углы между векторами, необходимо ознакомиться с определением вектора и понятием угла между векторами.
Вектором называют отрезок, имеющий направление, то есть отрезок, для которого определено его начало и конец.
Углом между двумя векторами на плоскости, имеющих общее начало, называют меньший из углов, на величину которого требуется переместить один из векторов вокруг общей точки, до положения, когда их направления совпадут.
Формула для решения
Поняв, что собой представляет вектор и как определяется его угол, можно вычислить угол между векторами. Формула решения для этого достаточно проста, и результатом её применения будет значение косинуса угла. Согласно определению, он равен частному скалярного произведения векторов и произведения их длин.
Скалярное произведение векторов считается как сумма помноженных друг на друга соответствующих координат векторов-сомножителей. Длина вектора, или его модуль, вычисляется как квадратный корень из суммы квадратов его координат.
Получив значение косинуса угла, вычислить величину самого угла можно с помощью калькулятора или воспользовавшись тригонометрической таблицей.
Пример
После того как вы разберетесь с тем, как вычислить угол между векторами, решение соответствующей задачи станет простым и понятным. В качестве примера стоит рассмотреть несложную задачу о нахождении величины угла.
Первым делом удобнее будет вычислить необходимые для решения значения длин векторов и их скалярного произведения. Воспользовавшись описанием, представленным выше, получим:
Подставив полученные значения в формулу, вычислим значение косинуса искомого угла:
Это число не является одним из пяти распространённых значений косинуса, поэтому для получения величины угла, придётся воспользоваться калькулятором или тригонометрической таблицей Брадиса. Но перед тем, как получить угол между векторами, формула может быть упрощена, чтобы избавиться от лишнего отрицательного знака:
Итоговый ответ для сохранения точности можно оставить в таком виде, а можно вычислить значение угла в градусах. По таблице Брадиса его величина составит примерно 116 градусов и 70 минут, а калькулятор покажет значение 116,57 градуса.
Вычисление угла в n-мерном пространстве
При рассмотрении двух векторов в трёхмерном пространстве, понять, о каком угле идёт речь гораздо сложнее, если они не лежат в одной плоскости. Для упрощения восприятия можно начертить два пересекающихся отрезка, которые образуют наименьший угол между ними, он и будет искомым. Несмотря на наличие третьей координаты в векторе, процесс того, как вычисляются углы между векторами, не изменится. Вычислите скалярное произведение и модули векторов, арккосинус их частного и будет являться ответом на данную задачу.
В геометрии нередко встречаются задачи и с пространствами, имеющими больше трёх измерений. Но и для них алгоритм нахождения ответа выглядит аналогично.
Разница между 0 и 180 градусами
Одна из распространённых ошибок при написании ответа на задачу, рассчитанную на то чтобы вычислить угол между векторами, — решение записать, что векторы параллельны, то есть искомый угол получился равен 0 или 180 градусам. Этот ответ является неверным.
Получив по итогам решения значение угла 0 градусов, правильным ответом будет обозначение векторов как сонаправленных, то есть у векторов будет совпадать направление. В случае получения 180 градусов векторы будут носить характер противоположно направленных.
Специфические векторы
Найдя углы между векторами, можно встретить один из особых типов, помимо описанных выше сонаправленных и противоположно направленных.
- Несколько векторов параллельных одной плоскости называются компланарными.
- Векторы, одинаковые по длине и направлению, называются равными.
- Векторы, лежащие на одной прямой, независимо от направления, именуются коллинеарными.
- Если длина вектора равна нулю, то есть его начало и конец совпадают, то его называют нулевым, а если единице, то единичным.
www.syl.ru
Формула угла между векторами
Угол между двумя векторами
Рассмотрим понятие угла между двумя направлениями в пространстве.
Как и на плоскости, в пространстве направлением называется множество всех лучей, каждый из которых сонаправлен с данным. Таким образом, любой луч из данного множества сонаправленных лучей вполне определяет это направление (подобно тому, как любой направленный отрезок вполне определяет вектор, который он изображает). Поэтому направление в пространстве обычно задают при помощи только одного луча.
Углом между двумя направлениями называется величина наименьшего угла между любыми лучами этих направлений с общим началом.
Угол между лучами l1 и l2 обозначается \(\widehat{l_1; l_2}\). По определению угол между двумя направлениями находится в промежутке [0°; 180°].
Углом между двумя ненулевыми векторами называется угол между направлениями этих векторов. Угол между векторами а и b (рис. 21) обозначается \(\widehat{a; b}\)
Если угол между векторами а и b равен 90°, то эти векторы называют перпендикулярными (или ортогональными) и пишут: а ⊥ b.
Отметим, что если а\(\upuparrows\)b, то \(\widehat{a; b}\) = 0°, а если а\(\uparrow\downarrow\)b, то \(\widehat{a; b}\) =180°.
Рассмотрим некоторую прямую l, на которой выбрана единица измерения длины. Пусть А и В — некоторые точки прямой l такие, что |АВ| = 1.
Тогда векторы \(\overrightarrow{AB}\) и \(\overrightarrow{BA}\) называются единичными векторами прямой l (рис.22).
Единичные векторы прямой задают на ней два направления. Одно из них называется положительным, другое — отрицательным.
Прямая, на которой выбрана точка О (начало отсчета), задано положительное направление и задана единица измерения длины, называется осью. Вектор е (|е| = 1), задающий направление оси, называется единичным вектором оси (рис. 23).
Углом между вектором и осью, называется величина угла между направлением оси и направлением вектора (рис. 24).
Вычисление угла между двумя векторами.
По определению скалярного произведения
а • b = | а | • | b | cos\(\widehat{(a; b)}\).
Следовательно, если а =/= 0 и b =/= 0, то
$$ cos\widehat{(a; b)} = \frac{a \cdot b}{|a|\cdot|b|} \;\; (1) $$т. е. косинус угла между ненулевыми векторами а и b равен скалярному произведению этих векторов, деленному на произведение их длин.
Пусть в пространстве имеется прямоугольная декартова система координат, и пусть заданы векторы а = (x1 ; y
и поэтому, используя равенство (1), получим формулу
$$ cos\widehat{(a; b)} = \frac{ x_1 x_2 + y_1 y_2 + z_1 z_2}{\sqrt{{x_1}^2 + {y_1}^2 + {z_1}^2}\cdot\sqrt{{x_2}^2 + {y_2}^2 + {z_2}^2} } \;\; (2)$$Эта формула позволяет вычислить косинус угла между векторами а и b по координатам этих векторов.
Если векторы а = (x1 ; y1 ) и b = (x2 ; y2) заданы в прямоугольной декартовой системе координат на плоскости, то косинус угла между ними вычисляется по формуле
$$ cos\widehat{(a; b)} = \frac{ x_1 x_2 + y_1 y_2}{\sqrt{{x_1}^2 + {y_1}^2}\cdot\sqrt{{x_2}^2 + {y_2}^2}} \;\; (3)$$Задача 1. Даны два вектора а = (3; 4) и b = (4; 3). Найти угол между ними.
Подставив координаты векторов в формулу (3), получим
$$ cos\widehat{(a; b)} = \frac{3\cdot 4 + 4\cdot 3}{\sqrt{{3}^2 + {4}^2}\cdot\sqrt{{4}^2 + {3}^2}} = \frac{24}{25} $$откуда (по таблице) \(\widehat{(a; b)}\) ≈ 16°.
Задача 2. Найти косинус угла между векторами
а = 2i + 2j — k, b = i — 2j + 2k .
Используя формулу (2), получим
$$ cos\widehat{(a; b)} = \frac{ 2\cdot 1 + 2\cdot(-2) + (-1)\cdot 2}{\sqrt{{2}^2 + {2}^2 + {-1}^2}\cdot\sqrt{{1}^2 + {-2}^2 + {2}^2}} = -\frac{4}{9} $$razdupli.ru
Угол между векторами.
Навигация по странице:
Определение. Углом между двумя векторами, отложенными от одной точки, называется кратчайший угол, на который нужно повернуть один из векторов вокруг своего начала до положения сонаправленности с другим вектором.
Формула вычисления угла между векторами
Примеры задач на вычисление угла между векторами
Примеры вычисления угла между векторами для плоских задачи
Пример 1. Найти угол между векторами a = {3; 4} и b = {4; 3}.Решение: Найдем скалярное произведение векторов:
a·b = 3 · 4 + 4 · 3 = 12 + 12 = 24.Найдем модули векторов:
|a| = √32 + 42 = √9 + 16 = √25 = 5|b| = √42 + 32 = √16 + 9 = √25 = 5
Найдем угол между векторами:
| cos α = | a · b | = | 24 | = | 24 | = 0.96 |
| |a| · |b| | 5 · 5 | 25 |
Решение: Найдем скалярное произведение векторов:
a·b = 5 · 7 + 1 · 5 = 35 + 5 = 40.Найдем модули векторов:
|a| = √72 + 12 = √49 + 1 = √50 = 5√2|b| = √52 + 52 = √25 + 25 = √50 = 5√2
Найдем угол между векторами:
| cos α = | a · b | = | 40 | = | 40 | = | 4 | = 0.8 |
| |a| · |b| | 5√2 · 5√2 | 50 | 5 |
Примеры вычисления угла между векторами для пространственных задач
Пример 3. Найти угол между векторами a = {3; 4; 0} и b = {4; 4; 2}.Решение: Найдем скалярное произведение векторов:
a·b = 3 · 4 + 4 · 4 + 0 · 2 = 12 + 16 + 0 = 28.Найдем модули векторов:
|a| = √32 + 42 + 02 = √9 + 16 = √25 = 5|b| = √42 + 42 + 22 = √16 + 16 + 4 = √36 = 6
Найдем угол между векторами:
| cos α = | a · b | = | 28 | = | 14 |
| |a| · |b| | 5 · 6 | 15 |
Решение: Найдем скалярное произведение векторов:
a·b = 1 · 5 + 0 · 5 + 3 · 0 = 5.Найдем модули векторов:
|a| = √12 + 02 + 32 = √1 + 9 = √10|b| = √52 + 52 + 02 = √25 + 25 = √50 = 5√2
Найдем угол между векторами:
| cos α = | a · b | = | 5 | = | 1 | = | √5 | = 0.1√5 |
| |a| · |b| | √10 · 5√2 | 2√5 | 10 |
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
0oq.ru
Угол между векторами, онлайн калькулятор
Наш онлайн калькулятор помогает найти угол и косинус угла между векторами всего за несколько минут. Для нахождения угла между двумя векторами выберите их размерность, введите все координаты и нажмите кнопку «Вычислить», калькулятор выдаст подробный ход решения и ответ! Калькулятор сам посчитает скалярное произведение векторов, вычислит косинус угла и сам угол. Каждый шаг будет детально расписан, это поможет вам проверить свое решение и понять, как был получен ответ.
Введите данные для вычисления угла между векторами Размерность вектора:2 3
Форма представления векторов:
координатами точками
Формула : |
| Понравился сайт? Расскажи друзьям! | |||
Вычислить угол между векторами
Вычислить угол между векторами. В этой публикации хочу вам показать один способ определения угла между двумя векторами. В условии для каждого из векторов задаются координаты начала и конца. Векторы могут быть построены на координатной плоскости или без того. Конечно же, данную задачу обычно (и это естественно) решают применяя формулу скалярного произведения векторов, и такой подход был показан в этой статье.
Но если пофантазировать и представить, что вдруг вы напрочь забыли эту формулу или вообще в решении задач с векторами как-то давно не практиковались, то на помощь может прийти нижеизложенный способ. Это вполне достойная альтернатива. Чем у вас будет больше «инструментов» в запасе, тем лучше.
Найти угол между векторами. Ответ дать в градусах.
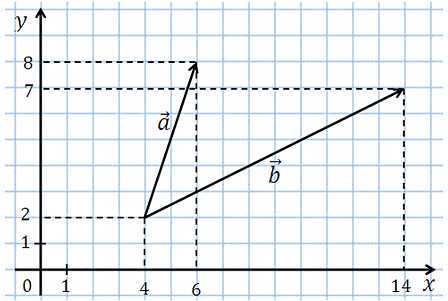
Идея очень простая: мы строим треугольник (соединяем концы векторов) и далее используем способ изложенный в этой статье. Его суть такова – в полученном треугольнике вычисляем стороны и для далее вычисления искомого угла используем теорему косинусов.
Приступим! Строим треугольник, далее описываем около него прямоугольник. Затем прямо на эскизе обозначаем длины катетов в образовавшихся прямоугольных треугольниках:

Вычисляем стороны. По теореме Пифагора:
Теорема косинусов: квадрат любой стороны треугольника равен сумме квадратов двух других сторон, без удвоенного произведения этих сторон на косинус угла между ними.
Вычисляем угол:
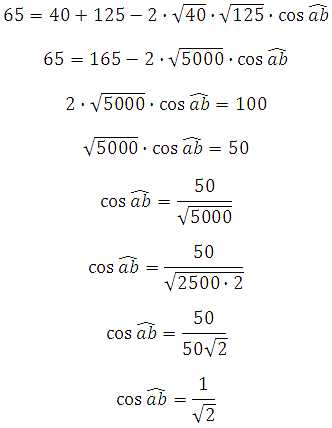
Таким образом, угол между векторами равен 45 градусам.
Ответ: 45
Решение через формулу скалярного произведения
Сама формула:

Известна следующая формула.
Скалярным произведением векторов на плоскости в прямоугольной системе координат называется число равное сумме произведений соответствующих координат векторов.
Значит:
Вычислим координаты векторов:
Подставим их в формулу:
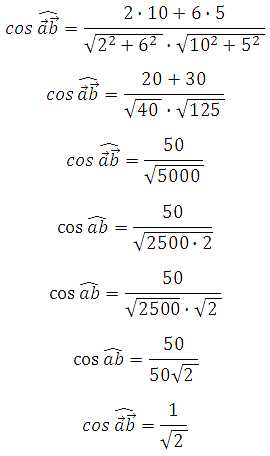
Таким образом, угол между векторами равен 45 градусам.
Ответ: 45
*Если векторы будут расположены на координатной плоскости не касаясь друг друга, то один из них всегда можно сдвинуть параллельным переносом и далее уже действовать как описано выше.
**Если они будут построены схематично на координатной плоскости, а не на листе в клетку и при этом будут указаны координат концов, то треугольник построить несложно.
С уважением, Александр.
В школе урок математики. Учитель:
— Петя, назови двузначное число!
— Сорок шесть.
— Теперь поменяй местами цифры и скажи, что получилось.
— Не знаю…
— Садись, два! Вовочка, назови двузначное число!
— Тридцать три, и можете начинать свои фигли-мигли!
*Делитесь информацией в социальных сетях!
matematikalegko.ru
