Действия с дробями | LAMPA
Как же теперь привести дроби 27\frac{2}{7}72 и 34\frac{3}{4}43 к знаменателю 282828?
Вспоминаем, что если умножить и числитель, и знаменатель дроби на одно и то же число, то значение дроби не изменится. Например, 15\frac{1}{5}51 и 210\frac{2}{10}102 — это одно и тоже число.
То есть нужно домножить числитель и знаменатель дроби на такое число, чтобы в знаменателе получился общий знаменатель дробей (в случае дробей 27\frac{2}{7}72 и 34\frac{3}{4}43 — число 282828).
Числитель и знаменатель дроби 27\frac{2}{7}72 нужно умножить на 444:
27=2⋅47⋅4=828\frac{2}{7}=\frac{2\cdot 4}{7\cdot 4}=\frac{8}{28}72=7⋅42⋅4=288,
— а числитель и знаменатель 34\frac{3}{4}43 — на 777:
34=3⋅74⋅7=2128\frac{3}{4}=\frac{3\cdot 7}{4\cdot 7}=\frac{21}{28}43=4⋅73⋅7=2821.
Теперь можно без труда сложить получившиеся дроби: 828+2128=2928=1128\frac{8}{28}+\frac{21}{28}=\frac{29}{28}=1 \frac{1}{28}288+2821=2829=1281.
Общая формула, которой можно пользоваться для сложения дробей: ab+cd=ad+bcbd\frac{a}{b}+\frac{c}{d}=\frac{ad+bc}{bd}ba+dc=bdad+bc
Пользуясь этой формулой, мы получим, что 13+16=1⋅6+3⋅13⋅6=918\frac{1}{3}+\frac{1}{6}=\frac{1\cdot 6+3\cdot 1}{3\cdot 6}=\frac{9}{18}31+61=3⋅61⋅6+3⋅1=189. Как мы видим, эту дробь можно сократить на 999. Получится 12\frac{1}{2}21.
Наименьший общий знаменатель
Можно ли сразу получить дробь, которую не надо было бы сокращать, то есть дробь с наименьшим возможным знаменателем?
Да, можно! Для этого вместо перемножения знаменателей необходимо вычислить их . То есть наименьшее число, которое делится на оба знаменателя. Наименьшее общее кратное чисел bbb и ddd обозначается НОК(b,d)\text{НОК}(b,d)НОК(b,d).
Например:
НОК(3,6)=6\text{НОК}(3,6)=6НОК(3,6)=6
НОК(10,15)=30\text{НОК}(10,15)=30НОК(10,15)=30.
Для того чтобы вычислить НОК, требуется разложить числа на простые множители, а затем для каждого простого делителя, который входит в разложение хотя бы одного из чисел, выбрать максимальную степень, в которой он входит в разложения.
Например, чтобы вычислить НОК(45,30)\text{НОК}(45,30)НОК(45,30), разложим числа на множители:
45=3⋅3⋅545=3\cdot 3\cdot 545=3⋅3⋅5,
30=2⋅3⋅530=2\cdot 3\cdot 530=2⋅3⋅5.
Число 333 входит в разложения в максимальной степени 222, а числа 222 и 555 — в степени 111. Поэтому НОК равно 2⋅32⋅5=902\cdot 3^2\cdot 5=902⋅32⋅5=90.
lampa.io
Правила действий с дробями 5 класс | Правила действий с дробями 5 класс |
|
|
|
|
| 3. Чтобы умножить одну дробь на другую, следует перемножить их числители и знаменатели |
| 4.Чтобы разделить одну дробь на другую, нужно первую дробь умножить на дробь, обратную второй. |
| 5. Чтобы сложить смешанные числа, надо сложить отдельно целые части и отдельно дробные части и полученные результаты сложить. Если в результате сложения дробная часть станет неправильной дробью, то из нее надо выделить целую часть и прибавить к целой части результата. |
| 6.Если дробные части смешанных чисел имеют разные знаменатели, то их сначала надо привести к общему знаменателю, а потом применить правило сложения смешанных чисел. |
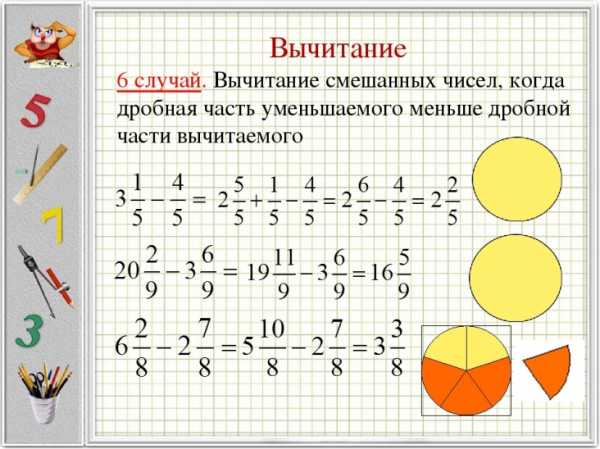
| 7. Если дробная часть уменьшаемого меньше дробной части вычитаемого, то у целой части уменьшаемого надо занять единицу, представить ее в виде дроби с тем же знаменателем и добавить ее к дробной части уменьшаемого. Затем применить правило вычитания дробей. |
| 8. Чтобы умножить или разделить смешанные числа, можно представить их в виде неправильных дробей, а затем применить правило умножения или деления обыкновенных дробей. |
infourok.ru
Действия с дробями
Условимся считать, что под «действиями с дробями» на нашем уроке будут пониматься действия с обыкновенными дробями. Обыкновенная дробь — это дробь, обладающая такими атрибутами, как числитель, дробная черта и знаменатель. Это отличает обыкновенную дробь от десятичной, которая получается из обыкновенной путём приведения знаменателя к числу, кратному 10. Десятичная дробь записывается с запятой, отделяющей целую часть от дробной. У нас пойдёт речь о действиях с обыкновенными дробями, так как именно они вызывают наибольшие затруднения у студентов, позабывших основы этой темы, пройденной в первой половине школьного курса математики. Вместе с тем при преобразованиях выражений в высшей математике используются в основном именно действия с обыкновенными дробями. Одни сокращения дробей чего стоят! Десятичные же дроби особых затруднений не вызывают. Итак, вперёд!
Две дроби и называются равными, если .
Например, , так как
Равными также являются дроби и (так как ), и (так как ).
Очевидно, равными являются и дроби и . Это означает, что если числитель и знаменатель данной дроби умножить или разделить на одно и то же натуральное число, то получится дробь, равная данной: .
Это свойство называется основным свойством дроби.
Основное свойство дроби можно использовать для перемены знаков у числителя и знаменателя дроби. Если числитель и знаменатель дроби умножить на -1, то получим . Это означает, что значение дроби не изменится, если одновременно изменить знаки у числителя и знаменателя. Если же изменить знак только у числителя или только у знаменателя, то и дробь изменит свой знак:
;
.
Пользуясь основным свойством дроби, можно заменить данную дробь другой дробью, равной данной, но с меньшим числителем и знаменателем. Такую замену называют сокращением дроби.
Пусть, например, дана дробь . Числа 36 и 48 имеют наибольший общий делитель 12. Тогда
.
В общем случае сокращение дроби возможно всегда, если числитель и знаменатель не являются взаимно простыми числами. Если числитель и знаменатель — взаимно простые числа, то дробь называется несократимой.
На сайте есть калькулятор онлайн для вычисления наибольшего общего делителя и наименьшего общего кратного двух чисел.
Итак, сократить дробь — это значит разделить числитель и знаменатель дроби на общий множитель. Всё вышесказанное применимо и к дробным выражениям, содержащим переменные.
Пример 1. Сократить дробь
.
Решение. Для разложения числителя на множители, представив предварительно одночлен — 5xy в виде суммы — 2xy — 3xy, получим
Для разложения знаменателя на множители используем формулу разности квадратов:
.
В результате
.
Далее, изменяя знаки в числителе и знаменателе дроби, получим
Пусть даны две дроби и . Они имеют разные знаменатели: 5 и 7. Пользуясь основным свойством дроби, можно заменить эти дроби другими, равными им, причём такими, что у полученных дробей будут одинаковые знаменатели. Умножив числитель и знаменатель дроби на 7, получим
.
Умножив числитель и знаменатель дроби на 5, получим
.
Итак, дроби приведены к общему знаменателю:
.
Но это не единственное решение поставленной задачи: например, данные дроби можно привести также к общему знаменателю 70:
,
и вообще к любому знаменателю, делящемуся одновременно на 5 и 7.
Рассмотрим ещё один пример: приведём к общему знаменателю дроби и . Рассуждая, как в предыдущем примере, получим
,
.
Но в данном случае можно привести дроби к общему знаменателю, меньшему, чем произведение знаменателей этих дробей. Найдём наименьшее общее кратное чисел 24 и 30: НОК(24, 30) = 120.
Так как 120:4=5, то чтобы записать дробь со знаменателем 120, надо и числитель, и знаменатель умножить на 5, это число называется дополнительным множителем. Значит .
Далее, получаем 120:30=4. Умножив числитель и знаменатель дроби на дополнительный множитель 4, получим .
Итак, данные дроби приведены к общему знаменателю.
Наименьшее общее кратное знаменателей этих дробей является наименьшим возможным общим знаменателем.
На сайте есть калькулятор онлайн для вычисления наибольшего общего делителя и наименьшего общего кратного двух чисел.
Для дробных выражений, в которые входят переменные, общим знаменателем является многочлен, который делится на знаменатель каждой дроби.
Сложение дробей определяется следующим образом:
.
Например,
.
Если b = d, то
.
Это значит, что для сложения дробей с одинаковым знаменателем достаточно сложить числители, а знаменатель оставить прежним. Например,
.
Если же складываются дроби с разными знаменателями, то обычно приводят дроби к наименьшему общему знаменателю, а потом складывают числители. Например,
.
На сайте есть калькулятор онлайн для вычисления наибольшего общего делителя и наименьшего общего кратного двух чисел.
Теперь рассмотрим пример сложения дробных выражений с переменными.
Пример 3. Преобразовать в одну дробь выражение
.
Решение. Найдём наименьший общий знаменатель. Для этого сначала разложим знаменатели на множители:
1) ;
2) ;
3) .
Наименьший общий знаменатель:
Дополнительные множители, на которые умножаются числители дробей:
2) ;
3) .
Результат этого умножения:
.
Далее, раскрывая скобки и выполняя тождественные преобразования, получаем
.
Произведение двух дробей и равно дроби, числитель которой равен произведению числителей, а знаменатель — произведению знаменателей, т. е. .
Например,
.
При делении дроби на дробь числитель делимого умножается на знаменатель делителя, а знаменатель делимого — на числитель делителя, т. е. .
Например,
.
1. Произведение крайних членов пропорции равно произведению её средних членов, т. е. если , то .
2. Из пропорции вытекают следующие пропорции: , , , то есть в пропорции можно менять местами крайние и средние члены или те и другие одновременно.
3. Чтобы найти неизвестный средний (крайний) член пропорции, нужно произведение крайних (средних) членов пропорции разделить на известный средний (крайний) член пропорции: и .
В высшей математике это действие с дробями чаще всего применяется при интегрировании рациональных функций. Поэтому оно подробно разобрано в уроке Интегрирование рациональных функций и метод неопределённых коэффициентов.
Другие темы в блоке «Школьная математика»
function-x.ru
Правила арифметических действий над обыкновенными дробям
#1. Основное свойство дроби
Если числитель и знаменатель дроби умножить или разделить на одно и то же число, не равное нулю, то получится дробь, равная данной.
3/7=3*3/7*3=9/21, то есть 3/7=9/21
a/b=a*m/b*m — так выглядит основное свойство дроби.
Другими словами, мы получим дробь, равную данной, умножив или разделив числитель и знаменатель исходной дроби на одно и то же натуральное число.
Если ad=bc, то две дроби a/b=c/d считаются равными.
Например, дроби 3/5 и 9/15 будут равными, так как 3*15=5*9, то есть 45=45
Сокращение дроби — это процесс замены дроби, при котором новая дробь получается равной исходной, но с меньшим числителем и знаменателем.
Сокращать дроби принято, опираясь на основное свойство дроби.
Например, 45/60=15/20=9/12=3/4 (числитель и знаменатель делится на число 3, на 5 и на 15).
Несократимая дробь — это дробь вида 3/4, где числитель и знаменатель являются взаимно простыми числами. Основная цель сокращения дроби — сделать дробь несократимой.
2. Приведение дробей к общему знаменателю
Чтобы привести две дроби к общему знаменателю, надо:
1) разложить знаменатель каждой дроби на простые множители;
2) умножить числитель и знаменатель первой дроби на недостающие
множители из разложения второго знаменателя;
3) умножить числитель и знаменатель второй дроби на недостающие множители из первого разложения.
Примеры: приведите дроби к общему знаменателю .
Разложим знаменатели на простые множители: 18=3∙3∙2, 15=3∙5
умножили числитель и знаменатель дроби на недостающий множитель 5 из второго разложения.
числитель и знаменатель дроби на недостающие множители 3 и 2 из первого разложения.
= , 90 – общий знаменатель дробей .
3. Арифметические действия над обыкновенными дробями
3.1. Сложение обыкновенных дробей
а) При одинаковых знаменателях числитель первой дроби складывают с числителем второй дроби, оставляя знаменатель прежним. Как видно на примере:
a/b+c/b=(a+c)/b;
б) При разных знаменателях дроби сначала приводят к общему знаменателю, а затем выполняют сложение числителей по правилу а):
7/3+1/4=7*4/12+1*3/12=(28+3)/12=31/12
3.2. Вычитание обыкновенных дробей
а) При одинаковых знаменателях из числителя первой дроби вычитают числитель второй дроби, оставляя знаменатель прежним:
a/b-c/b=(a-c)/b;
б) Если же знаменатели дробей различны, то сначала дроби приводят к общему знаменателю, а затем повторяют действия как в пункте а).
3.3. Умножение обыкновенных дробей
Умножение дробей подчиняется следующему правилу:
a/b*c/d=a*c/b*d,
то есть перемножают отдельно числители и знаменатели.
Например:
3/5*4/8=3*4/5*8=12/40.
3.4. Деление обыкновенных дробей
Деление дробей производят следующим способом:
a/b:c/d=a*d/b*c,
то есть дробь a/b умножается на дробь, обратную данной, то есть умножается на d/c.
Пример: 7/2:1/8=7/2*8/1=56/2=28

4. Взаимно обратные числа
Если a*b=1, то число b является обратным числом для числа a.
Пример: для числа 9 обратным является 1/9, так как 9*1/9=1, для числа 5 — обратное число 1/5, так как 5*1/5=1.
5. Десятичные дроби
Десятичной дробью называется правильная дробь, знаменатель которой равен 10, 1000, 10 000, …, 10^n10,1000,10000,…,10n.
Например: 6/10=0,6; 44/1000=0,044.
Таким же способом пишутся неправильные со знаменателем 10^n или смешанные числа.
Например: 51/10=5,1; 763/100=7,63
В виде десятичной дроби представляется любая обыкновенная дробь со знаменателем, который является делителем некой степени числа 10.
менателем, который является делителем некой степени числа 10.
Пример: 5 — делитель числа 100, поэтому дробь 1/5=1 *20/5*20=20/100=0,20=0,2.
6. Арифметические действия над десятичными дробями
6.1. Сложение десятичных дробей
Для сложения двух десятичных дробей, нужно их расположить так, чтобы друг под другом оказались одинаковые разряды и запятая под запятой, а затем выполнить сложение дробей как обычных чисел.
6.2. Вычитание десятичных дробей
Выполняется аналогично сложению.
6.3. Умножение десятичных дробей
При умножении десятичных чисел достаточно перемножить заданные числа, не обращая внимания на запятые (как натуральные числа), а в полученном ответе запятой справа отделяется столько цифр, сколько их стоит после запятой в обоих множителях суммарно.
Давайте выполним умножение 2,7 на 1,3. Имеем 27 \cdot 13=35127⋅13=351. Отделяем справа две цифры запятой (у первого и второго числа — одна цифра после запятой; 1+1=21+1=2). В итоге получаем 2,7 \cdot 1,3=3,512,7⋅1,3=3,51.
Если в полученном результате получается меньше цифр, чем надо отделить запятой, то впереди пишут недостающие нули, например:
Для умножения на 10, 100, 1000, надо в десятичной дроби перенести запятую на 1, 2, 3 цифры вправо (в случае необходимости справа приписывается определенное число нулей).
Например: 1,47 \cdot 10 000 = 14 7001,47⋅10000=14700.
6.4. Деление десятичных дробей
Деление десятичной дроби на натуральное число производят также, как и деление натурального числа на натуральное. Запятая в частном ставится после того, как закончено деление целой части.
Если целая часть делимого меньше делителя, то в ответе получается нуль целых, например:
Рассмотрим деление десятичной дроби на десятичную. Пусть нужно разделить 2,576 на 1,12. Первым делом, умножим делимое и делитель дроби на 100, то есть перенесем запятую вправо в делимом и делителе на столько знаков, сколько их стоит в делителе после запятой (в данном примере на две). Затем нужно выполнить деление дроби 257,6 на натуральное число 112, то есть задача сводится к уже рассмотренному случаю:
Бывает так, что не всегда получается конечная десятичная дробь при делении одного числа на другое. В результате получается бесконечная десятичная дробь. В таких случаях переходят к обыкновенным дробям.
Например, 2,8 : 0,09= 28/10 : 9/100= 28*100/10*9=2800/90=280/9=31 1/9.
author: ЦР GrandE Студия
vekgivi.ru
Предмет | Математика | Класс | 5 | ||||||||
Тема урока | Примеры с дробями на все действия. | ||||||||||
Тип урока | Применение о обобщение полученных знаний. | ||||||||||
Цели |
| ||||||||||
Планируемые образовательные результаты | |||||||||||
Предметные | Метапредметные | Личностные | |||||||||
Уметь применять полученные знания на правила сложения, вычитания, умножения и деления дробей при решении упражнений и задач. . | Развивать умение видеть математическую задачу в контексте проблемной ситуации в других дисциплинах, в окружающей жизни; формировать умение работать в группах. | Развивать умение слушать; ясно, точно, грамотно излагать свои мысли в устной и письменной речи; развивать креативность мышления, инициативу, находчивость, активность при решении математических задач; формировать представления о математике как способе познания, сохранения и гармоничного развития мира, как части общечеловеческой культуры, о значимости математики в развитии цивилизации и современного общества. | |||||||||
Организационная структура урока | |||||||||||
№ | Этап урока | УУД | Деятельность | ЭОР | Время | ||||||
учителя | учащихся | ||||||||||
1 | Организационный | Коммуникативные: планирование учебного сотрудничества с учителем и сверстниками. Регулятивные: организация своей учебной деятельности Личностные: мотивация учения. | Приветствие, проверка подготовленности к учебному занятию, организация внимания детей. | Включаются в деловой ритм урока. | 1 мин | ||||||
2 | Мотивация и актуализация | Коммуникативные: планирование учебного сотрудничества с учителем и сверстниками; Познавательные: самостоятельное выделение и формулирование познавательной цели. Логические: – формулирование проблемы | Устные задания. «Третий лишний» Выбери лишнее, объясни почему. 1. 2. 3. 4. 1. Как называется элемент дроби, стоящий над чертой, под чертой. 2. Каким действием можно заменить дробную черту. 3. Для того чтобы сравнить дроби с разными знаменателями нужно… 4. Для нахождения общего знаменателя нужно найти НОК или НОД. 5. Какие числа называются взаимно обратными. 6. Как найти дробь от числа. 7. Как называется сотая часть числа. 8. Какая дробь называется правильной. 9. Расскажите правило деления дробей. | Отвечают на вопросы, дополняю, друг друга, обсуждают ответы. | 7-8 мин | ||||||
3 | Работа по теме урока | Коммуникативные: использование средств языка и речи для получения и передачи информации, участие в продуктивном диалоге; Познавательные: анализ, логические рассуждения, выбор наиболее эффективных способов решения задач. | №940 (б) Решение:
№938 (1 ст) Решение: а) 4*(1/5+3/7-1/35)=4*(7/35+15/35-1/35)=4/1*21/35= =84/35. в) 3/2*(5/6+10/9-13/18)=3/2*(15/18+20/18-13/18) =3/2*22/18=66/36. | 1 ученик у доски, стальные решаю самостоятельно. | 15 мин | ||||||
4 | Закрепление знаний и навыков.С/р | Познавательные: анализ, логические рассуждения, выбор наиболее эффективных способов решения задач. Регулятивные: проявляют познавательную инициативу Коммуникативные: использование средств языка и речи для получения и передачи информации, участие в продуктивном диалоге. | Задача №1. Могла ли одна девочка съесть 2/3 торта, а другая ¾ этого же торта? (нет не могла, так как сумма данных дробей больше единицы) Задача №2. Определи количество учеников в классе, если 3/8 всех учеников увлекаются математикой, 1/8 историей, 2/8 географией, а остальные 7 человек — биологией (Данную задачу можно предложить для самостоятельного решения с дальнейшей самопроверкой. Ответ: 28 человек) Задача №3. Витя 2/5 летних каникул провел в спортивном лагере, а остальные45 дней отдыхал дома. Найти продолжительность всех каникул. (Дополнительная задача. Ответ:75 дней) | 1 ученик у доски, стальные решаю самостоятельно. | 20 мин | ||||||
5 | Подведение итогов. Домашнее задание. | Личностные: проводят самооценку Познавательные: сформирован навык для правильного выполнения домашнего задания Коммуникативные: планируют сотрудничество, определяют кому нужна помощь | Дает краткое пояснение каждого номера домашнего задания. № 938 (2 ст), 933 | Записывают домашнее задание в дневник, делая необходимые пометки. | 1 мин | ||||||
6 | Рефлексия | Личностные: проводят самооценку, учатся адекватно принимать причины успеха (неуспеха) Познавательные: проводят рефлексию способов и условий своих действий Коммуникативные: планируют сотрудничество, используют критерии для обоснования своих суждений | Задает вопросы: На уроке — Было трудно … — Было интересно … — Я научился … — Меня удивило | Выделение и осознание учащимися того, что уже усвоено и что ещё подлежит усвоению, осознание качества и уровня усвоения Выражают свои мысли | 2 мин | ||||||
multiurok.ru
|
oldskola1.narod.ru
Подготовка школьников к ЕГЭ и ОГЭ в учебном центре «Резольвента» (Справочник по математике — Арифметика
Сложение и вычитание дробей
При сложении (вычитании) дробей с одинаковыми знаменателями получается дробь с тем же знаменателем, а её числитель равен сумме (разности) числителей рассматриваемых дробей.
Например,
При сложении (вычитании) дробей с разными знаменателями предварительно нужно привести их к общему знаменателю. Для упрощения вычислений желательно приводить дроби к наименьшему общему знаменателю, хотя это не является обязательным.
Например,
(в уголках сверху здесь обозначены дополнительные множители).
Умножение и деление дробей
При умножении дробей получается дробь, числитель которой равен произведению числителей, а знаменатель – произведению знаменателей.
Например,
Деление дробей осуществляется в соответствии со следующим правилом:
Иногда это правило формулируют так: для того, чтобы разделить первую дробь на вторую, нужно первую дробь умножить на перевернутую вторую.
В частности,
Действия со смешанными числами
Для того, чтобы избежать ошибок при выполнении арифметических действий со смешанными числами, рекомендуется сначала обратить смешанные числа в неправильные дроби, затем выполнить нужные арифметические действия, а потом, если это требуется, обратить результат в смешанное число.
Пример. Найти сумму, разность, произведение и частное смешанных чисел
и
Решение. Преобразуем эти числа в неправильные дроби:
Далее получаем:


На нашем сайте можно также ознакомиться с разработанными преподавателями учебного центра «Резольвента» учебными материалами для подготовки к ЕГЭ и ОГЭ по математике.
Приглашаем школьников (можно вместе с родителями) на бесплатное тестирование по математике, позволяющее выяснить, какие разделы математики и навыки в решении задач являются для ученика «проблемными». Запись по телефону (495) 509-28-10 |
Для школьников, желающих хорошо подготовиться и сдать ЕГЭ /span> или ОГЭ по математике или русскому языку на высокий балл, учебный центр «Резольвента» проводит
У нас также для школьников организованы
МОСКВА, СВАО, Учебный центр «РЕЗОЛЬВЕНТА»
www.resolventa.ru











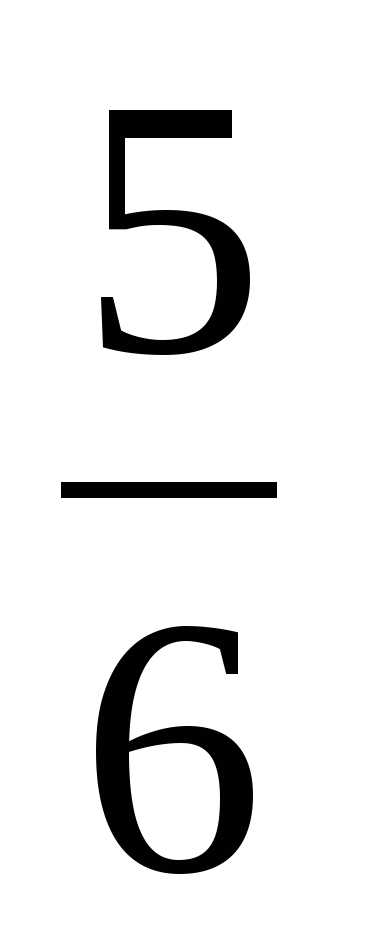 ;
;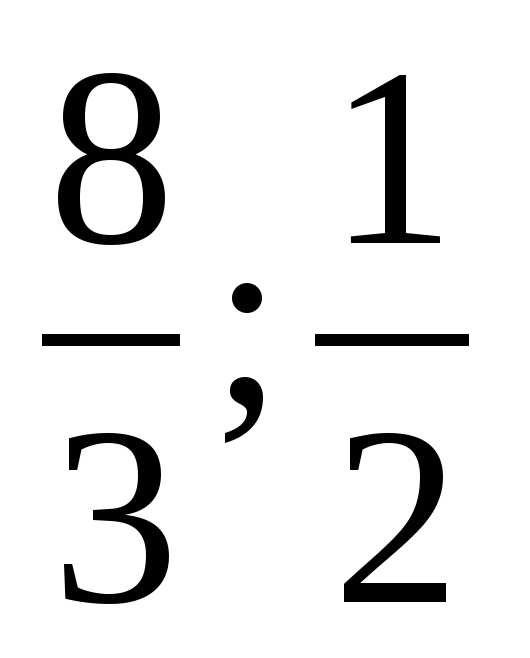 лишняя 8/3 т.к она неправильная
лишняя 8/3 т.к она неправильная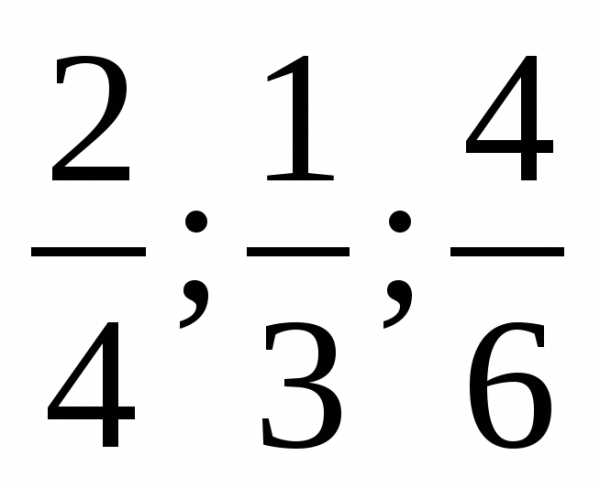 лишняя 1/3 т.к она несократима.
лишняя 1/3 т.к она несократима.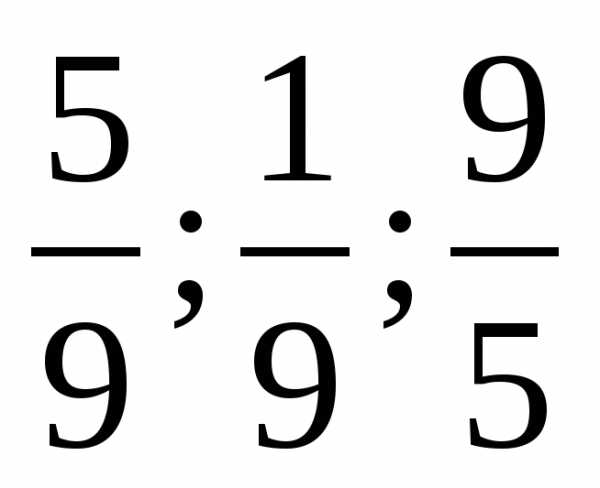 лишняя 1/9 т.к 5/9 и 9/5 взаимообратные
лишняя 1/9 т.к 5/9 и 9/5 взаимообратные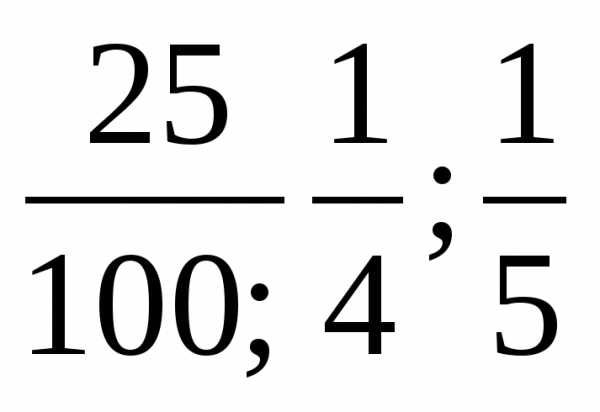 лишняя 1/5 т.к 25/100 и ¼ это равные дроби
лишняя 1/5 т.к 25/100 и ¼ это равные дроби