Какие функции – .

Понятие функции | Алгебра

Понятие функции в математике — одно из основных. Выражает зависимость одних переменных величин от других.

Определение.

Функция — это соответствие между двумя множествами, при котором каждому элементу одного множества соответствует единственный элемент другого множества.

Пусть каждому числу x из множества значений D поставлено в соответствие число y из множества значений E.

«Поставлено в соответствие» — значит, указан определённый способ (правило), по которому для каждого x∈D  находят y∈E. (∈ — знак принадлежности. Запись x∈D читают «икс принадлежит дэ»).

Чаще всего этот способ обозначают как y=f(x). Для обозначения функции применяют и другие буквы: y=g(x), s=f(t) и т.д.

Если функция задана соответствием y=f(x), переменная x называется независимой переменной или аргументом, y — зависимой переменной или функцией.

Множество значений D, которые может принимать x, называется

областью определения функции.

Множество значений E, которые может принимать y, называется областью значений функции.

Функцию можно задать несколькими способами:

— аналитическим (с помощью формулы),

— графическим,

— табличным,

— описанием с помощью словесной формулировки).

Функции, в которых значения аргумента и значения функции — числа, называются числовыми функциями. В курсе алгебры изучаются, в основном, числовые функции.

Примеры функций.

1) При движении автомобиля с постоянной скоростью пройденный путь является функцией от времени .

Например, если автомобиль движется с постоянной скоростью 60 км/ч, зависимость пути от времени можно задать формулой s=60t, где s — пройденный путь (в километрах), t — время (в часах).

2) Периметр квадрата является функцией от его стороны.

Зависимость периметра от стороны квадрата можно задать формулой P=4a, где P — периметр, a — длина стороны.

 

www.algebraclass.ru

Функции и графики — Математика — Теория, тесты, формулы и задачи

Оглавление:

 

Основные теоретические сведения

Координаты и базовые понятия о функциях

К оглавлению…

Длина отрезка на координатной оси находится по формуле:

Длина отрезка на координатной плоскости ищется по формуле:

Для нахождения длины отрезка в трёхмерной системе координат используется следующая формула:

Координаты середины отрезка (для координатной оси используется только первая формула, для координатной плоскости — первые две формулы, для трехмерной системы координат — все три формулы) вычисляются по формулам:

Функция – это соответствие вида y = f(x) между переменными величинами, в силу которого каждому рассматриваемому значению некоторой переменной величины x (аргумента или независимой переменной) соответствует определенное значение другой переменной величины,

y (зависимой переменной, иногда это значение просто называют значением функции). Обратите внимание, что функция подразумевает, что одному значению аргумента х может соответствовать только одно значение зависимой переменной у. При этом одно и то же значение у может быть получено при различных х.

Область определения функции – это все значения независимой переменной (аргумента функции, обычно это х), при которых функция определена, т.е. ее значение существует. Обозначается область определения D(y). По большому счету Вы уже знакомы с этим понятием. Область определения функции по другому называется областью допустимых значений, или ОДЗ, которую Вы давно умеете находить.

Область значений функции – это все возможные значения зависимой переменной данной функции. Обозначается Е(у).

Функция возрастает на промежутке, на котором большему значению аргумента соответствует большее значение функции. 

Функция убывает на промежутке, на котором большему значению аргумента соответствует меньшее значение функции.

Промежутки знакопостоянства функции – это промежутки независимой переменной, на которых зависимая переменная сохраняет свой положительный или отрицательный знак.

Нули функции – это такие значения аргумента, при которых величина функции равна нулю. В этих точках график функции пересекает ось абсцисс (ось ОХ). Очень часто необходимость найти нули функции означает необходимость просто решить уравнение. Также часто необходимость найти промежутки знакопостоянства означает необходимость просто решить неравенство.

Функцию y = f(x) называют четной, если она определена на симметричном множестве и для любого х из области определения выполняется равенство:

Это означает, что для любых противоположных значений аргумента, значения четной функции равны. График чётной функции всегда симметричен относительно оси ординат ОУ.

Функцию y = f(x) называют нечетной, если она определена на симметричном множестве и для любого х из области определения выполняется равенство:

Это означает, что для любых противоположных значений аргумента, значения нечетной функции также противоположны. График нечётной функции всегда симметричен относительно начала координат.

Сумма корней чётной и нечетной функций (точек пересечения оси абсцисс ОХ) всегда равна нулю, т.к. на каждый положительный корень х приходится отрицательный корень –х.

Важно отметить: некоторая функция не обязательно должна быть четной либо нечетной. Существует множество функций не являющихся ни четными ни нечетными. Такие функции называются функциями общего вида, и для них не выполняется ни одно из равенств или свойств приведенных выше.

 

График линейной функции

К оглавлению…

Линейной функцией называют функцию, которую можно задать формулой:

График линейной функции представляет из себя прямую и в общем случае выглядит следующим образом (приведен пример для случая когда k > 0, в этом случае функция возрастающая; для случая k < 0 функция будет убывающей, т.е. прямая будет наклонена в другую сторону — слева направо):

 

График квадратичной функции (Парабола)

К оглавлению…

График параболы задается квадратичной функцией:

Квадратичная функция, как и любая другая функция, пересекает ось ОХ в точках являющихся её корнями: (x₁; 0) и (x₂; 0). Если корней нет, значит квадратичная функция ось ОХ не пересекает, если корень один, значит в этой точке (x₀; 0) квадратичная функция только касается оси ОХ, но не пересекает её. Квадратичная функция всегда пересекает ось OY в точке с координатами: (0;

c). График квадратичной функции (парабола) может выглядеть следующим образом (на рисунке примеры, которые далеко не исчерпывают все возможные виды парабол):

При этом:

• если коэффициент a > 0, в функции y = ax² + bx + c, то ветви параболы направлены вверх;
• если же a < 0, то ветви параболы направлены вниз.

Координаты вершины параболы могут быть вычислены по следующим формулам. Икс вершины (p — на рисунках выше) параболы (или точка в которой квадратный трехчлен достигает своего наибольшего или наименьшего значения):

Игрек вершины (q — на рисунках выше) параболы или максимальное, если ветви параболы направлены вниз (a < 0), либо минимальное, если ветви параболы направлены вверх (a > 0), значение квадратного трехчлена:

 

Графики других функций

К оглавлению…

Степенной функцией называют функцию, заданную формулой:

Приведем несколько примеров графиков степенных функций:

Обратно пропорциональной зависимостью называют функцию, заданную формулой:

В зависимости от знака числа k график обратно пропорциональной зависимости может иметь два принципиальных варианта:

Асимптота — это линия, к которой линия графика функции бесконечно близко приближается, но не пересекает. Асимптотами для графиков обратной пропорциональности приведенных на рисунке выше являются оси координат, к которым график функции бесконечно близко приближается, но не пересекает их.

Показательной функцией с основанием а называют функцию, заданную формулой:

В зависимости от того больше или меньше единицы число a график показательной функции может иметь два принципиальных варианта (приведем также примеры, см. ниже):

Логарифмической функцией называют функцию, заданную формулой:

В зависимости от того больше или меньше единицы число a график логарифмической функции может иметь два принципиальных варианта:

График функции y = |x| выглядит следующим образом:

 

Графики периодических (тригонометрических) функций

К оглавлению…

Функция у = f(x) называется периодической, если существует такое, неравное нулю, число Т, что f(x + Т) = f(x), для любого х из области определения функции f(x). Если функция f(x) является периодической с периодом T, то функция:

где: A, k, b – постоянные числа, причем k не равно нулю, также периодическая с периодом

T₁, который определяется формулой:

Большинство примеров периодических функций — это тригонометрические функции. Приведем графики основных тригонометрических функций. На следующем рисунке изображена часть графика функции y = sinx (весь график неограниченно продолжается влево и вправо), график функции y = sinx называют синусоидой:

График функции y = cosx называется косинусоидой. Этот график изображен на следующем рисунке. Так как и график синуса он бесконечно продолжается вдоль оси ОХ влево и вправо:

График функции y = tgx называют тангенсоидой. Этот график изображен на следующем рисунке. Как и графики других периодических функций, данный график неограниченно далеко повторяется вдоль оси ОХ влево и вправо.

Ну и наконец, график функции y = ctgx называется

котангенсоидой. Этот график изображен на следующем рисунке. Как и графики других периодических и тригонометрических функций, данный график неограниченно далеко повторяется вдоль оси ОХ влево и вправо.

educon.by

Что такое функция — материалы для подготовки к ЕГЭ по Математике

 

Понятие функции – одно из основных в математике.

На уроках математики вы часто слышите это слово. Вы строите графики функций, занимаетесь исследованием функции, находите наибольшее или наименьшее значение функции. Но для понимания всех этих действий давайте определим, что такое функция.

Определение функции можно дать несколькими способами. Все они будут дополнять друг друга.

1. Функция – это зависимость одной переменной величины от другой. Другими словами, взаимосвязь между величинами.

Любой физический закон, любая формула отражает такую взаимосвязь величин. Например, формула – это зависимость давления жидкости от глубины .

Чем больше глубина, тем больше давление жидкости. Можно сказать, что давление жидкости является функцией от глубины, на которой его измеряют.

Знакомое вам обозначение как раз и выражает идею такой зависимости одной величины от другой. Величина у зависит от величины по определенному закону, или правилу, обозначаемому .

Другими словами: меняем (независимую переменную, или аргумент) – и по определенному правилу меняется .

Совсем необязательно обозначать переменные и . Например, – зависимость длины от температуры , то есть закон теплового расширения. Сама запись означает, что величина зависит от .

2. Можно дать и другое определение.

Функция – это определенное действие над переменной.

Это означает, что мы берем величину , делаем с ней определенное действие (например, возводим в квадрат или вычисляем ее логарифм) – и получаем величину .

В технической литературе встречается определение функции как устройства, на вход которого подается – а на выходе получается .

Итак, функция – это действие над переменной. В этом значении слово «функция» применяется и в областях, далеких от математики. Например, можно говорить о функциях мобильного телефона, о функциях головного мозга или функциях депутата. Во всех этих случаях речь идет именно о совершаемых действиях.

3. Дадим еще одно определение функции – то, что чаще всего встречается в учебниках.

Функция – это соответствие между двумя множествами, причем каждому элементу первого множества соответствует один и только один элемент второго множества.

Например, функция каждому действительному числу ставит в соответствие число в два раза большее, чем .

 

Повторим еще раз: каждому элементу множества по определенному правилу мы ставим в соответствие элемент множества . Множество называется областью определения функции. Множество – областью значений.

Но зачем здесь такое длинное уточнение: «каждому элементу первого множества соответствует один и только один элемент второго»? Оказывается, что соответствия между множествами тоже бывают разные.

Рассмотрим в качестве примера соответствие между двумя множествами – гражданами России, у которых есть паспорта, и номерами их паспортов. Ясно, что это соответствие взаимно-однозначное – у каждого гражданина только один российский паспорт. И наоборот – по номеру паспорта можно найти человека.

В математике тоже есть такие взаимно-однозначные функции. Например, линейная функция . Каждому значению соответствует одно и только одно значение . И наоборот – зная , можно однозначно найти .

Могут быть и другие типы соответствий между множествами. Возьмем для примера компанию друзей и месяцы, в которые они родились:

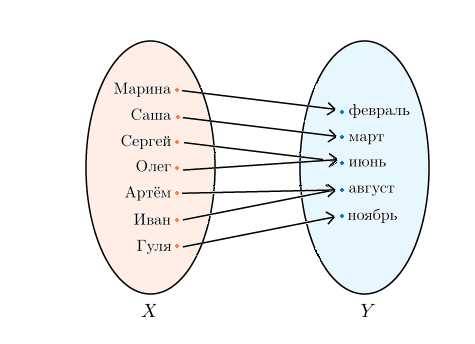
Каждый человек родился в какой-то определенный месяц. Но данное соответствие не является взаимно-однозначным. Например, в июне родились Сергей и Олег.

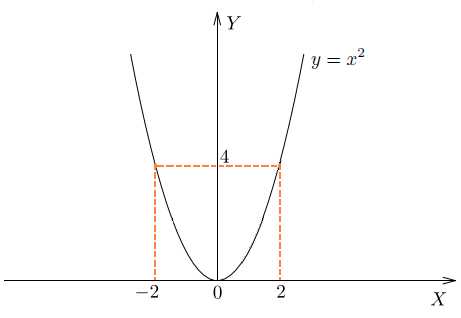
Пример такого соответствия в математике – функция . Один и тот же элемент второго множества соответствует двум разным элементам первого множества: и .

А каким должно быть соответствие между двумя множествами, чтобы оно не являлось функцией? Очень просто! Возьмем ту же компанию друзей и их хобби:

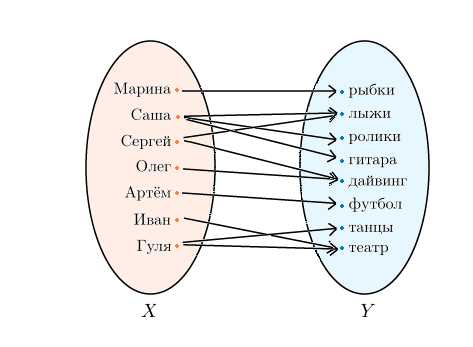
Мы видим, что в первом множестве есть элементы, которым соответствует два или три элемента из второго множества.

Очень сложно было бы описать такое соответствие математически, не правда ли?

Вот другой пример. На рисунках изображены кривые. Как вы думаете, какая из них является графиком функции, а какая – нет?

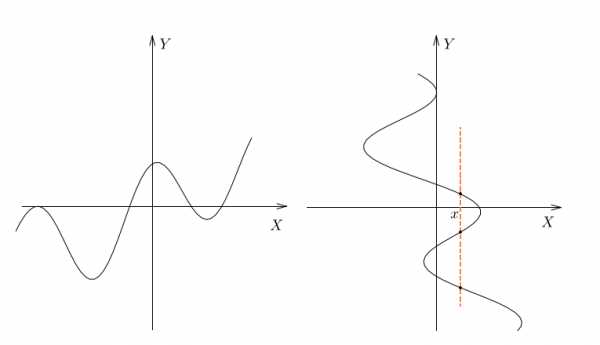
Ответ очевиден. Первая кривая – это график некоторой функции, а вторая – нет. Ведь на ней есть точки, где каждому значению соответствует не одно, а целых три значения .

Ты нашел то, что искал? Поделись с друзьями!

Перечислим способы задания функции.

1. С помощью формулы. Это удобный и привычный для нас способ. Например:

,

,

,

.

Это примеры функций, заданных формулами.

2. Графический способ. Он является самым наглядным. На графике сразу видно все – возрастание и убывание функции, наибольшие и наименьшие значения, точки максимума и минимума. В следующей статье будет рассказано об исследовании функции с помощью графика.

К тому же не всегда легко вывести точную формулу функции. Например, курс доллара (то есть зависимость стоимости доллара от времени) можно показать только на графике.

3. С помощью таблицы. С этого способа вы когда-то начинали изучение темы «Функция» — строили таблицу и только после этого – график. А при экспериментальном исследовании какой-либо новой закономерности, когда еще неизвестны ни формула, ни график, этот способ будет единственно возможным.

4. С помощью описания. Бывает, что на разных участках функция задается разными формулами. Известная вам функция задается описанием:

Звоните нам: 8 (800) 775-06-82 (бесплатный звонок по России)                        +7 (495) 984-09-27 (бесплатный звонок по Москве)

Или нажмите на кнопку «Узнать больше», чтобы заполнить контактную форму. Мы обязательно Вам перезвоним.

ege-study.ru

Виды функций и их графики

Поиск Лекций

---

Понятие функции

Зависимость одной переменной у от другой х, при которой каждому значению переменной х из определенного множества D соответствует единственное значение переменной у, называется функцией.

Общий вид функции: у = f(х),

где х – независимая переменная (аргумент), у – зависимая переменная (функция).

Область определения функции D(f)— множество, на котором задаётся функция. Другими словами: множество значений, которые может принимать аргумент.

Область значений функции E(f)— множество, состоящее из всех значений, которые принимает функция.

График функции – множество точек на координатной плоскости, координатами которых являются пары чисел (х; у), где х – значение аргумента, у – соответствующее ему значение функции.

Нули функции – значения аргумента, при которых функция равна 0.

Виды функций и их графики

ü Линейная функция y = kx + m

График функции – прямая.

Коэффициент k отвечает за угол наклона (k>0 – угол острый, k<0 – угол тупой, k=0 – горизонтальная прямая), m – за сдвиг графика вверх-вниз (m>0 – вверх, m<0 – вниз).

у = kx – частный случай линейной функции при m=0.

В этом случае график функции обязательно проходит через начало координат.

Свойства функции y = kx + m

1) D(f) = (-∞; +∞)

2) Возрастает, если k > 0; убывает, если k < 0

3) Не ограничена ни снизу, ни сверху

4) Нет ни наибольшего, ни наименьшего значений

5) E(f) = (-∞; +∞)

ü Функция y = kx² (k ≠ 0)График функции – парабола.

Свойства функции y = kx² Если k > 0

1) D(f) = (-∞; +∞)

2) Убывает на луче (-∞; 0], возрастает на луче [0; +∞)

3) Ограничена снизу, не ограничена сверху

4)

y наим = 0, у наиб не существует

5) Непрерывна

6) E(f) = [0; +∞)

Если k < 0

1)

D(f) = (-∞; +∞)

2) Возрастает на луче (-∞; 0], убывает на луче [0; +∞)

3) Не ограничена снизу, ограничена сверху

4) y наим не существует, у наиб = 0

5) Непрерывна

6) E(f) = (-∞; 0]

ü Квадратичная функция y = ax² + bx + c

График функции – парабола, у которой:

® вершинарасполагается в точке (x0; y0), где x0 = , y0 = f(x0)

® ветви, направлены вверх, если а > 0, и вниз, если а < 0

® прямая х = х0 является осью симметрии параболы.

Число с – ордината точки пересечения параболы с осью Оу.

Свойства функции y = ax² + bx + c

Если а > 0

1) D(f) = (-∞; +∞)

2)

Убывает на луче (-∞; — ], возрастает на луче [- ; +∞)

3) Ограничена снизу, не ограничена сверху

4) y наим = 0, у наиб не существует

5) Непрерывна

6) E(f) = [y0; +∞)

Если а > 0

1)

D(f) = (-∞; +∞)

2) Возрастает на луче (-∞; — ], убывает на луче [- ; +∞)

3) Не ограничена снизу, ограничена сверху

4) y_наим не существует, у_наиб = 0

5) Непрерывна

6) E(f) = (-∞; y₀]

ü

Функция обратной пропорциональности y =

График функции – гипербола.

Свойства функции y =

1) D(f) = (-∞; 0) (0; +∞)

2) Если k > 0, то функция убывает на промежутке (-∞; 0) (0; +∞)

Если k < 0, то функция возрастает на промежутке (-∞; 0) (0; +∞)

3) Не ограничена ни снизу, ни сверху

4) Нет ни наименьшего, ни наибольшего значений

5) Функция непрерывна на открытом луче (-∞; 0) и на открытом луче (0; +∞)

6) E(f) = (-∞; 0) (0; +∞)

ü Функция y =

График функции – ветвь параболы, перевернутая «набок».

Свойства функции y =

1) D(f) = [0; +∞)

2) Возрастает

3) Ограничена снизу, не ограничена сверху

4) y наим = 0, у наиб не существует

5) Непрерывна

6) E(f) = [0; +∞)

ü Функция y =

График функции – объединение двух лучей: y = x, x ≥ 0 и y = -x, x ≤ 0

Свойства функции y =

1) D(f) = (-∞; +∞)

2) Убывает на луче (-∞; 0], возрастает на луче [0; +∞)

3) Ограничена снизу, не ограничена сверху

4) y наим = 0, у наиб не существует

5) Непрерывна

6) E(f) = [0; +∞)

 

y = xⁿ (n = 3, 5, 7, 9…)

График функции – кубическая парабола (при n=3)

Свойства функции

1)

D(f) = (-∞; +∞)

2) Возрастает

3) Не ограничена ни снизу, ни сверху

4) Нет ни наименьшего, ни наибольшего значений

5) Непрерывна

6) E(f) = (-∞; +∞)

Преобразования графика функции y = f(x)

1) y = f(x) + a

Сдвиг вверх на а единиц, если a > 0

Cдвиг вниз, если a < 0

2) y = f(x + a)

Сдвиг влево на а единиц, если a > 0

Сдвиг вправо, если a < 0

3) — y = f(x)

Зеркальное отражение относительно Ох

4) y = f(-x)

Зеркальное отражение относительно Оу

5) y = a·f(x)

Растяжение вдоль Оу, если a > 1

Растяжение вдоль Ох, если 0 < a < 1

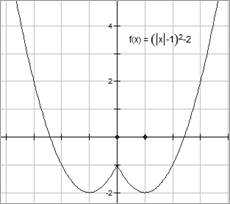
6) y = f(|x|)

Для x ≥ 0, y = f(x)

Для x < 0 – преобразование симметрии относительно Oy графика y = f(x), для x ≥ 0 симметричные части графика из правой полуплоскости в левую.

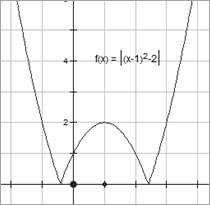
7) y = |f(x)|

Для f(x) ≥ 0, |f(x)| = f(x)

Для f(x) < 0, |f(x)| = -f(x)

Симметричное отображение части графика из нижней полуплоскости в верхнюю относительно Ox.

Рекомендуемые страницы:

Поиск по сайту

poisk-ru.ru

Виды функций

Постоянная функция. Эта функция задана формулой  у = b, где b – некоторое число. Графиком постоянной функции является прямая, параллельная оси абсцисс и проходящая через точку (0; b) на оси ординат. Графиком функции у = 0 является ось абсцисс.

Прямая пропорциональность. Эта функция задана формулой у = kx, где коэффициент пропорциональности k ≠ 0. Графиком прямой пропорциональности является прямая, проходящая через начало координат. 

Линейная функция. Такая функция задана формулой у = kx + b, где k и b – действительные числа. Графиком линейной функции является прямая.

Графики линейных функций могут пересекаться или быть параллельными.

Так, прямые графиков линейных функций у = k₁x + b₁ и у = k₂x + b₂ пересекаются, если k₁ ≠ k₂; если же k₁ = k₂, то прямые параллельны.

Обратная пропорциональность – это функция, которая задана формулой у = k/x, где k ≠ 0. K называется коэффициентом обратной пропорциональности. Графиком обратной пропорциональности является гипербола.

Функция у = х² представлена графиком, получившим название парабола: на промежутке [-~; 0] функция убывает, на промежутке [0; ~] функция возрастает.

Функция у = х³ возрастает на всей числовой прямой и графически представлена кубической параболой.

Степенная функция с натуральным показателем. Эта функция задана формулой у = хⁿ, где n – натуральное число. Графики степенной функции с натуральным показателем зависят от n. Например, если n = 1, то графиком будет прямая (у = х), если n = 2, то графиком будет парабола и т.д.

Степенная функция с целым отрицательным показателем представлена формулой у = х^—n, где n – натуральное число. Данная функция определена при всех х ≠ 0. График функции также зависит от показателя степени n.

Функция у = ˅х. Такая функция имеет смысл при х  > или = 0. Функция у = ˅х отличается тем, что она не является ни четной, ни нечетной.

Степенная функция с положительным дробным показателем. Эта функция представлена формулой у = х^r, где r – положительная несократимая дробь. Данная функция также не является ни четной, ни нечетной.

Закрепим изученный материал.

Задание 1.

Построим график функции у = х².

Решение.

Для этого выберем несколько значений х и найдем соответствующие им значения у.

1.Если х = 0, то у = 0.

2. Если х = 1, то у = 1.

3. Если х = 3, то у = 9.

4. Если х = 5, то у = 25.

5. Если х = -1, то у = 1.

6. Если х = -3, то у = 9.

7. Если х = -5, то у = 25 и т.д.

Следовательно, наши «опорные» точки имеют координаты (0; 0), (1; 1), (3; 9), (5; 25), (-1; 1) и т.д.

Ответ: нашим графиком будет парабола.

Задание 2.

Построим график функции у = х³.

Решение.

Для этого выберем несколько значений х и найдем им соответствующие значения у.

1.Если х = 0, то у = 0.

2. Если х = 1, то у = 1.

3. Если х = 2, то у = 8.

4. Если х = 3, то у = 27.

5. Если х = -1, то у = -1.

6. Если х = -2, то у = -8.

7. Если х = -3, то у = -27 и т.д.

Следовательно, наши «опорные» точки имеют координаты (0; 0), (1; 1), (2; 8), (3; 27), (-1; -1) и т.д.

Ответ: нашим графиком будет кубическая парабола.

© blog.tutoronline.ru, при полном или частичном копировании материала ссылка на первоисточник обязательна.

blog.tutoronline.ru

ФУНКЦИЯ — это… Что такое ФУНКЦИЯ?

ФУНКЦИЯ — (лат. functio – исполнение) обязанность, круг деятельности. «Функция – это существование, мыслимое нами в действии» (Гёте). Наука о функциях органов живых существ – физиология; специальная наука о функциях нервной системы – физиология органов… …   Философская энциклопедия

функция — Команда или группа людей, а также инструментарий или другие ресурсы, которые они используют для выполнения одного или нескольких процессов или деятельности. Например, служба поддержки пользователей. Этот термин также имеет другое значение:… …   Справочник технического переводчика

функция — См …   Словарь синонимов

ФУНКЦИЯ — (лат. functio). В физиологии: отправление каким либо органом ему одному свойственных действий, как напр., дыхание, пищеварение. 2) в математике: величина, зависящая от другой переменной величины. Словарь иностранных слов, вошедших в состав… …   Словарь иностранных слов русского языка

Функция — [function] 1. Зависимая переменная величина; 2. Соответствие y=f(x) между переменными величинами, в силу которого каждому рассматриваемому значению некоторой величины x (аргумента или независимой переменной) соответствует определенное значение… …   Экономико-математический словарь

Функция — (от латинского functio исполнение, осуществление), 1) деятельность, обязанность, работа; внешнее проявление свойств какого–либо объекта в данной системе отношений (например, функция органов чувств, функция денег). 2) Функция в социологии роль,… …   Иллюстрированный энциклопедический словарь

ФУНКЦИЯ — (от лат. functio исполнение осуществление),..1) деятельность, обязанность, работа; внешнее проявление свойств какого либо объекта в данной системе отношений (напр., функция органов чувств, функция денег)2)] Функция в социологии роль, которую… …   Большой Энциклопедический словарь

ФУНКЦИЯ — ФУНКЦИЯ, в математике одно из основных понятий, выражение, определяющее регулярную зависимость между двумя множествами переменных величин, заключающуюся в том, что каждому элементу одного множества соответствует определенная, единственная… …   Научно-технический энциклопедический словарь

ФУНКЦИЯ — (function) Взаимосвязь между двумя и более переменными. Если у является функцией от х и записывается в виде y=f(x), то, если значение аргумента х известно, функция позволяет показывает, как найти значение у. Если у – однозначная функция от х, то… …   Экономический словарь

ФУНКЦИЯ —         (от лат. исполняю, совершаю)         центр, понятие в методологии функционального и структурно функционального анализа об в. Понятие “Ф.” стало активно использоваться в социальных науках со вт. пол. 19 в. в связи с проникновением сначала… …   Энциклопедия культурологии

dic.academic.ru

Функции Excel (по категориям) — Служба поддержки Office

БЕССЕЛЬ.I	Возвращает модифицированную функцию Бесселя In(x).
БЕССЕЛЬ.J	Возвращает функцию Бесселя Jn(x).
БЕССЕЛЬ.K	Возвращает модифицированную функцию Бесселя Kn(x).
БЕССЕЛЬ.Y	Возвращает функцию Бесселя Yn(x).
ДВ.В.ДЕС	Преобразует двоичное число в десятичное.
ДВ.В.ШЕСТН	Преобразует двоичное число в шестнадцатеричное.
ДВ.В.ВОСЬМ	Преобразует двоичное число в восьмеричное.
БИТ.И	Возвращает результат операции поразрядного И для двух чисел.
БИТ.СДВИГЛ	Возвращает число со сдвигом влево на указанное число бит.
БИТ.ИЛИ	Возвращает результат операции поразрядного ИЛИ для двух чисел.
БИТ.СДВИГП	Возвращает число со сдвигом вправо на указанное число бит.
БИТ.ИСКЛИЛИ	Возвращает побитовое «исключающее или» двух чисел.
КОМПЛЕКСН	Преобразует коэффициенты при вещественной и мнимой частях комплексного числа в комплексное число.
ПРЕОБР	Преобразует число из одной системы счисления в другую.
ДЕС.В.ДВ	Преобразует десятичное число в двоичное.
ДЕС.В.ШЕСТН	Преобразует десятичное число в шестнадцатеричное.
ДЕС.В.ВОСЬМ	Преобразует десятичное число в восьмеричное.
ДЕЛЬТА	Проверяет равенство двух значений.
ФОШ	Возвращает функцию ошибки.
ФОШ.ТОЧН	Возвращает функцию ошибки.
ДФОШ	Возвращает дополнительную функцию ошибки.
ДФОШ.ТОЧН	Возвращает дополнительную функцию ошибки, проинтегрированную в пределах от x до бесконечности.
ПОРОГ	Проверяет, не превышает ли данное число пороговое значение.
ШЕСТН.В.ДВ	Преобразует шестнадцатеричное число в двоичное.
ШЕСТН.В.ДЕС	Преобразует шестнадцатеричное число в десятичное.
ШЕСТН.В.ВОСЬМ	Преобразует шестнадцатеричное число в восьмеричное.
МНИМ.ABS	Возвращает абсолютную величину (модуль) комплексного числа.
МНИМ.ЧАСТЬ	Возвращает коэффициент при мнимой части комплексного числа.
МНИМ.АРГУМЕНТ	Возвращает значение аргумента комплексного числа (тета) — угол, выраженный в радианах.
МНИМ.СОПРЯЖ	Возвращает комплексно-сопряженное комплексного числа.
МНИМ.COS	Возвращает косинус комплексного числа.
МНИМ.COSH	Возвращает гиперболический косинус комплексного числа.
МНИМ.COT	Возвращает котангенс комплексного числа.
МНИМ.CSC	Возвращает косеканс комплексного числа.
МНИМ.CSCH	Возвращает гиперболический косеканс комплексного числа.
МНИМ.ДЕЛ	Возвращает частное от деления двух комплексных чисел.
МНИМ.EXP	Возвращает экспоненту комплексного числа.
МНИМ.LN	Возвращает натуральный логарифм комплексного числа.
МНИМ.LOG10	Возвращает десятичный логарифм комплексного числа.
МНИМ.LOG2	Возвращает двоичный логарифм комплексного числа.
МНИМ.СТЕПЕНЬ	Возвращает комплексное число, возведенное в степень с целочисленным показателем.
МНИМ.ПРОИЗВЕД	Возвращает произведение от 2 до 255 комплексных чисел.
МНИМ.ВЕЩ	Возвращает коэффициент при вещественной (действительной) части комплексного числа.
МНИМ.SEC	Возвращает секанс комплексного числа.
МНИМ.SECH	Возвращает гиперболический секанс комплексного числа.
МНИМ.SIN	Возвращает синус комплексного числа.
МНИМ.SINH	Возвращает гиперболический синус комплексного числа.
МНИМ.КОРЕНЬ	Возвращает значение квадратного корня из комплексного числа.
МНИМ.РАЗН	Возвращает разность двух комплексных чисел.
МНИМ.СУММ	Возвращает сумму комплексных чисел.
МНИМ.TAN	Возвращает тангенс комплексного числа.
ВОСЬМ.В.ДВ	Преобразует восьмеричное число в двоичное.
ВОСЬМ.В.ДЕС	Преобразует восьмеричное число в десятичное.
ВОСЬМ.В.ШЕСТН	Преобразует восьмеричное число в шестнадцатеричное.

support.office.com

No related posts.