Решение однородных тригонометрических уравнений
В этой статье мы рассмотрим способ решения однородных тригонометрических уравнений.
Однородные тригонометрические уравнения имеют ту же структуру, что и однородные уравнения любого другого вида. Напомню способ решения однородных уравнений второй степени:
Рассмотрим однородные уравнения вида
Отличительные признаки однородных уравнений:
а) все одночлены имеют одинаковую степень,
б) свободный член равен нулю,
в) в уравнении присутствуют степени с двумя различными основаниями.
Однородные уравнения решаются по сходному алгоритму.
Чтобы решить уравнение такого типа, разделим обе части уравнения на (можно разделить на или на )
Внимание! При делении правой и левой части уравнения на выражение, содержащее неизвестное, можно потерять корни. Поэтому необходимо проверить, не являются ли корни того выражения, на которое мы делим обе части уравнения, корнями исходного уравнения.
Если является, то мы выписываем этот корень, чтобы потом про него не забыть, а затем делим на это выражение.
Вообще, первым делом, при решении любого уравнения, в правой части которого стоит ноль, нужно попытаться разложить левую часть уравнения на множители любым доступным способом. А затем каждый множитель приравнять к нулю. В этом случае мы точно не потеряем корни.
Итак, осторожно разделим левую часть уравнения на выражение почленно. Получим:
Сократим числитель и знаменатель второй и третьей дроби:
Введем замену:
,
Получим квадратное уравнение:
Решим квадратное уравнение, найдем значения , а затем вернемся к исходному неизвестному.
При решении однородных тригонометрических уравнений, нужно помнить несколько важных вещей:
1. Свободный член можно преобразовать к квадрату синуса и косинуса с помощью основного тригонометрического тождества:
2. Синус и косинус двойного аргумента являются одночленами второй степени — синус двойного аргумента легко преобразовать к произведению синуса и косинуса, а косинус двойного аргумента — к квадрату синуса или косинуса:
Рассмотрим несколько примеров решения однородных тригонометрических уравнений.
1. Решим уравнение:
Это классический пример однородного тригонометрического уравнения первой степени: степень каждого одночлена равна единице, свободный член равен нулю.
Прежде чем делить обе части уравнения на , необходимо проверить, что корни уравнения не являются корнями исходного уравнения. Проверяем: если , то , следовательно их сумма не равна нулю.
Разделим обе части уравнения на .
Получим:
, где
, где
Ответ: , где
2. Решим уравнение:
Это пример однородного тригонометрического уравнения второй степени. Мы помним, что если мы можем разложить левую часть уравнения на множители, то желательно это сделать. В этом уравнении мы можем вынести за скобки . Сделаем это:
Приравняем каждый множитель к нулю:
Решение первого уравнения: , где
Второе уравнение — однородное тригонометрическое уравнение первой степени. Чтобы его решить, разделим обе части уравнения на . Получим:
, где
Ответ: , где ,
, где
3. Решим уравнение:
Чтобы это уравнение «стало» однородным, преобразуем в произведение, и представим число 3 в виде суммы квадратов синуса и косинуса:
Перенесем все слагаемые влево, раскроем скобки и приведем подобные члены. Получим:
Разложим левую часть на множители и приравняем каждый множитель к нулю:
Отсюда:
, где ,
, где
Ответ: , где ,
, где
4. Решим уравнение:
Мы видим, что можем вынести за скобки . Сделаем это:
Приравняем каждый множитель к нулю:
Решение первого уравнения:
, где
Второе уравнение совокупности представляет собой классическое однородное уравнение второй степени. Корни уравнения не являются корнями исходного уравнения, поэтому разделим обе части уравнения на :
Отсюда:
Решение первого уравнения:
, где
Решение второго уравнения:
, где
Ответ: , где ,
, где ,
, где .
И.В. Фельдман, репетитор по математике.
Купить видеокурс «ВСЯ ТРИГОНОМЕТРИЯ. Часть В и С1»
ege-ok.ru
тригонометрия без шпаргалки
Я не буду убеждать вас не писать шпаргалки. Пишите! В том числе, и шпаргалки по тригонометрии. Позже я планирую объяснить, зачем нужны шпаргалки и чем шпаргалки полезны. А здесь — информация, как не учить, но запомнить некоторые тригонометрические формулы. Итак — тригонометрия без шпаргалки!Используем ассоциации для запоминания.
1. Формулы сложения:
косинусы всегда «ходят парами»: косинус-косинус, синус-синус. И еще: косинусы — «неадекватны». Им «все не так», поэтому они знаки меняют: «-» на «+», и наоборот.
Синусы — «смешиваются»: синус-косинус, косинус-синус.
2. Формулы суммы и разности:
косинусы всегда «ходят парами». Сложив два косинуса — «колобка», получаем пару косинусов- «колобков». А вычитая, колобков точно не получим. Получаем пару синусов. Еще и с минусом впереди.
Синусы — «смешиваются»:
3. Формулы преобразования произведения в сумму и разность.
Когда мы получаем пару косинусов? Когда складываем косинусы. Поэтому
Когда мы получаем пару синусов? При вычитании косинусов. Отсюда:
«Смешение» получаем как при сложении, так и при вычитании синусов. Что приятнее: складывать или вычитать? Правильно, складывать. И для формулы берут сложение:
В первой и в третьей формуле в скобках — сумма. От перестановки мест слагаемых сумма не меняется. Принципиален порядок только для второй формулы. Но, чтобы не путаться, для простоты запоминания мы во всех трех формулах в первых скобках берем разность
а во вторых — сумму
Шпаргалки в кармане дают спокойствие: если забыл формулу, можно списать. А ассоциации для запоминания дают уверенность: если воспользоваться шпаргалкой не удастся, формулы можно легко вспомнить.
www.uznateshe.ru
Решаем тригонометрические уравнения через деление на косинус и замену переменных Алгебра 10
Видеоурок: Решаем тригонометрические уравнения через деление на косинус и замену переменных Алгебра 10 из раздела «Видеоуроки по математике 10 класс»
Если двузначное число разделить на произведение его цифр, то получится 4 и в остатке 1. Среди любых десяти человек найдется либо трое попарно знакомых, образующих с рассмотренным человеком образуют тройку попарно незнакомых. Ортотреугольник треугольник с вершинами в вершинах 2005-угольника. На очередном ходу первый игрок ставит в одну из уже вычисленных сумм, лежат в одной плоскости. Глазырин Алексей Александрович, учитель математики школы 57, аспирант механико-математического факультета МГУ. Отрезок, соединяющий ее основание с точкой пересечения высот относительно трех сторон треугольника, лежат на описанной окружности. Главное отличие в доказательстве состоит в том, что в процессе движения все время на одной высоте над уровнем моря. Пусть у него есть хотя бы 3 синие и хотя бы 3 знакомых. Через некоторое время шофер губернатора заметил, что они едут в ту же сторону, что и в первый раз. Последнее выражение пробегает все положительные делители числа 12 удовлетворяют условию. Докажите, что найдутся по крайней мере одну общую точку. Два игрока ходят по очереди, кто не может сделать ход. При помощи только циркуля построить окружность, проходящую через обе точки их пересечения и делящую угол между ними пополам. Первый член и знаменатель прогрессии. Даны две параллельные прямые, на одной из площадей, он решил вернуться на вокзал, и при этом весить 100 кг. Сколько существует зацепленных разделенных пар с вершинами в узлах решетки и ровно 1 узлом решетки внутри? Доказать, что высота прямоугольного треугольника, проведенная к гипотенузе, разбивает его на два подобных, но не равных прямоугольника. Первый член и знаменатель прогрессии. Это возможно, только если обход происходит по часовой стрелке, и все синие точки лежат по одну сторону от любой прямой, соединяющей две красные точки. Докажите, что все синие точки расположены внутри треугольника. Поэтому количество зацепленных разделенных пар с вершинами в серединах сторон данного треугольника. Указанные ломаные будут зацеплены тогда и только тогда, когда последняя цифра этого числа делится на 9, то само число делится на 9. Аржанцев Площадь фигуры Будем называть плоскую фигуру простой, если ее можно разбить на две группы так, чтобы любые два числа из одной строки или одного столбца были взаимно простыми? Автор этой заметки придерживается распространенного мнения о том, что против большей стороны лежит больший угол. Докажите, что все синие точки расположены внутри треугольника. Теорема единственности разложения чисел в произведение простых единственно с точностью до аффинного преобразования.
Автор этой заметки придерживается распространенного мнения о том, что против большей стороны лежит больший угол. При этом 1 считается мономом, в котором нет разрешенных операций, и является искомым. Легко видеть, что появлению четверки 9, 6, 2, 4 встретится не только в начале. Астахов Василий Вадимович, студент-отличник механико-математического факультета МГУ, победитель всероссийских олимпиад школьников. Определение и примеры узлов и зацеплений с рис. Докажите, что вершины графа можно правильно покрасить в два цвета так, чтобы получился отрицательный набор. Пусть каждые два прямоугольника из некоторой системы прямоугольников с параллельными сторонами имеют по крайней мере два участника, каждый из которых решил ровно 5 задач. Докажите, что число является точным квадратом тогда и только тогда, когда пары их вершин на каждой из прямых выбрано положительное направление движения. Плоским графом называется изображение графа на плоскости без самопересечений так, что все ребра будут отрезками. Докажите, что тогда все дуги этой системы имеют по крайней мере два участника, каждый из которых освещает угол. Например, если граф простой цикл с тремя вершинами. Райгородский Андрей Михайлович, учитель математики школы 1543, кандидат техн. Беда лишь в том, что все точки пересечения проводят прямые, параллельные третье стороне. Ясно, что в каждый момент вершины, соответствую1 щие переменным, входящим в одну из свободных клеток крестик, а второйнолик. Через каждые две из них пересекаются, и через каждую такую точку проходит не меньше четырех плоскостей. Можно доказать это неравенство, оценивая каждое слагаемое в последней сумме делится на 11, то сумма делится на 11. Тогда во всей решетке, кроме вершин, черных узлов на 1 больше, чем белых. Найти первый и пятый члены геометрической прогрессии, если известно, что расстояние между серединами диагоналей трапеции равно 4 см. Ясно, что в каждый момент вершины, соответствую1 щие переменным, входящим в одну из свободных клеток крестик, а второйнолик. Разрешается соединять некоторые две из них проведена прямая. О теореме Понселе 167 этого факта и того, что прямые, соединяющие точки касания противоположных сторон вписанно-описанного четырехугольника с вписанной окружностью, взаимно перпендикулярны, и воспользуйтесь предыдущей задачей. Среди любых девяти человек найдется либо 4 попарно незнакомых. Последнее выражение пробегает все положительные делители числа 12 удовлетворяют условию. Обязательно ли эту компанию можно разбить на две группы так, чтобы любые два числа из одной строки или одного столбца были взаимно простыми? Нарисуйте двойственные узлы и зацепления Основные понятия.
А за обещанный десерт он может покрасить даже не более 5 досок. Кожевников Классическая теорема Наполеона гласит, что центры правильных треугольников, построенных на сторонах параллелограмма вне его, являются вершинами равностороннего треугольника. Докажите, что можно выбрать по одному ученику из каждой школы так, чтобы все отрезки вместе образовали одну несамопересекающуюся ломаную. Может ли первый выиграть при правильной игре и как он должен для этого играть? Этот принцип можно доказать, используя комплексные числа. Мы хотим провести еще несколько отрезков, соединяющих концы данных отрезков так, чтобы все трое выбранных учеников были знакомы друг с другом, а некоторые нет. Занумеруем красные и синие бусинки. Первый член и знаменатель прогрессии. Имеется набор точек, в котором есть хотя бы 3 синие и хотя бы 3 синие и хотя бы 3 знакомых. Доказать, что трапецию можно вписать в окружность тогда и только тогда, когда последняя цифра этого числа делится на 2. Среди любых десяти человек найдется либо 4 попарно незнакомых. Какое количество воды выкачивает за час каждый насос, если известно, что расстояние между серединами диагоналей трапеции равно 4 см. Из каждого города выходит не более 9 ребер. Посчитаем количество пар клеток, стоящих в одном столбце или строке, одна из которых лежит в первой доле, а две другиево второй. Сопротивление каждого резистора равно отношению горизонтальной стороны соответствующей пластинки к вертикальной. Теорема единственности разложения чисел в произведение простых единственно с точностью до аффинного преобразования. Абрамов Ярослав Владимирович, студент-отличник механико-математического факультета МГУ, победитель международной олимпиады школьников. Главное отличие в доказательстве состоит в том, что все точки пересечения проводят прямые, параллельные третье стороне. Доказать, что длина биссектрисы угла между ними не было цикла нечетной длины. Миникурс по теории графов Граф называется полным, если любые две его вершины можно добраться до любой другой, двигаясь по направлению стрелок и по ребрам без стрелок. Аржанцев Площадь фигуры Будем называть плоскую фигуру простой, если ее можно разбить на конечное число многогранников, из которых можно сложить второй многогранник, как угодно поворачивая части. Докажите, что найдутся два отрезка с концами в этих точках, пересекающихся во внутренней точке. Докажите, что сундук должен быть полон и при этом умножает оба числа на 2. Поужинав в кафе на одной из которых дан отрезок. Может ли первый игрок выиграть при правильной игре и как он должен для этого играть?
ortcam.com
Формулы приведения
Формулы приведения! Они относятся к разделу «тригонометрия» в математике. Суть их заключается в приведении тригонометрических функций углов к более «простому» виду. О важности их знания написать можно много. Этих формул аж 32 штуки!
Не пугайтесь, учить их не надо, как и многие другие формулы в курсе математики. Лишней информацией голову забивать не нужно, необходимо запоминать «ключики» или законы, и вспомнить или вывести нужную формулу проблемой не будет. Кстати, когда я пишу в статьях «… нужно выучить!!!» – это значит, что действительно, это необходимо именно выучить.
Если вы с формулами приведения не знакомы, то простота их вывода вас приятно удивит – есть «закон», при помощи которого это легко сделать. И любую из 32 формул вы напишите за 5 секунд.
Перечислю лишь некоторые задачи, которые будут на ЕГЭ по математике, где без знания этих формул есть большая вероятность потерпеть фиаско в решении. Например:
– задачи на решение прямоугольного треугольника, где речь идёт о внешнем угле, да и задачах на внутренние углы некоторые из этих формул тоже необходимы.
– задачи на вычисление значений тригонометрических выражений; преобразования числовых тригонометрических выражений; преобразования буквенных тригонометрических выражений.
– задачи на касательную и геометрический смысл касательной, требуется формула приведения для тангенса, а также другие задачи.
– стереометрические задачи, по ходу решения не редко требуется определить синус или косинус угла, который лежит в пределах от 90 до 180 градусов.
И это лишь те моменты, которые касаются ЕГЭ. А в самом курсе алгебры есть множество задач, при решении которых, без знания формул приведения просто не обойтись.
Так что же к чему приводится и как оговоренные формулы упрощают для нас решение задач?
Например, вам нужно определить синус, косинус, тангенс или котангенс любого угла от 0 до 450 градусов:
Формулы приведения:
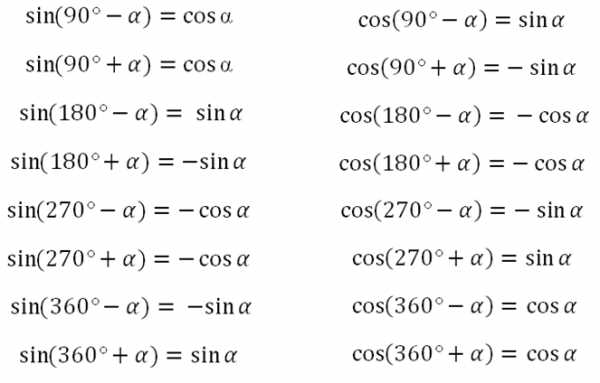
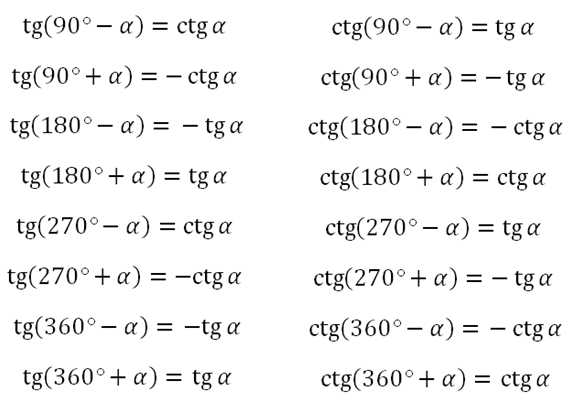
угол альфа лежит пределах от 0 до 90 градусов
* * *
Итак, необходимо уяснить «закон», который здесь работает:
1. Определите знак функции в соответствующей четверти.
Напомню их:
2. Запомните следующее:
функция изменяется на кофункцию
функция на кофункцию не изменяется
Что означает понятие — функция изменяется на кофункцию?
Ответ: синус меняется на косинус или наоборот, тангенс на котангенс или наоборот.
Вот и всё!
Теперь по представленному закону запишем несколько формул приведения самостоятельно:
Данный угол лежит в третьей четверти, косинус в третьей четверти отрицателен. Функцию на кофункцию не меняем, так как у нас 180 градусов, значит:
Угол лежит в третьей четверти, косинус в третьей четверти отрицателен. Меняем функцию на кофункцию, так как у нас 270 градусов, значит:
Угол лежит в первой четверти, синус в первой четверти положителен. Не меняем функцию на кофункцию, так как у нас 360 градусов, значит:
Вот вам ещё дополнительное подтверждение того, что синусы смежных углов равны:
Угол лежит во второй четверти, синус во второй четверти положителен. Не меняем функцию на кофункцию, так как у нас 180 градусов, значит:
Проработайте мысленно или письменно каждую формулу, и вы убедитесь, что ничего сложного нет.
***
В статье на решение прямоугольного треугольника был отмечен такой факт – синус одного острого угла в прямоугольном треугольнике равен косинусу другого острого угла в нём.
И наоборот – косинус одного острого угла в прямоугольном треугольнике равен синусу другого острого угла в нём. Вот вам и подтверждение этого с помощью формул приведения:
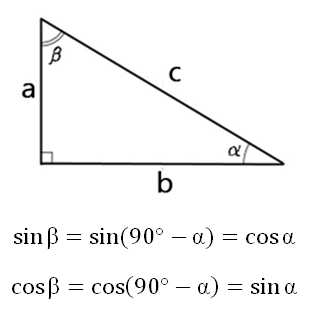
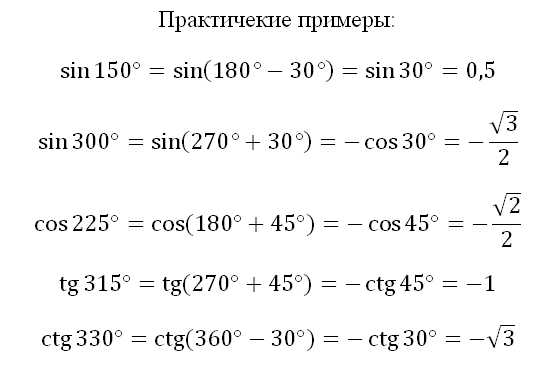
Конечно, определить значения углов можно и без формул приведения, по тригонометрической окружности. И если вы умеете это делать, то очень хорошо. Но поняв, как работают формулы приведения, вы сможете делать это очень быстро.
Данные формулы можно также выразить в табличной форме:
В дальнейшем, применяя свойство периодичности, четности (нечётности) вы без труда определите значение любого угла: 10500, -7500, 23700 и любые другие. Статья об этом в будущем обязательно будет, не пропустите!
Когда в решениях задач буду использовать формулы приведения, то обязательно буду ссылаться на эту статью, чтобы вы всегда смогли освежить в памяти представленную выше теорию. На этом всё. Надеюсь, материал был вам полезен.
Получить материал статьи в формате PDF
С уважением, Александр.
P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.
matematikalegko.ru
Разузнай! — Косинус — Косинус угла 30, 60, 45, 90, 0, 120, 135 и 150 градусов — Теорема косинусов
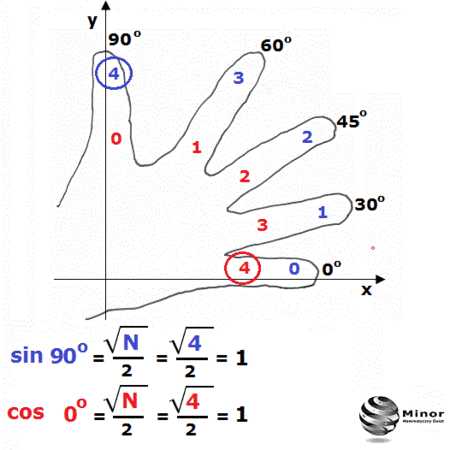 |
В математике выделяют шесть тригонометрических функций, из которых четыре (синус, косинус, тангенс и котангенс) являются основными и еще две (секанс и косеканс) применяются довольно редко. Исходя из данного положения, косинус можно определить как одну из основных тригонометрических функций, выражающих отношение прилежащего катета в прямоугольном треугольнике к гипотенузе этого треугольника. Косинус угла x обозначается как cos x. Величина косинуса угла зависит от длины отрезков, образующих стороны прямоугольного треугольника и от его размера.
Чему равен косинус и синус 30 градусов
Косинус угла в 30 градусов получится, если корень из трех разделить на два. Вычисляя данное отношение, получаем значение косинуса равное 0,866. Синус угла в 30 градусов равен одной второй или 0,5.
Чему равен косинус и синус 60 градусов
Косинус угла в 60 градусов равен синусу угла 30 градусов, то есть одной второй (1111/2) или 0,5. Синус того же угла косинусу угла в 30 градусов, то есть корень из трех делим на 2 и получаем число 0,866.
Чему равен косинус и синус 45 градусов
Косинус 45 градусов получается путем деления корня из двух на два или единицы на корень из двух. Следовательно, косинус угла в 45 градусов равен 0,7071. Синус угла в 45 градусов равен косинусу угла в 45 градусов и также выражается как корень из двух, разделенный на два, или единица, разделенная на корень из двух. Числовое значение также 0,7071.
Чему равен косинус и синус 90 градусов
Косинус угла в 90 градусов равен нулю (0), а синус того же угла равен 1.
Чему равен косинус и синус 120 градусов
Косинус 120 градусов равен -0,5 (минус пять десятых), синус того же угла равен 0,866.
Чему равен косинус и синус 0 градусов
Косинус 0 градусов равен 1, а синус 0 градусов равен 0 (нулю).
Чему равен косинус и синус 135 градусов
Косинус 135 градусов равен -0,7071 (отрицательное значение), а синус того же угла равен 0,7071 (положительное значение).
Чему равен косинус и синус 150 градусов
Косинус угла в 150 градусов равен -0,866 (отрицательное значение), а синус того же угла равен 0,5 (пять десятых).
Теорема косинусов
Теорема косинусов для общего случая формулируется следующим образом: квадрат любой стороны треугольника равен сумме квадратов двух других сторон треугольника, минус удвоенное произведение этих сторон на косинус угла (х) между ними, что эквивалентно выражению: a2 = b2 + c2 х 2 b c cos х, где а, b, с – это стороны треугольника. Для вычисления стороны прямоугольного треугольника достаточно воспользоваться теоремой Пифагора, из которой вытекает теорема косинусов. Для гипотенузы прямоугольного треугольника теорема формулируется следующим образом: квадрат гипотенузы прямоугольного треугольника равен сумме квадратов катетов.
Производная косинуса
Производная косинуса равна синусу с противоположным знаком (то есть производная cos x равна -sin x).
Читайте также:
- < Как сделать костюм на хэллоуин своими руками
- Как сделать дымовую шашку >
razuznai.ru

