Сочетания без повторений.
Поиск ЛекцийОсновные формулы комбинаторики
Задачи, в которых речь идет о тех или иных комбинациях объектов, их называют комбинаторными задачами. Область математики, в которой рассматриваются комбинаторные задачи, называют комбинаторикой.
Комбинаторика – область математики, в которой рассматриваются задачи о тех или иных комбинациях объектов.
Правило суммы
Пусть имеется n попарно непересекающихся множеств A1, A2,…An, содержащих m1, m2,…, mn элементов соответственно. Число способов, которыми можно выбрать один элемент из всех этих множеств, равно
m1 m2 … mn.
Пример. На курсе имеется 3 группы. В первой – 25 человек, во второй – 30, в третьей – 20. Сколькими способами из них можно выбрать одного студента?
Решение. Из первой группы одного человека можно выбрать 25 способами, из второй – 30, из третьей – 20. Чтобы найти ответ, нужно сложить все эти способы:
25 30 20=75.
Ответ: выбрать одного студента из трех групп можно 75 способами.
Правило произведения
Пусть имеется .n множеств A1, A2,…An,содержащих m1, m2,,…, mn элементов соответственно. Число способов, которыми можно выбрать по одному элементу из каждого множества
m1ּm2 ּ…ּmn.
Пример. На курсе имеется 3 группы. В первой – 25 человек, во второй – 30, в третьей – 20. Сколькими способами из каждой из них можно выбрать по одному студенту?
Решение. Из первой группы одного человека можно выбрать 25 способами, из второй – 30, из третьей – 20. Чтобы найти ответ, нужно перемножить эти числа:
25ּ30ּ20=15000.
Ответ: для того, чтобы из каждой группы выбрать по одному студенту, существует 15000 способов.
^ Если выбираем один элемент из нескольких множеств, то применяем правило суммы.
Если выбираем по одному элементу из нескольких множеств, то применяем правило произведения.
Факториаломчислаn называется последовательное произведение натуральных чисел от единицы до самого числа n:
Примечание: 0!=1.
Перестановки без повторений
Перестановками из n различных элементов называются размещения из этих n элементов по n. Перестановки — частный случай размещений.
Пример. Сколькими способами можно расставить в шеренгу студентов группы из 25 человек?
Решение. Число способов есть число перестановок из 25 элементов, то есть:
P25 = 25ּ24ּ23ּ…ּ1=25!=1,55ּ1025.
Ответ: расставить в шеренгу студентов группы из 25 человек можно 1,55ּ1025 способами.
Размещения без повторений
Различные упорядоченные подмножества по m элементов данного множества, содержащего n элементов, называются размещениями из n по m. Их число равно:
В частности: .
Пример. Из группы, состоящей из 25 человек, надо выбрать шахматную команду из четырех человек на I, II, III и IV доски. Сколькими способами это можно сделать?
Решение. Так как из 25 человек выбираются 4 и порядок важен, то число способов есть число размещений из 25 по 4, то есть:
.
Ответ: выбрать из 25 человек шахматную команду из четырех человек на I, II, III и IV доски можно 303600 способами.
Сочетания без повторений.
Различные неупорядоченные подмножества по m элементов из данного множества, содержащего n элементов, называются сочетаниями из n по m. Их число равно:
В частности, .
Пример. Сколькими способами из группы в 25 человек можно выбрать баскетбольную команду из пяти человек?
Решение. Так как из 25 человек выбираются 5 и порядок не важен, то число способов есть число сочетаний из 25 по 5, то есть:
Ответ: из группы в 25 человек можно выбрать баскетбольную команду 53130 способами.
Рекомендуемые страницы:
poisk-ru.ru
Число размещений без повторений
Число размещений без повторений из n по k – это число способов, сколькими можно из n различных элементов построить векторов с k различными координатами.
Число размещений без повторений находится по формуле:
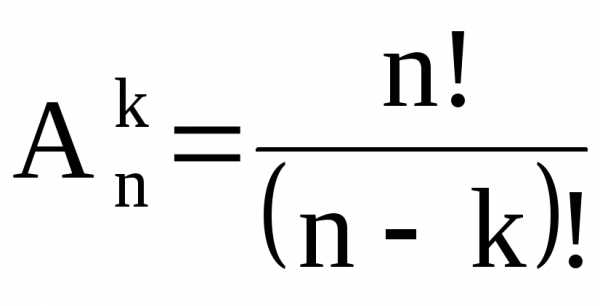 .
.
Пример: Сколькими способами можно построить 3-значное число с различными цифрами, не содержащее цифры 0?
Количество цифр 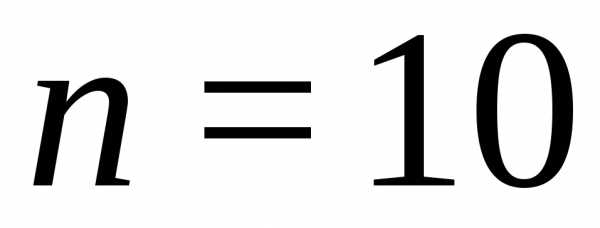 ,
размерность вектора с различными
координатами
,
размерность вектора с различными
координатами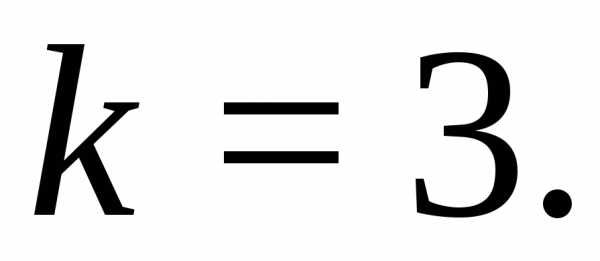
Число размещений с повторениями
Число размещений с повторениями из n по k – это число способов, сколькими можно из n различных элементов построить векторов с k координатами, среди которых могут быть одинаковые.
Число размещений с повторениями находится по формуле:
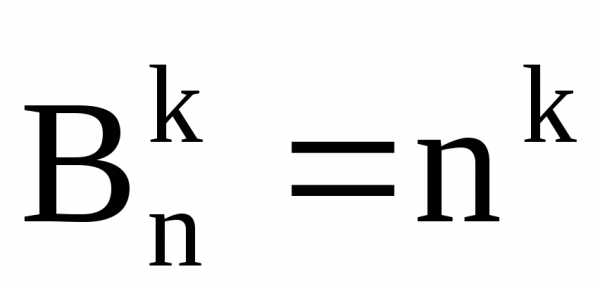
Пример: Сколько слов длины 6 можно составить из 26 букв латинского алфавита?
Количество букв 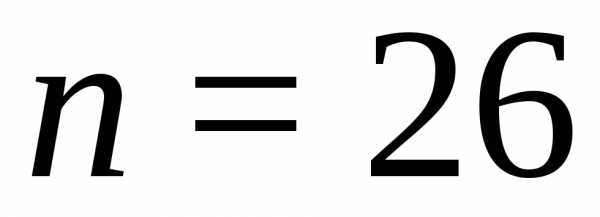 ,
размерность вектора
,
размерность вектора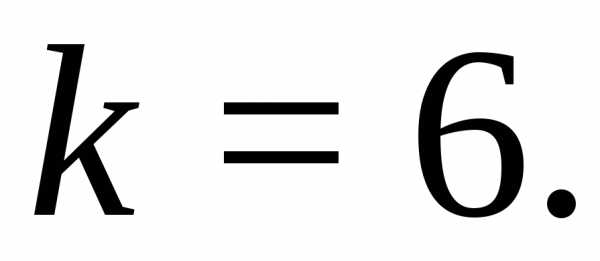
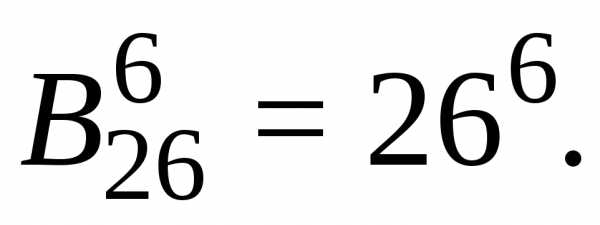
Число перестановок без повторений
Число перестановок без повторений из n элементов – это число способов, сколькими можно расположить на n различных местах n различных элементов.
Число перестановок без повторений находится по формуле:
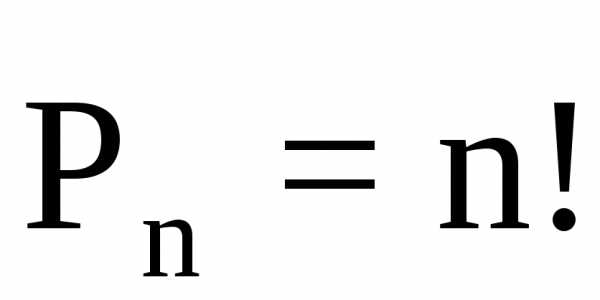 .
.
Замечание: Мощность искомого множества А удобно искать по формуле: , гдех – число способов выбрать нужные места;
Пример. Сколькими способами можно расставить на книжной полке 5 различных книг? В скольких случаях две определенные книги А и В окажутся рядом?
Всего способов
расставить 5 книг на 5-ти местах – равно 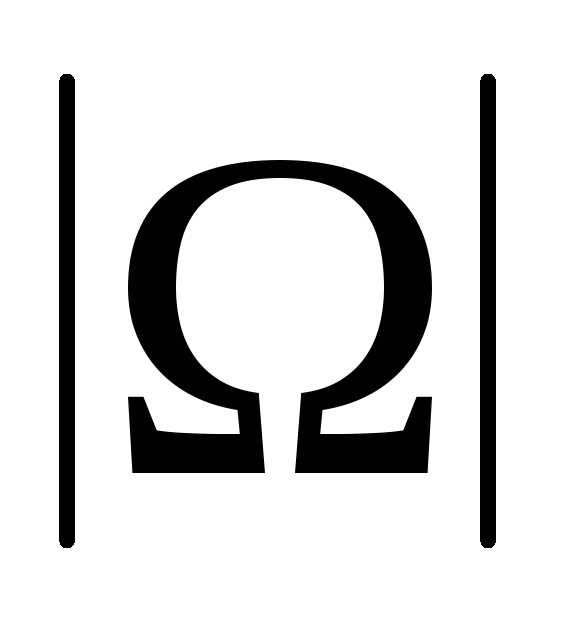 = 5! = 120.
= 5! = 120.
В задаче х – число способов выбрать два места рядом, х = 4; у – число способов расположить две книги на двух местах, у = 2! = 2; z – число способов расположить остальные 3 книги на оставшихся 3-х местах, z = 3! = 6. Значит = 48.
Число сочетаний без повторений
Число сочетаний без повторений из n по k – это число способов, сколькими можно из n различных элементов выбрать k
штук без учета порядка.Число сочетаний без повторений находится по формуле:
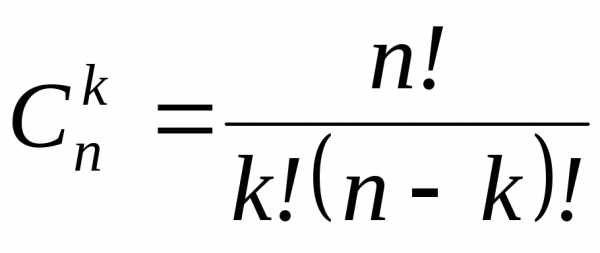 .
.
Свойства:
1) 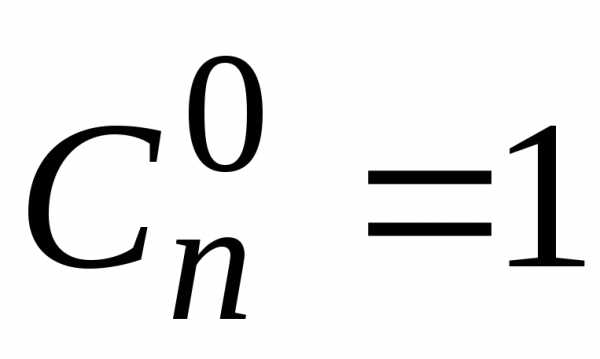 ;
2)
;
2)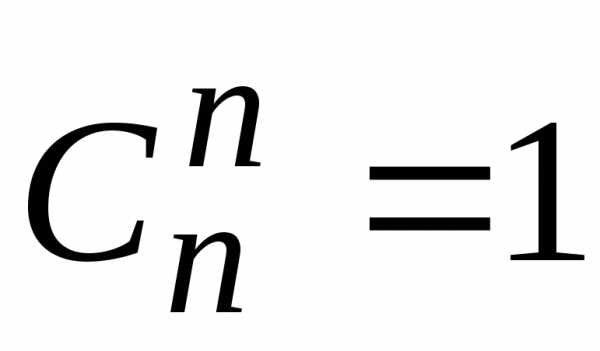 ;
3)
;
3)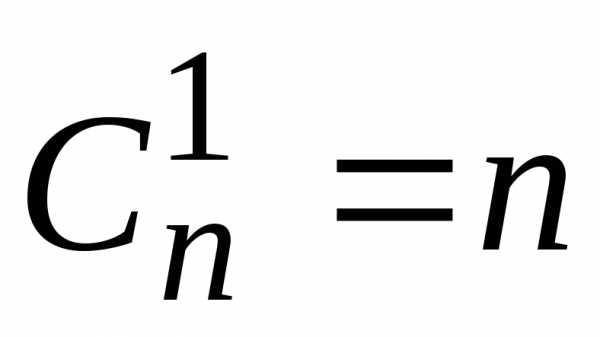 ;
;
4) 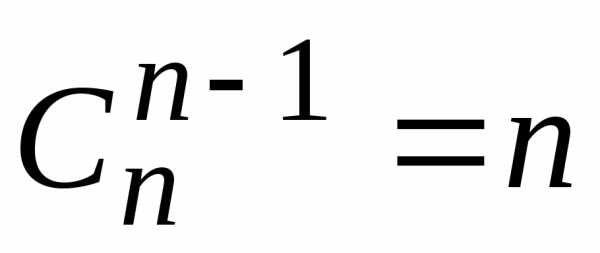 ;
5)
;
5)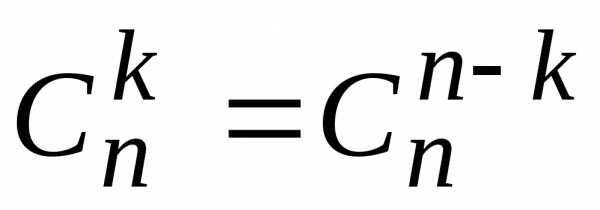 ;
6)
;
6)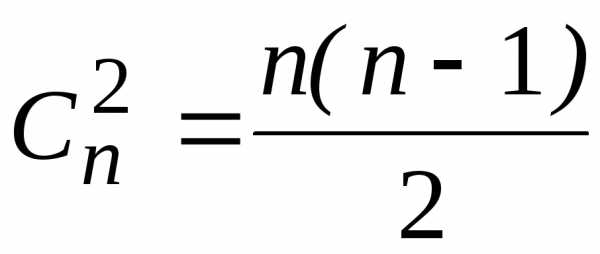 .
.
Пример. В урне 7 шаров. Из них 3 белых. Наугад выбирают 3 шара. Сколькими способами это можно сделать? В скольких случаях среди них будет ровно один белый.
Всего способов
.
Чтобы получить число способов выбрать
1 белый шар (из 3-х белых) и 2 черных шара
(из 4-х черных), надо перемножить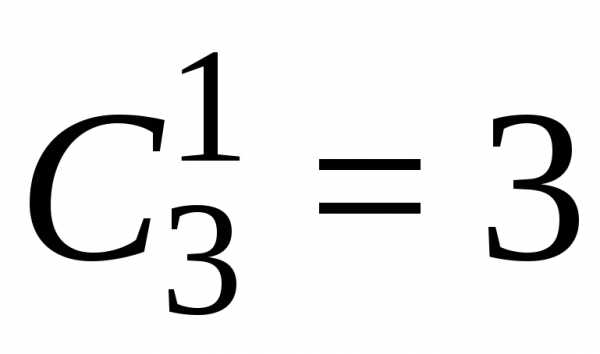
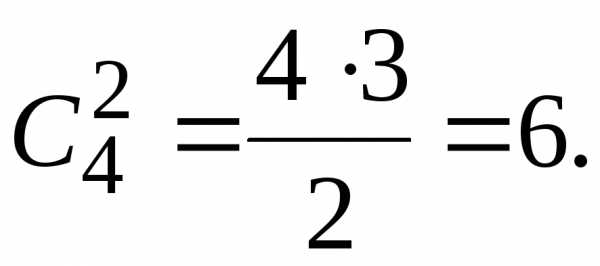 Таким образом искомое количество
способов
Таким образом искомое количество
способов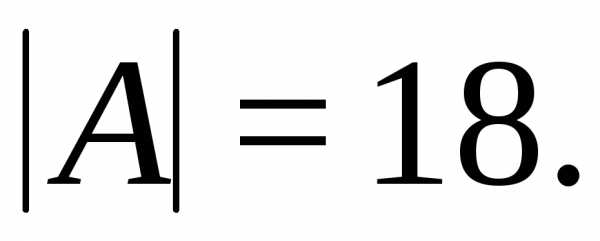
Упражнения
1. Из 35 учащихся класс по итогам года имели “5” по математике – 14 человек; по физике – 15 человек; по химии – 18 человек; по математике и физике – 7 человек; по математике и химии – 9 человек; по физике и химии – 6 человек; по всем трем предметам – 4 человек. Сколько человек имеют “5” по указанным предметам? Сколько человек не имеет “5” по указанным предметам? Имеет “5” только по математике? Имеет “5” только по двум предметам?
2. В группе из 30 студентов каждый знает, по крайней мере, один иностранный язык – английский или немецкий. Английский знают 22 студента, немецкий – 17. Сколько студентов знают оба языка? Сколько студентов знают немецкий язык, но не знают английский?
3. В 20 комнатах общежития института Дружбы Народов живут студенты из России; в 15 – из Африки; в 20 – из стран Южной Америки. Причем в 7 – живут россияне и африканцы, в 8 – россияне и южноамериканцы; в 9 – африканцы и южноамериканцы; в 3 – и россияне, и южноамериканцы, и африканцы. В скольких комнатах живут студенты: 1) только с одного континента; 2) только с двух континентов; 3) только африканцы.
4. Каждый из 500 студентов обязан посещать хотя бы один из трех спецкурсов: по математике, физике и астрономии. Три спецкурса посещают 10 студентов, по математике и физике – 30 студентов, по математике и астрономии – 25; спецкурс только по физике – 80 студентов. Известно также, что спецкурс по математике посещают 345 студентов, по физике – 145, по астрономии – 100 студентов. Сколько студентов посещают спецкурс только по астрономии? Сколько студентов посещают два спецкурса?
5. Староста курса представил следующий отчет по физкультурной работе. Всего – 45 студентов. Футбольная секция – 25 человек, баскетбольная секция – 30 человек, шахматная секция – 28 человек. При этом, 16 человек одновременно посещают футбольную и баскетбольную секции, 18 – футбольную и шахматную, 17 – баскетбольную и шахматную, 15 человек посещают все три секции. Объясните, почему отчет не был принят.
6. В аквариуме 11 рыбок. Из них 4 красных, остальные золотые. Наугад выбирают 4 рыбки. Сколькими способами это можно сделать? Найти число способов сделать это так, чтобы среди них будет: 1) ровно одна красная; 2) ровно 2 золотых; 3) хотя бы одна красная.
7. В списке 8 фамилий. Из них 4 – женские. Сколькими способами их можно разделить на две равные группы так, чтоб в каждой была женская фамилия?
8. Из колоды в 36 карт выбирают 4 . Сколько способов сделать это так, чтобы: 1) все карты были разных мастей; 2) все карты были одной масти; 3) 2 красные и 2 черные.
9. На карточках разрезной азбуки даны буквы К, К, К, У, У, А, Е, Р. Сколько способов сложить их в ряд так, что бы получилось «кукареку».
10. Даны карточки разрезанной азбуки с буквами О, Т, О, Л, О, Р, И, Н, Г, О, Л, О, Г. Сколько способов сложить их так, что бы получилось слово «отолоринголог».
11. Даны карточки нарезной азбуки с буквами Л, И, Т, Е, Р, А, Т, У, Р, А. Сколько способов сложить их в ряд так, что бы получилось слово «литература».
12. 8 человек становятся в очередь. Сколько способов сделать это так, что бы два определенных человека А и Б оказались: 1) рядом; 2) на краях очереди;
13. 10 человек садятся за круглый стол на 10 мест. Сколькими способами это можно сделать так, чтоб рядом оказались: 1) два определенных человека А и Б; 2) три определенных человека А, Б и С.
14. Из 10 арабских цифр составляют 5-значный код. Сколькими способами это можно сделать так, чтобы: 1) все цифры были разными; 2) на последнем месте четная цифра.
15. Из 26 букв латинского алфавита (среди них 6 гласных) составляется шестибуквенное слово. Сколькими способами это можно сделать так, чтобы в слове были: 1) ровно одна буква «а»; 2) ровно одна гласная буква; ровно две буквы «а»; в) ровно две гласные.
16. Сколько четырехзначных чисел делятся на 5?
17. Сколько четырехзначных чисел с различными цифрами делятся на 25?
19. Брошены 3 игральные кости. В скольких случаях выпала: 1) ровно 1 «шестерка»; 2) хотя бы одна «шестерка».
20. Брошены 3 игральные кости. В скольких случаях будет: 1) все разные; 2) ровно два одинаковых числа очков.
21. Сколько слов с различными буквами можно составить из алфавита а, в, с, d. Перечислить их все в лексикографическом порядке: abcd, abcd….
studfiles.net
Число сочетаний без повторений
Число сочетаний без повторений из n по k – это число способов, сколькими можно из n различных элементов выбрать k штук без учета порядка.
Число сочетаний без повторений находится по формуле:
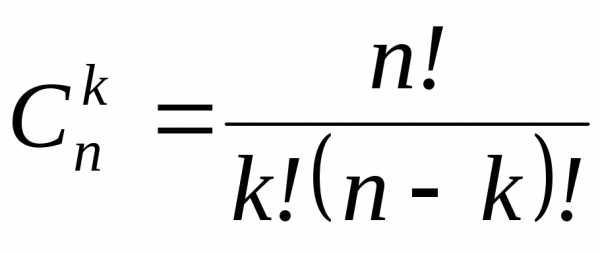 .
.
Свойства:
1) 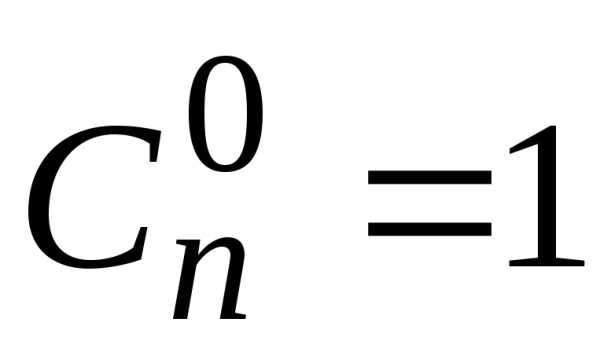 ;
2)
;
2)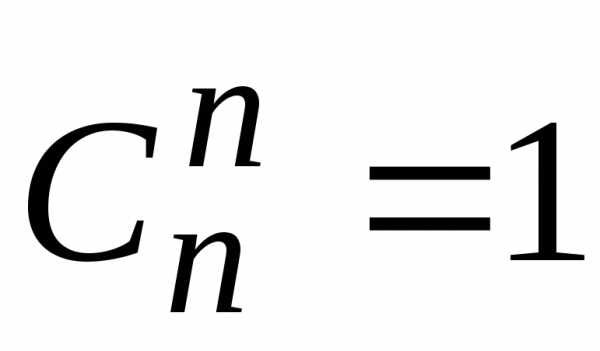 ;
3)
;
3)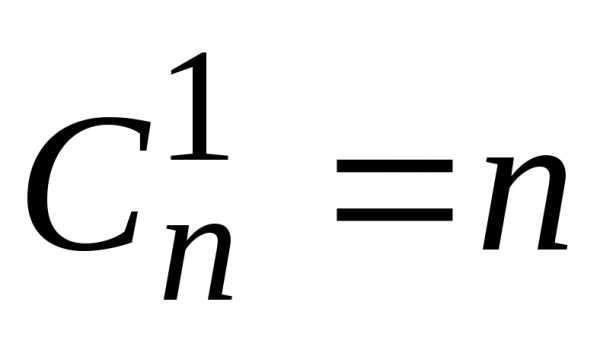 ;
;
4) 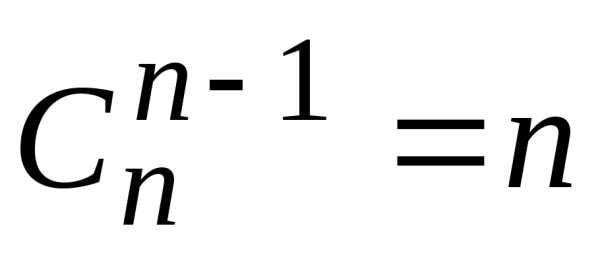 ;
5)
;
5)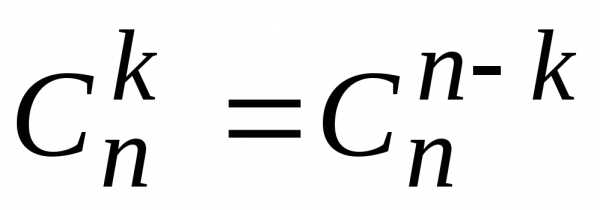 ;
6)
;
6)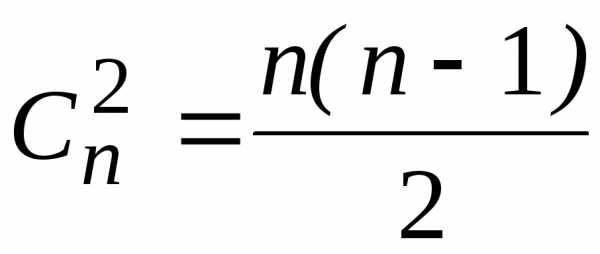 .
.
Пример. В урне 7 шаров. Из них 3 белых. Наугад выбирают 3 шара. Сколькими способами это можно сделать? В скольких случаях среди них будет ровно один белый.
Всего способов
.
Чтобы получить число способов выбрать
1 белый шар (из 3-х белых) и 2 черных шара
(из 4-х черных), надо перемножить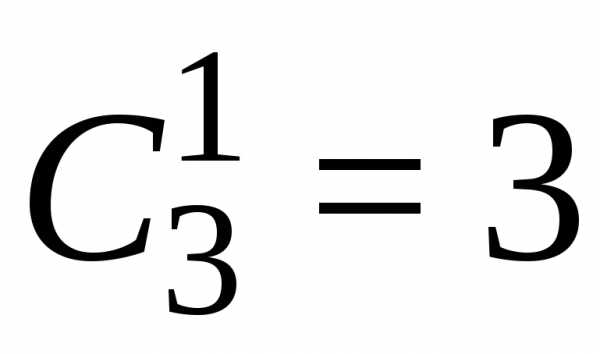 и
и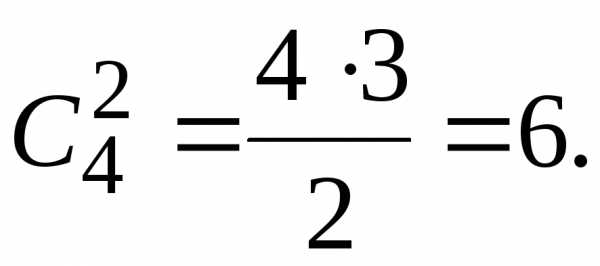 Таким образом искомое количество
способов
Таким образом искомое количество
способов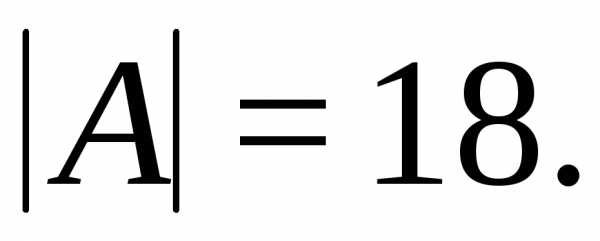
Упражнения
1. Из 35 учащихся класс по итогам года имели “5” по математике – 14 человек; по физике – 15 человек; по химии – 18 человек; по математике и физике – 7 человек; по математике и химии – 9 человек; по физике и химии – 6 человек; по всем трем предметам – 4 человек. Сколько человек имеют “5” по указанным предметам? Сколько человек не имеет “5” по указанным предметам? Имеет “5” только по математике? Имеет “5” только по двум предметам?
2. В группе из 30 студентов каждый знает, по крайней мере, один иностранный язык – английский или немецкий. Английский знают 22 студента, немецкий – 17. Сколько студентов знают оба языка? Сколько студентов знают немецкий язык, но не знают английский?
3. В 20 комнатах общежития института Дружбы Народов живут студенты из России; в 15 – из Африки; в 20 – из стран Южной Америки. Причем в 7 – живут россияне и африканцы, в 8 – россияне и южноамериканцы; в 9 – африканцы и южноамериканцы; в 3 – и россияне, и южноамериканцы, и африканцы. В скольких комнатах живут студенты: 1) только с одного континента; 2) только с двух континентов; 3) только африканцы.
4. Каждый из 500 студентов обязан посещать хотя бы один из трех спецкурсов: по математике, физике и астрономии. Три спецкурса посещают 10 студентов, по математике и физике – 30 студентов, по математике и астрономии – 25; спецкурс только по физике – 80 студентов. Известно также, что спецкурс по математике посещают 345 студентов, по физике – 145, по астрономии – 100 студентов. Сколько студентов посещают спецкурс только по астрономии? Сколько студентов посещают два спецкурса?
5. Староста курса представил следующий отчет по физкультурной работе. Всего – 45 студентов. Футбольная секция – 25 человек, баскетбольная секция – 30 человек, шахматная секция – 28 человек. При этом, 16 человек одновременно посещают футбольную и баскетбольную секции, 18 – футбольную и шахматную, 17 – баскетбольную и шахматную, 15 человек посещают все три секции. Объясните, почему отчет не был принят.
6. В аквариуме 11 рыбок. Из них 4 красных, остальные золотые. Наугад выбирают 4 рыбки. Сколькими способами это можно сделать? Найти число способов сделать это так, чтобы среди них будет: 1) ровно одна красная; 2) ровно 2 золотых; 3) хотя бы одна красная.
7. В списке 8 фамилий. Из них 4 – женские. Сколькими способами их можно разделить на две равные группы так, чтоб в каждой была женская фамилия?
8. Из колоды в 36 карт выбирают 4 . Сколько способов сделать это так, чтобы: 1) все карты были разных мастей; 2) все карты были одной масти; 3) 2 красные и 2 черные.
9. На карточках разрезной азбуки даны буквы К, К, К, У, У, А, Е, Р. Сколько способов сложить их в ряд так, что бы получилось «кукареку».
10. Даны карточки разрезанной азбуки с буквами О, Т, О, Л, О, Р, И, Н, Г, О, Л, О, Г. Сколько способов сложить их так, что бы получилось слово «отолоринголог».
11. Даны карточки нарезной азбуки с буквами Л, И, Т, Е, Р, А, Т, У, Р, А. Сколько способов сложить их в ряд так, что бы получилось слово «литература».
12. 8 человек становятся в очередь. Сколько способов сделать это так, что бы два определенных человека А и Б оказались: 1) рядом; 2) на краях очереди;
13. 10 человек садятся за круглый стол на 10 мест. Сколькими способами это можно сделать так, чтоб рядом оказались: 1) два определенных человека А и Б; 2) три определенных человека А, Б и С.
14. Из 10 арабских цифр составляют 5-значный код. Сколькими способами это можно сделать так, чтобы: 1) все цифры были разными; 2) на последнем месте четная цифра.
15. Из 26 букв латинского алфавита (среди них 6 гласных) составляется шестибуквенное слово. Сколькими способами это можно сделать так, чтобы в слове были: 1) ровно одна буква «а»; 2) ровно одна гласная буква; ровно две буквы «а»; в) ровно две гласные.
16. Сколько четырехзначных чисел делятся на 5?
17. Сколько четырехзначных чисел с различными цифрами делятся на 25?
19. Брошены 3 игральные кости. В скольких случаях выпала: 1) ровно 1 «шестерка»; 2) хотя бы одна «шестерка».
20. Брошены 3 игральные кости. В скольких случаях будет: 1) все разные; 2) ровно два одинаковых числа очков.
21. Сколько слов с различными буквами можно составить из алфавита а, в, с, d. Перечислить их все в лексикографическом порядке: abcd, abcd….
studfiles.net
Сочетания с повторением
Пусть имеется множество N из n элементов. Всевозможные неупорядоченные подмножества из m элементов, составленные так, что любой элемент множества N может входить в эти подмножества от 1 до m раз, либо вообще отсутствовать, называются сочетаниями с повторением. Их число подсчитывают по формуле:
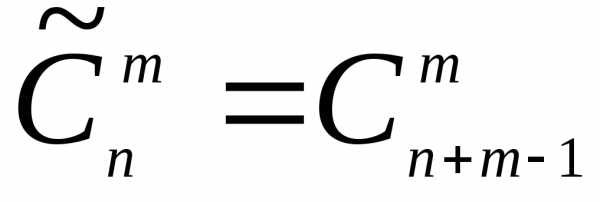
Пример 4. Сколько существует различных прямоугольных параллелепипедов, длина каждого ребра которых есть любое число от 1 до 10?
Решение: Всякий параллелепипед определяется тремя взаимно перпендикулярными ребрами и не зависит от их порядка. Тогда применима формула числа сочетаний с повторением: .
Перестановки с повторением
Пусть дано множество X = {x1, x2, …, xr}. Составим кортеж длиной n, в который элемент x1 входит n1 раз, x2 – n2 раза,…, xr — nr раз. Назовем составом этого кортежа новый кортеж (n1, n2, …, nr). Кортежи данного состава называют перестановками с повторением из n1 элементов х1, n2 элементов х2,…, nr элементов xr. Их число выражается формулой
,
где .
Лекция 2. Пространство элементарных событий. Классическое определение вероятности
Реализация некоторой совокупности условий называется испытанием, а результат испытания – событием. События будем обозначать большими латинскими буквами A, B, C, D,… Все события делят на три вида: достоверные, невозможные и случайные.
Достоверным называется событие, которое обязательно произойдет при выполнении данного комплекса условий.
Пример 1. При бросании игральной кости выпало число очков не более 6 – есть достоверное событие.
Невозможным называется событие, которое заведомо не произойдет, если будут выполнены данные условия.
Пример 2. При бросании игральной кости выпало число очков равное 8 – есть событие невозможное.
Случайным называется событие, которое может произойти или не произойти при выполнении данного комплекса условий.
Пример 3. При бросании игральной кости выпало 5 очков – это случайное событие.
Каждое случайное событие зависит от многих причин, но законы воздействия некоторых из них на конечный результат, как правило, неизвестны. Так, результат бросания монеты зависит от силы бросания, вращающего момента, ровности поверхности и т. д.
Поэтому заранее предугадать исход отдельного испытания невозможно, да этого и не требуется на практике. Например, для анализа деятельности предприятия неважно, является ли конкретная деталь стандартной или нет. Гораздо важнее знать, как часто встречается брак в выпускаемых изделиях. Или, при посеве семян, важно знать какой процент семян взойдет. Результат отдельного испытания для отдельного зернышка никакой практической ценности не имеет.
В рассмотренных примерах, во-первых, мы имеем дело с так называемыми массовыми испытаниями, которые состоят из повторения большого числа подобных между собой единичных испытаний, при соблюдении определенных условий их проведения. Во-вторых, в этих массовых однородных испытаниях мы не пытаемся предсказать исход отдельного испытания.
Массовые однородные случайные события, наступающие в результате описанных испытаний, подчиняются определенным закономерностям, которые называют вероятностными законами.
Предметом теории вероятностей является изучение закономерностей массовых, однородных, случайных событий.
studfiles.net
§2. Комбинаторика без повторений.
Для построения соответствующих математических моделей комбинаторных задач будем использовать математический аппарат теории множеств. Может случиться, что в данном множестве порядок следования элементов не важен, а важен только состав множества. Но есть задачи, в которых прядок элементов является существенным.
Определение
1: Порядок во множестве 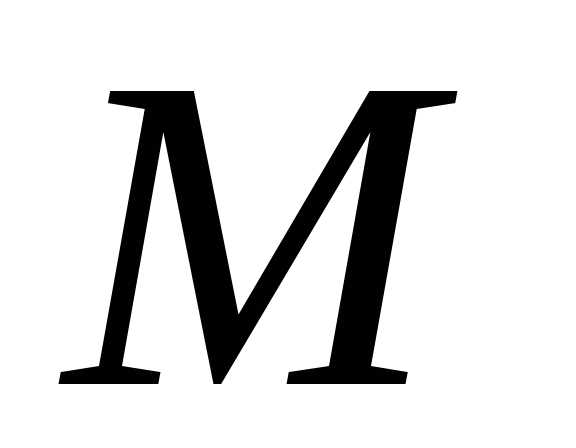 из
из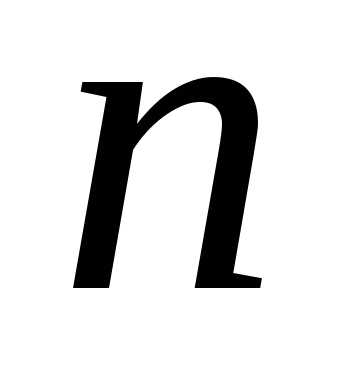 элементов – это нумерация его элементов
натуральными числами, т.е. отображение
множества
элементов – это нумерация его элементов
натуральными числами, т.е. отображение
множества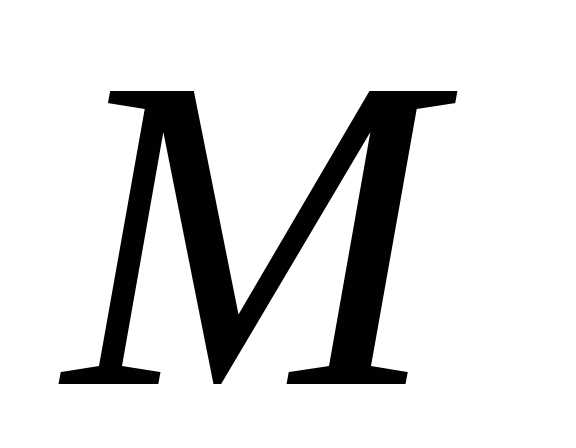 на множество
на множество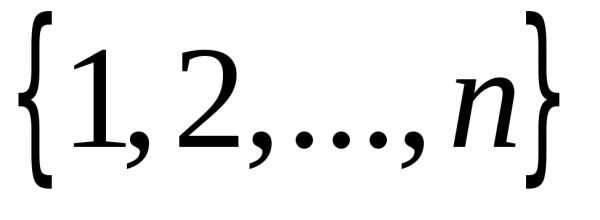 .
.
Определение 2: Множество с заданным на нем порядком называется упорядоченным множеством.
Очевидно, что множество, содержащее более одного элемента, можно упорядочить не единственным способом.
Например,
из двух букв  и
и можно построить упорядоченное множество
двумя различными способами:
можно построить упорядоченное множество
двумя различными способами:
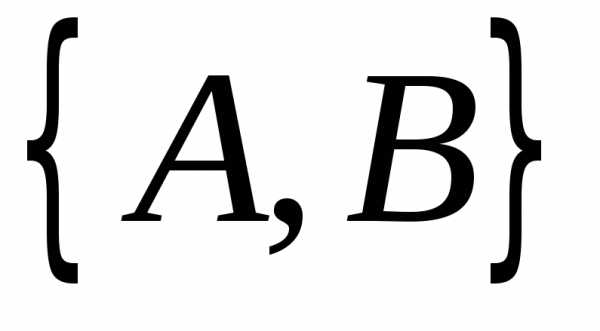 и
и 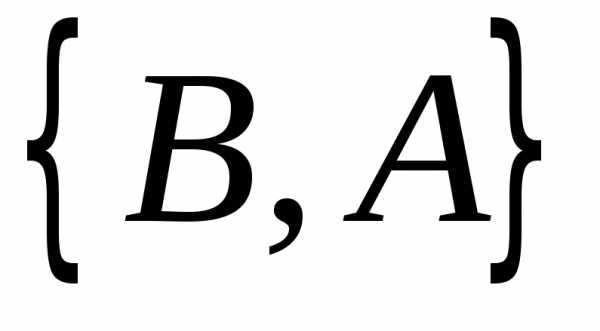 .
.
Три
буквы  ,
, и
и можно расположить в виде последовательности
шестью способами:
можно расположить в виде последовательности
шестью способами:
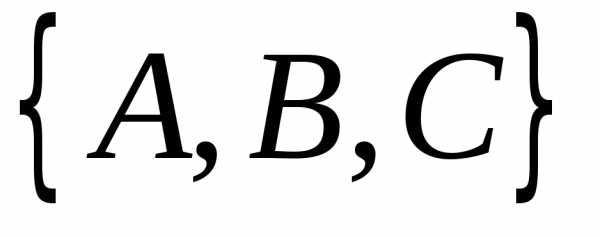 ,
, 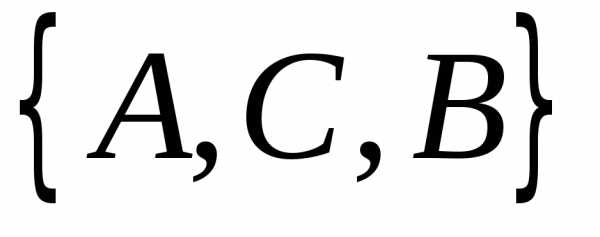 ,
,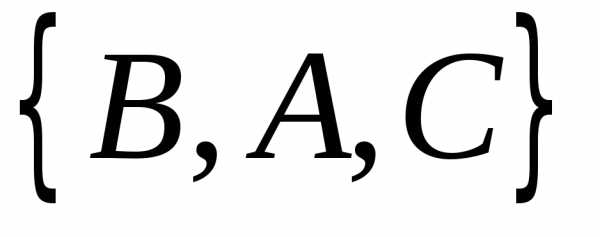 ,
,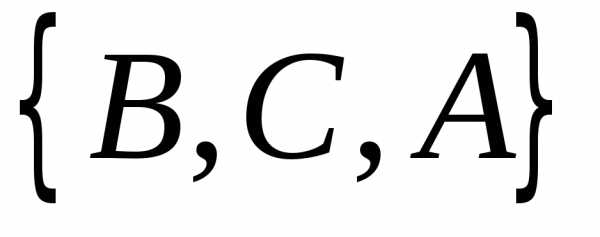 ,
,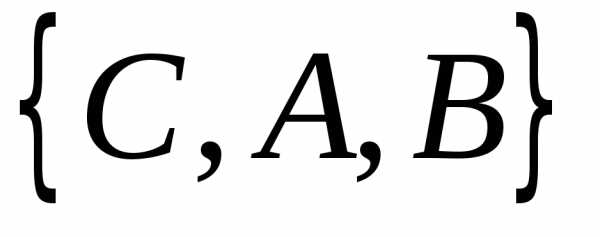 ,
,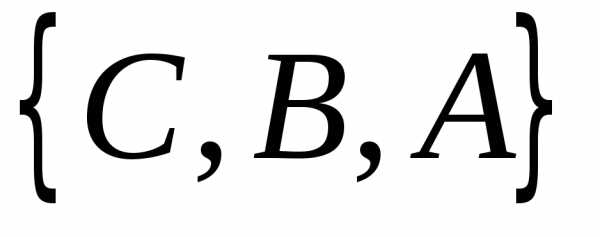 .
.
Для четырех букв путем перебора получим уже 24 различных упорядоченных последовательностей.
Упорядоченные последовательности элементов некоторого множества можно рассматривать как распределения или расстановки этих элементов в последовательности.
Определение
3: Пусть
дано конечное множество 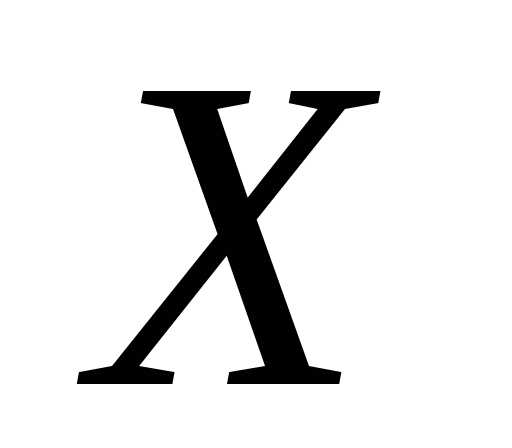 из
из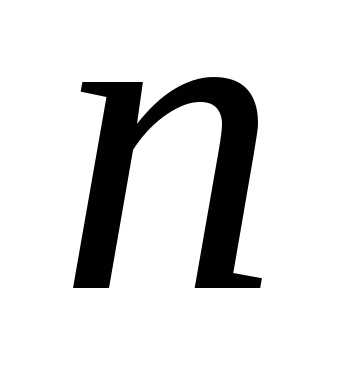 элементов. Всякий набор из
элементов. Всякий набор из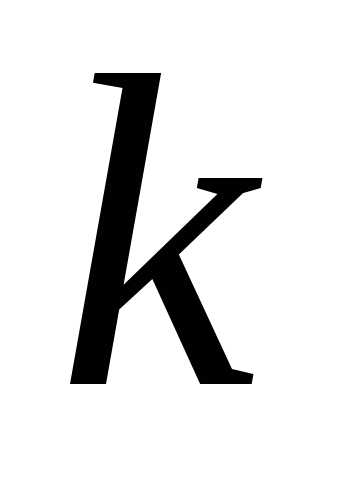 элементов данного множества (при этом
элементы в наборе могут и повторяться)
будем называть
элементов данного множества (при этом
элементы в наборе могут и повторяться)
будем называть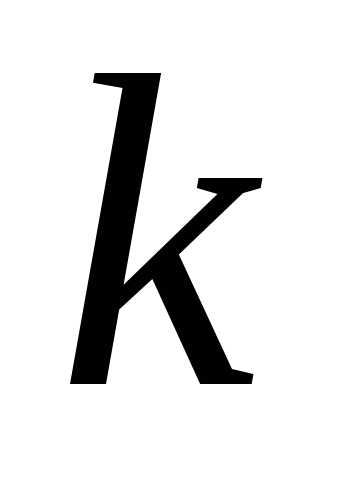 —расстановками.
—расстановками.
Через понятие расстановки вводятся основные определения комбинаторики: сочетания, размещения и перестановки. При этом каждое из этих понятий может быть с повторениями и без повторений. В данном параграфе будут рассмотрены комбинаторные формулы без повторений.
Перестановки без повторений.
Определение
4: Пусть
— конечное множество из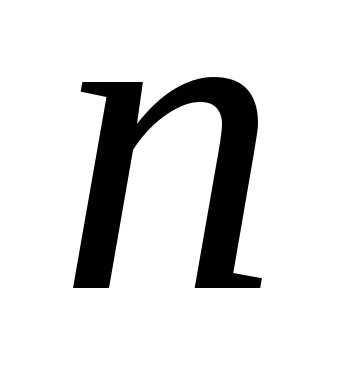 элементов.Перестановками из
элементов.Перестановками из 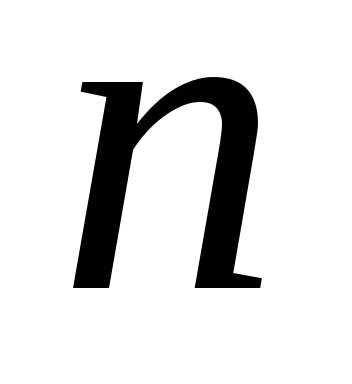 различных элементов множества
различных элементов множества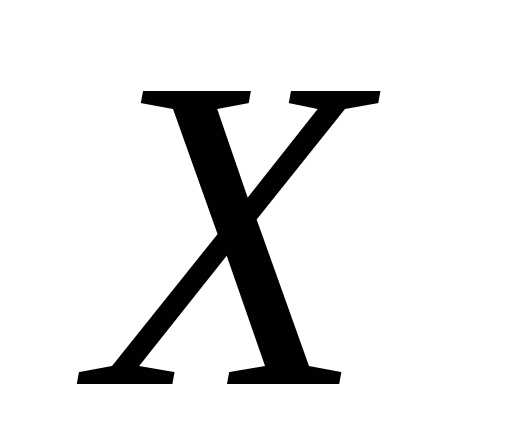 называются все расположения
называются все расположения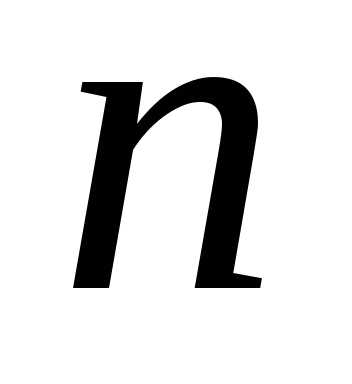 элементов в определенном порядке.
Обозначается:
элементов в определенном порядке.
Обозначается: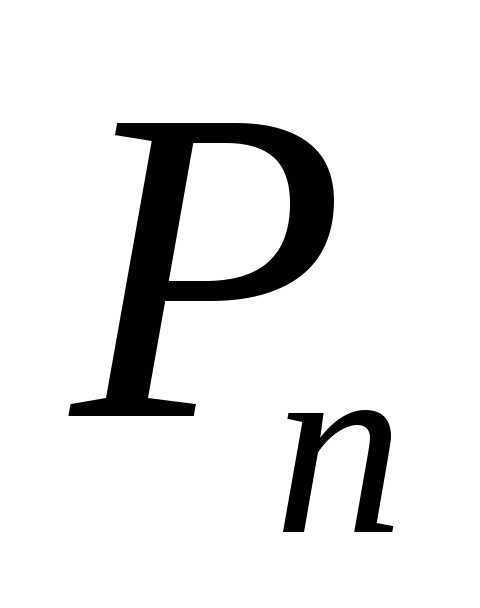 (от французского словаpermutation — перестановка).
(от французского словаpermutation — перестановка).
Упорядоченные множества считаются различными, если они отличаются либо своими элементами, либо их порядком.
Определение 5: Различные упорядоченные множества, которые отличаются лишь порядком элементов, называются перестановками этого множества.
Последнее определение сформулировано с позиции теории множеств.
Определение
6: Произведение 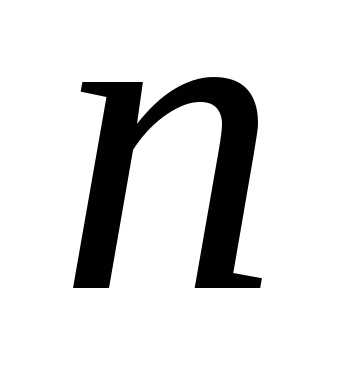 последовательных натуральных чисел в
математике обозначают
последовательных натуральных чисел в
математике обозначают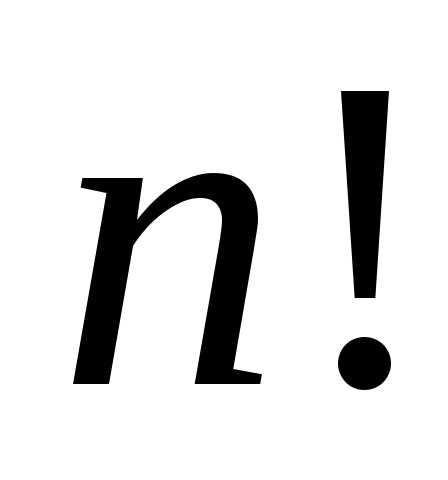 и называютфакториалом.
и называютфакториалом.
Выбор
для обозначения 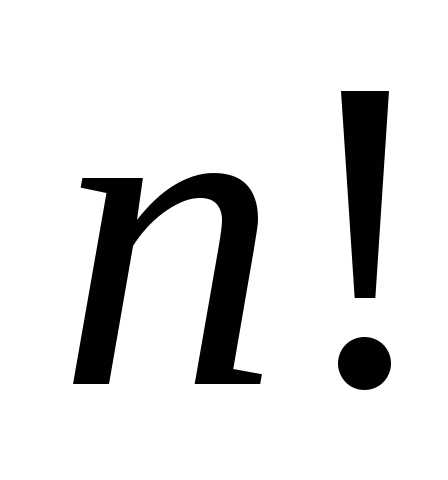 восклицательного знака, возможно, связан
с тем, что даже для сравнительно небольших
значений
восклицательного знака, возможно, связан
с тем, что даже для сравнительно небольших
значений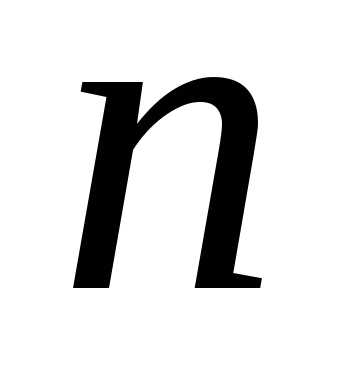 число
число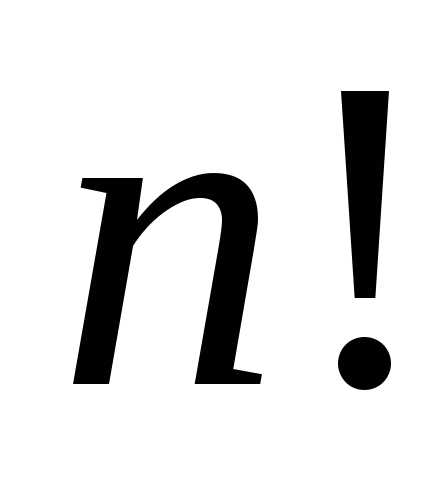 очень велико. Например,
очень велико. Например,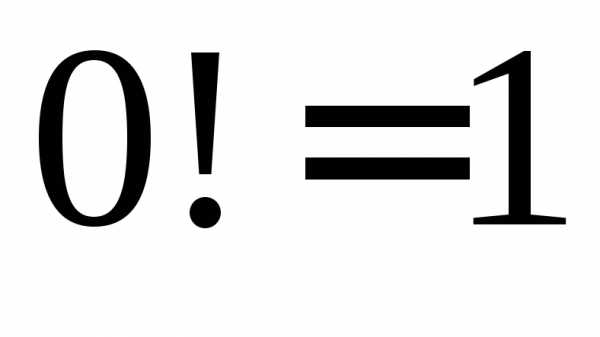 ,
,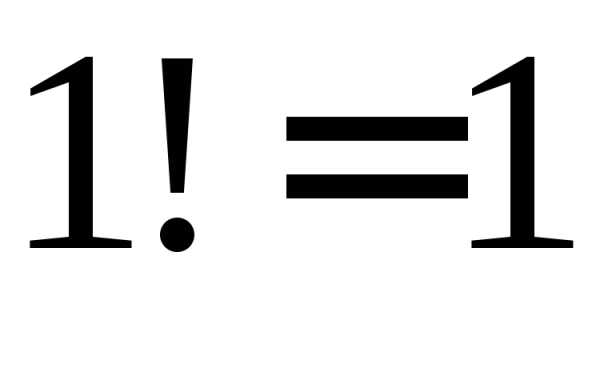 ,,,,,и т.д.
,,,,,и т.д.
Теорема
1: Число
перестановок из 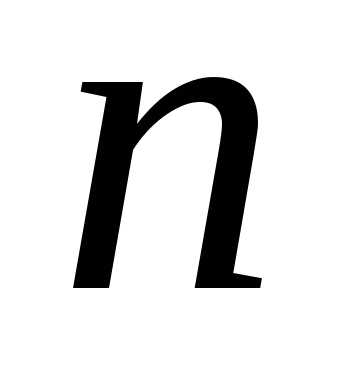 различных элементов вычисляется по
формуле:
различных элементов вычисляется по
формуле:
(1)
Доказательство. Рассмотрим произвольное множество из 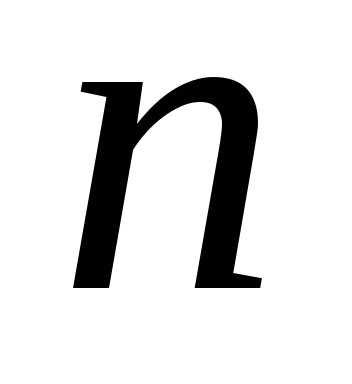 элементов. Построим всевозможные
расстановки из этих
элементов. Построим всевозможные
расстановки из этих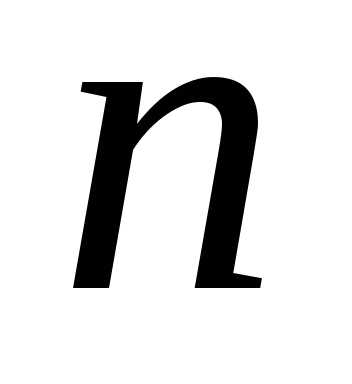 элементов.
На первое
место
расстановки можно поставить любой из
элементов.
На первое
место
расстановки можно поставить любой из 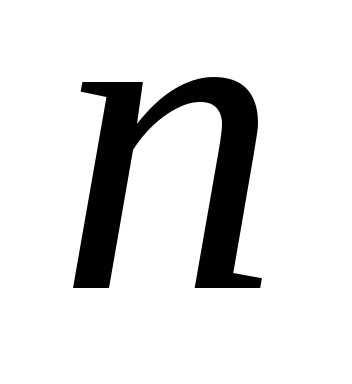 элементов (
элементов (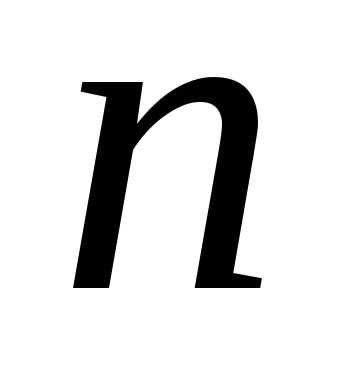 способов выбора первого элемента). После
того, как первый элемент выбран и
независимо как он выбран, второй элемент
можно выбрать
способов выбора первого элемента). После
того, как первый элемент выбран и
независимо как он выбран, второй элемент
можно выбрать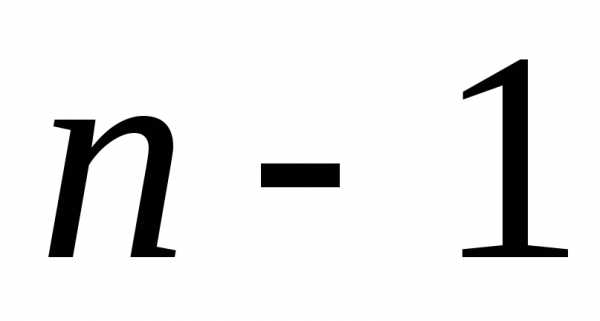 способом. Для выбора третьего элемента
остается
способом. Для выбора третьего элемента
остается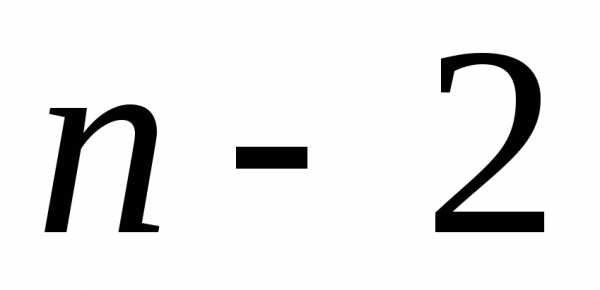 способа и т.д. Последний элемент выбирается
соответственно одним способом. Тогда,
в силу комбинаторного принципа умножения,
количество таких расстановок будет
равно:
способа и т.д. Последний элемент выбирается
соответственно одним способом. Тогда,
в силу комбинаторного принципа умножения,
количество таких расстановок будет
равно:
Теорема доказана.
Пример 1: Сколькими способами трое друзей могут занять в кинотеатре места с номерами 1, 2 и 3.
Решение. Количество искомых способов будет равно числу перестановок без повторений из трех элементов: способов. При необходимости эти способы можно перебрать.
Перестановки букв некоторого слова называют анаграммами. Открытые еще в ІІІ веке до нашей эры греческим грамматиком Ликофроном анаграммы до сих пор привлекают внимание языковедов, поэтов и любителей словесности. Мастера словесных игр помимо эрудиции и большого запаса слов знают много секретов, связанных с комбинаторными навыками, один из которых – анаграммы. Часто требуется среди всех перестановок выбрать те, которые обладают определенным свойством. Например, среди анаграмм слова «крот», которых всего , только одна, не считая самого слова«крот», имеет смысл в русском языке – «корт».
Кроме линейных перестановок, можно рассматривать перестановки круговые (или циклические). В этом случае перестановки, переходящие друг в друга при вращении, считаются одинаковыми и не должны засчитываться.
Теорема
2: Число
круговых перестановок из 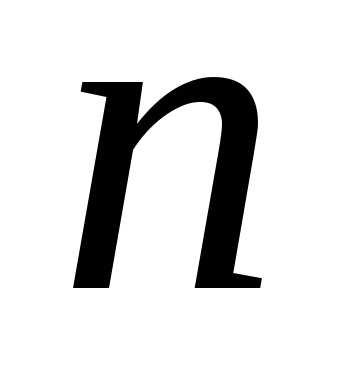 различных элементов равно
различных элементов равно
Пример 2: Сколькими способами 7 детей могут стать в хоровод?
Решение. Число линейных перестановок 7 детей
будет равно 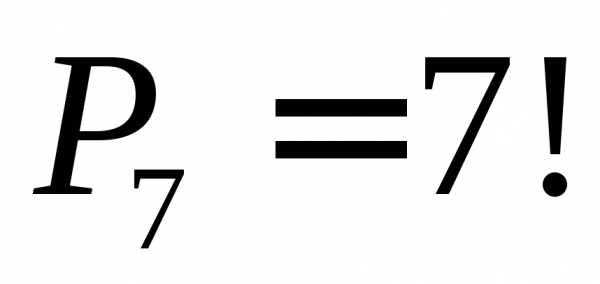 .
Если хоровод уже сформирован, тогда для
него существует 7 круговых перестановок,
переходящих друг в друга при повороте.
Эти перестановки не должны быть засчитаны,
поэтому круговых перестановок из 7
элементов будет
.
Если хоровод уже сформирован, тогда для
него существует 7 круговых перестановок,
переходящих друг в друга при повороте.
Эти перестановки не должны быть засчитаны,
поэтому круговых перестановок из 7
элементов будет .
.
Размещения без повторений.
Определение
7: Пусть
имеется 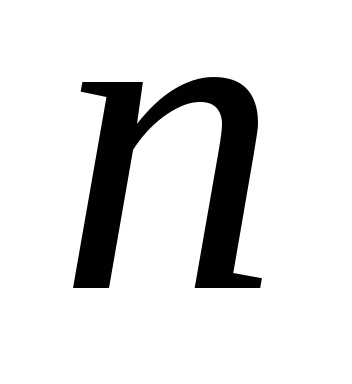 различных предметов. Расстановки из
различных предметов. Расстановки из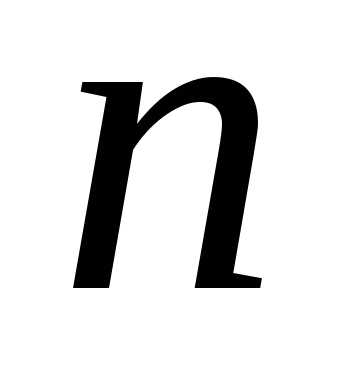 элементов по
элементов по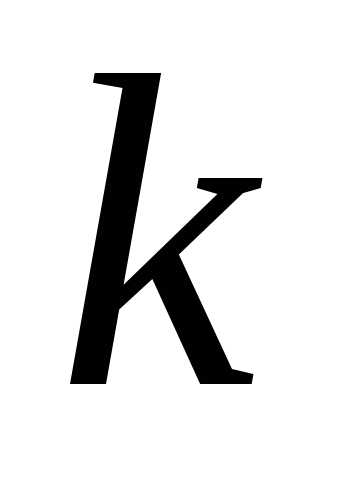 элементов (
элементов ( )
называютсяразмещениями
без повторений.
Обозначают:
)
называютсяразмещениями
без повторений.
Обозначают: 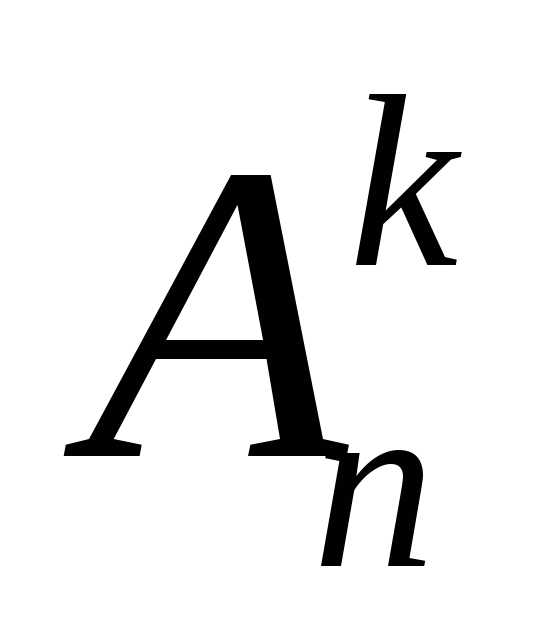 .
Здесь имеется в виду, что элементы в
расстановках не повторяются.
.
Здесь имеется в виду, что элементы в
расстановках не повторяются.
В данном определении существенной является следующая позиция: две расстановки различны, если они отличаются хотя бы одним элементом или порядком элементов.
Приведем еще одно определение размещений, эквивалентное исходному, более простое для понимания.
Определение 8: Конечные упорядоченные множества называются размещениями.
Теорема
3: Количество
всех размещений из 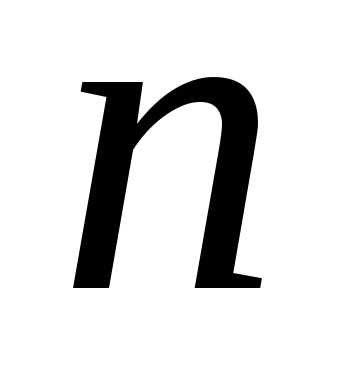 элементов по
элементов по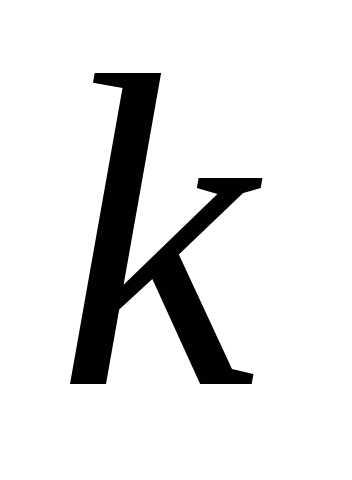 элементов без повторений вычисляется
по формуле:
элементов без повторений вычисляется
по формуле:
. (2)
Доказательство. Пусть имеется произвольное множество 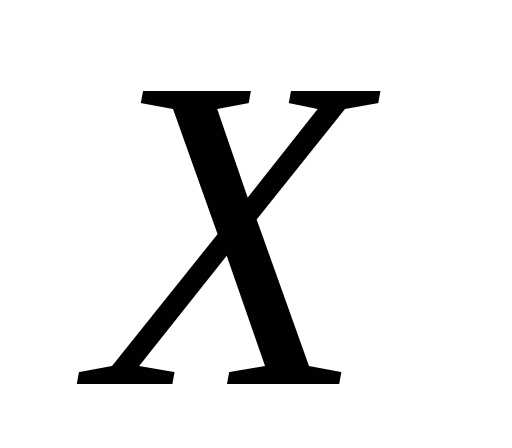 ,
состоящее из
,
состоящее из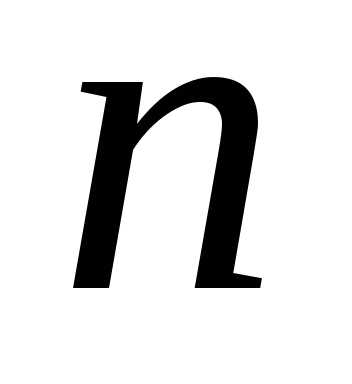 элементов. Необходимо выбрать из этого
множества
элементов. Необходимо выбрать из этого
множества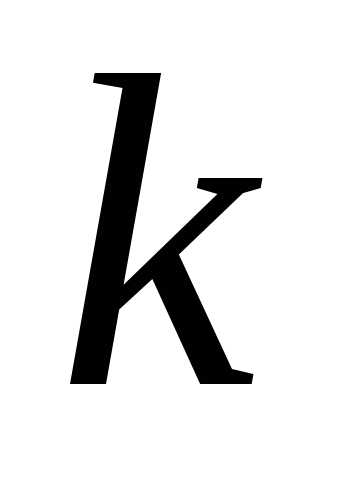 различных элементов. Причем, важен
порядок выбора.
различных элементов. Причем, важен
порядок выбора.
Выбор
элементов осуществляется поэтапно.
Первый элемент расстановки можно выбрать 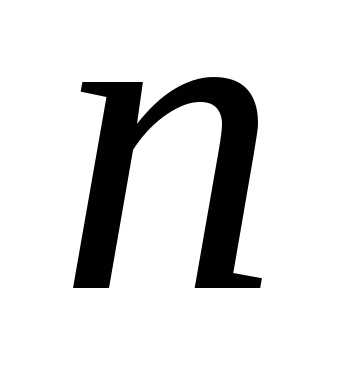 различными способами. Тогда из оставшихся
элементов множества
различными способами. Тогда из оставшихся
элементов множества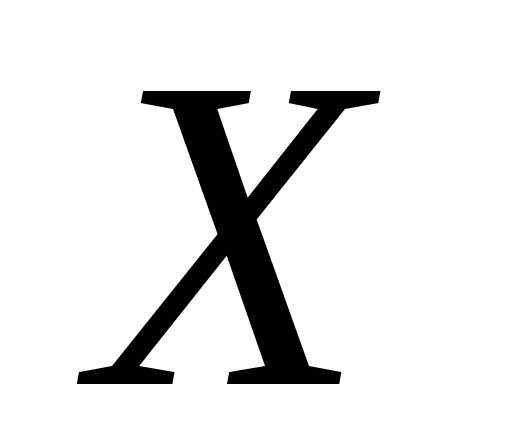 второй элемент расстановки выбирается
второй элемент расстановки выбирается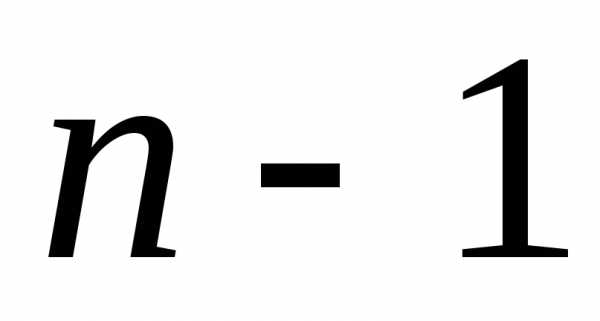 способом. Для выбора третьего элемента
возможно
способом. Для выбора третьего элемента
возможно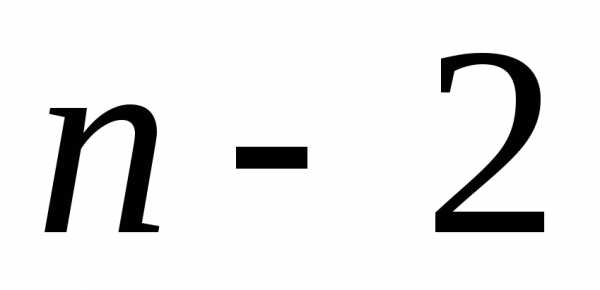 способа и т.д. Тогда для выбора
способа и т.д. Тогда для выбора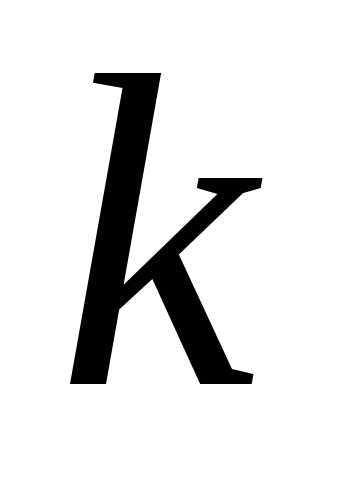 —
го элемента имеемспособ. Следовательно, согласно правилу
умножения, количество таких расстановок
будет равно:
—
го элемента имеемспособ. Следовательно, согласно правилу
умножения, количество таких расстановок
будет равно:
.
По определению, такие расстановки являются размещениями. Что и требовалось доказать.
Пример 3: Собрание из 25 человек выбирает президиум из 3 человек: 1) председатель, 2) заместитель, 3) секретарь. Сколько возможно вариантов выбора президиума?
Решение. Выбирая трех человек из 25, замечаем, что важен порядок выбора, поэтому количество президиумов будет равно:
.
Замечание: Число размещений без повторений можно также находить по формуле:
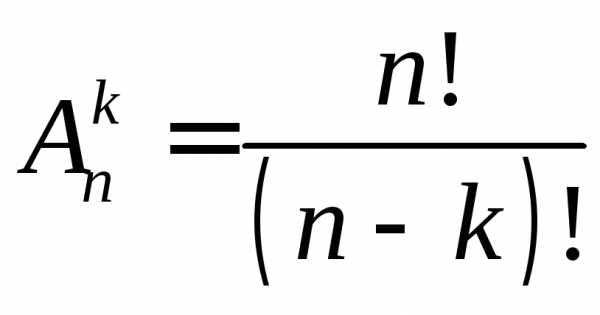 . (3)
. (3)
Если
в знаменателе дроби из формулы (3) 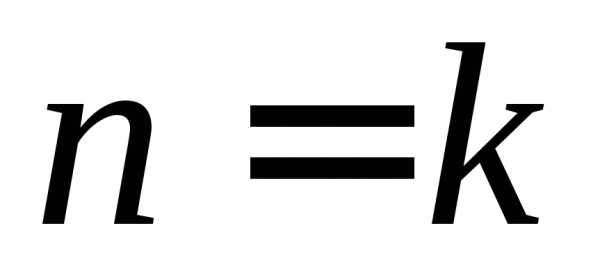 ,
то принято считать
,
то принято считать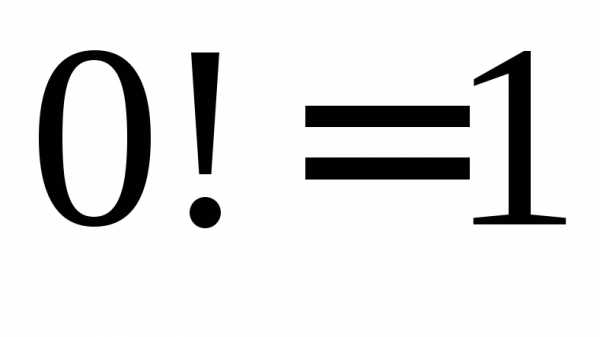 .
.
Замечание: Формула (3) отличается компактностью, но при решении задач удобнее использовать формулу (2). Дробь, стоящая в правой части формулы (3), может быть сокращена до целого числа. Это число равно числу из правой части формулы (2).
Пример 4: Сколько можно составить двухбуквенных слов (буквы не повторяются) из 33 букв русского алфавита?
Решение. В данном случае мы имеем дело не со словами в лингвистическом понимании, а с буквенными комбинациями произвольного состава.
Тогда количество различных комбинаций из 2 букв, выбранных из 33 букв алфавита, будет равно:
.
В данном случае важен порядок букв. Если поменять 2 буквы в слове, то получим новое слово.
Замечание: Перестановка без повторений – это
частный случай размещений без повторений
при 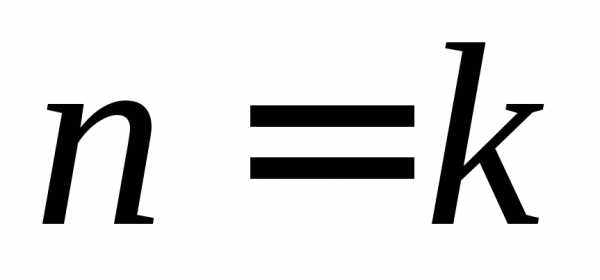 .
Можно сказать, что перестановка из
.
Можно сказать, что перестановка из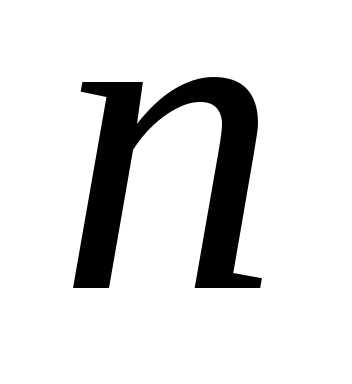 элементов – это размещение из
элементов – это размещение из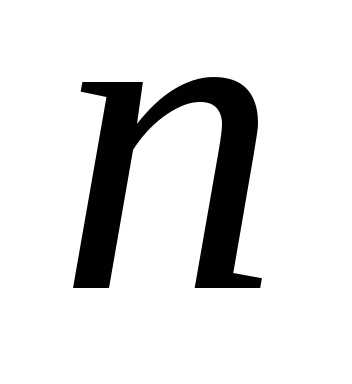 элементов по
элементов по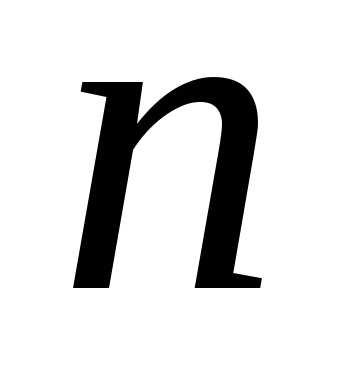 элементов:
элементов:
В некоторых задачах по комбинаторике не имеет значения порядок расположения объектов в той или иной совокупности. Важно лишь то, какие именно элементы ее составляют. В таких ситуациях мы имеем дело с сочетаниями.
Сочетания без повторений.
Определение
9: Сочетания без
повторений из 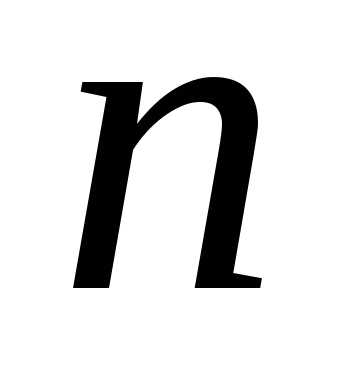 элементов некоторого множества по
элементов некоторого множества по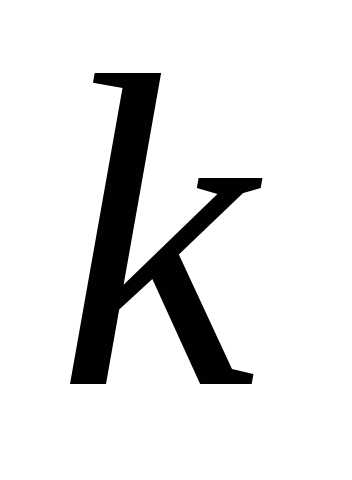 элементов (
элементов ( )
– это расстановки, отличающиеся друг
от другасоставом,
но не порядком элементов. Обозначают:
)
– это расстановки, отличающиеся друг
от другасоставом,
но не порядком элементов. Обозначают: 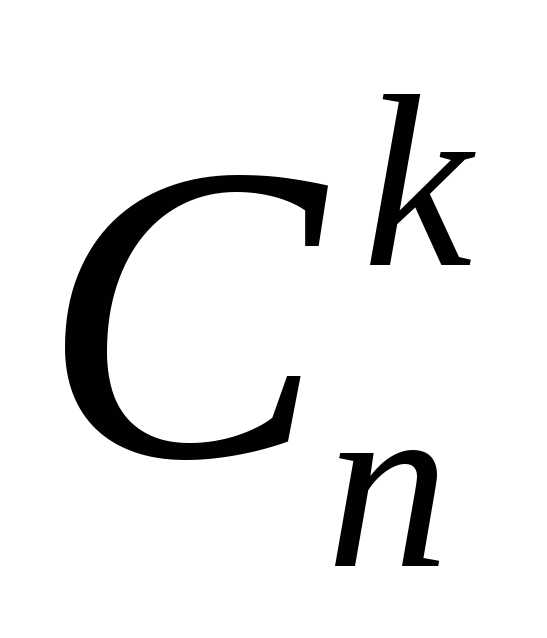 (от французского словаcombinaison – сочетание).
(от французского словаcombinaison – сочетание).
В данном случае в расстановках важен состав, а не порядок элементов в подмножестве. Если две расстановки отличаются только порядком следования элементов, то с точки зрения сочетаний они не различимы. Элементы в этих расстановках не повторяются.
С точки зрения теории множеств определение сочетаний можно сформулировать иначе.
Определение 10: Конечные неупорядоченные множества называются сочетаниями.
Таким образом, сочетания – это такая выборка элементов, при которой их порядок совершенно не важен.
Сочетаний
из 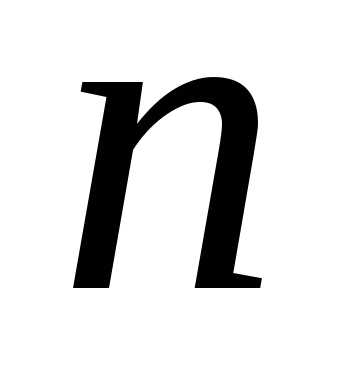 элементов по
элементов по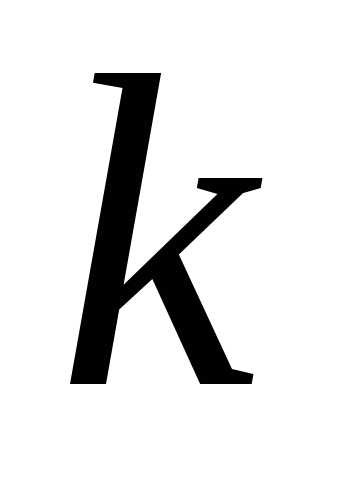 элементов должно быть меньше, чем
соответствующих размещений. Это следует
из того, что не надо засчитывать
расстановки одинакового состава.
элементов должно быть меньше, чем
соответствующих размещений. Это следует
из того, что не надо засчитывать
расстановки одинакового состава.
Теорема
4: Число
сочетаний 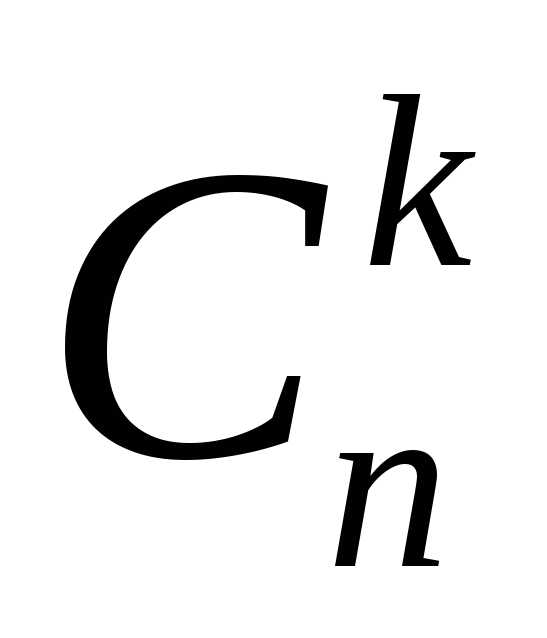 находится по следующей формуле:
находится по следующей формуле:
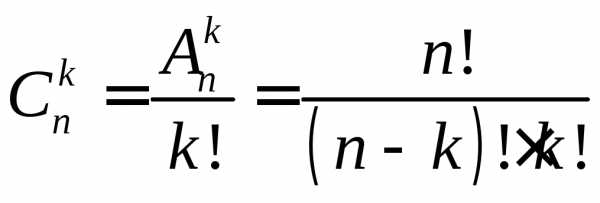 . (4)
. (4)
Доказательство. Если из произвольного 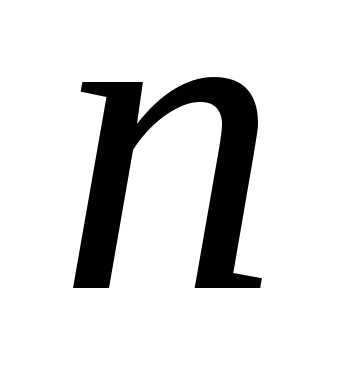 -элементного
множества выбраны
-элементного
множества выбраны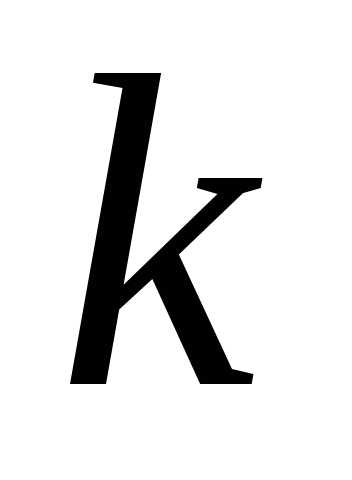 элементов, то их можно пронумеровать
номерами
элементов, то их можно пронумеровать
номерами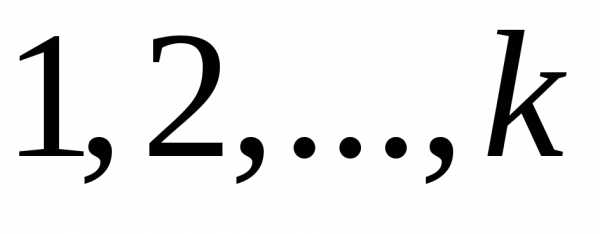 числом способов, равным
числом способов, равным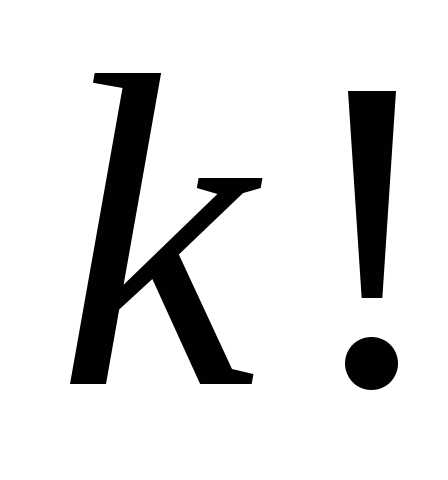 .
Оставшиеся
.
Оставшиеся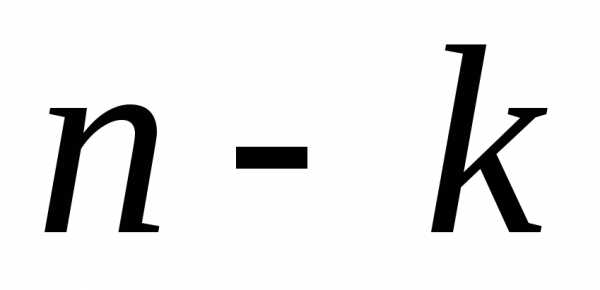 элементов можно занумеровать номерами
элементов можно занумеровать номерами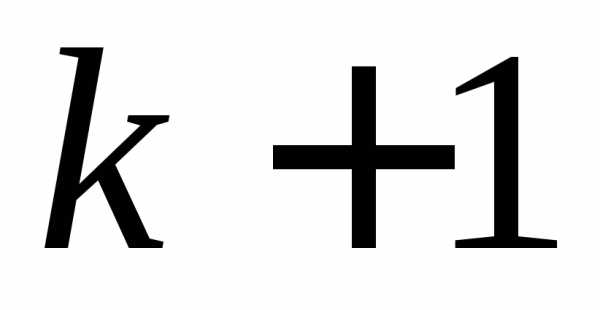 ,
,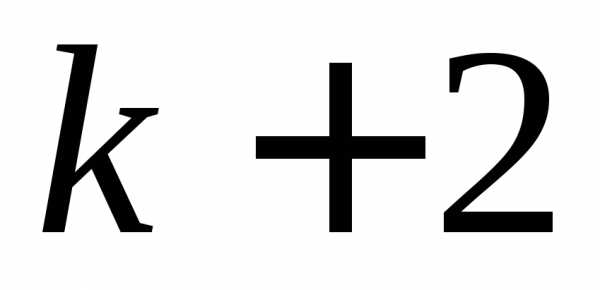 ,
…,
,
…,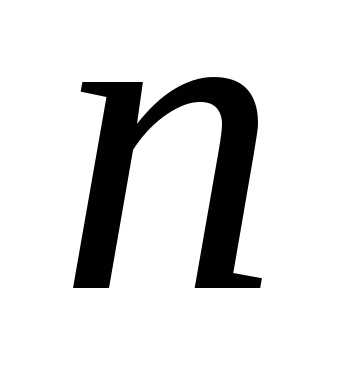 всего
всего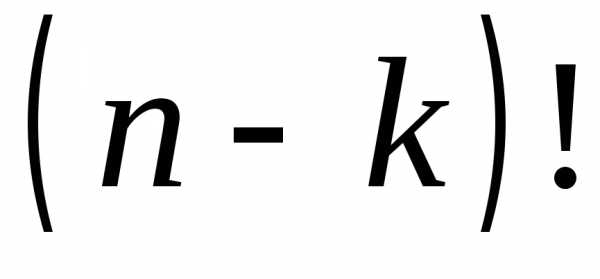 способами. Кроме того, сам отбор
способами. Кроме того, сам отбор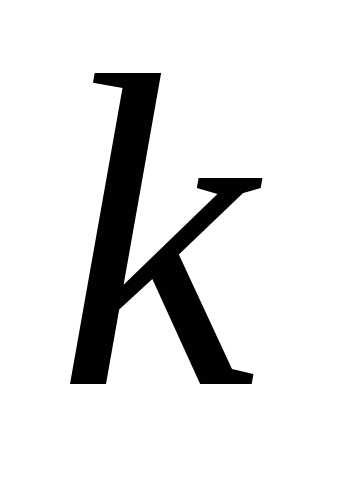 элементов из
элементов из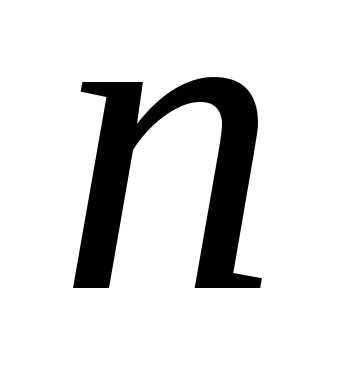 элементов можно осуществить
элементов можно осуществить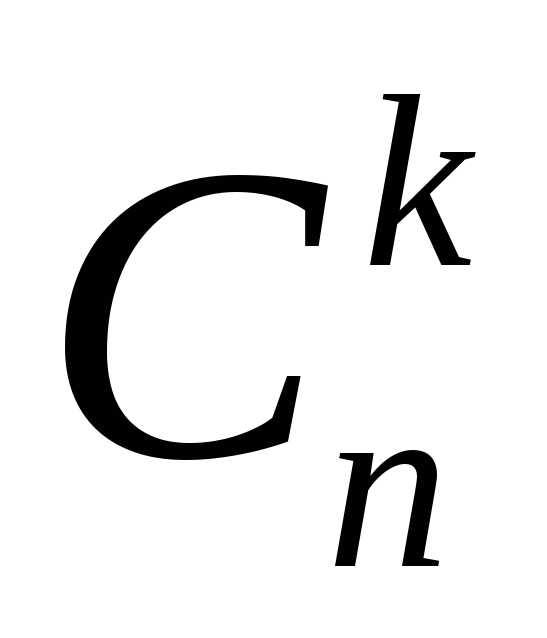 способами. Таким образом, мы получили вариантов нумерации полного множества
из
способами. Таким образом, мы получили вариантов нумерации полного множества
из 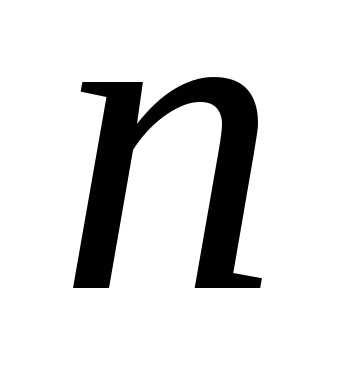 элементов, которых всего
элементов, которых всего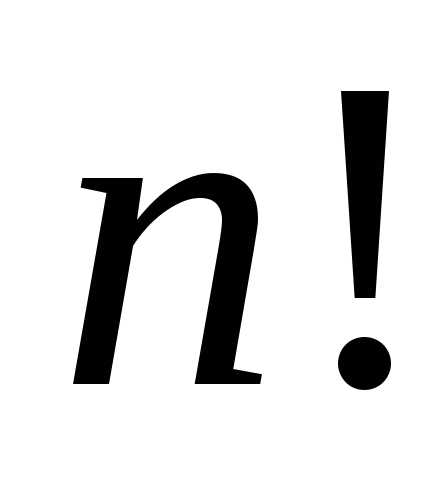 .
Поэтому имеем,
откуда получаем:
.
Поэтому имеем,
откуда получаем:
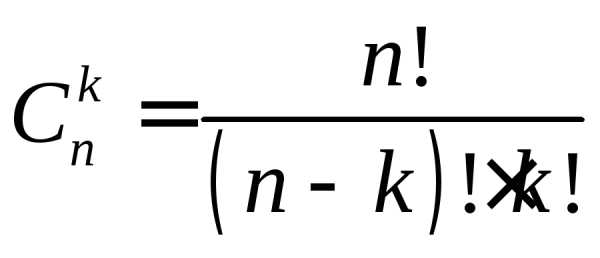 .
.
Теорема доказана.
Замечание: Дробь, стоящая в правой части (4), может быть сокращена до целого числа.
Из формулы числа сочетаний следует:
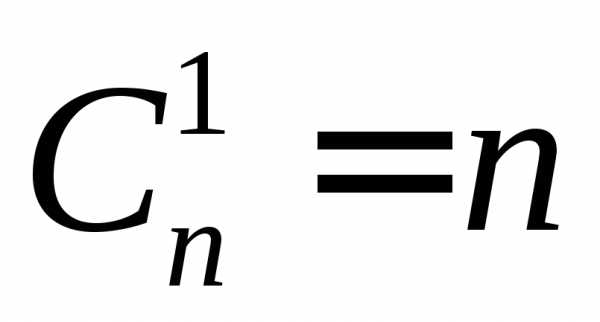 ,
, 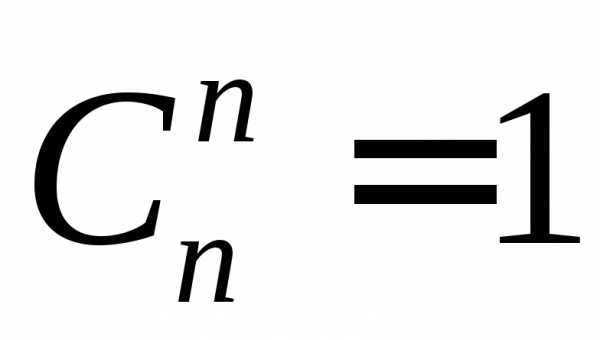 ,
,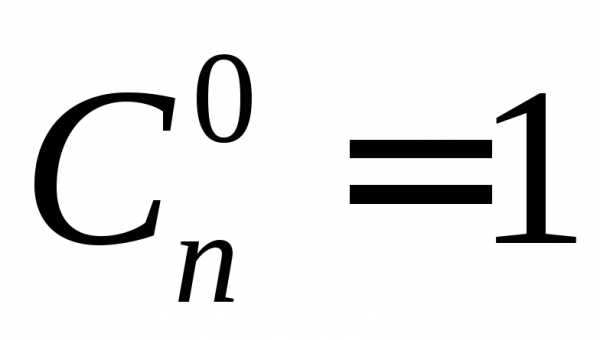 .
.
Формула
(4) может быть преобразована к виду:
.
Отсюда видно, что число размещений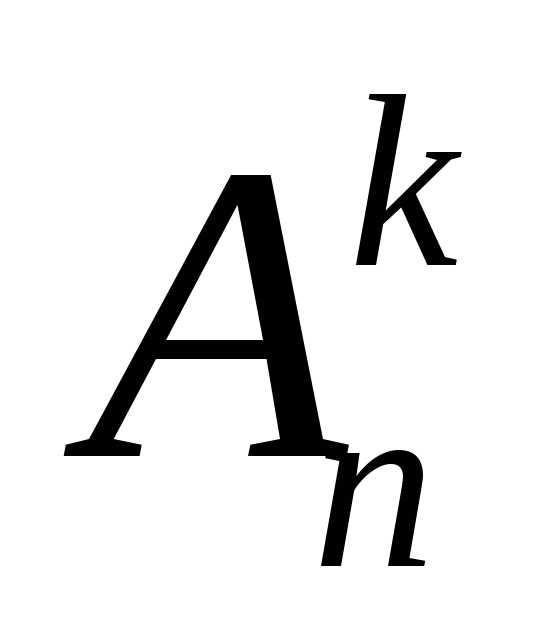 в
в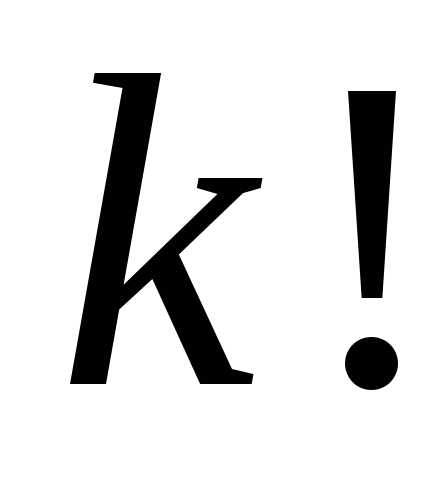 раз больше числа соответствующих
сочетаний
раз больше числа соответствующих
сочетаний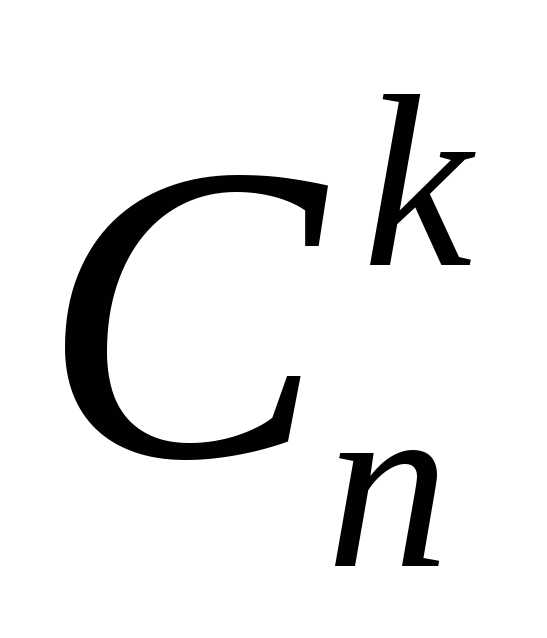 .
Другими словами, чтобы посчитать все
сочетания
.
Другими словами, чтобы посчитать все
сочетания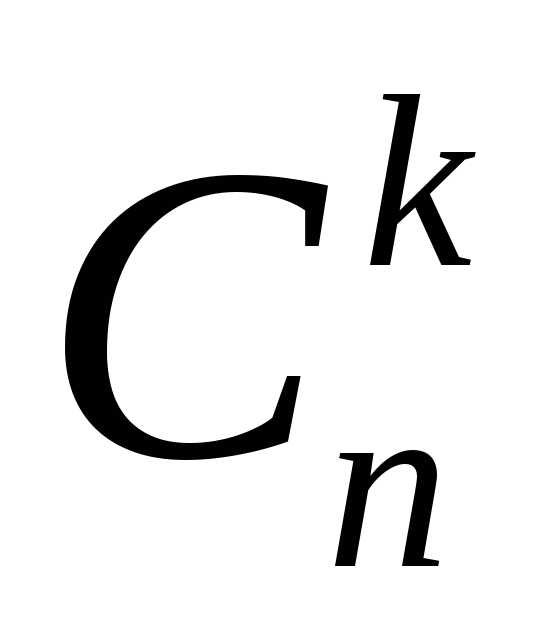 ,
нужно исключить из всех размещений
,
нужно исключить из всех размещений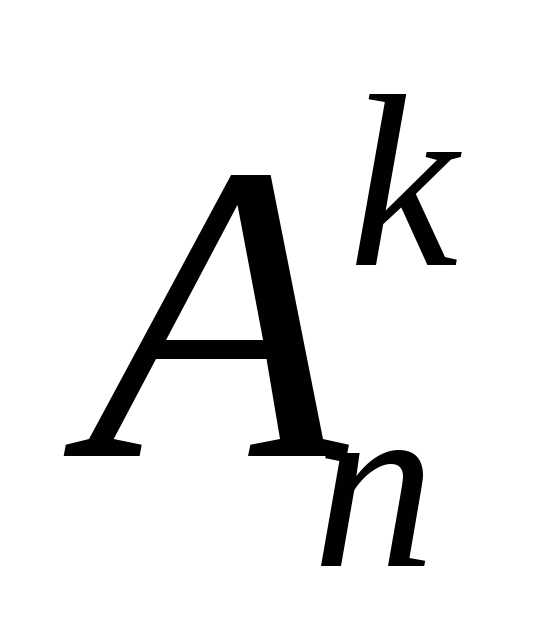 подмножества, отличающиеся порядком
(их будет
подмножества, отличающиеся порядком
(их будет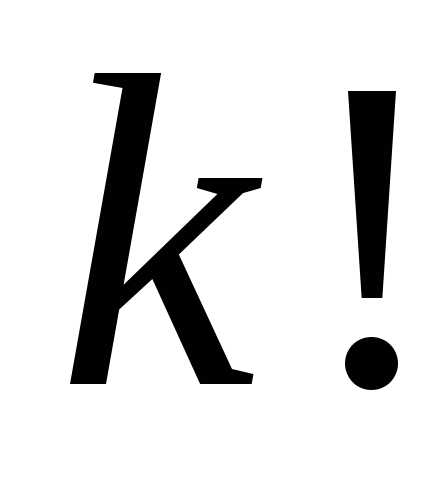 штук), т.е.
штук), т.е.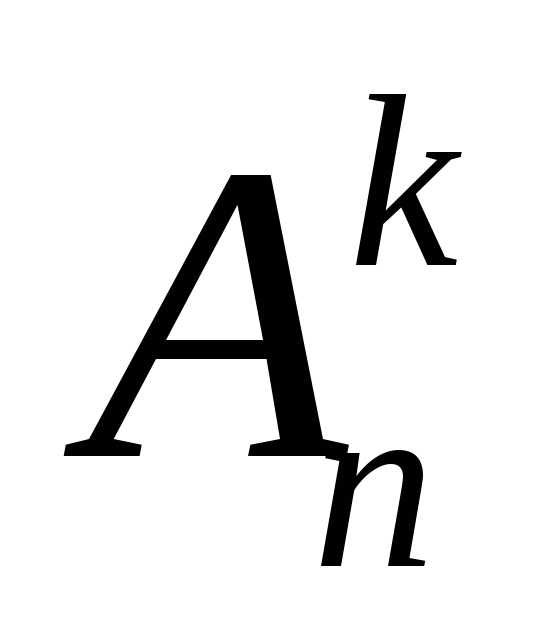 делят на
делят на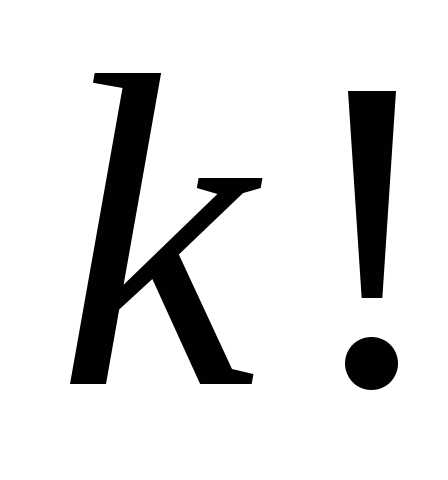 .
.
Пример 5: Сколькими способами можно выбрать 3 различные краски из имеющихся пяти.
Решение. Порядок выбора красок не важен. Важно
только какие краски выбраны. Поэтому
количество вариантов равно: 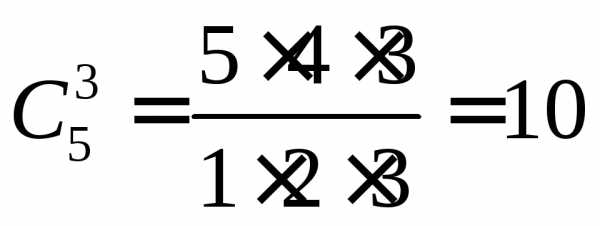 .
.
Пример 6: Сколькими способами можно пошить трехцветные полосатые флаги, если имеется материал пяти различных цветов.
Решение. Порядок выбора полос важен, поэтому количество таких флагов равно: .
studfiles.net
Число сочетаний без повторений
Поиск ЛекцийКОМБИНАТОРИКА
1. Правило суммы.Классическая формулировка
Если элемент можно выбрать k способами, а элемент можно выбрать m способами.
Тогда или можно выбрать k +m способами.
Теорема о мощности объединения множеств (современная формулировка)
Количество элементов объединения двух множеств равно сумме количества элементов в первом и во втором множестве, за вычетом количества элементов их пересечения: .
Причем, если множества не пересекаются, то теорема приобретает вид, аналогичный классической формулировке: .
Для трех множеств теорема имеет вид: .
Пример: Из 35 учащихся класс по итогам года имели “5” по математике – 14 человек; по физике – 15 человек; по химии – 18 человек; по математике и физике – 7 человек; по математике и химии – 9 человек; по физике и химии – 6 человек; по всем трем предметам – 4 человек.
Сколько человек имеют “5” по указанным предметам? Сколько человек не имеет “5” по указанным предметам? Имеет “5” только по математике? Имеет “5” только по двум предметам?
2. Правило произведения. Классическая формулировка
Если элемент можно выбрать k способами, а элемент можно выбрать m способами.
Тогда и можно выбрать km способами.
Теорема о мощности прямого произведения множеств (современная формулировка)
Количество элементов прямого произведения двух множеств равно произведению количества элементов первого и второго множества: .
Пример: Из 3 экземпляров учебника алгебры, 7 экземпляров учебника геометрии и 6 экземпляров учебника физики, надо выбрать комплект, содержащий все учебники по одному разу. Сколькими способами это можно сделать?
Число размещений без повторений
Число размещений без повторений из n по k – это число способов, сколькими можно из n различных элементов построить векторов с k различными координатами.
Число размещений без повторений находится по формуле: .
Пример: Сколькими способами можно построить 3-значное число с различными цифрами, не содержащее цифры 0?
Число размещений с повторениями
Число размещений с повторениями из n по k – это число способов, сколькими можно из n различных элементов построить векторов с k координатами, среди которых могут быть одинаковые.
Число размещений с повторениями находится по формуле: .
Пример: Сколько слов длины 6 можно составить из 26 букв латинского алфавита?
Число перестановок без повторений
Число перестановок без повторений из n элементов – это число способов, сколькими можно расположить на n различных местах n различных элементов.
Число перестановок без повторений находится по формуле: .
Пример: Сколькими способами можно расставить на книжной полке 5 различных книг? В скольких случаях две определенные книги А и В окажутся рядом?
Замечание: , где х – число способов выбрать нужные места; у- число способов расположить на них нужные элементы; z- число способов расположить остальные элементы на оставшихся местах.
Число сочетаний без повторений
Число сочетаний без повторений из n по k – это число способов, сколькими можно из n различных элементов выбрать k штук без учета порядка.
Число сочетаний без повторений находится по формуле: .
Свойства: 1) ; 2) ; 3) ; 4) ; 5) ; 6) .
Пример:В урне 7 шаров. Из них 3 белых. Наугад выбирают 3 шара. Сколькими способами это можно сделать? В скольких случаях среди них будет: 1) один белый; 2) два белых; 3) все белые.
Задачи
1) В аквариуме 11 рыбок. Из них 4 красных, остальные золотые. Наугад выбирают 4 рыбки. Сколькими способами это можно сделать? Найти число способов сделать это так, чтобы среди них будет: а) ровно одна красная; б) ровно 2 золотых; в) хотя бы одна красная.
2) В списке 8 фамилий. Из них 4 – женские. Сколькими способами их можно разделить на две равные группы так, чтоб в каждой была женская фамилия?
3) Из колоды в 36 карт выбирают 4 . Сколько способов сделать это так, чтобы: а) все карты были разных мастей; б) все карты были одной масти; в) 2 красные и 2 черные.
4) На карточках разрезной азбуки даны буквы К, К, К, У, У, А, Е, Р. Сколько способов сложить их в ряд так, что бы получилось « кукареку ».
5) Даны карточки разрезанной азбуки с буквами О, Т, О, Л, О, Р, И, Н, Г, О, Л, О, Г. Сколько способов сложить их так, что бы получилось слово « отолоринголог ».
6) Даны карточки нарезной азбуки с буквами Л, И, Т, Е, Р, А, Т, У, Р, А. Сколько способов сложить их в ряд так, что бы получилось слово « литература ».
7) 8 человек становятся в очередь. Сколько способов сделать это так, что бы два определенных человека А и Б оказались: а) рядом; б) на краях очереди;
8) 10 человек садятся за круглый стол на 10 мест. Сколькими способами это можно сделать так, чтоб рядом оказались: а) два определенных человека А и Б; б) три определенных человека А, Б и С.
9) Сколькими способами можно расположить на 10 путях станции 1 товарный и 2 пассажирских поезда так, чтоб товарный не находился на соседнем пути ни с одним из пассажирских поездов.
10) Из 10 арабских цифр составляют 5-значный код. Сколькими способами это можно сделать так, чтобы: а) все цифры были разными; б) на последнем месте четная цифра.
11) Из 26 букв латинского алфавита( среди них 6 гласных ) составляется шестибуквенное слово. Сколькими способами это можно сделать так, чтобы в слове были: а) ровно одна буква «а»; б) ровно одна гласная буква; ровно две буквы «а»; в) ровно две гласные.
12) Сколько четырехзначных чисел делятся на 5?
13) Сколько четырехзначных чисел с различными цифрами делятся на 25?
14) В скольких десятизначных числах сумма цифр ровна 3?
15) Брошены 3 игральные кости. В скольких случаях выпала: а) ровно 1 « шестерка »; б) хотя бы одна « шестерка ».
16) Брошены 3 игральные кости. В скольких случаях будет: а) все разные; б) ровно два одинаковых числа очков.
17) Сколько слов с различными буквами можно составить из алфавита а, в, с, d. Перечислить их все в лексикографическом порядке: abcd, abcd….
18) Записать прямое произведение множеств А= В= .
19) В классе 8 человек имеют «5» по литературе; 9 человек – по английскому; 10 человек – по истории. Кроме того известно, что 6 человек имеют «5» по литературе и истории; 5 – по литературе и английскому; 5 – по истории и английскому; 3 – по всем предметам. Сколько человек имеют «5»: а) только по литературе; б) только по двум предметам; в) не имеют «5» по английскому.
20) В 20 комнатах общежития института Дружбы Народов живут студенты из России; в 15 – из Африки; в 20 – из стран Южной Амери ки.Причем в 7 – живут россияне и африканцы, в 8 – россияне и южноамериканцы; в 9 – африканцы и южноамериканцы. В 3х комнатах живут и россияне, и южноамериканцы, и африканцы. В скольких комнатах живут студенты:
а) только с одного континента;
б) только с двух континентов;
в) только африканцы.
Рекомендуемые страницы:
poisk-ru.ru
Выборки элементов без повторений
Рассмотрим сначала некоторые общие термины.
- Пусть некоторая совокупность содержит n элементов, из которых выбирают k элементов. Каждый такой набор будем называть выборкой объема k из n элементов.
- Будем различать выборки с возвращением и без возвращения. Пусть имеется совокупность n пронумерованных элементов:
- если отобранный элемент после выбора не возвращается в исходную совокупность и не может повторяться в данной выборке больше одного раза, то такая выборка называется выборкой без возвращения или без повторения;
- если отобранный элемент после фиксации номера снова возвращается в исходную совокупность и, таким образом, может вновь оказаться в данной выборке, то говорят о выборке с возвращением или с повторением.
- Выборка называется упорядоченной, если порядок следования элементов в ней задан. Если две упорядоченные выборки отличаются только порядком следования элементов, то они считаются разными (например: 12 и 21).
- Выборка называется неупорядоченной, если порядок элементов в ней не имеет значения (т. е. 12 и 21 неразличимы).
Размещения без повторений.
Размещениями без повторений называются упорядоченные выборки, содержащие k различных элементов из данных n элементов.
Обратим внимание на следующие важные положения:
- Любой элемент может оказаться на любом из k мест, но использоваться может в выборке только один раз.
- Порядок элементов в выборке важен.
Формула для определения числа размещений без повторений:
Задача. Дана последовательность символов А, Б, С. Сколько вариантов кода, состоящего из двух разных символов, можно составить из заданной последовательности?
Решение.По условию код состоит «из двух разных символов», при этом коды АБ и БА – не одинаковые, поэтому, выборки – размещения без повторений.
Выборка осуществляется из 3 элементов по 2. Значит, n = 3, k = 2.
Действительно, комбинаций, удовлетворяющих условию, всего шесть: {АБ, АС, БА, БС, СА, СБ}
Перестановки без повторений.
Нетрудно заметить, что размещения, в которые входят все n разных элементов заданного множества (т. е. k = n), будут отличаться только порядком следования входящих элементов. Такие размещения называют перестановками.
Перестановками без повторений называются всевозможные упорядоченные выборки, составленные из всех данных n элементов.
Формула для определения числа перестановок без повторений
Pn = n! = n * (n − 1) * (n − 2) *…* 2 * 1
Задача. Сколько вариантов кода длиной 3 символа можно составить из трех букв А, Б, С, если каждая буква входит в последовательность не более одного раза?
Решение. Так как «каждая буква входит в последовательность не более одного раза», то выборки – перестановки без повторений.
Pn = 3! = 3 * 2 * 1 = 6 {АБC, АCБ, БАС, БСА, САБ, СБА}
Сочетания без повторений.
Сочетаниями без повторений называются неупорядоченные выборки, содержащие k различных элементов из данных n элементов.
Отметим, что
- …«выборки неупорядоченные», т.е. выборки AB и ВА – это одно и тоже сочетание.
- Любой элемент может оказаться на любом из k мест, но использоваться может в выборке только один раз.
Формула для определения числа сочетаний без повторений:
Задача. Из 4-х кандидатов происходят выборы участников конференции. Сколько существует вариантов выбора делегации?
Решение. Очевидно, один и тот же кандидат в данную выборку может быть избран только один раз. При этом набор А, Б и Б, А – это одни те же участники. Поэтому выборки есть сочетания без повторений.
Воспользуемся формулой для расчета числа различных сочетаний без повторений:
informatics-lesson.ru
