Комплексные числа
Содержание
§ 1.Комплексные числа: определения, геометрическая интерпретация, действия в алгебраической, тригонометрической и показательной формах
Определение комплексного числа
Комплексные равенства
Геометрическое изображение комплексных чисел
Модуль и аргумент комплексного числа
Алгебраическая и тригонометрическая формы комплексного числа
Арифметические действия над комплексными числами
Показательная форма комплексного числа
Формулы Эйлера
§ 2.Целые функции (многочлены) и их основные свойства. Решение алгебраических уравнений на множестве комплексных чисел
Определение алгебраического уравнения -й степени
Основные свойства многочленов
Примеры решения алгебраических уравнений на множестве комплексных чисел
Вопросы для самопроверки
Глоссарий
§ 1. Комплексные числа: определения, геометрическая интерпретация, действия в алгебраической, тригонометрической и показательной формах
Определение комплексного числа (Сформулируйте определение комплексного числа )
Комплексным числомz называется выражение следующего вида:
Комплексное число в алгебраической форме,(1)
Где x, y Î;
i — это мнимая единица , определяемая равенством i 2 = –1.
Основные термины:
x = Re z — действительная часть комплексного числа z ;
y = Im z — мнимая часть комплексного числа z ;
— комплексно сопряженное число числу z ; — противоположное число числу z ; — комплексный ноль ; – так обозначается множество комплексных чисел.Примеры
1)z = 1 + i Þ Re z = 1, Im z = 1,
= 1 – i, = –1 – i ;2)z = –1 +
i Þ Re z = –1, Im z = , = –1 – i, = –1 –i ;3)z = 5 + 0i = 5 Þ Re z = 5, Im z = 0,
= 5 – 0i = 5, = –5 – 0i = –5Þ если Imz = 0, то z = x — действительное число;
4)z = 0 + 3i = 3i Þ Re z = 0, Im z = 3, = 0 – 3i = –3i , = –0 – 3i = – 3iÞ если Rez = 0, то z = iy — чисто мнимое число .
Комплексные равенства (Сформулируйте смысл комплексного равенства )
1)
;2)
.Одно комплексное равенство равносильно системе двух действительных равенств. Эти действительные равенства получаются из комплексного равенства разделением действительных и мнимых частей.
Примеры
1)
;2)
.Геометрическое изображение комплексных чисел (В чём состоит геометрическое изображение комплексных чисел? )
Комплексное число z изображается точкой (x , y ) на комплексной плоскости или радиус-вектором этой точки.
Знак z во второй четверти означает, что система декартовых координат будет использоваться как комплексная плоскость.Модуль и аргумент комплексного числа (Что такое модуль и аргумент комплексного числа? )
Модулем комплексного числа
называется неотрицательное действительное число .(2)Геометрически модуль комплексного числа — это длина вектора, изображающего число z , или полярный радиус точки (x , y ).
Аргумент комплексного числа z — это угол между положительным направлением действительной оси и вектором z (геометрически – это полярный угол точки (x , y )).
Обозначение
, причем , или .Для вычисления аргумента комплексного числа используется формула
Аргумент комплексного числа ,(3)
причем, при определении угла
по его тангенсу обязательно нужно учитывать, в какой четверти на комплексной плоскости расположено число z :Алгебраическая и тригонометрическая формы комплексного числа (Что такое алгебраическая и тригонометрическая формы комплексного числа? )
Так как геометрически очевидно, что
и , тоТригонометрическая форма комплексного числа .(4)
Запись z = x + iy называется алгебраической формой комплексного числа z ; запись z = r (cosj + i sinj ) называется тригонометрической формой комплексного числа z .
Примеры
Изобразить на комплексной плоскости следующие числа и записать их в тригонометрической форме.
1)z = 1 + i Þ
, ÞÞ
;2)
Þ ,mirznanii.com
комплексные числа
§1. Комплексные числа
1°. Определение. Алгебраическая форма записи.
Определение 1. Комплексными
числами называются упорядоченные пары
действительных чисел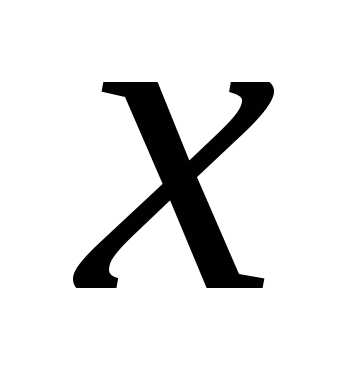 и
и
1) Два числа
иравны тогда и только тогда, когда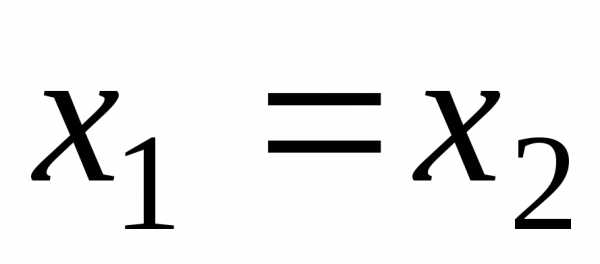 ,
,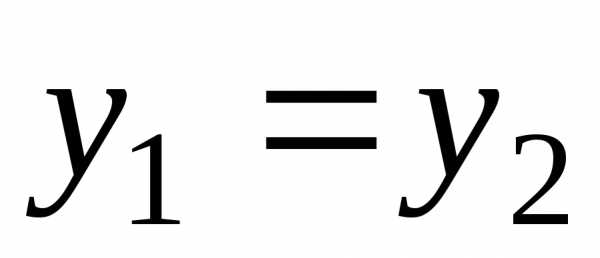 ,
т.е.
,
т.е.
2) Суммой комплексных
чисел
иназывается число, обозначаемое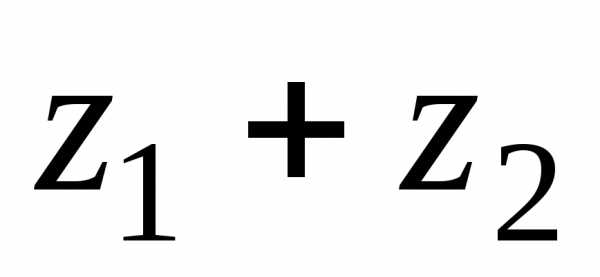 и равное,
т.е.
и равное,
т.е.
3) Произведением
комплексных чисел
иназывается число, обозначаемое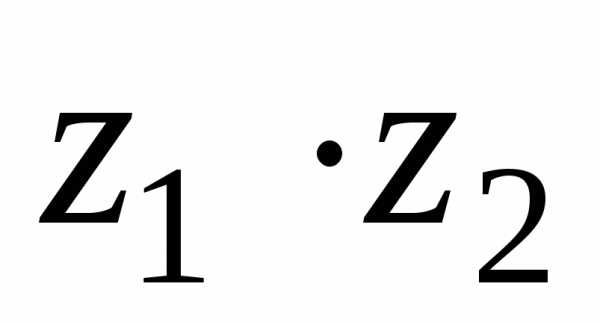 и равное,
т.е.
и равное,
т.е.
Множество комплексных
чисел обозначается C. 
Формулы (2),(3) для
чисел вида 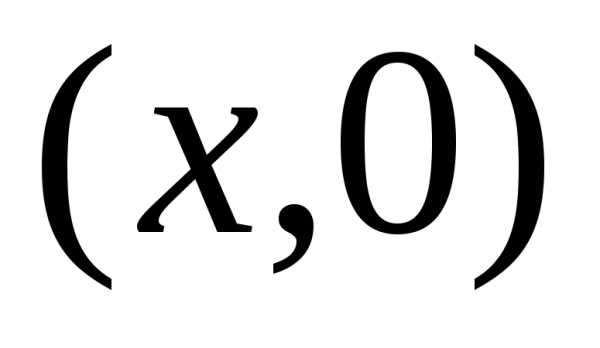 принимают
вид
принимают
вид
,
откуда следует,
что операции сложения и умножения для
чисел вида 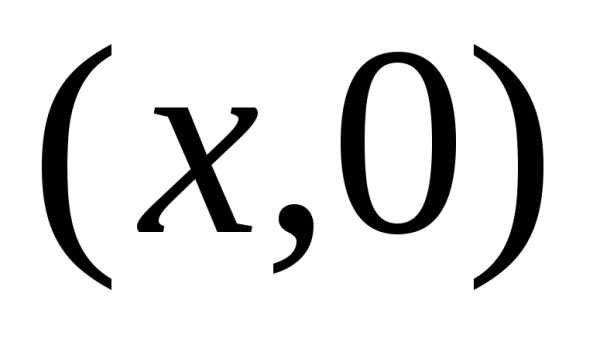
 отождествляется с вещественным числом
отождествляется с вещественным числом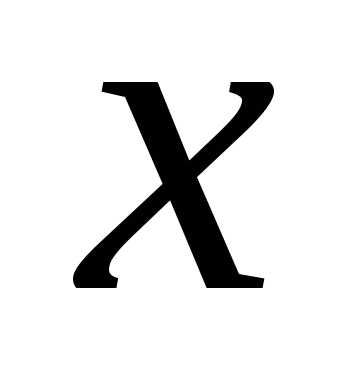 .
. Комплексное число
называетсямнимой
единицей и
обозначается 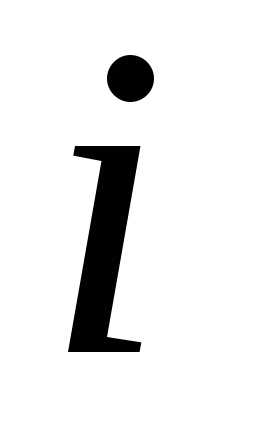 ,
т.е.
,
т.е.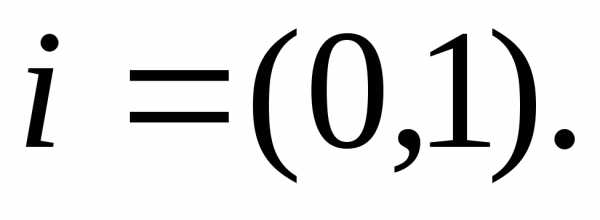 Тогда
из (3)
Тогда
из (3)
Из (2),(3) что и значит
(4) |
Выражение (4) называется алгебраической формой записи комплексного числа.
В алгебраической форме записи операции сложения и умножения принимают вид:
.
Комплексное число
обозначают
,
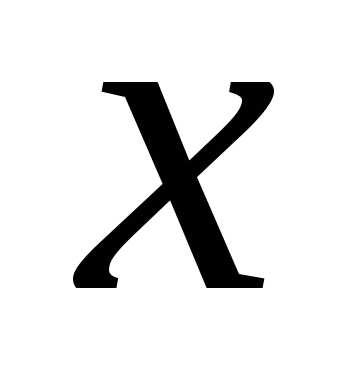
 – мнимая часть,
– мнимая часть, – чисто мнимое число. Обозначение:,
– чисто мнимое число. Обозначение:,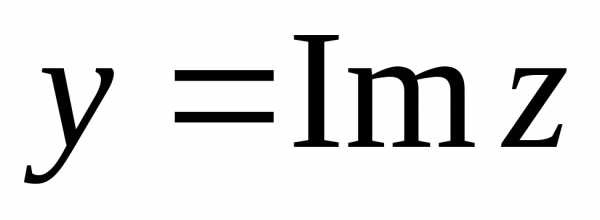 .
. Определение 2.
Комплексное число  называетсясопряженным с комплексным числом
.
называетсясопряженным с комплексным числом
.
Свойства комплексного сопряжения.
1)
2) .
3) Если , то.
4) 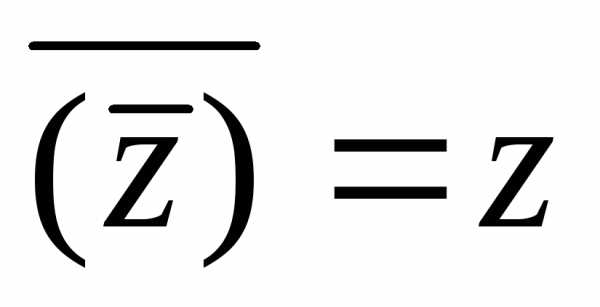 .
.
5) – вещественное число.
Доказательство проводится непосредственным вычислением.
Определение 3.
Число  называетсямодулем комплексного числа
и обозначается.
называетсямодулем комплексного числа
и обозначается.
Очевидно, что 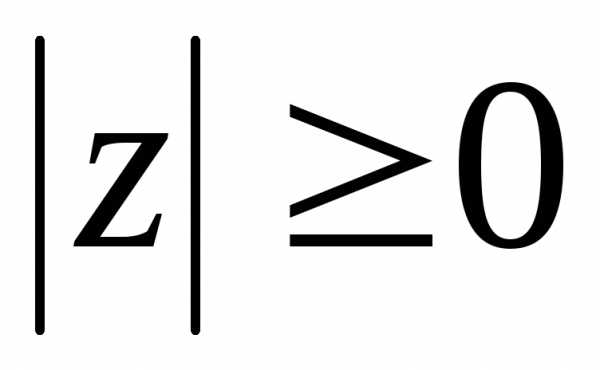 ,
причем
,
причем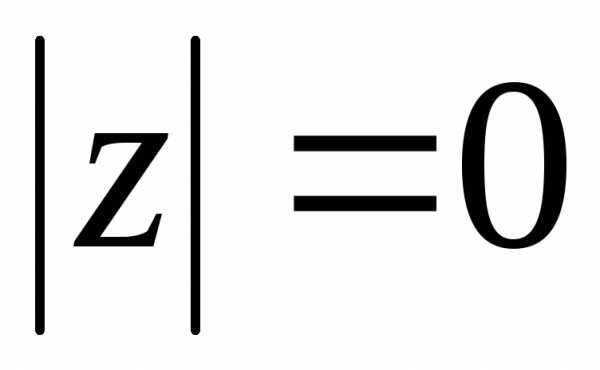

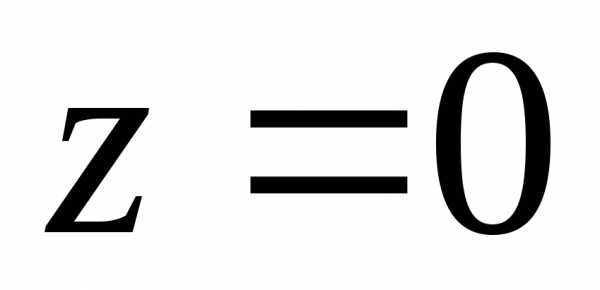 .
Также очевидны формулы:
.
Также очевидны формулы: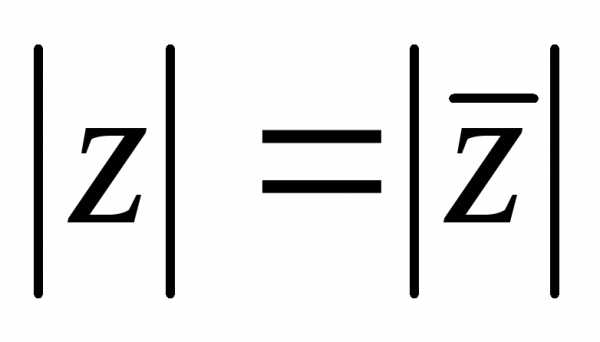 и
и  .
.
2°. Свойства операций сложения и умножения.
1) Коммутативность: , .
2) Ассоциативность:, .
3) Дистрибутивность: .
Доказательство 1) – 3) проводится непосредственными вычислениями на основе аналогичных свойств для вещественных чисел.
4) , .
5) 
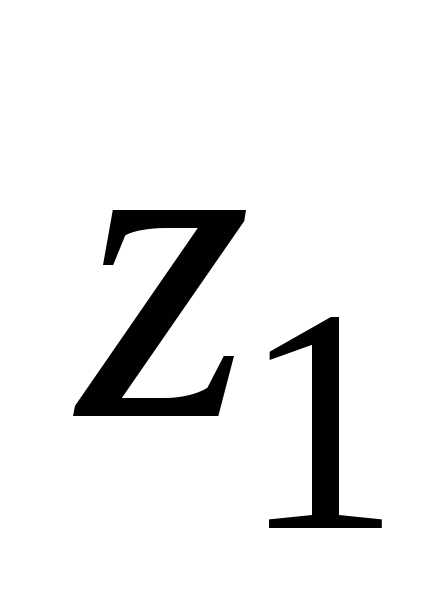 ,
, 
 C
C  !
! 
.
6) 
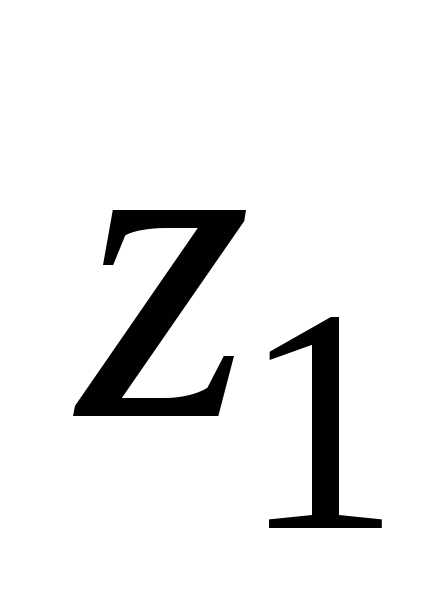 ,
,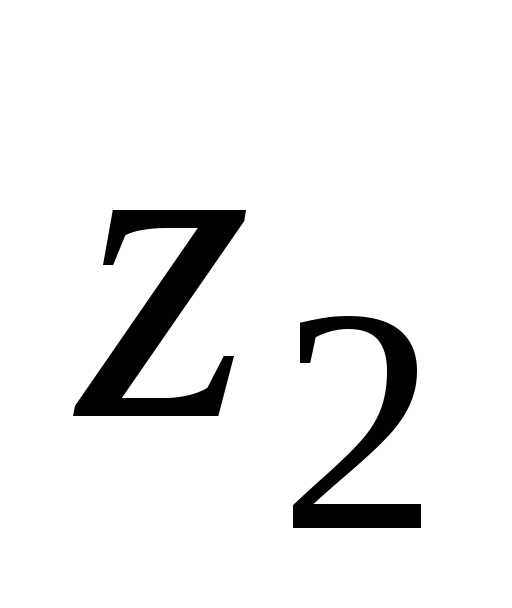
 C,
C, 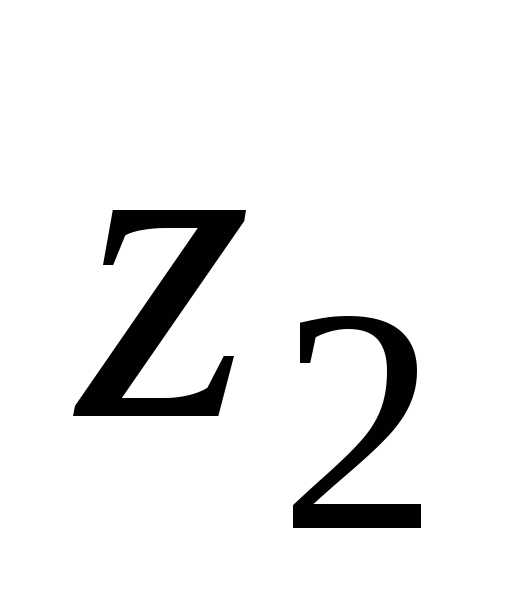
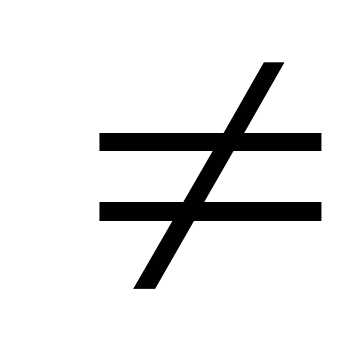 0,
0, 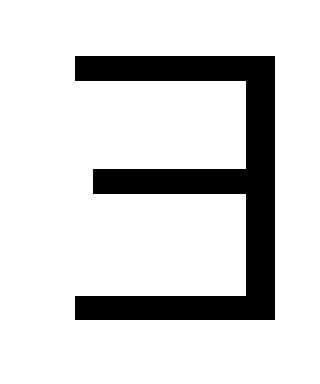 !
!  :
: 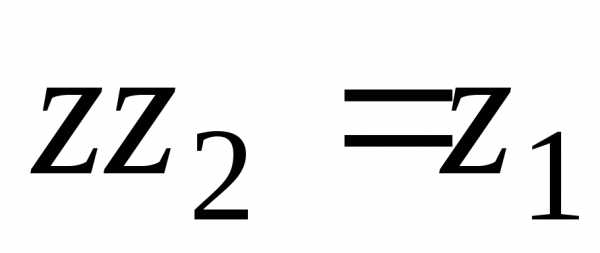 .
Такое
.
Такое  находится умножением
уравнения на
находится умножением
уравнения на 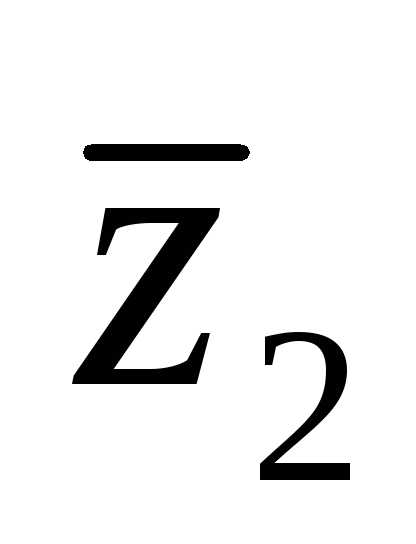

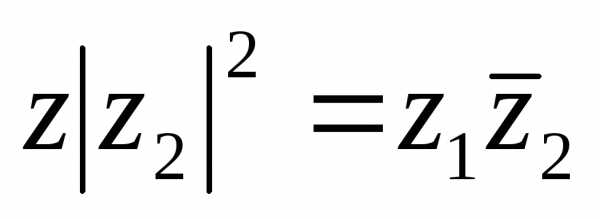

Пример. Представим
комплексное число  в
алгебраической форме. Для этого умножим
числитель и знаменатель дроби на число,
сопряженное знаменателю. Имеем:
в
алгебраической форме. Для этого умножим
числитель и знаменатель дроби на число,
сопряженное знаменателю. Имеем:
3°. Геометрическая интерпретация комплексных чисел. Тригонометрическая и показательная форма записи комплексного числа.
Пусть на плоскости
задана прямоугольная система координат.
Тогда 
 C можно
поставить в соответствие точку на
плоскости с координатами
.(см.
рис. 1). Очевидно, что такое соответствие
является взаимно однозначным. При этом
действительные числа лежат на оси
абсцисс, а чисто мнимые − на оси
ординат. Поэтому ось абсцисс называютдействительной
осью, а ось
ординат − мнимой
осью.
Плоскость, на которой лежат комплексные
числа, называется
C можно
поставить в соответствие точку на
плоскости с координатами
.(см.
рис. 1). Очевидно, что такое соответствие
является взаимно однозначным. При этом
действительные числа лежат на оси
абсцисс, а чисто мнимые − на оси
ординат. Поэтому ось абсцисс называютдействительной
осью, а ось
ординат − мнимой
осью.
Плоскость, на которой лежат комплексные
числа, называется
Отметим, что  и
и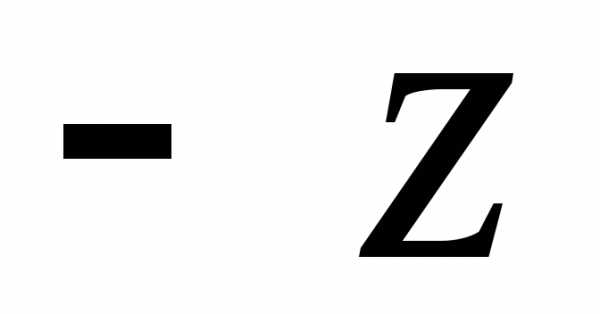 симметричны относительно начала
координат, а
симметричны относительно начала
координат, а и
и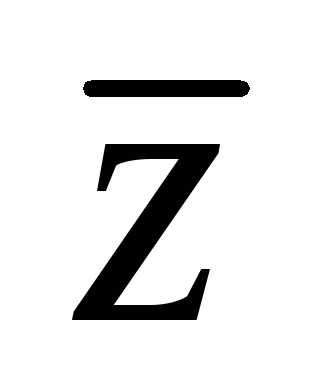 симметричны относительноOx.
симметричны относительноOx.
Каждому комплексному
числу (т.е. каждой точке на плоскости)
можно поставить в соответствие вектор
с началом в точке O
и концом в точке 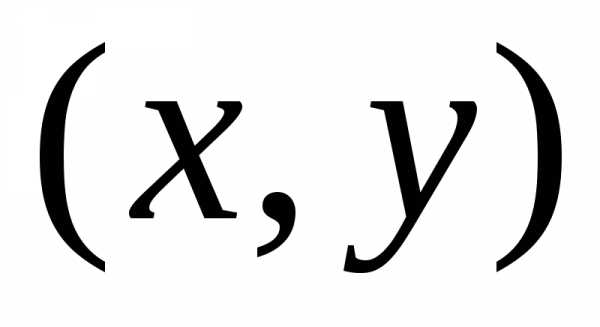 .
Соответствие между векторами и
комплексными числами является взаимно
однозначным. Поэтому вектор, соответствующий
комплексному числу
.
Соответствие между векторами и
комплексными числами является взаимно
однозначным. Поэтому вектор, соответствующий
комплексному числу ,
обозначается той же буквой
,
обозначается той же буквой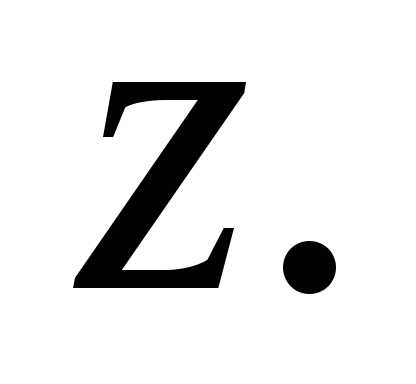
Длина
вектора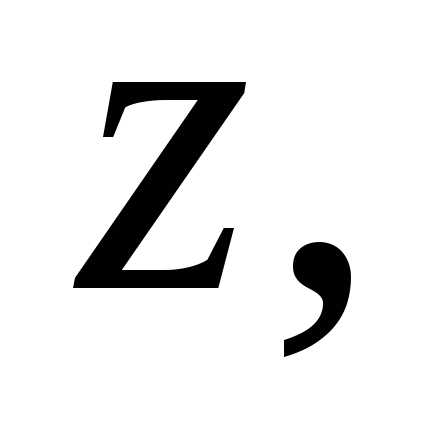 соответствующего комплексному числу,
равна,
причем,.
соответствующего комплексному числу,
равна,
причем,.
С помощью векторной
интерпретации можно видеть, что вектор 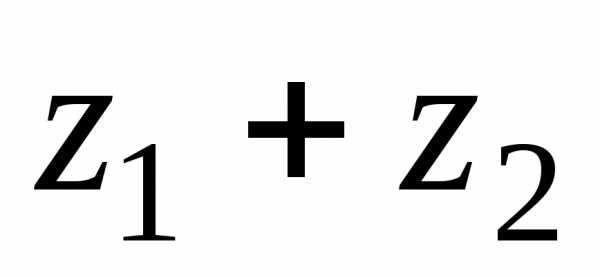 − сумма векторов
− сумма векторов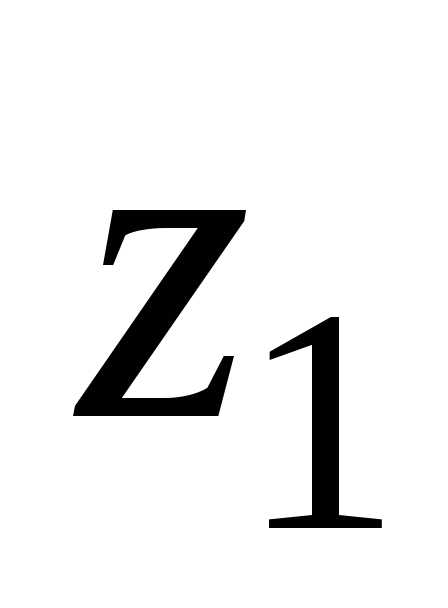 и
и ,
а
,
а −
сумма векторов
−
сумма векторов и
и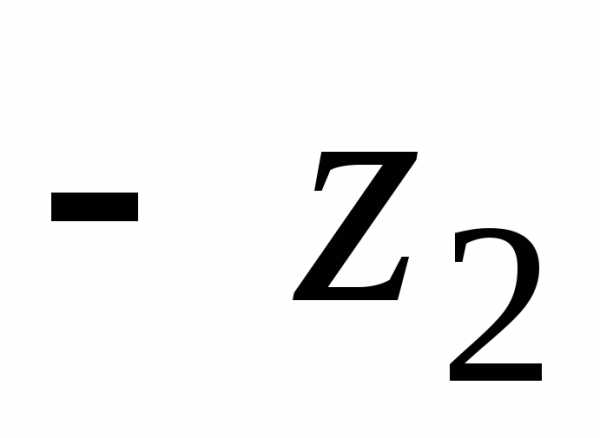 .(см.
рис. 2). Поэтому справедливы неравенства:
,
.(см.
рис. 2). Поэтому справедливы неравенства:
,
.
Наряду с длиной 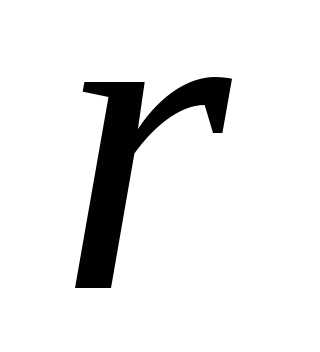 вектора
вектора введем в рассмотрение угол
введем в рассмотрение угол между вектором
между вектором и осьюOx,
отсчитываемый от положительного
направления оси Ox:
если отсчет ведется против часовой
стрелки, то знак величина угла
рассматривается положительной, если
по часовой стрелке – то отрицательной.
Этот угол называется аргументом
комплексного числа и обозначается
.
Угол
и осьюOx,
отсчитываемый от положительного
направления оси Ox:
если отсчет ведется против часовой
стрелки, то знак величина угла
рассматривается положительной, если
по часовой стрелке – то отрицательной.
Этот угол называется аргументом
комплексного числа и обозначается
.
Угол определяется не однозначно, а с точностью…
. Для
определяется не однозначно, а с точностью…
. Для аргумент не определяется.
аргумент не определяется.
При этом
, . | (5) |
Следовательно,
любое комплексное число 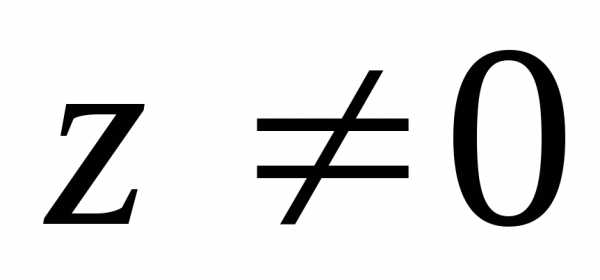 можно
представить в виде
можно
представить в виде
. | (6) |
Формулы (6) задают так называемую тригонометрическую форму записи комплексного числа.
Из (5) следует, что если ито
| (7) |
Из (5)  что по
что по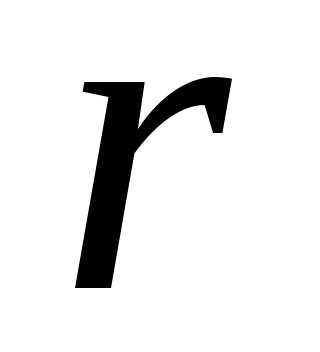 и
и комплексное число определяется
однозначно. Обратное неверно: а именно,
по комплексному числу
комплексное число определяется
однозначно. Обратное неверно: а именно,
по комплексному числу его модуль
его модуль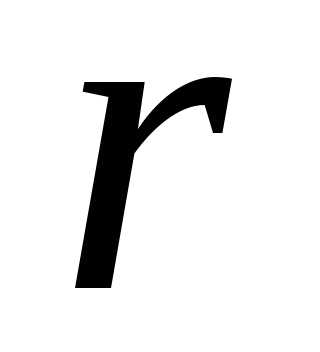 находится однозначно, а аргумент
находится однозначно, а аргумент ,
в силу (7), − с точностью
,
в силу (7), − с точностью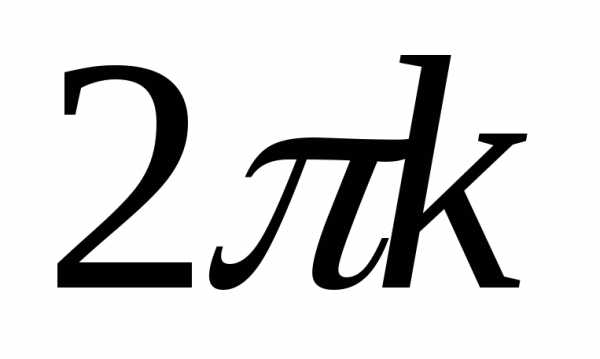 .
Также из (7) следует, что аргумент
.
Также из (7) следует, что аргумент может быть найден как решение уравнения
может быть найден как решение уравнения

Однако не все решения этого уравнения являются решениями (7).
Среди всех значений
аргумента комплексного числа выбирается
одно, которое называется главным
значением аргумента и обозначается 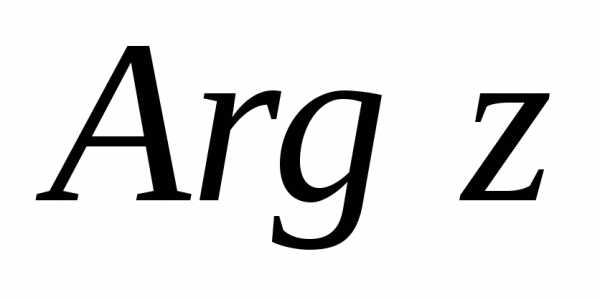 .
Обычно главное значение аргумента
выбирается либо в интервале,
либо в интервале
.
Обычно главное значение аргумента
выбирается либо в интервале,
либо в интервале
В тригонометрической форме удобно производить операции умножения и деления.
Теорема 1. Модуль произведения комплексных чисел 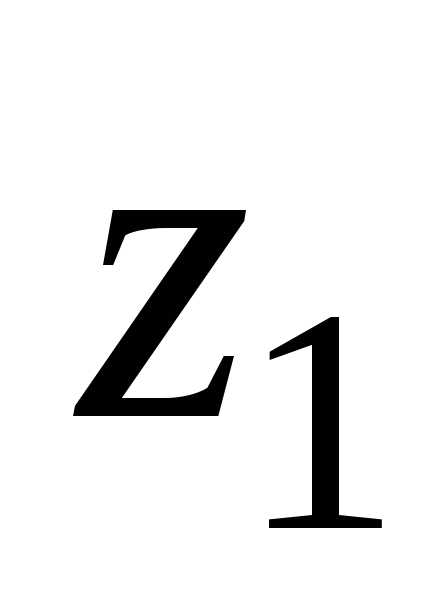 и
и 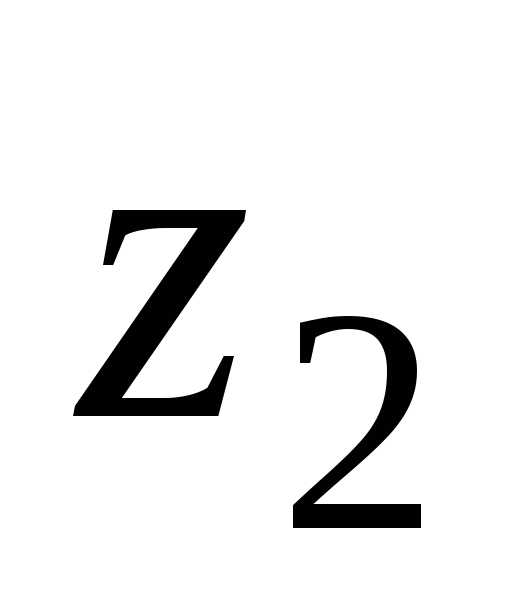 равен произведению
модулей, а аргумент – сумме аргументов,
т.е.
равен произведению
модулей, а аргумент – сумме аргументов,
т.е.
, а .
Аналогично
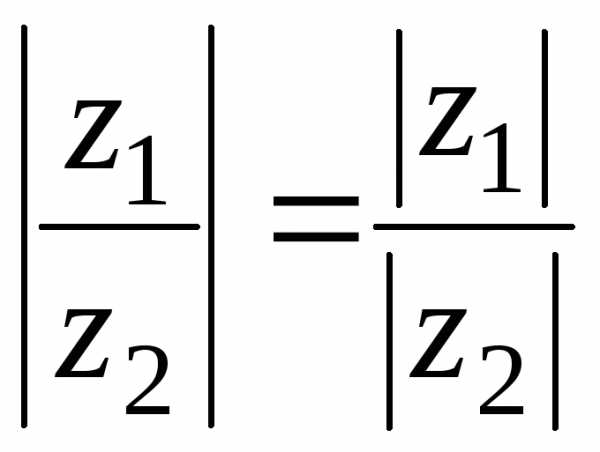 ,
,
Доказательство. Пусть ,. Тогда непосредственным умножением получаем:
.
Аналогично
.■
Следствие (формула Муавра). Для 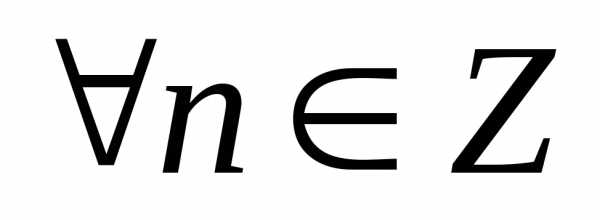 справедлива
формула Муавра
справедлива
формула Муавра
.
П
y
ример.Пусть Найдем геометрическое местоположение точки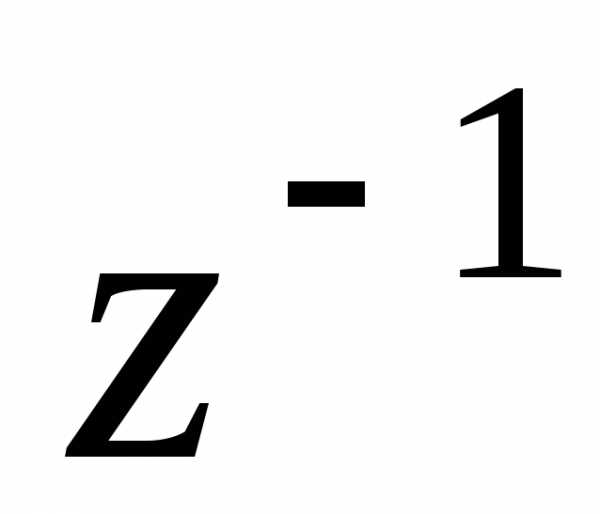 .
Из теоремы 1 следует, что
.
.
Из теоремы 1 следует, что
. Поэтому для ее
построение необходимо вначале построить
точку  ,
являющуюся инверсией
,
являющуюся инверсией  относительно
единичной окружности, а затем найти
точку, симметричную ей относительно
оси Ox.
относительно
единичной окружности, а затем найти
точку, симметричную ей относительно
оси Ox.
Пусть  ,т.е.
Комплексное число
обозначается
,
т.е.
,т.е.
Комплексное число
обозначается
,
т.е.

 R справедлива формула Эйлера
R справедлива формула Эйлера
(8) |
Так как
,
то,.
Из теоремы 1 что с функцией
что с функцией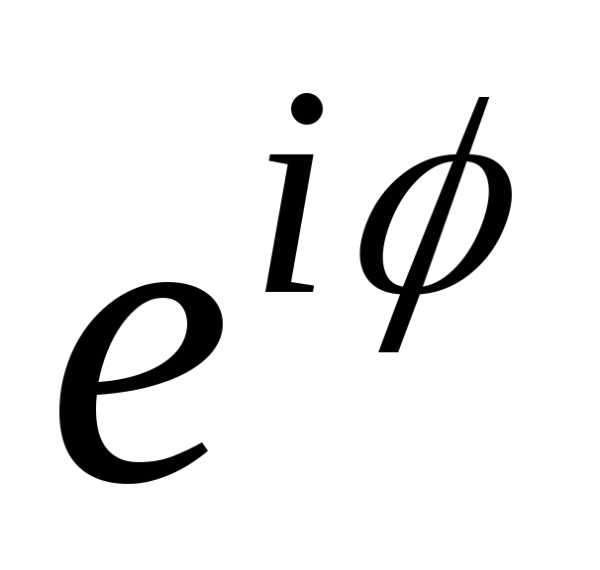 можно работать как с обычной показательной
функцией, т.е. справедливы равенства
можно работать как с обычной показательной
функцией, т.е. справедливы равенства
, 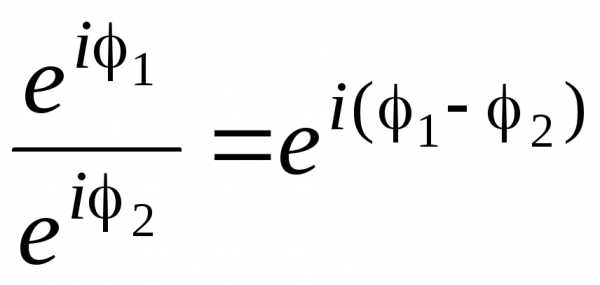 , .
, .
Из (8)  показательная
форма записи комплексного числа
показательная
форма записи комплексного числа
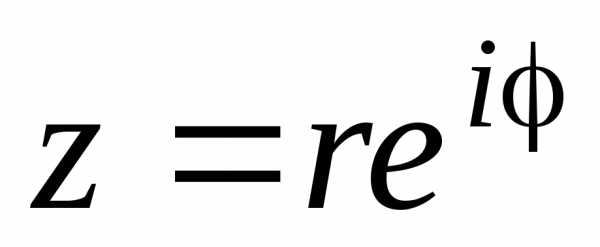 ,
где
,
где 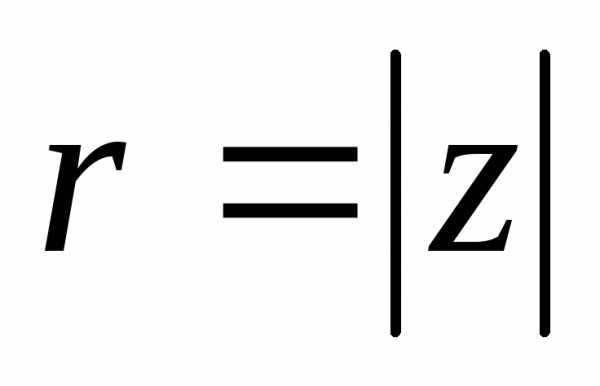 ,
,
Пример. .
4°. Корни 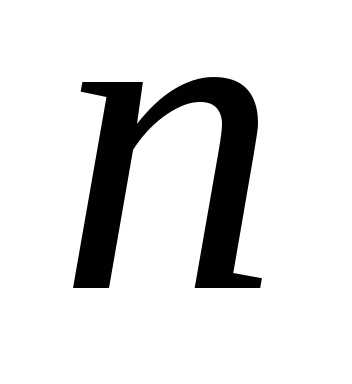 -ой
степени из комплексного числа.
-ой
степени из комплексного числа.
Рассмотрим уравнение
Пусть 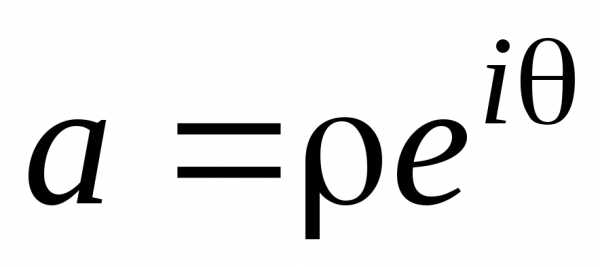 ,
а решение уравнения (9) ищется в виде
,
а решение уравнения (9) ищется в виде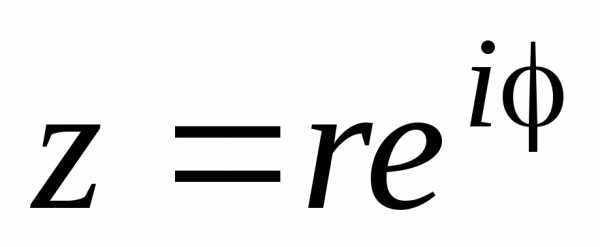 .
Тогда (9) принимает вид,
откуда находим, что
.
Тогда (9) принимает вид,
откуда находим, что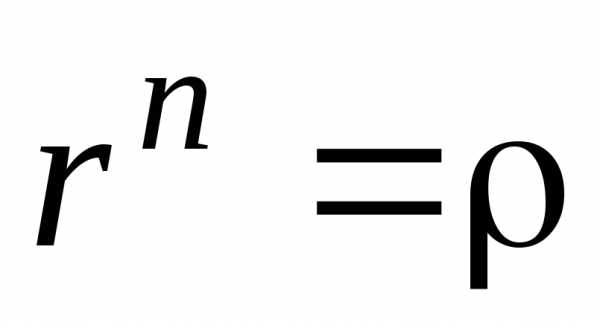 ,
,
т.е.
,
,
т.е.
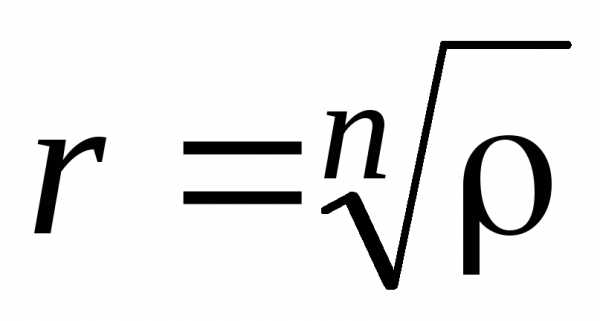 ,
, 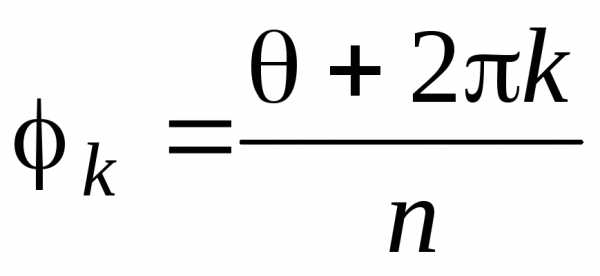 , .
, .
Таким образом, уравнение (9) имеет корни
| (10) |
Покажем, что среди
(10) имеется ровно 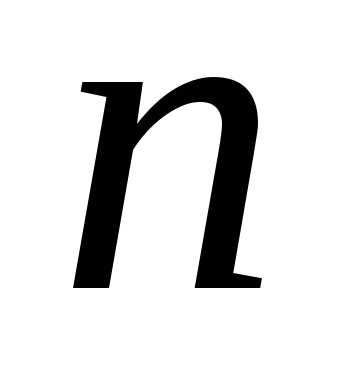 различных
корней. Действительно,
различных
корней. Действительно, 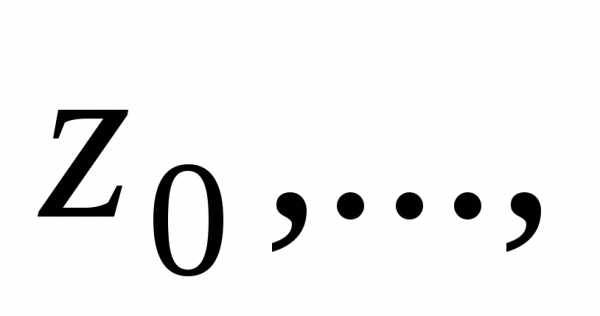
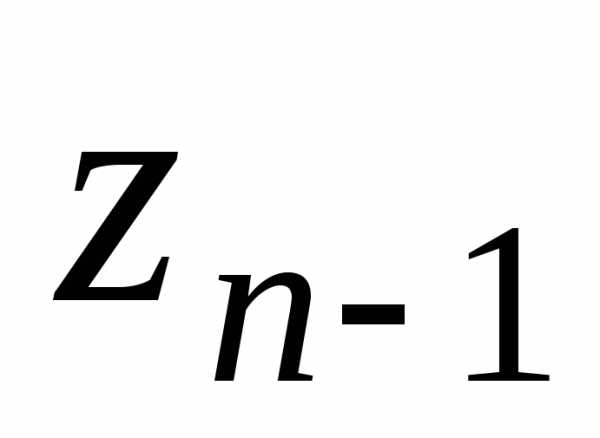 различны,
т.к. их аргументыразличны и отличаются меньше, чем на
различны,
т.к. их аргументыразличны и отличаются меньше, чем на .
Далее,
.
Далее, 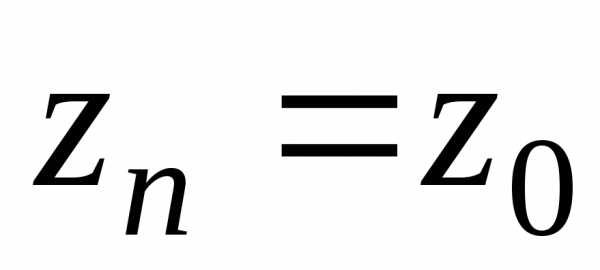 ,
т.к.
.
Аналогично.
,
т.к.
.
Аналогично.
Таким образом,
уравнение (9) при  имеет
ровно
имеет
ровно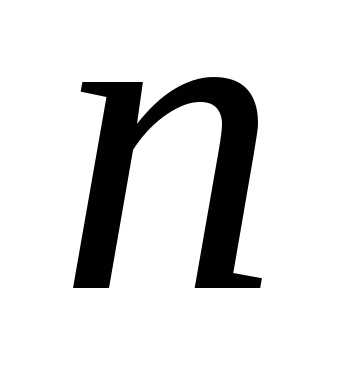 корней,
расположенных в вершинах правильного
корней,
расположенных в вершинах правильного -угольника,
вписанного в окружность радиуса
-угольника,
вписанного в окружность радиуса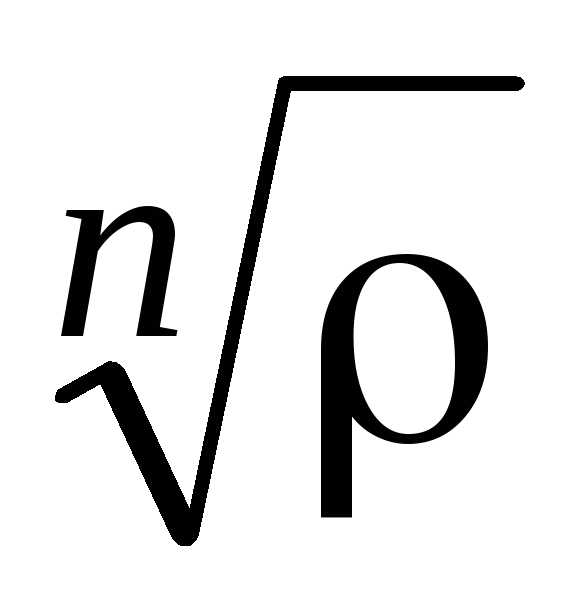 с центром в т.O.
с центром в т.O.
Таким образом, доказана
Теорема 2. Извлечение корня 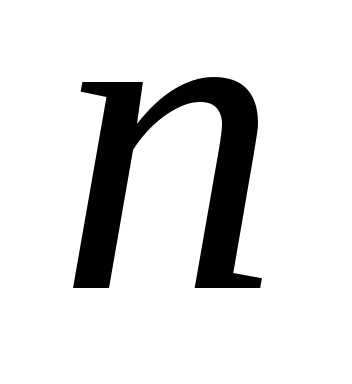 -ой
степени из комплексного числа
-ой
степени из комплексного числа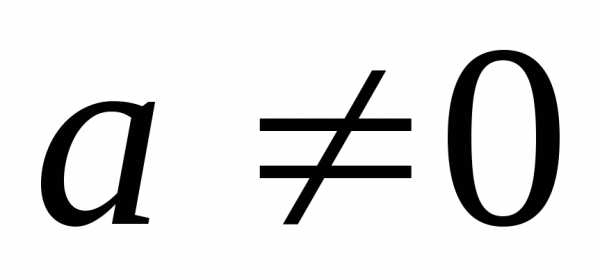 всегда
возможно. Все значения корня
всегда
возможно. Все значения корня  -ой
степени из
-ой
степени из расположены в вершинах правильного
расположены в вершинах правильного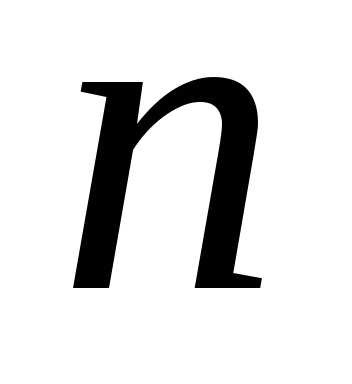 -угольника,
вписанного в окружность с центром в
нуле и радиуса
-угольника,
вписанного в окружность с центром в
нуле и радиуса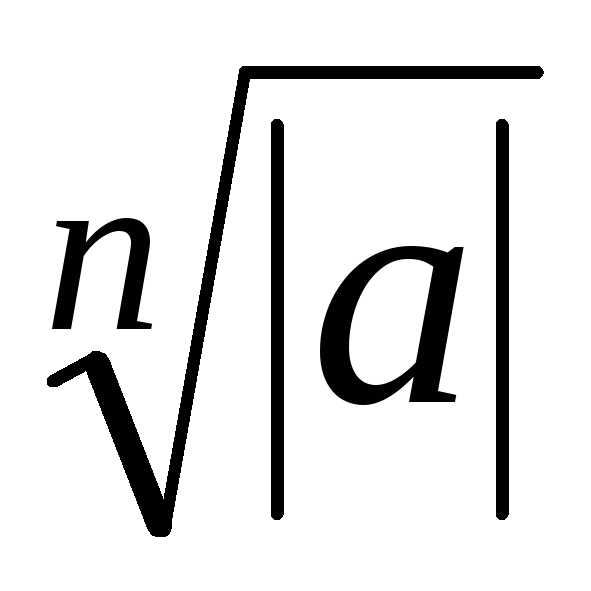 .
При этом,
.
При этом,
.
Следствие. Корни 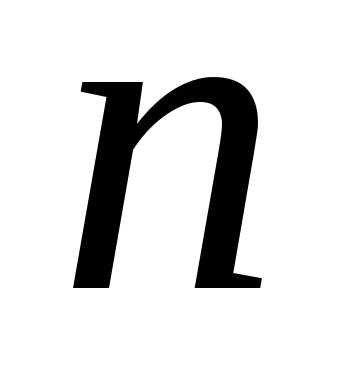 –ой
степени из 1 выражаются формулой
–ой
степени из 1 выражаются формулой
.
Произведение двух
корней из 1 является корнем, 1 – корень  -ой
степени из единицы,
-ой
степени из единицы, корня
корня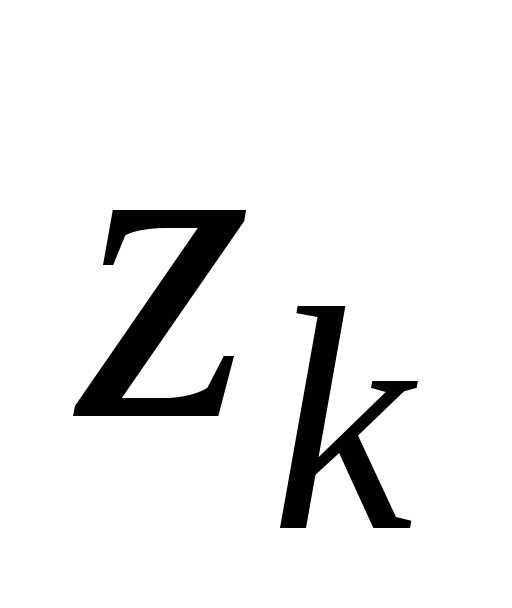

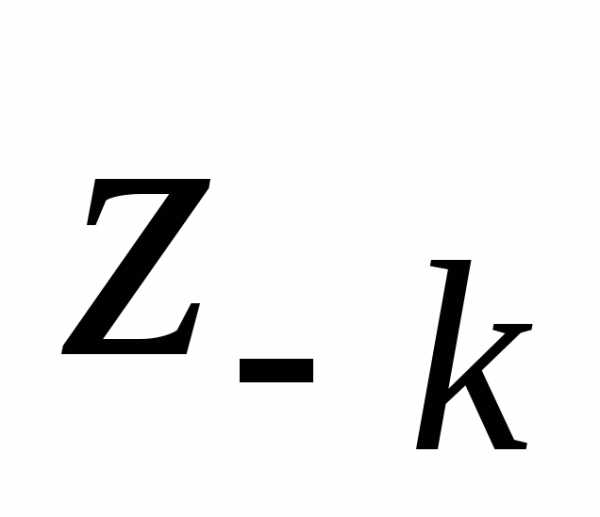 :
: 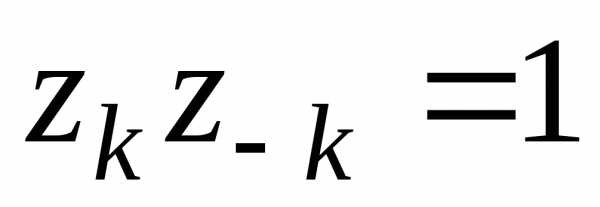 .
.
studfiles.net
Комплексное число — Традиция
Компле́ксные чи́сла[1] — расширение множества вещественных чисел, обычно обозначается \(\mathbb{C}\). Любое комплексное число может быть представлено как формальная сумма \(x + iy\), где \(x\) и \(y\) — вещественные числа, \(i\) — мнимая единица, то есть одно из чисел, удовлетворяющих уравнению \(i^2=-1\). Общепринятым произношением является компле́ксное число́, хотя произношение ко́мплексное число́ также встречается.
Комплексные числа образуют алгебраически замкнутое поле — это означает, что многочлен степени \(n\) с комплексными коэффициентами имеет ровно \(n\) комплексных корней, то есть верна основная теорема алгебры.
Стандартное[править]
Формально, комплексное число \(z\) — это упорядоченная пара вещественных чисел \((x, y)\) с введёнными на них следующим образом операциями сложения и умножения:
- \( (x , y) + (x’ , y’) = (x + x’ , y + y’) \,\)
- \( (x , y) \cdot (x’ , y’) = (xx’ — yy’ , xy’ + yx’). \,\)
Мнимая единица в такой системе представляется парой \(i=(0,1) \,\). Поэтому ошибочно определение числа \(i\) как единственного числа, удовлетворяющего уравнению \( i^2=-1 \), так как число \( (-i) \) также удовлетворяет этому уравнению. Следует также заметить, что выражение вида \( i=\sqrt{-1}\) некорректно, так как алгебраический корень определяется над множеством неотрицательных чисел.
Матричное[править]
Комплексные числа можно также определить как семейство вещественных матриц вида $$ \begin{pmatrix} x & y \\ -y & \;\; x \end{pmatrix} $$ с обычным матричным сложением и умножением. Действительной единице будет соответствовать $$ \begin{pmatrix} 1 & 0 \\ 0 & \;\; 1 \end{pmatrix} $$ , мнимой единице — $$ \begin{pmatrix} 0 & 1 \\ -1 & \;\; 0 \end{pmatrix} $$
все эти определения приводят к изоморфным расширениям поля вещественных чисел \(\mathbb{R}\), как и любые другие конструкции поля разложения многочлена x²+1
Действия над комплексными числами[править]
- Сложение
- \((a + bi) + (c + di) = (a + c) + (b + d)i\)
- Вычитание
- \((a + bi) — (c + di) = (a — c) + (b — d)i\)
- Умножение
- \((a + bi) (c + di) = ac + bci + adi + bd i^2 = (ac — bd) + (bc + ad)i\)
- Деление
- \(\,\frac{(a + bi)}{(c + di)} = \left({ac + bd \over c^2 + d^2}\right) + \left( {bc — ad \over c^2 + d^2} \right)i\,\)
Связанные определения[править]
Комплексная переменная обычно обозначается \(z\). Пусть \(x\) и \(y\) суть вещественные числа, такие, что \(z=x+iy\). Тогда
- Числа \(x = \Re(z)\) или \(\operatorname{Re}(z)\) и \(y = \Im(z)\) или \(\operatorname{Im}(z)\) называются соответственно вещественной (Real) и мнимой (Imaginary) частями \(z\).
- Если \(x=0\), то \(z\) называется мнимым или чисто мнимым.
- Комплексное число \(\bar z=x-iy\) называется сопряжённым (или комплексно сопряжённым) к \(z\).
- Число \(|z| = \sqrt{x^2+y^2} = \sqrt{z\bar z}\) называется модулем числа \(z\)
- Угол \(\varphi\) такой, что \(\cos \varphi = x \cdot |z|^{-1}\) и \(\sin \varphi = y \cdot |z|^{-1}\), называется аргументом \(z\).
Представление комплексных чисел[править]
Алгебраическая форма[править]
Запись комплексного числа \(z\) в виде \(x + iy\), \(x,y \in \mathbb{R}\), называется алгебраической формой комплексного числа.
Сумма и произведение комплексных чисел может быть вычислена непосредственным суммированием и перемножением таких выражений, с учётом тождества \(i^2 = -1\).
Тригонометрическая и показательная формы[править]
Если вещественную \(x\) и мнимую \(y\) части комплексного числа выразить через модуль \(r=|z|\) и аргумент \(\varphi\) (\(x=r\cos\varphi\), \(y=r\sin\varphi\)), то комплексное число \(z\) можно записать в тригонометрической форме $$z=r(\cos\varphi+i \sin\varphi).$$ Также может быть полезна следующая форма записи комплексных чисел, тесно связанная с тригонометрической через формулу Эйлера $$z=re^{i\varphi},$$ где \(e^{i\varphi}\) — расширение экспоненты для случая комплексного показателя степени.
Геометрическое представление[править]
Если на плоскости по оси абсцисс расположить действительную часть, а по оси ординат — мнимую, то комплексному числу будет соответствовать точка с декартовыми координатами \(x\) и \(y\) (или её радиус-вектор, что тоже самое), а модуль и аргумент будут полярными координатами этой точки.
- В геометрическом представлении сумма комплексных чисел соответствует векторной сумме соответствующих векторов. При перемножении комплексных чисел их модули перемножаются, а аргументы складываются. Отсюда, в частности, получается Формула Муавра.
Формула Муавра[править]
Формула, позволяющая возводить в степень комплексное число, представленное в тригонометрической форме. Формула Муавра имеет вид: $$z^n=[r(\cos \varphi +i\sin \varphi)]^n = r^n(\cos n\varphi +i\sin n\varphi),$$
где \(r\) — модуль, а \(\varphi\) — аргумент комплексного числа. В современной символике она опубликована Эйлером в 1722 г.
Эта формула применима при вычислении корней n-ой степени из комплексного числа.
$$z^{1/n}=[r(\cos (\varphi+2\pi k) +i\sin (\varphi+2\pi k))]^{1/n} = $$
\( =
r^{1/n}\left(\cos \frac{\varphi+2\pi k}{n} +i\sin \frac{\varphi+2\pi k}{n}\right),\)
\( \quad k=0,1..n-1\)
Георгий Александров нашел самый общий вид формулы Муавра: $$(x+y\,i)^n=\sqrt{(x^2+y^2)^n}\bigg [\cos\bigg(\frac{n\pi}{2}-\frac{n\pi}{2}\frac{|x|}{x} +n\operatorname{arctg}{\frac{|y|}{x} } \bigg )+i \, \frac{|y|}{y}\sin\bigg(\frac{n\pi}{2}-\frac{n\pi}{2}\frac{|x|}{x} +n\operatorname{arctg}{\frac{|y|}{x}} \bigg) \bigg]$$
где x,y,n — любые действительные числа.
Сопряжённые числа[править]
Геометрическое представление сопряжённых чиселЕсли комплексное число \(z=x+iy\), то число \(\bar z=x-iy\) называется сопряжённым (или комплексно сопряжённым) к \(z\) (часто обозначается также \(z^*\)). На комплексной плоскости сопряжённые числа получаются зеркальным отражением друг друга относительно вещественной оси. Модуль сопряжённого числа такой же, как у исходного, а их аргументы отличаются знаком. Отметим, что сумма и произведение двух сопряженных комплексных чисел являются действительными числами: $$ (x+iy)+(x-iy)=2x $$ $$ (x+iy)(x-iy)=x^2+y^2 $$ Однако, при делении двух сопряженных комплексных чисел получим число комплексное: $$\frac{x+iy}{x-iy}=\frac{x^2-y^2}{x^2+y^2}+i \, \frac{2xy}{x^2+y^2}$$ В 2016 году российский математик Георгий Александров выявил, что выражение $$ (x+iy)^n+(x-iy)^n $$ также является действительным числом при любой действительной степени n. Тождество Александрова: $$ (x+iy)^n+(x-iy)^n=2\sqrt{(x^2+y^2)^n} \cos \left [\frac{n\pi}{2}\left (1-\frac{|x|}{x} \right )+n \cdot \operatorname{arctg}\left (\frac{|y|}{x} \right ) \right ] $$
Впервые, по-видимому, мнимые величины появились в известном труде «Великое искусство, или об алгебраических правилах» Кардано (1545), который счёл их непригодными к употреблению.
Пользу мнимых величин, в частности, при решении кубического уравнения, в так называемом неприводимом случае (когда вещественные корни выражаются через кубические корни из мнимых величин), впервые оценил Бомбелли (1572). Он же дал некоторые простейшие правила действий с комплексными числами.
Выражения вида \(a+b\sqrt{-1}\), появляющиеся при решении квадратных и кубических уравнений, стали называть «мнимыми» в XVI-XVII веках, однако даже для многих крупных ученых XVII века алгебраическая и геометрическая сущность мнимых величин представлялась неясной. Известно, например, что Ньютон не включал мнимые величины в понятие числа, а Лейбницу принадлежит фраза: «Мнимые числа — это прекрасное и чудесное убежище божественного духа, почти что амфибия бытия с небытием»[Источник?].
Задача о выражении корней степени \(n\) из данного числа была в основном решена в работах Муавра (1707) и Котса (1722).
Символ \(i=\sqrt{-1}\) предложил Эйлер (1777, опубл. 1794), взявший для этого первую букву слова imaginarius. Он же высказал в 1751 году мысль об алгебраической замкнутости поля комплексных чисел. К такому же выводу пришел Д’Аламбер (1747), но первое строгое доказательство этого факта принадлежит Гауссу (1799). Гаусс и ввёл в широкое употребление термин «комплексное число» в 1831 г, хотя этот термин ранее использовал в том же смысле французский математик Лазар Карно в 1803 году.
Геометрическое истолкование комплексных чисел и действий над ними появилось впервые в работе Весселя ([[::en:Caspar Wessel|англ.]]), (1799). Первые шаги в этом направлении были сделаны Валлисом (Англия) в 1685 году.
Геометрическое представление комплексных чисел, иногда называемое «диаграммой Аргана», вошло в обиход после опубликования в 1806-м и 1814-м годах работы (Аргана (фр.)), повторявшей независимо выводы Весселя.
Арифметическая теория комплексных чисел как пар вещественных чисел была построена Гамильтоном (1837). Ему же принадлежит обобщение комплексных чисел — кватернионы, алгебра которых некоммутативна.
Функции комплексного переменного[править]
- ↑ Иногда ударение ставят на первый слог (в Московской школе)
- Понтрягин Л., «Комплексные числа», Квант, № 3, 1982.
- Арнольд В. И., «Геометрия комплексных чисел, кватернионов и спинов», МЦНМО, 2002
- Простой калькулятор комплексных чисел
- CaRevol Jet — Формульный калькулятор комплексных чисел под Windows.
- Елисеев В.И., «Введение в методы теории функций пространственного комплексного переменного», Центр научно-технического творчества молодежи Алгоритм. — М.:, НИАТ. — 1990. Шифр Д7-90/83308
traditio.wiki
Комплексные числа и алгебраические действия над ними
Комплексные числа и алгебраические действия над ними
- Комплексные числа
Рассмотрим квадратное уравнение .
Определим его корни .
Не существует действительного числа, квадрат которого равен -1. Но если формулой определить оператор i как мнимую единицу, то решение этого уравнения можно записать в виде . При этом и — комплексные числа, в которых -1 это действительная часть, 2 или во втором случае -2 – мнимая часть. Мнимая часть – это также действительное (вещественное) число. Мнимая часть, умноженная на мнимую единицу, означает уже мнимое число.
В общем виде комплексное число имеет вид
z = x + iy ,
где x, y – вещественные числа, – мнимая единица. В ряде прикладных наук, например, в электротехнике, электронике, теории сигналов мнимая единица обозначается через j. Вещественные числа x = Re{z} и y = Im{z} называются вещественной и мнимой частями числа z. Выражение называется алгебраической формой записи комплексного числа.
Любое действительное число есть частный случай комплексного числа в виде . Мнимое число тоже частный случай комплексного числа .
Определение множества комплексных чисел С
.
Это выражение читается следующим образом: множество С, состоящее из элементов , таких что x и y принадлежат множеству действительных чисел R и — это мнимая единица. Отметим, что и т.д.
Два комплексных числа и равны, если и только если равны их действительные и мнимые части, т.е. и .
Комплексные числа и функции широко используются в науке и технике, в частности, в механике, анализе и расчете цепей переменного тока, аналоговой электронике, в теории и обработке сигналов, в теории автоматического управления и др. прикладных науках.
- Арифметика комплексных чисел
Сложение двух комплексных чисел состоит в сложении их действительных и мнимых частей, т.е.
.
Соответственно разность двух комплексных чисел
.
Комплексное число называется комплексно сопряженным числу z = x + iy.
Комплексно сопряженные числа z и z* отличаются знаками мнимой части. Очевидно, что
.
Отсюда
.
Любое равенство между комплексными выражениями остается справедливым, если в этом равенстве всюду i заменить на —i, т.е. перейти к равенству сопряженных чисел. Числа i и –i алгебраически неразличимы, поскольку .
Произведение (умножение) двух комплексных чисел может быть вычислено следующим образом:
.
Поэтому
.
Деление двух комплексных чисел:
.
Пример:
.
- Комплексная плоскость
Комплексное число графически можно представить в прямоугольной системе координат. Зададим в плоскости прямоугольную систему координат (x, y).
На оси Ox будем располагать действительные части x , она называется действительной (вещественной) осью, на оси Oy –мнимые части y комплексных чисел. Она носит название мнимой оси. При этом каждому комплексному числу соответствует определенная точка плоскости, и такая плоскость называется комплексной плоскостью. Точке А комплексной плоскости будет соответствовать вектор ОА.
Число x называется абсциссой комплексного числа , число y – ординатой.
Пара комплексно сопряженных чисел отображается точками, расположенными симметрично относительно действительной оси.
Если на плоскости задать полярную систему координат, то каждое комплексное число z определяется полярными координатами . При этом модуль числа – это полярный радиус точки, а угол — её полярный угол или аргумент комплексного числа z.
Модуль комплексного числа всегда неотрицательный. Аргумент комплексного числа не определяется однозначно. Главное значение аргумента должно удовлетворять условию . Каждой точке комплексной плоскости соответствует также общее значение аргумента . Аргументы, отличающиеся значением, кратным 2π, считаются равными. Аргумент числа нуль не определен.
Главное значение аргумента определяют по выражениям:

Очевидно, что
При этом
, .
Представление комплексного числа z в виде
называется тригонометрической формой комплексного числа.
Пример.
- Показательная форма комплексных чисел
Разложение в ряд Маклорена для функций действительного аргумента имеет вид:

Для экспоненциальной функции комплексного аргумента z разложение имеет аналогичный характер
.
Разложение в ряд Маклорена для экспоненциальной функции мнимого аргумента можно представить как
Получившееся тождество называется формулой Эйлера.
Для отрицательного аргумента оно имеет вид
.
Комбинируя эти выражения, можно определить следующие выражения для синуса и косинуса
.
Пользуясь формулой Эйлера, из тригонометрической формы представления комплексных чисел
можно получить показательную (экспоненциальную, полярную) форму комплексного числа, т.е. его представление в виде
,
где — полярные координаты точки с прямоугольными координатами (x,y).
Число, сопряженное комплексному числу , в показательной форме записывается следующим образом .
Для показательной формы легко определить следующие формулы умножения и деления комплексных чисел
,
,
Т.е., в показательной форме произведение и деление комплексных чисел выполняется проще, чем в алгебраической форме. При умножении модули сомножителей перемножаются, а аргументы складываются. Это правило распространяется на любое число сомножителей. В частности, при умножении комплексного числа z на i вектор z поворачивается против часовой стрелки на 90
При делении модуль числителя делится на модуль знаменателя, и из аргумента числителя вычитается аргумент знаменателя.
Используя показательную форму комплексных чисел, можно получить выражения для известных тригонометрических тождеств. Например, из тождества
с помощью формулы Эйлера можно записать
Приравнивая действительную и мнимую части в данном выражении, получаем выражения для косинуса и синуса суммы углов
- Степени, корни и логарифмы комплексных чисел
Возведение комплексного числа в натуральную степень n производится по формуле
, т.е.,
.
Пример. Вычислим .
Представим число в тригонометрической форме
’
Применяя формулу возведения в степень, получим
.
Положив в выражении значение r = 1, получим так называемую формулу Муавра , при помощи которой можно определять выражения синусов и косинусов кратных углов.
Корень n–й степени из комплексного числа z имеет n различных значений, определяемых по выражению
Пример. Найдем .
Для этого выразим комплексное число () к тригонометрической форме
.
По формуле вычисления корня из комплексного числа, получаем
Логарифм комплексного числа z – это число w, для которого . Натуральный логарифм комплексного числа имеет бесконечное множество значений и вычисляется по формуле
При этом ln(r)– обычный вещественный логарифм модуля r.
Пример.
.
Справедливо равенство .
- Комплексные функции от вещественного аргумента
В электротехнике, электронике, обработке сигналов и др. областях часто используются функции, для которых независимая переменная вещественная, но функция принимает комплексные значения, например, а) , б) .
Подобную функцию можно разложить на вещественную и мнимую части, например,
Таким образом, комплексная функция от вещественного аргумента представляется двумя вещественными функциями того же аргумента. Например, комплексное напряжение
состоит из действительной (косинусоидальной) и мнимой (синусоидальной) части. Такое напряжение можно представлять как вектор длиной Um , начальной фазой (углом) , вращающийся с угловой скоростью ω.
При этом если комплексные функции складываются, то складываются их вещественные и мнимые части. Если комплексная функция умножается на константу или вещественную функцию, то её вещественная и мнимая части умножаются на тот же множитель. Дифференцирование / интегрирование такой комплексной функции сводится к дифференцированию / интегрированию вещественной и мнимой части.
Например, дифференцирование выражения комплексного напряжения
заключается в умножении его на iω.
Поэтому проще и быстрее выполнять все вычисления над всей комплексной функцией, а в качестве окончательного выражения взять вещественную или мнимую часть от результата.
- Понятие о функциях комплексного переменного
Пусть Е – множество точек в плоскости , а G — множество точек в плоскости . На множестве Е задана функция комплексного переменного , если каждому числу по некоторому правилу поставлено в соответствие единственное число . Функцию f(z)_ можно записать в виде , где — вещественная часть функции f(z), а – мнимая часть функции. Примеры: .
Значение z изображается точкой в комплексной плоскости z, а соответствующее значение w — точкой в комплексной плоскости w. При отображении w = f(z) линии плоскости z переходят в линии плоскости w, фигуры одной плоскости в фигуры другой, но формы линий или фигур могут существенно измениться.
Упражнения:
- Привести к виду следующие
выражения:
а) б), в) . - Отобразите на комплексной плоскости числа
. - Приведите к тригонометрической и показательной формам
комплексные числа
а) , б) , в) . - Упростите выражение
. - Найдите корни уравнения (шесть значений корня из 1) и
покажите их расположение на комплексной плоскости
vunivere.ru
Что такое комплексные числа 🚩 зачем нужны комплексные числа 🚩 Математика
Если вам нужно назвать расстояние между двумя городами, то можно дать ответ, состоящий из одного числа в милях, километрах или в других единицах измерения линейных расстояний. Однако если вы должны описать, как добраться из одного города в другой, то необходимо дать больше информации, чем просто расстояние между двумя точками на карте. В этом случае стоит сказать о направлении, в котором надо двигаться и о времени движения.
Вид информации, которая выражает одномерное измерение, в науке называется скалярной величиной. Скаляры – это числа, используемые в большинстве математических расчетов. К примеру, масса и скорость, которыми обладает тот или иной объект являются скалярными величинами.
Для того чтобы успешно анализировать природные явления, мы должны работать с абстрактными объектами и методами, способными представлять многомерные величины. Здесь необходимо отказываться от скалярных чисел в пользу комплексных. Они дают возможность выразить два измерения одновременно.
Комплексные числа легче понять, когда они представлены в графическом виде. Если нарисовать линию, имеющую определенную длину и направление, то это и будет графическое представление комплексного числа. Оно также широко известно в физике как вектор.
Такие типы чисел, как целые, рациональные, иррациональные и реальные знакомы детям со школы. Им всем присуща одномерность. Прямолинейность числовой прямой иллюстрирует это графически. Вы можете перемещаться вверх или вниз по ней, но все «движения» по этой линии будут ограничиваются горизонтальной осью. Одномерных, скалярных цифр вполне достаточно для подсчета количества предметов, выражения веса или измерения постоянного напряжения батареи. Но они не могут обозначать что-то более сложное. Скалярами невозможно одновременно выразить расстояние и направление между двумя городами, или амплитуду с фазой. Представлять эти виды чисел необходимо уже в виде многомерной области значений. Другими словами, нам нужны векторные величины, которые могут иметь не только величину, но и направление распространения.
Скалярное число является типом математического объекта, который люди привыкли использовать в повседневной жизни — это температура, длина, вес и т.д. Комплексное число представляет собой значение, которое включает в себя два типа данных.
Вектор является графическим изображением комплексного числа. Он выглядит, как стрелка с начальной точкой, определенной длиной и направлением. Иногда слово «вектор» используется в радиотехнике, где он выражает фазовый сдвиг между сигналами.
www.kakprosto.ru

 ,
, 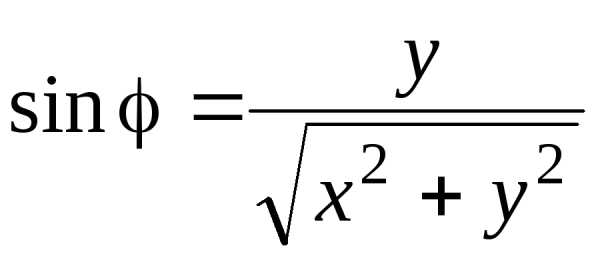 .
.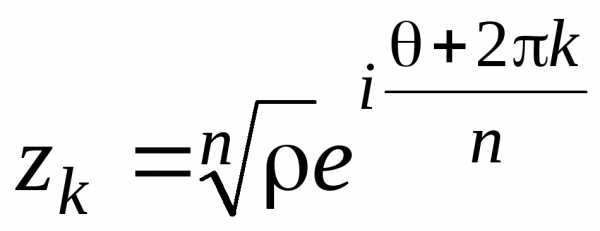 ,
.
,
.