Контрольная работа математика матрицы – Контрольная работа № 1 по теме: «Матрицы и определители»

Содержание

Контрольная работа « Матрицы и определители» для студентов 1 курса

Контрольная работа

«Матрицы и определители»

1). Дано: A,B. Найти:

а) 3A+B

б) AB

в)A ^-1

г)A ^-1A

2).Найти def A: а) методом треугольников;

б) приведением к каноническому виду

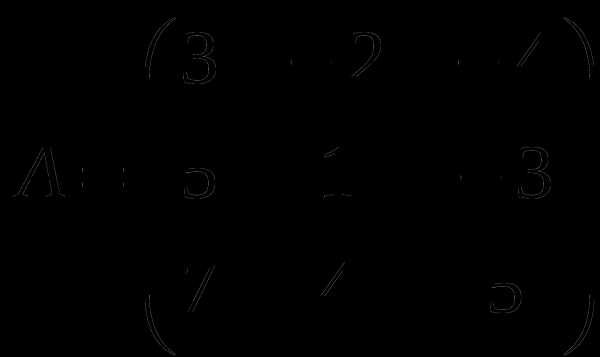
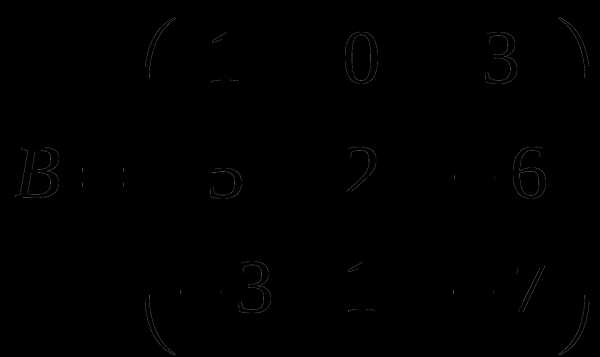
1). Дано: A,B. Найти:

а) -2A-B

б) BA

в)B ^-1

г) B ^-1B

2).Найти def A: а) приведением к каноническому виду;

б) методом треугольников;

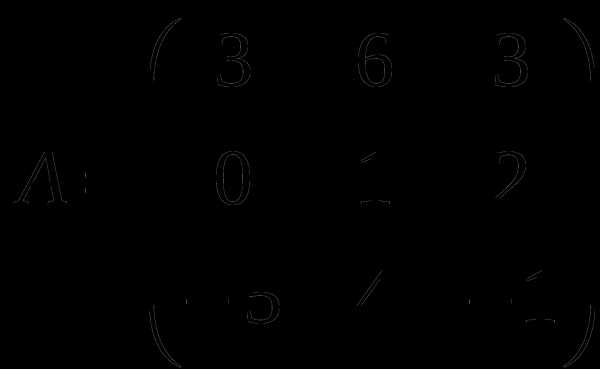
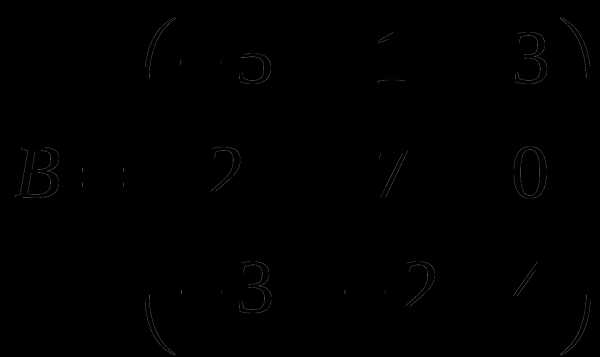
1). Дано: A,B. Найти:

а) 3B+A

б) BA

в)B ^-1

г)BB ^-1

2).Найти∆B: а) методом треугольников;

б) приведением к треугольному виду

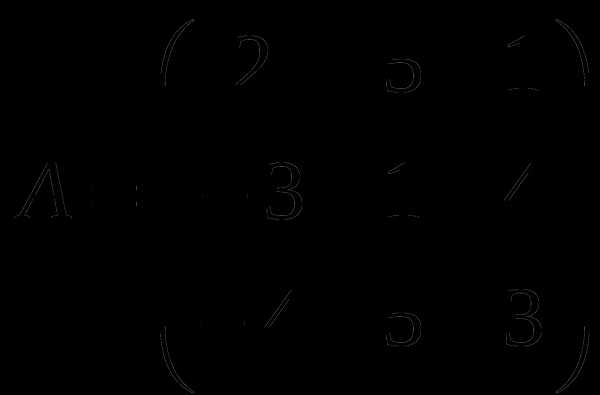
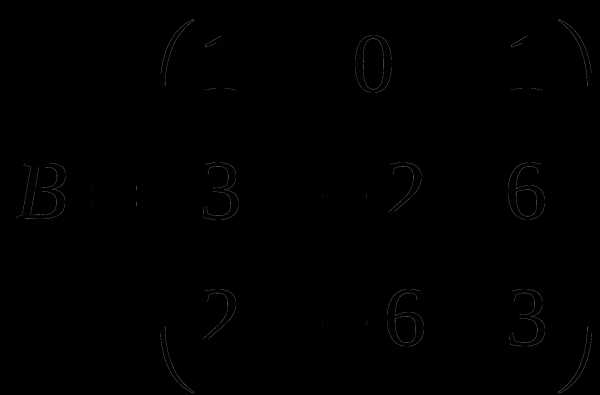
1). Дано: A,B. Найти:

а) 3A+B

б) AB

в)A ^-1

г)A ^-1A

2).Найти def B: а) методом треугольников;

б) приведением к каноническому виду

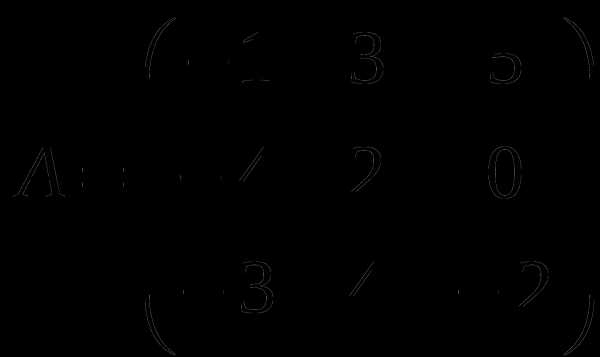
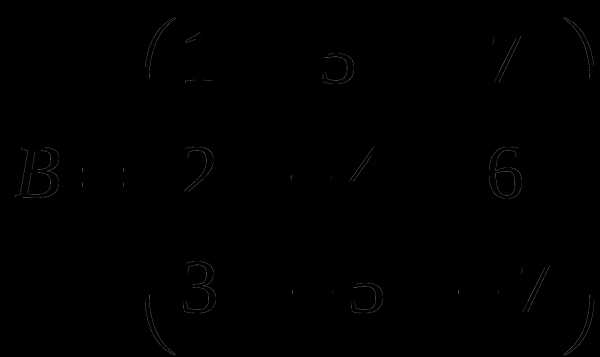
1). Дано: A,B. Найти:

а) 2A+B

б) AB

в)B ^-1

г) BB ^-1

2).Найти def A: а) методом треугольников;

б) приведением к треугольному виду;

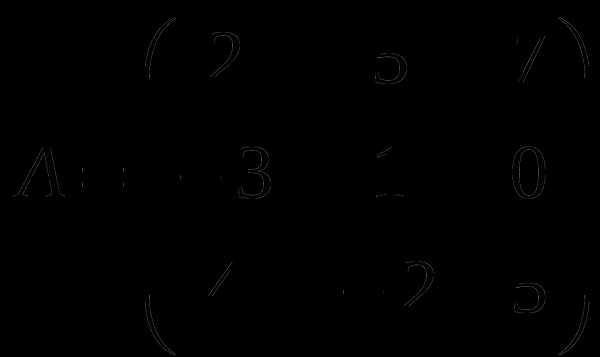
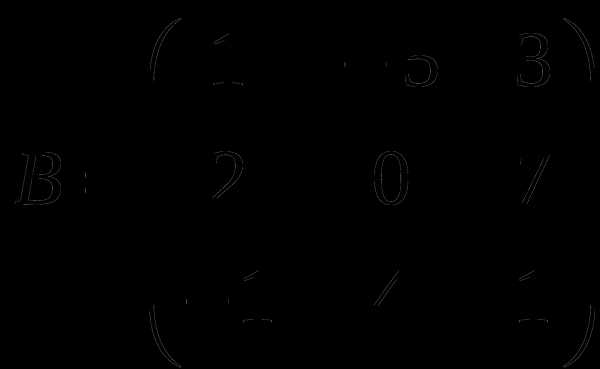
Контрольная работа № 1

1). Дано: A,B. Найти:

а) 3B-A

б) AB

в)A ^-1

г) AA ^-1

2).Найти ∆B: а) методом треугольников;

б) приведением к треугольному виду

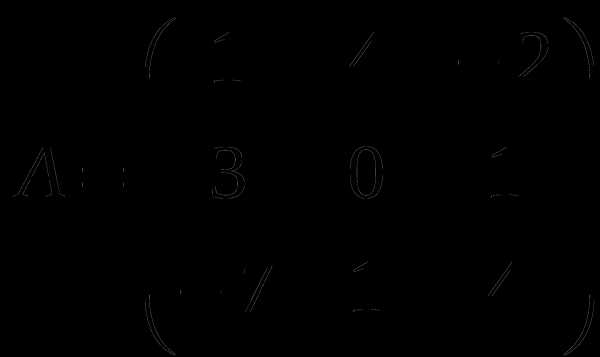
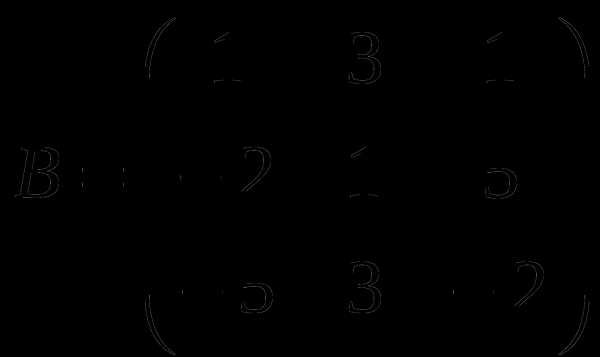
1). Дано: A,B. Найти:

а) 2B+3A

б) BA

в)A ^-1

г)A ^-1A

2).Найти∆B: а) методом треугольников;

б) приведением к треугольному виду

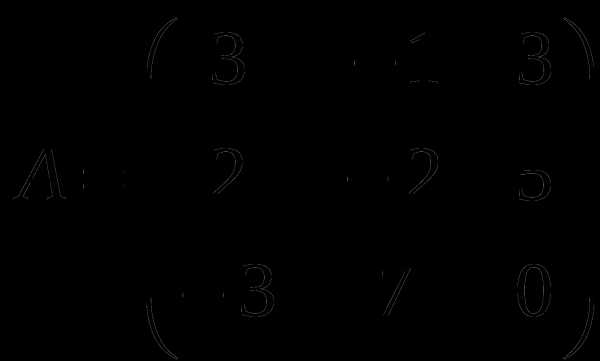
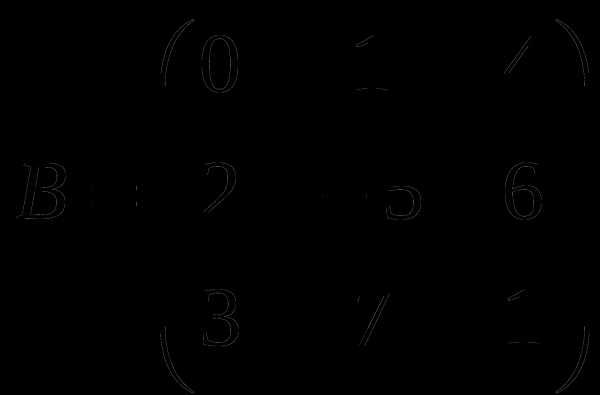
1). Дано: A,B. Найти:

а) 3B-A

б) AB

в)A ^-1

г)A ^-1A

2).Найти def B: а) методом треугольников;

б) приведением к треугольному виду

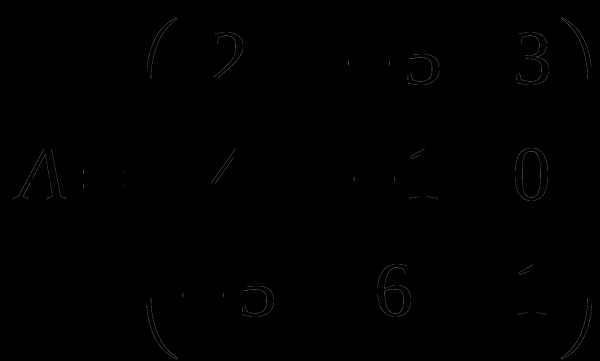
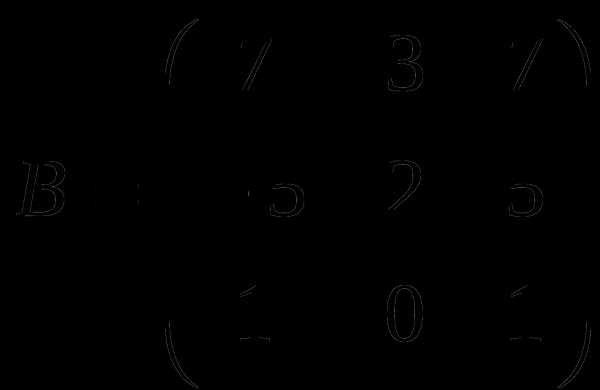
1). Дано: A,B. Найти:

а) 3B-A

б) AB

в)B ^-1

г) B ^-1B

2).Найти ∆ A: а) методом треугольников;

б) приведением к треугольному виду;

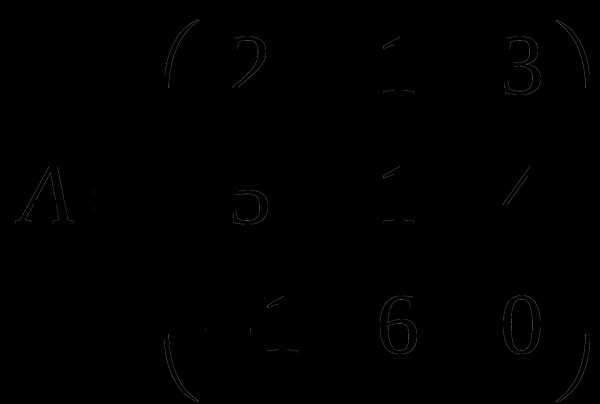
1). Дано: A,B. Найти:

а) 2B+2A

б) BA

в)A ^-1

г) AA ^-1

2).Найти ∆A: а) методом треугольников;

б) приведением к треугольному виду

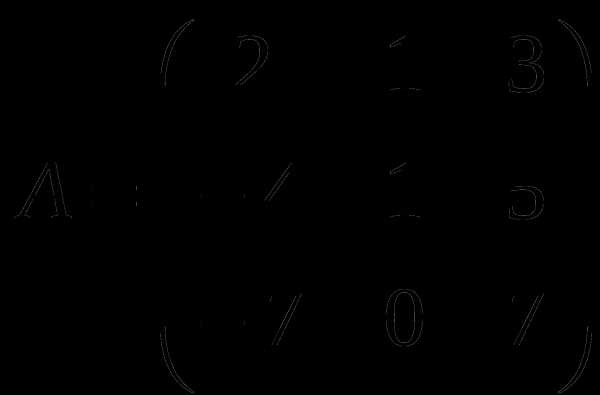
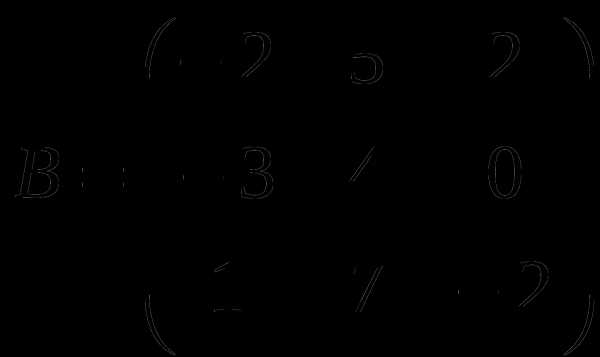
Контрольная работа № 1

1). Дано: A,B. Найти:

а) 2B-A

б) BA

в)B ^-1

г)B ^-1B

2).Найти def B: а) методом треугольников;

б) приведением к каноническому виду

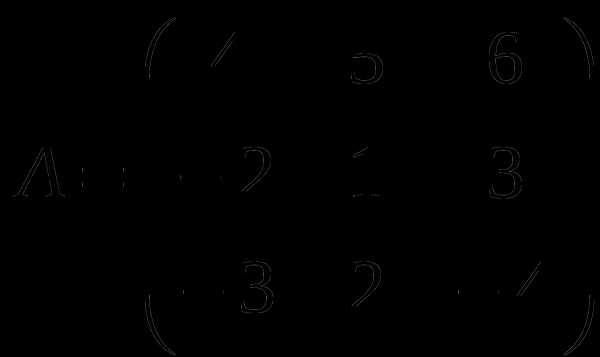
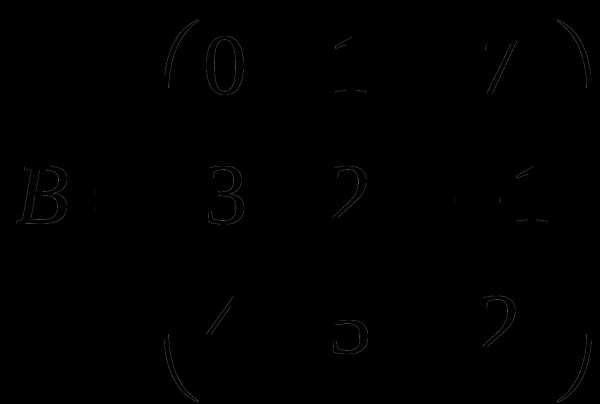
1). Дано: A,B. Найти:

а) 2B+A

б) AB

в)A ^-1

г)A ^-1A

2).Найти ∆ B: а) приведением к треугольному виду;

б) методом треугольников;

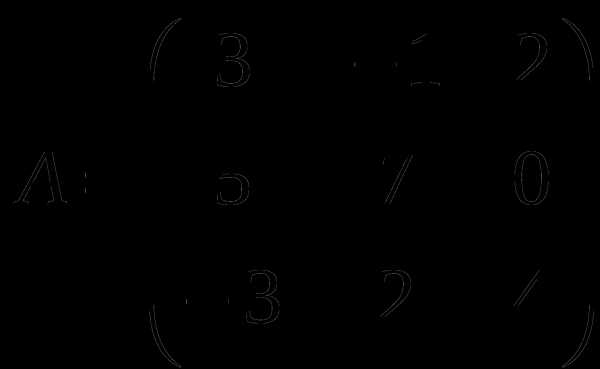
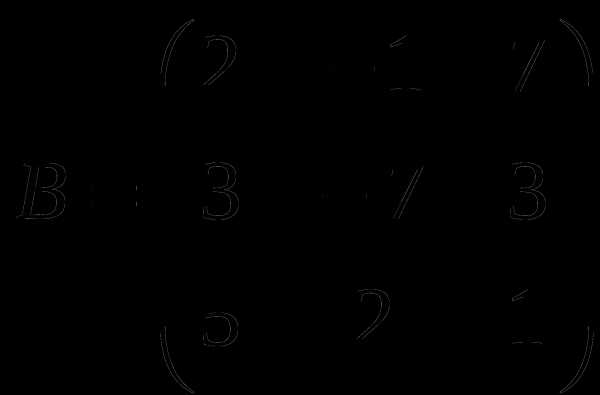
1). Дано: A,B. Найти:

а) 3A+B

б) AB

в)A ^-1

г) A ^-1A

2).Найти def B: а) методом треугольников;

б) приведением к треугольному виду

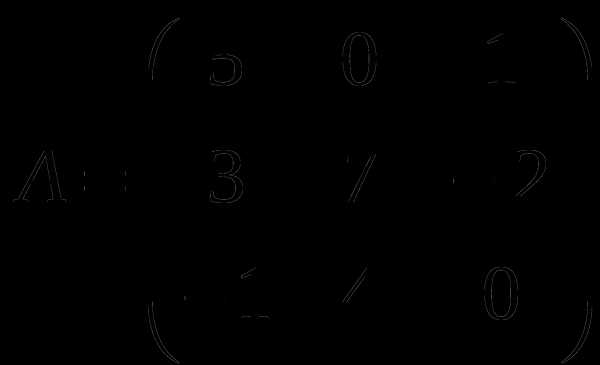
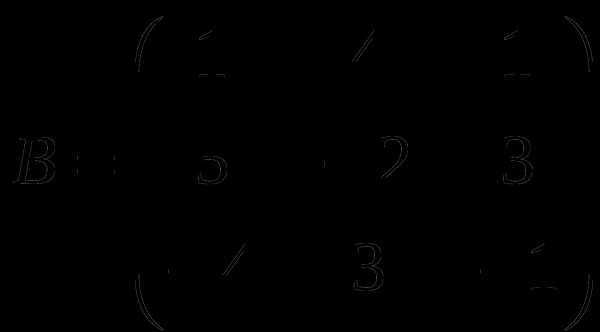
1). Дано: A,B. Найти:

а) 2B+3A

б) BA

в)B ^-1

г)B ^-1B

2).Найти ∆A: а) методом треугольников;

б) приведением к треугольному виду

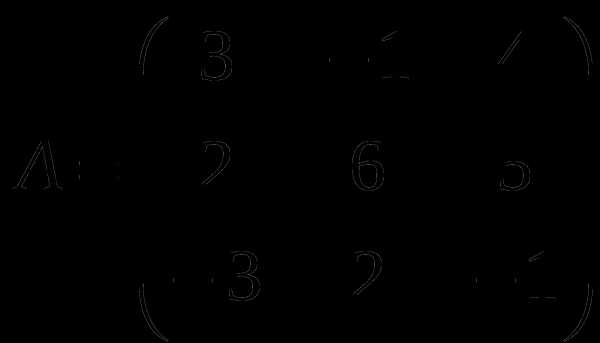
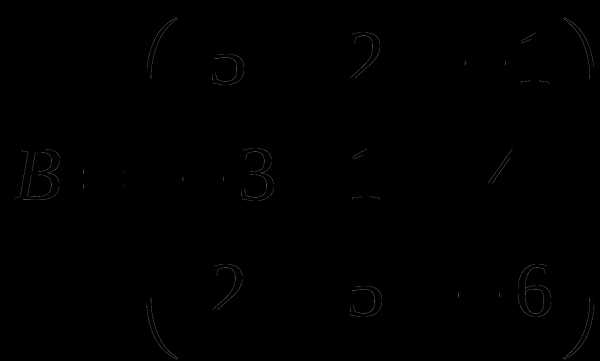
1). Дано: A,B. Найти:

а) 3A+B

б) BA

в)B ^-1

г)B ^-1B

2).Найти │A│: а) методом треугольников;

б) приведением к каноническому виду

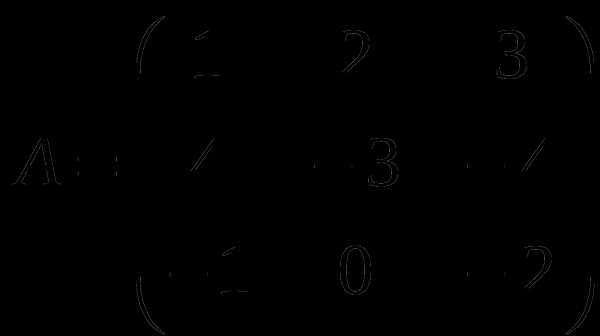
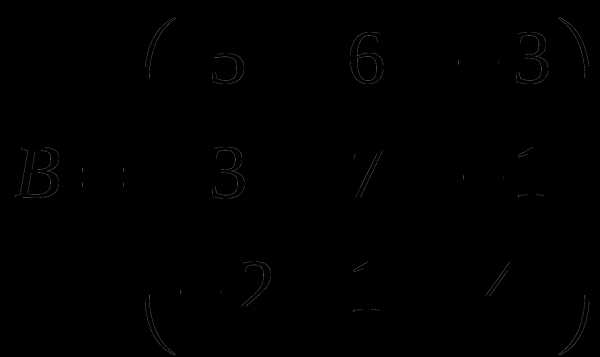
Контрольная работа № 1

1). Дано: A,B. Найти:

а) 2A+B

б) AB

в)A ^-1

г) AA ^-1

2).Найти def A: а) методом треугольников;

б) приведением к треугольному виду;

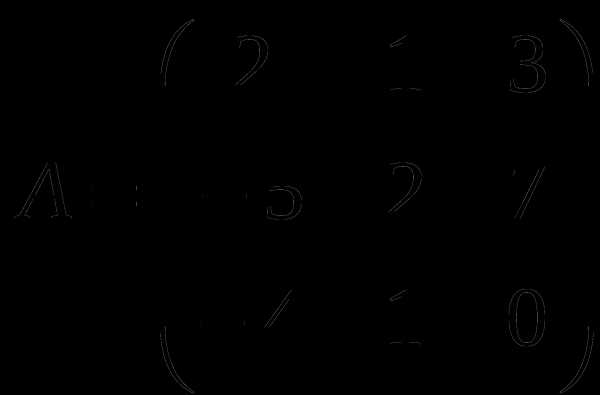
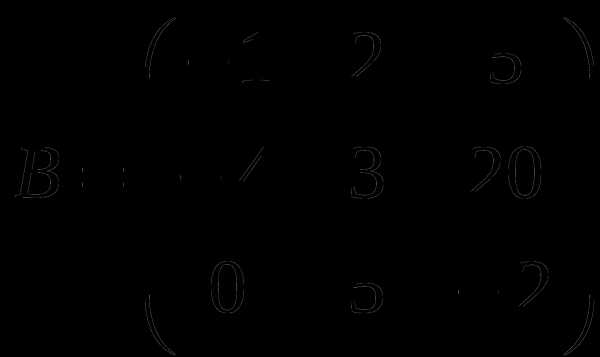
1). Дано: A,B. Найти:

а) 3A-B

б) AB

в)B ^-1

г) BB ^-1

2).Найти ∆A: а) методом треугольников;

б) приведением к треугольному виду

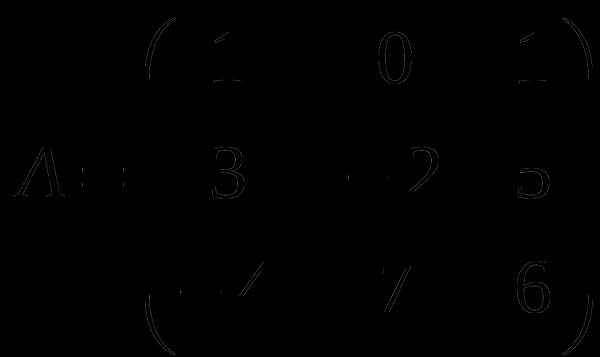
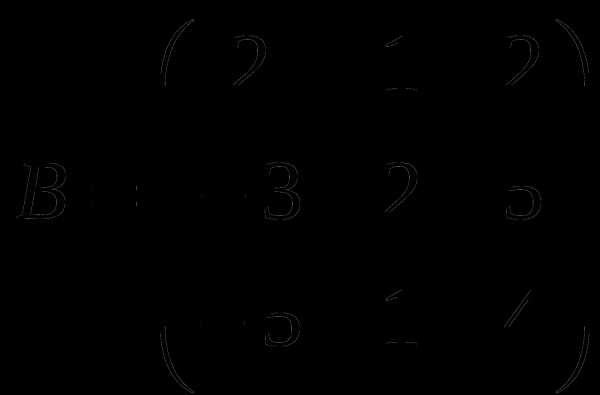
1). Дано: A,B. Найти:

а) A+2B

б) AB

в)B ^-1

г) B ^-1B

2).Найти def A: а) методом треугольников;

б) приведением к треугольному виду;

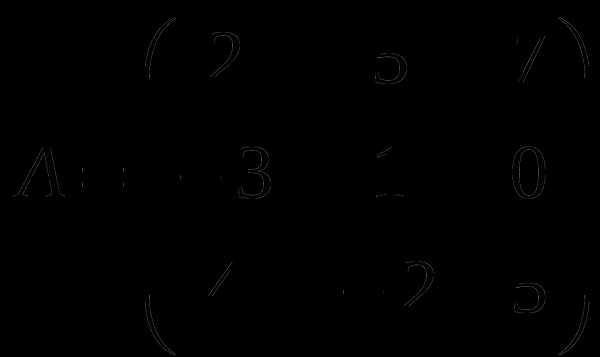
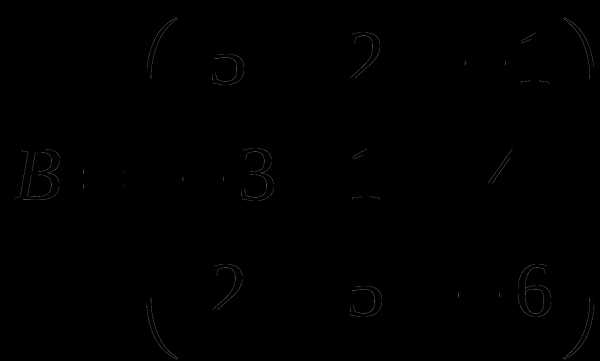
1). Дано: A,B. Найти:

а) B+3A

б) AB

в)B ^-1

г) BB ^-1

2).Найти def B: а) методом треугольников;

б) приведением к каноническому виду

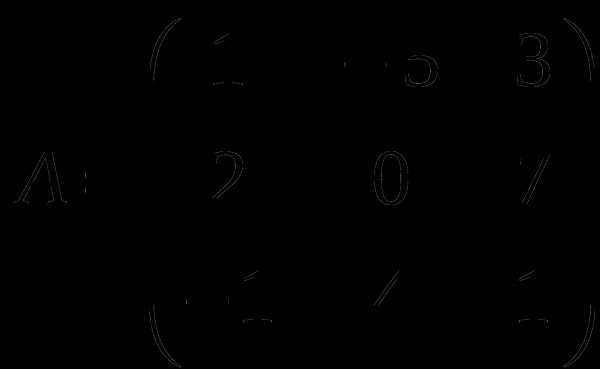
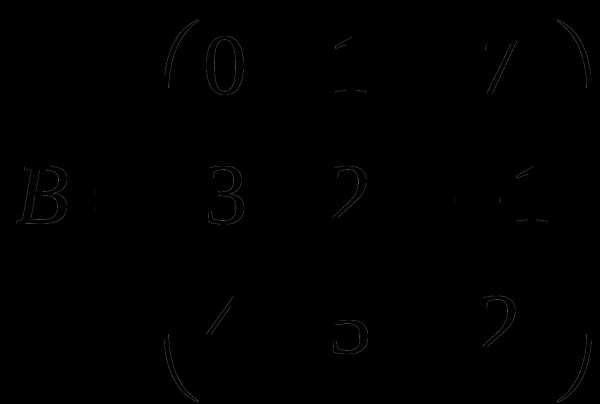
1). Дано: A,B. Найти:

а) 2A-B

б) AB

в)A ^-1

г) A ^-1A

2).Найти def A: а) методом треугольников;

б) приведением к треугольному виду;

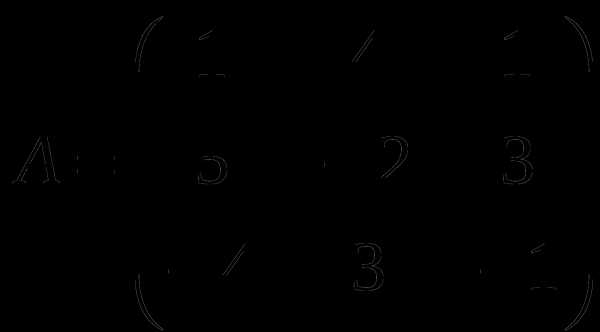
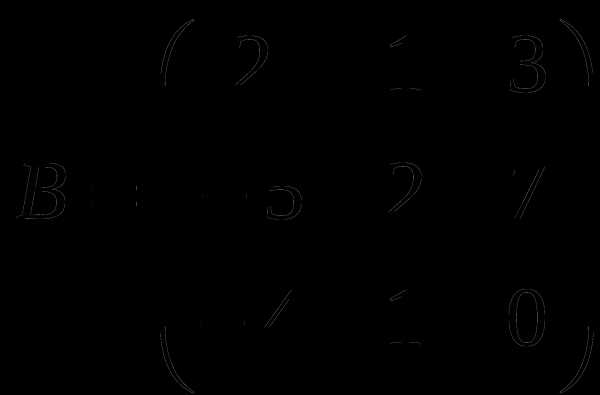
Контрольная работа № 1

infourok.ru

1. Самостоятельная работа матрицы

Самостоятельная работа №3

Системы линейных уравнений

ТЕМА 1. Системы линейных уравнений.

Матрицы и действия с ними.
Определители и их основные свойства.
Методы решения систем линейных уравнений.

СПИСОК ЛИТЕРАТУРЫ

Ильин В. А., Позняк Э. Г. Линейная алгебра: Учеб. для вузов.-5-е изд., стер. — М.: Физматлит, 2002. – 317 с.
Беклемишев Д. В. Курс линейной алгебры и аналитической геометрии: — М.: Физматлит, 2003. – 303 с.
Клетеник Д. В. Сборник задач по аналитической геометрии: Учеб. пособие для втузов / ред. Ефимов Н. В. – 17-е изд., стер. – СПб: Профессия, 2001. – 199 с.
Бугров Я.С., Никольский С.М. Высшая математика: Учеб.для вузов: в 3т.-5-е изд., стер.-М.:Дрофа.- (Высшее образование. Современный учебник). т.1. Элементы линейной алгебры и аналитической геометрии.-2003.-284 с.
Данко П.Е. и др. Высшая математика в упражнениях и задачах (с решениями): в 2 ч./ Данко П.Е., Попов А.Г., Кожевникова Т.Я -6-е изд..-М.: ОНИКС 21 век, ч.1. -2002.-304 с.

Решение типового варианта контрольной работы.

Задача 1. Вычислить определитель .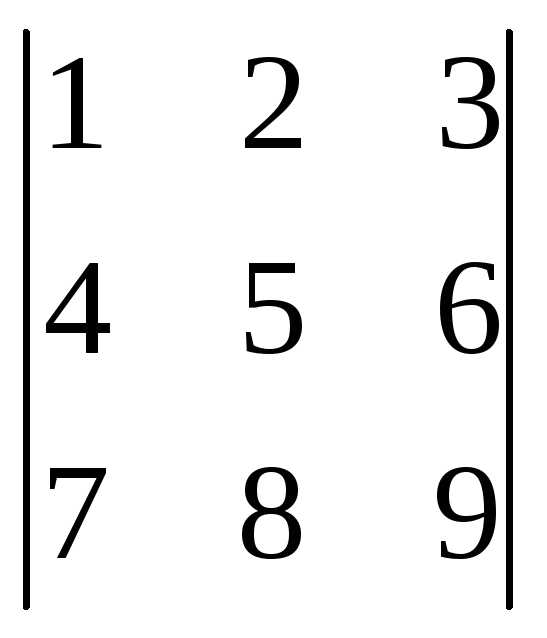

Решение. Для вычисления определителя третьего порядка будем использовать известную формулу Саррюса (правило треугольников), которое может быть записано следующей формулой:

Ответ: 0.

Задача 2. Решить систему методом Гаусса, матричным способом и используя правило Крамера.

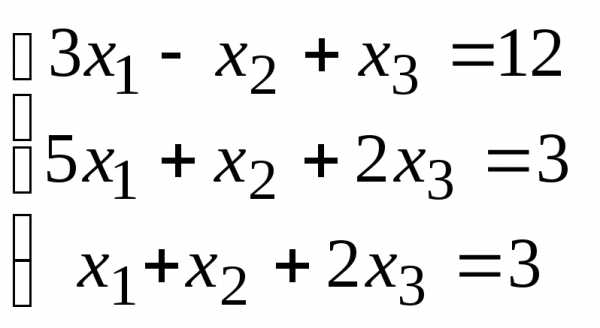
Решение:

Решим систему матричным способом, для этого вычислим обратную матрицу 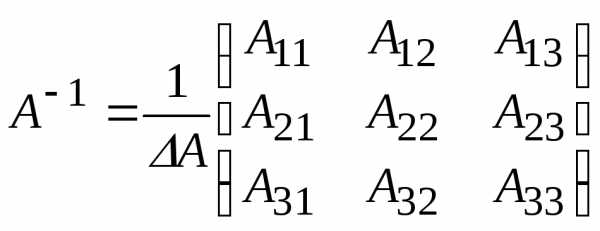, где— алгебраические дополнения к элементам матрицы.

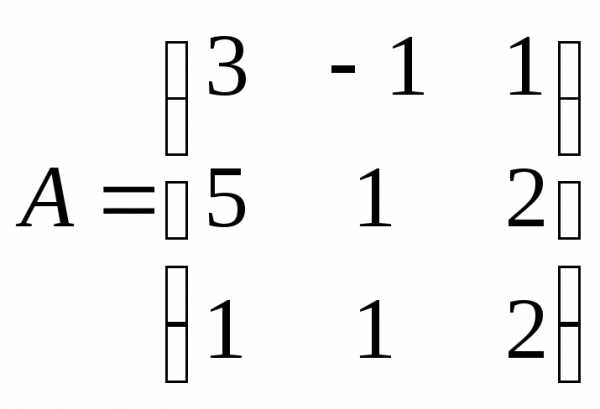
— матрица невырожденная.

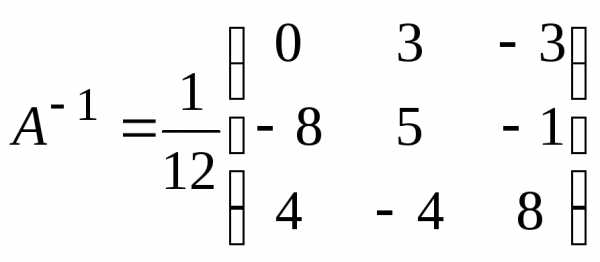
Решим систему методом Крамера. Главный определитель системы:

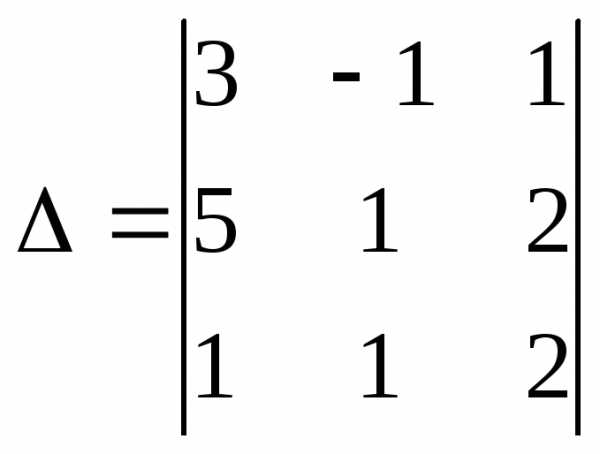. Разложим определитель по элементам первой строки, пользуясь формулой .

Запишем и вычислим вспомогательные определители

Тогда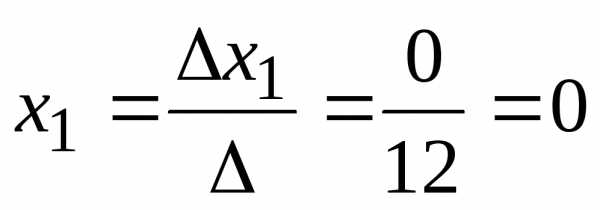

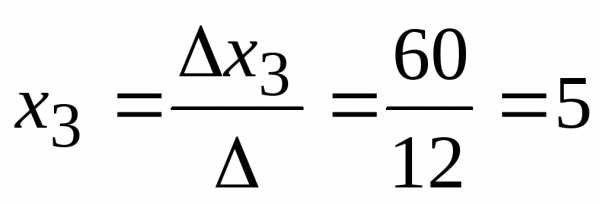
Ответ: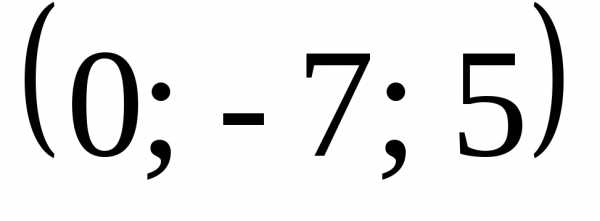

Решим систему методом Гаусса, для этого составим расширенную матрицу системы и упростим ее приведением к треугольному виду.



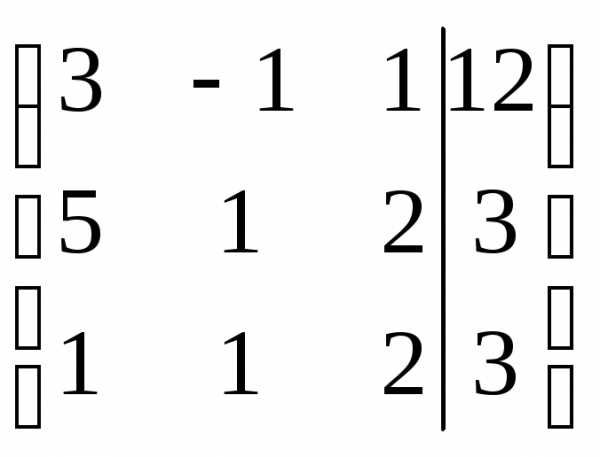
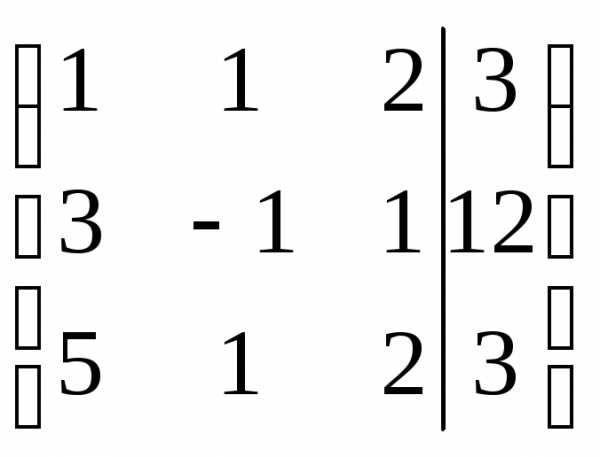
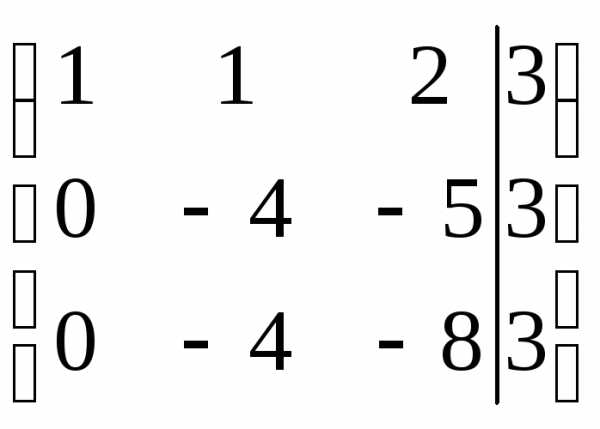
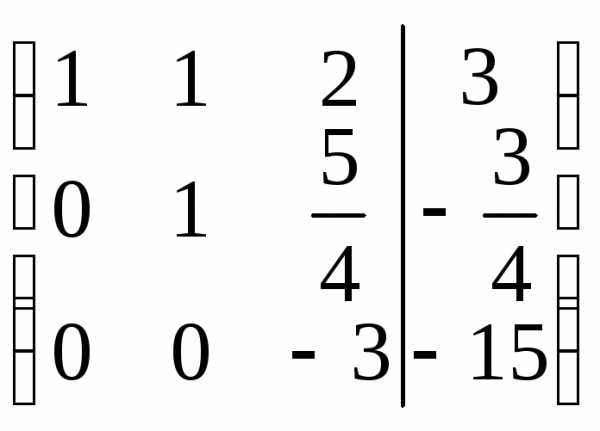
Таким образом, система равносильна системе

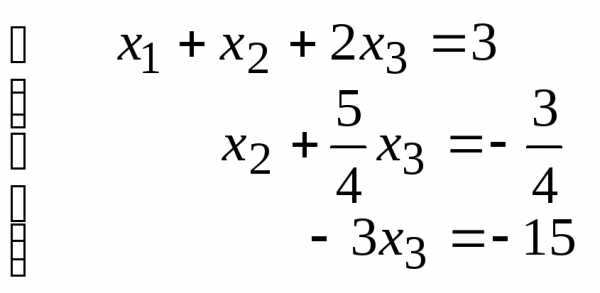
Находим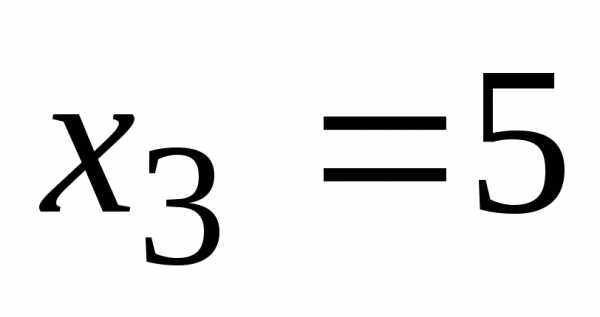

Ответ: ,,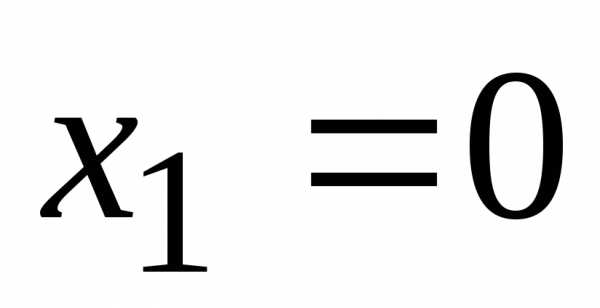

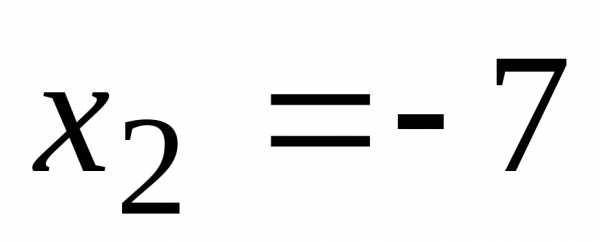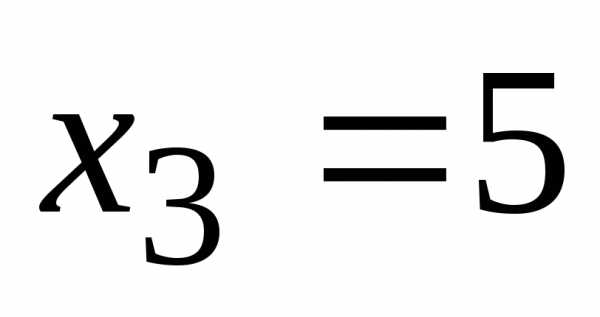
При решении всеми методами одной и той же системы, мы получим один ответ.

Задача 3. Выполнить действия:

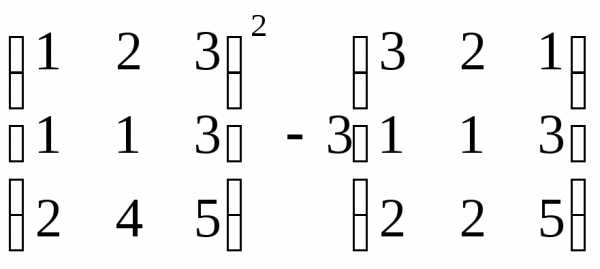
Решение. Выполним решение по действиям.

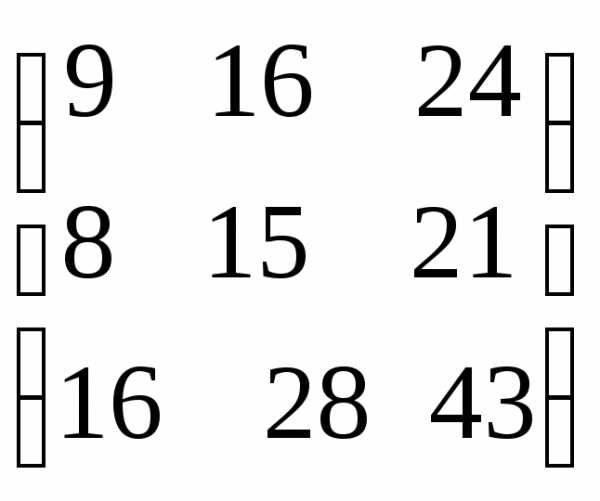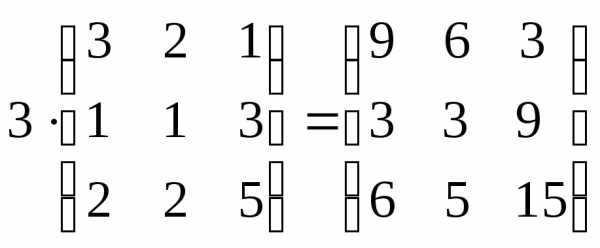Ответ: .

Операция умножения двух матриц вводится только для случая, когда число столбцов первой матрицы равно числу строк второй матрицы.

Если ,, то произведением матрицыназывается матрица, такая, что, где.

Пример: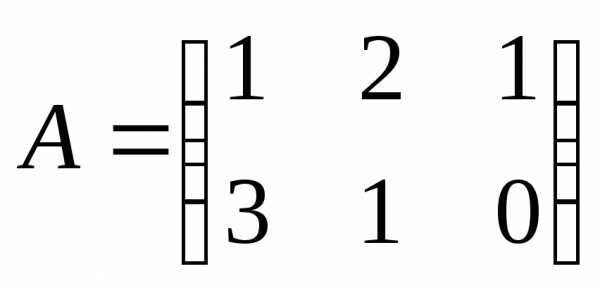

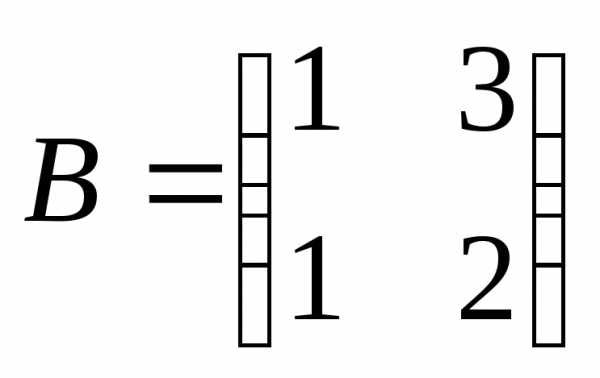
Произведение 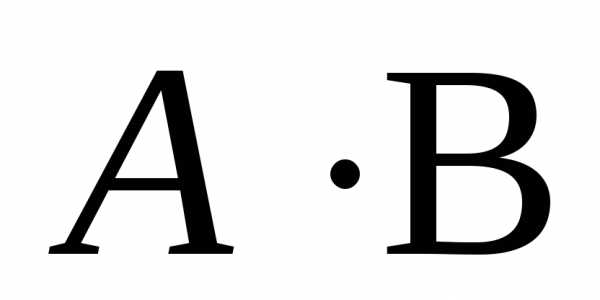не определено, так как число столбцов матрицыА (3) не совпадает с числом строк матрицы В (2).

Произведение 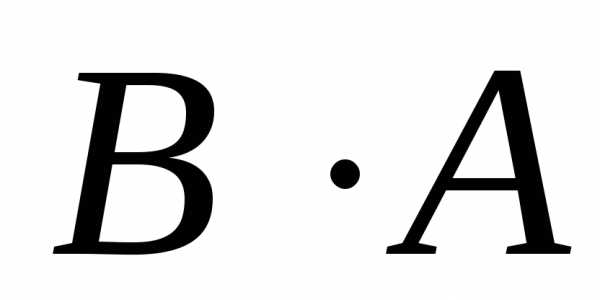определено.

Контрольная работа №1.

Вариант 1

Задача 1. Вычислить определитель:

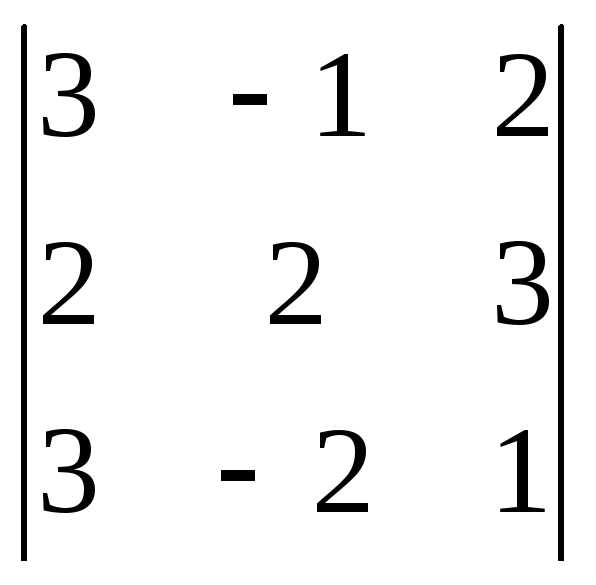
Задача 2. Решить систему методом Гаусса, матричным способом и используя правило Крамера.

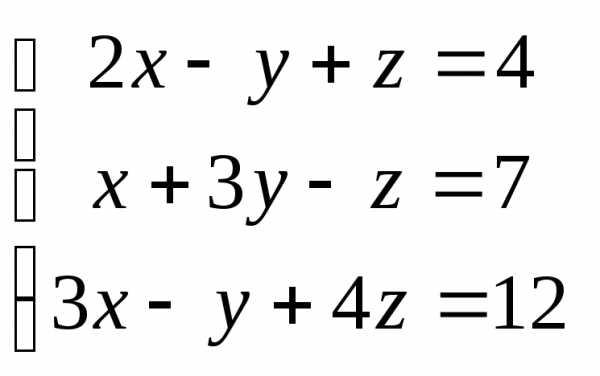
Задача 3. Выполнить действия:

Контрольная работа №1.

Вариант 2

Задача 1. Вычислить определитель:

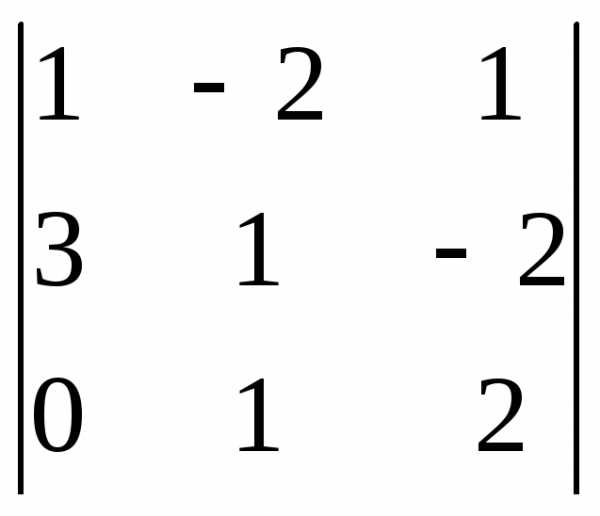
Задача 2. Решить систему методом Гаусса, матричным способом и используя правило Крамера.

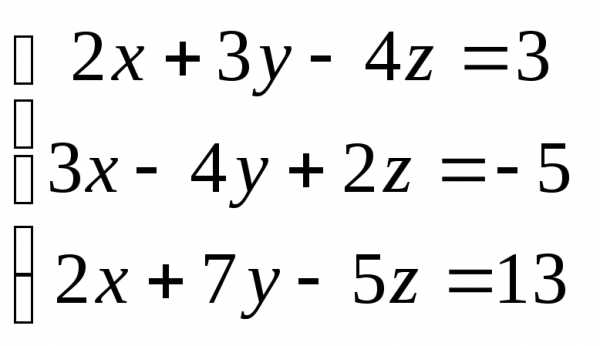
Задача 3. Выполнить действия:

Контрольная работа №1.

Вариант 3

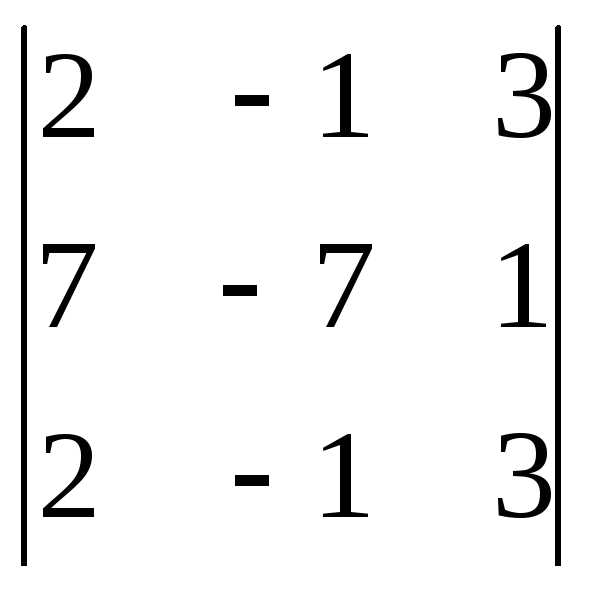
Задача 1. Вычислить определитель:

Задача 2. Решить систему методом Гаусса, матричным способом и используя правило Крамера.

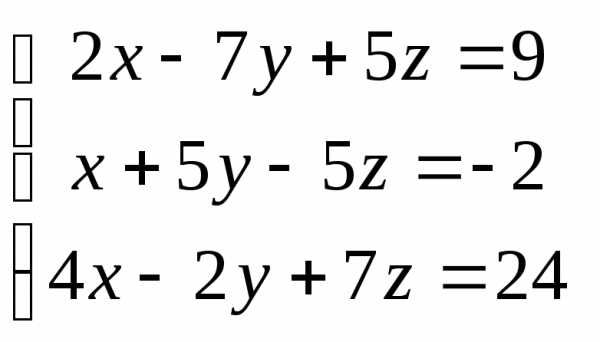
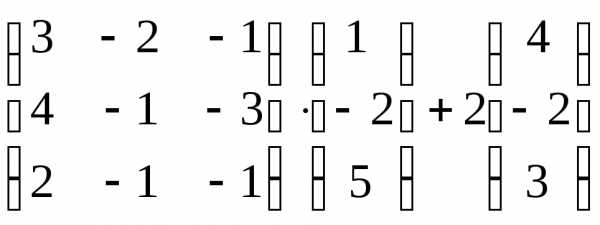
Задача 3. Выполнить действия:

Контрольная работа №1.

Вариант 4

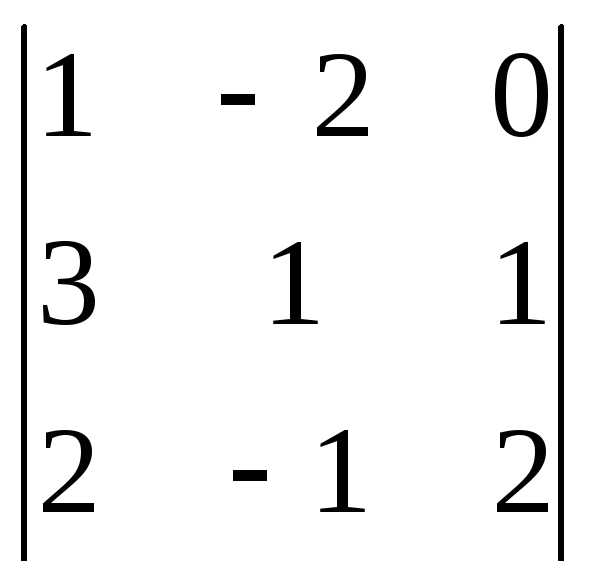
Задача 1. Вычислить определитель:

Задача 2. Решить систему методом Гаусса, матричным способом и используя правило Крамера.

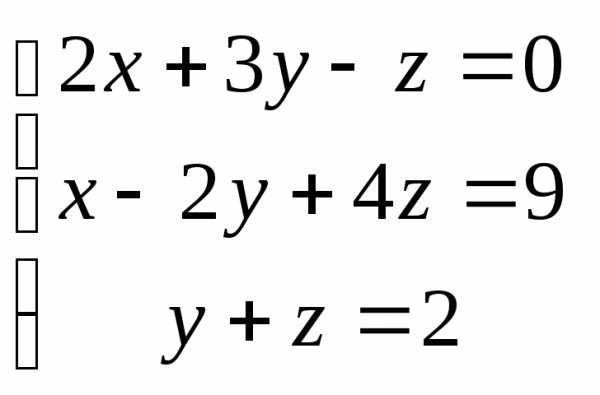
Задача 3. Выполнить действия:

Контрольная работа №1.

Вариант 5

Задача 1. Вычислить определитель:

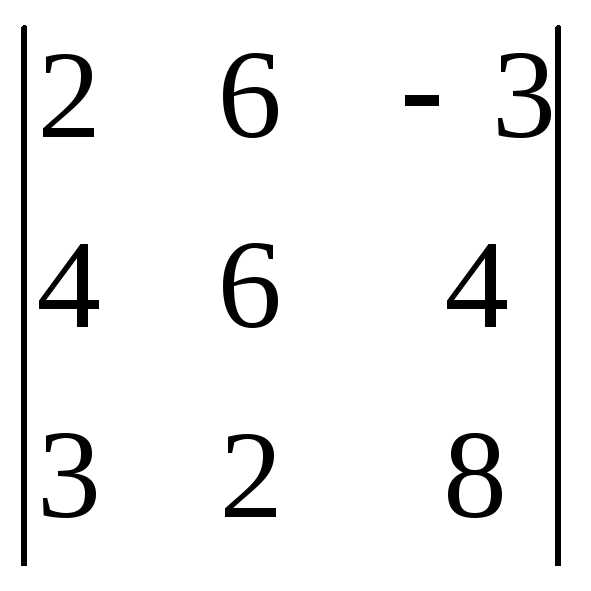
Задача 2. Решить систему методом Гаусса, матричным способом и используя правило Крамера.

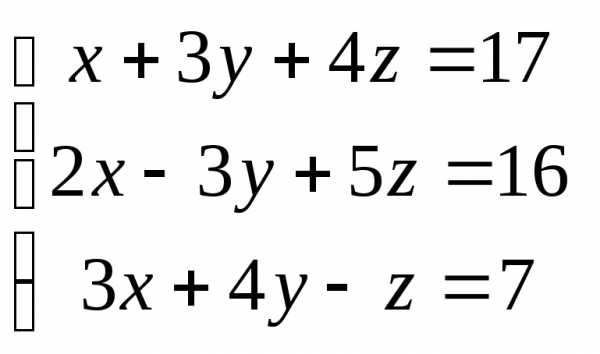
Задача 3. Выполнить действия:

Контрольная работа №1.

Вариант 6

Задача 1. Вычислить определитель:

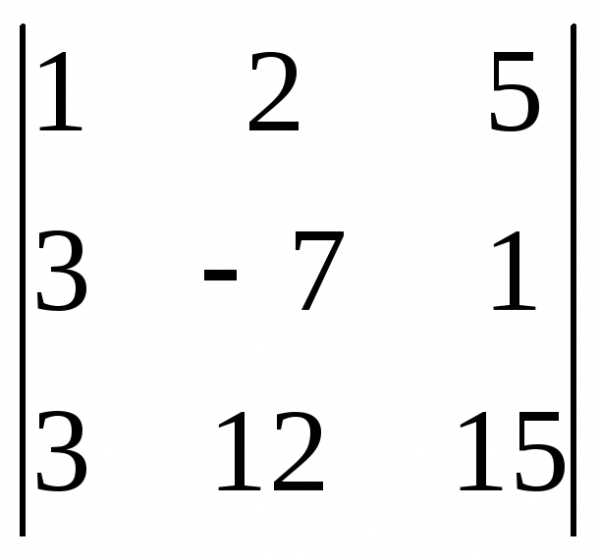
Задача 2. Решить систему методом Гаусса, матричным способом и используя правило Крамера.

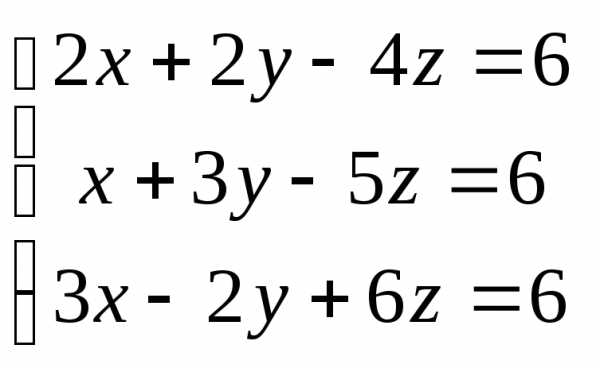
Задача 3. Выполнить действия:

Контрольная работа №1.

Вариант 7

Задача 1. Вычислить определитель:

Задача 2. Решить систему методом Гаусса, матричным способом и используя правило Крамера.

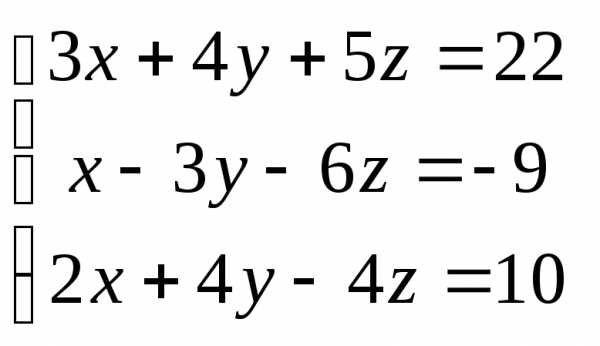
Задача 3. Выполнить действия:

Контрольная работа №1.

Вариант 8

Задача 1. Вычислить определитель:

Задача 2. Решить систему методом Гаусса, матричным способом и используя правило Крамера.

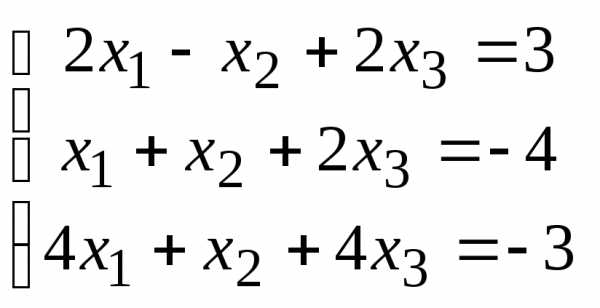
Задача 3. Выполнить действия:

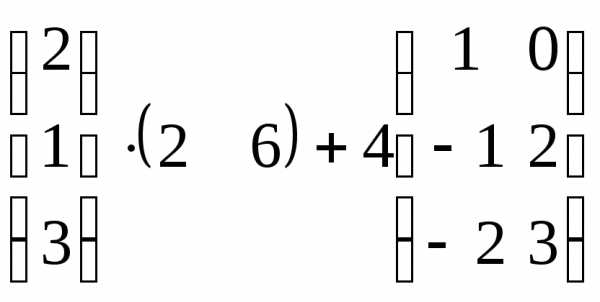
Контрольная работа №1.

Вариант 9

Задача 1. Вычислить определитель:

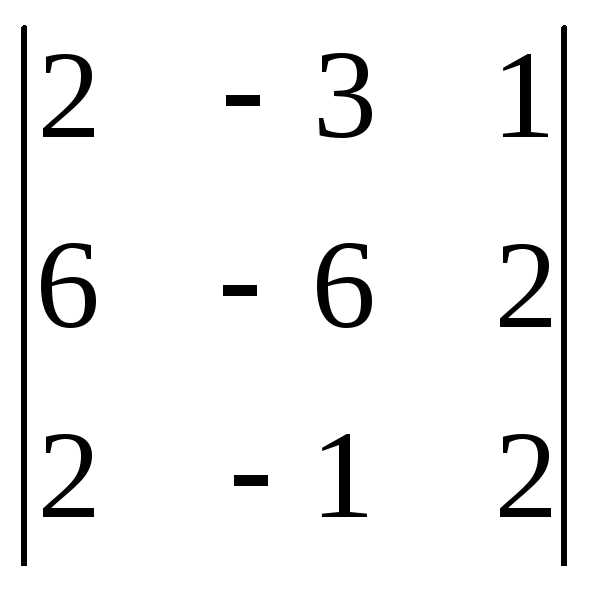
Задача 2. Решить систему методом Гаусса, матричным способом и используя правило Крамера.

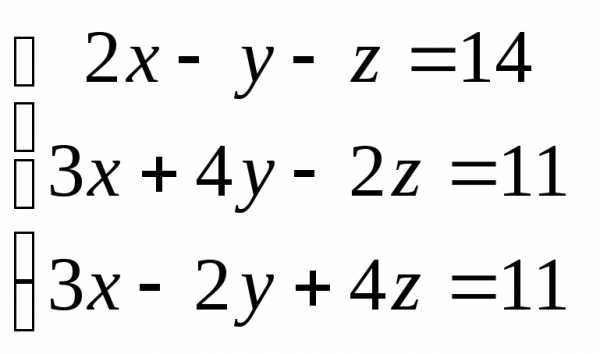
Задача 3. Выполнить действия:

Контрольная работа №1.

Вариант 10

Задача 1. Вычислить определитель:

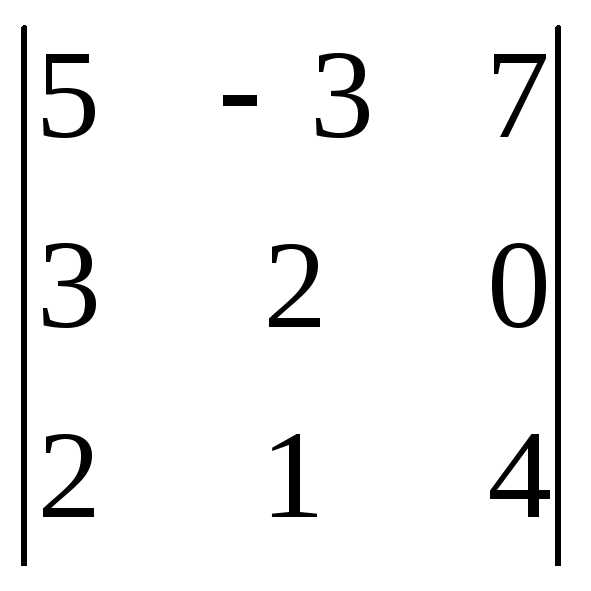
Задача 2. Решить систему методом Гаусса, матричным способом и используя правило Крамера.

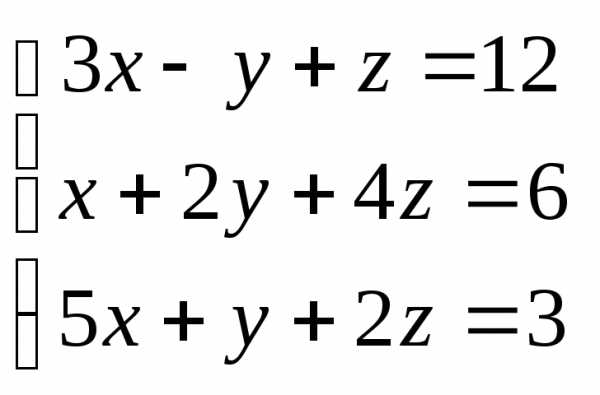
Задача 3. Выполнить действия:

Контрольная работа №1.

Вариант 11

Задача 1. Вычислить определитель:

Задача 2. Решить систему методом Гаусса, матричным способом и используя правило Крамера.

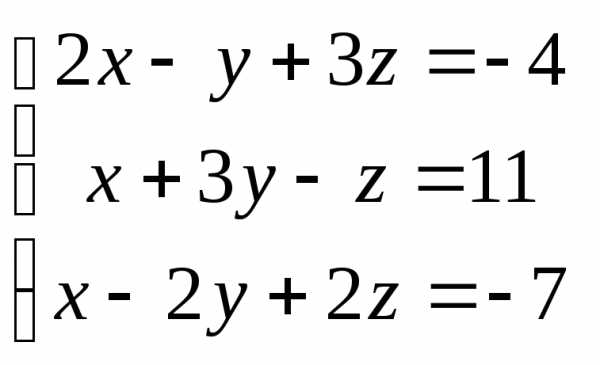
Задача 3. Выполнить действия:

Контрольная работа №1.

Вариант 12

Задача 1. Вычислить определитель:

Задача 2. Решить систему методом Гаусса, матричным способом и используя правило Крамера.

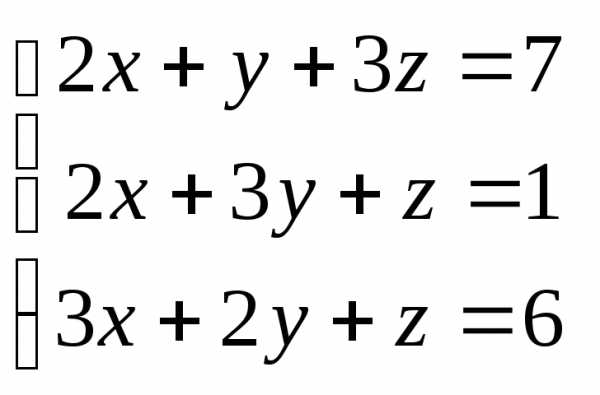
Задача 3. Выполнить действия:

Контрольная работа №1.

Вариант 13

Задача 1. Вычислить определитель:

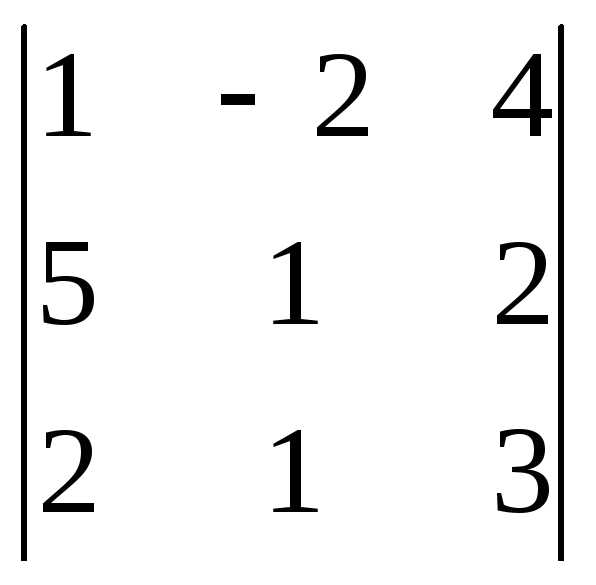
Задача 2. Решить систему методом Гаусса, матричным способом и используя правило Крамера.

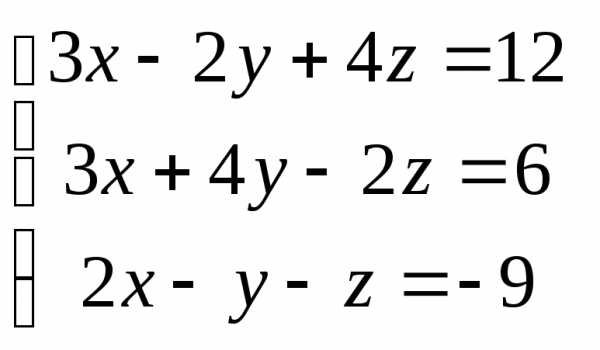
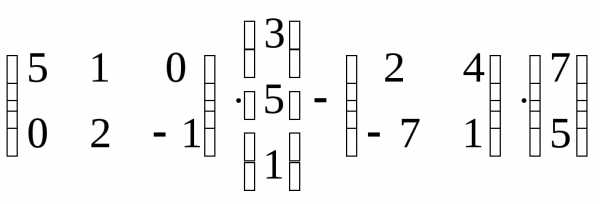
Задача 3. Выполнить действия:

Контрольная работа №1.

Вариант 14

Задача 1. Вычислить определитель:

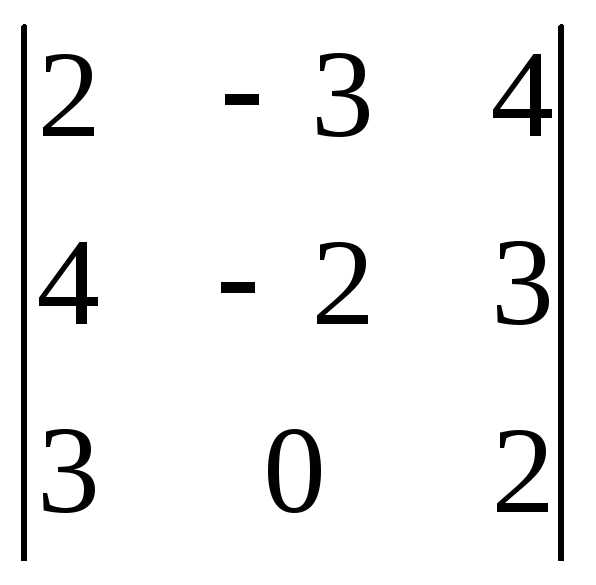
Задача 2. Решить систему методом Гаусса, матричным способом и используя правило Крамера.

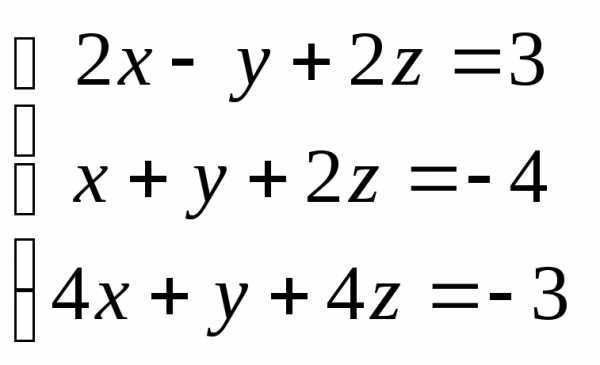
Задача 3. Выполнить действия:

Контрольная работа №1.

Вариант 15

Задача 1. Вычислить определитель:

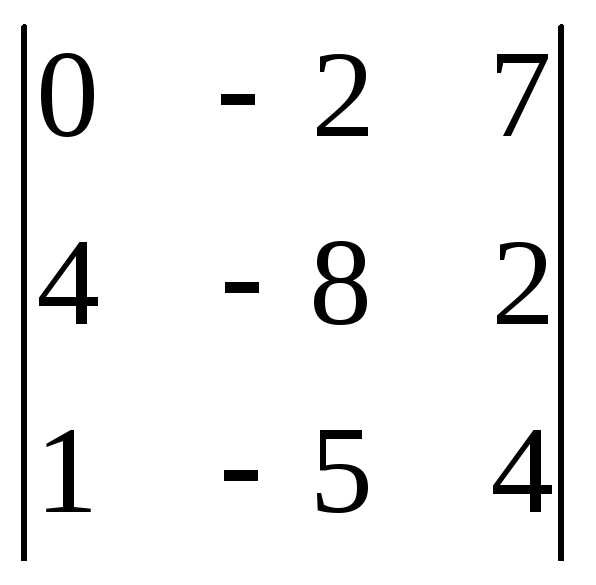
Задача 2. Решить систему методом Гаусса, матричным способом и используя правило Крамера.

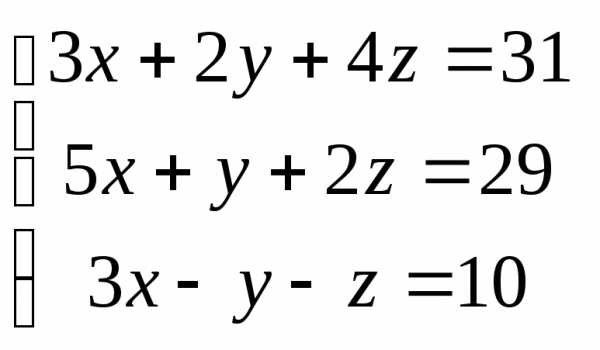
Задача 3. Выполнить действия:

Контрольная работа №1.

Вариант 16

Задача 1. Вычислить определитель:

Задача 2. Решить систему методом Гаусса, матричным способом и используя правило Крамера.

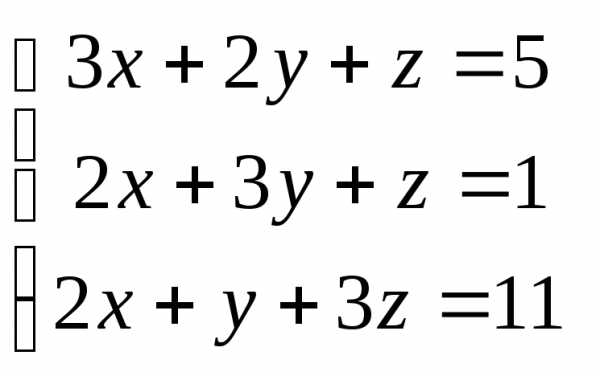
Задача 3. Выполнить действия:

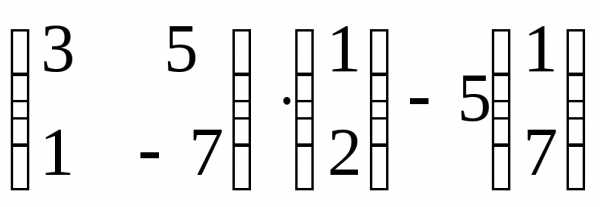
Контрольная работа №1.

Вариант 17

Задача 1. Вычислить определитель:

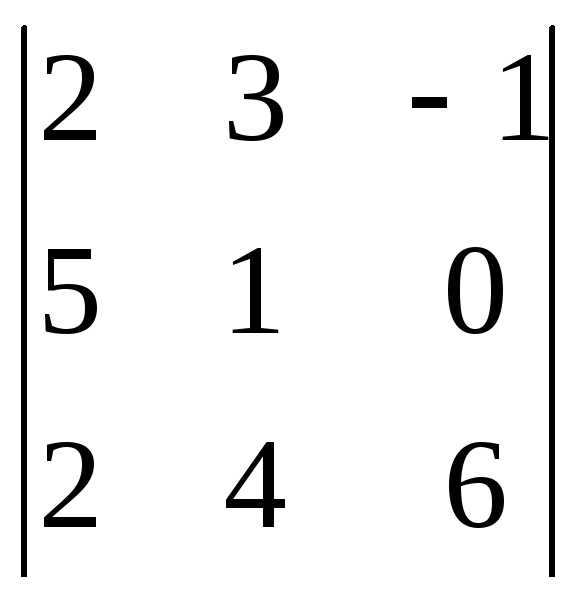
Задача 2. Решить систему методом Гаусса, матричным способом и используя правило Крамера.

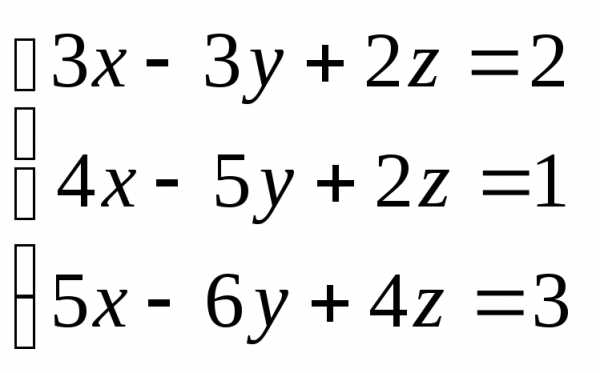
Задача 3. Выполнить действия:

Контрольная работа №1.

Вариант 18

Задача 1. Вычислить определитель:

Задача 2. Решить систему методом Гаусса, матричным способом и используя правило Крамера.

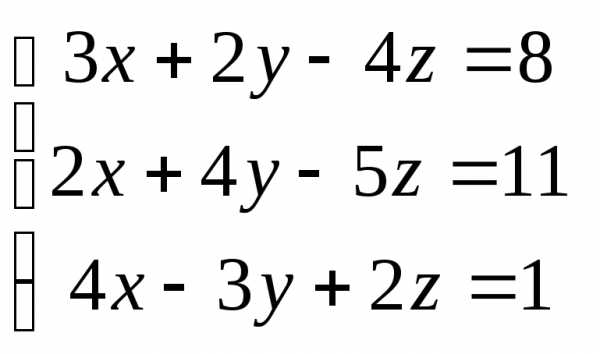
Задача 3. Выполнить действия:

Контрольная работа №1.

Вариант 19

Задача 1. Вычислить определитель:

Задача 2. Решить систему методом Гаусса, матричным способом и используя правило Крамера.

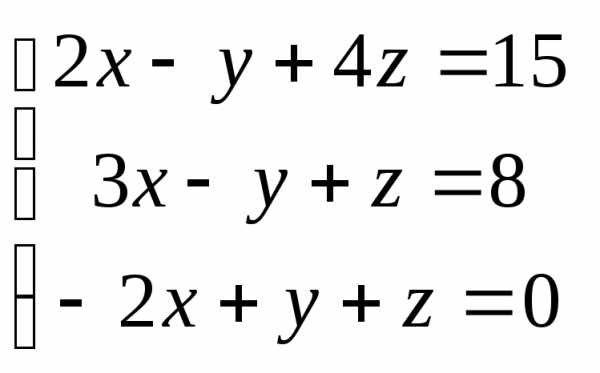
Задача 3. Выполнить действия:

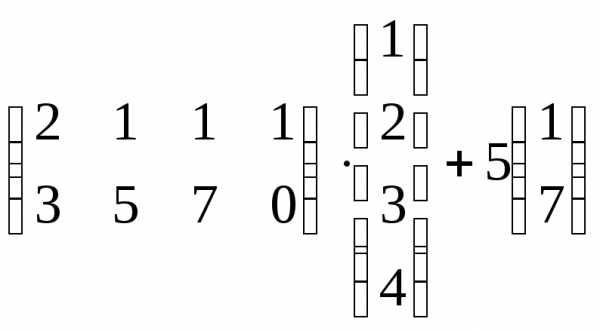
Контрольная работа №1.

Вариант 20

Задача 1. Вычислить определитель:

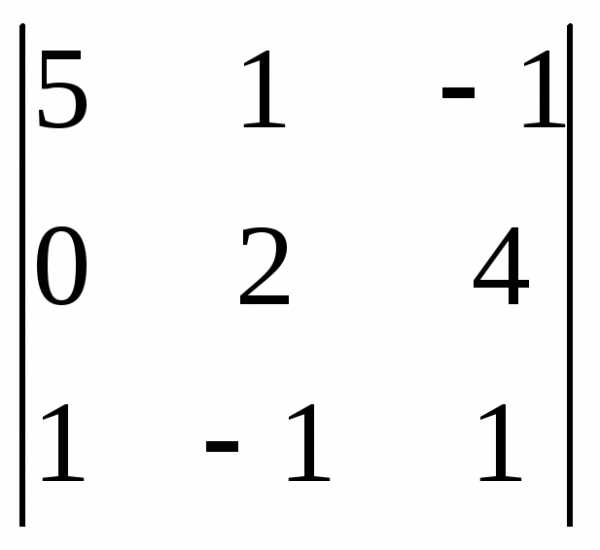
Задача 2. Решить систему методом Гаусса, матричным способом и используя правило Крамера.

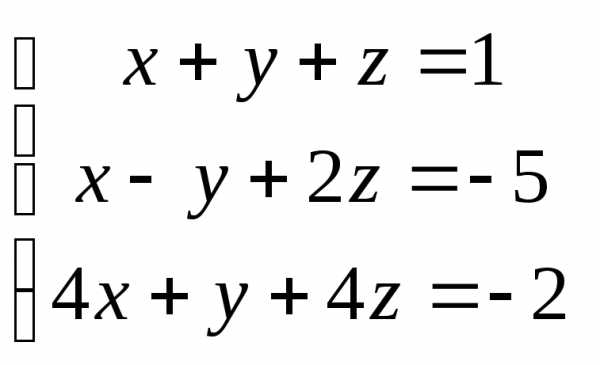
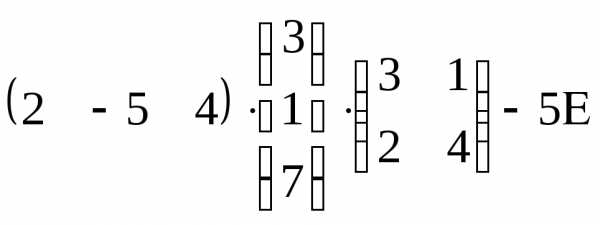
Задача 3. Выполнить действия:

Контрольная работа №1.

Вариант 21

Задача 1. Вычислить определитель:

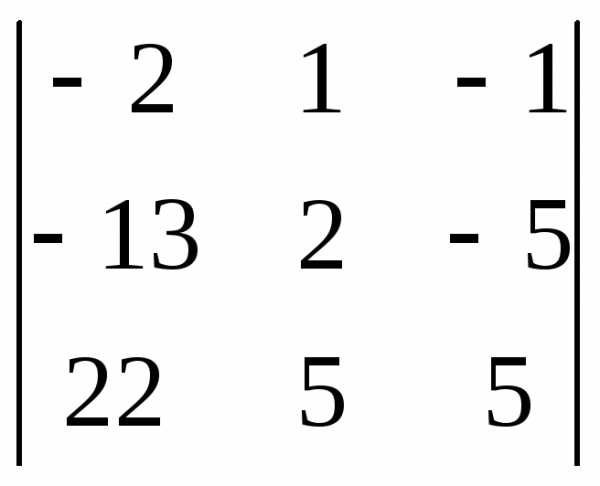
Задача 2. Решить систему методом Гаусса, матричным способом и используя правило Крамера.

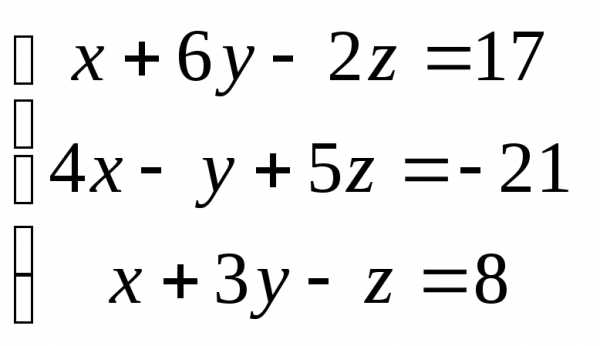
Задача 3. Выполнить действия:

Контрольная работа №1.

Вариант 22

Задача 1. Вычислить определитель:

Задача 2. Решить систему методом Гаусса, матричным способом и используя правило Крамера.

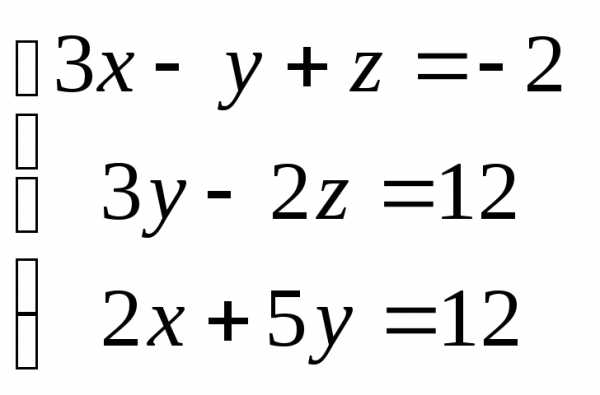
Задача 3. Выполнить действия:

Контрольная работа №1.

Вариант 23

Задача 1. Вычислить определитель:

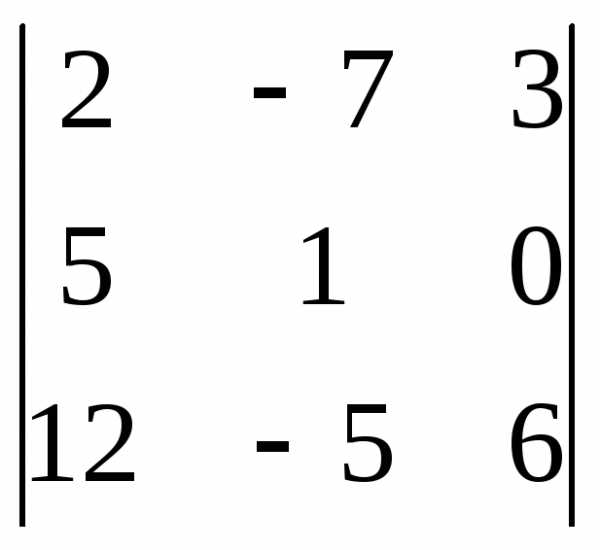
Задача 2. Решить систему методом Гаусса, матричным способом и используя правило Крамера.

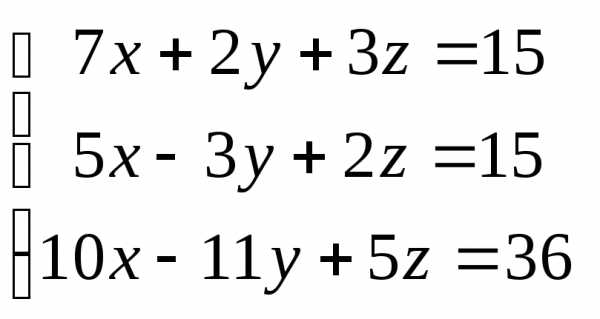
Задача 3. Выполнить действия:

Контрольная работа №1.

Вариант 24

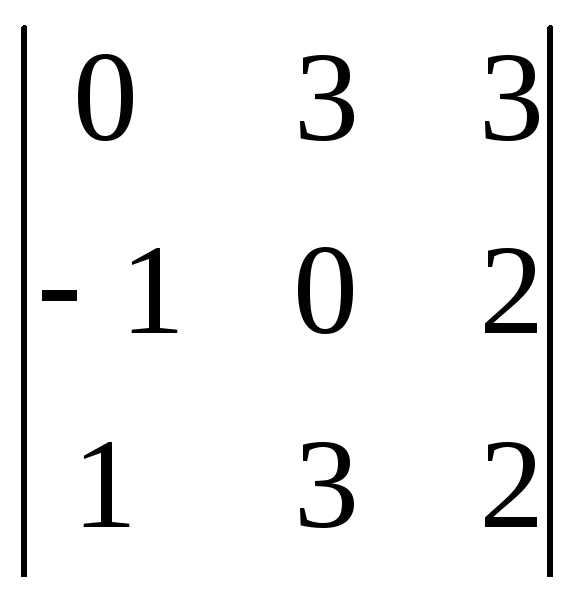
Задача 1. Вычислить определитель:

Задача 2. Решить систему методом Гаусса, матричным способом и используя правило Крамера.

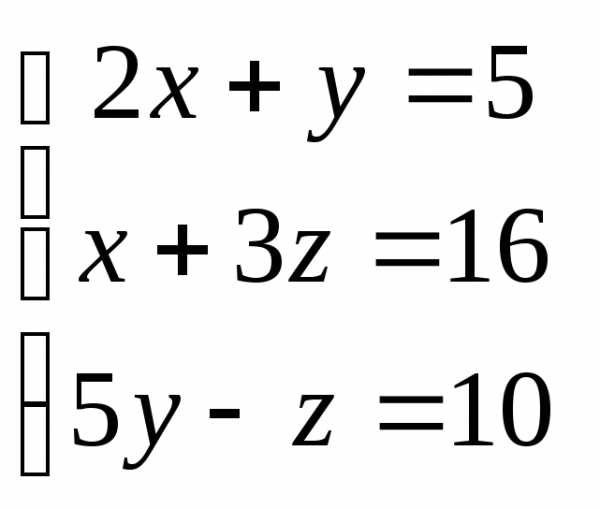
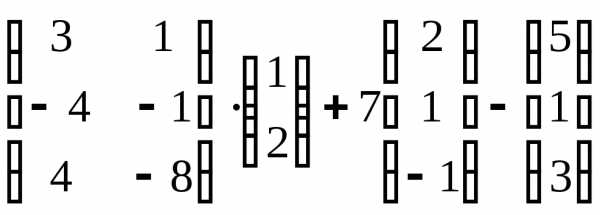
Задача 3. Выполнить действия:

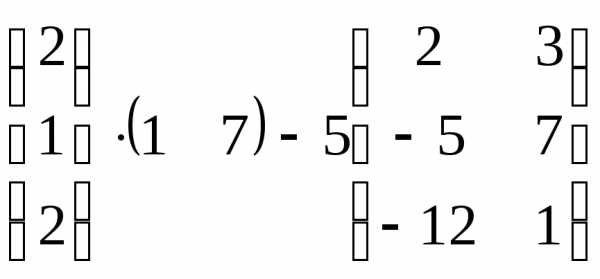
Контрольная работа №1.

Вариант 25

Задача 1. Вычислить определитель:

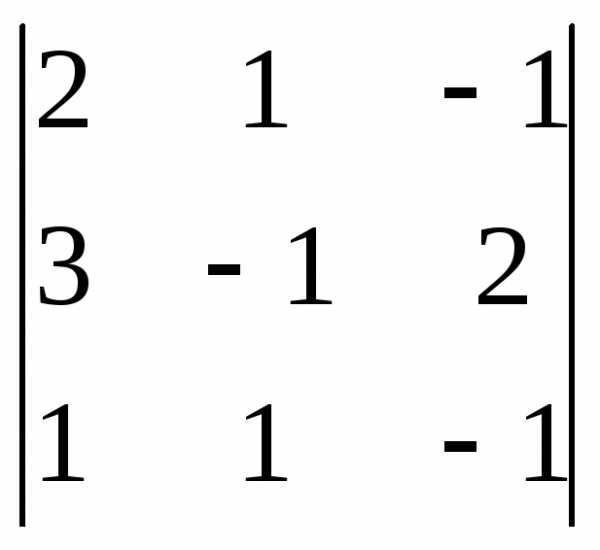
Задача 2. Решить систему методом Гаусса, матричным способом и используя правило Крамера.

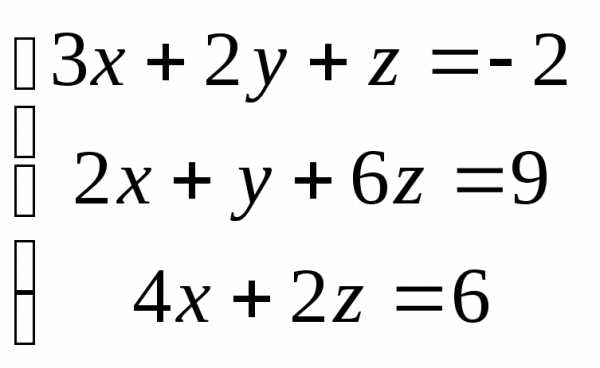
Задача 3. Выполнить действия:

Контрольная работа №1.

Вариант 26

Задача 1. Вычислить определитель:

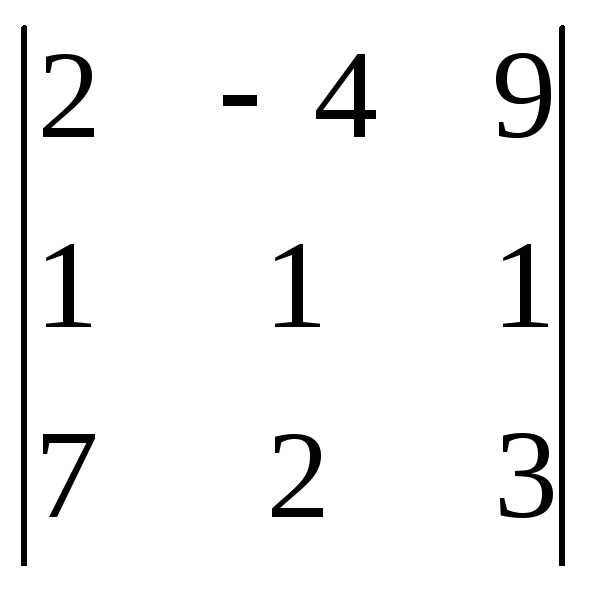
Задача 2. Решить систему методом Гаусса, матричным способом и используя правило Крамера.

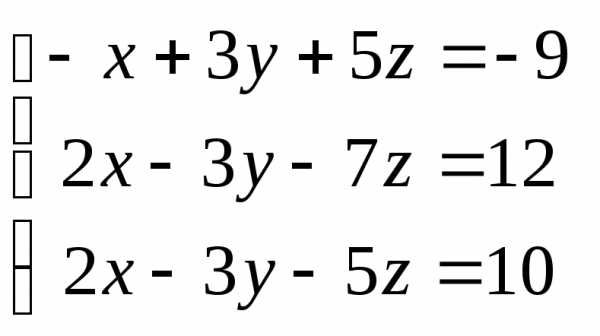
Задача 3. Выполнить действия:

Контрольная работа №1.

Вариант 27

Задача 1. Вычислить определитель:

Задача 2. Решить систему методом Гаусса, матричным способом и используя правило Крамера

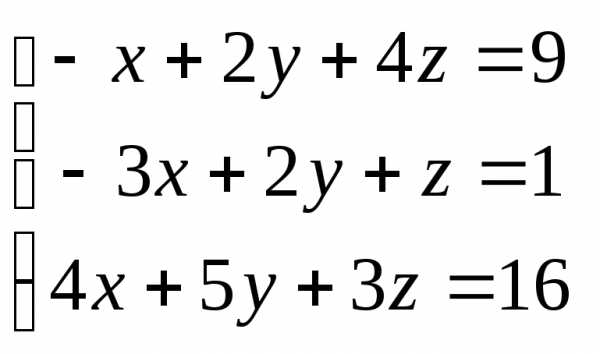
Задача 3. Выполнить действия:

Контрольная работа №1.

Вариант 28

Задача 1. Вычислить определитель:

Задача 2. Решить систему методом Гаусса, матричным способом и используя правило Крамера

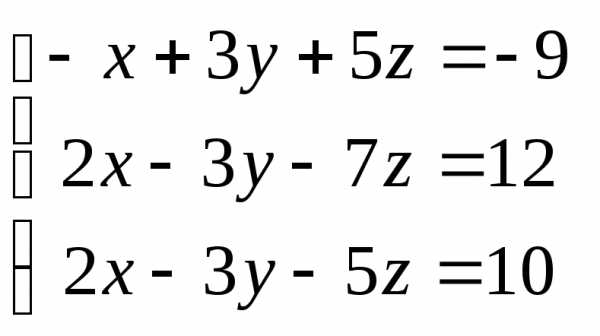
Задача 3. Выполнить действия:

Контрольная работа №1.

Вариант 29

Задача 1. Вычислить определитель:

Задача 2. Решить систему методом Гаусса, матричным способом и используя правило Крамера

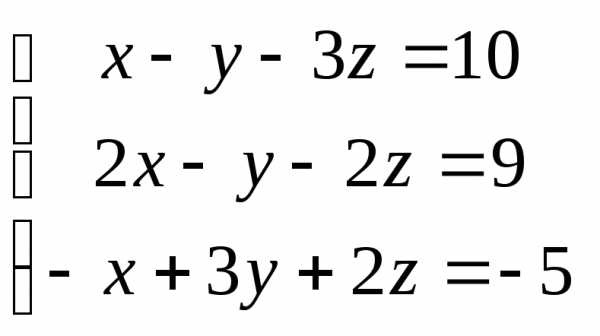
Задача 3. Выполнить действия:

Контрольная работа №1.

Вариант 30

Задача 1. Вычислить определитель:

Задача 2. Решить систему методом Гаусса, матричным способом и используя правило Крамера

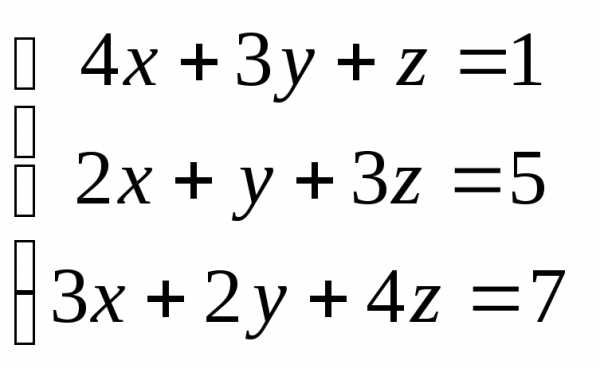
Задача 3. Выполнить действия:

studfiles.net

а) и , б ) 3А в) А – 2В, г) ВT , АT — Студопедия.Нет

Вариант

1. Даны матрицы. 1)Вычислить: а) и , б ) 3А в) А – 2В, г) В^T^{, А^T}

2) Вычислить: а) определители матриц А и В, б) найти обратные матрицы

1) А= В=

2) А = 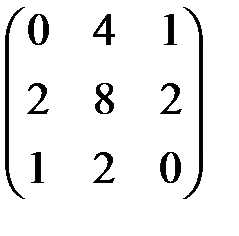, В = .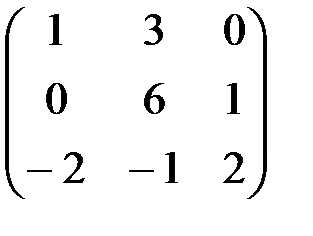

2. Решить систему уравнений а) Крамера б) Гаусса в) матричным

а) б)

3. Даны точки A(3,-5,4) B(-3,-4,0) C(-7,04) D(5,-6,1).

Найти: а) Координаты и длину вектора

б) координаты вектора

в) Найти площадь треугольника АВС и внутренний угол В

г) найти объем пирамиды ABCD и длину ее высоты, опущенной из вершины D

4. Векторы и образуют угол . Зная, что , вычислить .

5. Составить все виды уравнений (параметрическое, каноническое, общее, с угловым коэффициентом, через две точки, в отрезках) прямой, если известно, что она проходит через точку параллельно вектору .

6. Написать уравнение окружности, проходящей через три точки:

А (0; 2), В (1; 1), С (2; -2).

7. Составить каноническое уравнение эллипса, зная, что его большая ось равна 26, а фокусы лежат в точках F₁(10; 0) и F₂(14; 0).

8. Составить каноническое уравнение гиперболы, если ее действительная ось равна 6 и гипербола проходит через точку (9; -4).

9. Составить уравнение параболы, если вершина параболы в начале системы координат, парабола симметрична относительно оси ОУ и проходит через точку М (1; -2).

10. Составить уравнение сферы, если точки и являются концами одного из диаметров сферы.

Контрольная работа по математике за I семестр.

Вариант

1.Даны матрицы. 1)Вычислить: а) и , б ) 3А в) А – 2В, г) В^T^{, А^T}

2) Вычислить: а) определители матриц А и В, б) найти обратные матрицы

2) , ;

2. Решить систему уравнений а) Крамера б) Гаусса в) матричным

а) б)

3. Даны точки A(1,-2,-1) B(0,-5,4 ) C(3,-1,3 ) D(-1,0,3).

Найти а) Координаты и длину вектора

б) координаты вектора

в) Найти объем пирамиды ABCD и длину ее высоты, опущенной из вершины D

г) найти площадь треугольника АВС и внутренний угол В

4. Векторы и образуют угол . Зная, что , вычислить .

5. Составить все виды уравнений(параметрическое, каноническое, общее, с угловым коэффициентом, через две точки, в отрезках) прямой, если известно, что она проходит через точку параллельно вектору .

6. Написать уравнение окружности, проходящей через три точки:

А (0; 1), В (1; -1), С (3; -3).

7. Составить каноническое уравнение эллипса, зная, что его большая ось равна 16, а фокусы лежат в точках F₁(10; 0) и F₂(14; 0).

8. Составить каноническое уравнение гиперболы, если ее действительная ось равна 16 и гипербола проходит через точку (9; -4).

9. Составить уравнение параболы, если вершина параболы в начале системы координат, парабола симметрична относительно оси ОY и проходит через точку М (-1; -2).

10. Составить уравнение сферы, если точки и являются концами одного из диаметров сферы.

Контрольная работа по математике за I семестр.

Вариант

1. Даны матрицы. 1) Вычислить: а) и , б ) 3А в) А – 2В, г) В^T^{, А^T}

2) Вычислить: а) определители матриц А и В, б) найти обратные матрицы

, .

2. Решить систему уравнений а) Крамера б) Гаусса в) матричным

а) б)

3. Даны точки A(2,0,1) B(-1,0,3 ) C(1,1,1) D(-1,2,-1).

Найти: а) Координаты и длину вектора

б) координаты вектора

в) найти объем пирамиды ABCD и длину ее высоты, опущенной из вершины D

г) Найти площадь треугольника АВС и внутренний угол В

4. Векторы и образуют угол . Зная, что , вычислить

6. Написать уравнение окружности, проходящей через три точки:

А (1; 2), В (1; 2), С (2; -2).

7. Составить каноническое уравнение эллипса, зная, что его большая ось равна 6, а фокусы лежат в точках F₁(10; 1) и F₂(14; 1).

8. Составить каноническое уравнение гиперболы, если ее действительная ось равна 6 и гипербола проходит через точку (4; -4).

9. Составить уравнение параболы, если вершина параболы в начале системы координат, парабола симметрична относительно оси ОX и проходит через точку М (0; -2).

10.Составить уравнение сферы, если точки и являются концами одного из диаметров сферы.

studopedia.net

Итоговая работа по теме : «Матрицы»

1 вариант

2 вариант

Решить систему линейных уравнений

методом Гаусса

Решить систему линейных уравнений

методом Гаусса

Решить систему линейных уравнений

методом Гаусса

Найдите разность и сумму матриц: А+В, А-В, В-А.

Найдите разность и сумму матриц: А+В, А-В, В-А.

Найдите разность и сумму матриц: А+В, А-В, В-А.

Найти произведение матриц AB, если

Найти произведение матриц BA, если

Найти произведение матриц BA, если

Найдите определитель матрицы

Найдите определитель матрицы

Найдите определитель матрицы

Найдите обратную матрицу

Найдите обратную матрицу

Найдите обратную матрицу

intolimp.org

Контрольные — Контрольная по математике Матрицы

Выполнить нельзя, т. к. матрицы должны быть одной размерности

2) А’+В

Выполнить нельзя, т. к. матрицы должны быть одной размерности

3) А+В’

Выполнить нельзя, т. к. матрицы должны быть одной размерности

4) АВ

Выполнить можно, чисто столбцов А= числу строк В

5) ВА

Выполнить нельзя, чисто столбцов Вчислу строк А

6) А’В

Выполнить можно, чисто столбцов А’= числу строк В

7) АВ’

Выполнить нельзя, чисто столбцов Ачислу строк В’

8) А’B’

Выполнить нельзя, чисто столбцов А’числу строк В’

9) B’А’

Выполнить можно, число столбцов В’= числу строк А’

№2

Даны матрицы А= и В=. Найти B’А’ АВ

Решение:

А’= В’=

В’A’=

АВ=

B’А’ АВ=

№3

Дана матрица А=

Ответ С

№4

Дана матрица А=. Найти определитель матрицы В=А’А.

Решение:

А’=

В=

№5

Определить какая из приведенных ниже матриц имеют обратную.

1) 2) 3) 4)

Ответ

1) Матрица не квадратная, значит не имеет обратной

2) Определитель матрицы равен нулю, значит не имеет обратной

4) Определитель матрицы равен нулю, значит не имеет обратной

№6

При каком значении а матрица Д=будет равна матрице ВС, где А=

Ответ :

А=9.

№7

Найти С’ матрицы С=(АВ-B’A’+3E, где А= В= Е=.

Решение:

АВ=

(АВ)’=

В’= А’=

B’A’= 3Е=

С=

С’=

Системы линейных уравнений

№1

По формулам Крамера решить систему

Решение:

= =-3

Δ2 =

Δ3 =

x1 = Δ1/Δ = 1
x2 = Δ2/Δ = 2
x3 = Δ3/Δ = -1

№2

Решить матричное уравнение

Решение:

АХ=В

, значит матрица не вырождена, следовательно можно найти решение уравнения АХ=В с помощью. Умножая обе часть уравнения на слева, получим

Откуда

Вычислим алгебраические дополнения:

Отсюда

Х=

№3

Решить систему методом Гаусса:

edutext.net

Контрольная работа по математике 1 семестр

ВОПРОСЫ К ЗАЧЕТУ

по дисциплине «Математика»

1 семестр, I курс, 122 группа, 2013/2014 уч.год

Основные сведения о матрицах (определение, обозначения, виды — единичная, обратная и пр.)
Операции над матрицами (сложение, вычитание, умножение, возведение в степень, транспонирование)
Свойства операций над матрицами. Свойства умножения матриц
Определители матриц.
Правило Сарруса (правило треугольников)
Минор
Алгебраическое дополнение.
Теорема Лапласа
Свойства определителей
Обратная матрица
Необходимое и достаточное условие существования обратной матрицы
Алгоритм вычисления обратной матрицы
Ранг матрицы
Теорема о ранге матриц
Элементарные преобразования матриц
Система линейных уравнений. Матричное представление
Метод обратной матрицы
Теорема Крамера. Формулы Крамера
Метод Гаусса.
Теорема Кронекера-Капелли.

Вариант 1,6,11

Контрольная работа по математике

1 семестр (заочная форма обучения)

1. Найти произведение двух матриц AB и BA, если это возможно

2. Вычислить определитель матрицы А двумя методами:

а) применяя правило Сарруса

б) используя разложение по элементам третьей строки (по теореме Лапласа)

3. Найти матрицу, обратную данной

4. Найти ранг матрицы

5. Решить систему линейных уравнений

a) методом обратной матрицы

б) методом Крамера

6. Решить систему линейных уравнений методом Гаусса

Вариант 2,7,12

Контрольная работа по математике

1 семестр (заочная форма обучения)

1. Найти произведение двух матриц AB и BA, если это возможно

2. Вычислить определитель матрицы А двумя методами:

а) применяя правило Сарруса

б) используя разложение по элементам первой строки (по теореме Лапласа)

3. Найти матрицу, обратную данной

4. Найти ранг матрицы

5. Решить систему линейных уравнений

a) методом обратной матрицы

б) методом Крамера

6. Решить систему линейных уравнений методом Гаусса

Вариант 3,8,13

Контрольная работа по математике

1 семестр (заочная форма обучения)

1. Найти произведение двух матриц AB и BA, если это возможно

2. Вычислить определитель матрицы А двумя методами:

а) применяя правило Сарруса

б) используя разложение по элементам второй строки (по теореме Лапласа)

3. Найти матрицу, обратную данной

4. Найти ранг матрицы

5. Решить систему линейных уравнений

a) методом обратной матрицы

б) методом Крамера

6. Решить систему линейных уравнений методом Гаусса

Вариант 4,9,14

Контрольная работа по математике

1 семестр (заочная форма обучения)

1. Найти произведение двух матриц AB и BA, если это возможно

2. Вычислить определитель матрицы А двумя методами:

а) применяя правило Сарруса

б) используя разложение по элементам второго столбца (по теореме Лапласа)

3. Найти матрицу, обратную данной

4. Найти ранг матрицы

5. Решить систему линейных уравнений

a) методом обратной матрицы

б) методом Крамера

6. Решить систему линейных уравнений методом Гаусса

Вариант 5,10,15

Контрольная работа по математике

1 семестр (заочная форма обучения)

1. Найти произведение двух матриц AB и BA, если это возможно

2. Вычислить определитель матрицы А двумя методами:

а) применяя правило Сарруса

б) используя разложение по элементам третьего столбца (по теореме Лапласа)

3. Найти матрицу, обратную данной

4. Найти ранг матрицы

5. Решить систему линейных уравнений

a) методом обратной матрицы

б) методом Крамера

6. Решить систему линейных уравнений методом Гаусса

gigabaza.ru

Контрольная работа — Матрицы и определители

Дисциплина: Высшая математикаТема: Матрицы и определители

Понятие матрицы.

При изучении вопросов, связанных с действием над векторами,а также при изучении систем линейных уравнений приходится иметь дело стаблицами из чисел, которые называются матрицами.

Определение. Матрицей называется прямоугольная таблица изчисел, содержащая /> строк и /> столбцов.

Числа /> и /> называются порядкамиматрицы. Если />, то матрицаназывается квадратной. Для обозначения матрицы пользуются либо вертикальнымидвойными черточками, либо круглыми скобками:

/> или />.

Для краткого обозначения матрицы может быть использована иодна буква, например, />. Кроме того,вместо всей таблицы может быть написано:

/>, где />; />.

Числа /> называютсяэлементами матрицы, /> — номер строки, /> — номер столбца.

Для квадратной матрицы вводится понятие главной и побочнойдиагонали: главная диагональ идет из верхнего левого угла в нижний правый; побочная- из верхнего правого в нижний левый.

Ранг матрицы. Эквивалентные матрицы.

Дана прямоугольная матрица:

Выделим в этой матрице k произвольных строк и kпроизвольных столбцов (k Ј m, k Ј n).

Определение. Определитель k-го порядка, составленныйиз элементов матрицы A, расположенных на пересечении выделенных строк истолбцов, называется минором k-го порядка матрицы A. Матрица Aимеет C km*C kn миноров k-гопорядка.

Определение. Рассмотрим всевозможные миноры матрицы A,отличные от нуля. Рангом матрицы A называется наибольший порядокотличных от нуля миноров этой матрицы. Если все элементы матрицы равны нулю, торанг этой матрицы принимают равным нулю.

Определение. Всякий отличный от нуля минор матрицы, порядоккоторого равен рангу этой матрицы, называется базисным минором матрицы.

Ранг матрицы A будем обозначать через r (A). Еслиr (A) = r (B), то матрицы A и B называются эквивалентными.

Полезно иметь ввиду, что ранг матрицы не изменяется отэлементарных преобразований. Под элементарными преобразованиями понимаются:

1) замена строк столбцами, а столбцов соответствующимистроками;

2) перестановка строк матрицы;

3) вычеркивание строки, все элементы которой равны нулю;

4) умножение какой-либо строки на число, отличное от нуля;

5) прибавление к элементам одной строки соответствующихэлементов другой строки.

Действия над матрицами.

Определение. Две матрица называются равными, если ониимеют одинаковые порядки и все их соответствующие элементы совпадают.

Определение. Суммой двух матриц /> (/>) и /> (/>) одинаковых порядков /> называется матрица /> (/>) того же порядка, элементыкоторой равны />.

На письме это действие может быть записано так: />. Операция сложенияобладает, очевидно, обычными свойствами: перестановочным />; сочетательным />.

Определение. Произведением матрицы /> на число /> называется матрица />, элементы которой равны />.

Умножение матрицы на число может быть записано: /> или />.

Эта операция обладает следующими свойствами: сочетательнымотносительно числового множителя />; распределительнымотносительно суммы матриц />; распределительнымотносительно суммы чисел />.

После первых двух действий необходимо отметить, чтовычитание матриц производится аналогично сложению, а деление матрицы на числоможет быть определено как умножение на обратное число.

Определение. Произведением матрицы /> (/>), имеющей порядок />, на матрицу /> (/>), имеющую порядок />, называется матрица /> (/>), имеющая порядок />, элементы которой равны />, где />.

Записывается это действие так />.Из сказанного выше следует, что для нахождения элемента />, в произведении /> необходимо попарноперемножить все соответствующие элементы />-ойстроки матрицы /> на элементы />-го столбца матрицы />, а затем все это сложить. Изопределения также следует, что для умножения двух матриц необходимо, чтобычисло столбцов матрицы /> было равно числустрок матрицы />. Отсюда следует,что одновременно произведение /> и /> существует только лишь втом случае, когда число столбцов /> равночислу строк />, а число столбцов /> равно числу строк />. В этом случае /> и /> будут квадратнымиматрицами, но разных порядков. Чтобы оба произведения были одинакового порядка,необходимо, чтобы /> и /> были квадратными матрицамиодинакового порядка.

Произведение матриц /> имеетсвойства: сочетательное />; распределительное/>. Перестановочным свойствомв общем случае произведение матриц не обладает. Оно выполняется лишь внекоторых случаях.

Среди квадратных матриц необходимо выделить важный классдиагональных матриц.

Определение. Диагональной называется квадратная матрица,все элементы которой, расположенные вне главной диагонали, равны 0:

/>.

В том случае, если />,то для любой квадратной матрицы /> порядка/> справедливо />. Действительно, для /> получаем />. Для /> — />. Отсюда, />.

Среди диагональных матриц с равными друг другу элементамиособое место занимают две матрицы: единичная и нулевая. У единичной матрицы />, обозначается она — />, у нулевой />, обозначается она — />.

Как было показано />, />. Перемножив эти матрицы,можно убедиться, что />; />. Таким образом, матрицы /> и /> выполняют ту же роль, чтои 1 и 0 среди чисел. Вообще нулевой называют любую матрицу, элементы которойравны нулю.

Понятие определителя.

Выше было показано, что матрица — это прямоугольная таблица,составленная из чисел. Особое место среди матриц занимают квадратные матрицы. Рассмотримпроизвольную квадратную матрицу порядка /> илипросто />:

/> (3.1.1)

Оказывается, что с такой матрицей всегда можно связатьвполне определенную численную характеристику.

Определение. Численная характеристика квадратной матрицыназывается ее определителем.

Рассмотрим матрицу первого порядка />.

Определение. Численной характеристикой матрицы первогопорядка, то есть определителем первого порядка, называется величина ее элемента/>.

Обозначается определитель одним из символов />.

Рассмотрим матрицу второго порядка

/>.

Определение. Определителем второго порядка,соответствующим матрице второго порядка, называется число, равное />.

Обозначается определитель одним из символов

/> (3.1.2)

Очевидно, что для составления определителя второго порядка,необходимо найти разность произведения элементов, стоящих на главной диагоналиматрицы, и произведения элементов, стоящих на побочной диагонали этой матрицы.

Поскольку одна из форм обозначения определителя иобозначения матрицы имеют много общего (записывается таблица из чисел), то также, как и у матрицы, говорят о столбцах, строках и элементах определителя.

После того как рассмотрены определители 1-го и 2-гопорядков, можно перейти к понятию определителя любого порядка. Но перед этимвведем понятие минора.

Определение. Минором любого элемента /> квадратной матрицы порядка/> называется определительпорядка />, соответствующий тойматрице, которая получается из первоначальной в результате вычеркивания />-ой строки и />-го столбца, на пересечениикоторых стоит элемент />.

Обычно минор элемента /> обозначается/>.

Определение. Определителем порядка />, соответствующим матрицепорядка />, называется число, равное

/>.

Обозначается определитель одним из символов

(3.1 3)

Приведенное выражение представляет собой правило вычисленияопределителя />-го порядка по элементампервой строки соответствующей ему матрицы и по минорам элементов этой строки,которые являются определителями порядка />.Для /> это правило дает:

/>.

В приведенном правиле вычисления определителя фигурируетлишь первая строка. Возникает вопрос, а нельзя ли вычислить определитель,используя элементы других строк?

Теорема. Каков бы ни был номер строки /> (/>), для определителя />-го порядка справедливаформула

/>,

называемая разложением этого определителя по />-ой строке.

Нетрудно заметить, что в этой формулировке степень при (-1) равнасумме номеров строки и столбца, на пересечении которых стоит элемент />.

Докажем эту теорему для />.В этом случае /> может быть равно только 2,так как /> входит в основноеопределение величины определителя. Итак:

/>.

Полученное выражение совпадает с тем, которое было дано вопределении, следовательно, для определителя 2-го порядка теорема доказана.

Для произвольного /> даннаятеорема доказывается методом математической индукции.

Итак, показано, что определитель может быть разложен полюбой строке. Возникает вопрос, а нельзя ли сделать то же самое, использовавпроизвольный столбец.

Теорема. Каков бы ни был номер столбца /> (/>), для определителя />-го порядка справедливаформула />, называемая разложениемэтого определителя по />-му столбцу.

Докажем теорему для />:

/>.

Данное выражение равно величине определителя, введенной поопределению.

Итак, на основании теорем можно сказать, что для вычисленияопределителя />-го порядка необходимо егоразложить по произвольной строке или столбцу.

В заключение введем еще одно определение.

Определение. Алгебраическим дополнением данного элемента /> определителя />-го порядка называетсячисло, равное />, котороеобозначается />.

Значит, алгебраическое дополнение отличается отсоответствующего минора только лишь знаком. Теперь величину определителя можновычислить с помощью формул:

/>.

Литература

1. Лобоцкая Н.Л. Основы высшей математики. Минск, «Высшая школа»,1973.

2. Минорский В.П. Сборник задач по высшей математики.

3. Кудрявцев В.А., Демидович Б.П. Краткий курс высшей математики. М.,«Наука», 1986.

4. Гмурман В.Е. Теория вероятностей и математическая статистика. М., «Высшаяшкола» изд. 5, 1977.

5. Гмурман В.Е. Руководство к решению задач по теории вероятностей иматематической статистике. М., «Высшая школа» изд.2.

6. Баврин И.И. Высшая математика — 1980 г.3

7. Дж. Голуб, Ч. Ван Лоун Матричные вычисления. — М.: Мир, 1999.

8. Беллман Р. Введение в теорию матриц. — М.: Мир, 1969.

9. Гантмахер Ф.Р. Теория матриц (2-е издание). — М.: Наука, 1966.

10. Ланкастер П. Теория матриц. — М.: Наука, 1973.

11. Соколов Н.П. Пространственные матрицы и их приложения. — М.: ГИФМЛ, 1960.

ronl.org

Контрольная работа « Матрицы и определители» для студентов 1 курса

1. Самостоятельная работа матрицы

СПИСОК ЛИТЕРАТУРЫ

а) и , б ) 3А в) А – 2В, г) ВT , АT — Студопедия.Нет

Итоговая работа по теме : «Матрицы»

Контрольные — Контрольная по математике Матрицы

Контрольная работа по математике 1 семестр

Контрольная работа — Матрицы и определители

Добавить комментарий Отменить ответ