Контрольная работа по Статистике 4
Белорусский Национальный Технический Университет
Факультет Технологий управления и гуманитаризации
Контрольная работа
По дисциплине Статистика
Выполнил: Власов А.Р.
Проверила: Вербицкая Е.Н.
Минск 2010
Содержание:
1. Теоретическая часть…………………………………………………………………стр.3
2. Практическая часть…………………………………………………..стр.8
3. Литература………………………………………………………….стр.19
1. Теоретическая часть.
Понятие о рядах динамики, их виды, элементы и правила построения.
Понятие о статистических рядах динамики .
Ряды динамики – статистические данные , отображающие развитие во времени изучаемого явления . Их также называют динамическими рядами , временными рядами .
В каждом ряду динамики имеется два основных элемента :
1) показатель времени t ;
2) соответствующие им уровни развития изучаемого явления y;
В качестве показаний времени в рядах динамики выступают либо определенные даты (моменты), либо отдельные периоды (годы , кварталы, месяцы, сутки).
Уровни рядов динамики отображают количественную оценку (меру) развития во времени изучаемого явления . Они могут выражаться абсолютными , относительными или средними величинами .
Ряды динамики различаются по следующим признакам :
1) По времени . В зависимости от характера изучаемого явления уровни рядов динамики могут относиться или к определенным датам (моментам) времени, или к отдельным периодам . В соответствии с этим ряды динамики подразделяются на моментные и интервальные .
Моментные ряды динамики отображают состояние изучаемых явлений на определенные даты (моменты) времени . Примером моментного ряда динамики является следующая информация о списочной численности работников магазина в 1991 году (таб. 1):
Таблица 1
Списочная численность работников магазина в 1991 году
Особенностью моментного ряда динамики является то , что в его уровни могут входить одни и те же единицы изучаемой совокупности . Хотя и в моментном ряду есть интервалы – промежутки между соседними в ряду датами , — величина того или иного конкретного уровня не зависит от продолжительности периода между двумя датами . Так , основная часть персонала магазина , составляющая списочную численность на 1.01.1991 , продолжающая работать в течение данного года , отображена в уровнях последующих периодов . Поэтому при суммировании уровней моментного ряда может возникнуть повторный счет .
Посредством моментных рядов динамики в торговле изучаются товарные запасы , состояние кадров , количество оборудования и других показателей , отображающих состояние изучаемых явлений на отдельные даты (моменты) времени .
Интервальные ряды динамики отражают итоги развития (функционирования) изучаемых явлений за отдельные периоды (интервалы) времени .
Примером интервального ряда могут служить данные о розничном товарообороте магазина в 1987 – 1991 гг. (таб. 2):
Таблица 2
Объем розничного товарооборота магазина в 1987 — 1991 гг.
Каждый уровень интервального ряда уже представляет собой сумму уровней за более короткие промежутки времени . При этом единица совокупности , входящая в состав одного уровня , не входит в состав других уровней .
Особенностью интервального ряда динамики является то , что каждый его уровень складывается из данных за более короткие интервалы (субпериоды) времени . Например , суммируя товарооборот за первые три месяца года , получают его объем за Iквартал , а суммируя товарооборот за четыре квартала , получают его величину за год , и т. д. При прочих равных условиях уровень интервального ряда тем больше , чем больше длина интервала , к которому этот уровень относится .
Свойство суммирования уровней за последовательные интервалы времени позволяет получить ряды динамики более укрупненных периодов .
Посредством интервальных рядов динамики в торговле изучают изменения во времени поступления и реализации товаров , суммы издержек обращения и других показателей , отображающих итоги функционирования изучаемого явления за отдельные периоды .
Статистическое отображение изучаемого явления во времени может быть представлено рядами динамики с нарастающими итогами. Их применение обусловлено потребностями отображения результатов развития изучаемых показателей не только за данный отчетный период , но и с учетом предшествующих периодов . При составлении таких рядов производится последовательное суммирование смежных уровней . Этим достигается суммарное обобщение результата развития изучаемого показателя с начала отчетного периода (года , месяца , квартала и т. д.) .
Ряды динамики с нарастающими итогами строятся при определении общего объема товарооборота в розничной торговле . Так , обобщением товарно – денежных отчетов за последние операционные периоды (пятидневки , недели , декады и т. д.) .
2) По форме представления уровней . Могут быть построены также ряды динамики , уровни которых представляют собой относительные и средние величины . Они также могут быть либо моментными либо интервальными .
В интервальных рядах динамики относительных и средних величин непосредственное суммирование уровней само по себе лишено смысла , так как относительные и средние величины являются производными и исчисляются через деление других величин .
3) По расстоянию между датами или интервалам времени выделяют полные или неполные ряды динамики .
Полные ряды динамики имеют место тогда , когда даты регистрации или окончания периодов следуют друг за другом с равными интервалами . Это равноотстоящие ряды динамики . Неполные – когда принцип равных интервалов не соблюдается .
4) По числу показателей можно выделить изолированные и комплексные (многомерные) ряды динамики . Если ведется анализ во времени одного показателя , имеем изолированный ряд динамики . Комплексный ряд динамики получается в том случае , когда в хронологической последовательности дается система показателей , связанных между собой единством процесса или явления .
Требования , предъявляемые к рядам динамики :
1) Сопоставимость статистических данных
Основным условием для получения правильных выводов при анализе рядов динамики является сопоставимость его элементов .
Ряды динамики формируются в результате сводки и группировки материалов статистического наблюдения . Повторяющиеся во времени ( по отчетным периодам) значения одноименных показателей в ходе статистической сводки систематизируются в хронологической последовательности .
При этом каждый ряд динамики охватывает отдельные обособленные периоды , в которых могут происходить изменения , приводящие к несопоставимости отчетных данных с данными других периодов . Поэтому для анализа ряда динамики необходимо приведение всех составляющих его элементов к сопоставимому виду . Для этого в соответствии с задачами исследования устанавливаются причины , обусловившие несопоставимость анализируемой информации , и применяется соответствующая обработка , позволяющая производить сравнение уровней ряда динамики .
Несопоставимость в рядах динамики вызывается различными причинами . Это могут быть разновеликость показаний времени, неоднородность состава изучаемых совокупностей во времени , изменения в методике первичного учета и обобщения исходной информации , различия применяемых в различное время единиц измерения и т. д.
Так , при изучении динамики товарооборота по внутригодовым периодам несопоставимость возникает при неодинаковой продолжительности показаний времени (месяцев , кварталов , полугодий)
При отсутствии информации о фактическом времени работы для получения сопоставимых среднесуточных показателей используется режимное время работы . Последнее различно в зависимости от выполняемых торговлей функций и обслуживаемого контингента .
Для розничной торговли возможны следующие варианты режимного времени :
a) Предприятия , работающие без перерыва в праздничные и выходные дни (например , дежурные продуктовые и хлебобулочные магазины , рестораны , кафе) . Их фонд рабочего времени соответствует календарному ;
b) Предприятия , не работающие в праздничные дни ( например , городские рынки) . Их фонд рабочего времени меньше календарного на число ежегодных праздничных дней ;
c) Предприятия , не работающие в праздничные и общевыходные дни (например, городские промтоварные магазины , предприятия общественного питания на фабриках , в учреждениях и т. д.) . Величина их рабочего времени зависит от размещения в каждом календарном году праздничных и выходных дней ;
d) Предприятия , работающие в отдельные периоды времени , сезоны года (например , городские овощные базары , торговля в местах массового летнего отдыха и т. д.) .
2) Величины временных интервалов должны соответствовать интенсивности изучаемых процессов . Чем больше вариация уровней во времени , тем чаще следует делать замеры . Соответственно для стабильных процессов интервалы можно увеличить .
Так , переписи населения достаточно проводить один раз в десять лет ; учет национального дохода , урожая ведется один раз в год ; ежедневно регистрируются курсы покупки и продажи валют , и т. д.
3)Числовые уровни рядов динамики должны быть упорядоченными во времени . Не допускается анализ рядов с пропусками отдельных уровней , если же такие пропуски неизбежны , то их восполняют условными расчетными значениями.
mirznanii.com
Контрольная работа Статистика — вариант 2
Т.е. производительность труда увеличилась на 4%.
Разность числителя и знаменателя рассчитанного индекса показывает экономию живого труда (количество высвобожденных работников) за счет роста производительности:
∆Т = 1640 – 1570 = 70 чел.
Задача 7
Имеются следующие данные:
Год | Часовая выработка на одного рабочего, ед. | Продолжительность рабочего дня, ч | Продолжительность рабочего месяца, дн. |
Базисный | 100 | 7,7 | 20 |
Отчетный | 120 | 7,8 | 22 |
Определите: а) влияние динамики часовой выработки одного рабочего, продолжительности рабочего дня и рабочего месяца на динамику среднемесячной выработки; б) влияние каждого фактора в абсолютном выражении на функцию.
Решение.
Производительность труда одного работника за месяц (W) равна его среднечасовой выработке (а), умноженной на среднюю продолжительность дня (b) и на среднюю продолжительность рабочего месяца (с).
W = cba.
Система многофакторных индексов:
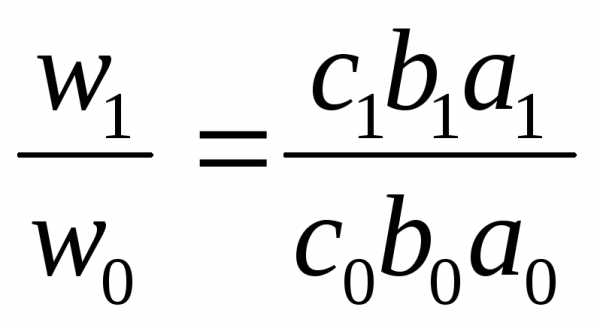
 =
=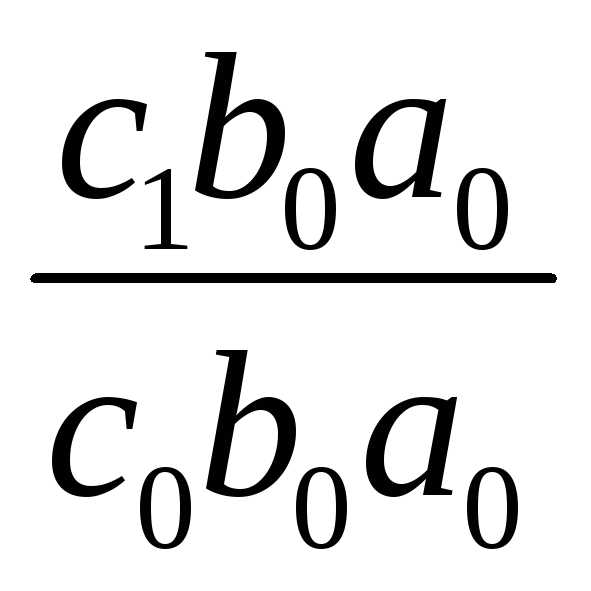 .
.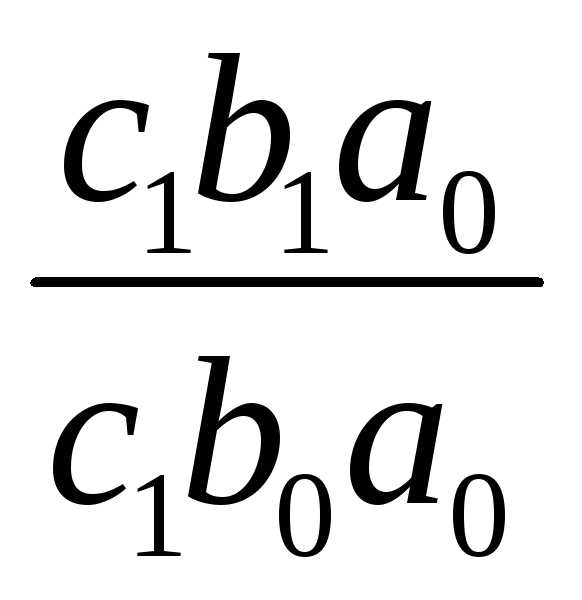 .
.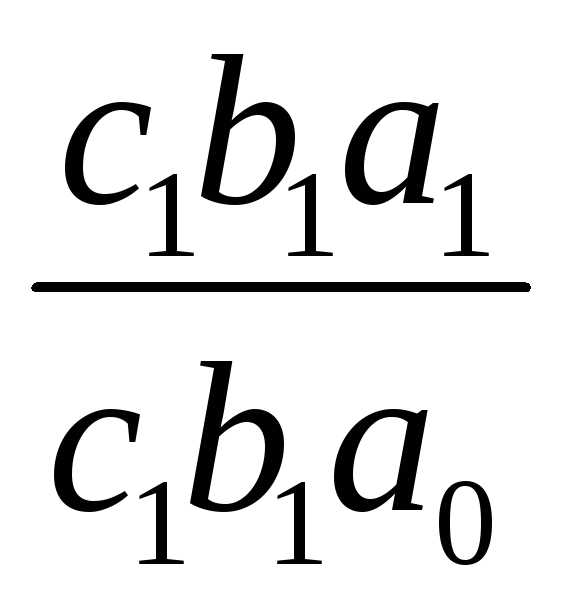
Таким образом, производительность труда в базисном периоде составила:
W0 = 100 . 7,7 . 20 = 15400 ед.
в отчетном периоде:
W1 = 120 . 7,8 . 22 = 20592 ед.
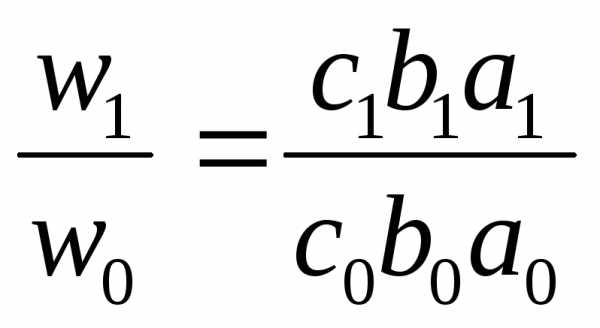
1,337 = 1,1 . 1,013 . 1,2
Абсолютное изменение выработки:
ΔW = 20592 – 15400 = 5192 ед.
Количество продукции (в абсолютном выражении) в расчете на одного рабочего, полученное за счет роста часовой выработки одного рабочего:
ΔWа = (120 – 100)* 7,7 * 20 = 3080 ед.
Количество продукции (в абсолютном выражении) в расчете на одного рабочего, полученное за счет снижения продолжительности рабочего дня:
ΔWb = 120 * (7,8 – 7,7) * 20 = 240 ед.
Количество продукции (в абсолютном выражении) в расчете на одного рабочего, полученное за счет снижения продолжительности рабочего месяца:
ΔWс = 120* 7,8 * (22 – 20) = 1872 ед.
Проверка:
ΔW = ΔWа + ΔWb + ΔWс
5192 = 3080 + 240 + 1872
5192 = 5192
Задача 8
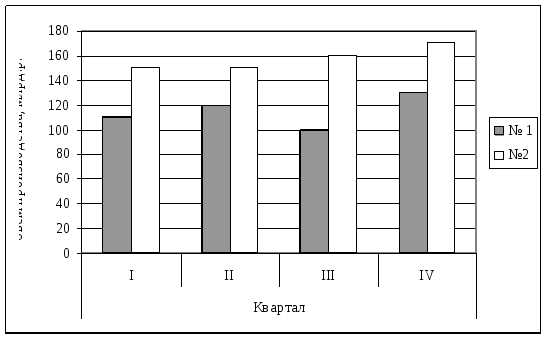
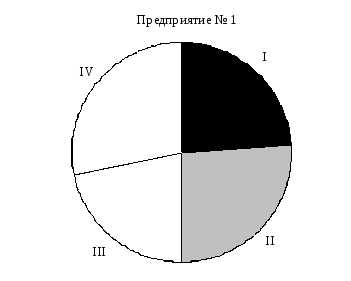
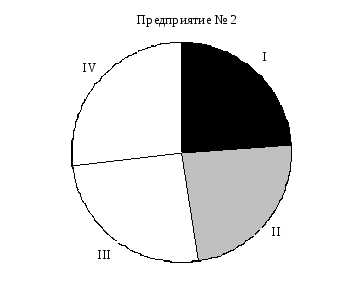
Изобразите данные задачи 2 с помощью столбиковых графиков, круговых графиков и ломаной кривой. Какой из этих графиков наиболее наглядно изображает динамику и структуру объема продукции в квартальном разрезе?
Решение.
Столбиковый график:
Круговой график:
Ломаная кривая:
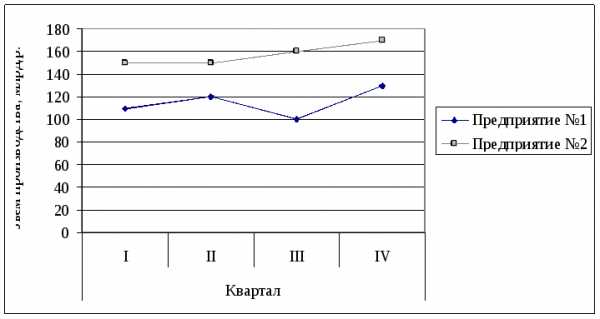
Таким образом, наиболее наглядным является график в виде ломаной кривой.
Задача 9
При 20%-ной разработке (по способу случайной бесповоротной выборки) данных текущего учета населения города удельный вес жителей в возрасте свыше 60 лет составил 8%, удельный вес населения в возрасте до 16 лет — 14%, удельный вес рабочих (без членов их семей) — 18%. Определите с вероятностью 0,954: а) предельную ошибку выборки удельного веса каждой из групп жителей; б) пределы (доверительный интервал), в которых будет находиться доля каждой из указанных групп жителей; в) какова должна быть доля выборки (объем выборки), чтобы предельная ошибка в оценке доли по указанным группам жителей была не более 0,20 %. Общая численность населения города составляет 300 тыс. человек.
Решение.
Возможные границы генеральной доли определяется по формуле:

где w – выборочная доля (удельный вес единиц в выборке, обладающих исследуемым признаком; w = m/n)
–предельная ошибка выборочной доли (для бесповторного отбора).
Так, удельный вес жителей в возрасте свыше 60 лет равен 0,08.
w = 0,08.
Предельная ошибка выборочной доли:
Тогда границы удельного веса данной группы:
0,031 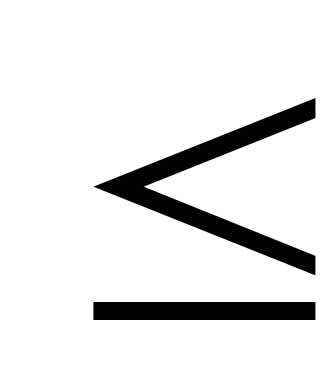 р
р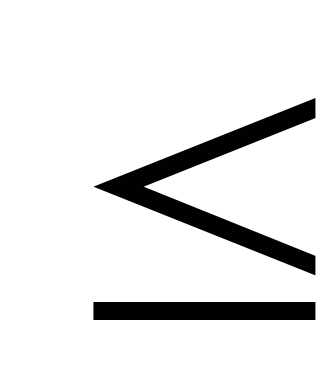 0,129
0,129
Т.е. доля жителей в возрасте свыше 60 лет находится в пределах от 3,1% до 12,9%.
Удельный вес населения в возрасте до 16 лет:
w = 0,14.
Предельная ошибка выборочной доли:
Тогда границы удельного веса данной группы:
0,078 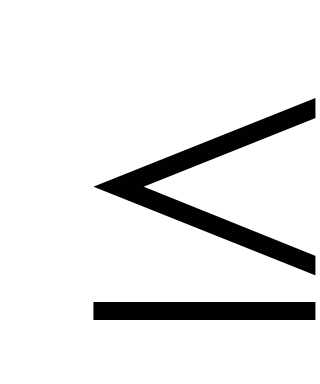 р
р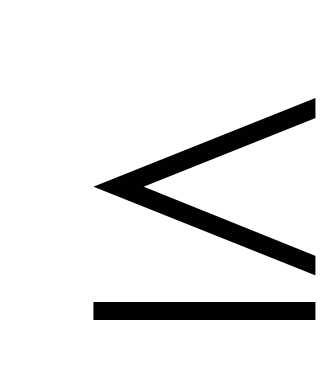 0,202
0,202
Т.е. доля жителей в возрасте до 16 лет находится в пределах от 7,8% до 20,2%.
Удельный вес рабочих:
w = 0,18.
Предельная ошибка выборочной доли:
Тогда границы удельного веса данной группы:
0,112 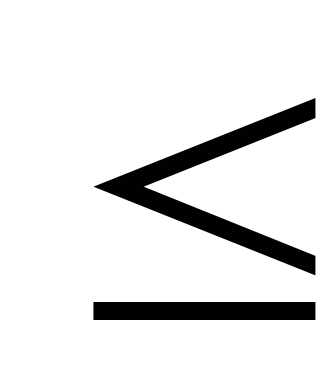 р
р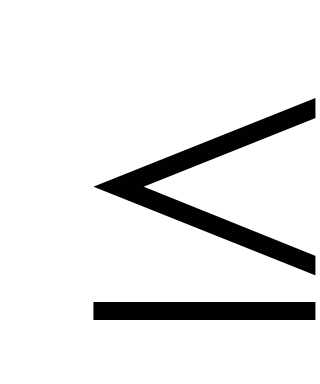 0,248
0,248
Т.е. доля рабочих находится в пределах от 11,2% до 24,8%.
Необходимый объем выборки рассчитаем по формуле:
Объем выборки, чтобы предельная ошибка в оценке доли жителей в возрасте свыше 60 лет была не более 0,2%:
59 101 чел.
Доля выборки = 59101 / 300000 . 100 = 19,7%.
Объем выборки, чтобы предельная ошибка в оценке доли жителей в возрасте до 16 лет была не более 0,2%:
85 918 чел.
Доля выборки = 85918 / 300000 . 100 = 28,6%.
Объем выборки, чтобы предельная ошибка в оценке доли жителей в возрасте до 16 лет была не более 0,2%:
98 928 чел.
Доля выборки = 98928 / 300000 . 100 = 33%.
Задача 10
Имеются следующие данные о связи между произведенной продукцией (в отпускных ценах) и переработкой сырья по 12 предприятиям:
Номер предприятия | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
Валовая продукция, млрд р. | 2,4 | 2,8 | 3,4 | 3,6 | 4,0 | 4,4 | 4,8 | 5,3 | 5,5 | 6,0 | 6,2 | 6,5 |
Переработано сырья, тыс. ц | 0,6 | 0,9 | 1,2 | 0,8 | 1,4 | 1,8 | 1,6 | 2,0 | 2,4 | 2,7 | 2,9 | 3,2 |
Составьте линейное уравнение регрессии, вычислите параметры и оцените тесноту корреляционной связи.
Решение.
Видно, что при росте размера предприятия возрастает фондоотдача, т.е. между этими показателями существует прямая корреляционная зависимость.
Коэффициент парной корреляции определяет тесноту связи между результативным и факторным показателями:
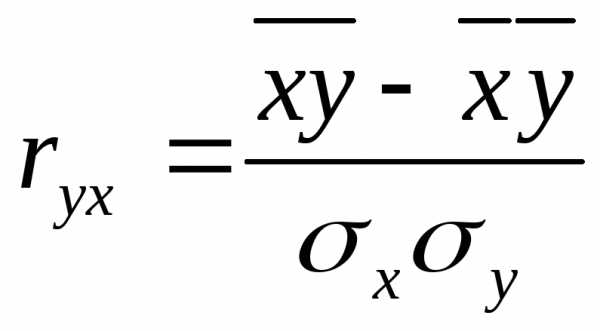
Расчет показателя тесноты связи
Номер предпряития | Валовая продукция, млрд р. | Переработано сырья, тыс. ц. | Линейные
отклонения у, | Линейные
отклонения х, | Квадрат
линейного отклонения у, | Квадрат
линейного отклонения х, | Произведение у на х, ху | Квадрат значения фактора, х2 |
1 | 2,4 | 0,6 | -2,175 | -1,192 | 4,731 | 1,420 | 1,44 | 0,36 |
2 | 2,8 | 0,9 | -1,775 | -0,892 | 3,151 | 0,795 | 2,52 | 0,81 |
3 | 3,4 | 1,2 | -1,175 | -0,592 | 1,381 | 0,350 | 4,08 | 1,44 |
4 | 3,6 | 0,8 | -0,975 | -0,992 | 0,951 | 0,983 | 2,88 | 0,64 |
5 | 4 | 1,4 | -0,575 | -0,392 | 0,331 | 0,153 | 5,6 | 1,96 |
6 | 4,4 | 1,8 | -0,175 | 0,008 | 0,031 | 0,000 | 7,92 | 3,24 |
7 | 4,8 | 1,6 | 0,225 | -0,192 | 0,051 | 0,037 | 7,68 | 2,56 |
8 | 5,3 | 2 | 0,725 | 0,208 | 0,526 | 0,043 | 10,6 | 4 |
9 | 5,5 | 2,4 | 0,925 | 0,608 | 0,856 | 0,370 | 13,2 | 5,76 |
10 | 6 | 2,7 | 1,425 | 0,908 | 2,031 | 0,825 | 16,2 | 7,29 |
11 | 6,2 | 2,9 | 1,625 | 1,108 | 2,641 | 1,228 | 17,98 | 8,41 |
12 | 6,5 | 3,2 | 1,925 | 1,408 | 3,706 | 1,983 | 20,8 | 10,24 |
Итого | 54,9 | 21,5 | 20,383 | 8,189 | 110,9 | 46,71 |
0,826
1,303
Т.к. 0<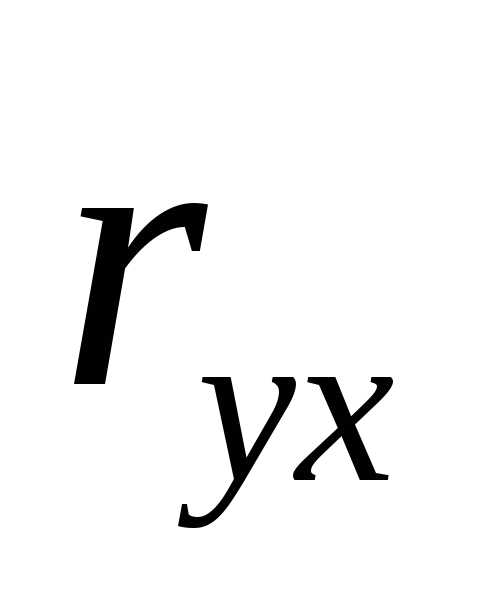 <1,
значит корреляция между x и y называется положительной, и она
показывает, что с ростом одного показателя
второй показатель возрастает. Связь
между показателями довольно тесная
<1,
значит корреляция между x и y называется положительной, и она
показывает, что с ростом одного показателя
второй показатель возрастает. Связь
между показателями довольно тесная
Определим параметры a и b уравнения регрессии y = a + bх
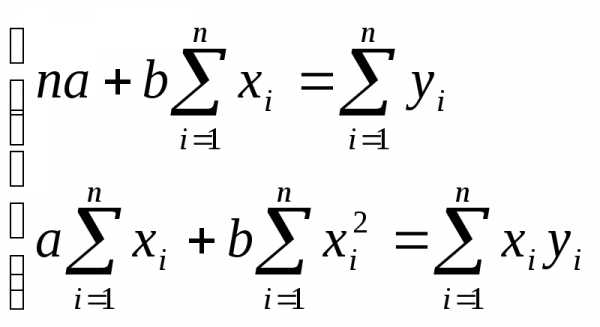
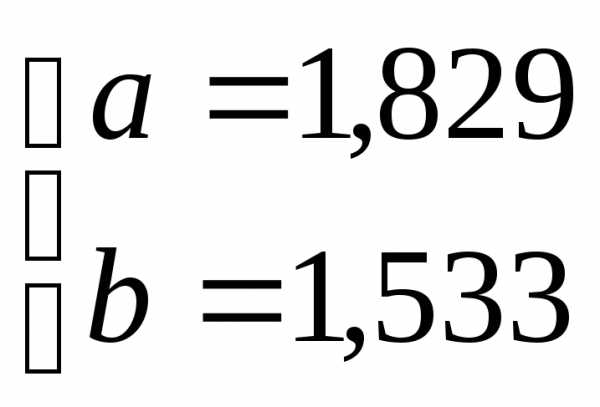
Уравнение регрессии y = 1,829 + 1,533х.
Графики, соответствующие эмпирическому ряду данных и уравнению
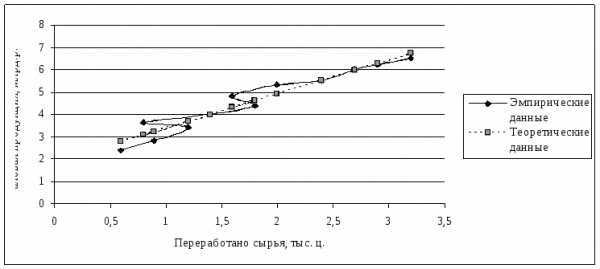
Проанализировав зависимость валовой продукции от количества переработанного сырья, можно сказать, что зависимость между этими показателями прямая и очень тесная. Это подтверждается значением коэффициента корреляции и при графическом анализе направления и тесноты связи.
Список использованных источников
Гусаров В.М. Статистика: Учебное пособие для вузов. – М.: ЮНИТИ-ДАНА, 2001.
Елисеева И.И., Юзбашев М.М. Общая теория статистики: Учебник. – М.: Финансы и статистика, 2000.
Ефимова М.Р., Рябцев В.М. Общая теория статистики. – М.: Финансы и статистика, 1991.
Теория статистики: Учебник / Под ред. Р.А. Шмойловой. – М.: Финансы и статистика, 1999.
studfiles.net
Контрольная работа по теме» Статистика»
Контрольная работа
1 вариант
1. На соревнованиях по прыжкам в высоту среди девочек 14 лет были показаны результаты: 100; 140; 130; 80; 110; 130; 120; 125; 140; 125.Найдите статистические характеристики этого набора чисел.
2. Фрезеровщики бригады затратили на обработку одной детали разное время( в мин), представленное в виде ряда данных: 40; 37; 35; 36; 32; 42; 32; 38; 32. На сколько медиана этого набора отличается от среднего арифметического?
3. В течение четверти Дима получил следующие отметки по физике: 2, 3, 3, 4, 2, 5, 4, 4, 3, 4, 5, 3, 3, 5, 4.
Найдите средний балл и медиану оценок. В ответе запишите разность медианы и среднего балла.
4. Построить столбчатую диаграмму выпадения осадков /мм/ за год в Чистополе.
Месяц
Январь
Февраль
Март
Апрель
Май
Июнь
Июль
Август
Сентябрь
Октябрь
Ноябрь
Декабрь
Кол-во осадков /мм/
85
65
52
57
76
106
106
146
143
105
76
88
5. Построить круговую диаграмму “Нормы питания девочек 11-13 лет”. Девочки 11-13 лет должны получать в день 85г белков, 85г жиров, 340г углеводов.
2 вариант
1. Записан рост (в сантиметрах) восьми учащихся: 149; 136; 163; 152; 145, 148, 136, 151. Найдите статистические характеристики этого ряда чисел.
2. Каждые полчаса гидролог замеряет температуру воды в водоеме и получает следующий ряд значений: 12,8; 13,1; 12,7; 13,2; 12,7; 13,3; 12,6; 12,9; 12,7; 13; 12,7. На сколько медиана этого набора отличается от размаха?
3. В течении четверти Маша получила следующие отметки по химии: 2, 3, 5, 4, 2, 5, 4, 4, 3, 2, 4, 5, 5, 5, 5 Найдите сумму среднего балла и медианы его оценок.
4. Построить полигон выпадения осадков /мм/ за год в Чистополе.
Месяц
Январь
Февраль
Март
Апрель
Май
Июнь
Июль
Август
Сентябрь
Октябрь
Ноябрь
Декабрь
Кол-во осадков /мм/
85
65
52
57
76
106
106
146
143
105
76
88
5. Построить круговую диаграмму “Нормы питания мальчиков 11-13 лет”. Мальчики 11-13 лет должны получать в день 120г белков, 120г жиров, 460г углеводов.
2 вариант
1. Записан рост (в сантиметрах) восьми учащихся: 149; 136; 163; 152; 145, 148, 136, 151. Найдите статистические характеристики этого ряда чисел.
2. Каждые полчаса гидролог замеряет температуру воды в водоеме и получает следующий ряд значений: 12,8; 13,1; 12,7; 13,2; 12,7; 13,3; 12,6; 12,9; 12,7; 13; 12,7. На сколько медиана этого набора отличается от размаха?
3. В течении четверти Маша получила следующие отметки по химии: 2, 3, 5, 4, 2, 5, 4, 4, 3, 2, 4, 5, 5, 5, 5 Найдите сумму среднего балла и медианы его оценок.
4. Построить полигон выпадения осадков /мм/ за год в Чистополе.
Месяц
Январь
Февраль
Март
Апрель
Май
Июнь
Июль
Август
Сентябрь
Октябрь
Ноябрь
Декабрь
Кол-во осадков /мм/
85
65
52
57
76
106
106
146
143
105
76
88
5. Построить круговую диаграмму “Нормы питания мальчиков 11-13 лет”. Мальчики 11-13 лет должны получать в день 120г белков, 120г жиров, 460г углеводов.
Контрольная работа
1 вариант
1. На соревнованиях по прыжкам в высоту среди девочек 14 лет были показаны результаты: 100; 140; 130; 80; 110; 130; 120; 125; 140; 125.Найдите статистические характеристики этого набора чисел.
2. Фрезеровщики бригады затратили на обработку одной детали разное время( в мин), представленное в виде ряда данных: 40; 37; 35; 36; 32; 42; 32; 38; 32. На сколько медиана этого набора отличается от среднего арифметического?
3. В течение четверти Дима получил следующие отметки по физике: 2, 3, 3, 4, 2, 5, 4, 4, 3, 4, 5, 3, 3, 5, 4.
Найдите средний балл и медиану оценок. В ответе запишите разность медианы и среднего балла.
4. Построить столбчатую диаграмму выпадения осадков /мм/ за год в Чистополе.
Месяц
Январь
Февраль
Март
Апрель
Май
Июнь
Июль
Август
Сентябрь
Октябрь
Ноябрь
Декабрь
Кол-во осадков /мм/
85
65
52
57
76
106
106
146
143
105
76
88
5. Построить круговую диаграмму “Нормы питания девочек 11-13 лет”. Девочки 11-13 лет должны получать в день 85г белков, 85г жиров, 340г углеводов.
2 вариант
1. Записан рост (в сантиметрах) восьми учащихся: 149; 136; 163; 152; 145, 148, 136, 151. Найдите статистические характеристики этого ряда чисел.
2. Каждые полчаса гидролог замеряет температуру воды в водоеме и получает следующий ряд значений: 12,8; 13,1; 12,7; 13,2; 12,7; 13,3; 12,6; 12,9; 12,7; 13; 12,7. На сколько медиана этого набора отличается от размаха?
3. В течении четверти Маша получила следующие отметки по химии: 2, 3, 5, 4, 2, 5, 4, 4, 3, 2, 4, 5, 5, 5, 5 Найдите сумму среднего балла и медианы его оценок.
4. Построить полигон выпадения осадков /мм/ за год в Чистополе.
Месяц
Январь
Февраль
Март
Апрель
Май
Июнь
Июль
Август
Сентябрь
Октябрь
Ноябрь
Декабрь
Кол-во осадков /мм/
85
65
52
57
76
106
106
146
143
105
76
88
5. Построить круговую диаграмму “Нормы питания мальчиков 11-13 лет”. Мальчики 11-13 лет должны получать в день 120г белков, 120г жиров, 460г углеводов.
Контрольная работа
1 вариант
1. На соревнованиях по прыжкам в высоту среди девочек 14 лет были показаны результаты: 100; 140; 130; 80; 110; 130; 120; 125; 140; 125.Найдите статистические характеристики этого набора чисел.
2. Фрезеровщики бригады затратили на обработку одной детали разное время( в мин), представленное в виде ряда данных: 40; 37; 35; 36; 32; 42; 32; 38; 32. На сколько медиана этого набора отличается от среднего арифметического?
3. В течение четверти Дима получил следующие отметки по физике: 2, 3, 3, 4, 2, 5, 4, 4, 3, 4, 5, 3, 3, 5, 4.
Найдите средний балл и медиану оценок. В ответе запишите разность медианы и среднего балла.
4. Построить столбчатую диаграмму выпадения осадков /мм/ за год в Чистополе.
Месяц
Январь
Февраль
Март
Апрель
Май
Июнь
Июль
Август
Сентябрь
Октябрь
Ноябрь
Декабрь
Кол-во осадков /мм/
85
65
52
57
76
106
106
146
143
105
76
88
5. Построить круговую диаграмму “Нормы питания девочек 11-13 лет”. Девочки 11-13 лет должны получать в день 85г белков, 85г жиров, 340г углеводов.
infourok.ru
Контрольная работа по Статистике 16
Задание 1. С целью изучения общественного мнения по вопросу содержания и качества телевизионных программ принято решение провести опрос населения.
1) Определите объект наблюдения, единицу наблюдения, отчетную единицу.
2) Какие признаки следует регистрировать при проведении данного наблюдения?
3) Укажите, к какому виду относится данное наблюдение по времени, охвату и способу получения данных.
Решение:
Статистическое наблюдение выступает как один из главных методов статистики и как одна из важнейших стадий статистического исследования. Под статистическими данными (информацией) понимают совокупность количественных характеристик социально-экономических явлений и процессов, полученных в результате статистического наблюдения, их обработки или соответствующих расчетов.
Цель наблюдения . Статистические наблюдения чаще всего преследуют практическую цель — получение достоверной информации для выявления закономерностей развития явлений и процессов. В нашем случае, целью было получение данных о содержания телевизионных программ.
Задача наблюдения – проанализировать потребности населения в содержании телевизионных программ.
Объект наблюдения – жители города N.
Для формирования выборочной совокупности из общего числа жителей можно применить типическую выборку, которая предполагает предварительное разделение генеральной совокупности на однородные группы, которые образуются посредством специально проведенной типической, группировки единиц генеральной совокупности. Единицей измерения в данном случае будет покупатель магазина. Численность покупателей можно разделить на мужчин и женщин, выделяя их по возрасту и другим признакам и в каждой полученной группе провести отбор, пропорциональный численности групп.
Для получения дополнительных сведений о зрителях в выборочной совокупности можно провести анкетирование. Определяя необходимый круг вопросов надо исходить из цели анкетирования — получения дополнительной информации для улучшения качества телепрограмм. Таким образом, в анкету следует включить вопросы о возрасте, цене, тематике и продолжительности программ. Следует выяснить по результатам анкетирования численность зрителей удовлетворенных имеющимся предложением и неудовлетворенных. Распространив результаты выборочного наблюдения на генеральную совокупность, можно определить особенности спроса на телепрограммы. Если включить в анкету вопрос о требованиях к тематике, то можно определить оптимальное содержание программ.
Задание 2. При 5%-ном выборочном обследовании страховых организаций получены следующие данные:
На основе приведенных данных:
1)проведите группировку страховых организаций по числу договоров страхования, выделив четыре группы с равными интервалами;
2)по каждой выделенной группе и по совокупности в целом рассчитайте:
· число страховых организаций,
· среднее число договоров страхования на одну организацию,
· размер страховых взносов по группе и в среднем на одну организацию,
· количество страховых случаев по группе и в среднем на одну организацию.
Результаты группировки представьте в таблице. Проанализируйте показатели таблицы. Установите характер связи между: числом договоров и количеством страховых случаев. Для измерения тесноты связи между этими показателями исчислите эмпирическое корреляционное отношение. Сделайте выводы.
Решение:
Проведем группировку страховых организаций по числу страховых случаев и построим интервальный ряд распределения.
Для построения интервального вариационного ряда, характеризующего распределение страховых организаций по числу договоров страхования, необходимо вычислить величину и границы интервалов ряда.
При построении ряда с равными интервалами величину интервала h определяем по формуле
,
где – наибольшее и наименьшее значения признака в исследуемой совокупности, k — число групп интервального ряда.
Определение величины интервала по формуле при заданных k = 4, xmax = 140, xmin = 60:
При h = 20 границы интервалов ряда распределения имеют следующий вид:
Для построения интервального ряда необходимо подсчитать число страховых организаций, входящих в каждую группу (частоты групп). При этом возникает вопрос, в какую группу включать единицы совокупности, у которых значения признака выступают одновременно и верхней, и нижней границами смежных интервалов. Отнесение таких единиц к одной из двух смежных групп осуществляем по принципу полуоткрытого интервала [ ). Т.к. при этом верхние границы интервалов не принадлежат данным интервалам, то соответствующие им единицы совокупности включаются не в данную группу, а в следующую. В последний интервал включаются и нижняя, и верхняя границы.
Построим рабочую таблицу:
На основе рабочей таблицы составим аналитическую:
Таким образом, можно сделать вывод, что размер страховых выплат на одну организацию, число договоров страхования на одну организацию, размер страховых взносов на одну организацию растут пропорционально росту числа договоров страхования.
Установим характер связи между числом договоров и количеством страховых случаев. Для измерения тесноты связи между этими показателями исчислим эмпирическое корреляционное отношение.
Для измерения тесноты связи между факторным и результативным признаками рассчитывают специальные показатели – эмпирический коэффициент детерминации
и эмпирическое корреляционное отношение .Эмпирический коэффициент детерминации
оценивает, насколько вариация результативного признака Y объясняется вариацией фактора Х (остальная часть вариации Y объясняется вариацией прочих факторов). Показатель рассчитывается как доля межгрупповой дисперсии в общей дисперсии по формулеmirznanii.com
Темы контрольных работ по дисциплине «статистика» 2015
Темы контрольных работ по дисциплине «Статистика»
1. Статистика цен и инфляции
2. Статистика государственного бюджета
3. Статистика денежного обращения
4. Статистика кредита
5. Статистика финансов предприятия
6. Статистика основных фондов
7. Статистика фондового рынка
8. Статистика внешней торговли
9. Статистика уровня жизни населения
10. Статистика природных ресурсов
11. Статистика рынка труда
12. Статистика оплаты труда и издержек на рабочую силу
13. Банковская статистика
14. Статистика сберегательного дела
15. Статистика страхования
16. Статистическая методология оценки и анализа эффективности инвестиций
17. Система показателей социально-демографической статистики
18. Система национальных счетов
19. Валовой внутренний продукт (ВВП): общая характеристика, методы расчета
20. Экономические индексы
Вариант контрольной работы выбирается в соответствии с порядковым номером в учебном журнале группы.
Теоретическая часть контрольной работы должна сопровождаться необходимыми расчетами.
Темы контрольных работ по дисциплине «Статистика»
1. Статистика цен и инфляции
2. Статистика государственного бюджета
3. Статистика денежного обращения
4. Статистика кредита
5. Статистика финансов предприятия
6. Статистика основных фондов
7. Статистика фондового рынка
8. Статистика внешней торговли
9. Статистика уровня жизни населения
10. Статистика природных ресурсов
11. Статистика рынка труда
12. Статистика оплаты труда и издержек на рабочую силу
13. Банковская статистика
14. Статистика сберегательного дела
15. Статистика страхования
16. Статистическая методология оценки и анализа эффективности инвестиций
17. Система показателей социально-демографической статистики
18. Система национальных счетов
19. Валовой внутренний продукт (ВВП): общая характеристика, методы расчета
20.Экономические индексы
Вариант контрольной работы выбирается в соответствии с порядковым номером в учебном журнале группы.
Теоретическая часть контрольной работы должна сопровождаться необходимыми расчетами.
matematiku5.ru

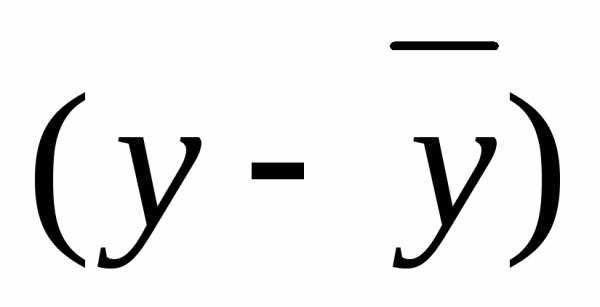
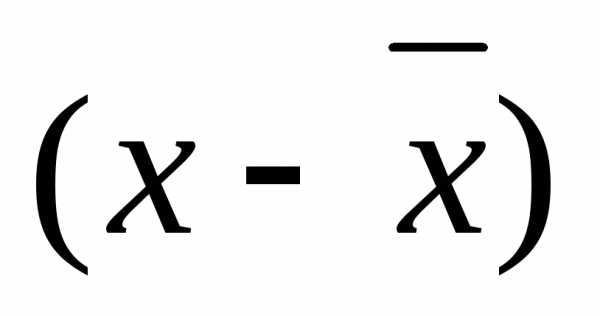
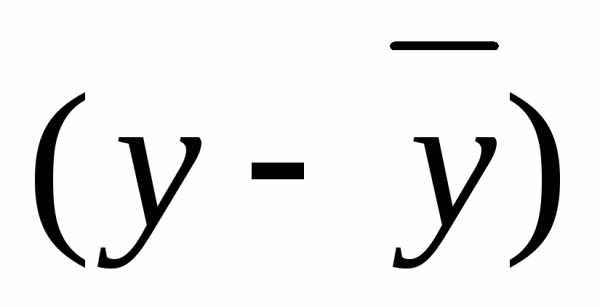 2
2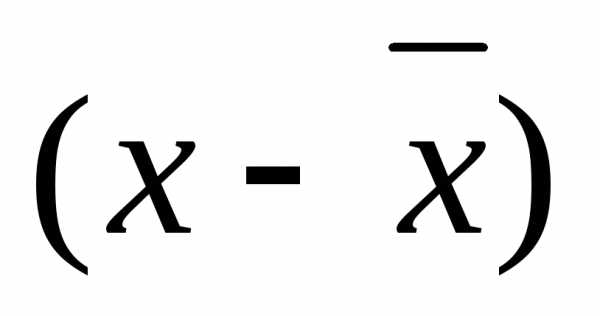 2
2