Син кос танг – , ,

Sin Cos Tan: Введение в тригонометрию

На колесе есть две точки, где вы будете находиться на нужной высоте (две красные точки на рисунке). Следовательно, существует два нужных нам угла α ₁ и α₂. Обратите внимание на два прямоугольных треугольника, выделенных зелёным цветом. Они одинаковые, так как являются зеркальным отображением друг друга. Давайте так же зеркально отобразим правый треугольник, но уже «вверх». Этот треугольник, выделенный красным цветом, имеет гипотенузу равную 1 (радиус колеса) и противолежащий катет (высота над центром) равный 1/2. В силу того, что все три треугольника одинаковые, они имеют одинаковые острые углы. Давайте найдём острый угол красного треугольника, при котором его синус равен 1/2. Поступим также, как древние астрономы, и заглянем в таблицу значений синуса для различных углов. Итак, sin α = 1/2 при = 30°. Интуитивно понятно, что наши три угла и значения их синусов связаны. Но как?

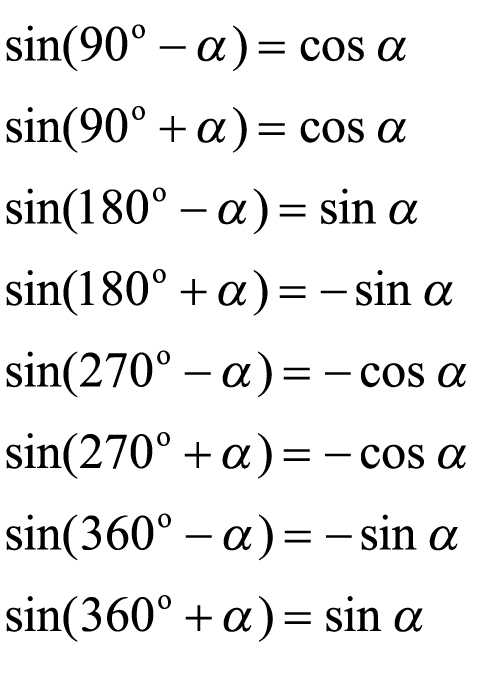
Полный круг составляет 360°. Разделим его на четыре четверти по 90° и пронумеруем их. Первая точка находится в третьей четверти. Так как две четверти в общем дают 180°, а угол α = 30°, то искомый угол α ₁ = 210°. Нашли первый угол. Вторая точка находится в четвертой четверти. Три четверти в общем дают 270°, но прибавлением 30° тут не отделаешся, так как нужно прибавить угол β, а не угол α. Так как угол α + β= 90°, то угол β = 90°− 30°=60°. И второй искомый угол равен 270°+ 60°=330°. Остался один маленький ньюанс. Помните, как мы говорили о том, что тригонометрические функции описывают повторяющиеся процессы? Если наше колесо не остановится после того, как совершит полный оборот в 360°, то с каждым новым оборотом вы будет проходить через две точки, находящиеся на уровне –1/2. Эти точки определяются простым прибавлением 360° к найденным нами углам.

При этом n – любое целое число, то есть, на нашем примере это количество оборотов колеса. Стоит заметить, что число n может быть и отрицательным, если колесо крутится в обратную сторону.

Равенстно sin α=−1/2 мы решили. Перейдем к неравенству sin α ≥ −1/2. Если для решения равенства мы нашли значения углов, при которых наша высота над центром колеса равна −1/2, то для решения неравенства нам нужно найти все углы, при которых наша высота больше либо равна −1/2. Помните мы говорили о том, что угол может быть отрицательным? Сейчас нам это пригодится. Определим угол α₂ не как 330°, а как −30° (330°−360°) На рисунке эта область выделена зелёным цветом. 

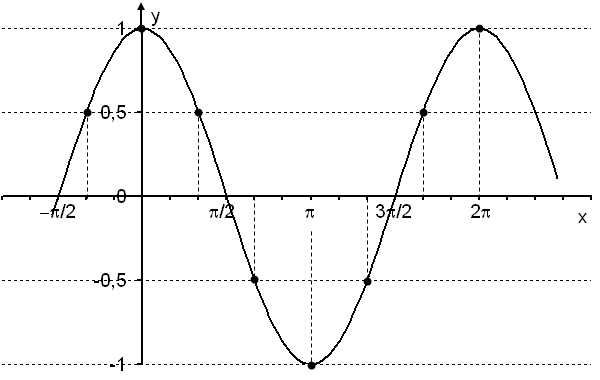
Для того, чтобы правильно записать решение неравенства, обратите внимание на рисунок синусоиды и прямой y=−1/2(высота). Нас интересуют области синусоиды, которые выше прямой y=−1/2. На рисунке они заштрихованы красным цветом. Обратите внимание на точки, которые выделяют эти отрезки. Это те же точки, которые мы получили при решении равенства sin α=−1/2 и они повторяются каждые 360°. Ответ можно записать так:

Дело осталось за малым. Во-первых, вспомнить, что математики обозначают 180° как π, когда записывают формулы с углами, и переписать решение так:

Во-вторых, произвести обратную замену α на 3x − π/4.

Путём нехитрых алгебраических преобразований, а именно прибавления π/4 и деления на 3 ко всем частям неравенства, получаем:

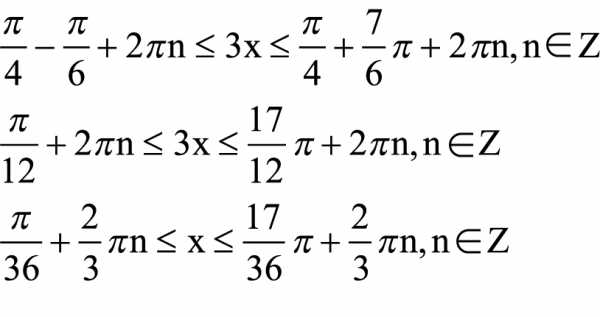
Ответ:

Миссия выполнена!

oyla.xyz

Формулы которыми пользуются учащиеся 10 класс для функций син и кос х

График функции синус, y = sin x

График функции косинус, y = cos x

Свойства синуса и косинуса

Периодичность

Функции   y = sin x   и   y = cos x   периодичны с периодом   2π.

Четность

Функция синус – нечетная. Функция косинус – четная.

Области определения и значений, экстремумы, возрастание, убывание

Основные свойства синуса и косинуса представлены в таблице (n — целое).

 

y = sin x

y = cos x

Область определения

– ∞ < x + ∞

– ∞ < x + ∞

Область значений

–1 ≤ y ≤ 1

–1 ≤ y ≤ 1

Возрастание

Убывание

Максимумы,

y = 1

Минимумы, y = –1

Нули, y = 0

Точки пересечения с осью ординат, x = 0

y = 0

y = 1

Основные формулы, содержащие синус и косинус

Сумма квадратов

Формулы синуса и косинуса суммы и разности

Формулы произведения синусов и косинусов

Формулы суммы и разности

Выражения через тангенс

При , где n — целое:

При :

Таблица синусов и косинусов, тангенсов и котангенсов

В данной таблице представлены значения синусов и косинусов при некоторых значениях аргумента.

infourok.ru

Ответы@Mail.Ru: косинусы синусы тангенсы котангенсы

косину 360 это 1 синус 360 это 0 тангенс это синус разделить на косинус, то есть 0 котангенс это косинус разделить на синус, то есть 1/0, а число на ноль делить нелзя, значит не определено 🙂 синус 410 это синус (360+50) синус 50 равняется 0,76604444311897803520239265055542 косинус 410 это косинус (360+50) то есть косинус 50 равняется 0,64278760968653932632264340990726 а тангенс решая точно таким же способом как и 360 градусов, будет вот так тангенс 410 : 1,1917535925942099587053080718604 котангенс 410 : 0,83909963117728001176312729812348

ну ты вощееееее летом ШКОЛА беееее!!!

Функции эти периодические. Вычитайте период и считайте значения.

танг=син/кос катанг=кос/син син410=кос (360-410)=кос (-50) Это по спец таблицам или на калькуляторе Остальное также

1)sin360=0;2)сos360=1;3)tg360=0;4)ctg360-не сущ.; 5)sin410=sin(360+50)=sin50;6)соs410=соs(360+50)=соs50;7)tg410=tg50;8)сtg410=сtg50.

согласна с анастасией. открой на компе калькулятор, там все и посчитаешь

sin360=0; сos360=1; tg360=0; ctg360-не сущ. ; sin410=sin(360+50)=sin50; соs410=соs(360+50)=соs50; tg410=tg50; сtg410=сtg50.

touch.otvet.mail.ru

Определение тангенса и котангенса запомнить легко! |

Определение тангенса и котангенса запомнить легко!

Вопросу о том,  как запомнить тригонометрические формулы и значения тригонометрических функций , на сайте “Математический Тандем” было уже уделено некоторое внимание.

Одним из методов, как запоминать формулы, был предложен метод с помощью образов. 

Отметим, что создавать и запоминать образы в стихотворной форме бывает гораздо легче.

Вот пример.

Определение тангенса и котангенса запомнить легко!

Тригонометрическая окружность нам показывает, что :

Тангенс угла α  – это отношение ординаты точки А к ее абсциссе.

Котангенс угла α  – это отношение абсциссы точки А к ее ординате

.

 

 

А вот как это может выглядеть в стихах:

 

[pwal description=»Чтобы увидеть остальную часть статьи, нажмите, пожалуйста, одну их кнопок социальных сетей.»]

 

Синее небо

Косматые облака,

Танго танцуют

Берег и река.

Косматый пес, 

С синевою нос,

Кота схватил 

Вчера за нос.

[/pwal]

 

 (Примечание: Син – синус, кос- косинус, тан- тангенс, кот- котангенс)

Автор : Панишева О.В.

 

Как видите, такие четверостишия помогают определение тангенса и котангенса запомнить легко!  А синус и косинус запомнить навсегда желаете? Тогда Вам сюда.

Попробуйте!

Огромной помощью  в запоминании формул тригонометрии для ученика может служить Мини-курс “Как запомнить 35 формул тригонометрии легко и надолго”.

Вы можете прямо сейчас скачать курс, введя свое имя и адрес электронной почты в форму ниже:

  ]]>

repetitor-problem.net

No related posts.