Извлечение корня из комплексного числа
Невозможно однозначно извлечь корень из комплексного числа, поскольку он имеет число значений, равное его степени.
Комплексные числа возводят в степень в тригонометрической форме, для которой верна формула Муавра:
Аналогично применяют данную формулу для вычисления корня степени из комплексного числа (не равного нулю):
Если комплексное число не равно нулю, то корни степени существуют всегда, и их можно изобразить на комплексной плоскости: они будут представлять собой вершины -угольника, который вписан в окружность с центром в начале координат и радиусом .
Примеры решения задач
| Понравился сайт? Расскажи друзьям! | |||
Извлечение корня из комплексного числа — энциклопедический справочник и словарь для студента от А до Я
Невозможно однозначно извлечь корень из комплексного числа, так как оно имеет ряд значений, равных его степени.
Сложные числа подняты до степени тригонометрической формы, для которой справедлива формула Моиварда:
Аналогично, эта формула используется для вычисления корня степени k из комплексного числа (не равного нулю):
Если комплексное число не равно нулю, то корни степени k всегда существуют, и их можно представить на комплексной плоскости: они будут вершинами k-угольника, вписанными в круг с центром в начале координат и радиус
Примеры решения проблем
ПРИМЕР 1 Найти корень третьей степени из числа z = -1.
Модуль комплексного числа z — это число:
Аргумент вычисляется по формуле:
Следовательно, тригонометрическая форма комплексного числа равна:
Тогда корень 3-й степени выглядит следующим образом:
При n = 0 получаем:
При n = 1 получаем:
При n = 2 получаем:
ПРИМЕР 2 Чтобы извлечь корень 2-й степени из числа Начнем с того, что мы выражаем комплексное число в тригонометрической форме. Действительной частью комплексного числа является число , мнимая часть . Чтобы найти тригонометрическую форму написания комплексного числа, вам нужно найти его модуль и аргумент. Модуль комплексного числа г — это число: Аргумент: Следовательно, тригонометрическая форма комплексного числа: Применяя формулу для извлечения корня 2-й степени, получаем: При n = 0 получаем: При n = 1 получаем:
sciterm.ru
Извлечение корня из комплексного числа
Извлечение корня из некоторого комплексного числа выполняется для чисел, которые представлены в тригонометрической форме.
Определение 1
Выражение вида $z=a+bi$, где $a$ и $b$ — вещественные числа, а $i$ — «мнимая единица», называется комплексным числом $z$. Мнимая единица определяется равенством $i=\sqrt{-1} $ или $i^{2} =-1$.
Определение 2
Запись некоторого комплексного числа $z$ в следующем виде $z=r\cdot (\cos \varphi +i\sin \varphi )$ называется тригонометрической формой записи, где число $r$ — модуль комплексного числа $z$, который определяется по формуле $r=|z|=|a+bi|=\sqrt{a^{2} +b^{2} } $, $\varphi $ — аргумент комплексного числа $z$, который определяется по формуле $\varphi =arctg\frac{b}{a} $.
Определение 3
Корень $n$-ой степени из некоторого комплексного числа $z$ — это такое комплексное число $w$, $n$-я степень которого равна $z$, то есть \[w^{n} =z.\]
Примечание 1
Корень $n$-ой степени из некоторого комплексного числа $z$ обозначают как $\sqrt[{n}]{z} $; на множестве всех комплексных чисел корень $n$-ой степени из этого комплексного числа $z$ имеет в точности $n$ значений.
Примечание 2
Однозначно извлечь корень из некоторого комплексного числа невозможно, так как он имеет количество значений, равное его степени.
Примечание 3
С геометрической точки зрения все значения корня $n$-ой степени из некоторого комплексного числа $z$ лежат на некоторой окружности радиуса $\sqrt[{n}]{z} $, центр которой находится в начале координат О(0;0), и образуют правильный $n$-угольник (рис. 1).

Рис. 1
Все комплексные числа, представленные в тригонометрической форме, можно возвести в некоторую степень по формуле Муавра:
\[z^{n} =r^{n} \cdot (\cos n\varphi +i\sin n\varphi ),\, \, \, \, \, \forall n\in N.\]Аналогично применяя формулу Муавра для вычисления корня $n$-ой степени из некоторого комплексного числа $z$ (не равного нулю) получаем:
\[\sqrt[{n}]{z} =\sqrt[{n}]{r} \cdot (\cos \frac{\varphi +2\pi k}{n} +i\sin \frac{\varphi +2\pi k}{n} ),\, \, \, k=0..n-1.\]Определение 4
Корнем $n$-й степени из некоторого комплексного числа $z=r\cdot (\cos \varphi +i\sin \varphi )$ является комплексное число, которое определяется равенством
\[\sqrt[{n}]{z} =\sqrt[{n}]{r} \cdot (\cos \frac{\varphi +2\pi k}{n} +i\sin \frac{\varphi +2\pi k}{n} ),\, \, \, k=0..n-1.\]Примечание 4
Если некоторое комплексное число $z$ отлично от нуля, то корень $n$-й степени существует всегда.
Пример 1
Выполнить действие $\sqrt[{3}]{z} $, где $z=2\cdot (\cos \pi +i\cdot \sin \pi )$.
Решение:
Воспользуемся формулой из определения 4.
Для $k=0$ получаем: $w_{1} =\sqrt[{3}]{z} =\sqrt[{3}]{2} \cdot \left(\cos \frac{\pi }{3} +i\cdot \sin \frac{\pi }{3} \right)$.
Для $k=1$ получаем: $w_{2} =\sqrt[{3}]{z} =\sqrt[{3}]{2} \cdot \left(\cos \frac{\pi +2\pi }{3} +i\cdot \sin \frac{\pi +2\pi }{3} \right)=\sqrt[{3}]{2} \cdot \left(\cos \pi +i\cdot \sin \pi \right)$.
Для $k=2$ получаем: $w_{3} =\sqrt[{3}]{z} =\sqrt[{3}]{2} \cdot \left(\cos \frac{\pi +4\pi }{3} +i\cdot \sin \frac{\pi +4\pi }{3} \right)=\sqrt[{3}]{2} \cdot \left(\cos \frac{5\pi }{3} +i\cdot \sin \frac{5\pi }{3} \right)$.
Определение 5
Запись некоторого комплексного числа $z$ в следующем виде $z=a+bi$ называется алгебраической формой записи (или алгебраической записью) комплексного числа. При этом:
- $a$ — вещественная (действительная) часть, обозначение $Rez=a$;
- $b$ — мнимая часть, обозначение $Imz=b$.
Алгоритм 1
Чтобы извлечь корень $n$-ой степени из некоторого комплексного числа $z$, представленного в алгебраической форме, необходимо выполнить следующие действия:
- записать данное число в тригонометрической форме;
- извлечь корни, используя определение.
Алгоритм 2
Чтобы комплексное число $z$, записанное в алгебраической форме, привести к тригонометрической форме записи, необходимо выполнить следующее:
- вычислить модуль и аргумент;
- подставить полученные значения в выражение $z=r(\cos \varphi +i\cdot \sin \varphi )$.
Пример 2
Выполнить операцию извлечения корня $\sqrt[{3}]{z} $ для заданных комплексных чисел в алгебраической форме представления:
\[z=\frac{1}{2} +\frac{1}{2} \cdot i.\]Решение:
Тригонометрическая форма записи некоторого комплексного числа имеет вид $z=r(\cos \varphi +i\cdot \sin \varphi )$.
По условию $a=\frac{1}{2} ,b=\frac{1}{2} $.
Вычислим модуль исходного комплексного числа:
\[r=\sqrt{\left(\frac{1}{2} \right)^{2} +\left(\frac{1}{2} \right)^{2} } =\sqrt{\frac{1}{4} +\frac{1}{4} } =\sqrt{\frac{1}{2} } =\frac{\sqrt{2} }{2} \]Вычислим аргумент исходного комплексного числа, используя формулу (*):
\[\varphi =\arg z=arctg\frac{1/2}{1/2} =arctg1=\frac{\pi }{4} .\]Подставим полученные значения и получим:
\[z=\frac{\sqrt{2} }{2} \cdot (\cos \frac{\pi }{4} +i\sin \frac{\pi }{4} ).\]Воспользуемся формулой из определения 4.
Для $k=0$ получаем: $w_{1} =\sqrt[{3}]{z} =\sqrt[{3}]{\frac{\sqrt{2} }{2} } \cdot \left(\cos \frac{\pi }{12} +i\cdot \sin \frac{\pi }{12} \right)$.
Для $k=1$ получаем:
\[w_{2} =\sqrt[{3}]{z} =\sqrt[{3}]{\frac{\sqrt{2} }{2} } \cdot \left(\cos \frac{\pi /4+2\pi }{3} +i\cdot \sin \frac{\pi /4+2\pi }{3} \right)=\sqrt[{3}]{\frac{\sqrt{2} }{2} } \cdot \left(\cos \frac{3\pi }{4} +i\cdot \sin \frac{3\pi }{4} \right).\]Для $k=2$ получаем:
\[w_{3} =\sqrt[{3}]{z} =\sqrt[{3}]{\frac{\sqrt{2} }{2} } \cdot \left(\cos \frac{\pi /4+4\pi }{3} +i\cdot \sin \frac{\pi /4+4\pi }{3} \right)=\sqrt[{3}]{\frac{\sqrt{2} }{2} } \cdot \left(\cos \frac{17\pi }{12} +i\cdot \sin \frac{17\pi }{12} \right).\]Определение 6
Запись комплексного числа $z$ в следующем виде $z=r\cdot e^{i\varphi } $ называется показательной формой записи, где число $r$ — модуль комплексного числа $z$, который определяется по формуле $r=|z|=|a+bi|=\sqrt{a^{2} +b^{2} } $, $\varphi $ — аргумент комплексного числа $z$, который определяется по формуле $\varphi =arctg\frac{b}{a} $.
Алгоритм 3
Чтобы извлечь корень $n$-ой степени из некоторого комплексного числа $z$, представленного в показательной форме, необходимо выполнить следующие действия:
- записать число в тригонометрической форме;
- извлечь корни, используя определение.
Алгоритм 4
Чтобы комплексное число $z$, записанное в показательной форме, привести к тригонометрической форме записи, необходимо выполнить следующее:
- определить из показательной записи числа значения модуля и аргумента;
- подставить полученные значения в выражение $z=r(\cos \varphi +i\cdot \sin \varphi )$.
Пример 3
Выполнить операцию извлечения корня $\sqrt{z} $ для заданных комплексных чисел в показательной форме представления:
\[z=3\cdot e^{\frac{\pi }{3} \cdot i} .\]Решение:
Тригонометрическая форма записи некоторого комплексного числа имеет вид $z=r(\cos \varphi +i\cdot \sin \varphi )$.
Определим значения модуля и аргумента: $r=3,\, \, \varphi =\frac{\pi }{3} $.
Запись числа в тригонометрической форме имеет вид: $z=3\cdot (\cos \frac{\pi }{3} +i\sin \frac{\pi }{3} )$.
Воспользуемся формулой из определения 4.
Для $k=0$ получаем: $w_{1} =\sqrt{z} =\sqrt{3} \cdot \left(\cos \frac{\pi }{6} +i\cdot \sin \frac{\pi }{6} \right)$.
Для $k=1$ получаем:
\[w_{2} =\sqrt{z} =\sqrt{3} \cdot \left(\cos \frac{\pi /3+2\pi }{2} +i\cdot \sin \frac{\pi /3+2\pi }{2} \right)=\sqrt{3} \cdot \left(\cos \frac{7\pi }{6} +i\cdot \sin \frac{7\pi }{6} \right).\]spravochnick.ru
Формула Муавра. Извлечение корня из комплексного числа
Используя формулу умножения комплексных чисел (3.3), получим формулу возведения комплексного числа в степень, называемую формулой Муавра:
(3.5) |
Из нее следует, что для возведения комплексного числа в любую натуральную степень его модуль нужно возвести в эту степень, а аргумент умножить на показатель этой степени.
Перейдем
к процедуре извлечения корней. Известно,
что во множестве действительных чисел
не из всякого действительного числа
можно извлечь корень. Например, 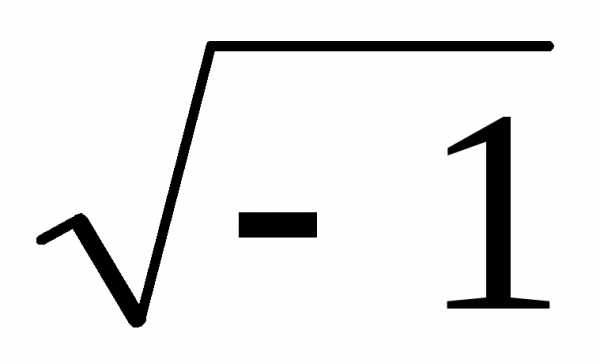 не существует. В множестве комплексных
чисел дело обстоит иначе.
не существует. В множестве комплексных
чисел дело обстоит иначе.
Пусть
.
Комплексное числоназывается корнем -й
степени из
-й
степени из ,
если
,
если ,
т.е.:
,
т.е.:
или
.
Модуль
комплексного числа определяется
однозначно, поэтому 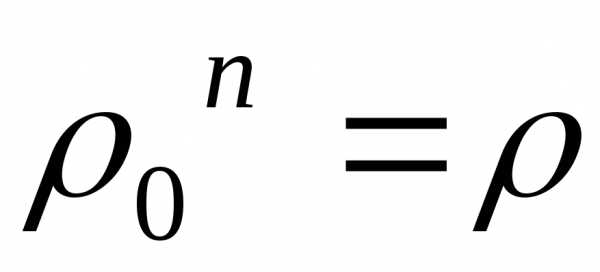 или
или (здесь имеется в виду арифметический
корень).
(здесь имеется в виду арифметический
корень).
Аргумент комплексного числа определяется с точностью до . Следовательно,, а.
Таким
образом, комплексное число  ,
которое является корнем
,
которое является корнем -й
степени из
-й
степени из имеет вид:
имеет вид:
(3.6) |
Придавая 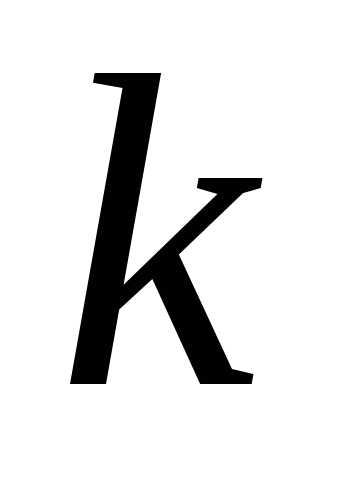 различные значения, мы не всегда будем
получать различные корни. Действительно,
различные значения, мы не всегда будем
получать различные корни. Действительно, можно записать в виде,
где.
Тогда:
можно записать в виде,
где.
Тогда:
,
Т.е.
значение аргумента при данном 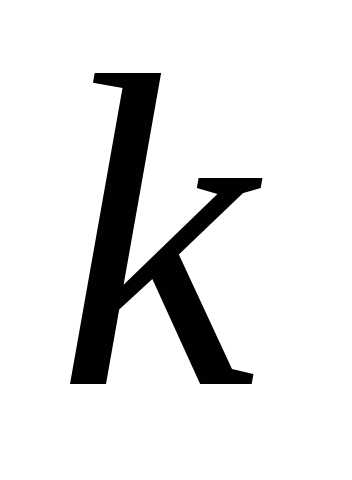 отличается от значения аргумента при
отличается от значения аргумента при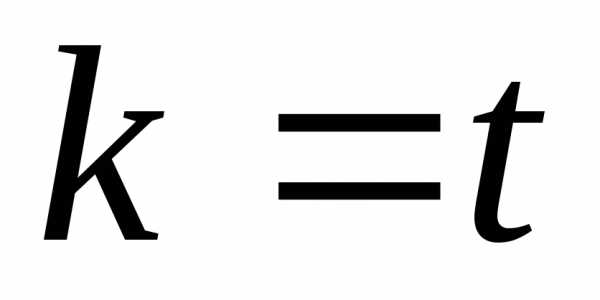 на число, кратное
на число, кратное .
Следовательно, в формуле (2) можно
ограничится лишь значениями.
При таких значениях
.
Следовательно, в формуле (2) можно
ограничится лишь значениями.
При таких значениях получаются различные корни, так как
разность между их аргументами по
абсолютной величине меньше
получаются различные корни, так как
разность между их аргументами по
абсолютной величине меньше
Итак,
для каждого ненулевого числа  существует ровно
существует ровно 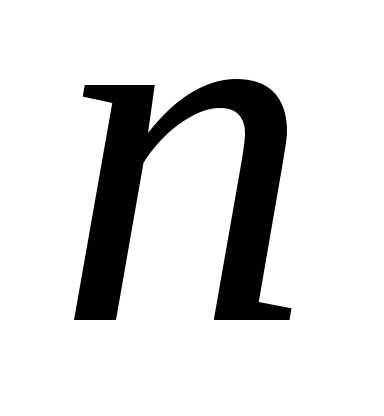 корней
корней  -й
степени из
-й
степени из  .
.
Пример.
Вычислить .
.
Представим число, стоящее под знаком корня, в тригонометрической форме:

.
Извлечем далее корень третьей степени из этого комплексного числа:
.
Отсюда полагая, что , получим:
;
;
.
Контрольные вопросы к лекции №3
Счетные и несчетные числовые множества.
Ограниченные множества.
Границы и грани множеств.
Соединения элементов.
Вычисление числа размещений, перестановок и сочетаний.
Понятие комплексного числа.
Понятие мнимой единицы (числа
 ).
).Основные операции над комплексными числами.
Представление комплексного числа в тригонометрической форме.
Понятие модуля комплексного числа.
Понятие аргумента комплексного числа.
Охарактеризовать умножение и деление комплексных чисел в тригонометрической форме.
Формула Муавра.
Тема 2. Аналитическая геометрия Лекция 4. Векторы
Основные понятия:
скалярная величина; векторная величина; коллинеарные векторы; компланарные векторы; единичный вектор; сложение векторов; проекция вектора; линейная комбинация векторов; линейная зависимость векторов; базис; координаты вектора; базисные орты; правая система координат; направляющие косинусы; скалярное произведение; векторное произведение; смешанное произведение.
Основные понятия
Понятие вектора широко применяется в экономике, математике, физике и других науках, при этом одинаково широко используется как алгебраическая концепция изложения векторного анализа, так и его геометрическая интерпретация, в рамках которой различаются величины двух видов: скалярные и векторные.
Скалярной величинойили скаляром называется величина, которая полностью определяется одним числом, выражающим отношение этой величины к соответствующей единице измерения, например, цена, количество проданного товара, стоимость и т.д.
Векторной величинойили вектором называется величина, для задания которой кроме численного значения необходимо указать и ее направление в пространстве, например, изменение темпов производства (рост или падение), колебание курса акций на бирже и т.д.
Векторная величина графически обычно изображается как связанный векторилинаправленный отрезок, т.е. отрезок прямой, у которого указано, какая из ограничивающих точек является его началом, а какая концом. Но в отличие от направленного отрезка, для описания которого необходимо указать начальную точку, длину и направление,свободный векторили простовекторпредставляет собой множество всех эквивалентных между собой связанных векторов и вполне характеризуется:
Для задания такого множества достаточно указать какой-либо один из связанных векторов этого множества – представитель вектора, в качестве которого обычно выбирается связанный вектор с началом, совпадающим с началом координат.
Вектор
обозначается одной маленькой буквой
со стрелкой сверху, например, 
 ,
где точка
,
где точка есть начало вектора (его точка приложения),
а
есть начало вектора (его точка приложения),
а ‑ его конец.
‑ его конец.Длина
вектора называется его модулем,
обозначается или
или и равна длине любого его представителя,
т.е. расстоянию между начальной и конечной
точками связного вектора
и равна длине любого его представителя,
т.е. расстоянию между начальной и конечной
точками связного вектора .
Вектор, длина которого равна нулю,
называетсянуль-вектороми обозначается
.
Вектор, длина которого равна нулю,
называетсянуль-вектороми обозначается .
.
Два вектора называются равными, если:
равны их длины;
они параллельны;
они направлены в одну сторону.
Иными словами, равные векторы получаются один из другого параллельным переносом в пространстве.
Векторы называются коллинеарными, если они расположены на одной или на параллельных прямых, икомпланарными, если они лежат на одной или на параллельных плоскостях.
Вектор,
длина которого равна единице, называется единичным вектором илиортом.
Орт обозначатся .
.
studfiles.net
Извлечение корня из комплексного числа — Мегаобучалка
Корнем n-ой степени, n Î N, n ³ 2, из числа z называется любое комплексное число u, для которого n-ая степень равна z:
.
В поле комплексных чисел справедлива следующая теорема.
Для любого z ≠ 0 извлечение корня n-ой степени, n ³ 2, из числа z всегда возможно и имеет ровно n различных значений.
Пусть z = r(cosj + isinj). Искомый корень n-ой степени обозначим
u = r(cosq + isinq).
По определению корня имеем un= z. Откуда следует, что
rn (cosnq + isinnq) = r(cosj + isinj).
Из равенства комплексных чисел получаем:
Так как .
Таким образом, модуль комплексного числа u определяется как арифметический корень из действительного положительного числа r, а аргумент находят по формуле
Общая формула Муавра
,
Пример.
Вычислить u = .
Представим число z = в тригонометрической форме:
Поэтому согласно общей формуле Муавра
,
где k = 0, 1, 2, 3, 4, 5.
Таким образом, значения корней:
,
,
Геометрически корни можно интерпретировать как числа, изображающие в комплексной плоскости вершины правильного n угольника (в рассмотренном примере – шестиугольника ), вписанного в окружность радиусом (в рассмотренном примере – радиусом ), с центром в начале координат.
Примеры.
Найти: 1) , 2) , 3) .
Решение.
1) ,
u0 = cos0 + isin0 = 1,
,
,
.
2)
, k = 0, 1, 2.
3) , k = 0, 1, 2.
Формула Эйлера. Показательная форма комплексного числа
Помимо алгебраической и тригонометрической имеется еще показательная форма записи комплексного числа, которая широко используется в различных приложениях, в частности в электротехнике.
Пусть , зависит от действительной переменной φ.
Сопоставим взаимно однозначным образом каждому комплексному числу комплексно показательное выражение . С помощью операций дифференцирования можно показать, что эти выражения имеют одну и ту же логическую сущность, в связи с этим полагают по определению
.
Эта формула называется формулой Эйлера и представляет собой определение комплексной показательной функции , где φ – любое действительное число.
Пусть дано комплексное число z =r (cosφ + isinφ). Сопоставляя это с предыдущей формулой, получаем
.
Такая форма записи комплексного числа называется показательной формой комплексного числа.
В этой форме записи удобно осуществлять операции умножения, деления, возведения в степень и извлечения корня. Соответствующие формулы записываются следующим образом.
Пусть . Тогда
Примеры.
1. Найти показательную форму чисел:
а) z1 = 1 + i; б) z2 = .
Решение.
а) r = , .
б) .
2. Найти алгебраическую форму чисел:
а) , б) , в) .
Решение.
а) ,
б) ,
в) .
3. Найти z1z2 и , результат записать в тригонометрической форме:
а) ; б) .
Решение.
а) ,
,
б)
.
4. Вычислить: а) z4 , б) , где .
Решение:
а) ,
б)
Теория комплексных чисел может быть использована при решении геометрических задач на плоскости; и обратно, факты геометрического характера позволяют доказывать некоторые соотношения и тождества для комплексных чисел.
Примеры.
1. Пусть . Доказать, что .
Поскольку , то
.
Геометрически этот факт означает, что сумма квадратов длин диагоналей ромба равна сумме квадратов длин всех его сторон.
 |
Действительно, точки плоскости, соответствующие комплексным числам 0, z1, z2 и z1 + z2, являются вершинами ромба, для которого и – длины его сторон, а и – длины его диагоналей.
2. Пусть z1, z2, z3, z4 – различные комплексные числа и . Доказать, что .
Имеем:
=
= ,
т. к. число вещественно и положительно (докажите это самостоятельно). Кроме того,
= = .
Доказанное равенство известно в планиметрии как теорема Птолемея: произведение длин диагоналей выпуклого вписанного в окружность четырехугольника равно сумме парных произведений длин его противолежащих сторон.
megaobuchalka.ru
11. Формула Муавра. Извлечение корня из комплексного числа
Используя формулу умножения комплексных чисел (3.3), получим формулу возведения комплексного числа в степень, называемую Формулой Муавра:
(3.5) |
Из нее следует, что Для возведения комплексного числа в любую натуральную степень его модуль нужно возвести в эту степень, а аргумент умножить на показатель этой степени.
Перейдем к процедуре извлечения корней. Известно, что во множестве действительных чисел не из всякого действительного числа можно извлечь корень. Например, не существует. В множестве комплексных чисел дело обстоит иначе.
Пусть . Комплексное число называется корнем -й степени из , если , т. е.:
Или
.
Модуль комплексного числа определяется однозначно, поэтому или (здесь имеется в виду арифметический корень).
Аргумент комплексного числа определяется с точностью до . Следовательно, , а .
Таким образом, комплексное число , которое является корнем -й степени из имеет вид:
(3.6) |
Придавая различные значения, мы не всегда будем получать различные корни. Действительно, можно записать в виде , где . Тогда:
,
Т. е. значение аргумента при данном отличается от значения аргумента при на число, кратное . Следовательно, в формуле (2) можно ограничится лишь значениями . При таких значениях получаются различные корни, так как разность между их аргументами по абсолютной величине меньше .
Итак, для каждого ненулевого числа существует ровно корней -й степени из .
Пример. Вычислить .
Представим число, стоящее под знаком корня, в тригонометрической форме:
.
Извлечем далее корень третьей степени из этого комплексного числа:
.
Отсюда полагая, что , получим:
;
;
.
Контрольные Вопросы к лекции №3
1. Счетные и несчетные числовые множества.
2. Ограниченные множества.
3. Границы и грани множеств.
4. Соединения элементов.
5. Вычисление числа размещений, перестановок и сочетаний.
6. Понятие комплексного числа.
7. Понятие мнимой единицы (числа ).
8. Основные операции над комплексными числами.
9. Представление комплексного числа в тригонометрической форме.
10. Понятие модуля комплексного числа.
11. Понятие аргумента комплексного числа.
12. Охарактеризовать умножение и деление комплексных чисел в тригонометрической форме.
13. Формула Муавра.
| < Предыдущая | Следующая > |
|---|
matica.org.ua
4.3. Формула Муавра и извлечение корня п-ой степени из комплексного числа
Вычислив произведение комплексных чисел, записанных в тригонометрической форме, можно убедиться, что модуль и аргумент комплексного числа обладают следующими свойствами:
 .
Модуль произведения комплексных чисел
равен произведению модулей этих чисел:
.
.
Модуль произведения комплексных чисел
равен произведению модулей этих чисел:
.
 .
Аргумент произведения комплексных
чисел равен сумме аргументов этих чисел:
.
.
Аргумент произведения комплексных
чисел равен сумме аргументов этих чисел:
.
Используя эти свойства, легко можно получить формулу возведения комплексного числа в целую положительную степень, а именно:
если , то
–формула Муавра,
или в показательной форме записи:
.
Определение. Корнем п-ой
степени из комплексного числа  называется такое комплексное число
называется такое комплексное число ,
которое, будучи возведено в степеньп даст число
,
которое, будучи возведено в степеньп даст число  .
.
Из определения и
формулы Муавра ясно, что модуль искомого
корня будет  ,
а аргумент
,
а аргумент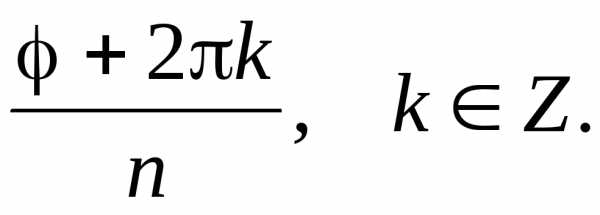
Таким образом,
(1)
Придавать  значения, большие
значения, большие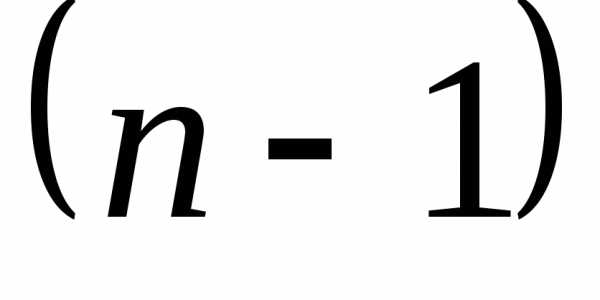 ,
не имеет смысла, так как будем получать
уже имеющиеся значения аргумента (с
точностью до
,
не имеет смысла, так как будем получать
уже имеющиеся значения аргумента (с
точностью до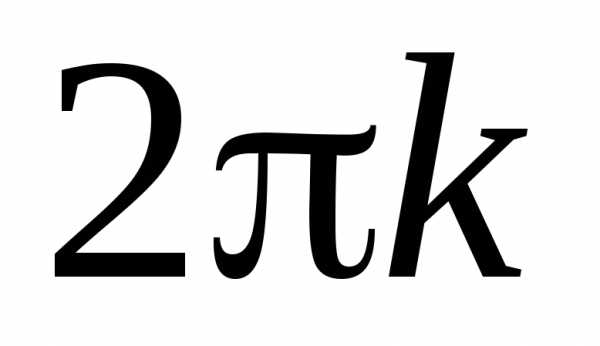 ).
).
Следовательно,
корень п-ой
степени из комплексного числа  имеетп различных
значений, модули которых одинаковы (
имеетп различных
значений, модули которых одинаковы ( ),
т.е. все значения корня лежат на окружности
с центром в начале координат радиуса
),
т.е. все значения корня лежат на окружности
с центром в начале координат радиуса ,
а аргументы последовательных значений
отличаются на угол
,
а аргументы последовательных значений
отличаются на угол .
.
Пример 4. Используя формулу Муавра, вычислить:
а)  ;
б)
;
б)
Решение. а) Представим число в тригонометрической форме. Имеем:
. Значит,
–тригонометрическая форма записи комплексного числа .
Применяя формулу Муавра, получим:
б) Представим
число  в тригонометрической форме. Имеем:.
Поэтому
в тригонометрической форме. Имеем:.
Поэтому
–тригонометрическая
форма записи комплексного числа  .
.
Применяя формулу Муавра, получим:
Пример 5. Найти
все значения корня:  .
.
Решение. Представим
комплексное число  в тригонометрической форме. ЗдесьПоэтому
в тригонометрической форме. ЗдесьПоэтому
.
По формуле (1) находим:
где
Полагая , получим:
Найденным корням соответствуют вершины правильного пятиугольника, вписанного в окружность радиуса с центром в начале координат (рис. 3).
Рис. 3.
4.4. Функции комплексного переменного
Говорят, что в
области  определена функция
определена функция ,
если каждой точке
,
если каждой точке поставлено в соответствие одно
(однозначная функция) или несколько
(многозначная функция) значений
поставлено в соответствие одно
(однозначная функция) или несколько
(многозначная функция) значений .
.
Пусть
и.
Тогда зависимость между комплексной функцией
между комплексной функцией и комплексной переменной
и комплексной переменной может быть описана с помощью двух
действительных функций
может быть описана с помощью двух
действительных функций и
и действительных переменных
действительных переменных и
и :,.
:,.
Таким образом,
функцию 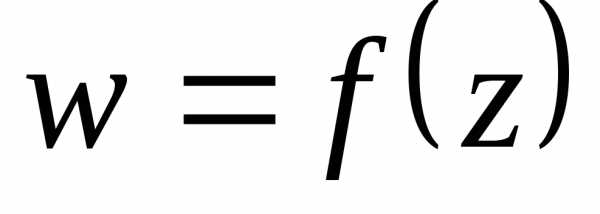 можно записать в виде:
можно записать в виде:
,
где
– действительная часть ;– мнимая часть
;– мнимая часть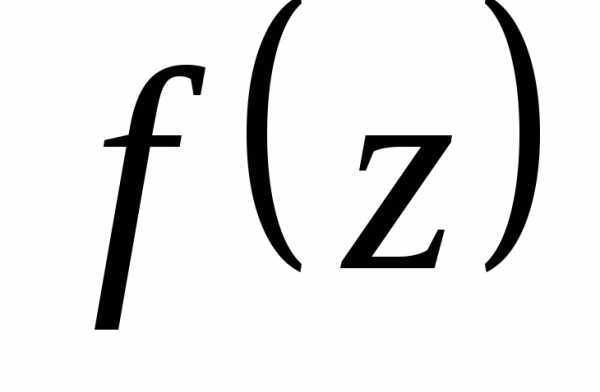 .
.
Основные элементарные функции комплексного переменного
1. Показательная функция
где
.
Свойства показательной функции:
Непрерывна на всей комплексной плоскости;
Периодична с периодом
 т.е.;
т.е.;Принимает все значения, кроме нуля, т.е. уравнение
 разрешимо для любого
разрешимо для любого ;
;;
studfiles.net

 ).
). т.е.;
т.е.;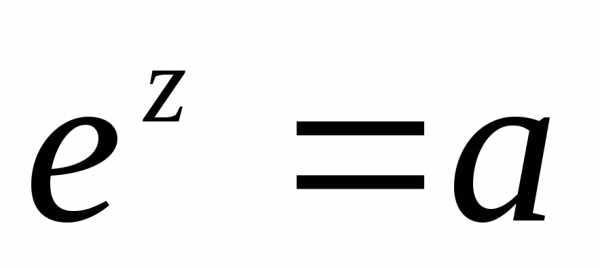 разрешимо для любого
разрешимо для любого ;
;