Задачи на теорему синусов и косинусов – Задачи на теорему косинусов — задачи с решениями

Ключевые задачи по теме «теорема синусов и косинусов»

Тогда 0-y.

Применяем теорему косинусов к треугольнику АВМ:

АВ²=АМ²+ВМ²-2∙АМ∙ВМ∙cosy.

2. Применяем теорему косинусов к треугольнику АСМ:

АС²=АМ²+СМ²-2∙АМ∙СМ∙cos(180⁰-y).

3. Получили систему уравнений:

с²=x²+0,25a²-2∙0,5a∙x∙cosy, b²=x²+0,25a²+2∙0,5a∙x∙cosy.

Сложив эти равенства, получаем:

С²+b²=2x²+0,5a².

.

Переход к выбору раздела.

Материалы по третьей ключевой задаче

Анализ третьей ключевой задачи

В этом разделе проводится анализ такой задачи: Четырехугольник АВСД вписан в окружность. Известно, что АВ=3, ВС=4, СД=5 и АД=2. Найти диагональ АС.

1. Так как АВСД вписан в окружность, то сумма углов В и Д равна 180

0.

2. Сторона АС принадлежит двум треугольникам АВС и АДС.

3. Так как известны длины сторон АВ, ВС и АД, СД, то можно получить уравнение для определения косинуса угла В.

4. Это позволяет предложить такой план решения:

А) Применить теорему косинусов к треугольнику АВС.

Б) применить теорему косинусов к треугольнику АДС.

В) составить и решить уравнение относительно косинуса угла В.

Г) найти длину АС.

Переход к выбору ключевой задачи.

Решение третьей ключевой задачи

В этом разделе проводится решение такой задачи: Четырехугольник АВСД вписан в окружность. Известно, что АВ=3, ВС=4, СД=5 и АД=2. Найти диагональ АС.

На основе анализа задачи был составлен такой план решения:

А) Применить теорему косинусов к треугольнику АВС.

Б) применить теорему косинусов к треугольнику АДС.

В) составить и решить уравнение относительно косинуса угла В.

Г) найти длину АС.

Реализация плана решения.

А) Пусть угол АВС равен х, тогда угол АДС равен 180⁰-х. Применяем теорему косинусов к треугольнику АВС. Получаем:

АС²=АВ²+ВС²-2∙АВ∙ВС∙cosx.

Б) Применяем теорему косинусов к треугольнику АДС. Получаем:

АС²=АД²+ДС²+2∙АД∙ДС∙cosx.

С учетом известной информации получаем уравнение относительно cosx:

9+16-2∙3∙4∙cosx=4+25+2∙2∙5∙cosx.

cosx=-.

В) Теперь вычисляем АС:

АС²=9+16+2∙3∙4∙=.

Ответ: .

Переход к выбору ключевой задачи.

Обобщение третьей ключевой задачи

В этом разделе проводится обобщение такой задачи: Четырехугольник АВСД вписан в окружность. Известно, что АВ=3, ВС=4, СД=5 и АД=2. Найти диагональ АС.

Обобщение выполним, рассматривая четырехугольник АВСД, вписанный в окружность: Четырехугольник АВСД вписан в окружность. Известно, что АВ=a, ВС=b, СД=c и АД=d. Найти диагональ АС.

Реализуем известный план решения:

А) Применить теорему косинусов к треугольнику АВС.

Б) применить теорему косинусов к треугольнику АДС.

В) составить и решить уравнение относительно косинуса угла В.

Г) найти длину АС.

Реализация плана решения.

А) Пусть угол АВС равен х, тогда угол АДС равен 180⁰-х. Применяем теорему косинусов к треугольнику АВС. Получаем:

АС²=АВ²+ВС²-2∙АВ∙ВС∙cosx.

Б) Применяем теорему косинусов к треугольнику АДС. Получаем:

АС²=АД²+ДС²+2∙АД∙ДС∙cosx.

С учетом известной информации получаем уравнение относительно cosx:

a²+b²-2∙a∙b∙cosx=c²+d²+2∙c∙d∙cosx.

cosx=.

В) Теперь вычисляем АС:

АС²=a²+b²-2∙a∙b∙=

.

Ответ: .

Переход к выбору ключевой задачи.

Материалы по четвертой ключевой задаче

Анализ четвертой ключевой задачи

Вас интересует анализ такой задачи: Дан треугольник АВС, в котором АС=10 и ABC=60⁰. Найти радиус окружности, проходящей через центр вписанной в треугольник АВС окружности и вершины А и С.

Пусть О – центр окружности, вписанной в треугольник АВС. Тогда известно, что АО и СО – биссектрисы внутренних углов треугольника АВС.

Так как известен угол В, то можно вычислить градусную меру угла АОС. Так как известна длина АС и угол АОС, то, применив теорему синусов, для треугольника АОС можно найти радиус окружности, проходящей через точки О, А и С.

Эти соображения позволяют предложить такой план решения:

1. Вычислить градусную меру угла АОС.

2. Применить теорему синусов к треугольнику АОС.

3. Вычислить искомый радиус.

Переход к выбору ключевой задачи.

Решение четвертой ключевой задачи

В разделе приводитя решение такой задачи: Дан треугольник АВС, в котором АС=10 и ABC=60⁰. Найти радиус окружности, проходящей через центр вписанной в треугольник АВС окружности и вершины А и С.

Пусть О – центр окружности, вписанной в треугольник АВС, R – радиус окружности, проходящей через точки А, О, С.

На основе анализ задачи был предложен такой план решения:

1. Вычислить градусную меру угла АОС.

2. Применить теорему синусов к треугольнику АОС.

3. Вычислить искомый радиус.

Реализуем этот план.

1. Из треугольника АОС найдем угол АОС:

⁰-0-0,5(0-0,5(180⁰—0.

2. Применяем теорему синусов к треугольнику АОС. Имеем:

.

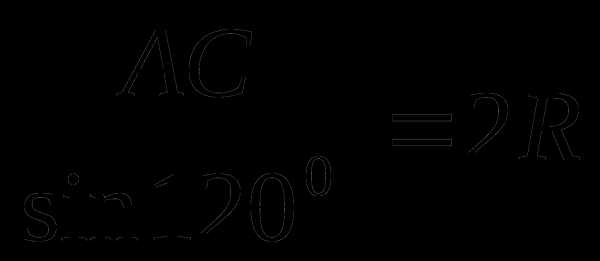3. Находим радиус R: R=.

Переход к выбору ключевой задачи.

Материалы по пятой ключевой задаче

Анализ пятой ключевой задачи

Вас интересует анализ такой задачи: Внутри квадрат АВСД через вершины А и Д проведены прямые, образующие угол в 15⁰ со стороной АД. Эти прямые пересекаются в точке Е.

Доказать, что треугольник ВЕС – равносторонний.

В ситуации задачи имеются:

1. Треугольники АЕД, АВЕ, ДЕС, ВСЕ.

2. Нет линейных размеров. Но их недостаток можно компенсировать, введя обозначение для стороны квадрата.

3. После введения обозначения для стороны квадрата в треугольнике АЕД известна сторона и все углы, поэтому могут быть найдены все стороны.

4. В треугольнике ВЕД, после вычисления стороны АЕ, можно вычислить сторону ВЕ и сравнить ее длину с длиной стороны квадрата.

Отсюда такой план:

1. Из треугольника АДЕ находим АЕ.

2. Из треугольника АВЕ находим ВЕ.

3. Сравниваем ВЕ с АВ.

Переход к выбору раздела.

Решение пятой ключевой задачи

Вас интересует решение такой задачи: Внутри квадрат АВСД через вершины А и Д проведены прямые, образующие угол в 15⁰ со стороной АД. Эти прямые пересекаются в точке Е.

Доказать, что треугольник ВЕС – равносторонний.

На основе анализ был предложен такой план:

4. Из треугольника АДЕ находим АЕ.

5. Из треугольника АВЕ находим ВЕ.

6. Сравниваем ВЕ с АВ.

Реализуем этот план.

1. Пусть АВ=а. В треугольнике АЕД: 0=0. Применим теорему синусов к треугольнику АЕД:

.

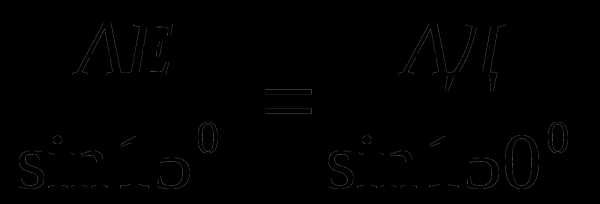АЕ=2аsin15⁰.

2. Применим теорему косинусов к треугольнику АВЕ. Получаем:

=.

3. Так как cos75⁰=sin15⁰ , получаем:

.

Аналогично доказывается, что СЕ=а.

Утверждение доказано.

Переход к выбору раздела.

gigabaza.ru

Теорема косинусов. Решение задач.

Теорема косинусов. Решение задач.

Цели: научить учащихся применять теорему косинусов и следствия из неё
при решении задач.

Ход урока

1. Организационный момент.

2. Актуализация опорных знаний
   1. Сформулировать теорему о площади треугольника (вычисление площади по двум сторонам и углу между ними).
   2. Сформулировать теорему синусов.
   3. Сформулировать теорему косинусов.
   4. При решении, каких задач, мы уже использовали теорему косинусов? (Нахождение стороны по двум другим заданным сторонам и углу между ними; нахождение угла треугольника по трём известным сторонам.)

3. Решение задач и создание проблемных ситуаций при их решении.
   № 1. Найдите неизвестную сторону и площадь треугольника АВС,
   
   

№ 2. Найдите угол А треугольника АВС, если АВ =АС =1 м, ВС = м. Решение.
Пользуясь теоремой косинусов, получаем: так как

AC = b = 1 м, AB = c = 1м , BC = а = м, то

№ 3. Решить задачу № 1031 (в). Выясните, является ли треугольник остроугольным, прямоугольным или тупоугольным, если его стороны равны:
9, 5, 6. (По ходу решения учитель задаёт наводящие вопросы.)

Решение. Пусть

Все ли углы нужно находить?
( Достаточно найти наибольший угол — он лежит против большей из сторон, то есть в данной задаче это угол А.)

Можно ли определить вид треугольника, не вычисляя углы треугольника?
(Вариантов ответа только два: «нет» и «да». Но объяснить почему можно иначе — не могут.)
Рассмотрим теорему косинусов и проведём её исследование при различных значениях угла между сторонами a и b:

1. Если угол С

   острый, то следовательно, .

2. Если угол С прямой, то следовательно, .

3. Если угол С тупой, то следовательно, .

Воспользуемся полученными следствиями из теоремы косинусов при решении следующих задач.

№ 4. Решить задачу № 1031(б). Выясните, является ли треугольник остроугольным, прямоугольным или тупоугольным, если его стороны равны: 17, 8, 15.
Решение.

Пусть

Наибольшая сторона треугольника с, поэтому сравним её квадрат с суммой квадратов двух других сторон.

то есть , следовательно, угол С прямой.

треугольник прямоугольный.

№ 5. В треугольнике АВС угол С равен 45^о, АС = 5 см, ВС = 9 см. Найдите угол А.

Решение.
Найдём сторону АВ по теореме косинусов:

;
.
Как будем искать угол А? (Мнения разделились: одни предлагают по теореме синусов, другие – по теореме косинусов. Предлагаю решить 1 варианту по теореме косинусов, а варианту 2 – по теореме синусов.) Двое учащихся у доски воспроизводят свои варианты решений.

Решение 1 варианта.
, тогда

угол А – тупой, А.

Решение 2 варианта.

; тогда
А

Почему получились разные значения одного и того же угла? Задача имеет несколько решений? (Некоторые из учащихся заметили, что сумма получившихся значений угла А равна 180^о и сообщили, что во 2-ом варианте надо было брать угол не 78^о , а 102^о , так как их синусы равны.)

При решении по теореме синусов необходимо было вначале выяснить вид угла А, воспользовавшись следствиями из теоремы косинусов. В нашем случае: , т.к. ; ,
следовательно угол А – тупой.

тогда А.

4. Подведение итогов урока.
   

5. Домашнее задание: выучить материал пунктов 100-102 (стр. 252-254), решить задачи № 1031(а), 1025(е).

infourok.ru

Теорема косинусов. Пример решения задачи

Теорема косинусов формулируется следующим образом: квадрат любой стороны треугольника равен сумме квадратов двух других сторон без удвоенного произведения этих сторон на косинус угла между ними.

Задача

Одна из сторон треугольника больше другой на 8 сантиметров, а угол между ними равен 120 градусам. Найдите периметр треугольника, если длин третьей стороны равна 28 см.

Решение.

Обозначим одну из сторон треугольника как x, тогда величина другой равна x+8 см.

Исходя из теоремы косинусов, получим:
28² = x² + (x+8)²-2x(x+8)cos120^o
784 = x² + x² +16x + 64 — 2x(x+8)(-0,5)
784 = 2x²+16x + 64 + x(x+8)
720 = 3x² + 16x + 8x
3x² + 24x +720 = 0
D=9216
x₁=((-24)+96)/6=12 (второй корень является отрицательным числом и не имеет смысла в рамках решения задачи)

Таким образом, периметр треугольника P=12+(12+8)+28 = 60 см.

Ответ: 60 см

Задача   

В треугольнике АВС сторона АС равна 7√3 см, сторона ВС равна 1 см. Угол С равен 150 градусам. Найти длину стороны АВ.

Решение.
Применим теорему косинусов и соответствующую формулу (см.выше)
AB²  = (7√3)² + 1²  — 2 (7√3) cos 150º

Значение косинуса 150 градусов найдем по таблице значений тригонометрических функций.
AB² = 147 + 1 — 14√3 (-√3/2) 
AB² = 148 + 21 = 169
AB = 13

Ответ: 13 см

 Теорема косинусов и ее доказательство. | Описание курса | Тангенс и его свойства 

   

profmeter.com.ua

«Теорема синусов и косинусов в задачах с практическим содержанием»

Обобщающий урок по теме:

«Теорема синусов и косинусов в задачах
с практическим содержанием»

Цель:

1. Обобщить знания, умения и навыки учащихся в решении задач с практическим содержанием.

2. Показать связь теории с практикой.

ХОД УРОКА

Орг. Момент. Актуализация знаний

1. Учитель: Ребята! Сегодня у нас обобщающий урок по теме: «Соотношения между сторонами и углами треугольника». (Записать в тетрадях число и тему урока)

2. Исходя из формулировки темы, какие цели вы должны поставить перед собой на сегодняшний урок?

Ученик: Необходимо повторить весь теоретический материал и применить его при решении задач.

3. Для этого, какие поставим перед собой цели?

Ученики:

• Знать теорему синуса, теорему косинуса.

• Знать табличные значения синуса, косинуса.

• Уметь решить треугольник, по каким- то трем данным элементам, определяющим треугольник.

• Уметь применять основные формулы раздела при решении задач.

Разминка

-Сформулировать теорему синусов и записать на доске и в тетрадях соответствующую формулу

— Сформулировать теорему косинусов и записать на доске и в тетрадях соответствующую формулу

— Чему равна сумма углов треугольника?

— Записать на доске формулу для нахождения косинуса угла треугольника.

— Какими формулами приведения мы пользуемся при решении треугольников? Запишите на доске

sin (180-a)= sin a

cos (180-a)= -cos a

2. Два ученика работают у доски по карточкам у доски.

Карточка № 1

Карточка № 2

1. В  АВС сторона АВ = 8 см,
С = 60 В = 45.

Найдите сторону АС.

2. Сформулируйте теорему косинусов.

1. В  АВС сторона АВ = 7 см,
В = 45 ВС = 5 см.

Найдите сторону АС.

2. Сформулируйте теорему синусов.

Три ученика работают по карточкам № 3-5 индивидуально.

Карточка № 3	Карточка № 4	Карточка № 5
В  АВС сторона АВ = 4 см, С= 30 В = 45. Найдите сторону АС. В  PQR сторона PQ = 7,5 м, QR = 9,4 cм, PR = 11,3 м. Какой угол треугольника наибольший, какой наименьший?	В  СDМ сторона СD = 10 см, D= 45 М = 60. Найдите сторону СМ. Стороны треугольника равны 7 см, 9 см. Может ли угол, противолежащий стороне 7 см, быть тупым? Почему?	В  KPD сторона PD = 6 см, K= 60 P = 45. Найдите сторону KD. Стороны треугольника равны 8 см, 6 см. Может ли угол, противолежащий стороне 6 см, быть прямым? Почему?

3. Остальные учащиеся в это время слушают сообщение на тему: «Геометрия в древних практических задачах» (журнал «Математика в школе», № 5. — 1995).

Ученик: На первых этапах своего развития геометрия представляла собой набор полезных, но не связанных между собой правил, формул для решения задач, с которыми люди сталкивались в повседневной жизни.

Лишь много веков спустя учёными Древней Греции была создана теоретическая основа геометрии. Но и тогда прикладная геометрия не утратила своего значения, поскольку была незаменима для землемерия, мореплавания и строительства.

Таким образом, написанные в древности, руководства по геометрии, содержащие «рецепты» решения практических задач, сопровождали человечество на протяжении всей истории существования.

Р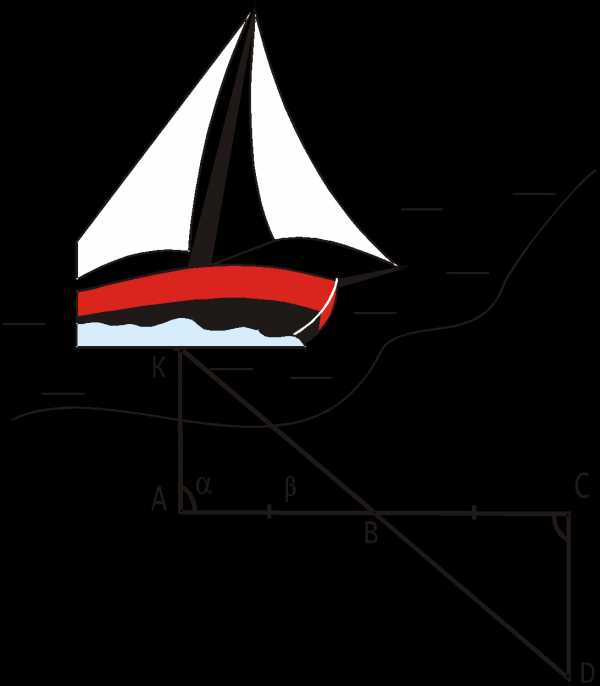ешение отдельных старинных задач практического характера могут найти применение и в настоящее время, а поэтому заслуживают внимания. История хранит немало приёмов решения задач на нахождение расстояний, определение расстояний до кораблей, находящихся в море, – одна из таких задач, решаемая двумя способами. Предполагают, что оба способа принадлежат древнегреческому учёному, путешественнику и купцу Фалесу Милетскому (VI век до н.э.).

Задача

1-ый способ основан на одном из признаков равенства треугольников. Пусть корабль находится в точке К, а наблюдатель – в точке А. Требуется определить расстояние КА.

Построив в точке А прямой угол, необходимо отложить на берегу два рав­ных отрезка АВ=ВС. В точке С вновь построить, прямой угол, причём наблюдатель должен идти по перпендикуляру до тех пор, пока не дойдет до точки D, из которой корабль К и точка В были бы видны лежащими на одной прямой.

Прямоугольные  ВСD и  ВAK равны, следовательно, СD = АК, а отрезок СD можно непосредственно измерить.

Ученик: 2-ой способ, получивший название метода триангуляции, нашёл применение в астрономии. С его помощью измерялись расстояния до небесных тел. Этот метод состоит из трёх этапов.

1. Измерение углов  и  и расстояния АВ.

2. Построение  АВК с углами  и  при вершинах А и В соответственно.

3. Учитывая подобие треугольников АВК и АВК, рассматриваем равенство: АК:АВ = АК: АВ, по известным длинам отрезков АВ и АВ нетрудно найти длину АК.

После этого сообщения учитель собирает самостоятельную работу учеников, а работающие у доски объясняют своё решение и отвечают на вопросы.

4. Сообщения учеников.

1. Решение задачи на определение недоступных расстояний. Задача

В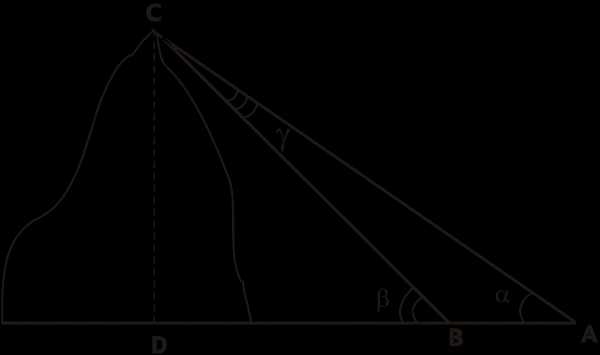ершина горы видна из точки А под углом 3842, а при приближении к горе на 200м вершина стала видна под углом 42. Найдите высоту горы.

Дано: АВ = 200м,

САВ =  = 3842,

СВD =  = 42, СD  DА

Найти СD.

Решение:

1. Из СВА по теореме синусов имеем равенство: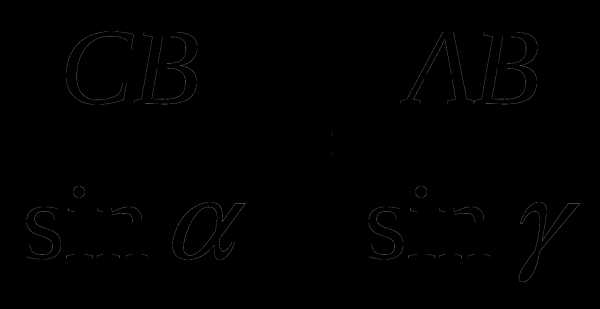

2. Угол  – внешний угол АВС, поэтому  =  + , откуда  =  – .

3. .

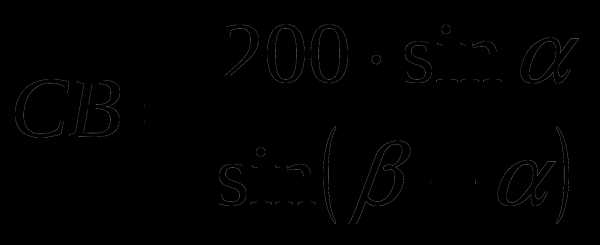4. Из СВD находим (м)

Ответ: м

2. Решение задачи на движение

В 7 часов утра пассажирский самолёт вылетел из города А. После получасовой остановки в городе В в 8 часов 10 минут самолёт сделал поворот на 35 вправо и в 9 часов совершил посадку в городе С.

Найти расстояние между городами А и С, если средняя скорость самолёта на каждом участке полёта была равна 320км/час.

Д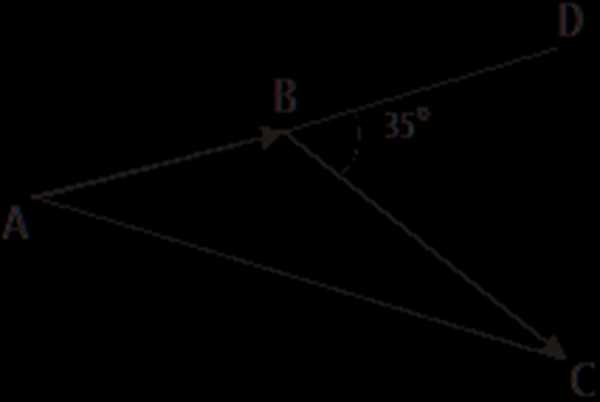ано: СВD = 35,

V = 320 км/час, t₁ = 7 ч.,

t₂ = 8 ч. 10 мин, t₃ = 9 ч.

t_ост = 30 мин.

Найти АС.

Решение:

1. ; (км)

2. ; (км)

3. АВС + DВС = 180 (как смежные)

АВС = 180 – 35, АВС = 145

По теореме косинусов из АСВ находим АС:

АС² = АВ² + ВС² – 2АВ * ВС cos 145

Ответ: АС  458 км.

5. Учитель:  Подведем итог этого этапа урока, ответим на вопросы:

1. Что значит решить треугольник?

Ученик : Решить треугольник означает определить стороны, углы и другие элементы треугольника, если даны некоторые из них.

2. Какие теоремы, таблицы используем при этом?

Ученик: теоремы синусов, косинусов, теорему Пифагора, теорему о сумме углов треугольника. Используем таблицы значений синусов и косинусов.

3. Какие типы задач при этом можно выделить?

Ученик: по стороне и двум прилежащим к ней углам; по двум сторонам и углу между ними; по трём сторонам

3. Самостоятельная работа по группам.

Учитель: Вам предстоит на практике показать ваши умения решать прикладные задачи.

Цель: проверить умение учащихся применять знания по изученной теме при решении задач

Группа 1

Найти расстояние от точки А, находящейся на берегу, до корабля К.

Дано: А = , В = , АВ = а.

Найти АК.

Решение:

К = 180 – ( + ), из  АВК по теореме синусов находим расстояние АК: , .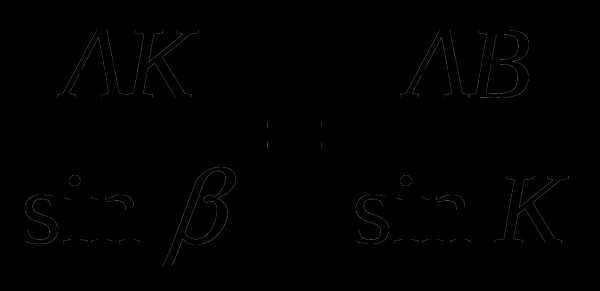

Г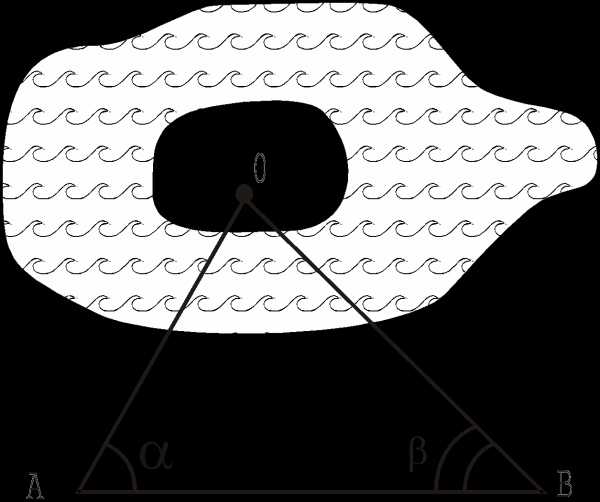руппа 2: Найти расстояние от острова, находящегося на озере, до пункта В на берегу (остров О принят за точку).

Дано: А = ,

В = ,

АВ = в.

Найти ОВ.

Решение:

О = 180 – ( + ), из АОВ по теореме синусов находим расстояние ОВ: , .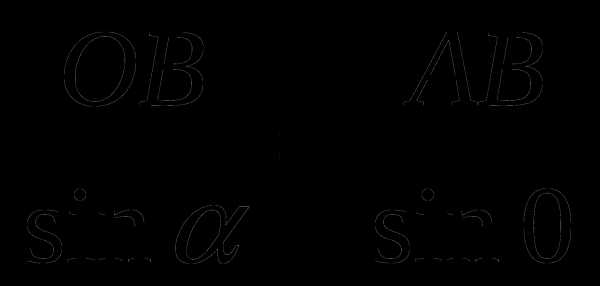

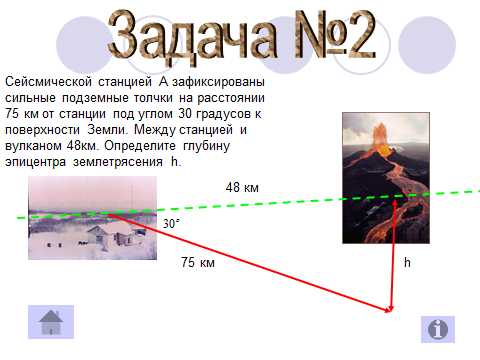
Военно-прикладные задачи.

Группа 3

Группа 4

Группа 5

Группа 6

Проверка решений по слайдам.

Рефлексия на листочках

Ребята сдают листочки с работами в группах учителю.

– Итак, где можно применить полученные знания на практике и в жизни?

Учитель:  Существует множество областей, в которых применяются тригонометрия и тригонометрические функции. Например, метод триангуляции используется в астрономии для измерения расстояния до ближайших звезд, в географии для измерения расстояний между объектами, а также в спутниковых навигационных системах. Синус и косинус имеют фундаментальное значение для теории периодических функций, например при описании звуковых и световых волн.
Тригонометрия или тригонометрические функции используются в астрономии (особенно для расчётов положения небесных объектов, когда требуется сферическая тригонометрия), в морской и воздушной навигации, в теории музыки, в акустике, в оптике, в анализе финансовых рынков, в электронике, в теории вероятностей, в статистике, в биологии, в медицинской визуализации (например, компьютерная томография и ультразвук), в аптеках, в химии, в теории чисел (следовательно, и в криптологии), в сейсмологии, в метеорологии, в океанографии, во многих физических науках, в межевании и геодезии, в архитектуре, в фонетике, в экономике, в электротехнике, в машиностроении, в гражданском строительстве, в компьютерной графике, в картографии, в кристаллографии, в разработке игр и многих других областях.

В старших классах каждый школьник
Изучает треугольник.
Три каких-то уголка,
А работы – на века.

Учитель:  Сегодня мы с вами обобщили тему «Решение треугольника». Кроме того узнали где можно применить полученные знания на практике и в жизни. Запишите домашнее задание.

Оценки за урок
– Спасибо за урок! 

Дополнительные вопросы:

1. Почему теорема косинусов является обобщённой теоремой Пифагора? (Когда треугольник АВС прямоугольный с прямым углом при вершине С; C = 90º, cos 90º = 0 => а² + b² = c²).

2. Как, используя теорему косинусов определить вид треугольника? (достаточно определить знак косинуса, соответствующего наибольшему углу, если сторона а наибольшая, то достаточно определить знак величины в² + с² – а²)

3. В треугольнике АВС,  АВ = 8,4 cм,  ВС = 13,2 см,  АС = 7,5 см. Какой угол треугольника наибольший, какой наименьший?

4. Стороны треугольника 12 см, 15 см, 9 см. Может ли угол, противолежащий стороне 9 см, быть тупым? Почему?

5. Стороны треугольника 9 см и 12 см. Может ли угол, противолежащий стороне равной 9 см, быть прямым? Почему?

infourok.ru

Задачи с практическим содержанием на применение теорем синусов и косинусов.

Урок геометрии в 9 классе по теме «Задачи с практическим содержанием на применение теорем синусов и косинусов»

Климочкина Галина Николаевна, учитель математики

Тип урока: урок систематизации и закрепления знаний.

Цель урока: показать связь теории с практикой, способствовать совершенствованию навыков решения практических задач, применяя теоремы синусов и косинусов.

Задачи:

— использовать теоремы синусов и косинусов для нахождения неизвестных величин в реальной ситуации;

— приобрести опыт решения задач практического содержания;

— формировать коммуникативную компетенцию учащихся;

— способствовать развитию наблюдательности, умению анализировать, сравнивать, делать выводы.

Ход урока.

1. Вступление.

Часто возникает спор о том, нужны ли задачи с занимательным условием, задачи, оперирующие с конкретными, взятыми из жизни, примерами? Здесь не может быть двух мнений: такие задачи нужны. Практические задачи позволяют показать важность геометрических знаний в повседневной жизни и быту. Сегодня на уроке мы рассмотрим задачи с практическим содержанием на применение теорем синусов и косинусов.

Блез Паскаль сказал: «Среди равных умов при одинаковости прочих условий превосходит тот, кто знает геометрию». Это девиз нашего урока.

А теперь перейдем к разминке.

2. Разминка.

1 блок. Знай!!!

Задание 1. Как продолжить утверждение, чтобы оно стало верным?

«Стороны треугольника пропорциональны…».

Задание 2. Продолжите фразу так, чтобы утверждение стало верным? «Квадрат стороны треугольника равен…».

Итак, мы повторили теоремы синусов и косинусов.

2 блок. Подумай!!!

Задание 1. Найдите ошибки в записи формул.

Задание 2. Установите соответствие формул с их названиями.

1) 2) 3)

А) теорема синусов Б) теорема Пифагора В) теорема косинусов

Ответ: 231.

3 блок. Примени!!!

Задание 1. Дано: АВ=5, АС=4, ВАС=60⁰. Найти: ВС.

Задание 2. Дано: АВ=, ВС=, ВАС=60⁰. Найти: угол С.

4 блок. Сообрази!!!

Задание 1. В ΔАВС АВ=8,4 см, ВС=13,2 см, АС=7,5 см. Какой угол треугольника наибольший, какой наименьший?

Задание 2. Известны стороны треугольника 9 см и 12 см. Может ли угол, противолежащий стороне 9 см, быть прямым? Почему?

5 блок. Напрягись!!!

Задание 1. Подберите условие задачи к данному чертежу:

1) В треугольнике АВС А=30°, АВ=8, АС=6. Найдите длину стороны ВС.

2) В треугольнике АВС А=30°, АВ=8, АС=6. Найдите S(АВС).

3) В треугольнике АВС А=30°, АВ=8, АС=6. Найдите длину медианы, проведенной к стороне АС.

Задание 2. Составьте условие задачи по данному чертежу.

А теперь перейдем к основной теме нашего урока «Задачи с практическим содержанием на применение теорем синусов и косинусов».

3. Решение задач.

Повторим алгоритм решения практических задач.

1. Выполнить рисунок.

2. Построить математическую модель (чертеж).

3. Решить геометрическую задачу.

Задача 1. Найдите ширину озера АВ, если АС=12 м, угол С=60⁰, ВС=15 м. В ответе укажите целое число метров.

Задача 2. Футбольный мяч находится у Ежика , который расположился на расстояниях 12 м от одной штанги ворот и 14 м от другой. Ширина ворот 7 м. Найдите угол попадания мяча в ворота.

Задача 3. Как мальчику найти расстояние до пальмы на острове, если у него есть рулетка и астролябия для измерения углов?

Алгоритм нахождения расстояния до недоступного предмета.

1) Наметить 2 точки, расстояние между которыми можно измерить.

2) Выполнить измерение углов.

3) Построить математическую модель (чертеж).

4) Решить геометрическую задачу, используя теорему синусов

Мы с вами рассмотрели практические задачи на применение теорем синусов и косинусов. А теперь рассмотрим применение этих теорем в стереометрической задаче. Такие задачи вы будете решать в старших классах.

Задача 4. В тетраэдре DАВС DВС=DВА=60⁰, ВА=ВС=5 см, DВ=8 см, АС=8 см. Найдите S(АDС).

Тетраэдр – это многогранник, составленный из 4-х треугольников. Перед вами модель тетраэдра.

Как можно найти S(АDС)?

1) SΔ =, где р = — полупериметр (формула Герона),

2) SΔ = аh_a, 3) SΔ = аbsinγ.

1 способ.

Найдем S(АDС) по формуле Герона.

S =

2 способ.

Давайте найдем S(АDС) по следующей формуле:

S(АDС) = АD∙DН, где DН-высота ΔАDС

3 способ.

Найдем S(АDС) по формуле:

S(АDС) = AD∙AC∙sinDAC

Итак, мы нашли S(АDС) тремя различными способами.

4. Применение полученных знаний на практике и в жизни.

Где можно применить полученные знания на практике и в жизни?

Существует множество областей, в которых применяются тригонометрия и тригонометрические функции. Например, в географии для измерения высоты предмета, в спутниковых навигационных системах. Синус и косинус имеют фундаментальное значение для теории периодических функций, например при описании звуковых и световых волн. Тригонометрия или тригонометрические функции используются в астрономии (особенно для расчётов положения небесных объектов, когда требуется сферическая тригонометрия), в морской и воздушной навигации, в оптике, в теории вероятностей, в статистике, в биологии, в медицинской визуализации (например, компьютерная томография и ультразвук), в теории чисел (следовательно, и в криптологии), в архитектуре, в электротехнике, в компьютерной графике, в разработке игр, в кристаллографии и многих других областях.

5. Заключение.

Сегодня на уроке мы повторили теоремы синусов и косинусов, применили эти теоремы для решения практических задач, так как каждому из нас в дальнейшем придется решать не только геометрические задачи.

Правильный путь таков: усвой то, что сделали твои предшественники и иди дальше. Л.Н.Толстой.

Спасибо за урок!

infourok.ru

Задачи на теорему синусов

Задача 1 В ABC мы имеем AB = 30 cм и γ = 45°. Найдите длину радиуса описанной окружности.
Ответ: 15√2cм.

Задача 2 Радиус описанной окружности вокруг ABC равен R = 2√3/3 cм. Найдите величину угла α, если BC = 2 cм.
Ответ: 60°.

Задача 3 В ABC α : β : γ = 1 : 3: 8. Найдите длину AC, если AB = 10 cм.
Ответ: 10√63 cм.

Задача 4 В окружности с радиусом 7 cм, дуга AB равна 120°. Найдите хорду AB.
Ответ: 7√3cм.

Задача 5 В равнобедренном треугольнике ABC основа AB = 12 cм, а угол при вершине равен 30°. На боковой стороне BC взята точка D так, что CAD : DAB = 1 : 4. Найдите длину радиуса описанной окружности вокруг ABD.
Ответ: 6√2cм.

Задача 6 Основа равнобедренного треугольника равна 10 cм, а угол возле основы равен 2α. Найдите биссектрису угла возле основы.
Угол: 10sin2α/sin3α.

Задача 7 В ABC мы имеем AB = 12 cм и γ = 60°. Найдите радиус описанной вокруг ABL окружности, если точка L есть пересечением биссектрис ABC.
Ответ: 4√3cм.

Задача 8В окружность с радиусом 50 cм вписан четырехугольник. Два из его углов равны 45° и 120°. Найдите его диагонали.
Ответ: 50√2cм или 50√3cм.

Задача 9 В ABC мы имеем have α = 45°, β = 30°. На стороне AB мы выбрали точку M. Радиус описанной окружности вокруг AMC равен R. Найдите радиус описанной вокруг MBC окружности.
Ответ: R√2cм.

www.math10.com

Урок «Применение теорем синусов и косинусов»

Разделы: Математика

---

Цели и задачи урока:

актуализировать опорные знания учащихся по теме урока;
повторить свойства биссектрисы треугольника, формул площади треугольника, определение синуса острого угла в прямоугольном треугольнике, понятие окружности описанной около треугольника;
продемонстрировать применение теорем синусов и косинусов в решении задач повышенного уровня;
показать межпредметную связь между науками: тригонометрией и геометрией;
провести итоговый контроль знаний учащихся в форме теста;
активизировать познавательную деятельность учащихся, развивать их инициативу и творчество;
сформировать зависимые характеристики ученика: разумность, сознательность, абстрактность, прочность, — на основе творческих характеристик.

Ход урока:

Мотивационный этап.

(сообщается тема урока, цели и задачи, основные этапы урока)

Актуализация опорных знаний.

Задача 1.

B ABC: B = 30⁰, AB = 12 см. Найдите высоту, опущенную из вершины С, если внешний угол при вершине А равен 60⁰.

Решение:

1способ:

Т.к. СAD = 60⁰ – внешний угол ABC, то ACB = 30⁰. Следовательно, AC = AB = 12 cм.

B CDA: DA = Ѕ AC = 6 cм по т. Пифагора CD = ; CD = 6 cм

Ответ: 6 cм

2 способ:

Т.к. СAD = 60⁰ – внешний угол ABC, то ACB = 30⁰. Следовательно, AC = AB = 12 cм.

B ABC по определению синуса острого угла в прямоугольном треугольнике:

CD = AC sin A

CD = 6 cм

Ответ: 6 cм

Задача 2.

Дано: ABC, AL = b – биссектриса, AB = C, LC = K, BAC = 2. Найти: BC и AC (составьте алгоритм решения данной задачи)

Решение:

Задача 3.

В равнобедренном треугольнике ABC с основанием AB, боковая сторона AC = b, угол лежащий против основания 2. Найдите радиус описанной окружности (составьте алгоритм решения задачи).

Решение:

Решение задач повышенного уровня c применением теоремы синусов и косинусов

Задача 1.

В равнобедренном треугольнике ABC длины боковых сторон AB и AC = b, угол при вершине A = 2. Прямая, проходящая через вершину B и центр O описанной около треугольника ABC окружности, пересекает сторону AC в точке D. Найдите длину отрезка BD.

Дано: ABC – равнобедренный с основанием BC

угол BAC = 2, AB = AC = b

т.O – центр описанной около ABC окружности,

т.D AC, т.O BD.

Найти: BD

Решение:

1 способ

Вопрос: На пересечении каких прямых лежит центр описанной около треугольника окружности?

Итак, т.к. т.О – центр описанной около треугольника ABC окружности, то он лежит на биссектрисе AK (AK перпендикулярен BC и BK = KC). Следовательно, угол BAK = Ѕ угла BAK = .

B треугольнике BOA: ВО =OA следовательно, угол BAK = углу ABD = .

Решение:

Задача 2.

Точка N лежит на стороне AC правильного треугольника ABC. Найдите отношение радиусов окружностей, описанных около треугольников ABN и ABC, если AN: AC = n.

Дано: ABC – правильный,

т. N AC, AN: AC = n,

ABC и ABN вписаны в окружности с радиусами R₁ и R_2.

Найти: R₁ и R₂

Решение:

Пусть R₁ – радиус окружности, описанной около ABN, а R₂ – радиус окружности, описанной около

ABC. Обозначим через а сторону AC, тогда AN = nа.

 

Контроль за оформлением умственных действий.

Практический тест.

В треугольнике ABС угол A тупой и sinA = 3/5, AB = 3 см, AC = 5 см. Найдите длину сторон BC.

В равнобедренном треугольнике основание равно 5 cм, а угол при основании равен 75⁰. Найдите радиус описанной окружности.

В треугольнике ABС заданы: AB = 4 cм, cos B = 1/3, sin С = 2/3. Найдите длину АС.

В ABС со сторонами AB = 15 см, AС = 12 см и BС = 9 см из вершины С провели медиану и высоту. Найти площадь треугольника, заключенного между медианой и высотой.

Ответ: а) 15, 12 см²  б) 0,81 см²   в) 7, 56 см²   г)7,16 см²

Нормы оценок:

За 2 задачи – “3”

За 3 задачи – “4”

За 5 задач – “5”

 

Решение теста

 

Код текста: б, в, а, с

Подведение итогов урока, домашнее задание:

В окружности проведены три хорды: МА=6 см, МВ=4 см, МС=1 см.

Хорда МВ делит угол АМС пополам. Найти радиус окружности.

7.10.2003

urok.1sept.ru

No related posts.