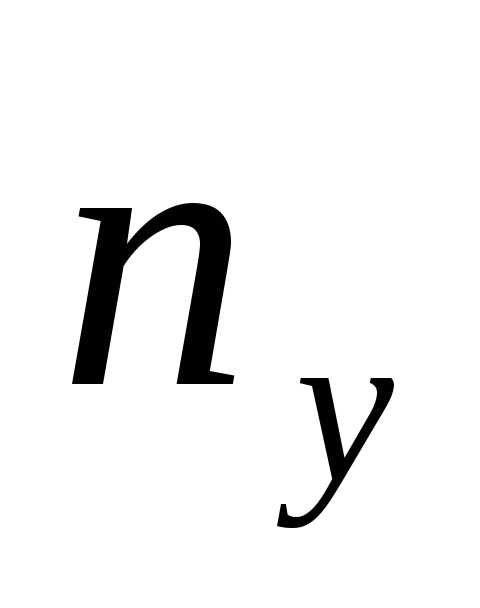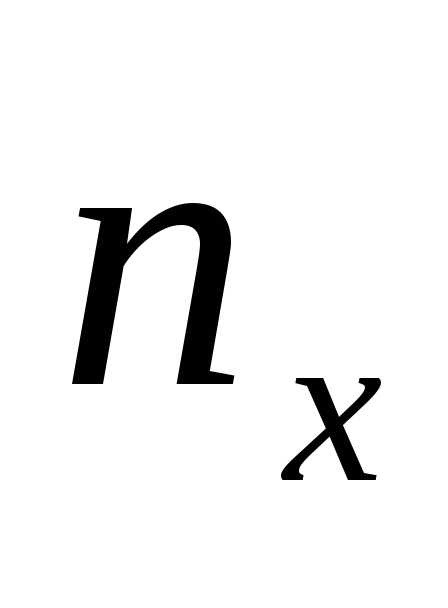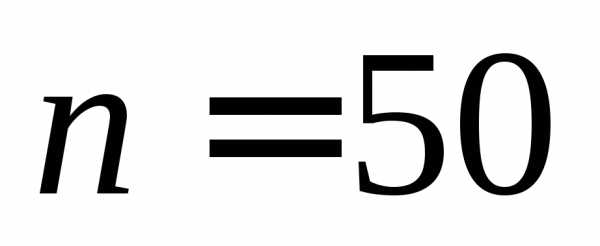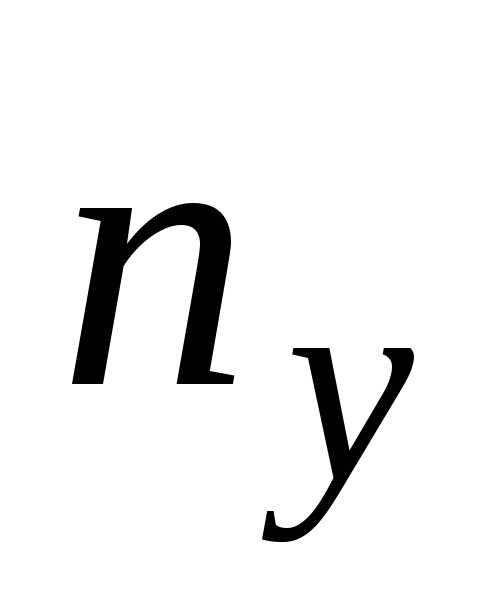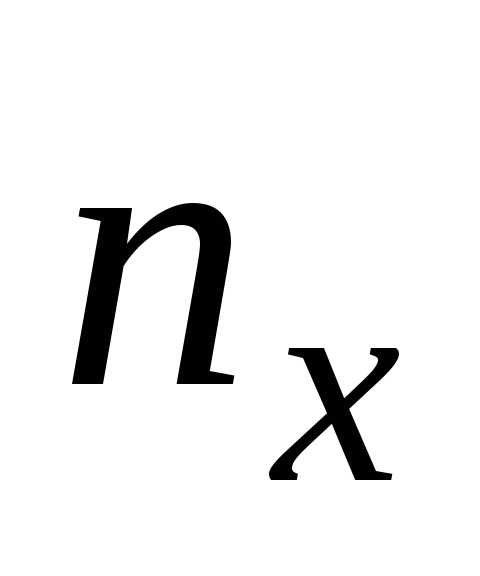4.3. Корреляционная таблица
При большом числе
наблюдений одно и то же значение случайной
величины Х может встретиться 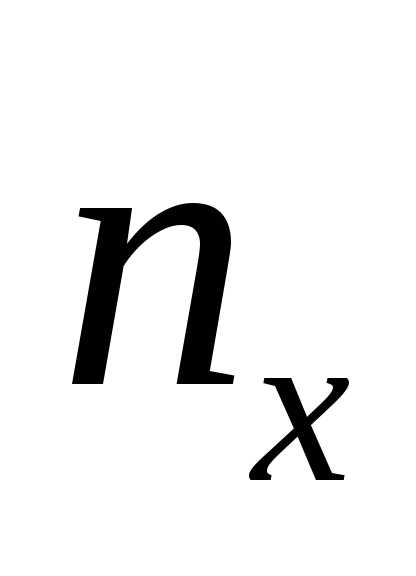 раз, одно и то же значение случайной
величиныY может встретиться
раз, одно и то же значение случайной
величиныY может встретиться 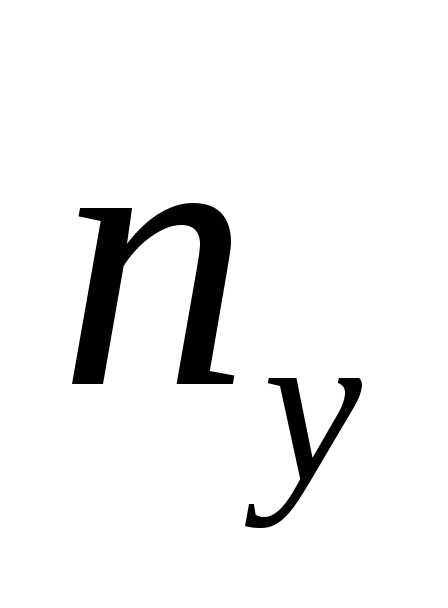 раз, а одна и та же пара чисел (х, у)
может наблюдаться
раз, а одна и та же пара чисел (х, у)
может наблюдаться 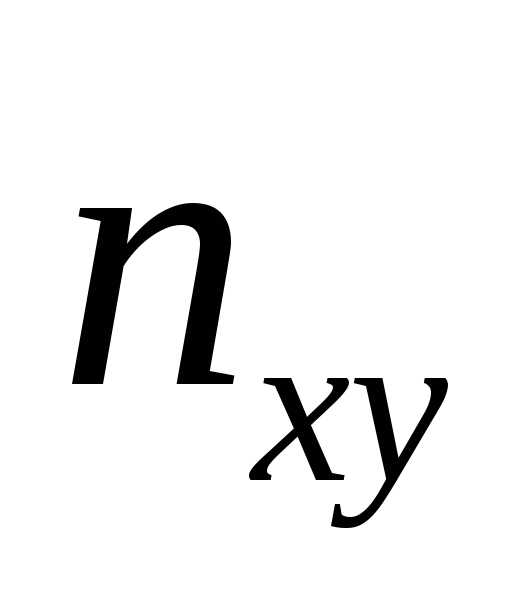 раз. Поэтому данные наблюдений группируют,
т.е. подсчитывают частоты
раз. Поэтому данные наблюдений группируют,
т.е. подсчитывают частоты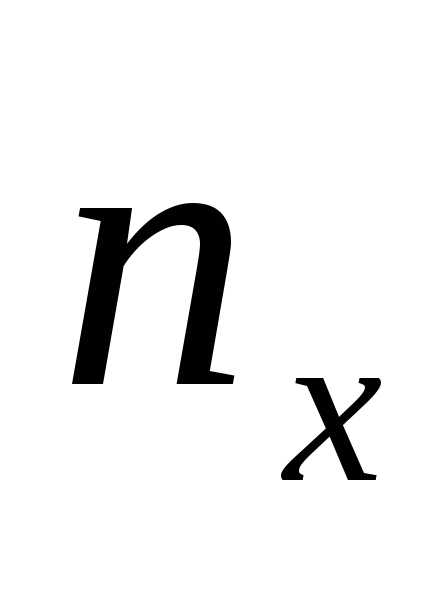 ,,
,,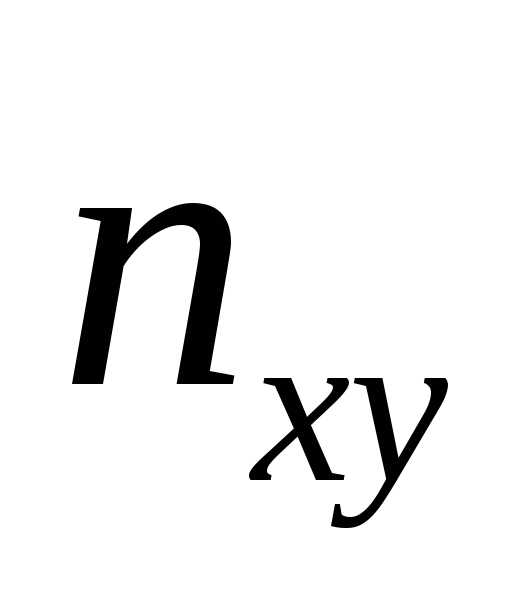 . Все сгруппированные данные за-писывают
в виде таблицы, которую называют корреляционной.
. Все сгруппированные данные за-писывают
в виде таблицы, которую называют корреляционной.
Поясним ее строение на простом примере. Имеем таблицу:
Y X | 1 | 2 | 3 | 4 | 5 |
|
1 | 6 | 4 | 10 | |||
0 | 1 | 4 | 6 | 11 | ||
1 | 5 | 9 | 5 | 19 | ||
2 | 3 | 7 | 10 | |||
| 3 | 12 | 10 | 15 | 10 |
|
В
первой строке указаны наблюдаемые
значения (1,
2, 3, 4, 5)
слу-чайной величины Х,
а в первом столбце таблицы – наблюдаемые
значения (1,
0,
1,
2)
случайной величины Y. На пересечении строк и столбцов находятся
частоты 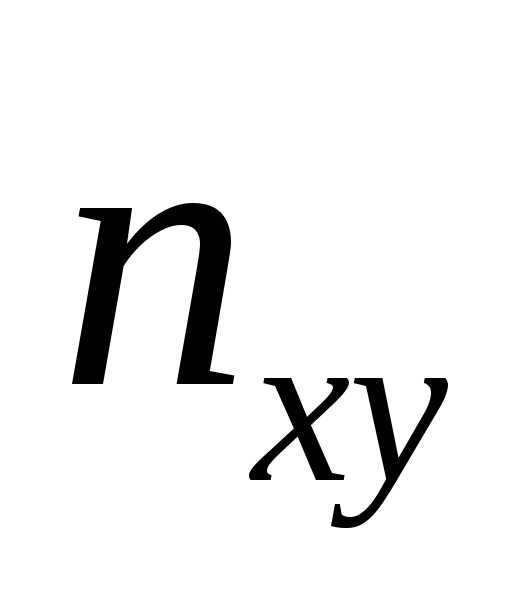
В последнем столбце записаны суммы частот строк. Например, сумма частот второй строки равна — это число указывает, что значение случайной величины Y, равное 0 (в сочетании с различными значениями случайной величины Х ), наблюдалось 11 раз.
В последней строке записаны суммы частот столбцов. Например, сумма частот четвертого столбца равна — это число указывает, что значение случайной величины Х, равное 4 (в сочетании с различными значениями случайной величины Y ), наблюдалось 15 раз.
Общее
число наблюдений 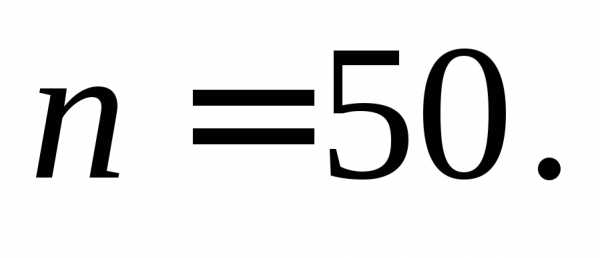
4.4. Выборочный коэффициент корреляции
Ранее мы полагали, что значения Х и соответствующие им значения Y наблюдались по одному разу. На практике, безусловно, одна пара случайных величин (х, у) может наблюдаться любое число раз.Поэтому формула для коэффициента регрессии (4.4) примет вид
(4.5)
где в сумме 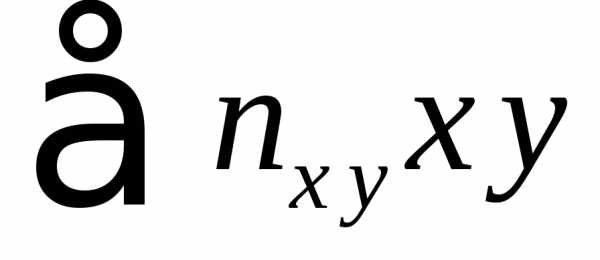 учтено, что пара
(х, у)
наблюдалась
учтено, что пара
(х, у)
наблюдалась 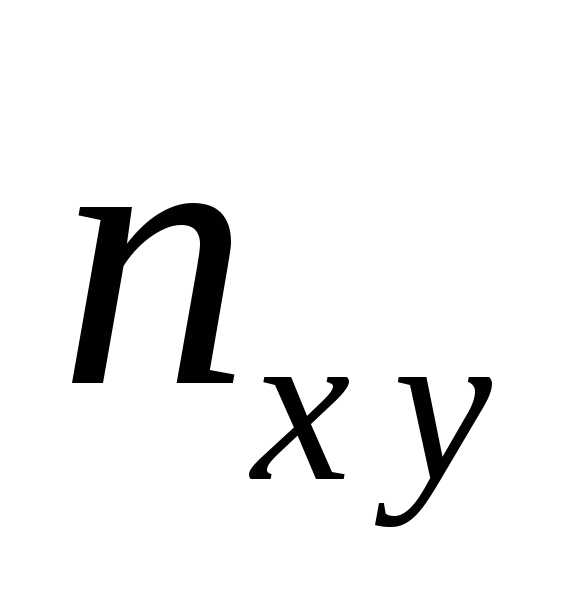 раз, а
и
раз, а
и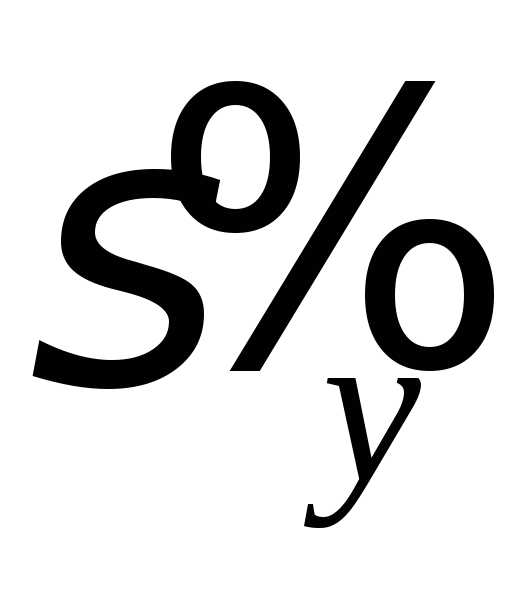
выборочные средние квадратические
отклонения случайных величин Х и Y.
выборочные средние квадратические
отклонения случайных величин Х и Y.
Умножим обе части
равенства (4.5) на дробь 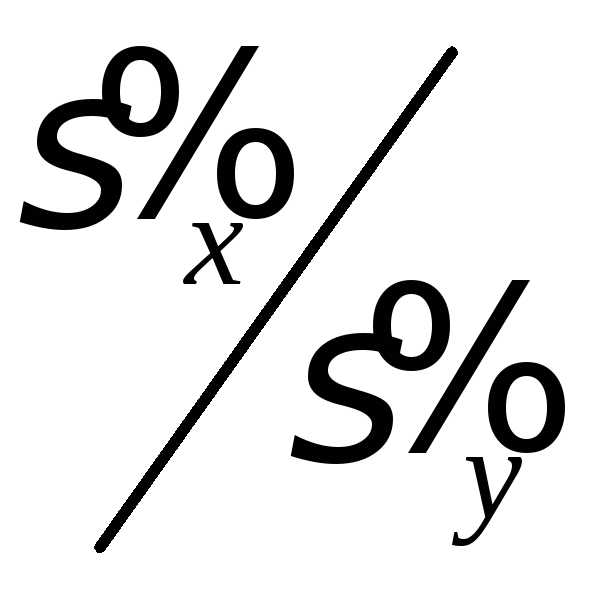 и назовем это выражение выборочным
коэффициентом корреляции
и назовем это выражение выборочным
коэффициентом корреляции
Тогда уравнение линейной регрессии Y на Х будет иметь вид
Замечание 2. Выборочный коэффициент корреляции является безраз-мерной оценкой коэффициента регрессии
Таким образом,
основная задача корреляционного анализа
состоит в оценке степени линейной связи
между случайными величинами Х и Y, которая
устанавливается при помощи выборочного
коэффициента корре-ляции 
Если выборочный
коэффициент корреляции  мал, то линейная связь считается слабой
и ее можно не принимать во внимание.
Если же выборочный коэффициент корреляции
мал, то линейная связь считается слабой
и ее можно не принимать во внимание.
Если же выборочный коэффициент корреляции близок к1,
то линейная связь сильная и к ней следует
относиться практически как к функциональной.
В противном случае, связь принято считать
статистической. И, наконец, при
близок к1,
то линейная связь сильная и к ней следует
относиться практически как к функциональной.
В противном случае, связь принято считать
статистической. И, наконец, при 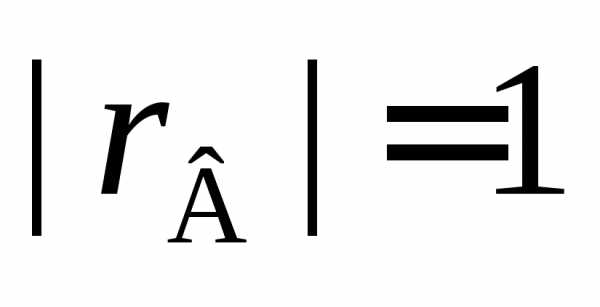
Замечание. Выборочный коэффициент корреляции  является лишь оценкой теоретического
коэффициента корреляции
является лишь оценкой теоретического
коэффициента корреляции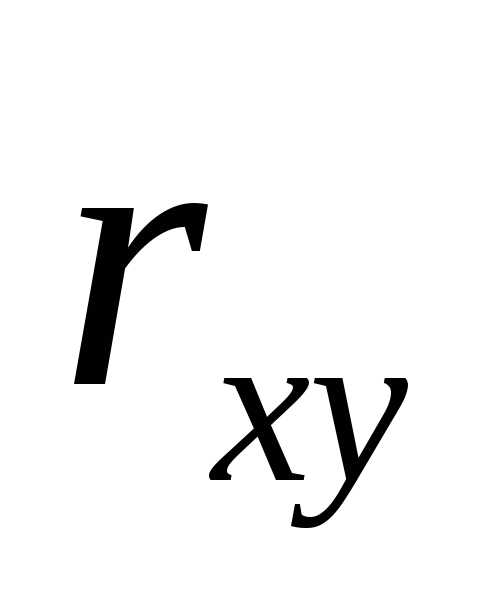 генеральной сово-купности, поэтому
возникает необходимость проверить
гипотезу о значи-мости выборочного
коэффициента корреляции
генеральной сово-купности, поэтому
возникает необходимость проверить
гипотезу о значи-мости выборочного
коэффициента корреляции . Однако, если
выборка имеет достаточно большой
объем и хорошо представляет генеральную
совокупность, т.е. является репрезентативной,
то вывод (гипотезу) о ли-нейной зависимости
между случайными величинами Х и Y , полученный по данным выборки, можно
распространить и на всю генеральную
сово-купность
. Однако, если
выборка имеет достаточно большой
объем и хорошо представляет генеральную
совокупность, т.е. является репрезентативной,
то вывод (гипотезу) о ли-нейной зависимости
между случайными величинами Х и Y , полученный по данным выборки, можно
распространить и на всю генеральную
сово-купность
Например, для
оценки теоретического коэффициента
корреляции 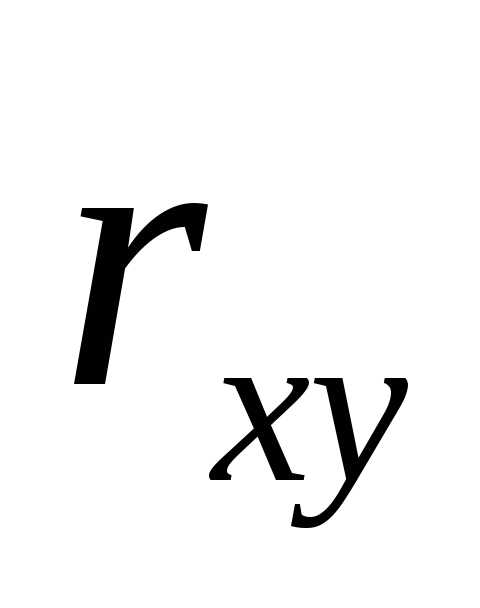 генеральной
совокупности (если она распределена
нормально) можно воспользоваться
формулой
генеральной
совокупности (если она распределена
нормально) можно воспользоваться
формулой
studfiles.net
Корреляционная таблица | Высшая математика | Студенту | Статьи и обсуждение вопросов образования в Казахстане | Образовательный сайт Казахстана
На практике в результате независимых наблюдений над величинами X и Y, как правило, имеют дело не со всей совокупностью всех возможных пар значений этих величин, а лишь с ограниченной выборкой из генеральной совокупности, причем объем n выборочной совокупности определяется как количество имеющихся в выборке пар.Первоочередной задачей статистической обработки экспериментального материала является систематизация полученных данных и выяснение формы соответствующей генеральной совокупности.
Пусть величина Х в выборке принимает значения x 1, x2,….xm, где количество различающихся между собой значений этой величины, причем в общем случае каждое из них в выборке может повторяться. Пусть величина Y в выборке принимает значения y1, y2,….yk, где k — количество различающихся между собой значений этой величины, причем в общем случае каждое из них в выборке также может повторяться. В этом случае данные заносят в таблицу с учетом частот встречаемости. Такую таблицу с группированными данными называют корреляционной.
Первым этапом статистической обработки результатов является составление корреляционной таблицы (таблица 1).
| Y\X | x1 | x2 | … | xm | ny |
| y1 | n12 | n21 | nm1 | ||
| y2 | n22 | nm2 | ny2 | ||
| … | |||||
| yk | n1k | n2k | nmk | nyk | |
| nx | nx1 | nx2 | nxm | n |
В первой строке основной части таблицы в порядке возрастания перечисляются все встречающиеся в выборке значения величины X. В первом столбце также в порядке возрастания перечисляются все встречающиеся в выборке значения величины Y. На пересечении соответствующих строк и столбцов указываются частоты nij (i=1,2,…,m; j=1,2,…,k) равные количеству появлений пары (xi;yi) в выборке. Например, частота n12 представляет собой количество появлений в выборке пары (x 1;y1).
Так же nxinij, 1≤i≤m, сумма элементов i-го столбца, nyjnij, 1≤j≤k, — сумма элементов j-ой строки и nxi=nyj=n
Аналоги формул (3), полученные по данным корреляционной таблицы, имеют вид:
(6)
Пример 3. Изучалась зависимость между качеством стандартности товаров Y(%) и количеством товаров (X) шт. Результаты наблюдений приведены в виде корреляционной таблицы.
| Y\X | 18 | 22 | 26 | 30 | ny |
| 70 | 5 | 5 | |||
| 75 | 7 | 46 | 1 | 54 | |
| 80 | 29 | 72 | 101 | ||
| 85 | 8 | 37 | |||
| 90 | 3 | 3 | |||
| nx | 12 | 75 | 102 | 11 | 200 |
Требуется:
1) Найти выборочное уравнение прямой регрессии Y на X.
2) Определить выборочные аналоги функции регрессии.
3) Сравнить между собой при каждом значении Х приближения средних значений Y, полученные по функции регрессии и по уравнению прямой регрессии.
Решение: Пользуясь данными, приведенными в этой таблице, по формулам (6), находим:
Следовательно,
a=79.475-1.111•24.24=79.475-26.930=52.544
Таким образом, выборочное уравнение прямой регрессии Y на X выражается формулой:
Y=79.475+1.111(x-24.24)=79.475+1.111x-26.930=52.545+1.111x
Откуда:
| X | 18 | 22 | 26 | 30 |
| Yлин | 72.5 | 76.98 | 81.45 | 85.92 |
| Yx | 72.91 | 76.93 | 81.37 | 86.36 |
где Yлин(x=x1)=52.545+1.111•18=72.5 и т.д. yx1=(5•70+7•75)/12=72.91 и т.д.
Сопоставляя полученные результаты, приходим к выводу, что значения, вычисленные по уравнению выборочной регрессии и по линейной зависимости хорошо согласуются.
Заключение. Величины, вычисленные путем подстановки возможных значений Х в уравнение прямой регрессии и в функцию регрессии, практически совпадают.
Замечание. Для упрощения вычислений в корреляционной табл. удобно от (xi;yi) перейти к новым переменным (ui;vi), положив ui=(xi-x0)/h1; vj=(yj-y0)/h2 (*)
где x0 и y0 варианты соответствующие наибольшим частотам соответственно xi и yi. hi=xi+1-xi.
Обратный пересчет осуществляется по формулам:
testent.ru
Таблица корреляции
В таблице корреляций представлены критические значения коэффициента корреляции r-Пирсона и коэффициента корреляции r-Спирмена
Критические значения коэффициентов корреляции
| n | p | |||
| 0,1 | 0,05 | 0,01 | 0,001 | |
| 5 | 0,805 | 0,878 | 0,959 | 0,991 |
| 6 | 0,729 | 0,811 | 0,917 | 0,974 |
| 7 | 0,669 | 0,754 | 0,875 | 0,951 |
| 8 | 0,621 | 0,707 | 0,834 | 0,925 |
| 9 | 0,582 | 0,666 | 0,798 | 0,898 |
| 10 | 0,549 | 0,632 | 0,765 | 0,872 |
| 11 | 0,521 | 0,602 | 0,735 | 0,847 |
| 12 | 0,497 | 0,576 | 0,708 | 0,823 |
| 13 | 0,476 | 0,553 | 0,684 | 0,801 |
| 14 | 0,458 | 0,532 | 0,661 | 0,780 |
| 15 | 0,441 | 0,514 | 0,641 | 0,760 |
| 16 | 0,426 | 0,497 | 0,623 | 0,742 |
| 17 | 0,412 | 0,482 | 0,606 | 0,725 |
| 18 | 0,400 | 0,468 | 0,590 | 0,708 |
| 19 | 0,389 | 0,456 | 0,575 | 0,693 |
| 20 | 0,378 | 0,444 | 0,561 | 0,679 |
| 21 | 0,369 | 0,433 | 0,549 | 0,665 |
| 22 | 0,360 | 0,423 | 0,537 | 0,652 |
| 23 | 0,352 | 0,413 | 0,526 | 0,640 |
| 24 | 0,344 | 0,404 | 0,515 | 0,629 |
| 25 | 0,337 | 0,396 | 0,505 | 0,618 |
| 26 | 0,330 | 0,388 | 0,496 | 0,607 |
| 27 | 0,323 | 0,381 | 0,487 | 0,597 |
| 28 | 0,317 | 0,374 | 0,479 | 0,588 |
| 29 | 0,311 | 0,367 | 0,471 | 0,579 |
| 30 | 0,306 | 0,361 | 0,463 | 0,570 |
| 31 | 0,301 | 0355 | 0,456 | 0,562 |
| 32 | 0,296 | 0,349 | 0,449 | 0,554 |
| 33 | 0,291 | 0,344 | 0,442 | 0,547 |
| 34 | 0,287 | 0,339 | 0,436 | 0,539 |
| 35 | 0,283 | 0,334 | 0,430 | 0,532 |
| 36 | 0,279 | 0,329 | 0,424 | 0,525 |
| 37 | 0,275 | 0,325 | 0,418 | 0,519 |
| 38 | 0,271 | 0,320 | 0,413 | 0,513 |
| 39 | 0,267 | 0,316 | 0,408 | 0,507 |
| 40 | 0,264 | 0,312 | 0,403 | 0,501 |
| 41 | 0,260 | 0,308 | 0,398 | 0,495 |
| 42 | 0,257 | 0,304 | 0,393 | 0,490 |
| 43 | 0,254 | 0,301 | 0,389 | 0,484 |
| 44 | 0,251 | 0,297 | 0,384 | 0,479 |
| 45 | 0,248 | 0,294 | 0,380 | 0474 |
| 46 | 0,246 | 0,291 | 0,376 | 0,469 |
| 47 | 0,243 | 0,288 | 0,372 | 0,465 |
| 48 | 0,240 | 0,285 | 0,368 | 0,460 |
| 49 | 0,238 | 0,282 | 0,365 | 0,456 |
| 50 | 0,235 | 0,279 | 0,361 | 0,451 |
| 51 | 0,233 | 0,276 | 0,358 | 0,447 |
| 52 | 0,231 | 0,273 | 0,354 | 0,443 |
| 53 | 0,228 | 0,271 | 0,351 | 0,439 |
| 54 | 0,226 | 0,268 | 0,348 | 0,435 |
| 55 | 0,224 | 0,266 | 0,345 | 0,432 |
| 56 | 0,222 | 0,263 | 0,341 | 0,428 |
| 57 | 0,220 | 0,261 | 0,339 | 0,424 |
| 58 | 0,218 | 0,259 | 0,336 | 0,421 |
| 59 | 0,216 | 0,256 | 0,333 | 0,418 |
| 60 | 0,214 | 0,254 | 0,330 | 0,414 |
| 61 | 0,213 | 0,252 | 0,327 | 0,411 |
| 62 | 0,211 | 0,250 | 0,325 | 0,408 |
| 63 | 0,209 | 0,248 | 0,322 | 0,405 |
| 64 | 0,207 | 0,246 | 0,320 | 0,402 |
| 65 | 0,206 | 0,244 | 0,317 | 0,399 |
| 66 | 0,204 | 0,242 | 0,315 | 0,396 |
| 67 | 0,203 | 0,240 | 0,313 | 0,393 |
| 68 | 0,201 | 0,239 | 0,310 | 0,390 |
| 69 | 0,200 | 0,237 | 0,308 | 0,388 |
| 70 | 0,198 | 0,235 | 0,306 | 0,385 |
| 80 | 0,185 | 0,220 | 0,286 | 0,361 |
| 90 | 0,174 | 0,207 | 0,270 | 0,341 |
| 100 | 0,165 | 0,197 | 0,256 | 0,324 |
| 110 | 0,158 | 0,187 | 0,245 | 0,310 |
| 120 | 0,151 | 0,179 | 0,234 | 0,297 |
| 130 | 0,145 | 0,172 | 0,225 | 0,285 |
| 140 | 0,140 | 0,166 | 0,217 | 0,275 |
| 150 | 0,135 | 0,160 | 0,210 | 0,266 |
| 200 | 0,117 | 0,139 | 0,182 | 0,231 |
| 250 | 0,104 | 0,124 | 0,163 | 0,207 |
| 300 | 0,095 | 0,113 | 0,149 | 0,189 |
| 350 | 0,088 | 0,105 | 0,138 | 0,175 |
| 400 | 0,082 | 0,098 | 0,129 | 0,164 |
| 450 | 0,078 | 0,092 | 0,121 | 0,155 |
| 500 | 0,074 | 0,088 | 0,115 | 0,147 |
| 600 | 0,067 | 0,080 | 0,105 | 0,134 |
statpsy.ru
Мат.статистика. Лекция №3
Лекция 3. Корреляционный анализ
В
реальном мире многие явления природы
происходят в обстановке действия
многочисленных факторов, влияние каждого
из них ничтожно, а число их велико. В
этом случае возникает статистическая
связь между случайными величинами, т.е.
случайная переменная реагирует на
изменение другой переменной изменением
своего ряда распределения. В результате
, она . переходит не в определенное
состояние, а в одно из возможных своих
состояний. Для изучения статистической
зависимости нужно знать аналитический
вид двумерного распределения. Нахождение
аналитического вида двумерного
распределения по выборке ограниченного
объема громоздко и может привести к
значительным ошибкам. Поэтому на
практике при исследовании зависимостей
между случайными переменными 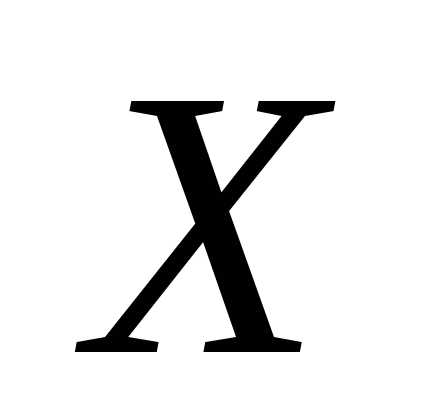 и
и ограничиваются изучением зависимости
между одной из них и условным математическим
ожиданием другой. Знание статистической зависимости
позволяет прогнозировать, что значение
зависимой случайной переменной будет
находиться в некотором интервале, если
независимая переменная примет определенное
значение. С помощью вероятностных
методов можно вычислить вероятность
того, что ошибка прогноза не выйдет за
определенные границы.
ограничиваются изучением зависимости
между одной из них и условным математическим
ожиданием другой. Знание статистической зависимости
позволяет прогнозировать, что значение
зависимой случайной переменной будет
находиться в некотором интервале, если
независимая переменная примет определенное
значение. С помощью вероятностных
методов можно вычислить вероятность
того, что ошибка прогноза не выйдет за
определенные границы.
При изучении статистических зависимостей форму связи можно характеризовать функцией регрессии (линейной, квадратной, показательной и т.д.)
Кривой
регрессии 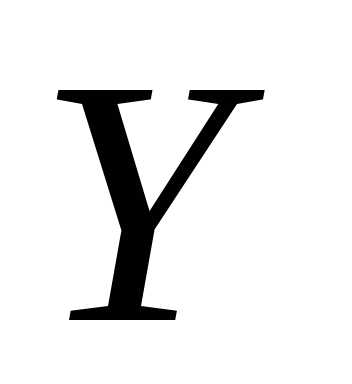 по
по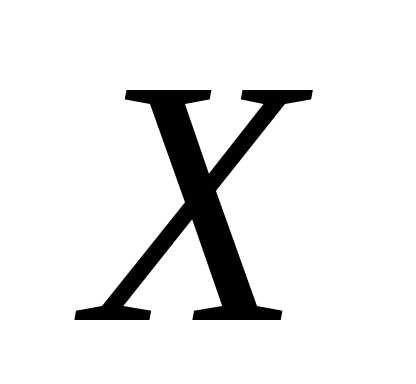 (или
(или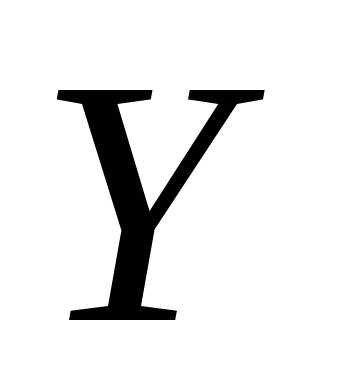 на
на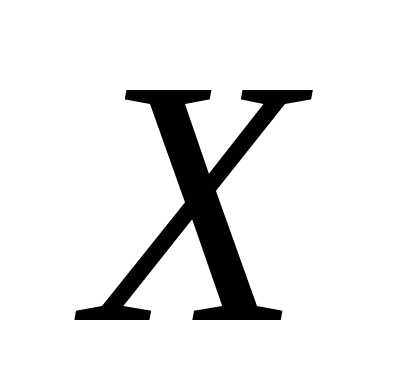 ) называется условное среднее значение
случайной переменной
) называется условное среднее значение
случайной переменной 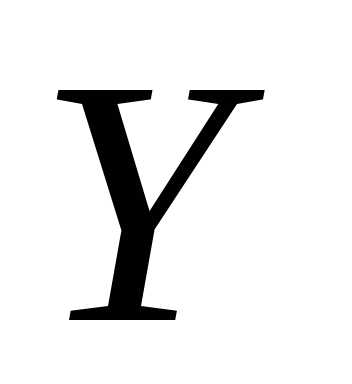 как функция
как функция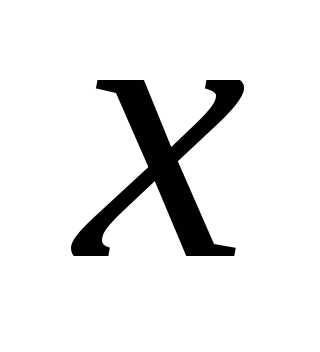 и некоторого числа параметров, которые
находятся методом наименьших квадратов
по наблюденным значениям двумерной
случайной величины
и некоторого числа параметров, которые
находятся методом наименьших квадратов
по наблюденным значениям двумерной
случайной величины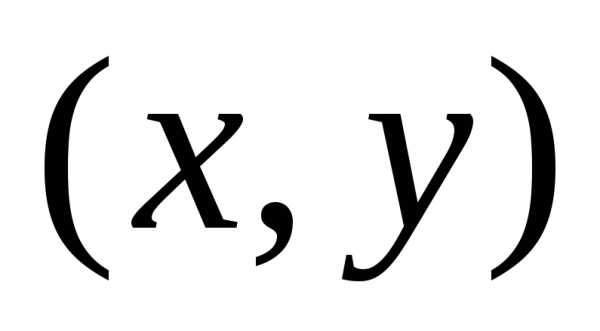 .
Эта кривая называется такжеэмпирическим
уравнением регрессии или просто уравнением регрессии.
.
Эта кривая называется такжеэмпирическим
уравнением регрессии или просто уравнением регрессии.
Статистические связи между переменными можно изучать методом корреляционного и регрессионного анализа. Основная задача корреляционного анализа – выявление связи между случайными переменными путем точечной и интервальной оценки парных коэффициентов корреляции, вычисления функции регрессии одной случайной величины на другую. Корреляционный анализ статистических данных включает следующие этапы: 1) построение корреляционного поля и составление корреляционной таблицы; 2) вычисление выборочных коэффициентов корреляции и корреляционных отношений; 3) проверка статистической гипотезы значимости связи.
Поле корреляции. Корреляционная таблица
Рассмотрим
простейший случай корреляционного
анализа – двумерную модель. Пусть 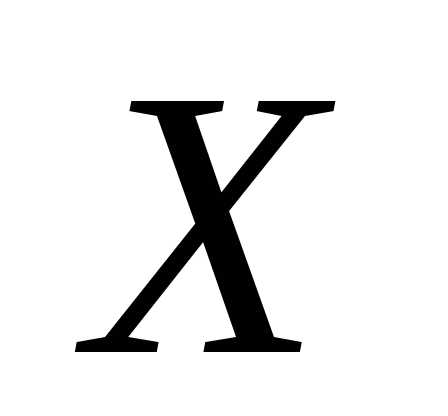 и
и случайные переменные, Пару случайных
чисел
случайные переменные, Пару случайных
чисел
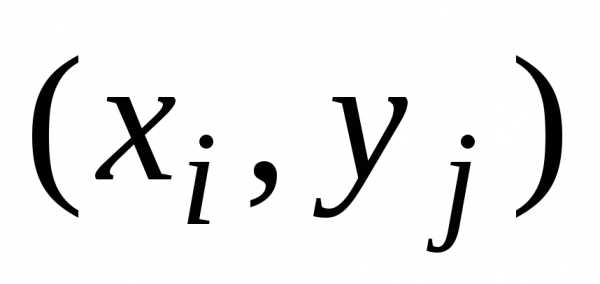 можно
изобразить графически в виде точки с
координатами
можно
изобразить графически в виде точки с
координатами 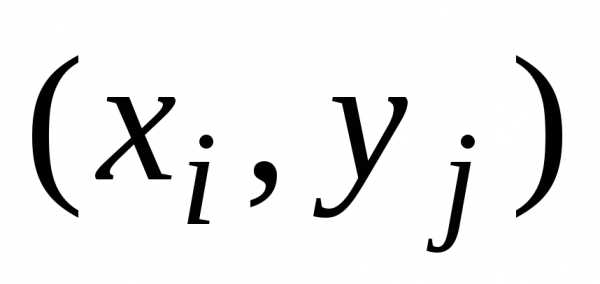 .
Аналогично можно изобразить всю выборку.
.
Аналогично можно изобразить всю выборку.
Декартова
плоскость с нанесенными на нее точками
с координатами 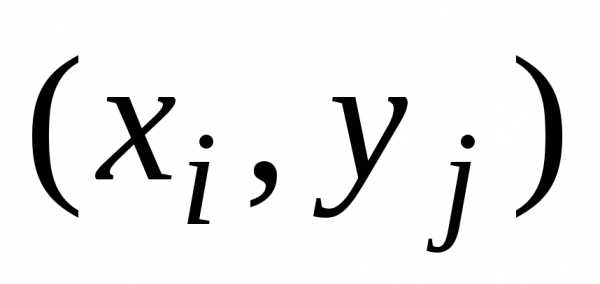 называетсякорреляционным
полем .
называетсякорреляционным
полем .
По
виду корреляционного поля иногда можно
судить о виде зависимости между случайными
величинами 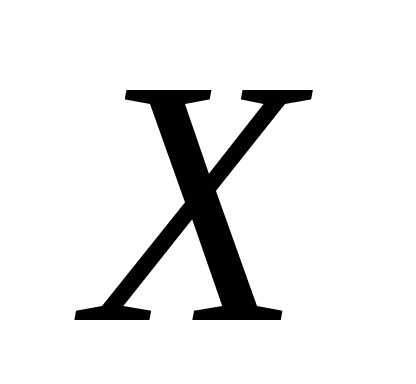 и
и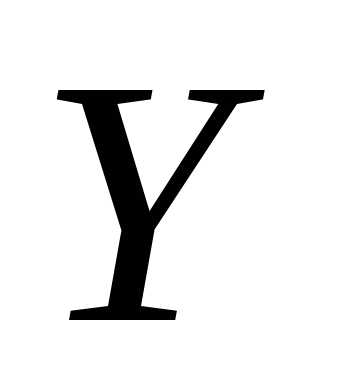 ,
если она существует.
,
если она существует.
В
данном случае представлено корреляционное
поле для дискретного случайного вектора.
При большом объеме выборки построение
поля корреляции становится очень
громоздкой задачей. Задача упрощается,
если выборку упорядочить, т.е. переменные
сгруппировать. В результате получится
сгруппированный статистический ряд.
Сгруппированный ряд может быть дискретным
или интервальным. Сгруппированному
ряду соответствует корреляционная
таблица. Пусть, например  — объем выполненных работ,
— объем выполненных работ,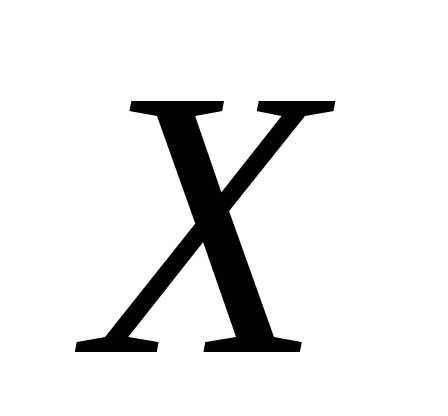 – накладные расходы. Для случайного
вектора (
– накладные расходы. Для случайного
вектора (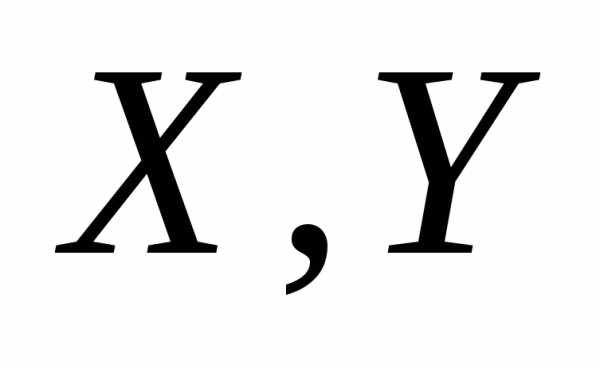 )
получена выборка, которую можно
представить с помощью корреляционной
таблицы
)
получена выборка, которую можно
представить с помощью корреляционной
таблицы
| 1-2 1.5 | 2-3 2.5 | 3-4 3.5 | 4-5 4.5 | 5-6 5.5 | 6-7 6.5 | 7-8 7.5 | 8-9 8.5 |
|
10-20 15 | 4 | 5 | 9 | ||||||
20-30 25 | 1 | 3 | 1 | 5 | |||||
30-40 35 | 2 | 3 | 6 | 5 | 3 | 1 | 20 | ||
40-50 45 | 5 | 9 | 19 | 8 | 7 | 2 | 1 | 51 | |
50-60 55 | 1 | 2 | 7 | 16 | 9 | 4 | 2 | 41 | |
60-70 65 | 1 | 5 | 6 | 4 | 2 | 2 | 20 | ||
70-80 75 | 1 | 3 | 4 | ||||||
| 7 | 17 | 19 | 36 | 33 | 21 | 9 | 8 | 150 |
Эта
таблица построена на основе интервального
ряда. В первой строке и первом столбце
таблицы помещают интервалы изменения 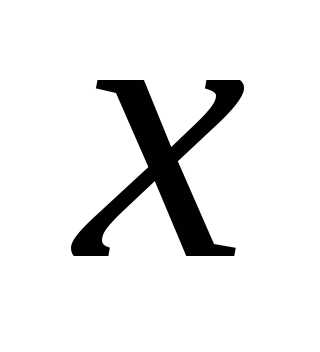 и
и и значения середин интервалов. В ячейки,
образованные пересечением строк и
столбцов помещают частоты
и значения середин интервалов. В ячейки,
образованные пересечением строк и
столбцов помещают частоты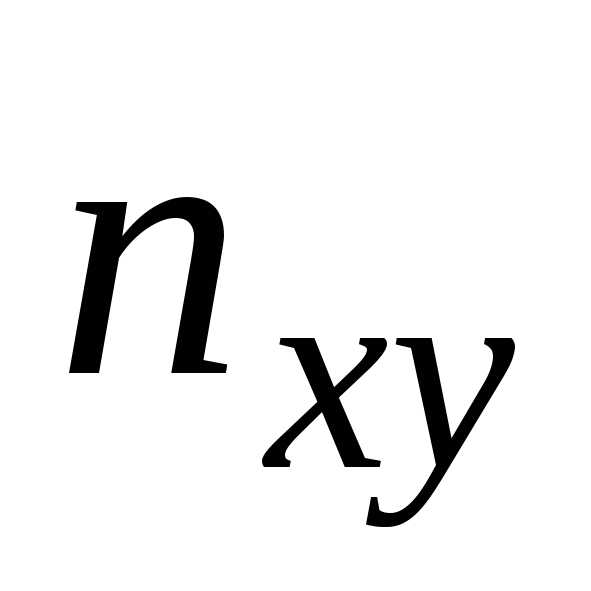 попадания пар значений
попадания пар значений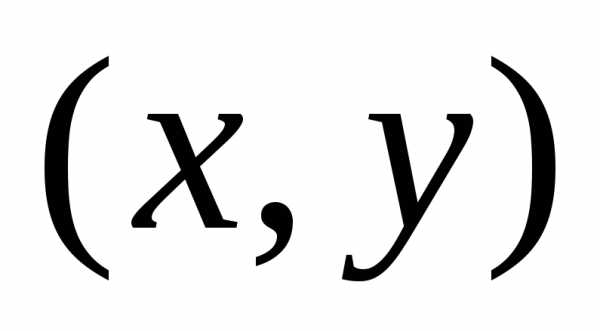 в соответствующие интервалы. В последней
строке и последнем столбце находятся
значения
в соответствующие интервалы. В последней
строке и последнем столбце находятся
значения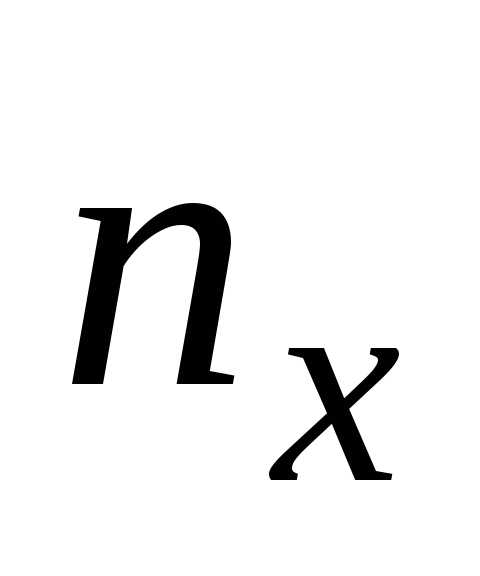 и
и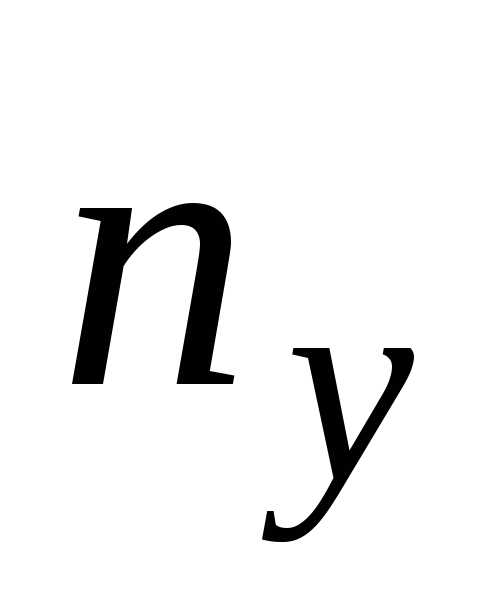 — суммы
— суммы по соответствующим столбцу и строке ,
где
по соответствующим столбцу и строке ,
где 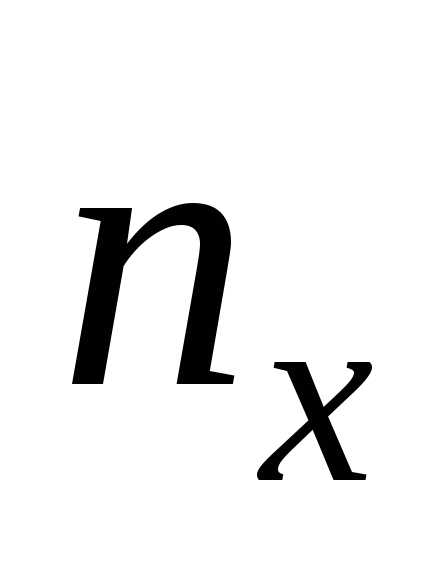 – суммарная частота наблюдаемого
значения признака
– суммарная частота наблюдаемого
значения признака 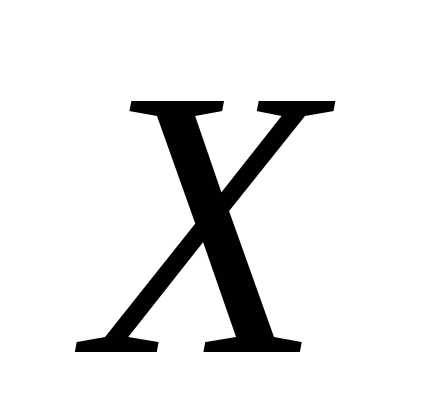 при всех значениях
при всех значениях ,
, 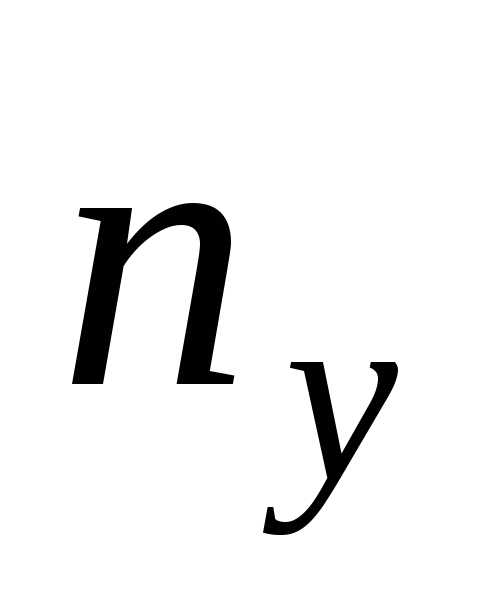 – суммарная частота наблюдаемого
значения признака
– суммарная частота наблюдаемого
значения признака  при
всех значениях
при
всех значениях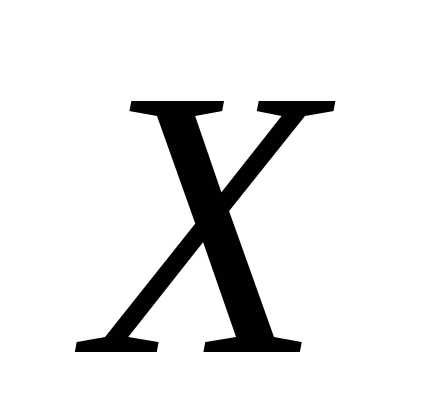 ,
, 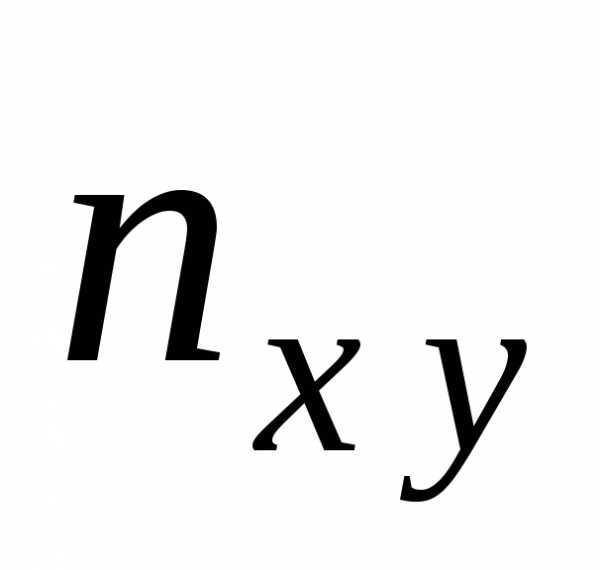 –частота
появления пары значений признаков
–частота
появления пары значений признаков 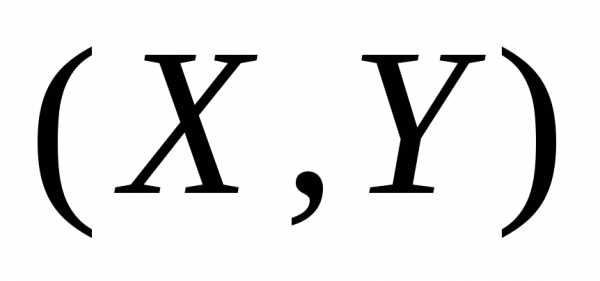 .При
этом выполняются равенства
.При
этом выполняются равенства
, (1)
где 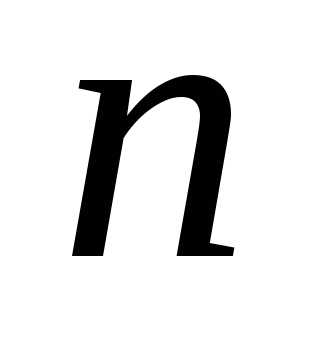 —
объем выборки.
—
объем выборки.
Вычислим статистические оценки параметров распределения случайного вектора. Статистической оценкой математического ожидания является среднее арифметическое, а статистической оценкой дисперсии является статистическая дисперсия. Вычисление этих величин в данном случае проводится по формулам
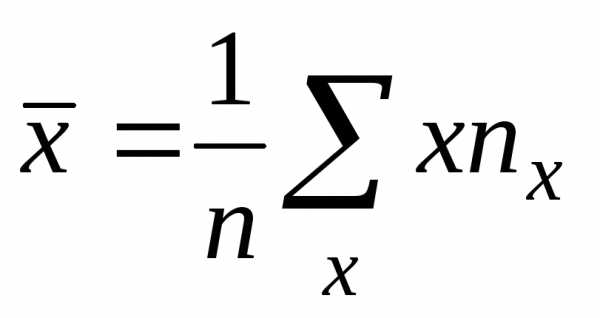 ,
, 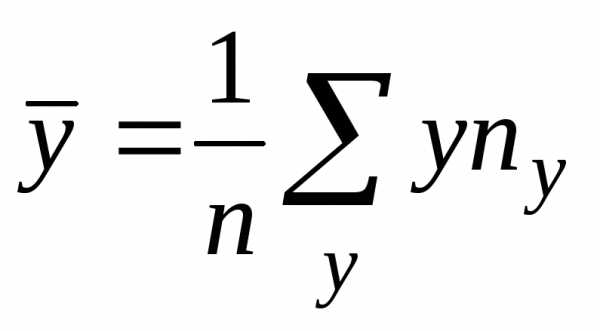 ,
(2)
,
(2)
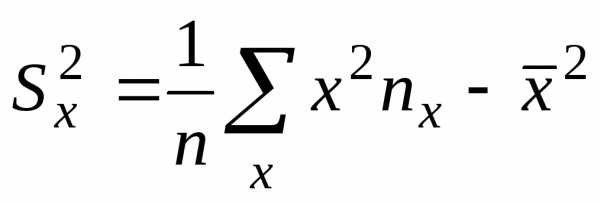 ,
, 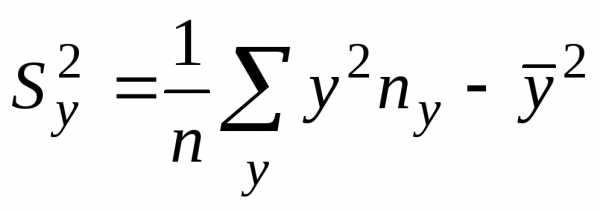 .
(3)
.
(3)
Оценкой коэффициента корреляции является выборочный коэффициент корреляции, который определяется равенством
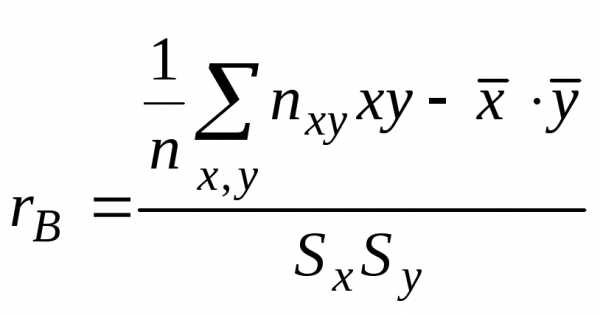 (4)
(4)
В данном примере
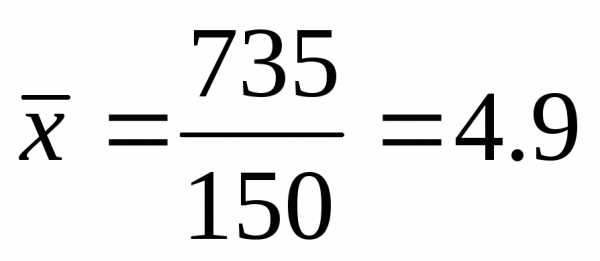 ,
, 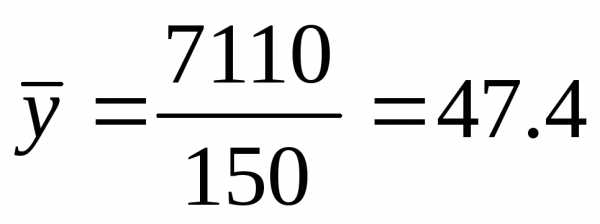
,
.
Величина
выборочного коэффициента корреляции
не зависит от порядка следования
переменных, т.е. 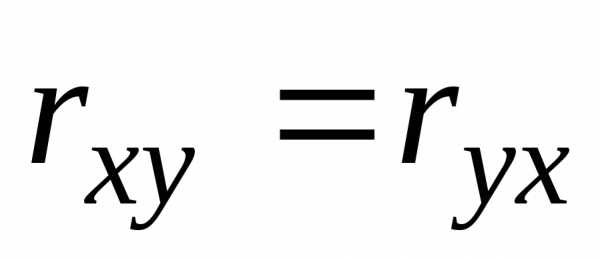 ,
поэтому выборочный коэффициент корреляции
обозначают просто
,
поэтому выборочный коэффициент корреляции
обозначают просто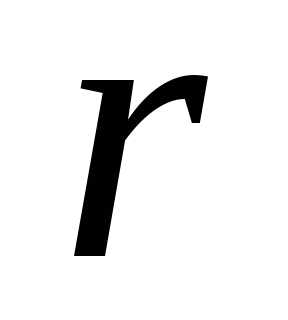 .
.
Если
генеральная совокупность имеет нормальное
распределение, т. е. совместная функция
распределения 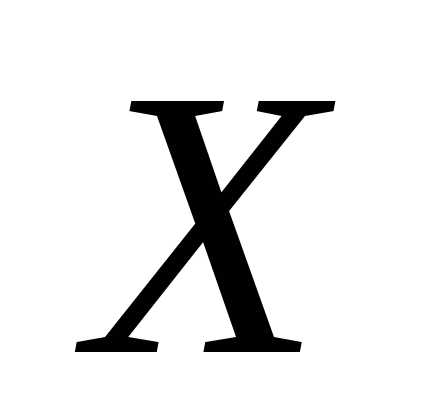 и
и подчиняется
нормальному закону,
подчиняется
нормальному закону,
то
функция регрессии линейны. Функция
регрессии 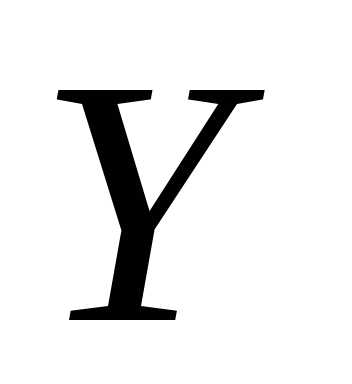 на
на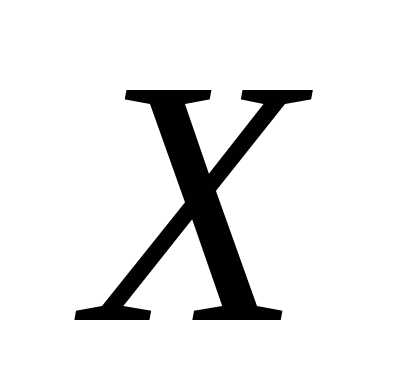 имеет вид
имеет вид
, (5)
а
функция регрессии 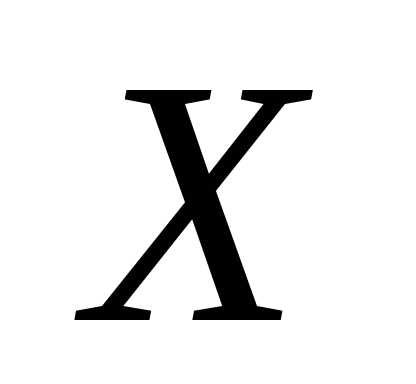 на
на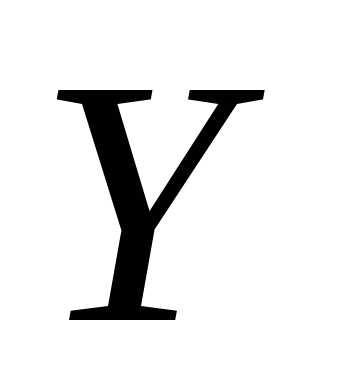 имеет вид
имеет вид
. (6)
Выражения 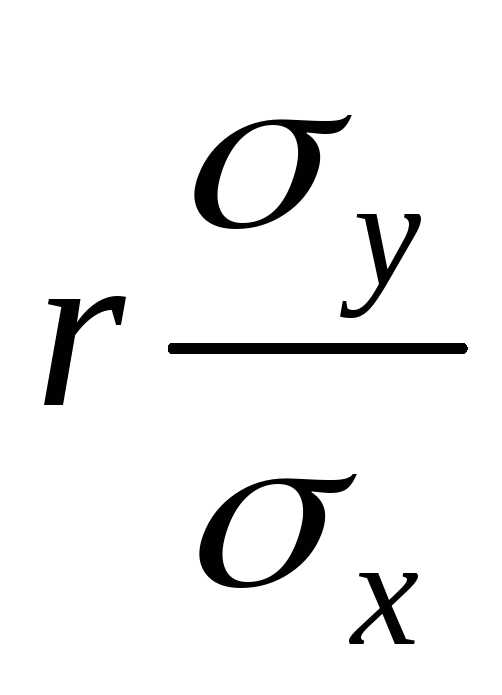 и
и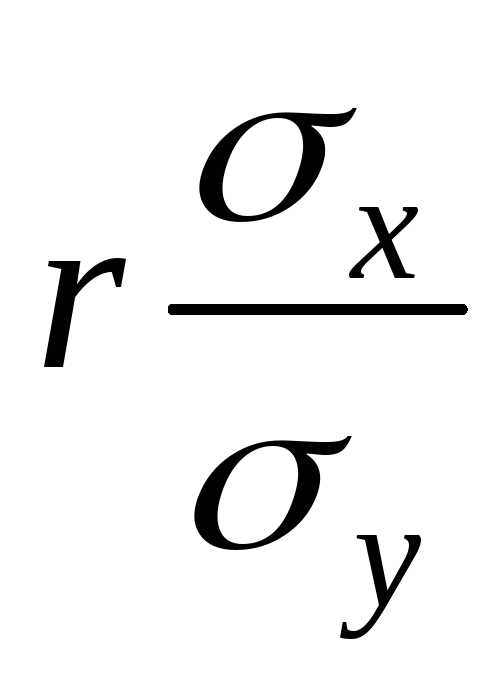 называются коэффициентами регрессии.
называются коэффициентами регрессии.
Уравнения
регрессии  наи
наи на
на имеют вид
имеют вид
, (7)
В
данном примере уравнение регрессии  на
на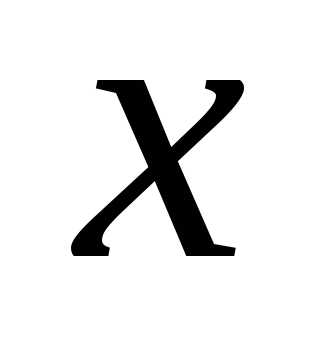
,
уравнение
регрессии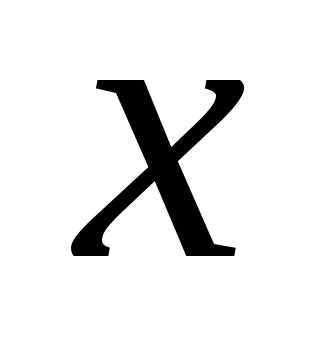 на
на
.
Полученные
уравнения регрессии показывают, как в
среднем изменяется 
(или 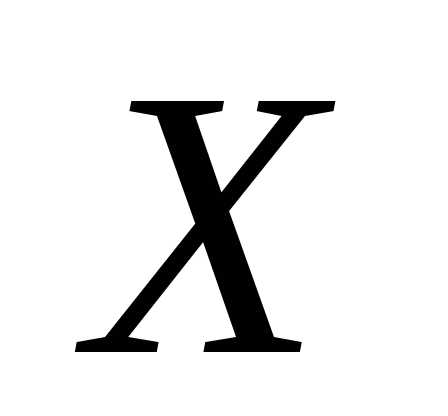 )
в зависимости от изменения аргумента
)
в зависимости от изменения аргумента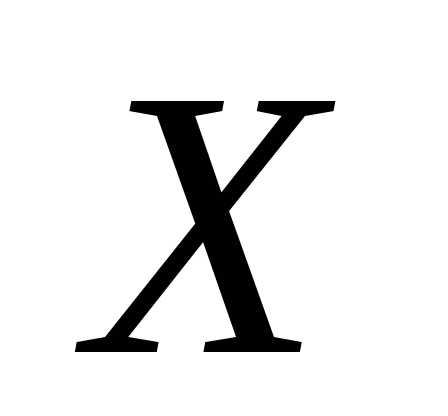 (или
(или ).
).
Проверка гипотезы о значимости коэффициента корреляции.
Выборочный
коэффициент корреляции является точечной
оценкой коэффициента корреляции. Он
служит для оценки силы линейной связи
между 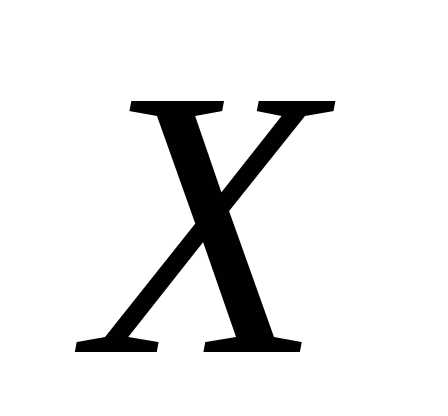 и
и .
Равенство нулю выборочного коэффициента
корреляции еще не свидетельствует о
равенстве нулю самого коэффициента
корреляции, а, следовательно, о
некоррелированности случайных величин
.
Равенство нулю выборочного коэффициента
корреляции еще не свидетельствует о
равенстве нулю самого коэффициента
корреляции, а, следовательно, о
некоррелированности случайных величин и
и .
Чтобы выяснить, находятся ли случайные
величины в корреляционной зависимости,
нужно проверить значимость выборочного
коэффициента корреляции
.
Чтобы выяснить, находятся ли случайные
величины в корреляционной зависимости,
нужно проверить значимость выборочного
коэффициента корреляции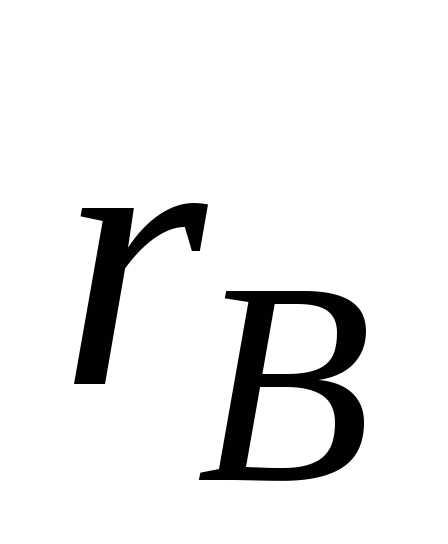 ,
т.е. установить, достаточна ли его
величина для обоснованного вывода о
наличии корреляционной связи. Для этого
проверяют нулевую гипотезу
,
т.е. установить, достаточна ли его
величина для обоснованного вывода о
наличии корреляционной связи. Для этого
проверяют нулевую гипотезу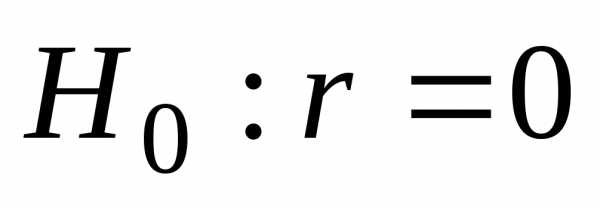 ,
т.е. случайные величины в генеральной
совокупности не коррелированы.
Альтернативная гипотеза.
Предполагая, что имеется двумерное
нормальное распределение случайных
переменных, вычисляют статистику
,
т.е. случайные величины в генеральной
совокупности не коррелированы.
Альтернативная гипотеза.
Предполагая, что имеется двумерное
нормальное распределение случайных
переменных, вычисляют статистику
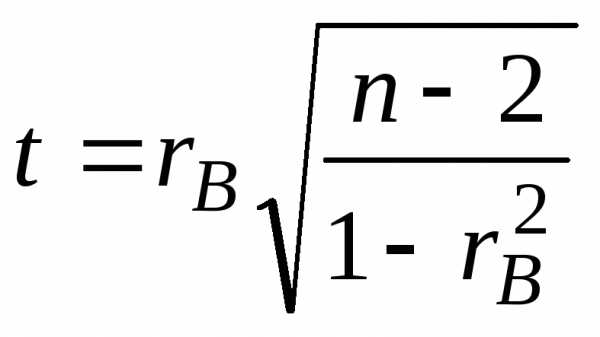 ,
(8)
,
(8)
которая
имеет распределение Стьюдента с
степенями свободы. Для проверки нулевой
гипотезы по уровню значимости и числу степеней свободынаходят по таблицам распределения
Стьюдента критическое значение
и числу степеней свободынаходят по таблицам распределения
Стьюдента критическое значение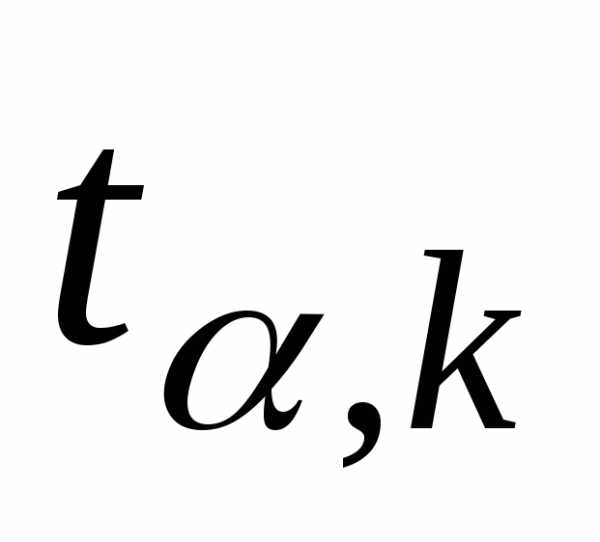 ,
удовлетворяющее условию.
Если
,
удовлетворяющее условию.
Если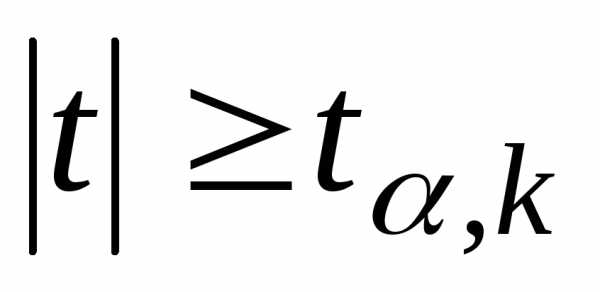 ,
то нулевую гипотезу об отсутствии
корреляционной связи между переменными
,
то нулевую гипотезу об отсутствии
корреляционной связи между переменными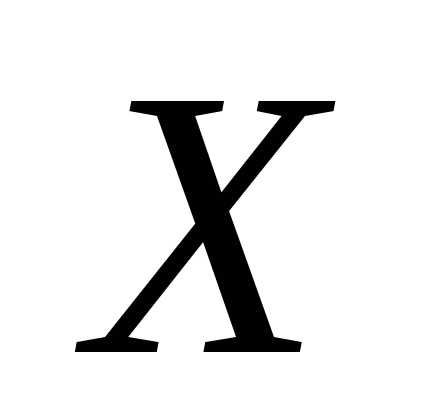 и
и следует отвергнуть. В этом случае
переменные являются зависимыми. Если
следует отвергнуть. В этом случае
переменные являются зависимыми. Если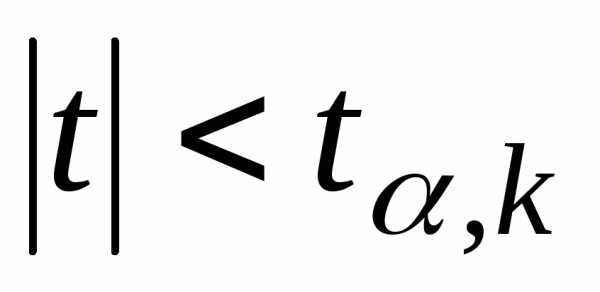 ,
то нет оснований отвергать нулевую
гипотезу.
,
то нет оснований отвергать нулевую
гипотезу.
В
нашем примере зададим
.
По формуле (8) найдем статистику.
Из таблиц распределения критических
точек Стьюдента по заданному уровню
значимости и числу степеней свободынайдем критическую точку
и числу степеней свободынайдем критическую точку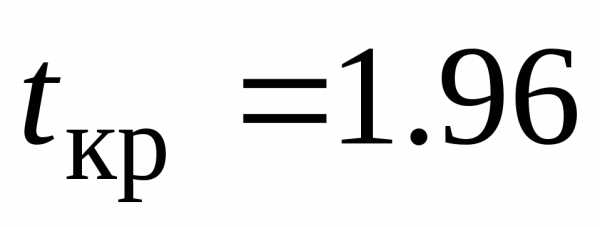 .
Так как
.
Так как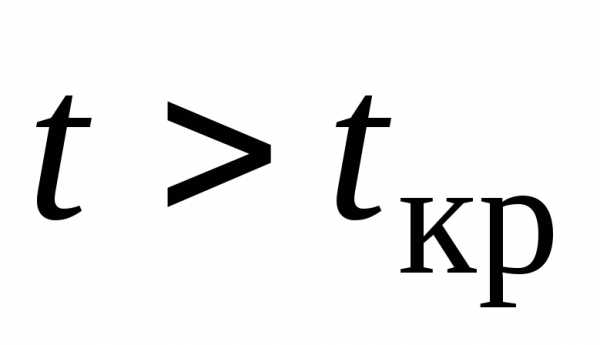 ,
то нулевая гипотеза отвергается.
Рассматриваемые случайные величины
являются коррелированными и , следовательно,
зависимыми.
,
то нулевая гипотеза отвергается.
Рассматриваемые случайные величины
являются коррелированными и , следовательно,
зависимыми.
В случае значимого выборочного коэффициента корреляции можно построить доверительный интервал для коэффициента корреляции.
Плотность вероятности выборочного коэффициента корреляции имеет сложный вид. Поэтому прибегают к специально подобранным функциям от выборочного коэффициента корреляции, которые сводятся хорошо изученным распределениям, например, к нормальному или Стьюдента.
Чаще всего используют преобразование Фишера.
По
выборочному коэффициенту корреляции
вычисляют статистику 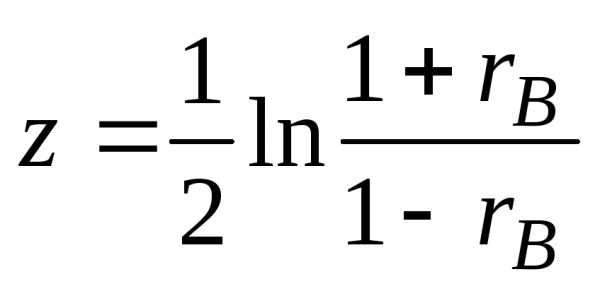 .
Отсюда.
.
Отсюда.
Распределение
статистики  хорошо аппроксимируется нормальным
распределением с параметрамии
хорошо аппроксимируется нормальным
распределением с параметрамии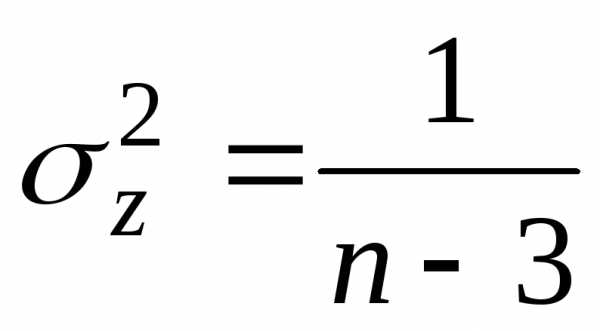 .
.
В
этом случае доверительный интервал для 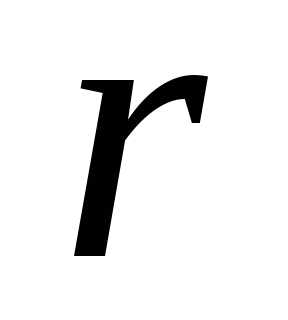 имеет вид.
Величины
имеет вид.
Величины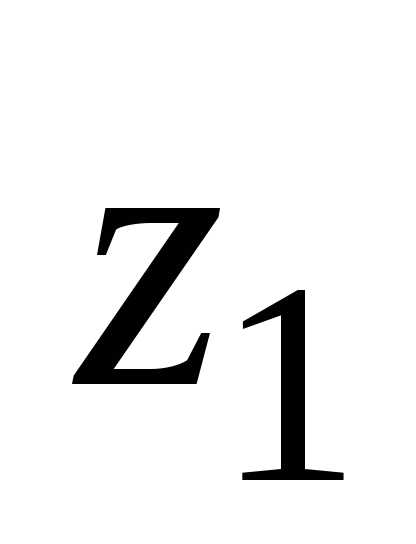 и
и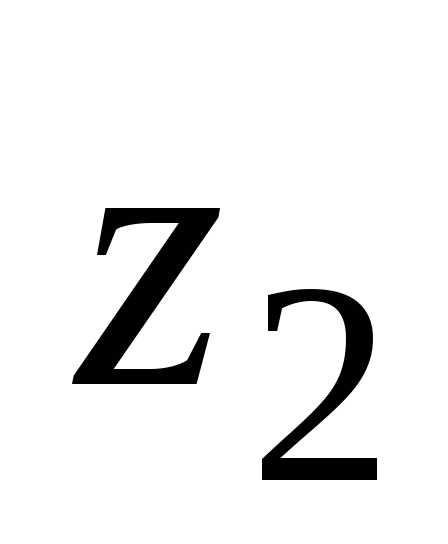 находят по таблицам
находят по таблицам
где 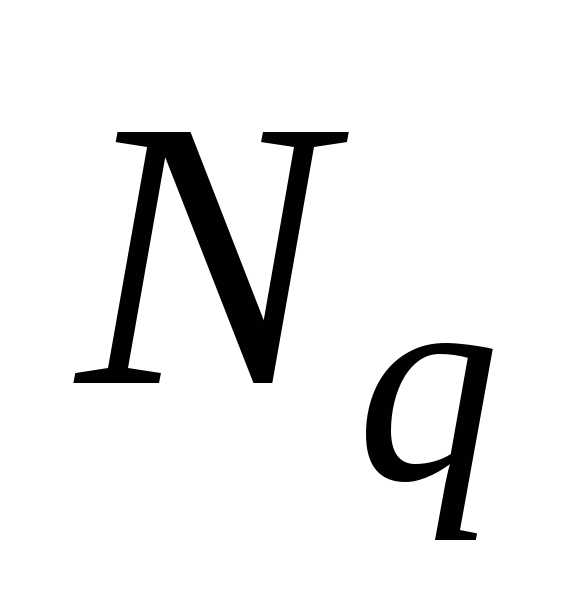 –
нормированная функция Лапласа для
–
нормированная функция Лапласа для %
доверительного интервала.
%
доверительного интервала.
Если коэффициент корреляции значим, то коэффициенты регрессии значимо отличаются от нуля. Интервальные оценки для них имеют вид
Где 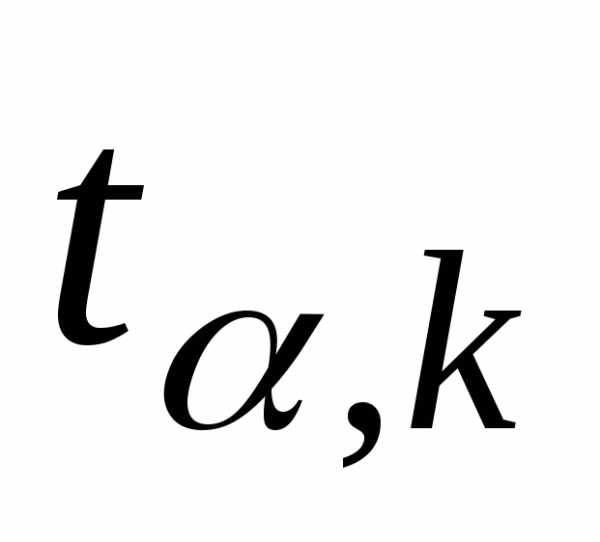 имеет распределение Стьюдента сстепенями свободы. Регрессионный анализ
имеет распределение Стьюдента сстепенями свободы. Регрессионный анализ
Основная
задача регрессионного анализа– изучение
зависимости между результативным
признаком  и наблюдавшимся признаком
и наблюдавшимся признаком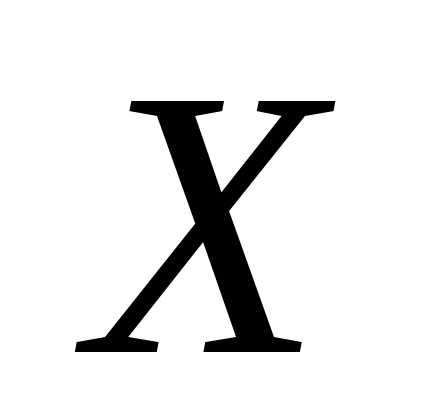 ,
оценка функции регрессии. Рассмотрим
вначале линейный регрессионный анализ
в котором условное математическое
ожидание можно представить в виде
линейной функции от оцениваемых
параметров
,
оценка функции регрессии. Рассмотрим
вначале линейный регрессионный анализ
в котором условное математическое
ожидание можно представить в виде
линейной функции от оцениваемых
параметров
. (9)
Это
выражение называется функцией регрессии
или модельным уравнением регрессии.
Параметры 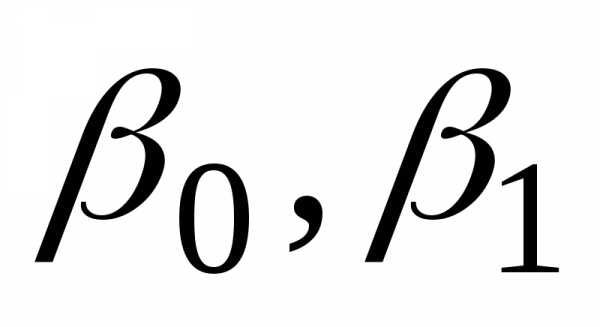 называются коэффициентами регрессии.
Оценки этих параметров обозначим
называются коэффициентами регрессии.
Оценки этих параметров обозначим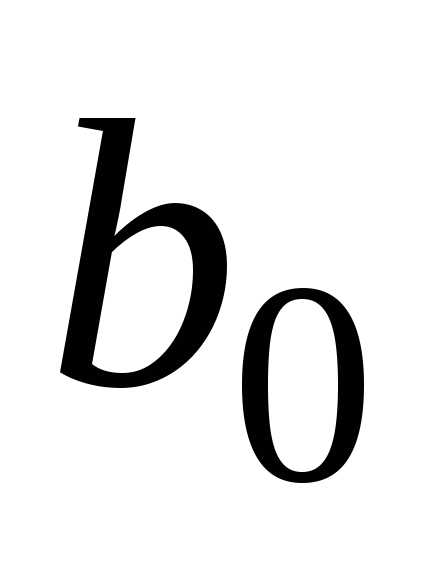 и
и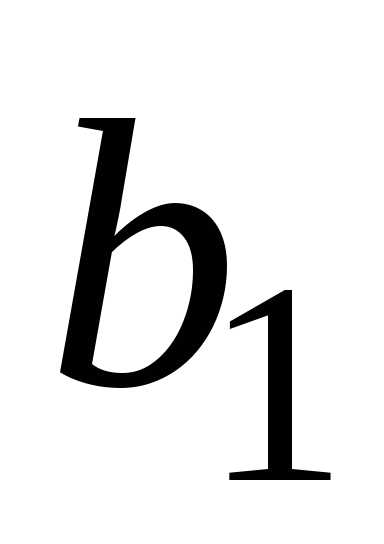 .
Подставляя эти оценки в формулу (9)
вместо параметров, получим линейное
уравнение регрессии
.
Подставляя эти оценки в формулу (9)
вместо параметров, получим линейное
уравнение регрессии
, (10)
коэффициенты
которого найдем методом наименьших
квадратов из условия минимума суммы
квадратов отклонений измеренных значений
результативного признака  от вычисленных по уравнению регрессии
от вычисленных по уравнению регрессии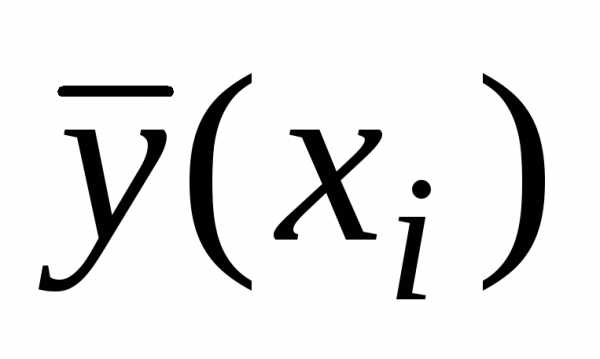 ,
т. е. условия минимума величины
,
т. е. условия минимума величины
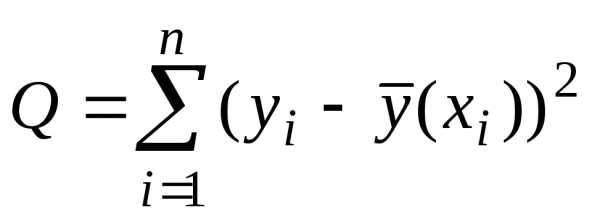 (11)
(11)
Подставляя в (11) выражение (10), получим
(12)
В
соответствии с необходимым условием
минимума функции приравняем нулю
частные производные функции  по переменным
по переменным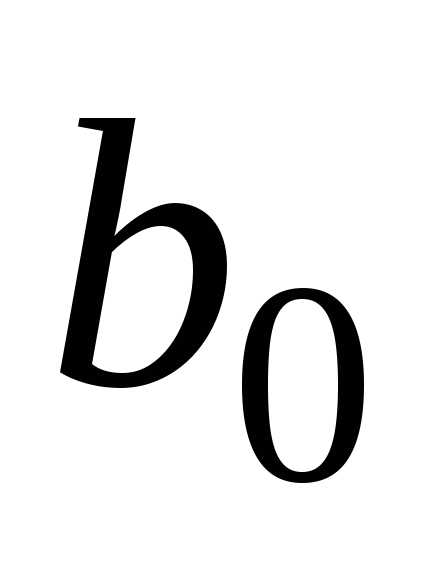 и
и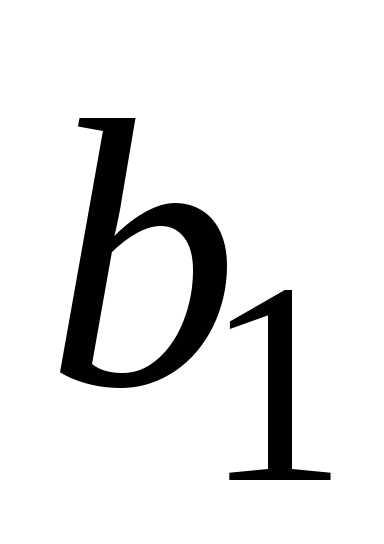 .
В результате получим систему нормальных
уравнений
.
В результате получим систему нормальных
уравнений
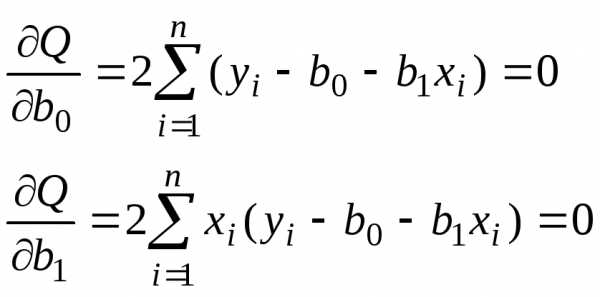 (13)
(13)
После упрощения система уравнений (13) приводится к виду
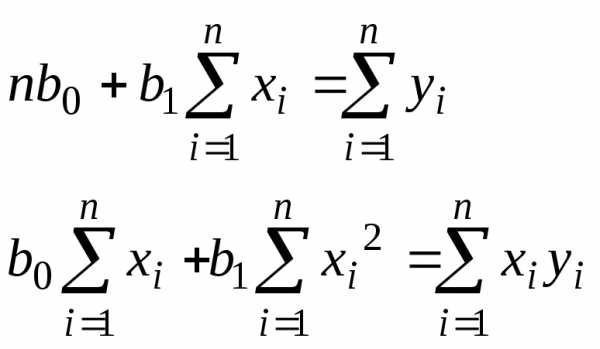 (14)
(14)
Оценки, полученные по методу наименьших квадратов, обладают наименьшей дисперсией в классе линейных оценок. В случае, когда наблюдавшиеся данные представлены корреляционной таблицей, нужно произвести следующие замены в уравнениях (14)
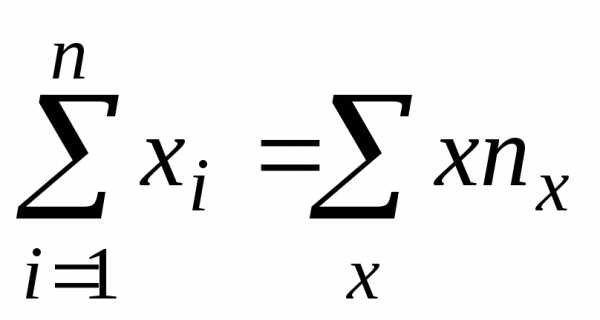 ,
,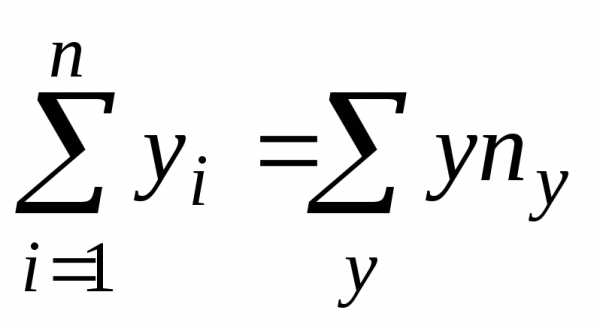 ,
,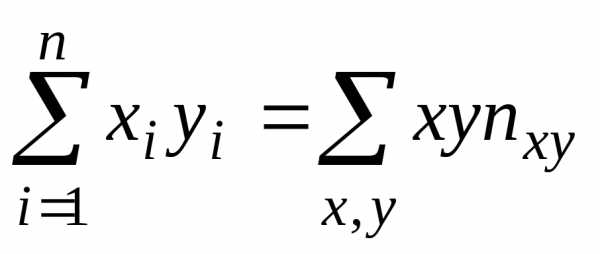 ,
,
.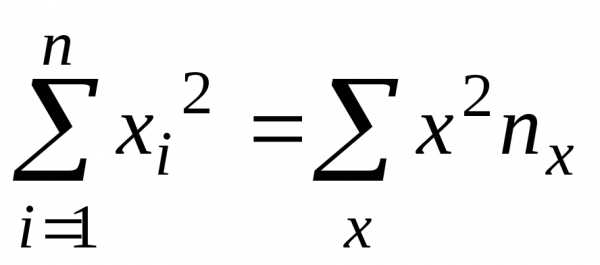 (15)
(15)
где 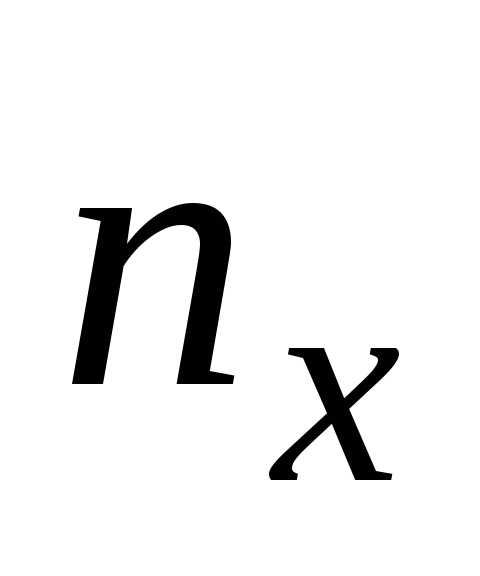 ,
,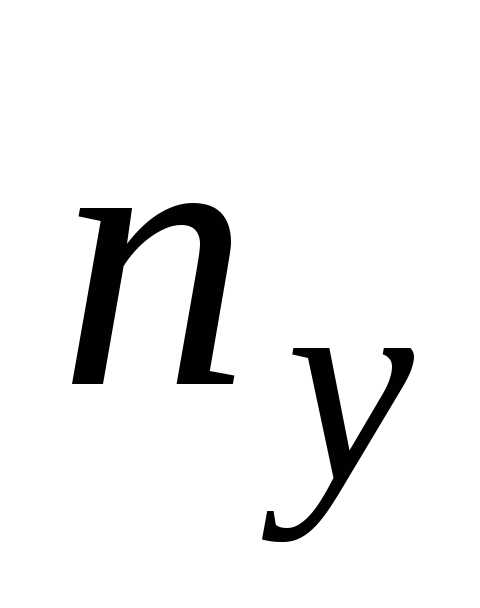 ,
,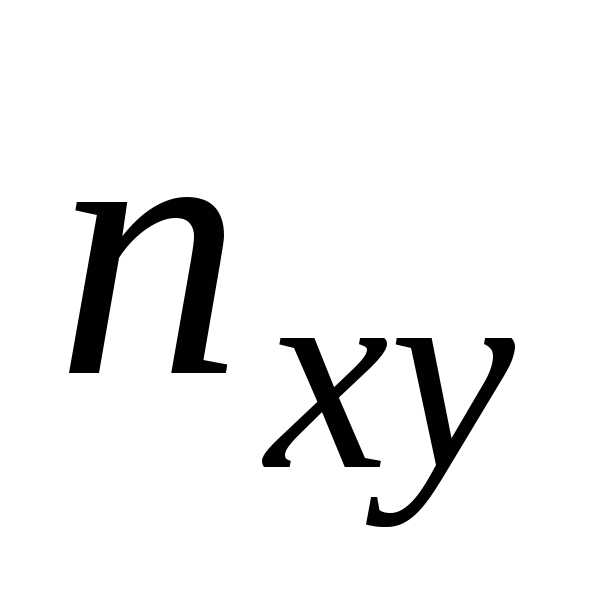 соответствующие частоты:
соответствующие частоты:
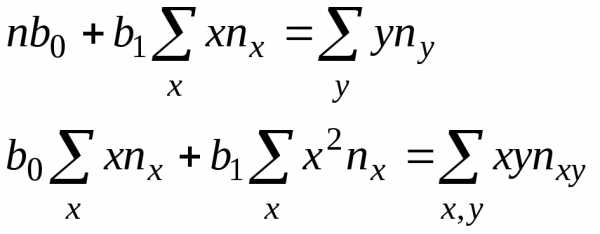 (16)
(16)
Решая
уравнения (16), найдем значения параметров 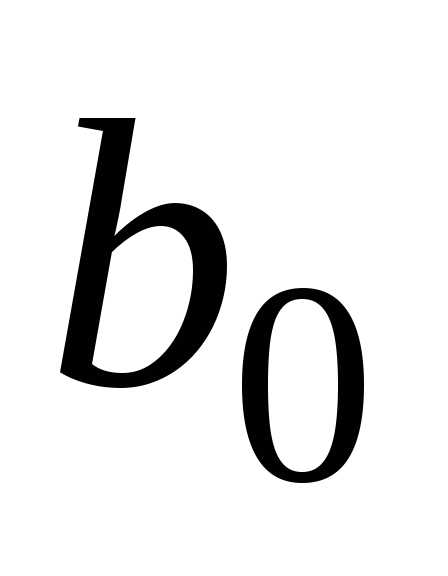 и
и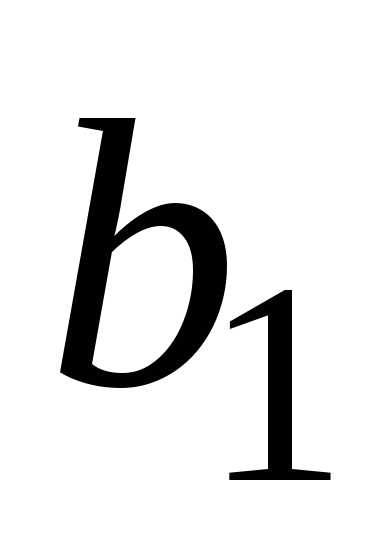 и уравнение регрессии.
и уравнение регрессии.
В примере 1 ,. Уравнение регрессии имеет вид
.
Нелинейная регрессия
Линейная
регрессия часто оказывается
неудовлетворительной. Тогда используют
криволинейную регрессию, график которой
есть некоторая подходящим образом
выбранная кривая, вид которой определяют
по корреляционному полю. Если зависимость
между признаками 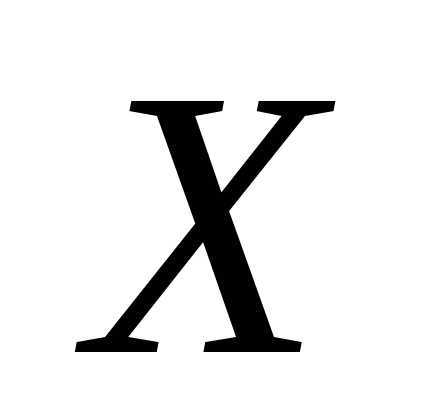 и
и нелинейная,
то условное математическое ожидание
является нелинейной функцией. Пусть,
например,.
Оценки параметров
нелинейная,
то условное математическое ожидание
является нелинейной функцией. Пусть,
например,.
Оценки параметров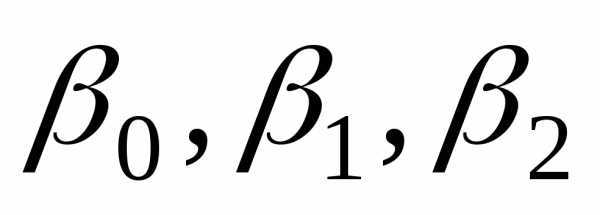 обозначим
обозначим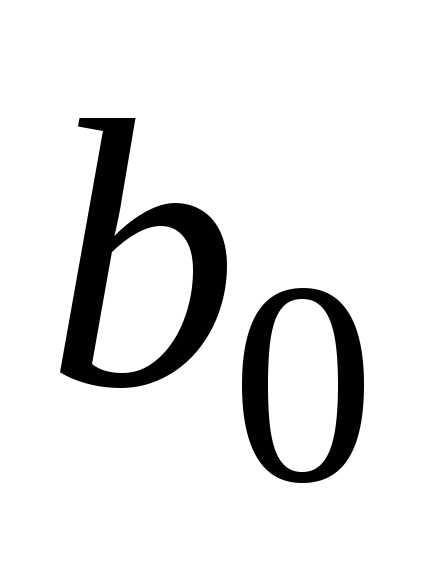 ,
,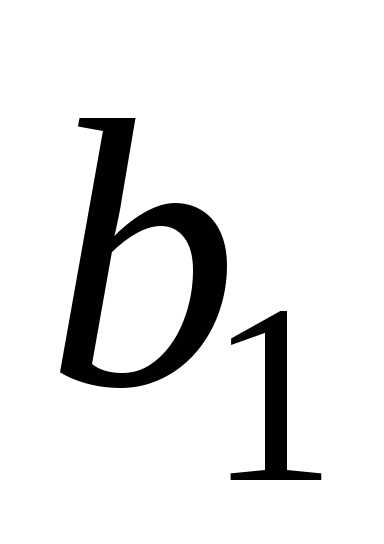 ,
,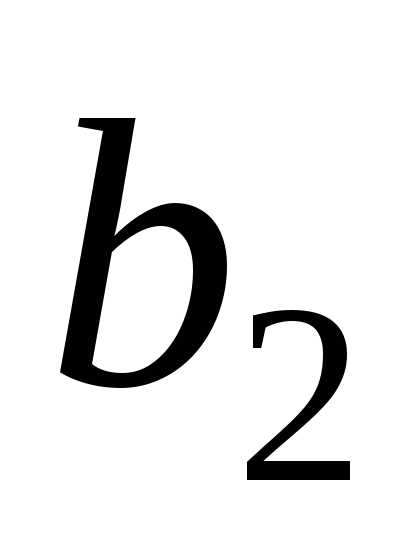 .
В этом случае система нормальных
уравнений имеет вид
.
В этом случае система нормальных
уравнений имеет вид
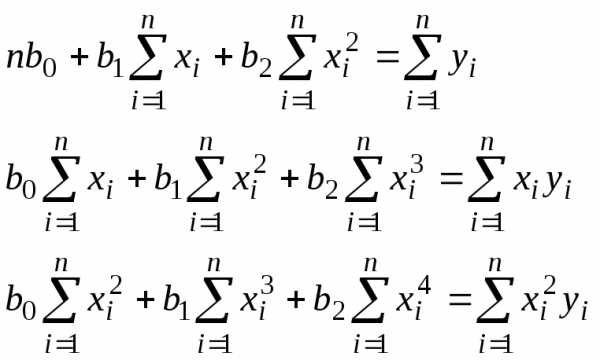 (17)
(17)
Если наблюдавшиеся данные представлены корреляционной таблицей, нужно произвести замену (15) в уравнениях (17)
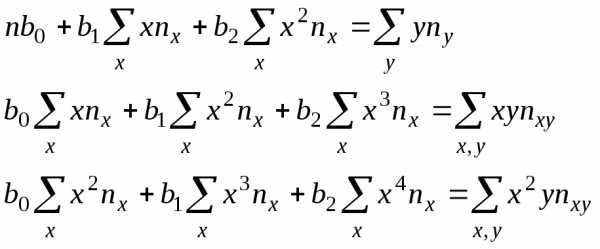 (18)
(18)
Корреляционное отношение
Корреляционное отношение определяется равенством
,
которое может быть записано в виде
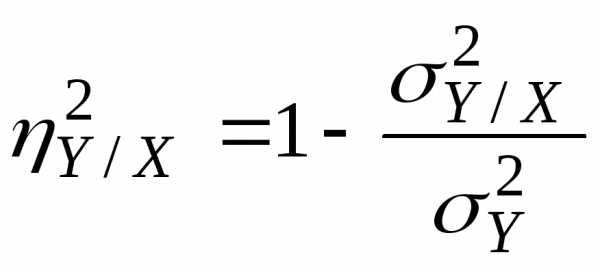
При
вычислении корреляционного отношения
по выборочным данным получается
выборочное корреляционное отношение 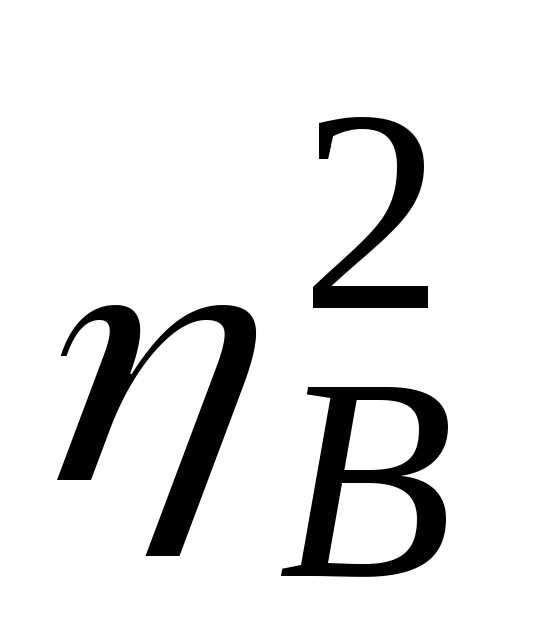 .
В этом случае вместо дисперсий используются
их статистические оценки. Тогда
.
В этом случае вместо дисперсий используются
их статистические оценки. Тогда
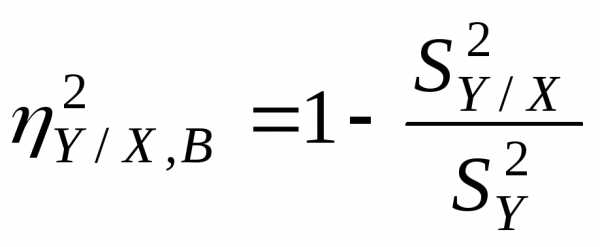 (19)
(19)
где
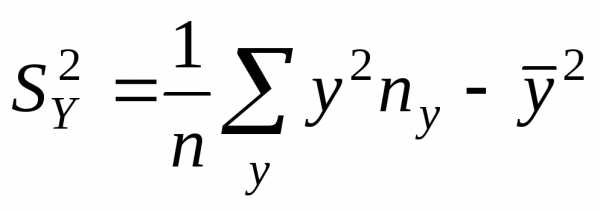 ,
,
Выборочное
значение 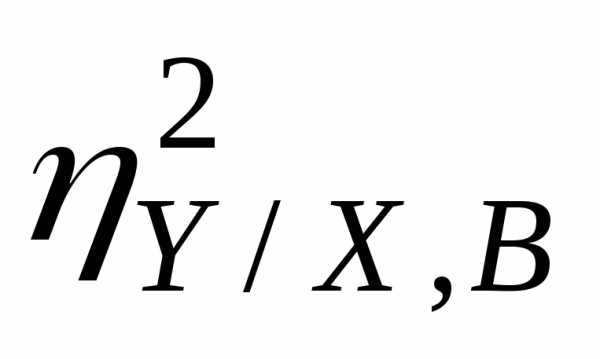 вычисляется по данным корреляционной
таблицы с помощью формулы
вычисляется по данным корреляционной
таблицы с помощью формулы
,
где
числитель характеризует рассеяние
условных средних значений 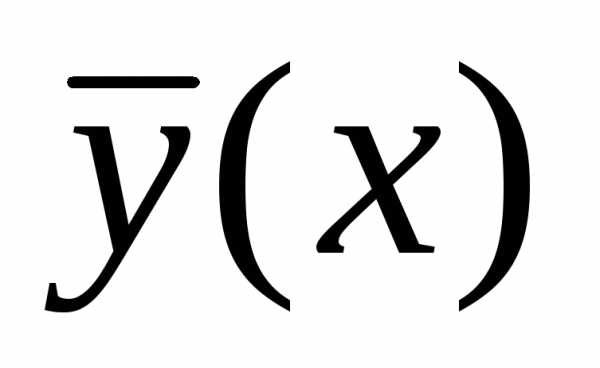 относительно безусловного среднего
арифметического
относительно безусловного среднего
арифметического .
.
9
studfiles.net
Корреляционная таблица — это… Что такое Корреляционная таблица?
- Корреляционная таблица
- таблица сопряженности признаков) один из основных способов описания корреляционных связей между признаками, используемых для упорядочения информации о распределении изучаемой совокупности индивидов по двум признакам. К. т. имеет прямоугольную форму, число строк ее nопределяется количеством значений одного признака, а число столбцов m количеством значений другого. На пересечении, например, второй строки и третьего столбца в таблице проставляется число индивидов, у которых первый признак принимает второе значение из своего списка, а второй признак третье из своего Таблица имеет n m внутренних клеток. Кроме того, выделяются два маргинала (на полях-правом и нижнем). Первый маргинал это m 1-ый столбец, заполненный числами индивидов, у которых первый признак принимает свое первое значение (независимо от того, какое значение принимает второй признак, это сумма элементов первой внутренней строки), второе значение и т.
д. до п.-ого.
Второй маргинал это n 1-ая строка, заполненная суммами элементов соответствующих столбцов. Сумма элементов каждого маргинала равна числу индивидов. Такого рода распределения называют двумерными. Если п=, то говорят об одномерном распределении ( оно показывает, как распределены индивиды по одному, в данном случае второму признаку). Изучают и трехмерные распределения: для каждого значения третьего признака составляют свои двумерные распределения по первому и второму признакам и т. д. Таким образом, основной формой представления является двумерная К. т. Характер распределения индивидов по ее клеткам определяется характером связи между признаками. Поэтому по эмпирической таблице восстанавливают характер связи. Если связи нет, то число индивидов, попадающих в данную клетку таблицы, равно произведению маргиналов строки и столбца с соответствующими номерами, деленному на число всех индивидов [1, 72]. Таблицу, заполненную такими частотами, называют теоретической. Если связь есть, то эмпирическая таблица отличается от теоретической. Мерой отличия, характеризующей связь, является критерий Пирсона X2 (см. Анализ таблиц сопряженности, корреляция).
Социологический справочник. — К.: Политиздат Украины. Под ред. В. И. Воловича. 1990.
- Конфликт социальный
- Корреляция
Смотреть что такое «Корреляционная таблица» в других словарях:
ТАБЛИЦА СОПРЯЖЕННОСТИ — таблица, содержащая частоты совместного появления значения двух признаков (обозначим их как X и У), измеренных в данной совокупности единиц анализа (в качестве синонимов для обозначения таких таблиц используются такие названия, как комбинационная … Российская социологическая энциклопедия
Матрица корреляционная — средство представления структуры связей между переменными, квадратная таблица, в которой указываются коэффициенты между каждой парой переменных … Социологический словарь Socium
Корреляция (в матем. статистике) — Корреляция в математической статистике, вероятностная или статистическая зависимость, не имеющая, вообще говоря, строго функционального характера. В отличие от функциональной, корреляционная зависимость возникает тогда, когда один из признаков… … Большая советская энциклопедия
Корреляция — I Корреляция (от позднелат. correlatio соотношение) термин, применяемый в различных областях науки и техники для обозначения взаимозависимости, взаимного соответствия, соотношения понятий, предприятий, предметов, функций. См. также… … Большая советская энциклопедия
Корреляционный анализ — совокупность основанных на математической теории корреляции (См. Корреляция) методов обнаружения корреляционной зависимости между двумя случайными признаками или факторами. К. а. экспериментальных данных заключает в себе следующие… … Большая советская энциклопедия
СССР. Естественные науки — Математика Научные исследования в области математики начали проводиться в России с 18 в., когда членами Петербургской АН стали Л. Эйлер, Д. Бернулли и другие западноевропейские учёные. По замыслу Петра I академики иностранцы… … Большая советская энциклопедия
КОРРЕЛЯЦИЯ — зависимость между случайными величинами, не имеющая, вообще говоря, строго функционального характера. В отличие от функциональной зависимости К., как правило, рассматривается тогда, когда одна из величин зависит не только от данной другой, но и… … Математическая энциклопедия
КОРРЕЛЯЦИЯ — зависимость между числовыми случайными величинами, не имеющая, вообще говоря, строго функционального характера. В отличие от функциональной зависимости К., как правило, рассматривается тогда, когда по крайней мере одна из величин зависит не… … Российская социологическая энциклопедия
Корреляция — (Correlation) Корреляция это статистическая взаимосвязь двух или нескольких случайных величин Понятие корреляции, виды корреляции, коэффициент корреляции, корреляционный анализ, корреляция цен, корреляция валютных пар на Форекс Содержание… … Энциклопедия инвестора
Коэффициент корреляции — (Correlation coefficient) Коэффициент корреляции это статистический показатель зависимости двух случайных величин Определение коэффициента корреляции, виды коэффициентов корреляции, свойства коэффициента корреляции, вычисление и применение… … Энциклопедия инвестора
sociological_guide.academic.ru
Корреляционная таблица
Y X | y1 | y2 | … | yi | ni |
x1 | m11 | m12 | … | m1l | n1 |
x2 | m21 | m22 | … | m2l | n2 |
xk | mk1 | mk2 | … | mkl | nk |
mj | m1 | m2 | … | ml | n |
В случае, когда случайные величины являются непрерывными (т.е. могут принимать любое значение из соответствующих интервалов), составляется интервальная корреляционная таблица.
Условным среднимназывают среднее арифметическое значенийY, соответствующих значениюX=x. Например,
.
Корреляционной зависимостьюYотXназывают зависимость:
(8)
Уравнение (8) называют эмпирическим уравнением регрессииYнаX; функцию f(x)называютэмпирическойрегрессиейYнаX, а ее график — линией регрессииYна X.
Аналогично определяются условная средняя и корреляционная зависимостьXотY:
(9)
Распределение системы (X,Y)характеризуется числовыми параметрами: математическими ожиданиями компонентmx, my; дисперсиями,; корреляционным моментом (ковариацией); коэффициентом корреляции,.
Здесь и дальше, будем считать, что двумерная случайная величина (X,Y) распределена нормально, тогда уравнения линейной регрессии YнаXи X наYимеют вид:
и
По корреляционной таблице 6, найдем оценки параметров линейной регрессии:
;; (10)
; (11)
; (12)
; (13)
— выборочный коэффициент корреляции .
Выборочный коэффициент корреляции характеризует тесноту линейной связи междуи. Если, то элементы выборки,лежат на прямой линии, аисчитаются практически линейно зависимы. Чем ближек 1, тем связь сильнее; чем ближек 0, тем связь слабее. ЕслиXиYнезависимы, то.
Эмпирическая функция линейной регрессии YнаXиXнаYсоответственно задаётся уравнениями
;.
Замечание 1.Если построить на одном корреляционном поле две линии регрессииYнаXиXнаY, то они пересекутся в точкеO, и угол между этими прямыми тем меньше, чем ближе коэффициент корреляции к.
Замечание 2.В случае, когда данные наблюденийXиYзаписаны в виде интервальной корреляционной таблицы в формулах (10) – (13) вместоxiиyiобычно берут середины, соответствующих интервалов.
Для проверки соответствия линейной регрессии результатам наблюдений вычисляется наблюдаемое значение критерия
и по таблице критических точек распределения Стьюдента (таблица 7) по заданному уровню значимости α и числу степеней свободы k=n–2 , находится. Затем сравнивается наблюдаемое значение критерия с табличным.
Таблица 7
t-Распределение Стьюдента.
Число степеней свободы, υ | Уровень значимости,α | Число степеней свободы, υ | Уровень значимости,α | ||
0,1 | 0,05 | 0,1 | 0,05 | ||
1 | 6,31 | 12,7 | 17 | 1,74 | 2,11 |
2 | 2,92 | 4,3 | 18 | 1,73 | 2,10 |
3 | 2,35 | 3,18 | 19 | 1,73 | 2,09 |
4 | 2,13 | 2,78 | 20 | 1,73 | 2,09 |
5 | 2,01 | 2,57 | 21 | 1,72 | 2,06 |
6 | 1,94 | 2,45 | 22 | 1,72 | 2,07 |
7 | 1,89 | 2,36 | 23 | 1,71 | 2,07 |
8 | 1,86 | 2,31 | 24 | 1,71 | 2,06 |
9 | 1,83 | 2,26 | 25 | 1,71 | 2,06 |
10 | 1,81 | 2,23 | 26 | 1,71 | 2,06 |
11 | 1,80 | 2,2 | 27 | 1,71 | 2,05 |
12 | 1,78 | 2,18 | 28 | 1,70 | 2,05 |
13 | 1,77 | 2,16 | 29 | 1,70 | 2,05 |
14 | 1,76 | 2,14 | 30 | 1,70 | 2,04 |
15 | 1,75 | 2,13 | 40 | 1,68 | 2,02 |
16 | 1,75 | 2,12 | 60 | 1,67 | 2,00 |
120 | 1,66 | 1,98 | |||
Если , то гипотеза о некоррелированности составляющихXиYотвергается. Если же, то нет основания отвергать гипотезу о некоррелированности случайных величинXиY.
studfiles.net
Корреляционная таблица это что такое Корреляционная таблица: определение — Социология.НЭС
Корреляционная таблица
таблица сопряженности признаков) один из основных способов описания корреляционных связей между признаками, используемых для упорядочения информации о распределении изучаемой совокупности индивидов по двум признакам. К. т. имеет прямоугольную форму, число строк ее nопределяется количеством значений одного признака, а число столбцов m количеством значений другого. На пересечении, например, второй строки и третьего столбца в таблице проставляется число индивидов, у которых первый признак принимает второе значение из своего списка, а второй признак третье из своего Таблица имеет n m внутренних клеток. Кроме того, выделяются два маргинала (на полях-правом и нижнем). Первый маргинал это m+1-ый столбец, заполненный числами индивидов, у которых первый признак принимает свое первое значение (независимо от того, какое значение принимает второй признак, это сумма элементов первой внутренней строки), второе значение и т. д. до п.-ого. Второй маргинал это n+1-ая строка, заполненная суммами элементов соответствующих столбцов. Сумма элементов каждого маргинала равна числу индивидов. Такого рода распределения называют двумерными. Если п=, то говорят об одномерном распределении ( оно показывает, как распределены индивиды по одному, в данном случае второму признаку). Изучают и трехмерные распределения: для каждого значения третьего признака составляют свои двумерные распределения по первому и второму признакам и т. д. Таким образом, основной формой представления является двумерная К. т. Характер распределения индивидов по ее клеткам определяется характером связи между признаками. Поэтому по эмпирической таблице восстанавливают характер связи. Если связи нет, то число индивидов, попадающих в данную клетку таблицы, равно произведению маргиналов строки и столбца с соответствующими номерами, деленному на число всех индивидов [1, 72]. Таблицу, заполненную такими частотами, называют теоретической. Если связь есть, то эмпирическая таблица отличается от теоретической. Мерой отличия, характеризующей связь, является критерий Пирсона X2 (см. Анализ таблиц сопряженности, корреляция).
Оцените определение:
Источник: Социологический справочник
voluntary.ru