что это такое, каковы его свойства и чему равна сумма его уголов
Если на плоскости имеются четыре точки, из которых никакие три не принадлежит одной прямой, то их можно попарно соединить отрезками. В результате получится фигура с четырьмя углами, содержащая две диагонали, при пересечении которых получится выпуклый четырехугольник.
Виды
Существует несколько видов фигур с четырьмя углами, но не все они являются выпуклыми. Слева рисунок отображает выпуклый четырехугольник, все его внутренние точки находятся в одной полуплоскости относительно прямой l, на которой лежит сторона AD. Для среднего данное условие выполняется, но его нельзя считать выпуклым, потому что его стороны пересекаются. Такие четырехугольники называются самопересекающимися. Правый тоже не является выпуклым, так как две его точки B и C лежат в разных полуплоскостях относительно разбиения прямой l.
На основании вышесказанного дадим определение. Выпуклым четырехугольником называется фигура, состоящая из четырех точек и четырех отрезков, которые последовательно их соединяют. Главное условие: никакие три точки не должны одновременно лежать на одной прямой, а соединяющие отрезки пересекаться.
Виды выпуклых четырехугольников:
- прямоугольник;
- параллелограмм;
- трапеция;
- ромб;
- квадрат.
Перечисленные отношения между множествами фигур упрощают доказательства теорем (предложений, выражающих свойства). Например, если теорема доказана для параллелограмма (будет ли параллелограмм выпуклым? и т.д.), то она будет верна и для любого соответствующего подмножества фигур. Если же доказана более общая теорема для выпуклого четырехугольника, то она будет верна и для параллелограмма, и для трапеции.
Свойства
Главные признаки:
- сумма углов — 360 градусов;
- диагонали могут пересекаться в одной точке.
Если сумма углов равна 360, это следствие более общего случая – четырехугольника, не имеющего пересекающихся отрезков. Но для выпуклого обычно проводят отдельное и очень простое доказательство. Если внутри выпуклого четырехугольника провести диагональ, то она разобьет его на два треугольника. Как известно, сумма углов в треугольнике равна 180. Сложив все получившиеся углы, получаем величину 360.
Если взять средние точки всех сторон произвольного выпуклого четырехугольника и построить на них новый, то он окажется параллелограммом (Теорема Вариньона).
Доказательство на следующем фото. Выпуклый четырёхугольник ABCD имеет на каждой из сторон точку, делящую эту сторону пополам. Рассмотрим отрезок FG. Это средняя линия треугольника DAB, параллельная диагонали DB. Это следует из подобия треугольников DAB и FAG.
Аналогично проводятся рассуждения для треугольников DBC и EHC. Из чего следует параллельность DB и EH. Поскольку отрезки FG и EH параллельны диагонали DB, то и сами параллельны.
Аналогично доказывается, что отрезки FE и GH параллельны. Так как противолежащие стороны EFGH попарно параллельны, значит, это параллелограмм.
Обратите внимание! Теорема Вариньона справедлива для всех четырехугольников, невыпуклых и самопересекающихся. Если взять середины диагоналей, то можно построить еще два параллелограмма. Центры всех трех параллелограммов окажутся на одной прямой.
Если выпуклый четырёхугольник имеет свойство взаимной перпендикулярности своих диагоналей, то суммы квадратов его противоположных сторон у него равны. Это доказывается при помощи теоремы Пифагора, как показано на следующем чертеже:
Квадрат каждой из сторон выражается через сумму квадратов отрезков диагоналей, ограниченных вершинами и точкой пересечения. Для удобства мы обозначаем их малыми буквами латинского алфавита, совпадающими с названием вершин. Затем выписываем выражения для сумм квадратов противолежащих сторон:
В правой части каждого из выражений стоит одна и та же сумма слагаемых. Следовательно, равны и правые части между собой, что доказывает теорема.
Вписанные и описанные
Часто требуется проверить, не лежат ли вершины четырехугольника на окружности, или существует ли окружность, вписанная в 4-угольник. Центр описанной окружности находится в точке пересечения срединных перпендикуляров к сторонам, а центр вписанной – на пересечении биссектрис внутренних углов.
Если сумма противоположных углов составляет 180, то рядом с ними можно описать окружность, другими словами, существует окружность, на которой лежат все вершины четырехугольника. Его называют вписанным (подразумевается, что в окружность). Верно и обратное утверждение, то есть выраженное в теореме условие необходимое и достаточное.
Расчет площади
Площадь, которую имеет любой выпуклый четырёхугольник, равна половине произведения длин диагоналей на синус угла между ними. Докажем это правило.
Здесь опять поможет теорема Вариньона (мы имеем “большой” параллелограмм, о котором сразу не было сказано). Проведем прямые, параллельные диагоналям, через вершины A, B, C, D исходного прямоугольника. Мы получим параллелограмм EFGH. Его площадь равна сумме площадей параллелограммов AFBO, BGCO, CHDO, DEAO. Но каждый из перечисленных делится своей диагональю на пару треугольников с равными площадями. С другой стороны, в силу параллельности диагоналей ADCD сторонам внешнего параллелограмма, мы можем применить формулу площади:
Полезное видео
Подведем итоги
Фигуру, состоящую из четырех углов, можно часто увидеть в обычной жизни, такую форму обычно имеют земельные участки, здания, параллелограммы служат для построения векторных базисов на плоскости. Не случайно 4-угольники хорошо изучены и установлено большое число свойств, связанных с ними.
Вконтакте
Одноклассники
Мой мир
znaniya.guru
Подготовка школьников к ЕГЭ и ОГЭ в учебном центре «Резольвента» (Справочник по математике — Планиметрия
Типы четырёхугольников
Классификация треугольников изложена в разделе нашего справочника «Типы треугольников».
Целью данного раздела является классификация четырёхугольников.
Классификация четырёхугольников по типам представлена на схеме 1.
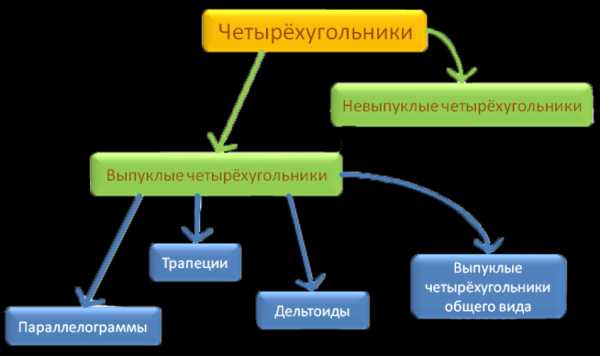
Схема 1
Рисунки и определения фигур, представленных на схеме 1, даны в следующей таблице.
| Фигура | Рисунок | Определение |
| Четырёхугольник | Четырёхугольник – это часть плоскости, ограниченная замкнутой ломаной линией с четырьмя звеньями без самопересечений. | |
| Выпуклый четырёхугольник | Выпуклый четырёхугольник – это четырёхугольник, который вместе с любыми двумя точками содержит и весь отрезок с концами в этих точках | |
| Невыпуклый четырёхугольник | Четырёхугольник называют невыпуклым, если он не является выпуклым. | |
| Параллелограмм | Параллелограмм – это четырёхугольник, у которого противолежащие стороны параллельны | |
| Трапеция | Трапеция – это четырёхугольник, у которого две стороны параллельны (основания), а две другие стороны не параллельны (боковые стороны). | |
| Дельтоид | Дельтоид – это выпуклый четырёхугольник, состоящий из двух различных равнобедренных треугольников с общим основанием, вершины которых лежат по разные стороны от этого основания. |
| Четырёхугольник |
Четырёхугольник – это часть плоскости, ограниченная замкнутой ломаной линией с четырьмя звеньями без самопересечений. |
| Выпуклый четырёхугольник |
Выпуклый четырёхугольник – это четырёхугольник, который вместе с любыми двумя точками содержит и весь отрезок с концами в этих точках |
| Невыпуклый четырёхугольник |
Четырёхугольник называют невыпуклым, если он не является выпуклым. |
| Параллелограмм |
Параллелограмм – это четырёхугольник, у которого противолежащие стороны параллельны |
| Трапеция |
Трапеция – это четырёхугольник, у которого две стороны параллельны (основания), а две другие стороны не параллельны (боковые стороны). |
| Дельтоид |
Дельтоид – это выпуклый четырёхугольник, состоящий из двух различных равнобедренных треугольников с общим основанием, вершины которых лежат по разные стороны от этого основания. |
Типы параллелограммов
На схеме 2 представлена классификация параллелограммов.
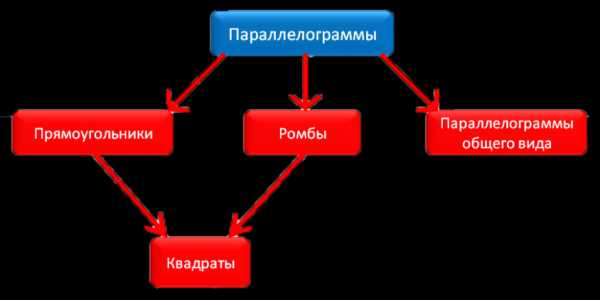
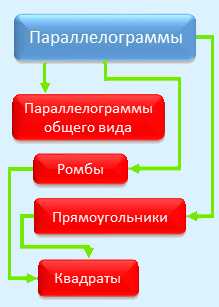
Схема 2
Рисунки и определения фигур, представленных на схеме 2, даны в следующей таблице.
| Фигура | Рисунок | Определение |
| Прямоугольник | Прямоугольник – это параллелограмм, у которого все углы прямые. | |
| Ромб | Ромб – это параллелограмм, у которого все стороны равны. | |
| Квадрат | Квадрат – это параллелограмм, у которого все углы прямые и все стороны равны. | |
| Параллелограмм общего вида | Параллелограмм – это четырёхугольник, у которого противолежащие стороны параллельны |
| Прямоугольник |
Прямоугольник – это параллелограмм, у которого все углы прямые. |
| Ромб |
Ромб – это параллелограмм, у которого все стороны равны. |
| Квадрат |
Квадрат – это параллелограмм, у которого все углы прямые и все стороны равны. |
| Параллелограмм общего вида |
Параллелограмм – это четырёхугольник, у которого противолежащие стороны параллельны |
Типы трапеций
На схеме 3 представлена классификация трапеций.
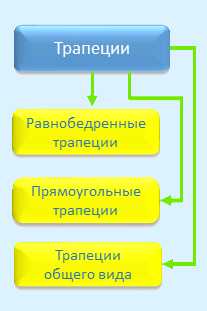
Схема 3
Рисунки и определения фигур, представленных на схеме 3, даны в следующей таблице.
| Фигура | Рисунок | Определение |
| Равнобедренная (равнобочная) трапеция | Равнобедренной называют трапецию, у которой боковые стороны равны. | |
| Прямоугольная трапеция | Прямоугольной называют трапецию, у которой одна из боковых сторон перпендикулярна основаниям. | |
| Трапеция общего вида | Трапеция – это четырёхугольник, у которого две стороны параллельны, а две другие стороны не параллельны. |
| Равнобедренная (равнобочная) трапеция |
Равнобедренной называют трапецию, у которой боковые стороны равны. |
| Прямоугольная трапеция |
Прямоугольной называют трапецию, у которой одна из боковых сторон перпендикулярна основаниям. |
| Трапеция общего вида |
Трапеция – это четырёхугольник, у которого две стороны параллельны, а две другие стороны не параллельны. |
На нашем сайте можно также ознакомиться с разработанными преподавателями учебного центра «Резольвента» учебными материалами для подготовки к ЕГЭ и ОГЭ по математике.
Приглашаем школьников (можно вместе с родителями) на бесплатное тестирование по математике, позволяющее выяснить, какие разделы математики и навыки в решении задач являются для ученика «проблемными». Запись по телефону (495) 509-28-10 |
Для школьников, желающих хорошо подготовиться и сдать ЕГЭ или ОГЭ по математике или русскому языку на высокий балл, учебный центр «Резольвента» проводит
У нас также для школьников организованы
МОСКВА, СВАО, Учебный центр «РЕЗОЛЬВЕНТА»
www.resolventa.ru
Ответы@Mail.Ru: что такое выпуклый четырёхугольник
Четырехугольник, и вообще любая плоская фигура, называется выпуклой, если любые две точки, принадлежащие этой фигуре, можно соединить отрезком, который тоже будет принадлежать этой фигуре (никакая из точек отрезка не будет находиться вне этой фигуры).
выпуклый многоугольник целиком лежит по одну сторону от каждой из своих сторон.
Выпуклый многоугольник — это многоугольник, все вершины которого находятся в одной полуплоскости относительно прямой, на которой лежит любая из его сторон 🙂
полностью соглашусь с гуру ПыхтачкомЭто трапеция! Не сомневайтесь! Это правильный ответ!!!!
touch.otvet.mail.ru
Четырёхугольник — Википедия
Четырёхугольник — это геометрическая фигура (многоугольник), состоящая из четырёх точек (вершин), никакие три из которых не лежат на одной прямой, и четырёх отрезков (сторон), попарно соединяющих эти точки. Различают выпуклые и невыпуклые четырёхугольники, невыпуклый четырёхугольник может быть самопересекающимся (см. рис.).
Виды четырёхугольников[править]
- Параллелограмм — четырёхугольник, у которого все противоположные стороны попарно равны и параллельны;
- Прямоугольник — четырёхугольник, у которого все углы прямые;
- Ромб — четырёхугольник, у которого все стороны равны;
- Квадрат — четырёхугольник, у которого все углы прямые и все стороны равны;
- Трапеция — четырёхугольник, у которого две противоположные стороны параллельны;
- Дельтоид — четырёхугольник, у которого две пары смежных сторон равны.
- Антипараллелограмм , или
Четырёхсторонник[править]
Хотя такое название может быть эквивалентно четырёхугольнику, в него часто вкладывают дополнительный смысл. Четвёрка прямых, никакие две из которых не параллельны и никакие три не проходят через одну точку, называется четырёхсторонником. Такая конфигурация встречается в некоторых утверждениях евклидовой геометрии (например, теорема Менелая, прямая Гаусса, прямая Обера, теорема Микеля и др.), в которых часто все прямые являются взаимозаменяемыми.
- Замечание. Многие теоремы планиметрии, сформулированные для четырёхсторонника, применимы также и для полного четырёхсторонника или пространственного четырёхсторонника, когда отмеченные выше четыре прямые общего положения располагаются не на плоскости, а в пространстве с теми же ограничениями: все прямые попарно пересекаются (на плоскости это условие почти всегда гарантировано), никакие две из них не параллельны и никакие три не проходят через одну точку.
Угловые соотношения[править]
- Сумма углов четырёхугольника равна .
Метрические соотношения[править]
Обобщенное неравенство четырехугольника[править]
В любом четырехугольнике (включая вырожденный) сумма длин трех его сторон не меньше длины четвертой стороны, то есть [1]:
причём равенство достигается тогда и только тогда, когда выпуклый четырехугольник вписан в окружность или его вершины лежат на одной прямой.
Если в четырёхугольнике две пары противоположных сторон не параллельны, то две середины его диагоналей лежат на прямой, которая проходит через середину отрезка, соединяющего две точки пересечения этих двух пар противоположных сторон (на рисунке точки показаны красным цветом). Указанная прямая называется прямой Гаусса (на рисунке она показана зеленым цветом). При этом прямая Гаусса всегда перпендикулярна прямой Обера.
Соотношения между сторонами и диагоналями четырехугольника[править]
- Шесть расстояний между четырьмя произвольными точками плоскости, взятыми попарно, связаны соотношением:
- .
Это соотношение можно представить в виде определителя:
- Замечание. Последний определитель с точностью до множителя 288 представляет собой выражение для квадрата объёма тетраэдра через длины его рёбер с помощью определителя Кэли-Менгера. Если тетраэдр уложен в плоскость, то он имеет нулевой объем и превращается в четырехугольник. Длины рёбер будут длинами сторон или диагоналей четырехугольника.
- Соотношения Бретшнайдера — соотношение между сторонами a, b, c, d и противоположными углами и диагоналями e, f простого (несамопересекающегося) четырёхугольника:
- ,
- ,
- .
Теоремы о средних линиях четырёхугольника[править]
Пусть G, H, I, J – середины сторон выпуклого четырёхугольника ABCD, а E, F – середины его диагоналей. Назовем три отрезка GH, IJ, EF соответственно первой, второй и третьей средними линиями четырёхугольника.
Точки E, K, F лежат на одной прямой, прямой Ньютона- Обобщенная теорема Ньютона. Все три средние линии четырёхугольника пересекаются в одной точке и делятся ею пополам. Указанная прямая называется прямой Ньютона.
- Теорема Вариньона (геометрия) [1]:
- Четырёхугольники GHIJ, EHFG, JEIG являются параллелограммами и называются параллелограммами Вариньона. Первый из них назовем большим параллелограммом Вариньона
- Центры всех трех параллелограммов Вариньона лежат на середине отрезка, соединяющего середины сторон исходного четырёхугольника (в этой же точке пересекаются отрезки, соединяющие середины противоположных сторон — диагонали вариньоновского параллелограмма).
- Периметр большого параллелограмма Вариньона равен сумме диагоналей исходного четырёхугольника.
- Площадь большого параллелограмма Вариньона
- .
- Площадь исходного четырёхугольника равна произведению первой и второй средних линий четырёхугольника на синус угла между ними, то есть
- .
- Сумма квадратов трех средних линий четырёхугольника равна четверти суммы квадратов всех его сторон и диагоналей:
- .
- Формула Эйлера: учетверённый квадрат расстояния между серединами диагоналей равен сумме квадратов сторон четырёхугольника минус сумма квадратов его диагоналей.
- Математически для рисунка слева с серым четырёхугольником ABCD формула Эйлера записывается в виде:
- .
- Четыре отрезка, каждый из которых соединяет вершину четырёхугольника с центроидом треугольника, образованного оставшимися тремя вершинами, пересекаются в центроиде четырёхугольника и делятся им в отношении 3:1, считая от вершин.
- См. также свойства центроида четырёхугольника.
Окружности девяти точек треугольников внутри четырехугольника[править]
В произвольном выпуклом четырехугольнике окружности девяти точек треугольников , на которые его разбивают две диагонали, пересекаются в одной точке [2].
Частные случаи четырехугольников[править]
Четырехугольники, вписанные в окружность[править]
- Говорят, что если около четырёхугольника можно описать окружность, то четырёхугольник вписан в эту окружность, и наоборот.
- Около четырёхугольника можно описать окружность тогда и только тогда, когда сумма противоположных углов равна 180°, то есть:
- .
- Две теоремы Птолемея. Для простого (несамопересекающегося) четырехугольника, вписанного в окружность, имеющего длины пар противоположных сторон: a и c, b и d, а также длины диагоналей e и f, справедливы:
1) Первая теорема Птолемея:
- ;
2) Вторая теорема Птолемея
- Если выпуклый четырёхугольник вписан в некоторую окружность, то в ту же самую окружность вписаны и пара треугольников, на которые разбивает четырехугольник любая из его диагоналей (связь с окружностями треугольника).
- Из последнего утверждения следует: если три из четырех медиатрис (или срединных перпендикуляров), проведенных к сторонам выпуклого четырёхугольника, пресекаются в одной точке, то в той же точке пресекается и медиатриса его четвертой стороны. Более того, такой четырехугольник вписан в некоторую окружность, центр которой находится в точке пресечения указанных медиатрис[3].
- Выпуклый четырёхугольник (см. рис. справа), образованный четырьмя данными прямыми Микеля, вписан в окружность тогда и только тогда, когда точка Микеля M четырёхугольника лежит на прямой, соединяющей две из шести точек пересечения прямых (те, которые не являются вершинами четырёхугольника). То есть, когда M лежит на EF.
- Прямая, антипараллельная стороне треугольника и пересекающая его, отсекает от него четырёхугольник, около которого всегда можно описать окружность.
- Площадь вписанного в окружность четырёхугольника:
- где p — полупериметр четырёхугольника.
- Последняя формула следует из общей формулы (1) в рамке в параграфе «Площадь», если в ней учесть, что
- Последняя формула есть обобщение формулы Герона на случай четырёхугольника.
- Формула Брахмагупты для площади вписанного в окружность четырёхугольника может быть записана через определитель[5]:
- Из последней формулы при d=0 автоматически получается формула Дроздова В. [6][7] для формулы Герона:
- Радиус окружности, описанной около четырёхугольника:
- Теорема[8]. Если во вписанном в окружность четырехугольнике провести диагональ, а в полученные два треугольника вписать две окружности, затем аналогично поступить, проведя вторую диагональ, тогда центры четырех образовавшихся окружностей являются вершинами прямоугольника.
- Теорема[9]. Пусть – вписанный четырёхугольник, – основание перпендикуляра, опущенного из вершины на диагональ ; аналогично определяются точки . Тогда точки лежат на одной окружности.
- Частными четырёхугольниками, вписанными в окружность, являются: прямоугольник, квадрат, равнобедренная или равнобочная трапеция, антипараллелограмм.
Четырехугольники, вписанные в окружность с перпендикулярными диагоналями (вписанные ортодиагональные четырехугольники)[править]
Если вписанный четырёхугольник имеет перпендикулярные диагонали, пересекающиеся в точке , то две пары его антимедиатрис проходят через точку .
Замечание. В этой теореме под антимедиатрисой[10] понимают отрезок четырехугольника на рисунке справа (по аналогии с серединным перпендикуляром (медиатрисой) к стороне треугольника). Он перпендикулярен одной стороне и одновременно проходит через середину противоположной ей стороны четырехугольника.
- Известна теорема: Если в четырехугольнике перпендикулярны диагонали, то на одной окружности (окружность восьми точек четырехугольника) лежат восемь точек: середины сторон и проекции середин сторон на противоположные стороны [11]. Из этой теоремы и теоремы Брахмагупты следует, что концы двух пар антимедиатрис (восемь точек) вписанного ортодиагонального четырехугольника лежат на одной окружности (окружность восьми точек четырехугольника).
- Частным вписанным ортодиагональным четырёхугольником является квадрат.
Четырехугольники, описанные около окружности[править]
- Говорят, что если в четырёхугольник можно вписать окружность, то четырёхугольник описан около этой окружности, и наоборот.
- Выпуклый четырёхугольник является описанным около окружности тогда и только тогда, когда суммы длин противоположных сторон равны, то есть: .
- Точки касания вписанной окружности с четырехугольником отсекают равные отрезки от углов четырёхугольника.
- Площадь описанного четырехугольника
- Условие означает, что .
Вводя понятие полупериметра p, имеем . Следовательно, также имеем . Далее можно заметить: Следовательно, Тогда по формуле (1) в рамке в параграфе «Площадь» имеем
- Поскольку четырёхугольник описан, то его площадь также равна половине периметра p, умноженной на радиус r вписанной окружности: .
- Если выпуклый четырёхугольник — не трапеция и не параллелограмм и он описан около некоторой окружности, то около этой же самой окружности описаны и пара треугольников, которые получаются при продолжении двух его пар противоположных сторон до их пересечения (связь с окружностями треугольника).
- Из последнего утверждения следует: если три из четырех биссектрис (или биссекторов), проведенных для внутренних углов выпуклого четырёхугольника, пресекаются в одной точке, то в той же точке пресекается и биссектриса его четвертого внутреннего угла. Более того такой четырехугольник описан около некоторой окружности, центр которой находится в точке пресечения указанных биссектрис[12].
- Если четырёхугольник является описанным около окружности, то центр его вписанной окружности лежит на прямой Ньютона. Более точное утверждение ниже.
- Во всяком описанном четырёхугольнике две середины диагоналей и центр вписанной окружности лежат на одной прямой (теорема Ньютона). На ней же лежит середина отрезка с концами в точках пересечения продолжений противоположных сторон четырёхугольника (если они не параллельны). Эта прямая называется прямой Гаусса. На рисунке (вторая группа рисунков сверху) она зеленая, диагонали красные, отрезок с концами в точках пересечения продолжений противоположных сторон четырёхугольника тоже красный.
- Центр описанной около четырёхугольника окружности — точка пересечения высот треугольника с вершинами в точке пересечения диагоналей и точках пересечения противоположных сторон (теорема Брокара).
- Частными четырёхугольниками, описанными около окружности, являются: ромб, квадрат, дельтоид.
Вписано-описанные четырехугольники[править]
Вписано-описанные четырехугольники — четырехугольники, которые могут быть одновременно описаны около некоторой окружности, а также вписаны в некоторую окружность.
Свойства:[править]
- Любое одно из двух указанных ниже условий по отдельности является необходимым, но не достаточным условием для того, чтобы данный выпуклый четырехугольник был вписанно-описанным для некоторых окружностей:
и .
- Выполнение двух последних условий одновременно для некоторого выпуклого четырехугольника является необходимым и достаточным для того, чтобы данный четырехугольник был вписанно-описанным.
- Площадь вписанно-описанного четырехугольника:
- Для радиусов R и r соответственно описанной и вписанной окружностей данного четырёхугольника и расстояния d между центрами этих окружностей выполняется соотношение, представляющее четырехугольниковый аналог теоремы Эйлера (аналогичная формула Эйлера есть для треугольника):
или
- .
- Частным вписанно-описанным четырехугольником является квадрат.
Четырехугольники с перпендикулярными сторонами[править]
- Две противоположные стороны четырёхугольника перпендикулярны тогда и только тогда, когда сумма квадратов двух других противоположных сторон равна сумме квадратов диагоналей.
- Если у выпуклого четырёхугольника перпендикулярны две пары смежных сторон (то есть два противоположных угла прямые), то этот четырёхугольник может быть вписан в некоторую окружность. Более того, диаметром этой окружности будет служить диагональ, на которую опираются одними концами указанные две пары смежных сторон.
- Частными четырёхугольниками с перпендикулярными сторонами являются: прямоугольник и квадрат.
Четырехугольники с перпендикулярными диагоналями[править]
- Четырехугольники с перпендикулярными диагоналями называются ортодиагональными четырёхугольниками.
- Диагонали четырёхугольника перпендикулярны тогда и только тогда, когда суммы квадратов противоположных сторон равны.
- Площадь ортодиагонального четырёхугольника равна половине произведения его диагоналей: .
- Средние линии четырёхугольника равны тогда и только тогда, когда равны суммы квадратов его противоположных сторон.
- Антимедиатрисой четырехугольника называются отрезок прямой, выходящий из середины одной его стороны и перпендикулярный противоположной ей стороне.
- Теорема Брахмагупты. Если у четырехугольника перпендикулярны диагонали и он может быть вписан в некоторую окружность, то четыре его антимедиатрисы пересекаются в одной точке. Более того, этой точкой пересечения антимедиатрис является точка пересечения его диагоналей.
- Если у четырехугольника перпендикулярны диагонали и он может быть вписан в некоторую окружность, то учетверенный квадрат её радиуса R равен сумме квадратов любой пары противоположных его сторон:
- Если у четырехугольника перпендикулярны диагонали и он может быть описан около некоторой окружности, то у него равны произведения двух пар противоположных сторон:
- Параллелограмм Вариньона с вершинами в серединах сторон ортодиагональныого четырёхугольника является прямоугольником.
- Если в четырехугольнике перпендикулярны диагонали, то на одной окружности (окружность восьми точек четырехугольника) лежат восемь точек: середины сторон и проекции середин сторон на противоположные стороны [13].
- Частными ортодиагональными четырёхугольниками являются: ромб, квадрат, дельтоид.
Внеописанный четырёхугольник[править]
- Внеописанный четырёхугольник — это выпуклый четырёхугольник, продолжения всех четырёх сторон которого являются касательными к окружности (вне четырёхугольника)[14]. Окружность называется вневписанной. Центр вневписанной окружности лежит на пересечении шести биссектрис.
- Замечание. Вписанную, описанную, а также вневписанную окружности можно провести не у всякого четырёхугольника. Если противоположные стороны выпуклого четырёхугольника ABCD пересекаются в точках E и F, то условием его внеописанности является любое из двух условий ниже:
- Площадь произвольного не самопересекающегося выпуклого четырёхугольника с диагоналями , и углом между ними (или их продолжениями), равна:
- Площадь произвольного выпуклого четырёхугольника равна произведению первой и второй средних линий четырёхугольника на синус угла между ними, то есть
- .
Замечание. Первая и вторая средние линии четырёхугольника — отрезки, соединяющие середины его противоположных сторон
- Площадь произвольного выпуклого четырёхугольника равна[4]:
- , где , — длины диагоналей, a, b, c, d — длины сторон.
- Площадь произвольного выпуклого четырёхугольника также равна
(1) |
где p — полупериметр, а есть полусумма противоположных углов четырёхугольника (Какую именно пару противоположных углов взять роли не играет, так как если полусумма одной пары противоположных углов равна , то полусумма двух других углов будет и ). Из этой формулы для вписанных 4-угольников следует формула Брахмагупты.
где p — полупериметр, e и f -диагонали четырёхугольника.
История[править]
В древности египтяне и некоторые другие народы использовали для определения площади четырёхугольника неверную формулу — произведение полусумм его противоположных сторон a, b, c, d[15]:
- .
Для непрямоугольных четырёхугольников эта формула даёт завышенное значение площади. Можно предположить, что она использовалась только для определения площади почти прямоугольных участков земли. При неточном измерении сторон прямоугольника эта формула позволяет повысить точность результата за счет усреднения исходных измерений.
- ↑ 1,01,1 Четырёхугольники.
- ↑ Математика в задачах. Сборник материалов выездных школ команды Москвы на Всероссийскую математическую олимпиаду/ Под редакцией А. А. Заславского, Д. А. Пермякова, А. Б. Скопенкова, М. Б. Скопенкова и А. В. Шаповалова. c. 118, задача 9
- ↑ Стариков В.Н. Заметки по геометрии// Научный поиск: гуманитарные и социально-экономические науки: сборник научных трудов. Выпуск 1/ Гл. ред. Романова И .В. Чебоксары: ЦДИП «INet», 2014. С. 38, правая колонка, пункт 7
- ↑ 4,04,1 Понарин, с. 74
- ↑ Стариков В.Н. Заметки по геометрии// Научный поиск: гуманитарные и социально-экономические науки: сборник научных трудов. Выпуск 1/ Гл. ред. Романова И.В. Чебоксары: ЦДИП «INet», 2014. С. 37-39
- ↑ Дроздов В. Геронов определитель. Занимательная страница // Математика в школе, 1995, № 5, обложка
- ↑ Мухлаев А. Возможно, Герон что-то утаил/ 38–я открытая областная научная конференция учащихся. Омск. 2006. C. 8/ http://gigabaza.ru/doc/66950.html
- ↑ Вокруг задачи Архимеда. Упр. 8, рис. 13, c. 6 / http://www.geometry.ru/articles/aymefeuerbach.pdf
- ↑ Вокруг задачи Архимеда. Упр. 7, рис. 11, следствие, c. 5 / http://www.geometry.ru/articles/aymefeuerbach.pdf
- ↑ Стариков В.Н. Заметки по геометрии// Научный поиск: гуманитарные и социально-экономические науки: сборник научных трудов. Выпуск 1/ Гл. ред. Романова И .В. Чебоксары: ЦДИП «INet», 2014. С. 37-39
- ↑ Математика в задачах. Сборник материалов выездных школ команды Москвы на Всероссийскую математическую олимпиаду/ Под редакцией А. А. Заславского, Д. А. Пермякова, А. Б. Скопенкова, М. Б. Скопенкова и А. В. Шаповалова. c. 118, задача 11
- ↑ Стариков В.Н. Заметки по геометрии// Научный поиск: гуманитарные и социально-экономические нау-ки: сборник научных трудов. Выпуск 1/ Гл ред. Романова И .В Чебоксары: ЦДИП «INet», 2014. С. 39, левая колонка, последний абзац
- ↑ Математика в задачах. Сборник материалов выездных школ команды Москвы на Всероссийскую математическую олимпиаду/ Под редакцией А. А. Заславского, Д. А. Пермякова, А. Б. Скопенкова, М. Б. Скопенкова и А. В. Шаповалова. c. 118, задача 11
- ↑ Mirko, Zoran, Vladimir, 2007, с. 33—52
- ↑ Г. Г. Цейтен История математики в древности и в средние века, ГТТИ, М-Л, 1932.
www.wikiznanie.ru
