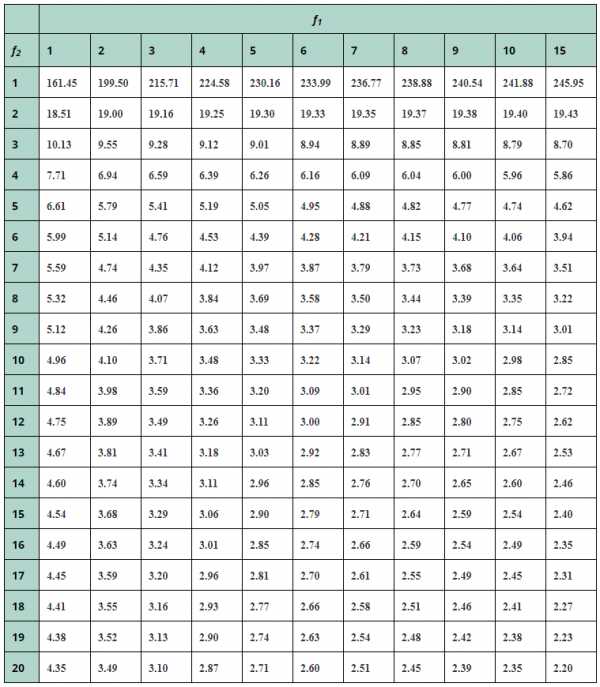
Таблица значений критерия Фишера (F-критерия) |
При α = 0.05
f1 — число степеней свободы большей дисперсии
f2 — число степеней свободы меньшей дисперсии:
| f1 | |||||||||||
| f2 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 15 |
| 1 | 161.45 | 199.50 | 215.71 | 224.58 | 230.16 | 233.99 | 236.77 | 238.88 | 240.54 | 241.88 | 245.95 |
| 2 | 18.51 | 19.00 | 19.16 | 19.25 | 19.30 | 19.33 | 19.35 | 19.37 | 19.38 | 19.40 | 19.43 |
| 3 | 10.13 | 9.55 | 9.28 | 9.12 | 9.01 | 8.94 | 8.89 | 8.85 | 8.81 | 8.79 | 8.70 |
| 4 | 7.71 | 6.94 | 6.59 | 6.39 | 6.26 | 6.16 | 6.09 | 6.04 | 6.00 | 5.96 | 5.86 |
| 5 | 6.61 | 5.79 | 5.41 | 5.19 | 5.05 | 4.95 | 4.88 | 4.82 | 4.77 | 4.74 | 4.62 |
| 5.99 | 5.14 | 4.76 | 4.53 | 4.39 | 4.28 | 4.21 | 4.15 | 4.10 | 4.06 | 3.94 | |
| 7 | 5.59 | 4.74 | 4.35 | 4.12 | 3.97 | 3.87 | 3.79 | 3.73 | 3.68 | 3.64 | 3.51 |
| 8 | 5.32 | 4.46 | 4.07 | 3.84 | 3.69 | 3.58 | 3.50 | 3.44 | 3.39 | 3.35 | 3.22 |
| 9 | 5.12 | 4.26 | 3.86 | 3.63 | 3.48 | 3.37 | 3.29 | 3.23 | 3.18 | 3.14 | 3.01 |
| 10 | 4.96 | 4.10 | 3.71 | 3.48 | 3.33 | 3.22 | 3.14 | 3.07 | 3.02 | 2.98 | 2.85 |
| 11 | 4.84 | 3.98 | 3.59 | 3.36 | 3.20 | 3.09 | 3.01 | 2.95 | 2.90 | 2.85 | 2.72 |
| 12 | 4.75 | 3.89 | 3.49 | 3.26 | 3.11 | 3.00 | 2.91 | 2.85 | 2.80 | 2.75 | 2.62 |
| 13 | 4.67 | 3.81 | 3.41 | 3.18 | 3.03 | 2.92 | 2.83 | 2.77 | 2.71 | 2.67 | 2.53 |
| 14 | 4.60 | 3.74 | 3.34 | 3.11 | 2.96 | 2.85 | 2.76 | 2.70 | 2.65 | 2.60 | 2.46 |
| 15 | 4.54 | 3.68 | 3.29 | 3.06 | 2.90 | 2.79 | 2.71 | 2.64 | 2.59 | 2.54 | 2.40 |
| 16 | 4.49 | 3.63 | 3.24 | 3.01 | 2.85 | 2.74 | 2.66 | 2.59 | 2.54 | 2.49 | 2.35 |
| 17 | 4.45 | 3.59 | 3.20 | 2.96 | 2.81 | 2.70 | 2.61 | 2.55 | 2.49 | 2.45 | 2.31 |
| 18 | 4.41 | 3.55 | 3.16 | 2.93 | 2.77 | 2.66 | 2.58 | 2.51 | 2.46 | 2.41 | 2.27 |
| 19 | 4.38 | 3.52 | 3.13 | 2.90 | 2.74 | 2.63 | 2.54 | 2.48 | 2.42 | 2.38 | 2.23 |
| 20 | 4.35 | 3.49 | 3.10 | 2.87 | 2.71 | 2.60 | 2.51 | 2.45 | 2.39 | 2.35 | 2.20 |
www.matematicus.ru
Распределение Фишера F-распределение для alpha=0.05
df1— число степеней свободы большей дисперсии
df2—число степеней свободы меньшей дисперсии
Уровень значимости a =0.05
|
df2/df1 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
12 |
15 |
20 |
24 |
30 |
40 |
60 |
120 |
INF |
|
1 |
161.4476 |
199.5000 |
215.7073 |
224.5832 |
230.1619 |
233.9860 |
236.7684 |
238.8827 |
240.5433 |
241.8817 |
243.9060 |
245.9499 |
248.0131 |
249.0518 |
250.0951 |
251.1432 |
252.1957 |
253.2529 |
254.3144 |
|
2 |
18.5128 |
19.0000 |
19.1643 |
19.2468 |
19.2964 |
19.3295 |
19.3532 |
19.3710 |
19.3848 |
19.3959 |
19.4125 |
19.4291 |
19.4458 |
19.4541 |
19.4624 |
19.4707 |
19.4791 |
19.4874 |
19.4957 |
|
3 |
10.1280 |
9.5521 |
9.2766 |
9.1172 |
9.0135 |
8.9406 |
8.8867 |
8.8452 |
8.8123 |
8.7855 |
8.7446 |
8.7029 |
8.6602 |
8.6385 |
8.6166 |
8.5944 |
8.5720 |
8.5494 |
8.5264 |
|
4 |
7.7086 |
6.9443 |
6.5914 |
6.3882 |
6.2561 |
6.1631 |
6.0942 |
6.0410 |
5.9988 |
5.9644 |
5.9117 |
5.8578 |
5.8025 |
5.7744 |
5.7459 |
5.7170 |
5.6877 |
5.6581 |
5.6281 |
|
5 |
6.6079 |
5.7861 |
5.4095 |
5.1922 |
5.0503 |
4.9503 |
4.8759 |
4.8183 |
4.7725 |
4.7351 |
4.6777 |
4.6188 |
4.5581 |
4.5272 |
4.4957 |
4.4638 |
4.4314 |
4.3985 |
4.3650 |
|
6 |
5.9874 |
5.1433 |
4.7571 |
4.5337 |
4.3874 |
4.2839 |
4.2067 |
4.1468 |
4.0990 |
4.0600 |
3.9999 |
3.9381 |
3.8742 |
3.8415 |
3.8082 |
3.7743 |
3.7398 |
3.7047 |
3.6689 |
|
7 |
5.5914 |
4.7374 |
4.3468 |
4.1203 |
3.9715 |
3.8660 |
3.7870 |
3.7257 |
3.6767 |
3.6365 |
3.5747 |
3.5107 |
3.4445 |
3.4105 |
3.3758 |
3.3404 |
3.3043 |
3.2674 |
3.2298 |
|
8 |
5.3177 |
4.4590 |
4.0662 |
3.8379 |
3.6875 |
3.5806 |
3.5005 |
3.4381 |
3.3881 |
3.3472 |
3.2839 |
3.2184 |
3.1503 |
3.1152 |
3.0794 |
3.0428 |
3.0053 |
2.9669 |
2.9276 |
|
9 |
5.1174 |
4.2565 |
3.8625 |
3.6331 |
3.4817 |
3.3738 |
3.2927 |
3.2296 |
3.1789 |
3.1373 |
3.0729 |
3.0061 |
2.9365 |
2.9005 |
2.8637 |
2.8259 |
2.7872 |
2.7475 |
2.7067 |
|
10 |
4.9646 |
4.1028 |
3.7083 |
3.4780 |
3.3258 |
3.2172 |
3.1355 |
3.0717 |
3.0204 |
2.9782 |
2.9130 |
2.8450 |
2.7740 |
2.7372 |
2.6996 |
2.6609 |
2.6211 |
2.5801 |
2.5379 |
|
11 |
4.8443 |
3.9823 |
3.5874 |
3.3567 |
3.2039 |
3.0946 |
3.0123 |
2.9480 |
2.8962 |
2.8536 |
2.7876 |
2.7186 |
2.6464 |
2.6090 |
2.5705 |
2.5309 |
2.4901 |
2.4480 |
2.4045 |
|
12 |
4.7472 |
3.8853 |
3.4903 |
3.2592 |
3.1059 |
2.9961 |
2.9134 |
2.8486 |
2.7964 |
2.7534 |
2.6866 |
2.6169 |
2.5436 |
2.5055 |
2.4663 |
2.4259 |
2.3842 |
2.3410 |
2.2962 |
|
13 |
4.6672 |
3.8056 |
3.4105 |
3.1791 |
3.0254 |
2.9153 |
2.8321 |
2.7669 |
2.7144 |
2.6710 |
2.6037 |
2.5331 |
2.4589 |
2.4202 |
2.3803 |
2.3392 |
2.2966 |
2.2524 |
2.2064 |
|
14 |
4.6001 |
3.7389 |
3.3439 |
3.1122 |
2.9582 |
2.8477 |
2.7642 |
2.6987 |
2.6458 |
2.6022 |
2.5342 |
2.4630 |
2.3879 |
2.3487 |
2.3082 |
2.2664 |
2.2229 |
2.1778 |
2.1307 |
|
15 |
4.5431 |
3.6823 |
3.2874 |
3.0556 |
2.9013 |
2.7905 |
2.7066 |
2.6408 |
2.5876 |
2.5437 |
2.4753 |
2.4034 |
2.3275 |
2.2878 |
2.2468 |
2.2043 |
2.1601 |
2.1141 |
2.0658 |
|
16 |
4.4940 |
3.6337 |
3.2389 |
3.0069 |
2.8524 |
2.7413 |
2.6572 |
2.5911 |
2.5377 |
2.4935 |
2.4247 |
2.3522 |
2.2756 |
2.2354 |
2.1938 |
2.1507 |
2.1058 |
2.0589 |
2.0096 |
|
17 |
4.4513 |
3.5915 |
3.1968 |
2.9647 |
2.8100 |
2.6987 |
2.6143 |
2.5480 |
2.4943 |
2.4499 |
2.3807 |
2.3077 |
2.2304 |
2.1898 |
2.1477 |
2.1040 |
2.0584 |
2.0107 |
1.9604 |
|
18 |
4.4139 |
3.5546 |
3.1599 |
2.9277 |
2.7729 |
2.6613 |
2.5767 |
2.5102 |
2.4563 |
2.4117 |
2.3421 |
2.2686 |
2.1906 |
2.1497 |
2.1071 |
2.0629 |
2.0166 |
1.9681 |
1.9168 |
|
19 |
4.3807 |
3.5219 |
3.1274 |
2.8951 |
2.7401 |
2.6283 |
2.5435 |
2.4768 |
2.4227 |
2.3779 |
2.3080 |
2.2341 |
2.1555 |
2.1141 |
2.0712 |
2.0264 |
1.9795 |
1.9302 |
1.8780 |
|
20 |
4.3512 |
3.4928 |
3.0984 |
2.8661 |
2.7109 |
2.5990 |
2.5140 |
2.4471 |
2.3928 |
2.3479 |
2.2776 |
2.2033 |
2.1242 |
2.0825 |
2.0391 |
1.9938 |
1.9464 |
1.8963 |
1.8432 |
|
21 |
4.3248 |
3.4668 |
3.0725 |
2.8401 |
2.6848 |
2.5727 |
2.4876 |
2.4205 |
2.3660 |
2.3210 |
2.2504 |
2.1757 |
2.0960 |
2.0540 |
2.0102 |
1.9645 |
1.9165 |
1.8657 |
1.8117 |
|
22 |
4.3009 |
3.4434 |
3.0491 |
2.8167 |
2.6613 |
2.5491 |
2.4638 |
2.3965 |
2.3419 |
2.2967 |
2.2258 |
2.1508 |
2.0707 |
2.0283 |
1.9842 |
1.9380 |
1.8894 |
1.8380 |
1.7831 |
|
23 |
4.2793 |
3.4221 |
3.0280 |
2.7955 |
2.6400 |
2.5277 |
2.4422 |
2.3748 |
2.3201 |
2.2747 |
2.2036 |
2.1282 |
2.0476 |
2.0050 |
1.9605 |
1.9139 |
1.8648 |
1.8128 |
1.7570 |
|
24 |
4.2597 |
3.4028 |
3.0088 |
2.7763 |
2.6207 |
2.5082 |
2.4226 |
2.3551 |
2.3002 |
2.2547 |
2.1834 |
2.1077 |
2.0267 |
1.9838 |
1.9390 |
1.8920 |
1.8424 |
1.7896 |
1.7330 |
|
25 |
4.2417 |
3.3852 |
2.9912 |
2.7587 |
2.6030 |
2.4904 |
2.4047 |
2.3371 |
2.2821 |
2.2365 |
2.1649 |
2.0889 |
2.0075 |
1.9643 |
1.9192 |
1.8718 |
1.8217 |
1.7684 |
1.7110 |
|
26 |
4.2252 |
3.3690 |
2.9752 |
2.7426 |
2.5868 |
2.4741 |
2.3883 |
2.3205 |
2.2655 |
2.2197 |
2.1479 |
2.0716 |
1.9898 |
1.9464 |
1.9010 |
1.8533 |
1.8027 |
1.7488 |
1.6906 |
|
27 |
4.2100 |
3.3541 |
2.9604 |
2.7278 |
2.5719 |
2.4591 |
2.3732 |
2.3053 |
2.2501 |
2.2043 |
2.1323 |
2.0558 |
1.9736 |
1.9299 |
1.8842 |
1.8361 |
1.7851 |
1.7306 |
1.6717 |
|
28 |
4.1960 |
3.3404 |
2.9467 |
2.7141 |
2.5581 |
2.4453 |
2.3593 |
2.2913 |
2.2360 |
2.1900 |
2.1179 |
2.0411 |
1.9586 |
1.9147 |
1.8687 |
1.8203 |
1.7689 |
1.7138 |
1.6541 |
|
29 |
4.1830 |
3.3277 |
2.9340 |
2.7014 |
2.5454 |
2.4324 |
2.3463 |
2.2783 |
2.2229 |
2.1768 |
2.1045 |
2.0275 |
1.9446 |
1.9005 |
1.8543 |
1.8055 |
1.7537 |
1.6981 |
1.6376 |
|
30 |
4.1709 |
3.3158 |
2.9223 |
2.6896 |
2.5336 |
2.4205 |
2.3343 |
2.2662 |
2.2107 |
2.1646 |
2.0921 |
2.0148 |
1.9317 |
1.8874 |
1.8409 |
1.7918 |
1.7396 |
1.6835 |
1.6223 |
|
40 |
4.0847 |
3.2317 |
2.8387 |
2.6060 |
2.4495 |
2.3359 |
2.2490 |
2.1802 |
2.1240 |
2.0772 |
2.0035 |
1.9245 |
1.8389 |
1.7929 |
1.7444 |
1.6928 |
1.6373 |
1.5766 |
1.5089 |
|
60 |
4.0012 |
3.1504 |
2.7581 |
2.5252 |
2.3683 |
2.2541 |
2.1665 |
2.0970 |
2.0401 |
1.9926 |
1.9174 |
1.8364 |
1.7480 |
1.7001 |
1.6491 |
1.5943 |
1.5343 |
1.4673 |
1.3893 |
|
120 |
3.9201 |
3.0718 |
2.6802 |
2.4472 |
2.2899 |
2.1750 |
2.0868 |
2.0164 |
1.9588 |
1.9105 |
1.8337 |
1.7505 |
1.6587 |
1.6084 |
1.5543 |
1.4952 |
1.4290 |
1.3519 |
1.2539 |
|
inf |
3.8415 |
2.9957 |
2.6049 |
2.3719 |
2.2141 |
2.0986 |
2.0096 |
1.9384 |
1.8799 |
1.8307 |
1.7522 |
1.6664 |
1.5705 |
1.5173 |
1.4591 |
1.3940 |
1.3180 |
1.2214 |
1.0000 |
Вернуться Статистические таблицы
helpstat.ru
Таблица критических точек F-распределения Фишера-Снедекора
F-критерий, используется для проверки гипотезы равенства дисперсий двух совокупностей, в дисперсионном анализе, регрессионном анализе, многомерном статистическом анализе. Ниже представлены таблицы критических точек F- распределения Фишера-Снедекора для двух уровней значимости α=0,01 и α=0,05.
– число степеней свободы большей дисперсии
– число степеней свободы меньшей дисперсии
| Уровень значимости α = 0,01 |
| k2\k1 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 1 | 4052 | 4999 | 5403 | 5625 | 5764 | 5889 | 5928 | 5981 | 6022 | 6056 | 6082 | 6106 |
| 2 | 98,49 | 99,01 | 90,17 | 99,25 | 99,33 | 99,3 | 99,34 | 99,36 | 99,36 | 99,4 | 99,41 | 99,42 |
| 3 | 34,12 | 30,81 | 29,46 | 28,71 | 28,24 | 27,91 | 27,67 | 27,49 | 27,34 | 27,23 | 27,13 | 27,05 |
| 4 | 21,2 | 18 | 16,69 | 15,98 | 15,52 | 15,21 | 14,98 | 14,8 | 14,66 | 14,54 | 14,45 | 14,37 |
| 5 | 16,26 | 13,27 | 12,06 | 11,39 | 10,97 | 10,67 | 10,45 | 10,27 | 10,15 | 10,05 | 9,96 | 9,89 |
| 6 | 13,74 | 10,92 | 9,78 | 9,15 | 8,75 | 8,47 | 8,26 | 8,1 | 7,98 | 7,87 | 7,79 | 7,72 |
| 7 | 12,25 | 9,55 | 8,45 | 7,85 | 7,46 | 7,19 | 7 | 6,84 | 6,71 | 6,62 | 6,54 | 6,47 |
| 8 | 11,26 | 8,65 | 7,59 | 7,01 | 6,63 | 6,37 | 6,19 | 6,03 | 5,91 | 5,82 | 5,74 | 5,67 |
| 9 | 10,56 | 8,02 | 6,99 | 6,42 | 6,06 | 5,8 | 5,62 | 5,47 | 5,35 | 5,26 | 5,18 | 5,11 |
| 10 | 10,04 | 7,56 | 6,55 | 5,99 | 5,64 | 5,39 | 5,21 | 5,06 | 4,95 | 4,85 | 4,78 | 4,71 |
| 11 | 9,86 | 7,2 | 6,22 | 5,67 | 5,32 | 5,07 | 4,88 | 4,74 | 4,63 | 4,54 | 4,46 | 4,4 |
| 12 | 9,33 | 6,93 | 5,95 | 5,41 | 5,06 | 4,82 | 4,65 | 4,5 | 4,39 | 4,3 | 4,22 | 4,16 |
| 13 | 9,07 | 6,7 | 5,74 | 5,2 | 4,86 | 4,62 | 4,44 | 4,3 | 4,19 | 4,1 | 4,02 | 3,96 |
| 14 | 8,86 | 6,51 | 5,56 | 5,03 | 4,69 | 4,46 | 4,28 | 4,14 | 4,03 | 3,94 | 3,86 | 3,8 |
| 15 | 8,68 | 6,36 | 5,42 | 4,89 | 4,56 | 4,32 | 4,14 | 4 | 3,89 | 3,8 | 3,73 | 3,67 |
| 16 | 8,53 | 6,23 | 5,29 | 4,77 | 4,44 | 4,2 | 4,03 | 3,89 | 3,78 | 3,69 | 3,61 | 3,55 |
| 17 | 8,4 | 6,11 | 5,18 | 4,67 | 4,34 | 4,1 | 3,93 | 3,79 | 3,68 | 3,59 | 3,52 | 3,45 |
| Уровень значимости α = 0,05 |
| k2\k1 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 1 | 161 | 200 | 216 | 225 | 230 | 234 | 237 | 239 | 241 | 242 | 243 | 244 |
| 2 | 18,51 | 19 | 19,16 | 19,25 | 19,3 | 19,33 | 19,36 | 19,37 | 19,38 | 19,39 | 19,4 | 19,41 |
| 3 | 10,13 | 9,55 | 9,28 | 9,12 | 9,01 | 8,94 | 8,88 | 8,84 | 8,81 | 8,78 | 8,76 | 8,74 |
| 4 | 7,71 | 6,94 | 6,59 | 6,39 | 6,26 | 6,16 | 6,09 | 6,04 | 6 | 5,96 | 5,93 | 5,91 |
| 5 | 6,61 | 5,79 | 5,41 | 5,19 | 5,05 | 4,95 | 4,88 | 4,82 | 4,78 | 4,74 | 4,7 | 4,68 |
| 6 | 5,99 | 5,14 | 4,76 | 4,53 | 4,39 | 4,28 | 4,21 | 4,15 | 4,1 | 4,06 | 4,03 | 4 |
| 7 | 5,59 | 4,74 | 4,35 | 4,12 | 3,97 | 3,87 | 3,79 | 3,73 | 3,68 | 3,63 | 3,6 | 3,57 |
| 8 | 5,32 | 4,46 | 4,07 | 3,84 | 3,69 | 3,58 | 3,5 | 3,44 | 3,39 | 3,34 | 3,31 | 3,28 |
| 9 | 5,12 | 4,26 | 3,86 | 3,63 | 3,48 | 3,37 | 3,29 | 3,23 | 3,18 | 3,13 | 3,1 | 3,07 |
| 10 | 4,96 | 4,1 | 3,71 | 3,48 | 3,33 | 3,22 | 3,14 | 3,07 | 3,02 | 2,97 | 2,94 | 2,91 |
| 11 | 4,84 | 3,98 | 3,59 | 3,36 | 3,2 | 3,09 | 3,01 | 2,95 | 2,9 | 2,86 | 2,82 | 2,79 |
| 12 | 4,75 | 3,88 | 3,49 | 3,26 | 3,11 | 3 | 2,92 | 2,85 | 2,8 | 2,76 | 2,72 | 2,69 |
| 13 | 4,67 | 3,8 | 3,41 | 3,18 | 3,02 | 2,92 | 2,84 | 2,77 | 2,72 | 2,67 | 2,63 | 2,6 |
| 14 | 4,6 | 3,74 | 3,34 | 3,11 | 2,96 | 2,85 | 2,77 | 2,7 | 2,65 | 2,6 | 2,56 | 2,53 |
| 15 | 4,54 | 3,68 | 3,29 | 3,06 | 2,9 | 2,79 | 2,7 | 2,64 | 2,59 | 2,55 | 2,51 | 2,48 |
| 16 | 4,49 | 3,63 | 3,24 | 3,01 | 2,85 | 2,74 | 2,66 | 2,59 | 2,54 | 2,49 | 2,45 | 2,42 |
| 17 | 4,45 | 3,59 | 3,2 | 2,96 | 2,81 | 2,7 | 2,62 | 2,55 | 2,5 | 2,45 | 2,41 | 2,38 |
100task.ru
|
matica.org.ua
Критерий Фишера — это… Что такое Критерий Фишера?
- Критерий Фишера
Критерий Фишера (F-критерий, φ*-критерий, критерий наименьшей значимой разности) — апостериорный статистический критерий, используемый для сравнения дисперсий двух вариационных рядов, то есть для определения значимых различий между групповыми средними в установке дисперсионного анализа.
Критерий Фишера широко применяется в задачах статистического оценивания, в частности в аналитической химии.
Пример таблицы критических значений F-критерия для уровня значимости 0.05[1]
f2\f1 1 2 3 4 5 6 7 8 9 10 12 1 161.45 199.50 215.71 224.58 230.16 233.99 236.77 238.88 240.54 241.88 245.95 2 18.51 19.00 19.16 19.25 19.30 19.33 19.35 19.37 19.38 19.40 19.43 3 10.13 9.55 9.28 9.12 9.01 8.94 8.89 8.85 8.81 8.79 8.70 4 7.71 6.94 6.59 6.39 6.26 6.16 6.09 6.04 6.00 5.96 5.86 5 6.61 5.79 5.41 5.19 5.05 4.95 4.88 4.82 4.77 4.74 4.62 6 5.99 5.14 4.76 4.53 4.39 4.28 4.21 4.15 4.10 4.06 3.94 7 5.59 4.74 4.35 4.12 3.97 3.87 3.79 3.73 3.68 3.64 3.51 8 5.32 4.46 4.07 3.84 3.69 3.58 3.50 3.44 3.39 3.35 3.22 9 5.12 4.26 3.86 3.63 3.48 3.37 3.29 3.23 3.18 3.14 3.01 10 4.96 4.10 3.71 3.48 3.33 3.22 3.14 3.07 3.02 2.98 2.85 11 4.84 3.98 3.59 3.36 3.20 3.09 3.01 2.95 2.90 2.85 2.72 12 4.75 3.89 3.49 3.26 3.11 3.00 2.91 2.85 2.80 2.75 2.62 13 4.67 3.81 3.41 3.18 3.03 2.92 2.83 2.77 2.71 2.67 2.53 14 4.60 3.74 3.34 3.11 2.96 2.85 2.76 2.70 2.65 2.60 2.46 15 4.54 3.68 3.29 3.06 2.90 2.79 2.71 2.64 2.59 2.54 2.40 16 4.49 3.63 3.24 3.01 2.85 2.74 2.66 2.59 2.54 2.49 2.35 17 4.45 3.59 3.20 2.96 2.81 2.70 2.61 2.55 2.49 2.45 2.31 18 4.41 3.55 3.16 2.93 2.77 2.66 2.58 2.51 2.46 2.41 2.27 19 4.38 3.52 3.13 2.90 2.74 2.63 2.54 2.48 2.42 2.38 2.23 20 4.35 3.49 3.10 2.87 2.71 2.60 2.51 2.45 2.39 2.35 2.20
См. также
Примечания
Внешние ссылки
Статистические показатели Описательная
статистикаСтатистический
вывод и
проверка
гипотезКорреляция Коэффициент корреляции Пирсона · Ранг корреляций (Коэффициент Спирмана для ранга корреляций, Коэффициент тау Кендалла для ранга корреляций) · Переменная смешивания Линейные модели Основная линейная модель · Обобщённая линейная модель · Анализ вариаций · Анализ ковариаций Регрессия Линейная · Нелинейная · Непараметрическая регрессия · Полупараметрическая регрессия · Логистическая регрессия Столбчатая диаграмма · Совмещённая диаграмма · Диаграмма управления · Лесная диаграмма · Гистограмма · Q-Q диаграмма · Диаграмма выполнения · Диаграмма разброса · Стебель-листья · Ящик с усами - Статистические критерии
Wikimedia Foundation. 2010.
- Киев (энциклопедический справочник)
- Кузьмицкий, Алексей Алексеевич
Смотреть что такое «Критерий Фишера» в других словарях:
критерий Фишера — Fišerio kriterijus statusas T sritis augalininkystė apibrėžtis Veiksnio arba veiksnių sąveikos įtakos bandymo rezultatams patikimumo rodiklis. atitikmenys: angl. Fisher’s test rus. критерий Фишера … Žemės ūkio augalų selekcijos ir sėklininkystės terminų žodynas
КРИТЕРИЙ ФИШЕРА — Показатель достоверности влияния изучаемых факторов на полученный результат. Определяется отношением факториальной вариансы к вариансе ошибок: где F показатель достоверности; || факториальная варианса; варианса ошибок. Уровень вероятности влияния … Термины и определения, используемые в селекции, генетике и воспроизводстве сельскохозяйственных животных
Критерий Фишера F-критерий — Критерий Фишера, F критерий * крытэрый Фішара, F крытэрый * Fisher’s criterion or F test критерий существенности индивидуального или совместного взаимодействия изучаемых факторов на конечный результат эксперимента. К. Ф. определяется отношением… … Генетика. Энциклопедический словарь
точный критерий Фишера — для таблицы сопряженности 22 используется при проверке гипотезы о независимости переменной строки и переменной столбца. В отличие от критерия хи квадрат, в котором уровень значимости рассчитывается на основе асимптотического распределения, в… … Словарь социологической статистики
F-критерий;критерий Фишера — Критерий, статистика которого подчиняется F распределению, если нулевая гипотеза верна. Примечание. Этот критерий применяется, например, для (см. дисперсионный анализ) : 1. проверки равенства дисперсий двух нормальных совокупностей на основе… … Словарь социологической статистики
Критерий φ* Фишера — Критерий Фишера (F критерий, φ* критерий, критерий наименьшей значимой разности) апостериорный статистический критерий, используемый для сравнения дисперсий двух вариационных рядов, то есть для определения значимых различий между групповыми… … Википедия
Критерий Краскела — Уоллиса предназначен для проверки равенства медиан нескольких выборок. Данный критерий является многомерным обобщением критерия Уилкоксона Манна Уитни. Критерий Краскела Уоллиса является ранговым, поэтому он инвариантен по отношению к любому… … Википедия
Критерий согласия Колмогорова — или Критерий согласия Колмогорова Смирнова статистический критерий, использующийся для определения того, подчиняются ли два эмпирических распределения одному закону, либо того, подчиняется ли полученное распределение предполагаемой модели.… … Википедия
Критерий Вальда — (максиминный критерий[1]) один из критериев принятия решений в условиях неопределённости. Критерий крайнего пессимизма. История Критерий Вальда был предложен Абрахамом Вальдом в 1955 году для выборок равного объема, а затем распространен на … Википедия
Критерий согласия Пирсона — Критерий Пирсона, или критерий χ² (Хи квадрат) наиболее часто употребляемый критерий для проверки гипотезы о законе распределения. Во многих практических задачах точный закон распределения неизвестен, то есть является гипотезой, которая… … Википедия
dic.academic.ru
Таблица значений критерия Фишера (F критерия)
Значения критерия Фишера (F-критерия) для уровня значимости p = 0.05
f1 — число степеней свободы большей дисперсии, f2 — число степеней свободы меньшей дисперсии
| f1 | |||||||||||
| f2 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 15 |
| 1 | 161.45 | 199.50 | 215.71 | 224.58 | 230.16 | 233.99 | 236.77 | 238.88 | 240.54 | 241.88 | 245.95 |
| 2 | 18.51 | 19.00 | 19.16 | 19.25 | 19.30 | 19.33 | 19.35 | 19.37 | 19.38 | 19.40 | 19.43 |
| 3 | 10.13 | 9.55 | 9.28 | 9.12 | 9.01 | 8.94 | 8.89 | 8.85 | 8.81 | 8.79 | 8.70 |
| 4 | 7.71 | 6.94 | 6.59 | 6.39 | 6.26 | 6.16 | 6.09 | 6.04 | 6.00 | 5.96 | 5.86 |
| 5 | 6.61 | 5.79 | 5.41 | 5.19 | 5.05 | 4.95 | 4.88 | 4.82 | 4.77 | 4.74 | 4.62 |
| 6 | 5.99 | 5.14 | 4.76 | 4.53 | 4.39 | 4.28 | 4.21 | 4.15 | 4.10 | 4.06 | 3.94 |
| 7 | 5.59 | 4.74 | 4.35 | 4.12 | 3.97 | 3.87 | 3.79 | 3.73 | 3.68 | 3.64 | 3.51 |
| 8 | 5.32 | 4.46 | 4.07 | 3.84 | 3.69 | 3.58 | 3.50 | 3.44 | 3.39 | 3.35 | 3.22 |
| 9 | 5.12 | 4.26 | 3.86 | 3.63 | 3.48 | 3.37 | 3.29 | 3.23 | 3.18 | 3.14 | 3.01 |
| 10 | 4.96 | 4.10 | 3.71 | 3.48 | 3.33 | 3.22 | 3.14 | 3.07 | 3.02 | 2.98 | 2.85 |
| 11 | 4.84 | 3.98 | 3.59 | 3.36 | 3.20 | 3.09 | 3.01 | 2.95 | 2.90 | 2.85 | 2.72 |
| 12 | 4.75 | 3.89 | 3.49 | 3.26 | 3.11 | 3.00 | 2.91 | 2.85 | 2.80 | 2.75 | 2.62 |
| 13 | 4.67 | 3.81 | 3.41 | 3.18 | 3.03 | 2.92 | 2.83 | 2.77 | 2.71 | 2.67 | 2.53 |
| 14 | 4.60 | 3.74 | 3.34 | 3.11 | 2.96 | 2.85 | 2.76 | 2.70 | 2.65 | 2.60 | 2.46 |
| 15 | 4.54 | 3.68 | 3.29 | 3.06 | 2.90 | 2.79 | 2.71 | 2.64 | 2.59 | 2.54 | 2.40 |
| 16 | 4.49 | 3.63 | 3.24 | 3.01 | 2.85 | 2.74 | 2.66 | 2.59 | 2.54 | 2.49 | 2.35 |
| 17 | 4.45 | 3.59 | 3.20 | 2.96 | 2.81 | 2.70 | 2.61 | 2.55 | 2.49 | 2.45 | 2.31 |
| 18 | 4.41 | 3.55 | 3.16 | 2.93 | 2.77 | 2.66 | 2.58 | 2.51 | 2.46 | 2.41 | 2.27 |
| 19 | 4.38 | 3.52 | 3.13 | 2.90 | 2.74 | 2.63 | 2.54 | 2.48 | 2.42 | 2.38 | 2.23 |
| 20 | 4.35 | 3.49 | 3.10 | 2.87 | 2.71 | 2.60 | 2.51 | 2.45 | 2.39 | 2.35 | 2.20 |
По материалам книги «Статистика в аналитической хими». К. Дерффель, Москва, «Мир», 1994
chemstat.com.ru
Таблица значений F-критерия Фишера при уровне значимости α =0,05
Продолжение
|
ignorik.ru
