Схема Бернулли. Примеры решения задач
Не будем долго размышлять о высоком — начнем сразу с определения.
Схема Бернулли — это когда производится n однотипных независимых опытов, в каждом из которых может появиться интересующее нас событие A, причем известна вероятность этого события P(A) = p. Требуется определить вероятность того, что при проведении n испытаний событие A появится ровно k раз.
Задачи, которые решаются по схеме Бернулли, чрезвычайно разнообразны: от простеньких (типа «найдите вероятность, что стрелок попадет 1 раз из 10») до весьма суровых (например, задачи на проценты или игральные карты). В реальности эта схема часто применяется для решения задач, связанных с контролем качества продукции и надежности различных механизмов, все характеристики которых должны быть известны до начала работы.
Вернемся к определению. Поскольку речь идет о независимых испытаниях, и в каждом опыте вероятность события A одинакова, возможны лишь два исхода:
- A — появление события A с вероятностью p;
- «не А» — событие А не появилось, что происходит с вероятностью q = 1 − p.
Важнейшее условие, без которого схема Бернулли теряет смысл — это постоянство. Сколько бы опытов мы ни проводили, нас интересует одно и то же событие A, которое возникает с одной и той же вероятностью p.
Между прочим, далеко не все задачи в теории вероятностей сводятся к постоянным условиям. Об этом вам расскажет любой грамотный репетитор по высшей математике. Даже такое нехитрое дело, как вынимание разноцветных шаров из ящика, не является опытом с постоянными условиями. Вынули очередной шар — соотношение цветов в ящике изменилось. Следовательно, изменились и вероятности.
Если же условия постоянны, можно точно определить вероятность того, что событие A произойдет ровно k раз из n возможных. Сформулируем этот факт в виде теоремы:
Теорема Бернулли. Пусть вероятность появления события A в каждом опыте постоянна и равна р. Тогда вероятность того, что в n независимых испытаниях событие A появится ровно k раз, рассчитывается по формуле:
где Cnk — число сочетаний, q = 1 − p.
Эта формула так и называется: формула Бернулли. Интересно заметить, что задачи, приведенные ниже, вполне решаются без использования этой формулы. Например, можно применить формулы сложения вероятностей. Однако объем вычислений будет просто нереальным.
Задача. Вероятность выпуска бракованного изделия на станке равна 0,2. Определить вероятность того, что в партии из десяти выпущенных на данном станке деталей ровно k будут без брака. Решить задачу для k = 0, 1, 10.
По условию, нас интересует событие A выпуска изделий без брака, которое случается каждый раз с вероятностью p = 1 − 0,2 = 0,8. Нужно определить вероятность того, что это событие произойдет k раз. Событию A противопоставляется событие «не A», т.е. выпуск бракованного изделия.
Таким образом, имеем: n = 10; p = 0,8; q = 0,2.
Итак, находим вероятность того, что в партии все детали бракованные (k = 0), что только одна деталь без брака (k = 1), и что бракованных деталей нет вообще (k = 10):
Задача. Монету бросают 6 раз. Выпадение герба и решки равновероятно. Найти вероятность того, что:
- герб выпадет три раза;
- герб выпадет один раз;
- герб выпадет не менее двух раз.
Итак, нас интересует событие A, когда выпадает герб. Вероятность этого события равна p = 0,5. Событию A противопоставляется событие «не A», когда выпадает решка, что случается с вероятностью q = 1 − 0,5 = 0,5. Нужно определить вероятность того, что герб выпадет k раз.
Таким образом, имеем: n = 6; p = 0,5; q = 0,5.
Определим вероятность того, что герб выпал три раза, т.е. k = 3:
Теперь определим вероятность того, что герб выпал только один раз, т.е. k = 1:
Осталось определить, с какой вероятностью герб выпадет не менее двух раз. Основная загвоздка — во фразе «не менее». Получается, что нас устроит любое k, кроме 0 и 1, т.е. надо найти значение суммы X = P6(2) + P6(3) + … + P6(6).
Заметим, что эта сумма также равна (1 − P6(0) − P6(1)), т.е. достаточно из всех возможных вариантов «вырезать» те, когда герб выпал 1 раз (k = 1) или не выпал вообще (k = 0). Поскольку P6(1) нам уже известно, осталось найти P6(0):
Задача. Вероятность того, что телевизор имеет скрытые дефекты, равна 0,2. На склад поступило 20 телевизоров. Какое событие вероятнее: что в этой партии имеется два телевизора со скрытыми дефектами или три?
Интересующее событие A — наличие скрытого дефекта. Всего телевизоров n = 20, вероятность скрытого дефекта p = 0,2. Соответственно, вероятность получить телевизор без скрытого дефекта равна q = 1 − 0,2 = 0,8.
Получаем стартовые условия для схемы Бернулли: n = 20; p = 0,2; q = 0,8.
Найдем вероятность получить два «дефектных» телевизора (k = 2) и три (k = 3):
\[\begin{array}{l}{P_{20}}\left( 2 \right) = C_{20}^2{p^2}{q^{18}} = \frac{{20!}}{{2!18!}} \cdot {0,2^2} \cdot {0,8^{18}} \approx 0,137\\{P_{20}}\left( 3 \right) = C_{20}^3{p^3}{q^{17}} = \frac{{20!}}{{3!17!}} \cdot {0,2^3} \cdot {0,8^{17}} \approx 0,41\end{array}\]
Очевидно, P20(3) > P20(2), т.е. вероятность получить три телевизора со скрытыми дефектами больше вероятности получить только два таких телевизора. Причем, разница неслабая.
Небольшое замечание по поводу факториалов. Многие испытывают смутное ощущение дискомфорта, когда видят запись «0!» (читается «ноль факториал»). Так вот, 0! = 1 по определению.
P. S. А самая большая вероятность в последней задаче — это получить четыре телевизора со скрытыми дефектами. Подсчитайте сами — и убедитесь.
Смотрите также:
- Локальная теорема Муавра — Лапласа
- Формула полной вероятности
- Тест к уроку «Сложение и вычитание дробей» (легкий)
- Решение задач B12: №448—455
- Уравнение плоскости в задаче C2. Часть 1: матрицы и определители
- Тест по задачам B14: легкий уровень, 1 вариант
www.berdov.com
20. Закон распределения Бернулли, его определение, свойства и примеры.
Дискретная случайная величина X имеет биномиальное распределение (или распределена по биномиальному закону), если она принимает значения 0, 1, 2, …, n, с соответствующими вероятностями:
, где,,.
Математическое ожидание и дисперсия случайной величины X, имеющей биномиальное распределение, находятся по формулам:
.
Из формулы Бернулли следует, что случайная величина – число наступлений событиявнезависимых испытаниях () – распределена по биномиальному закону.
21. Биномиальный закон распределения, его определение, свойства и примеры.
Пусть производится n независимых испытаний, в каждом из которых событиеAможет появиться или не появиться. Вероятность наступления события во всех испытаниях постоянна и равнаp(следовательно, вероятность непоявленияq = 1 — p).
Рассмотрим случайную величину X– число появлений событияAв этих испытаниях. Случайная величинаXпринимает значения0,1,2,…nс вероятностями, вычисленными по формуле Бернулли:, гдеk = 0,1,2,…n.
Определение:Биномиальнымназывают раcпределение вероятностей, определяемое формулой Бернулли.
Пример. По мишени производится три выстрела, причем вероятность попадания при каждом выстреле равна 0,8. Рассматривается случайная величинаX– число попаданий в мишень. Найти ее ряд распределения.
Решение: Случайная величинаXпринимает значения0,1,2,3 с вероятностями, вычисленными по формуле Бернулли, гдеn = 3, p = 0,8(вероятность попадания),q = 1 — 0,8 = = 0,2(вероятность непопадания).
Тогда
,
Таким образом, ряд распределения имеет следующий вид:
0 | 1 | 2 | 3 |
0,008 | 0,096 | 0,384 | 0,512 |
Пользоваться формулой Бернулли при больших значениях nдостаточно трудно, поэтому для подсчета соответствующих вероятностей используют локальную теорему Лапласа, которая позволяет приближенно найти вероятность появления события ровноkраз вnиспытаниях, если число испытаний достаточно велико.
22.Закон распределения Пуассона, его определение, свойства и примеры.
Определение. Будем говорить, что случайная величинаε распределена по закону Пуассона с параметромλ , если она принимает значения из множества { 0,1,…,n, …} с вероятностямиP{ε=m} = (λm/m!)*e—λ.
Теорема. Если случайная величинаε распределена по закону Пуассона с параметромλ , то и математическое ожидание, и дисперсия этой случайной величины равны параметруλ.
Свойства распределения Пуассона:
1. .
Действительно: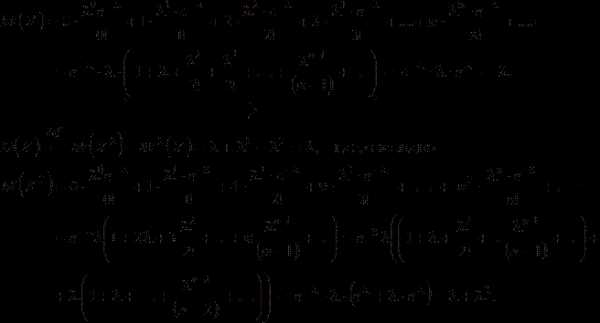
2. .
3. если , то из биномиального распределения следует закон распределения Пуассона.
ПРИМЕР 1.Завод отправил на базу 5000 доброкачественных изделий. Вероятность того, что в пути изделие повредится, равна 0,0002. Найти вероятность того, что на базу прибудут: а) три негодных изделия; б) не более трёх повреждённых изделия.
Решение: по условию n=5000, p=0,0002. Найдём .
а) k = 3. Искомая вероятность по формуле Пуассона приближённо равна
.
б) Пусть случайная величина Х – число изделий, повреждённых в пути, то есть . Очевидно, что данная случайная величина распределена по биномиальному закону. Следовательно, искомую вероятность можно вычислить по формуле
.
Но, так как , то по свойству 3о можем воспользоваться законом распределения Пуассона, то есть, можем записать:
.
Замечание.По формуле Пуассона можно вычислить вероятность того, что число событий, происшедших за время равно, если события образуют пуассоновский поток, причём– интенсивность потока, то есть среднее число событий, которые появляются в единицу времени:
.
ПРИМЕР 2. В течение часа коммутатор получает в среднем 60 вызовов. Какова вероятность того, что за время 30 сек, в течении которых телефонистка отлучилась, не будет ни одного вызова?
Решение: Найдём, прежде всего, – среднее число вызовов за 1 секунду:
.
Тогда, при , получим:
23.* Геометрическое распределение, его определение, свойства и примеры.
Пусть проводятся независимые испытания, каждое испытание может иметь два исхода: удача с вероятностью p и неудача с вероятностью q = 1 — p. Введем в рассмотрение случайную величину X — число испытаний до первого появления удачи. Эта случайная величина может принимать значения 1, 2, 3, 4 и так далее до бесконечности. Когда говорят, что случайная величина X имеет значение k, то это означает, что первые k — 1 испытание закончились неудачей, а k-ое испытание стало удачным. Вероятность того, что в серии независимых испытаний будет вначале k — 1 неудач, а в k-ое испытание — удача, равна . Таким образом мы получили закон распределения случайной величины X: значению k случайной величины соответствует вероятность. Этот закон распределения и называется геометрическим распределением. Название происходит из того, что величинапредставляет собой геометрическую прогрессию, с первым членом p и знаменателем q.Изучим теперь свойства этого распределения. С ростом k вероятности убывают. Используя формулу для суммы членов геометрической прогрессии, можем записать:, то есть условие, что сумма всех вероятностей в законе распределения равна единице, выполнено. Вычислим теперь математическое ожидание и дисперсию. По определению математического ожидания имеем:. Для вычисления суммы воспользуемся следующим приемом — заменимнаи вынесем производную за знак суммы, в итоге получим:. Оставшаяся сумма представляет собой сумму членов геометрической прогрессии и равна. Вычисляя производную, запишем:. Аналогично можно получить выражение для:. Заменяя сумму на ее значение, вычисляем:. Таким образом, имеем выражение для дисперсии:. Если вероятность удачи равна единице, то математическое ожидание числа испытаний до первой удачи равно 1, а дисперсия — 0. Если, наоборот, вероятность удачи равна нулю, то математическое ожидание — бесконечность (то есть нужно произвести бесконечное число испытаний до появления удачи).Пример 30.1Вероятность попадания в мишень из винтовки равна 0,8. Найти математическое ожидание и дисперсию случайной величины — количества выстрелов до первого попадания.Математическое ожидание, дисперсия. Полученные результаты означают, что при вероятности попадания 0,8 попадание будет в среднем с 1—2 выстрела.
24.Равномерный закон распределения, его определение, свойства и примеры. Законы распределения НСВ Плотности распределения НСВ называют также законами распределения. Часто встречаются законы равномерного, нормального и показательного распределений.
Определение.1. Закон распределения НСВ называется равномерным, если ее плотность распределения задается в виде:
1. Зная плотность распределения, и используя формулу ,
можно найти функцию распределения:
2. Если НСВ имеет равномерное распределение, то ее числовые характеристики могут быть найдены по формулам:
.
3. Вероятность попадания равномерно-распределенной НСВ в интервалможно определить по формуле:
.
Пример 1. Автобусы подходят к остановке с интервалом в 5 минут. Считая, что НСВ — время ожидания автобуса — распределена равномерно, найти среднее время ожидания (математическое ожидание), среднее квадратическое отклонение. Какова вероятность того, случайно подошедший на остановку пассажир будет ожидать автобус не более 4 минут, но и не менее 2 минут.
Решение:
;
.
studfiles.net
Схема повторных независимых испытаний. Формула Бернулли
Теория вероятностей имеет дело с такими экспериментами, которые можно повторять (по крайней мере теоретически) неограниченное число раз. Пусть некоторый эксперимент повторяется раз, причем результаты каждого повторения не зависят от исходов предыдущих повторений. Такие серии повторений называют независимыми испытаниями. Частным случаем таких испытаний являются независимые испытания Бернулли, которые характеризуются двумя условиями:
1) результатом каждого испытания является один из двух возможных исходов, называемых соответственно «успехом» или «неудачей».
2) вероятность «успеха», в каждом последующем испытании не зависит от результатов предыдущих испытаний и остается постоянной.
Теорема Бернулли
Если производится серия из независимых испытаний Бернулли, в каждом из которых «успех» появляется с вероятностью , то вероятность того, что «успех» в испытаниях появится ровно раз, выражается формулой:
где – вероятность «неудачи».
– число сочетаний элементов по (см. основные формулы комбинаторики)
Эта формула называется формулой Бернулли.
Формула Бернулли позволяет избавиться от большого числа вычислений — сложения и умножения вероятностей - при достаточно большом количестве испытаний.
Схему испытаний Бернулли называют также биномиальной схемой, а соответствующие вероятности – биномиальными, что связано с использованием биномиальных коэффициентов .
Распределение по схеме Бернулли позволяет, в частности, найти наивероятнейшее число наступления события.
Если число испытаний n велико, то пользуются:
Условие задачи
Всхожесть семян некоторого растения составляет 70%. Какова вероятность того, что из 10 посеянных семян взойдут: 8, по крайней мере 8; не менее 8?
Задали объемную контрольную? Скоро важный зачет/экзамен? Нет времени на выполнение работы или подготовку к зачету/экзамену, но есть деньги? На сайте 100task.ru можно заказать решение или онлайн-помощь на зачете/экзамене 〉〉
Решение задачи
Воспользуемся формулой Бернулли:
В нашем случае
Пусть событие – из 10 семян взойдут 8:
Пусть событие – взойдет по крайней мере 8 (это значит 8, 9 или 10)
Пусть событие – взойдет не менее 8 (это значит 8,9 или 10)
Ответ
P(A)=0.2335;P(B)=0.3828; P(C)=0.3828
К оглавлению решебника по теории вероятностей и математической статистике 〉
100task.ru
Распределение Бернулли — Howling Pixel
Распределе́ние Берну́лли в теории вероятностей и математической статистике — дискретное распределение вероятностей, моделирующее случайный эксперимент произвольной природы, при заранее известной вероятности успеха или неудачи.
| Распределение Бернулли | |
|---|---|
| Функция вероятности | |
| Функция распределения | |
| Параметры | p∈(0,1){\displaystyle p\in (0,1)} q≡1−p{\displaystyle q\equiv 1-p} |
| Носитель | k={0,1}{\displaystyle k=\{0,1\}} |
| Функция вероятности | qk=0p k=1{\displaystyle {\begin{matrix}q&k=0\\p~~&k=1\end{matrix}}} |
| Функция распределения | 0k<0q0≤k<11k≥1{\displaystyle {\begin{matrix}0&k<0\\q&0\leq k<1\\1&k\geq 1\end{matrix}}} |
| Математическое ожидание | p{\displaystyle p} |
| Мода | {0,q>p0,1,q=p1,q<p{\displaystyle {\begin{cases}0,&q>p\\0,1,&q=p\\1,&q<p\end{cases}}} |
| Дисперсия | pq{\displaystyle pq} |
| Коэффициент асимметрии | q−ppq{\displaystyle {\frac {q-p}{\sqrt {pq}}}} |
| Коэффициент эксцесса | 6p2−6p+1p(1−p){\displaystyle {\frac {6p^{2}-6p+1}{p(1-p)}}} |
| Дифференциальная энтропия | −qlnq−plnp{\displaystyle -q\ln q-p\ln p} |
| Производящая функция моментов | q+pet{\displaystyle q+pe^{t}} |
| Характеристическая функция | q+peit{\displaystyle q+pe^{it}} |
Определение
Случайная величина X{\displaystyle X} имеет распределение Бернулли, если она принимает всего два значения: 1{\displaystyle 1} и 0{\displaystyle 0} с вероятностями p{\displaystyle p} и q≡1−p{\displaystyle q\equiv 1-p} соответственно. Таким образом:
- P(X=1)=p{\displaystyle \mathbb {P} (X=1)=p},
- P(X=0)=q{\displaystyle \mathbb {P} (X=0)=q}.
Принято говорить, что событие {X=1}{\displaystyle \{X=1\}} соответствует «успеху», а событие {X=0}{\displaystyle \{X=0\}} — «неудаче». Эти названия условные, и в зависимости от конкретной задачи могут быть заменены на противоположные.
Моменты распределения Бернулли
- E[X]=p{\displaystyle \mathbb {E} [X]=p},
- D[X]=p(1−p)=pq{\displaystyle \operatorname {D} [X]=p(1-p)=pq}, так как: E(X2)−E(X)2=p−p2=p⋅(1−p)=pq{\displaystyle \operatorname {E} \left(X^{2}\right)-\operatorname {E} (X)^{2}=p-p^{2}=p\cdot (1-p)=pq}.
Вообще, легко видеть, что
- E[Xn]=p,∀n∈N{\displaystyle \mathbb {E} \left[X^{n}\right]=p,\;\forall n\in \mathbb {N} }.
Замечание
Если независимые случайные величины X1,…,Xn{\displaystyle X_{1},\ldots ,X_{n}}, имеют распределение Бернулли с вероятностью успеха p{\displaystyle p}, то
- Y=∑i=1nXi{\displaystyle Y=\sum \limits _{i=1}^{n}X_{i}}
имеет биномиальное распределение с n{\displaystyle n} степенями свободы.
См. также
Литература
- Hazewinkel, Michiel, ed. (2001), «Binomial distribution», Encyclopedia of Mathematics, Springer, ISBN 978-1-55608-010-4
Байесовская статистика — это теория в области статистики, основанная на байесовской интерпретации вероятности, когда вероятность отражает степень доверия событию, которая может измениться, когда новая информация будет собрана, в отличие от фиксированного значения, основанного на частотном подходе. Степень доверия может основываться на априорных знаниях о событии, таких как результаты предыдущих экспериментов или личное доверие событию. Это отличается от ряда других интерпретаций вероятности, таких как частотная интерпретация, которая рассматривает вероятность как предел относительной частоты выпадения события после большого числа испытаний.
БернуллиБерну́лли (Bernoulli) — фамилия.
Семья Бернулли — семья, многие члены которой внесли существенный вклад в науку.
Бернулли, Якоб (1655—1705) — швейцарский математик, профессор математики Базельского университета.
Бернулли, Иоганн (1667—1748) — младший брат Якоба.
Бернулли, Николай (1687—1759) — математик.
Бернулли, Николай (1695—1726) — юрист и математик.
Бернулли, Даниил (1700—1782) — сын Иоганна.
Бернулли, Иоганн II (1710—1790) — швейцарский математик и физик.
Бернулли, Иоганн III (1744—1807) — внук Иоганна Бернулли, математик, астроном и путешественник.
Бернулли, Якоб II (1759—1789) — племянник Даниила.
Бернулли — кратер на видимой стороне Луны.
Бернулли, ЯкобЯ́коб Берну́лли (нем. Jakob Bernoulli, 6 января 1655, Базель, — 16 августа 1705, там же) — швейцарский математик. Один из основателей теории вероятностей и математического анализа. Старший брат Иоганна Бернулли, совместно с ним положил начало вариационному исчислению. Доказал частный случай закона больших чисел — теорему Бернулли. Профессор математики Базельского университета (с 1687 года). Иностранный член Парижской академии наук (1699) и Берлинской академии наук (1702).
Бернулли (семья)Семья Берну́лли (Bernoulli) — швейцарская протестантская семья, многие члены которой в XVII-XVIII веках внесли существенный вклад в науку. В частности, к этой династии принадлежат 9 крупных математиков и физиков (из них 3 великих), а также известные историки, искусствоведы, архитекторы, юристы и др.
Историки насчитали в науке и культуре не менее 30 знаменитых представителей семьи Бернулли. Среди академиков Петербургской Академии наук — пятеро из семьи Бернулли. Кафедру математики Базельского университета в течение 105 лет почти без перерыва занимали представители семьи Бернулли.
Биномиальное распределениеБиномиа́льное распределе́ние в теории вероятностей — распределение количества «успехов» в последовательности из n{\displaystyle n} независимых случайных экспериментов, таких, что вероятность «успеха» в каждом из них постоянна и равна p{\displaystyle p}.
Дискретная случайная величинаДискретная случайная величина — это случайная величина, множество значений которой не более чем счётно (то есть конечно или счётно). Очевидно, значения дискретной случайной величины не содержат какой-либо непрерывный интервал на числовой прямой.
Примеры:
Любая случайная величина, принимающая целочисленные значения.
Моменты испускания альфа-частиц атомом радиоактивного элемента.
Достаточная статистикаДостаточная статистика для параметра θ∈Θ,{\displaystyle \theta \in \Theta ,\;} определяющая некоторое семейство Fθ{\displaystyle F_{\theta }} распределений вероятности — статистика T=T(X),{\displaystyle T=\mathrm {T} (X),\;} такая, что условная вероятность выборки X=X1,X2,…,Xn{\displaystyle X=X_{1},X_{2},\ldots ,X_{n}\;} при данном значении T(X){\displaystyle \mathrm {T} (X)\;} не зависит от параметра θ.{\displaystyle \theta \;.} То есть выполняется равенство:
- P(X∈X¯|T(X)=t,θ)=P(X∈X¯|T(X)=t),{\displaystyle \mathbb {P} (X\in {\bar {X}}|\mathrm {T} (X)=t,\theta )=\mathbb {P} (X\in {\bar {X}}|\mathrm {T} (X)=t),}
Достаточная статистика T(X),{\displaystyle \mathrm {T} (X),\;} таким образом содержит в себе всю информацию о параметре θ{\displaystyle \theta \;}, которая может быть получена на основе выборки X. Поэтому понятие достаточной статистики широко используется в теории оценки параметров.
Наиболее простой достаточной статистикой является сама выборка T(X)=X{\displaystyle \mathrm {T} (X)=X\;}, однако действительно важными являются случаи, когда размерность достаточной статистики значительно меньше размерности выборки, в частности, когда достаточная статистика выражается лишь несколькими числами.
Достаточная статистика S=S(X){\displaystyle S=\mathrm {S} (X)\;} называется минимально достаточной, если для каждой достаточной статистики T существует неслучайная измеримая функция g, что S(X)=g(T(X)){\displaystyle S(X)=g(T(X))} почти всюду.
Задача о разорении игрокаЗадача о разорении игрока — задача из области теории вероятностей. Подробно рассматривалась российским математиком А. Н. Ширяевым в монографии «Вероятность».
Качественная переменнаяКачественная, дискретная, или категорийная переменная — это переменная, которая может принимать одно из ограниченного и, обычно, фиксированного числа возможных значений, назначая каждую единицу наблюдения определённой группе или номинальной категории на основе некоторого качественного свойства. В информатике и некоторых других ветвях математики качественные переменные называются перечислениями или перечисляемыми типами. Обычно (хотя не в этой статье), каждое из возможных значений качественной переменной называется уровнем. Распределение вероятностей, связанное со случайной качественной переменной, называется категорийным распределением.
Логистическая регрессияЛогистическая регрессия или логит-регрессия (англ. logit model) — это статистическая модель, используемая для прогнозирования вероятности возникновения некоторого события путём подгонки данных к логистической кривой.
Мартингал де МуавраМартинга́л де Муа́вра в теории случайных процессов — это простейший пример мартингала.
Моральное ожиданиеМоральное ожидание — оценка жребия, впервые введенная швейцарским математиком Даниилом Бернулли. В отличие от математического ожидания (ожидаемой доходности) моральное ожидание зависит от состояния игрока и неявно учитывает фактор риска. Сам термин «моральное ожидание» принадлежит французскому математику Пьеру Симону Лапласу.
Правило СтёрджесаПравило Стёрджеса — эмпирическое правило определения оптимального количества интервалов, на которые разбивается наблюдаемый диапазон изменения случайной величины при построении гистограммы плотности её распределения. Названо по имени американского статистика Герберта Стёрджеса (Herbert Arthur Sturges, 1882—1958).
Количество интервалов n{\displaystyle n} определяется как:
- n=1+⌊log2N⌋{\displaystyle n=1+\lfloor \log _{2}N\rfloor },
где N{\displaystyle N} — общее число наблюдений величины, log2{\displaystyle \log _{2}} — логарифм по основанию 2, ⌊x⌋{\displaystyle \lfloor x\rfloor } — обозначает целую часть числа x{\displaystyle x}.
Часто встречается записанным через десятичный логарифм:
- n=1+⌊3.322lgN⌋{\displaystyle n=1+\lfloor 3.322\lg N\rfloor },
Основанием для него служит оценка количества событий с разными вероятностями в схеме испытаний Бернулли длительностью в n−1{\displaystyle n-1} этап. Если имеются серии испытаний с 2 альтернативными исходами с постоянной вероятностью каждого, то число видов серий, где в составе имеется k{\displaystyle k} исходов, принимающих первое из альтернативных значений, и, соответственно, n−k−1{\displaystyle n-k-1} — принимающих второе, равно: n{\displaystyle n} (от k=0{\displaystyle k=0} до k=n−1{\displaystyle k=n-1}), а общее число серий N=2n−1{\displaystyle N=2^{n-1}}.
Если аппроксимировать значения наблюдаемой случайной величины результатами сложения случайно выпадающих в серии испытаний значений двух чисел a{\displaystyle a} и b{\displaystyle b} (например 0{\displaystyle 0} и 1{\displaystyle 1}), соответствующих исходам схемы Бернулли, то каждой серии испытаний содержащей k{\displaystyle k} исходов с результатом a{\displaystyle a} и n−k−1{\displaystyle n-k-1} исходов с результатом b{\displaystyle b} будет соответствовать сумма ka+(n−k+1)b{\displaystyle ka+(n-k+1)b}. Количество различных значений (в рассматриваемом случае: a(n−1),a(n−2)+b,..a+b(n−2),b(n−1){\displaystyle a(n-1),a(n-2)+b,..a+b(n-2),b(n-1)}, для пары 0,1{\displaystyle 0,1} — 0,1,2,..n−1{\displaystyle 0,1,2,..n-1}) будет равно количеству последовательностей с различным числом исходов n{\displaystyle n}. Т.о., если ставить задачу, чтобы на каждый интервал между a{\displaystyle a} и b{\displaystyle b} приходилось в среднем не меньше одного значения суммы, а значит и не меньше одной серии испытаний, моделирующей получение случайной величины, то число этапов в серии, равное числу интервалов, на которые разбивается диапазон изменения наблюдаемых значений, должно быть не больше, чем n=1+⌊log2N⌋{\displaystyle n=1+\lfloor \log _{2}N\rfloor }
Распределение получившихся величин (распределение Бернулли) аппроксимируется при больших N{\displaystyle N} нормальным распределением согласно теореме Муавра — Лапласа, что дает основания при предположении о близости распределения исследуемой величины к нормальному и, соответственно, к аппроксимируемому им биномиальному применять оценку количества интервалов разбиения соответственно количеству ожидаемых дискретных значений для распределения Бернулли, что приводит к правилу Стёрджеса.
Производящая функция моментовПроизводя́щая фу́нкция моме́нтов — способ задания вероятностных распределений. Используется чаще всего для вычисления моментов.
Распределение вероятностейРаспределение вероятностей — это закон, описывающий область значений случайной величины и вероятности их исхода (появления).
Формула КеллиФормула Келли — формула, которая показывает оптимальную долю капитала, которой можно рискнуть в одной сделке. Применяется в управлении капиталом при игре на финансовых рынках, в азартных играх и др.
Рассматривается следующая ситуация. Участник при каждой сделке может с вероятностью p{\displaystyle p} получить прибыль в A{\displaystyle A} раз превышающую поставленный капитал x{\displaystyle x} или с вероятностью q=1−p{\displaystyle q=1-p} получить убыток в B{\displaystyle B} раз превышающий ставку x{\displaystyle x}. Ставится задача — какую долю общего капитала K{\displaystyle K} надо каждый раз ставить, чтобы максимизировать среднюю величину логарифма прибыли при большом числе повторяемых сделок.
Обозначим долю капитала f=x/K{\displaystyle f=x/K}.
Формула Келли гласит, что оптимальное значение
- f∗=pB−qA{\displaystyle f^{*}={\frac {p}{B}}-{\frac {q}{A}}}
(предполагается, что математическое ожидание сделки положительно, то есть pA−qB>0{\displaystyle pA-qB>0}).
Формулы Келли применимы только к результатам, имеющим распределение Бернулли (два возможных исхода). Применение формул Келли к иному распределению будет ошибкой и не даст оптимального f{\displaystyle f} .
Функция вероятностиФу́нкция вероя́тности в теории вероятностей — функция, возвращающая вероятность того, что дискретная случайная величина X{\displaystyle X} примет определённое значение. Например, пусть p:Rn→[0,1]{\displaystyle p:\mathbb {R} ^{n}\to [0,1]} функция вероятности, тогда вероятность того что X{\displaystyle X} примет значение равное 13, вычисляется подстановкой значения X=13{\displaystyle X=13} в функцию p(X)=p(13){\displaystyle p(X)=p(13)}, которая уже возвращает вероятность, например, 0.5 — это означает, что X{\displaystyle X} будет принимать значения равные 13 в 50% всех исходов.
Функция вероятности — это наиболее часто используемый способ охарактеризовать дискретное распределение. Стоит обратить внимание, что функция вероятности отличается от плотности вероятности в том, что последняя используется для вычисления вероятностей в случае непрерывной случайной величины; значения же самой функции плотности не вычисляются простой подстановкой значений X{\displaystyle X} в качестве аргумента (как было показано выше в дискретном случае), а должны наоборот быть проинтегрированы над интервалом значений, которые может принимать X{\displaystyle X}.
Характеристическая функция случайной величиныХарактеристи́ческая фу́нкция случа́йной величины́ — один из способов задания распределения. Характеристические функции могут быть удобнее в тех случаях, когда, например, плотность или функция распределения имеют очень сложный вид. Также характеристические функции являются удобным инструментом для изучения вопросов слабой сходимости (сходимости по распределению). В теорию характеристических функций внесли большой вклад Ю.В. Линник, И.В. Островский, С.Р. Рао, Б. Рамачандран.
This page is based on a Wikipedia article written by authors
(here).
Text is available under the CC BY-SA 3.0 license; additional terms may apply.
Images, videos and audio are available under their respective licenses.
howlingpixel.com
Формула Бернулли. Решение задач
Схема Бернулли возникает при повторных независимых испытаниях. Независимыми испытаниями называются такие, которые зависят друг от друга, и от результатов предыдущих испытаний. Они могут проводиться как в однотипных условиях, так и в разных. В первом случае вероятность появления какого-либо события во всех испытаниях одна и та же, во втором случае она меняется от опыта к опыту.
Пусть для каждого опыта вероятность появления события равна , вероятность противоположного события определяется зависимостью
Нужно найти вероятность появления события ровно раз в серии из испытаний. При этом следует отметить, что событие в серии опытов может чередоваться любым способом, главное чтобы исполнилась ровно раз.
Результаты испытаний для удобства обозначаем буквой в случае появления события и для противоположного.
Испытания в которых происходит раз и не происходит () раз по определению будут благоприятными. Их количество равно количеству способов выбора элементов с и определяется по формуле сочетания
Определим вероятность благоприятной комбинации (в серии из испытаний появления события ровно раз). Для простоты записи, рассмотрим случай, когда событие произошло в первых опытах и не состоялось в остальных . Схематично его можно обозначить следующим образом, а вероятность найти по теореме умножения вероятностей
для других благоприятных испытаний и вероятности будут такие же, только порядок их в серии из экспериментов будет постоянно меняться
Все благоприятные испытания являются попарно несовместимы, поэтому для нахождения общей вероятности их нужно просуммировать
или
Вывел ее впервые швейцарский математик Якоб Бернулли (1654 г.-1705 г.).
Если просуммировать вероятности всех испытаний в которых событие может произойти от нуля до раз в серии испытаний, то получим полную вероятность
Слагаемые этой суммы совпадают по виду с расписанием бинома Ньютона
Легко убедится, что
В литературе можно встретить термин «биномиальное распределение вероятностей», это как раз множество всех вероятностей, которые просуммированы выше.
Как последствия, из формулы Бернулли выводятся следующие формулы для популярных для практики задач:
1) вероятность появления события «хотя бы один раз» в серии из испытаний
2) вероятность появления события «хотя бы определенное количество раз» в серии из испытаний вычисляют по формуле
или согласно свойству биномиального разложения вероятностей
На основе данной зависимости вводят в рассмотрение сквозную функцию, которая дает возможность определить возможное количество появления события в серии из испытаний
По свойству сквозной функции множители при степени переменной () равны вероятности появления события в серии из опытов ровно раз. Это легко проследить по формуле суммирования вероятностей всех возможных испытаний по схеме Бернулли.
Если вероятности появления события в каждом опыте разные , а противоположного равны то по свойствам сквозной функции вероятность события произойти раз в серии из опытов равна множителю при в расписании функции по степеням
Она достаточно часто встречается при решении задач, в которых вероятности появления события в каждом последующем опыте меняются и позволяет при небольшом количестве появления события быстро найти вероятность (решение задачи).
Вероятное количество появлений события в схеме Бернулли лежит в интервале
Для применения схемы Бернулли нужно, чтобы выполнялись три условия:
1) опыты должны быть независимы между собой;
2) каждый опыт должен иметь два результата , и никаких других вариантов;
3) вероятность появления события должна быть одинаковой для каждого следующего опыта.
Рассмотрим решения типичных для данной схемы задач.
——————————
Пример 1. В тире стрелок проводит 7 выстрелов по мишени с вероятностью попадания каждого 0,8. Какова вероятность того, что будет: а) ровно 4 попадания б) не менее 5 попаданий в) не более двух попаданий.
Решение. а) проводится независимых друг от друга испытаний с вероятностью попадания в мишень в каждом из них . Вероятность того, что будет точно попаданий вычисляем по формуле Бернулли:
б) событие , которое заключается в том, что при выстрелах будет не менее 5 попаданий, можно рассматривать как сумму трех несовместных событий: – 5 попаданий из 7, событие – 6 попаданий с 7 и – все 7 выстрелов метки.
По формуле Бернулли находим вероятности событий
Тогда вероятность события равна сумме найденных вероятностей
в) Подобным образом, вероятность события – не более двух попаданий при семи выстрелах можно вычислить, как сумму вероятностей трех событий:
– 2 попадания из 7,
– 1 из 7 ,
– ни одного попадания из 7 выстрелов (7 промахов).
На практике студенты часто забывают рассматривать событие — подобное отсутствию попадений , поэтому не делайте подобных ошибок и хорошо запомните возможность возникновения такого варианта. Вероятности находим по знакомой уже формуле
Суммируя вероятности получим
Однако, события (не более двух попаданий при семи выстрелах) и (не менее 5 попаданий при семи выстрелах) противоположны друг другу, поэтому
——————————
Пример 2. Монета подбрасывают пять раз. Найти вероятность того, что герб выпадет не более трех раз.
Решение. Вероятность выпадения герба или решки считаем независимым событием с вероятностью . По аналогии с предыдущей задачей, искомая вероятность равна сумме трех следующих
Чтобы не искать столько слагаемых, из приведенных выше формул получим простую
——————————
Пример 3. Вероятность появления события в одном опыте равна 0,4. Сколько нужно провести опытов, чтобы вероятное количество появления события была равна 20.
Решение. Согласно условия выписываем данные
и проводим расчеты согласно неравенству
С него получим
три числа 49,50,51.
——————————
Пример 4. Три биатлониста независимо друг от друга делают по одному выстрелу в мишень. Вероятность попадания в мишень для первого равна 0,9, для второго — 0,85, для третьего — 0,8. Найти вероятность того, что будут закрыты две мишени из трех.
Решение. Вероятности попадания для стрелков разные, поэтому применяем образующую функцию. Для нее входные данные примут значения
После подстановки и разложения в ряд получим
Искомая вероятность входит в расписание множителем при
Из этого примера также легко убедиться, что сумма всех множителей при степенях равна полной вероятности (единицы).
——————————
Схема Бернулли на практике не сложная, важно уловить как в вычислениях реализовать задачи вида «не более раз», «не менее раз», «ровно раз» с . Как только Вы это поймете, все остальное сведется к суммирования, умножению и возведения в степень.
yukhym.com
Биномиальное распределение. Схема Бернулли.
Пусть
производятся независимые испытания и
при каждом испытании может быть 2 исхода:
успех с вероятностью 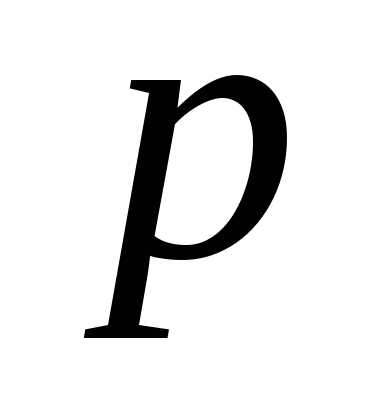 или неудача с вероятностью
или неудача с вероятностью ,
при этом (
,
при этом ( ).
).
Примеры
1) Стрельба по цели. При каждом выстреле 2 исхода: попадание или промах.
2) Проверка наугад выбранного изделия, которое может оказаться качественным или бракованным.
3) Подбрасывание симметричной монеты .Может выпасть герб или решетка.
Построим
вероятностную модель эксперимента в
случае 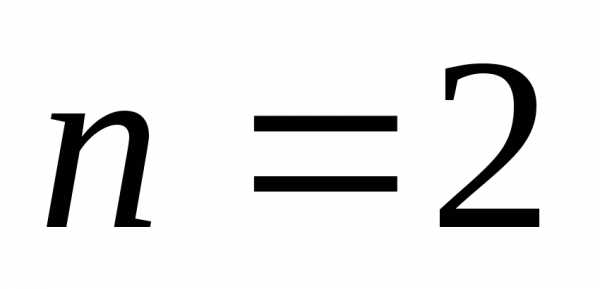 .
.
Пространство элементарных событий .
, ,,. Поскольку испытания независимы, то вероятности элементарных исходов определяются как произведение вероятностей.
В качестве случайной величины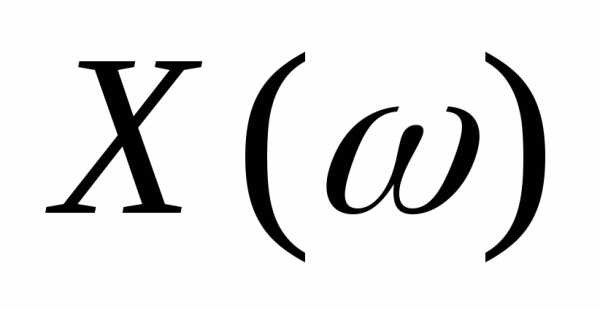 рассмотрим число успехов в серии из 2
испытаний. Построим ряд распределения
случайной величины
рассмотрим число успехов в серии из 2
испытаний. Построим ряд распределения
случайной величиныПри этом , так как.
Пусть
теперь опыт повторяется 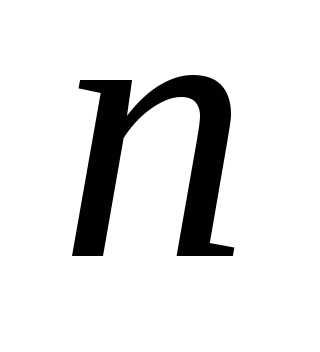 раз.
При каждом опыте событие А (успех)
происходит с вероятностью
раз.
При каждом опыте событие А (успех)
происходит с вероятностью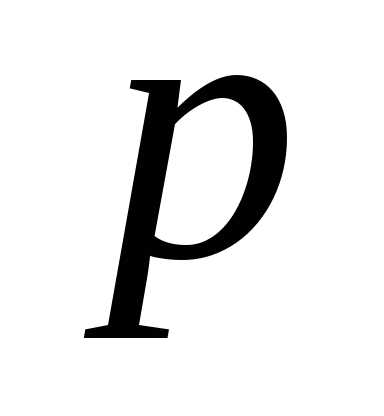 и не происходит с вероятностью
и не происходит с вероятностью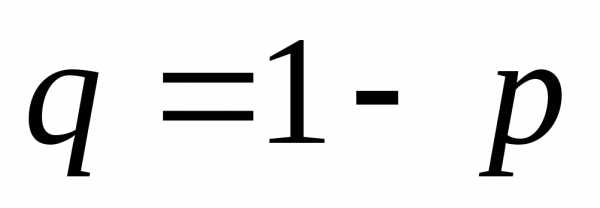 ,
причем эти вероятности от опыта к опыту
не меняются. Случайная
величина
,
причем эти вероятности от опыта к опыту
не меняются. Случайная
величина 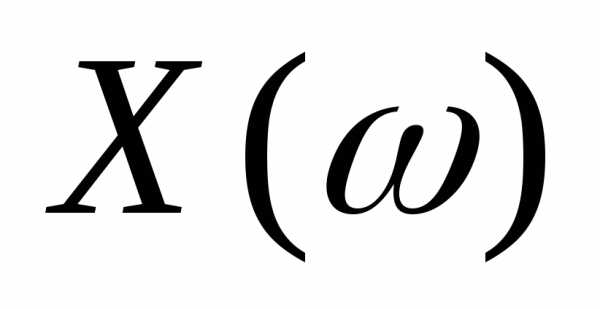 – число успехов в серии из
– число успехов в серии из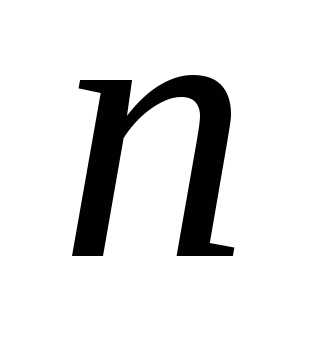 испытаний, Найдем вероятность того, что,
т.е. что событие А (успех) наступит
испытаний, Найдем вероятность того, что,
т.е. что событие А (успех) наступит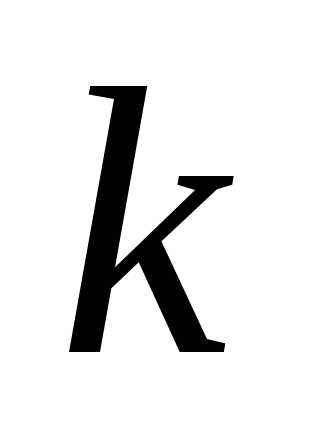 раз (а, следовательно, неуспех наступит
раз (а, следовательно, неуспех наступит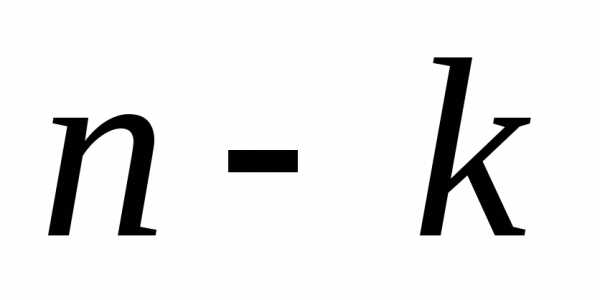 раз).Найдем вначале, что событие А
(успех) произойдет при первых
раз).Найдем вначале, что событие А
(успех) произойдет при первых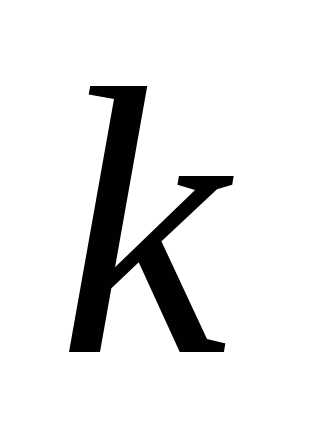 опытах и не произойдет при последних
опытах и не произойдет при последних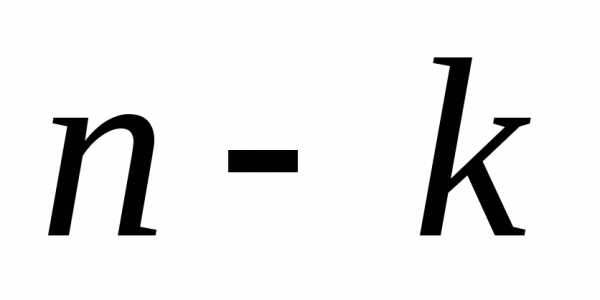 опытах. Применяя теорему умножения
вероятностей, получим.
Но событие А может произойти
опытах. Применяя теорему умножения
вероятностей, получим.
Но событие А может произойти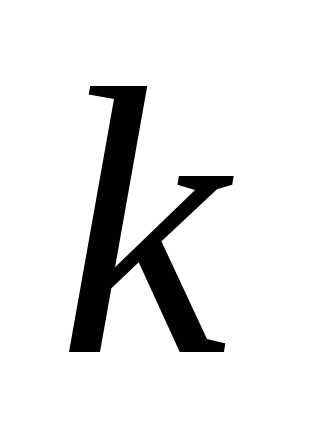 раз и в другой последовательности. Общее
число всех возможных последовательностей
равно
раз и в другой последовательности. Общее
число всех возможных последовательностей
равно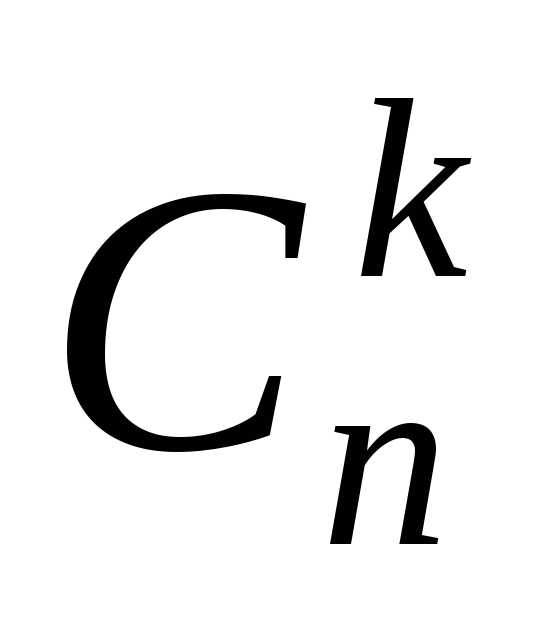 .
Вероятность появления события А для
каждой такой последовательности равна
.
Вероятность появления события А для
каждой такой последовательности равна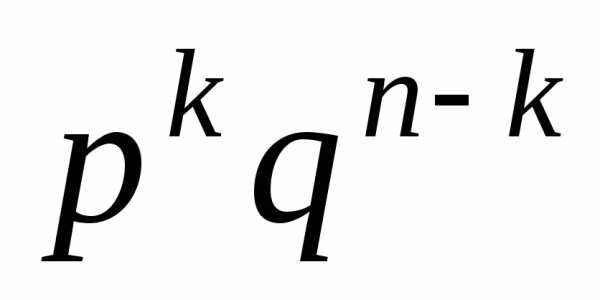 .
Вероятность появления какой либо одной
из этих последовательностей найдем с
помощью теоремы сложения вероятностей
.
Вероятность появления какой либо одной
из этих последовательностей найдем с
помощью теоремы сложения вероятностей
, где .
Полученная
формула является формулой для 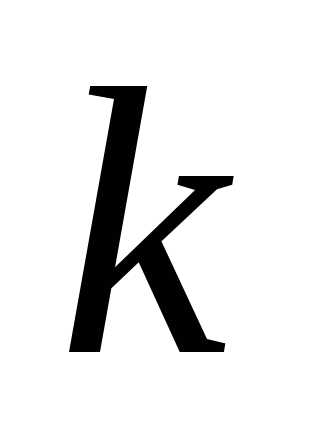 –го
члена бинома Ньютона
–го
члена бинома Ньютона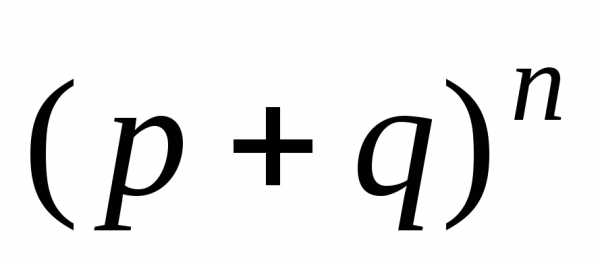 .
Поэтому такое распределение вероятностей
называется биномиальным. Впервые это
распределение подробно изучил Бернулли.
Поэтому стохастический эксперимент,
приводящий к биномиальному распределению,
называется схемой Бернулли.
.
Поэтому такое распределение вероятностей
называется биномиальным. Впервые это
распределение подробно изучил Бернулли.
Поэтому стохастический эксперимент,
приводящий к биномиальному распределению,
называется схемой Бернулли.
Функция распределения биномиального закона имеет вид
,
где 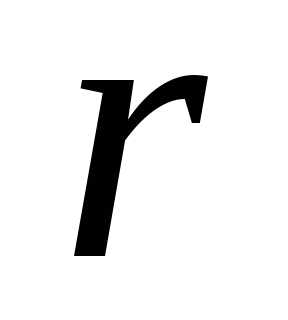 неотрицательное
целое число.
неотрицательное
целое число.
Пример.
Прибор состоит из четырех элементов.
Вероятность отказа каждого из них равна 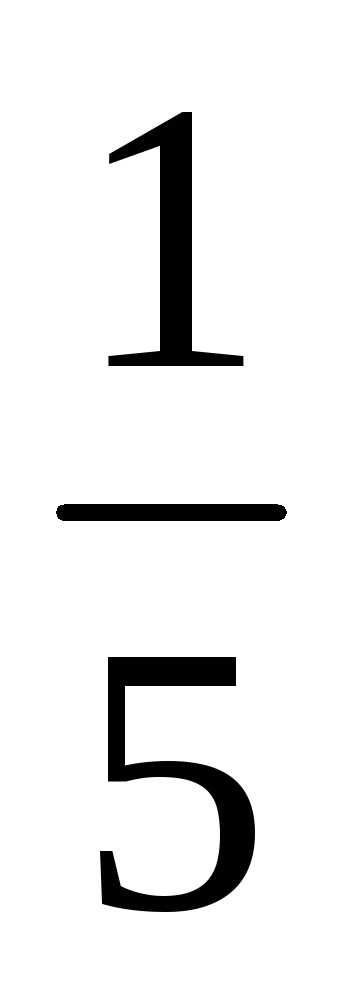 .
Найти вероятность отказа 0,1,2,3,4 элементов
во время работы прибора.
.
Найти вероятность отказа 0,1,2,3,4 элементов
во время работы прибора.
Сумма всех вероятностей равна 1, так как эта сумма есть вероятность достоверного события.
Геометрическое распределение.
Пусть
производятся независимые испытания и
при каждом испытании может быть 2 исхода:
успех с вероятностью 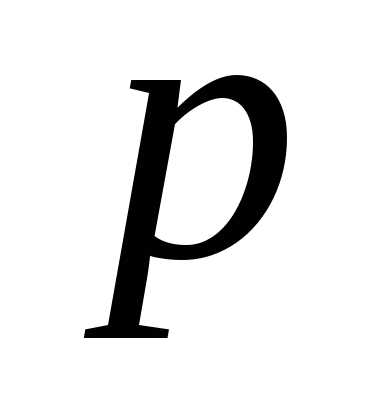 или неудача с вероятностью
или неудача с вероятностью ,
при этом (
,
при этом (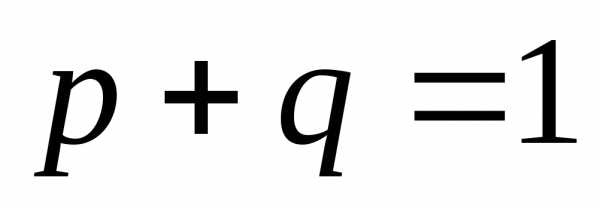 ).
Испытания проводятся до первого успеха.
Случайная величина
).
Испытания проводятся до первого успеха.
Случайная величина – число испытаний до первого успеха.
Найдем распределение случайной величины
– число испытаний до первого успеха.
Найдем распределение случайной величины .
Пространство элементарных событий
.
Пространство элементарных событий
. Согласно предположению о независимости испытаний в соответствии с теоремой умножения вероятностей . Это означает, что, где. Ряд распределения имеет вид
Такое распределение называется геометрическим, так как членами ряда распределения являются члены геометрической прогрессии.
Функция распределения случайной величины
.
Если случайная величина имеет геометрическое распределение, то справедливо равенство
.
Действительно,
Это
равенство означает отсутствие
последействия. Условная вероятность
того, что
,
если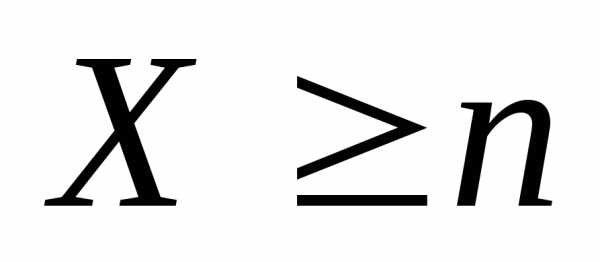 ,
совпадает с безусловной вероятностью
того, что
,
совпадает с безусловной вероятностью
того, что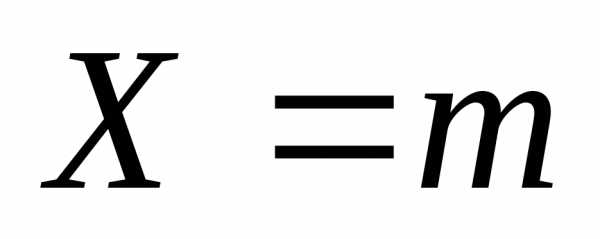 .
.
Пример
1. Телефонные разговоры. Пусть длительность
телефонного разговора измеряется целым
числом минут. В начале каждой минуты с
вероятностью 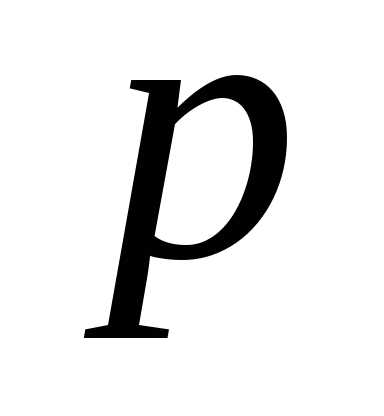 принимается решение закончить разговор
и с вероятностью
принимается решение закончить разговор
и с вероятностью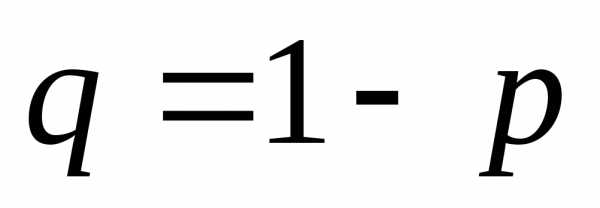 его продолжить. Тогда длительность
телефонного разговора будет случайной
величиной, имеющей геометрическое
распределение. Условная вероятность
того, что телефонный разговор будет
продолжаться ровно
его продолжить. Тогда длительность
телефонного разговора будет случайной
величиной, имеющей геометрическое
распределение. Условная вероятность
того, что телефонный разговор будет
продолжаться ровно минут, если известно, что он не закончился
за
минут, если известно, что он не закончился
за минуту, совпадает с безусловной
вероятностью того, разговор будет
продолжаться ровно
минуту, совпадает с безусловной
вероятностью того, разговор будет
продолжаться ровно минут, т.е. вероятность появления значения
случайной величиныне зависит от того, наступало событие
минут, т.е. вероятность появления значения
случайной величиныне зависит от того, наступало событие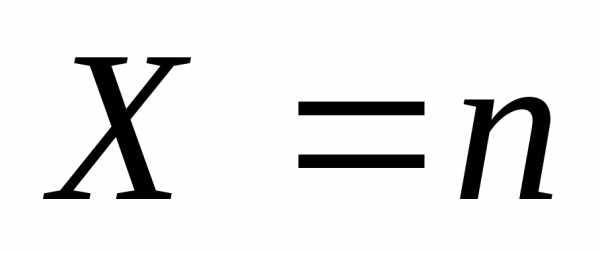 или нет. Это означает, что предыстория
не влияет на вероятность появления
события в ближайшем будущем
или нет. Это означает, что предыстория
не влияет на вероятность появления
события в ближайшем будущем
Среди всех дискретных распределений свойством отсутствия последействия обладает только геометрическое распределение.
Пример
2.
Пусть стохастический эксперимент –
бросание монеты до появления герба.
Вероятности успеха и неуспеха равны
соответственно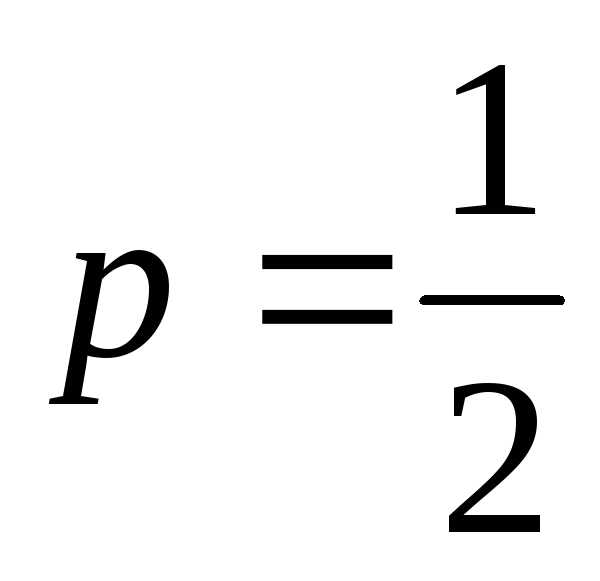 ,
,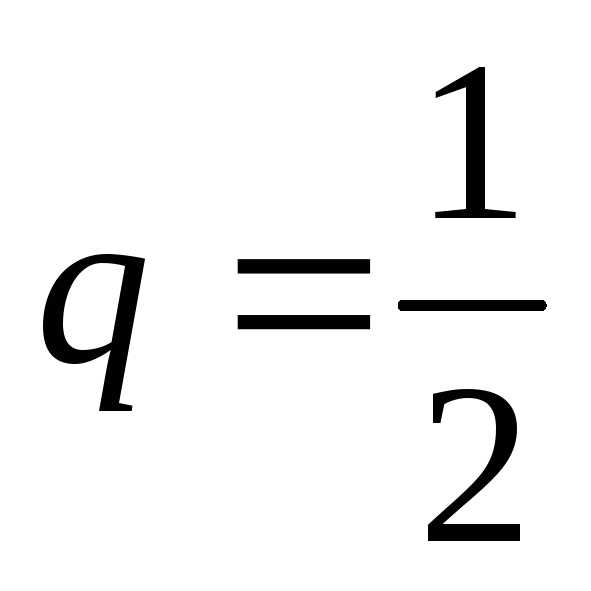 .
Случайная величина – число бросаний
до появления герба имеет геометрическое
распределение. Ряд распределения
.
Случайная величина – число бросаний
до появления герба имеет геометрическое
распределение. Ряд распределения
studfiles.net
Лекция №5
Лекция №5Лекция 5. Основные дискретные распределения |
1. Биномиальное распределение |
Определение 1.
Дискретная СВ X с реализациями xk= k, k = 0,n, имеет биномиальное распределение с параметрами n и p О [0,1], что символически обозначается как X ~ Bi(n, p), если вероятность события {X = xk} определяется формулой Бернулли:| pk | Δ = |
P{X = xk} | Δ = |
Pn(k) | Δ = |
Cnkpkqn-k , q = 1 — p. |
Замечание 1. Пусть
опыт G повторяется n раз в одних и тех же условиях, при этом событие A появляется при каждом повторении опыта с одной и той же вероятностью Тогда по теореме Л3.Р5.Т1 вероятность появления события A ровно k раз при n повторениях опыта G определяется формулой Бернулли Pn(k) = Cnkpkqn-k , т.е. случайная величина X, являющаяся числом появления события A при n повторениях опыта, имеет биномиальное распределение. Заметим, что формула Бернулли совпадает с выражением для (k + 1)-го слагаемого в разложении бинома Ньютона (p + q)n, и поэтому такое распределение и называется биномиальным.Замечание 2.
Характеристическая функция СВ X ~ Bi(n, p):g(t) |
Δ = |
n ∑ k=0 |
pkeitk = |
n ∑ k=0 |
Cnk(peit)kqn-k = |
mx |
Δ = |
ν1 = |
1 i |
d dt |
g(t) |
| | t =0 |
= |
1 i |
[ |
d dt |
(q + peit)n |
] |
| | t =0 |
= np(q + p)n-1 = np, |
| ν2 = | 1 i2 |
d2 dt2 |
g(t) |
| | t =0 | = |
1 i2 |
d2 dt2 |
(q + peit)n |
| | t =0 | = |
= |
np i |
[ |
d dt |
(q + peit)n-1eit |
] |
| | t =0 |
= |
= np2(n-1)[e2it(q + peit)n-2] |
| | t =0 |
+ np[(q + peit)n-1eit] |
| | t =0 |
= |
dx |
Δ = |
μ2 |
6)mx = |
ν2 — mx2 = n2p2 + npq — n2p2 = npq. |
Пример 1. Монету бросают три раза. Требуется найти
ряд распределения числа X выпавших «гербов». СВ X распределена по биномиальному закону с параметрами n = 3 , p = 1/2 . Поэтому p0 = C30(1/2)3 = 1/8, p2 = p1 = C31(1/2)3 = 3/8, p3 = 1 — (p0 + p1 + p2) = 1/8. Таким образом, получаем следующий ряд распределенияПример 2. Предположим требуется оценить эффективность начала работы магазина с 8 часов утра в течении 5 рабочих дней. Вероятность появления покупателей в это время суток известна и она равна p. Тогда вероятность прихода покупателей в это время k раз за неделю выражается формулой Бернулли. При этом, если, например, для k = 4 эта вероятность P5(4) окажется близкой к единице, то следует ожидать экономический эффект от открытия магазина в 8 часов утра.
2. Распределение Бернулли |
Определение 1.
Биномиальное распределение Bi(1, p) с параметрами n = 1 и p О [0,1] называется распределением Бернулли.Замечание 1. Для распределения
Bi(1, p) имеем по замечанию 2 из предыдущего раздела g(t) = q + peit, mx = p, dx = p(1-p).Замечание 2.
Распределение Бернулли Bi(1, p) играет фундаментальную роль в теории вероятностей и математической статистике, являясь математической моделью опыта с двумя исходами (см. замечание Л10.Р2.З6).Замечание 3. Если Xm, m = 1,n, — независимые
СВ (см. понятие Л9.Р1.О5) с распределением Bi(1, p), тогда СВX |
Δ = |
n ∑ m=1 |
Xm |
Пример 1. Пусть имеется партия некоторого товара, в котором товар с дефектами встречается с вероятностью 1 — p, а товар без дефектов — с вероятностью p. Положим x0 = 1, если попался товар без дефектов, и x1 = 0, если товар с дефектом. Тогда «качество» товара можно описать случайной величиной, имеющей распределение Бернулли Bi(1, p).
3. Распределение Пуассона |
Определение 1.
Дискретная СВ X с реализациями xk = k, k = 0,1,… имеет распределение Пуассона с параметром a > 0, что символически записывается как X ~ П(a), еслиpk |
Δ = |
P{X = xk } = |
ak k! |
e-a. |
Замечание 1.
Найдём Характеристическую функцию СВ X ~ П(а):g(t) |
Δ = |
∞ ∑ k=0 |
pkeitk = |
∞ ∑ k=0 |
ak k! |
e-aeitk = |
= e-a |
∞ ∑ k=0 |
(aeit)k k! |
= e-aeae | it | = ea(e |
it | -1) . |
mx |
Δ = |
ν1 = |
1 i |
d dt |
g(t) |
| | t =0 |
= |
1 i |
[a i eitea(e | it | -1)] |
| | t =0 |
= a ; |
| ν2 = | 1 i2 |
d2 dt2 |
g(t) |
| | t =0 | = |
a i |
[i eitea(e |
it | -1)] |
| | t =0 |
= a(1+a) ; |
Замечание 2. Для
распределения Пуассона характерно числовое равенство mx = dx = a, но при этом физические размерности mx и dx не совпадают.Замечание 3.
Распределение Пуассона широко используется в теории массового обслуживания. Приведем пример типичной ситуации, когда возникает такое распределение.Пример 1. Пусть на телеграфную станцию в
произвольные моменты времени случайным образом поступают заявки на переговоры
с городом N так, что выполняются два условия:
а) вероятность появления любого количества заявок за какой-либо
отрезок времени не зависит от того, сколько их поступило за любой другой, не
пересекающийся с ним отрезок, т.е. заявки распределяются на оси времени
t
независимо друг от друга. Это условие независимости;
б) вероятность появления за достаточно малый интервал времени
длины Δt двух и более заявок пренебрежимо мала по сравнению с
вероятностью поступления в течении этого интервала времени не более одной
заявки, которая пропорциональна Δt с коэффициентом пропорциональности
a. Это условие ординарности.
В данном случае можно показать, что
Пример 2. Пусть машина проехала Δ километров и X — число проколов шины на этом расстоянии. Тогда вероятность k проколов шины может быть найдена по формуле Пуассона (с соответствующим параметром a).
Замечание 4. Между
биномиальным распределением Bi(n, p) и распределением Пуассона П(a) имеется следующая связь.Теорема 1. (Пуассона) Пусть n → ∞, p → 0 и при этом np ≡ a = const. Тогда
Pn(k) → |
ak k! |
e-a , |
где Pn(k) |
Δ = |
Cnkpkqn-k , k = 0,n . |
Замечание 5. Докажем это утверждение, пользуясь замечательным пределом (1 — a/n)n → e-a при n → ∞. Так как здесь p = a/n, q = 1 — a/n, то по определению
Л5.Р1.О1 получаемl i m n → ∞ |
Pn(k) = |
l i m n→∞ |
n(n-1)…(n—k+1) k! |
(a/n)k(1-a/n)n—k = |
| = | ak k! |
l i m n→∞ |
n(n-1)…(n—k+1) nk |
(1-a/n)n (1-a/n)k |
= | ak k! |
e-a. |
Замечание 6. Таким образом, при больших n и малых p (при редких явлениях) выполняется закон малых чисел, в соответствии с которым сложное двухпараметрическое
биномиальное распределение Bi(n, p) можно приближенно заменить однопараметрическим распределением Пуассона П(а), где а = nр. При этом ошибка от такой замены не превышает np2, т.е.| |Cnkpkqn-k — | (np)k k! |
e-np | ≤ np2. |
Пример 3. Пусть некоторая система содержит 5000 независимо работающих элементов.
Вероятность отказа каждого равна 0.001. Найдем вероятность отказа системы, если известно, что он происходит при отказе двух и более ее элементов. Число отказавших элементов является СВ X ~ Bi(5000,0.001). Поскольку значение n = 5000 велико, p = 0.001 мало (а = np = 5) и, кроме того, np2 = 0.005 — приемлемая точность, то воспользуемся замечанием 4: P{X ≥ 2} = 1 — P{X ≤ 1} = 1 — P5000(0) - P5000(1) ≈ 0.9596.mytwims.narod.ru
