Кубический корень найти – 3

Как вычислить быстро кубический корень.

Из таблицы видно, что куб некоторого числа заканчивается цифрами 0, 1, 4, 5, 6, 9, то кубический корень заканчивается той же цифрой, если же число заканчивается одной из цифр 2, 3, 7, 8, то кубический корень из него дополнение этой цифры до 10. Поэтому цифра, стоящая в разряде единиц кубического корня, угадывается сразу. Чтобы найти следующую цифру корня, выделим в кубе класс тысяч: (ху)³ = 1000а + b. Теперь рассмотрим кубы однозначных чисел n из таблицы (1). Если , то х=n.

Пример 1. Пусть известно, что 493039 – куб двузначного числа. Запишем данное число иначе 493*1000+39 и обратимся к таблице (1). Мы видим, что 7³ = 343, 8³ = 512 и . Значит, в искомом корне цифра в разряде десятков – 7. Цифра в разряде единиц – 9, так как последняя цифра 9.

Следовательно, = 79.

Пример 2. Пусть известно, что 238328 – куб двузначного числа. Запишем данное число иначе 238*1000+328 и обратимся к таблице (1). Мы видим, что 6³ = 216, 7³ = 343 и. Значит, в искомом корне цифра в разряде десятков – 6. Цифра в разряде единиц – 2, так как последняя цифра 10 — 8=2.

Следовательно, = 62.

2. Отгадывание корня из куба трехзначного числа.

Для извлечения кубического корня свыше 1 млн. нужно знать кубы чисел от 11 до 20.

Таблица 2

Пример 3. Вычислить

Последняя цифра заданного числа равна 4, следовательно, и последняя цифра искомого числа равна 4. Отбрасываем последние три цифры, получим число . По таблице (2) мы видим, что . Меньшее из этих чисел 19 и дает первые две цифры искомого результата.

Следовательно, = 194.

Пример 4. Вычислить

Цифра в разряде единиц – 7, так как последняя цифра 10 – 3 = 7. Отбрасываем последние три цифры, получим число . Меньшее из этих чисел 15 и дает первые две цифры искомого результата. Следовательно, = 157.

Найдите самостоятельно: ;.

Литература:

1. Кордемский Б.А., Ахадов А.А..Удивительный мир чисел. Математические головоломки и задачи для любознательных, М.Просвещение, 1986.

infourok.ru

Как вычислять кубические корни 🚩 вычислить пределы с кубическим корнем 🚩 Математика

4 июня 2011

Автор КакПросто!

Когда перед средним (с точки зрения математических наклонностей ума) жителем интернета ставят задачу посчитать кубический корень, то звучит это немного устрашающе. Но если есть под рукой агрегат, выполняющий миллиарды математических операций то за время, пока мы набираем это самое слово «корень», задача сводится к тривиальному вопросу, что и в какой последовательности надо нажимать.

Статьи по теме:

Инструкция

Есть не один способ вычислить значение кубического корня числа. Пожалуй, наиболее простой из них — воспользоваться встроенным в ОС Windows калькулятором. Запустить это приложение можно так: сначала нажмите сочетание клавиш WIN + R. В результате откроется окно «Запуск программ», в поле ввода которого наберите короткую команду «calc» (без кавычек) и щелкните кнопку «OK» или нажмите клавишу Enter. Калькулятор по умолчанию будет запущен операционной системой в «обычном» виде. В этом варианте оформления в нем нет функции, нужной вам. Чтобы до нее добраться, надо переключить калькулятор в расширенный режим — в Windows XP и Vista он назван «инженерным», а в Windows 7 — «научным». Для этого в меню раскройте разделе «Вид» и выберите пункт «Инженерный» (либо «Научный»).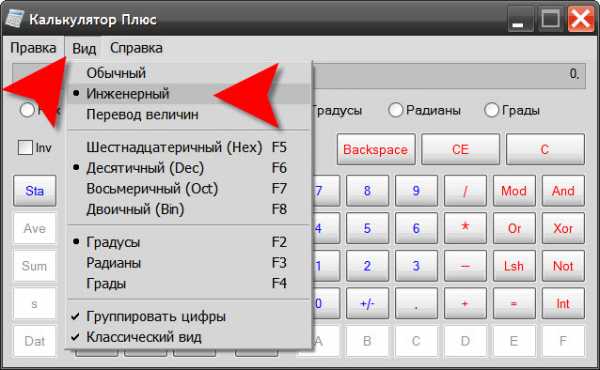 Функциональных кнопок в этом виде будет значительно больше, в числе новых будет и функция возведения чисел в куб — эта кнопка будет использоваться и при вычислении кубического корня. Но прежде чем нажать ее надо проделать еще несколько подготовительных манипуляций. Конечно же надо ввести число, из которого следует извлечь корень нужной степени. Это число можно набирать, щелкая кнопки калькулятора мышью, можно вводить с клавиатуры, можно скопировать и вставить в поле ввода — как вам удобнее это делать.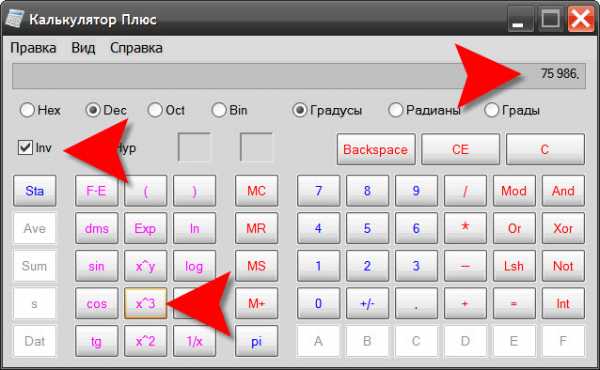

Затем поставьте отметку в поле чекбокса с надписью «Inv» — эта опция инвертирует операции, назначенные кнопкам калькулятора по умолчанию. То есть теперь, нажав кнопку возведения в третью степень (в куб), вы произведете обратную операцию — извлечение корня третьей степени (кубического). Что и требуется.

Видео по теме

Обратите внимание

Этот легкий и необычный способ позволяет вычислить корень кубический из числа, если ответ — целое число. Чтобы извлечь корень кубический из числа, число, стоящее под знаком корня, необходимо представить в виде суммы нечетных слагаемых. Количество таких слагаемых равно кубическому корню из этого числа (если ответ является целым числом).

Полезный совет

Кубический корень из комплексного числа (из любого числа) имеет ровно три значения (частный случай свойства корня n-ой степени): Здесь под понимается арифметический корень из положительного числа. В частности.  Далее найденный промежуточный ответ заменим буквой . Вычислите по формуле такое число , что его результат меньше нижнего числа, но при увеличении на 1 становиться больше. Запишите найденное справа от ответа.

Источники:

• вычислить кубометр

Операцию нахождения корня третьей степени обычно называют извлечением «кубического» корня, а заключается она в нахождении такого вещественного числа, возведение которого в куб даст значение равное подкоренному числу. Операция извлечения арифметического корня любой степени n эквивалентна операции возведения в степень 1/n. Для практического вычисления кубического корня можно использовать несколько способов.

Инструкция

Используйте онлайн-калькулятор для нахождения корня третьей степени. Например, чтобы сделать это с помощью сервиса, помещенного на странице http://csgnetwork.com/cuberootcubecalc.html, достаточно ввести число в поле Enter A Value и нажать кнопку Calculate. Этот калькулятор использует для вычислений JavaScript-сценарий, то есть все вычисления производятся непосредственно в вашем компьютере, поэтому результат вы получите мгновенно. Корень кубический из введенного числа будет помещен в поле Calculated Cube Root, где его можно скопировать и перенести в нужную вам программу.

Другой способ — использовать калькулятор, встроенный в поисковую систему Google. Например, для нахождения кубического корня из числа 1730 введите в поле поискового запроса 1730 ^ (1/3). Если надо находить корень из дробного числа, то в качестве разделителя целой и дробной части используйте точку, а не запятую.

Если нет доступа в интернет, то можно использовать калькулятор, встроенный в операционную систему Windows. Ссылка на его запуск упрятана не менее глубоко, чем смерть Кащея. Чтобы добраться до нее сначала раскройте главное меню на кнопке «Пуск», затем откройте раздел «Все программы», потом щелкните подраздел «Стандартные», после него — секцию «Служебные», а затем кликните пункт «Калькулятор». Можно сделать проще — нажать сочетание клавиш WIN + R, ввести команду calc и нажать Enter.

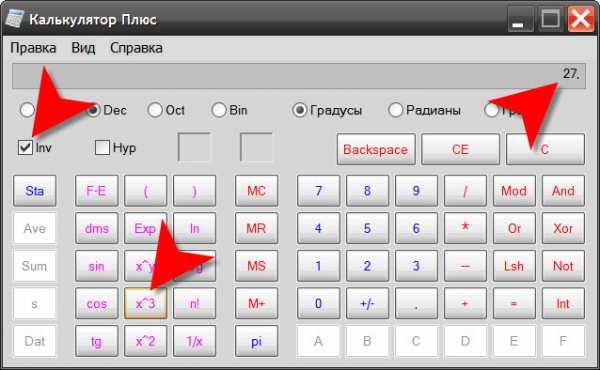
Откройте в меню калькулятора раздел «Вид» и выберите пункт «Инженерный» либо «Научный», так как нужная функция в обычном интерфейсе программы отсутствует. Затем введите число, из которого надо извлечь кубический корень.

Поставьте отметку в чекбоксе рядом с надписью Inv — так вы сообщите программе, что надо выполнять операции обратные тем, что указаны на функциональных кнопках его интерфейса. Затем щелкните кнопку с символами x^3 и калькулятор посчитает и покажет вам результат извлечения кубического корня из введенного числа.

Видео по теме

Источники:

• нахождение степени в

Математическая операция извлечения корня N-ой степени из числа (подкоренного выражения) означает подбор такого значения, которое при умножении на само себя (N-1) раз даст подкоренное выражение. Если при степени, равной двойке, подобрать такое значение в уме еще можно, то для пятой степени это будет довольно затруднительно. Один из наиболее простых способов решить проблему — воспользоваться встроенным в ОС программным калькулятором.

Вам понадобится

Инструкция

Запустите стандартный калькулятор, входящий в состав базового программного обеспечения операционной системы. В любой использующейся сегодня версии Windows это можно сделать через диалог запуска программ — вызовите его одновременным нажатием клавиш Win и R. В единственное поле диалога введите calc, щелкните по кнопке OK и калькулятор будет запущен. В ОС Windows 7 это же можно сделать, раскрыв главное меню (например, нажатием клавиши Win), введя в поле с надписью «Найти программы и файлы» буквы «кальк», а затем кликнув по ссылке «Калькулятор» в списке с результатами поиска. В других версиях Windows такую же ссылку надо искать в секции «Стандартные» раздела «Все программы» главного меню системы.

Нажмите сочетание клавиш Alt и 2 — так интерфейс этого приложения переключается в свой «инженерный» вариант, содержащий нужную вам функцию извлечения корня. Можно это сделать и через меню программы — соответствующий пункт помещен в раздел «Вид».

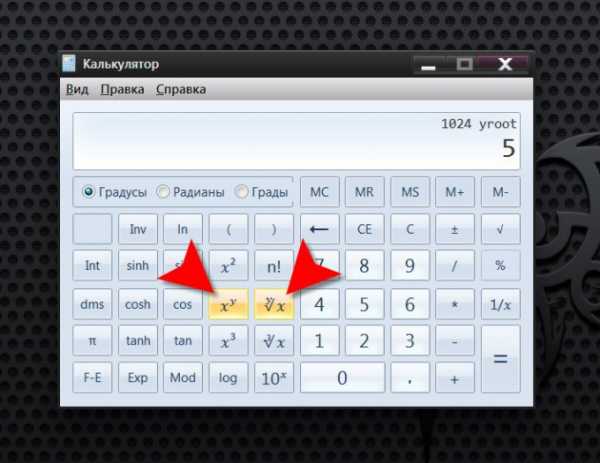
Введите число, из которого надо извлечь корень. Это можно сделать как с использованием клавиатуры, так и кликая мышкой соответствующие кнопки в интерфейсе на экране.

Нажмите кнопку, на которой размещен символ извлечения корня степени y из подкоренного значения x (ʸ√x). Затем введите пятерку и кликните знак равенства в интерфейсе приложения либо нажмите Enter на клавиатуре. Программа произведет вычисление и отобразит результат.

Вместо использованной на предыдущем шаге функции можно воспользоваться другой — возведением в степень. Возведение любого числа в дробную степень означает, в частности, извлечение из него корня с показателем, стоящим в знаменателе дроби. Поэтому, если вы возведете число в степень 1/5 или 0,2, то тоже получите нужный результат. Кликните в интерфейсе кнопку, отвечающую за запуск операции возведения числа x в степень y (xʸ), введите 0,2 и нажмите клавишу Enter. Программа рассчитает и отобразит тот же результат, что и в предыдущем шаге.

Видео по теме

Источники:

• вычисление корней степени n

Если у вас есть возможность пользоваться компьютером, наверняка есть и доступ к программе-калькулятору. Такие приложения включают все возможности обычного гаджета, добавляя к ним удобство использования, свойственное современному программному обеспечению. Например, вычисление корней в программном калькуляторе Windows возможно четырьмя способами.

Вам понадобится

Инструкция

Запустите программу-калькулятор. Соответствующую ссылку можно найти в главном меню ОС, но проще нажать клавишу Win, набрать «ка» и нажать клавишу Enter — система поймет вас с двух букв и откроет программный калькулятор. Для более ранних версий Windows — например, XP — этот метод можно заменить нажатием сочетания клавиш Win + R и вводом команды calc с последующим нажатием клавиши Enter. Если показатель степени корня, который требуется вычислить, равен двойке, сразу поле запуска приложения начинайте вводить подкоренное значение. Это можно делать как с клавиатуры, так и щелкая по кнопкам в интерфейсе программы. Закончив, кликните по кнопке с изображением радикала — второй сверху в правой колонке. Программа извлечет корень и отобразит результат.

Для расчета значения кубического корня возможностей запускаемого по умолчанию интерфейса недостаточно, поэтому активируйте более продвинутый — «инженерный». Для этого нажмите сочетание клавиш Ctrl + 2 или выберите соответствующий пункт в разделе «Вид» меню приложения. Затем введите число, корень которого следует рассчитать, и кликните по кнопке интерфейса, помеченной символами ³√x, и задача будет выполнена.

При извлечении корня с более высоким показателем степени операция ввода будет состоять из двух шагов. Сначала наберите подкоренное число, затем кликните по кнопке с символами ʸ√x, введите показатель степени и нажмите клавишу Enter. Результат появится в соответствующем поле интерфейса приложения.

Есть еще один способ извлечения корня произвольной степени, при котором используется операция возведения в степень с дробным показателем. Вы же знаете, что извлечение корня, например, четвертой степени равносильно возведению в степень 1/4. Поэтому введите сначала число, из которого надо извлечь корень, затем кликните по кнопке возведения в произвольную степень xʸ и наберите десятичную дробь, соответствующую единице, поделенной на показатель степени. Для корня четвертой степени это будет число 1/4=0,25. Нажмите Enter, и корень будет извлечен.

Источники:

• как посчитать корень на калькуляторе

www.kakprosto.ru

Как вычислить корень третьей степени

10 августа 2011

Автор КакПросто!

Во многих школьных и чисто практических задачах требуется вычислить корень третьей степени, называемый также кубическим корнем. Несмотря на внешнюю простоту задачи, вычислить корень третьей степени не так просто. Ведь на калькуляторах нет кнопки, вычисляющей эту функцию.

Статьи по теме:

Вам понадобится

Инструкция

Чтобы вычислить корень третьей степени, возьмите калькулятор, предназначенный для инженерных расчетов. Для вычисления корня третьей степени воспользуйтесь равнозначной функцией возведения в степень 1/3. Чтобы возвести число в степень 1/3, введите это число, затем нажмите на кнопку возведения в степень и наберите приблизительное значение числа 1/3 — 0,333. Такой точности вполне достаточно для большинства расчетов. Однако точность вычислений очень легко повысить – просто добавьте столько троек, сколько уместится на индикаторе калькулятора (например, 0,3333333333333333). Затем нажмите кнопку «=».

Чтобы вычислить корень третьей степени с помощью компьютера, запустите программу «калькулятор Windows». Порядок действий при вычислении корня третьей степени полностью аналогичен описанному выше. Единственное отличие – в дизайне кнопки возведения в степень. На виртуальной клавиатуре калькулятора она обозначена как «x^y».

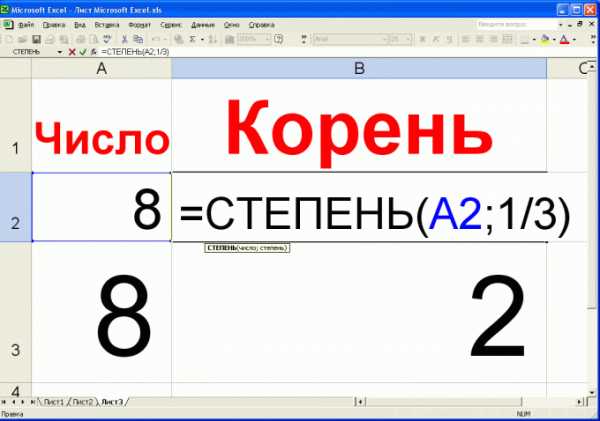
Корень третьей степени можно вычислить и в программе MS Excel. Для этого введите в любую клетку символ «=» и выберите значок «вставка функции» (fx). Выберите в появившемся окошке функцию «СТЕПЕНЬ» и нажмите кнопку «Ок». В появившемся окошке введите значение числа, для которого необходимо вычислить корень третьей степени. В окошко «Степень» введите число «1/3». Число 1/3 набирайте именно в таком виде – как обыкновенную дробь. После этого нажмите кнопку «Ок». В той клетке таблицы, где создавалась формула, появится кубический корень из заданного числа.

Если корень третьей степени приходится вычислять постоянно, то немного усовершенствуйте описанный выше метод. В качестве числа, из которого требуется извлечь корень, укажите не само число, а клетку таблицы. После этого, просто каждый раз вводите в эту клетку исходное число – в клетке с формулой будет появляться его кубический корень.

Видео по теме

Обратите внимание

Заключение. В данной работе были рассмотрены различные методы вычисления значений кубического корня. Выяснилось, что значения кубического корня можно находить с помощью метода итераций, также можно аппроксимировать кубический корень, возводить число в степень 1/3, искать значения корня третьей степени с помощью Microsoft Office Ecxel, задавая формулы в ячейках.

Полезный совет

Корни второй и третьей степени употребляются особенно часто и поэтому имеют специальные названия. Квадратный корень: В этом случае показатель степени обычно опускается, а термин «корень» без указания степени чаще всего подразумевает квадратный корень.  Практическое вычисление корней Алгоритм нахождения корня n-ной степени. Квадратные и кубические корни обычно предусмотрены во всех калькуляторах.

Источники:

• корень третий степени
• Как извлечь квадратный корень в N степени в Excel

www.kakprosto.ru

Как вычислить кубический корень

Вычисление кубического корня

10 последних вычислений

Если ваш калькулятор не обладает такой функцией, или его просто нет поблизости, а вычисления на бумаге займут огромное количество времени, а иногда и усилий, то на этом сайте можно одолеть задачу в считанные секунды. Он готов решать задачу прямо сейчас.

Онлайн вычисление корня совершенно бесплатно. Мы предусмотрели максимально полезный и удобный интерфейс с возможностью ввода чисел не только с помощью мыши, но и клавиатуры. Сложные математические расчеты станут настоящим удовольствием даже для тех, кто имел в школе двойку по математике!

Сколько гневных слов произнесено в его адрес? Порой кажется, что кубический корень невероятно сильно отличается от квадратного. На самом деле разница не настолько велика. Особенно, если понять, что они только частные случаи общего корня n-ой степени.

Зато с его извлечением могут возникнуть проблемы. Но чаще всего они связаны с громоздкостью вычислений.

Что нужно знать о корне произвольной степени?

Во-первых, определение этого понятия. Корнем n-ой степени из некоторого «а9raquo; называется такое число, которое при возведении в степень n дает исходное «а9raquo;.

Причем бывают четные и нечетные степени у корней. Если n — четное, то подкоренное выражение может быть только нулем или положительным числом. В противном случае вещественного ответа не будет.

Когда же степень нечетная, то существует решение при любом значении «а9raquo;. Оно вполне может быть и отрицательным.

Во-вторых, функцию корня всегда можно записать, как степень, показателем которой является дробь. Иногда это бывает очень удобным.

Например, «а9raquo; в степени 1/n как раз и будет корнем n-ой степени из «а9raquo;. В этом случае основание степени всегда больше нуля.

Аналогично «а9raquo; в степени n/m будет представлено, как корень m-ой степени из «а n ».

В-третьих, для них справедливы все действия со степенями.

• Их можно перемножать. Тогда показатели степеней складываются.
• Корни можно разделить. Степени нужно будет вычесть.
• И возвести в степень. Тогда их следует перемножить. То есть ту степень, которая была, на ту, в которую возводят.

В чем сходства и различия квадратного и кубического корней?

Они похожи, как родные братья, только степень у них разная. И принцип их вычисления одинаков, различие только в том, сколько раз должно число на себя умножиться, чтобы получить подкоренное выражение.

А о существенном отличии было сказано чуть выше. Но повториться не будет лишним. Квадратный извлекается только из неотрицательного числа. В то время, как вычислить кубический корень из отрицательной величины не составит труда.

Извлечение кубического корня на калькуляторе

Каждый человек хоть раз делал это для квадратного корня. А как быть если степень «39raquo;?

На обычном калькуляторе имеется только кнопочка для квадратного, а кубического — нет. Здесь поможет простой перебор чисел, которые трижды умножаются на себя. Получилось подкоренное выражение? Значит, это ответ. Не получилось? Подбирать снова.

А что в инженерном виде калькулятора в компьютере? Ура, здесь есть кубический корень. Эту кнопочку можно просто нажать, и программа выдаст ответ. Но это не все. Здесь можно вычислить корень не только 2 и 3 степени, но и любой произвольной. Потому что есть кнопка у которой в степени корня стоит «у9raquo;. То есть после нажатия этой клавиши потребуется ввести еще одно число, которое будет равно степени корня, а уже потом «=9raquo;.

Извлечение кубического корня вручную

Этот способ потребуется, когда калькулятора под рукой нет или воспользоваться им нельзя. Тогда для того чтобы вычислить кубический корень из числа, потребуется приложить усилия.

Сначала посмотреть, а не получается ли полный куб от какого-нибудь целого значения. Может быть под корнем стоит 2, 3, 5 или 10 в третьей степени?

В противном случае нужно будет считать столбиком. Алгоритм не самый простой. Но если немного попрактиковаться, то действия легко запомнятся. И вычислить кубический корень больше не будет проблемой.

1. Мысленно разделить подкоренное выражение на группы по три цифры от десятичной запятой. Чаще всего нужна дробная часть. Если ее нет, то нули нужно дописать.
2. Определить число, куб которого меньше целой части подкоренного выражения. Его записать в промежуточный ответ над знаком корня. А под этой группой расположить его куб.
3. Выполнить вычитание.
4. К остатку приписать первую группу цифр после запятой.
5. В черновике записать выражение: а 2 * 300 * х + а * 30 * х 2 + х 3 . Здесь «а9raquo; — это промежуточный ответ, «х9raquo; является числом, которое меньше получившегося остатка с приписанными к нему числами.
6. Число «х9raquo; нужно записать после запятой промежуточного ответа. А значение всего этого выражения записать под сравниваемым остатком.
7. Если точности достаточно, то расчеты прекратить. В противном случае нужно возвращаться к пункту под номером 3.

Наглядный пример вычисления кубического корня

Он нужен потому, что описание может показаться сложным. На рисунке ниже показано, как извлечь кубический корень из 15 с точностью до сотых.

Единственной сложностью, которую имеет этот метод, заключается в том, что с каждым шагом числа увеличиваются многократно и считать в столбик становится все сложнее.

1. 15> 2 3 , значит под целой частью записана 8, а над корнем 2.
2. После вычитания из 15 восьми получается остаток 7. К нему нужно приписать три нуля.
3. а = 2. Поэтому: 2 2 * 300 * х +2 * 30 * х 2 + х 3 2 + х 3 2 + х 3 2 + х 3

lotos-n.ru

Как вычислить кубический корень вручную Как? Так!

Содержимое:

3 части:

Если под рукой есть калькулятор, извлечь кубический корень из любого числа не составит никаких проблем. Но если калькулятора нет или вы просто хотите произвести впечатление на окружающих, извлеките кубический корень вручную. Большинству людей описываемый здесь процесс покажется довольно сложным, но с практикой извлекать кубические корни станет намного легче. Перед тем как приступить к чтению данной статьи, вспомните основные математические операции и вычисления с числами в кубе.

Шаги

Часть 1 Извлечение кубического корня на простом примере

1. 1 Запишите задачу. Извлечение кубического корня вручную похоже на деление в столбик, но с некоторыми нюансами. Сначала запишите задачу в определенной форме.
   • Запишите число, из которого нужно извлечь кубический корень. Число разбейте на группы по три цифры, причем отсчет начните с десятичной запятой. Например, нужно извлечь кубический корень из 10. Напишите это число так: 10, 000 000. Дополнительные нули призваны повысить точность результата.
   • Возле и над числом нарисуйте знак корня. Представьте, что это горизонтальная и вертикальная линии, которые вы рисуете при делении в столбик. Единственное отличие – это форма двух знаков.
   • Над горизонтальной линией поставьте десятичную запятую. Сделайте это непосредственно над десятичной запятой исходного числа.
2. 2 Запомните результаты возведения в куб целых чисел. Они будут использованы в вычислениях.
   • 13=1∗1∗1=1 3 Найдите первую цифру ответа. Выберите куб целого числа, который ближе всего, но меньше первой группы из трех цифр.
     • В нашем примере первая группа из трех цифр – это число 10. Найдите наибольший куб, который меньше 10. Таким кубом является 8, а кубический корень из 8 равен 2.
     • Над горизонтальной линией над цифрой 10 напишите цифру 2. Затем запишите значение операции 23 4
       Найдите следующую цифру ответа. К первому остатку припишите вторую группу из трех цифр, а слева от полученного числа проведите вертикальную черту. С помощью полученного числа вы найдете вторую цифру ответа. В нашем примере к первому остатку (2) нужно приписать вторую группу из трех цифр (000), чтобы получить число 2000.
       • Слева от вертикальной линии вы напишите три числа, сумма которых равна некоему первому множителю. Оставьте пустые пространства для этих чисел, а между ними поставьте знаки «плюс».
     • 5 Найдите первое слагаемое (из трех). В первом пустом пространстве запишите результат умножения числа 300 на квадрат первой цифры ответа (она записана над знаком корня). В нашем примере первой цифрой ответа является 2, поэтому 300*(2^2) = 300*4 = 1200. Напишите 1200 в первом пустом пространстве. Первым слагаемым является число 1200 (плюс еще два числа, которые нужно найти).
     • 6 Найдите вторую цифру ответа. Выясните, на какое число нужно умножить 1200, чтобы результат был близок, но не превышал 2000. Таким числом может быть только 1, так как 2*1200 = 2400, что больше 2000. Напишите 1 (вторая цифра ответа) после 2 и десятичной запятой над знаком корня.
     • 7 Найдите второе и третье слагаемые (из трех). Множитель состоит из трех чисел (слагаемых), первое из которых вы уже нашли (1200). Теперь нужно найти оставшиеся два слагаемых.
       • Умножьте 3 на 10 и на каждую цифру ответа (они записаны над знаком корня). В нашем примере: 3*10*2*1 = 60. Прибавьте этот результат к 1200 и получите 1260.
       • Наконец, возведите в квадрат последнюю цифру ответа. В нашем примере последней цифрой ответа является 1, поэтому 1^2 = 1. Таким образом, первый множитель равен сумме следующих чисел: 1200 + 60 + 1 = 1261. Запишите это число слева от вертикальной черты.
     • 8 Умножьте и вычтите. Умножьте последнюю цифру ответа (в нашем примере это 1) на найденный множитель (1261): 1*1261 = 1261. Запишите это число под 2000 и вычтите его из 2000. Вы получите 739 (это второй остаток).
     • 9 Подумайте, является ли полученный ответ достаточно точным. Делайте это каждый раз, после того как завершите очередное вычитание. После первого вычитания ответ был равен 2, что не является точным результатом. После второго вычитания ответ равен 2,1.
       • Чтобы проверить точность ответа, возведите его в куб: 2,1*2,1*2,1 = 9,261.
       • Если вы считаете, что ответ достаточно точный, вычисления можно не продолжать; в противном случае проделайте еще одно вычитание.
     • 10 Найдите второй множитель. Чтобы попрактиковаться в вычислениях и получить более точный результат, повторите действия, которые описаны выше.
       • Ко второму остатку (739) припишите третью группу из трех цифр (000). Вы получите число 739000.
       • Умножьте 300 на квадрат числа, которое записано над знаком корня (21): 300∗212 11 Умножьте последнюю цифру ответа на второй множитель. После того как вы нашли второй множитель и третью цифру ответа, действуйте следующим образом:
         • Умножьте последнюю цифру ответа на найденный множитель: 135475*5 = 677375.
         • Вычтите: 739000-677375 = 61625.
         • Подумайте, является ли полученный ответ достаточно точным. Для этого возведите его в куб: 2,15∗2,15∗2,15=9,94 12 Запишите ответ. Результат, записанный над знаком корня, является ответом с точностью до двух цифр после запятой. В нашем примере кубический корень из 10 равен 2,15. Проверьте ответ, возведя его в куб: 2,15^3 = 9,94, что приблизительно равно 10. Если вам нужна большая точность, продолжите вычисления (как описано выше).

Часть 2 Извлечение кубического корня методом оценок

1. 1 Используйте кубы чисел, чтобы определить верхний и нижний пределы. Если нужно извлечь кубический корень практически из любого числа, найдите кубы (некоторых чисел), которые близки к данному числу.
   • Например, нужно извлечь кубический корень из 600. Так как 83=512 2 Оцените второе число. Первое число вы нашли благодаря знанию кубов целых чисел. Теперь целое число превратите в десятичную дробь, приписав к нему (после десятичной запятой) некоторую цифру от 0 до 9. Необходимо найти десятичную дробь, куб которой будет близок, но меньше исходного числа.
     • В нашем примере число 600 находится между числами 512 и 729. Например, к первому найденному числу (8) припишите цифру 5. Получится число 8,5.
   • 3 Оцените полученное число, возведя его в куб. Сделайте это, чтобы проверить, что куб близок, но не больше исходного числа.
     • В нашем примере: 8,5∗8,5∗8,5=614,1. 4 Если нужно, оцените другое число. Сравните куб полученного числа с исходным числом. Если куб полученного числа больше исходного числа, попробуйте оценить меньшее число. Если же куб полученного числа намного меньше исходного числа, оценивайте большие числа до тех пор, пока куб одного из них не превысит исходное число.
       • В нашем примере: 8,53 5 Оцените следующее число, чтобы повысить точность ответа. К каждому числу, которое вы оценили последним, приписывайте цифру от 0 до 9 до тех пор, пока не получите точный ответ. В каждом оценочном раунде нужно найти верхний и нижний пределы, между которыми находится исходное число.
         • В нашем примере: 8,43=592,7 6 Если нужно, оцените другое число. Сравните куб полученного числа с исходным числом. Если куб полученного числа больше исходного числа, попробуйте оценить меньшее число. Короче говоря, нужно найти такие два числа, кубы которых чуть больше и чуть меньше исходного числа.
           • В нашем примере 8,44∗8,44∗8,44=601,2 7 Выполняйте описанный процесс до тех пор, пока не получите ответ, точность которого вас устроит. Оцените следующее число, сравните его с исходным, затем, если нужно, оцените другое число и так далее. Обратите внимание, что каждая дополнительная цифра после десятичной запятой повышает точность ответа.
             • В нашем примере куб числа 8,43 меньше исходного числа менее чем на 1. Если нужна большая точность, возведите в куб число 8,434 и получите, что 8,4343=599,93

               Часть 3 Объяснение описанного процесса вычисления

               1. 1 Вспомните биноминальный ряд. Биноминальный ряд – это результат возведения бинома (двучлена) в некоторую степень, в данном случае в куб. Чтобы понять описанный здесь алгоритм извлечения кубического корня, сначала вспомните, как возводится в куб двучлен. Скорее всего, вы изучали это в школе (и, вероятно, вскоре забыли, как большинство людей). Переменными A
               2. 2 Возведите двучлен в куб. Сделайте это для того, чтобы понять процесс извлечения кубического корня, который описан в первом разделе. Вычислите (10A+B)3
                  • Подробное объяснение можно найти .
               3. 3 Уясните алгоритм деления в столбик. Обратите внимание, что описанный здесь метод извлечения кубического корня очень напоминает деление в столбик. При делении в столбик нужно найти число (частное), при умножении которого на делитель получится делимое. В описанном методе в качестве частного выступает результат извлечения кубического корня (он записывается над знаком корня). То есть результат извлечения кубического корня можно представить как бином (10A + B). Точные значения А и В на данном этапе не важны: просто запомните, что результат можно записать в виде двучлена.
               4. 4 Посмотрите на биноминальный ряд.
                  Он представляет собой сумму четырех одночленов, благодаря которым можно понять принцип действия алгоритма извлечения кубического корня. Обратите внимание, что множитель каждого этапа извлечения корня равен сумме четырех слагаемых, которые нужно вычислить и сложить.
                  • Множителем первого члена является число 1000. Чтобы вычислить первую цифру ответа, сначала вы находите куб целого числа, который ближе всего, но меньше некоторого числа (а именно первой группы из трех цифр). Это определяет член 1000A^3 биноминального ряда.
                  • Множителем второго члена биноминального ряда является число 300 (3∗102 5 Обратите внимание на увеличение точности ответа. Чем больше этапов извлечения корня вы пройдете, тем точнее будет ответ. Например, в этой статье нужно было извлечь кубический корень из 10. На первом этапе ответ равен 2, так как 23

               Советы

               • Практикуйтесь, чтобы освоить описанные методы. Чем больше практики, тем быстрее вы справитесь с вычислениями.

               Предупреждения

               • В процессе вычисления довольно легко сделать ошибку. Поэтому обязательно проверьте ответ.

               Что вам понадобится

               • Ручка или карандаш
               • Лист бумаги
               • Линейка
               • Ластик

Прислал: Cr1stal . 2017-11-06 10:38:50

kak-otvet.imysite.ru

Как посчитать кубический корень 🚩 Корень кубический калькулятор 🚩 Математика

27 декабря 2018

Автор КакПросто!

В технических расчетах и при решении многих задач иногда требуется посчитать кубический корень, то есть найти такое число, куб которого равен исходному. Для подсчета значения кубического корня достаточно инженерного калькулятора. Однако даже на таком калькуляторе нет специальной клавиши для вычисления кубического корня. Но используя некоторые нехитрые приемы, можно обойтись и без такой кнопки.

Статьи по теме:

Вам понадобится

• инженерный калькулятор или компьютер

Инструкция

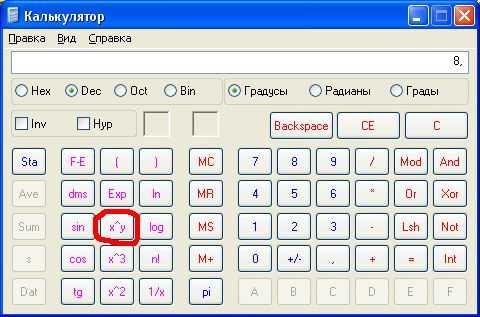
Чтобы посчитать кубический корень найдите такое число, которое при возведении в третью степень будет равно данному. То есть, например, если х – исходное число, а у – кубический корень из этого числа, то должно выполняться равенство:у³ = х Для того чтобы найти кубический корень с помощью калькулятора, возьмите инженерный калькулятор и наберите на нем исходное число. Затем, нажмите на кнопку возведения в степень. Теперь введите значение показателя степени. В данном случае он (теоретически) должен равняться 1/3. Но, так как использование обыкновенных дробей даже на инженерном калькуляторе затруднительно, то наберите округленное значение числа 1/3, то есть: 0,33. Затем нажмите на кнопку «=». На индикаторе калькулятора появится искомое значение. Чтобы получить более точное значение, набирайте не две тройки, а больше, например, 0,333333333333.

Чтобы посчитать кубический корень на компьютере, запустите программу «калькулятор». Если соответствующего значка нет на рабочем столе, проделайте следующее:
— нажмите кнопку «Пуск»;
— выберите пункт меню «Выполнить»;
— введите в появившемся окошке строку «calc».Если появившийся на рабочем столе калькулятор имеет обычный вид (напоминающий «бухгалтерский калькулятор»), то переведите его в режим выполнения инженер расчетов. Для этого, выберите строку «Вид» и укажите пункт «Инженерный».Теперь введите то число, из которого нужно извлечь кубический корень. Затем нажмите на калькуляторе кнопку «x^y». Далее наберите показатель степени, например, 0,33. Для получения более точного результата, можно набрать более длинное значение показателя степени, например, 0,333333333333. Чтобы получить точный результат, введите показатель степени «1/3» в скобках. То есть нажмите последовательно клавиши «(1/3)».

Расчет в программе Excel. Запустите саму программу, нажмите кнопку «=» и выберите функцию «СТЕПЕНЬ». Затем введите то число, из которого требуется извлечь корень третьей степени. После чего, в следующей строке появившегося окошка наберите дробь «1/3» и нажмите кнопку «Ок».

www.kakprosto.ru