Lim 0 бесконечность – , .

пределы на бесконечность на бесконечность

 

Рассмотрим  пределы на раскрытие неопределенности вида бесконечность на бесконечность.

Сначала учтем следующее:

— если при вычислении предела в числителе дроби  стоит число, то

   

— или

   

Выражение вида 

   

— это предел на неопределенность вида бесконечность, деленная на бесконечность (или просто бесконечность на бесконечность).

Чтобы найти предел,  надо раскрыть неопределенность вида бесконечность на бесконечность. Для этого и в числителе, и в знаменателе выносим за скобки степень с наибольшим показателем. Затем сокращаем на нее.

1)

   

В дальнейшем просто делим почленно числитель и знаменатель (то есть каждое слагаемое) на старшую степень икса.
2)

   

3)

   

4)

   

А теперь сделаем выводы. Пределы на неопределенность бесконечность на бесконечность сводятся к одному из трех вариантов:

   

Примеры для самопроверки: 

   

   

   

Показать решение

 

 

adminПредел функции

www.matematika.uznateshe.ru

Определение предела функции на бесконечности

Конечный предел функции на бесконечности

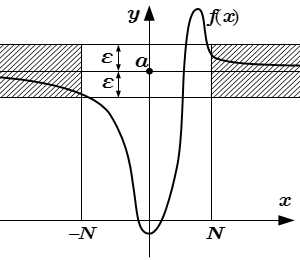
Предел функции на бесконечности:
|f(x) – a| < ε  при  |x| > N

Определение предела по Коши
Пусть функция f(x) определена в некоторой окрестности бесконечно удаленной точки, при |x| > K, где K – положительное число. Число a называется пределом функции f(x) при x стремящемся к бесконечности (), если для любого, сколь угодно малого положительного числа ε > 0, существует такое число N_ε> K, зависящее от ε, что для всех x, |x| > N_ε, значения функции принадлежат ε — окрестности точки a:
|f(x) – a| < ε.
Предел функции на бесконечности обозначается так:
.
Или     при   .

Также часто используется следующее обозначение:
.

Запишем это определение, используя логические символы существования и всеобщности:
.
Здесь подразумевается, что значения принадлежат области определения функции.

Односторонние пределы

Левый предел функции на бесконечности:
|f(x) – a| < ε  при  x < –N

Часто встречаются случаи, когда функция определена только для положительных или отрицательных значений переменной x (точнее в окрестности точки или ). Также пределы на бесконечности для положительных и отрицательных значений x могут иметь различные значения. Тогда используют односторонние пределы.

Левый предел в бесконечно удаленной точке или предел при x стремящемся к минус бесконечности () определяется так:
.
Правый предел в бесконечно удаленной точке или предел при x стремящемся к плюс бесконечности ():
.
Односторонние пределы на бесконечности часто обозначают так:
;   .

Бесконечный предел функции на бесконечности

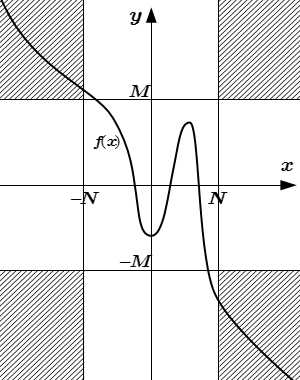
Бесконечный предел функции на бесконечности:
|f(x)| > M  при  |x| > N

Определение бесконечного предела по Коши
Пусть функция f(x) определена в некоторой окрестности бесконечно удаленной точки, при |x| > K, где K – положительное число. Предел функции  f(x)  при x стремящемся к бесконечности (), равен бесконечности, если для любого, сколь угодно большого числа M > 0, существует такое число N_M> K, зависящее от M, что для всех x, |x| > N_M, значения функции принадлежат окрестности бесконечно удаленной точки:
|f(x)| > M.
Бесконечный предел при x стремящемся к бесконечности обозначают так:
.
Или   при  .

С помощью логических символов существования и всеобщности, определение бесконечного предела функции можно записать так:
.

Аналогично вводятся определения бесконечных пределов определенных знаков, равных и :
.
.

Определения односторонних пределов на бесконечности.
Левые пределы.
.
.
.
Правые пределы.
.
.
.

Определение предела функции по Гейне

Пусть функция f(x) определена на некоторой окрестности бесконечно удаленной точки x₀, где или или .
Число a (конечное или бесконечно удаленное) называется пределом функции f(x) в точке x₀:
,
если для любой последовательности {x_n}, сходящейся к x₀: ,
элементы которой принадлежат окрестности , последовательность {f(x_n)} сходится к a:
.

Если в качестве окрестности взять окрестность бесконечно удаленной точки без знака: , то получим определение предела функции при x стремящемся к бесконечности, . Если взять левостороннюю или правостороннюю окрестность бесконечно удаленной точки x₀: или , то получим определение предела при x стремящемся к минус бесконечности и плюс бесконечности, соответственно.

Определения предела по Гейне и Коши эквивалентны.

Примеры

Пример 1

Используя определение Коши показать, что
.

Решение

Введем обозначения:
.
Найдем область определения функции . Поскольку числитель и знаменатель дроби являются многочленами, то функция определена для всех x кроме точек, в которых знаменатель обращается в нуль. Найдем эти точки. Решаем квадратное уравнение. ;
.
Корни уравнения:
;   .
Поскольку , то и .
Поэтому функция определена при . Это мы будем использовать в дальнейшем.

Выпишем определение конечного предела функции на бесконечности по Коши:
.
Преобразуем разность:
.
Разделим числитель и знаменатель на и умножим на –1:
.

Пусть .
Тогда
;
;
;
.

Итак, мы нашли, что при ,
.
Вводим положительные числа и :
.
Отсюда следует, что
  при ,    и  .

Поскольку всегда можно увеличить, то возьмем . Тогда для любого ,
  при  .
Это означает, что .

Пример 2

Пусть .
Используя определение предела по Коши показать, что:
1) ;
2) .

1) Решение при x стремящемся к минус бесконечности

Поскольку , то функция определена для всех x.
Выпишем определение предела функции при , равного минус бесконечности:
.

Пусть  . Тогда
;
.

Итак, мы нашли, что при ,
.
Вводим положительные числа и :
.
Отсюда следует, что для любого положительного числа M, имеется число , так что при ,
.

Это означает, что .

2) Решение при x стремящемся к плюс бесконечности

Преобразуем исходную функцию. Умножим числитель и знаменатель дроби на и применим формулу разности квадратов:
.
Имеем:

.
Выпишем определение правого предела функции при :
.

Введем обозначение: .
Преобразуем разность:
.
Умножим числитель и знаменатель на :
.

Пусть
.
Тогда
;
.

Итак, мы нашли, что при ,
.
Вводим положительные числа и :
.
Отсюда следует, что
  при   и  .

Поскольку это выполняется для любого положительного числа , то
.

Использованная литература:
С.М. Никольский. Курс математического анализа. Том 1. Москва, 1983.

Автор: Олег Одинцов.     Опубликовано: 17-05-2018

1cov-edu.ru

Ответы@Mail.Ru: А когда считаешь предел и получается ноль умножить на бесконечность

Мистер Бонд, прочтите первый том «Курса дифференциального и интегрального исчисления» Г. М. Фихтенгольца. Ноль * Бесконечность — это неопределенность. Она сводится к неопределенности типа 0 / 0 или Бесконечность / Бесконечность, которые дальше можно раскрыть, например, применяя правила Лопиталя. Не хотите открывать Фихтенгольца — суньтесь в Яндекс. Вот ссылочка первая же по запросу «Неопределенность, Правило Лопиталя» <a rel=»nofollow» href=»http://www.mathelp.spb.ru/book1/lopital.htm» target=»_blank»>http://www.mathelp.spb.ru/book1/lopital.htm</a> Успехов в решении! И не забывайте о том, что Джеймс Бонд всегда находил решения самых трудных задач.

ноль… т.к. если любое число из этого бесконечного ряда чисел умножать на ноль, все равно будет 0…

к сожалению только ноль…

А что у нас «ноль»? Ноль величина абстрактная и в природе не имеющая места быть вообще.

А это смотря как умножать…

нуль. Нуль деленная на беск-ть=неопред-ть.

не слушай троечников — неопределенность, разумеется! И может получиться любое число в результате.

Иногда так хочется,чтоб ноль стал бесконечностью…

Это вы предел не доразложили. Непонятно какой ноль и какая бесконечность. Например: 1. Lnx/x при x стремящемся к бесконечности — 0 2. e^x/x при x стремящемся к бесконечности — бесконечность 3. sin2x/x при x стремящемся к 0 равно 2 Поэтому, прежде чем считать предел типа f(x)/g(x) при x стремящемся к x0 надо провести разложение в окрестности x0 обоих функций и после сокращения в числителе или знаменателе у вас останется константа — а далее все просто.

Это неопределенность.

Это неопределенность. Одна сорокомиллионная — это практически ноль, а сорок миллионов — почти бесконечность,их перемножить, что получится?Если мы не знаем точно о сорока миллионах или о восьмидесяти идет речь? Неопределенность.

Это неопределенность типа ноль умножить на бесконечность.

Сколько раз ни складывай ноль с нулем, ноль никогда не сдвинется с места, даже если бесконечное число раз. Это очевидно, поэтому результат всегда равен нулю. Другие числа могут получиться, если считать предел произведения функций, одна из которых стремится к нулю, а другая к бесконечности, в этом случае все зависит от их скоростей стремления к нулю или к бесконечности.

0 на бесконечность умножать нельзя т. к возьмем 0 0/0=бесконечность А 1/0= тоже бесконечность любое число даже 0 деленное на 0 будет бесконечность и число умножая на бесконечность будет неопределимость бесконечностью не имеет значения поэтому 0 * бесконечность нельзя а 0 на себя можно

touch.otvet.mail.ru

7.Правила лопиталя для раскрытия неопределённостей вида 0/0 и бесконечность/бесконечность. Раскрытие неопределённостей вида 0*бесконечность, бесконечность-бесконечность, 1бесконечность, 00

Правило Лопиталя-пусть функция f(x) и g(x) имеют производные в окрестности точки х_о тогда: 1)если lim f(x)= lim g(x)=бесконечность, то limf(x)/g(x)=(бесконечность/бесконечность)= lim f’(x)/g’(x), при условии что последний предел существует. 2)если lim f(x)=lim g(x)=0, то lim f(x)/g(x)= (0/0)= lim f’(x)/g’(x), при условии что последний существует.

Следовательно если мы имеем неопределённости бесконечность/бесконечность, 0/0, воспользоваться правилом Лопиталя означает найти производные числителя и знаменателя, а затем вычислить новый предел.

Пример lim sin4x/x=(0/0)=lim(sin4x)’/x= lim4cos4x/1=4*cos0=4*1=4

3)0*бесконечность, пусть f стремиться к 0, g стремиться к бесконечности, тогда fg=f/ (1/g)= (0/0)=g/(1/f)= (бесконечность/бесконечность), т.е. мы свели данную неопределённость к 0/0 или бесконечность/бесконечность, после чего можно применять правило Лопиталя

4)бесконечность-бесконечность . Пусть f стремиться к бесконечности, g стремиться к бесконечности, тогда f-g=1/(1/f)- 1/(1/g)=(1/g)-(1/f)/(1/f)*(1/g)=(0/0)

5)1^{бесконечность},0⁰, бесконечность⁰. Данные неопределённости также сводятся к неопределённостям бесконечность/бесконечность или 0/0 . для этого можно воспользоваться формулой f^g=e^infg=eglnf, f>0. Так, если f стремиться к 1, g стремиться к бесконечности, то получаем неопределённость 0*бесконечность (так как ln1=0), после чего можно получить бесконечность/бесконечность или 0/0

8.Дифференциал функции.Связь дифференциала и производной.Использование дифференциала в приближенных вычислениях.

Функция f(x) называется дифференцируемой в точке х₀, если ее приращение в этой точке можно представить в виде дельта y=f(x₀+дельтаx)-f(x₀)=A*дельтаx+a(дельтаx)

Для того чтобы функция f(x) была дифференцируемой в точке х₀, необходимо и достаточно, чтобы в точке х₀ существовала произвлдная f’(x)=A.

F(x₀+дельтаx)-f(х₀)=f’(x₀)*дельтаx+a(дельтах)

Функция f’(x₀)*дельтаx есть главная линейная часть приращения функции f(x) в точке х₀.Эту главную линейную часть приращения функции f(x) и называется дифференциалом функции f(x) в точке х₀ и обозначают df(x₀)=f’(x₀)*дельтаХ, в частности для f(x)=x имеем df=dx=1*дельтаХ=дельтаХ, следовательно df(x₀)=f’(x₀)dx

Для дифференциалов функций f и g справедливы формулы, подобные формулам для производных функций:

1)d(f+g)=df+dg

2)d(f*g)=g*df+f*dg

3)d(f/g)=(gdf-fdg)/g²

Данные формулы будут широко применяться при вычислении интегралов функций. С помощью дифференциала можно также приближенно вычислить значения функции f для ч, близких к x₀, Так как отбросив бесконечно малую функцию в формуле 2, получаем: f(x₀+дельтаХ)=f(x₀)+f’(x₀)дельтаХ

9.Исследование на монотонность функции одной переменной. Точки экстремума. Необходимые и достаточные условия существования экстремума.

Пусть задана функция y=f(x) на множестве Х и х₀-внутренняя точка множества Х.

Обозначим через U(x₀) окрестность точки х₀.В точке х₀ функция f(x) имеет локальный максимум, если существует такая окрестность U(x₀) точки х₀, что для всех х из этой окрестности выполнено условие f(x)<=f(x₀).

Точки локальных максимума и минимума называются точки локальных экстремумов, а значения функции в них-локальными экстремумами функции.Пусть функция f(x) определена на отрезке[a,b] и имеет локальный экстремум на каком0то из концов этого отрезка.Тогда такой экстремум называется локальным односторонним или краевым экстремумом. В этом случае соответствующая окрестность является правой для точки а и левой для точки b полуокрестностью.

Критическими точками , т.е. точки подозрительные на экстремум функции на интервале [a,b] , являются точки,в которых производная существует и равна 0 либо она не существует или равна бесконечности.

Первое достаточное условие экстремума-пусть непрерывная функция диффиринцируема в некоторой проколотой окрестности U(x₀) точки х₀, тогда: 1)если f’(x)>0 при х<x_0, х принадлежит U(х₀) и f’(x)<0 при х>x₀, x принадлежит U(x₀), то в точке х₀-локальный максимум

2)если f’(x)<0 при x<x₀ х принадлежит U(x₀) и f’(x)>0при x>x₀ x принадлежит U(x₀), то в точке х₀

локальный минимум.

Функция называется n раз непрерывно-дифференцируемой на некотором промежутке, если на этом промежутке она имеет непрерывные производные до порядка n включительно (n=0,1,2,….)

Второе достаточное условие экстремума- пусть функция f(x) дважды непрерывно-дифференцируема. Если х₀-стационарная точка (f’(x₀)=0) в которой f’’(x₀)>0, то в точке х₀ функция имеет локальный минимум. Если же f’’(x₀)< 0 то в точке х₀ функция имеет локальный максимум.

studfiles.net

один в степени бесконечность | Математика

Рассмотрим, как раскрывается неопределенность один в степени бесконечность в другой форме записи 2 замечательного предела. В этом случае фактически имеем неопределенность один в степени один на ноль.

Второй замечательный предел иначе можно записать так:

 

   

а если α=f(x), при условии f(x)→0, при x→0, имеем:

   

Рассмотрим на примерах, как раскрыть неопределенность один в степени бесконечность в этом случае.

Найти пределы:

   

  Получили неопределенность один в степени один на ноль. Поскольку 

   

Чтобы воспользоваться модификацией второго замечательного предела и раскрыть неопределенность один в степени бесконечность, рассуждаем так:

   

   

(не забываем о требовании  f(x)→0, при x→0).

   

   

   

Чтобы избавиться от неопределенности ноль на ноль в показателе степени, в числителе выносим за скобки общий множитель x и сокращаем дробь на x:

   

Будьте внимательны! Если в примере нет неопределенности, предел вычисляем непосредственно:

   

   

Неопределенность вида ноль на ноль в показателе степени — первый замечательный предел:

   

 

 

www.matematika.uznateshe.ru

Раскрытие неопределенностей — Мегаобучалка

При определении пределов часто возникают ситуации, называемые неопределенностями. Мы рассмотрим неопределенности следующих видов

1) – неопределенность “ноль делить на ноль”.

2) – неопределенность “бесконечность делить на бесконечность”.

 

3) –неопределенность “ноль умножить на бесконечность”.

Нахождение пределов в этих случаях называется раскрытием неопределенностей.

Рассмотрим некоторые приемы раскрытия каждой неопределенности в отдельности.

Неопределенность появляется при нахождении предела отношения двух бесконечно малых функций .

Пример 1.4

.

Здесь = 4 – 10 + 6 = 0 и = 0. Числитель и знаменатель дроби являются бесконечно малыми при , т.е. имеет место неопределенность . Для раскрытия неопределенности в рассматриваемом случае числитель и знаменатель дроби разложим на множители и сократим на величину , дающую 0 в числителе и знаменателе:

= = = = = – .

Пример 1.5

Найти предел: .

Решение

Здесь также имеем дело с неопределенностью . Для раскрытия этой неопределенности умножим числитель и знаменатель дроби на выражение , которое называется сопряженным выражению , тогда

 

= = = =

= = = .

Для раскрытия неопределенности в некоторых случаях могут быть полезны следующие определения и теоремы.

Определение 1.1. Пусть и две БМ при . Если

,

(1.1)

 

то БМ и называются эквивалентными. Эквивалентность БМ и обозначается .

 

Теорема 1.1. (Первый замечательный предел). Можно показать

[ ], что

 

,

(1.2)

 

Предел (1.2) называется первым замечательным пределом. Из теоремы 1.1 и определения 1.1 следует, что . Приведем еще некоторые примеры эквивалентных БМ при a® 0:

Таблица 1.1

Теорема 1.2.

 

Предел отношения двух бесконечно малых величин равен пределу отношения бесконечно малых, эквивалентных данным.

Поясним, что утверждает теорема. Пусть и две бесконечно малые функции. Известны еще две БМ и , причем и . Тогда .

Доказательство:

= , что и требовалось. доказать.

Каждый из пределов в рамках равен единице, т.к. это пределы отношений эквивалентных бесконечно малых.

Пример 1.6

Найти .

 

Решение

Здесь имеет место неопределенность , которая раскрывается

переходом к эквивалентным величинам: sin5x~5x, sin3x~3x, по теореме 1.2 получаем:

= = = .

 

Неопределенность появляется при нахождении предела отношения двух бесконечно больших .

 

Пример 1.7

Найти .

 

Решение

Здесь имеет место неопределенность . Отметим, что самая большая степень, в которой переменная входит в числитель и знаменатель дроби. Для раскрытия неопределенности вынесем за скобки и в числителе и в знаменателе и сократим. Получим

= =

= .

Отметим, что в данном примере высшая степень в числителе равна высшей степени в знаменателе. Предел равен отношению коэффициентов при высших степенях в числителе и знаменателе.

Пример 1.8

= = = = 0.

Отметим, что в данном примере высшая степень в числителе меньше высшей степени в знаменателе. Предел равен нулю.

Пример 1.9

= = =

= = .

В данном примере высшая степень в числителе больше высшей степени в знаменателе. Предел равен бесконечности. В результате рассмотрения примеров 1.7, 1.8 и 1.9 сформулируем общее правило нахождения предела вида

=

=

 

Пример 1.10

.

 

Решение

Здесь , , , поэтому предел равен :

.

 

megaobuchalka.ru

Тема 20 раскрытие неопределенности вида «ноль на ноль». Раскрытие неопределенности «бесконечность на бесконечность»

КОНСПЕКТ 20

20.1 РАСКРЫТИЕ НЕОПРЕДЕЛЕННОСТИ ВИДА  

Пример 1

Решить предел Сначала попробуем подставить -1 в дробь:В данном случае получена так называемая неопределенность.

Общее правило:если в числителе и знаменателе находятся многочлены, и имеется неопределенности вида, то для ее раскрытиянужно разложить числитель и знаменатель на множители.

Для этого чаще всего нужно решить квадратное уравнение и (или) использовать формулы сокращенного умножения.

Разложим числитель на множители.

Пример 2

Вычислить предел

Разложим числитель и знаменатель на множители.

Числитель: Знаменатель:,

 

Метод умножения числителя и знаменателя на сопряженное выражение

Продолжаем рассматривать неопределенность вида

Следующий тип пределов похож на предыдущий тип. Единственное, помимо многочленов, у нас добавятся корни.

Пример 3

Найти предел

Умножим числитель и знаменатель на сопряженное выражение.

20.2 РАСКРЫТИЕ НЕОПРЕДЕЛЕННОСТИ ВИДА  

Сейчас мы рассмотрим группу пределов, когда , а функция представляет собой дробь, в числителе и знаменателе которой находятся многочлены

Пример 4

Вычислить предел

Согласно нашему правилу попытаемся подставить бесконечность в функцию. Что у нас получается вверху? Бесконечность. А что получается внизу? Тоже бесконечность. Таким образом, у нас есть так называемая неопределенность вида . Можно было бы подумать, что, и ответ готов, но в общем случае это вовсе не так, и нужно применить некоторый прием решения, который мы сейчас и рассмотрим.

Как решать пределы данного типа?

Сначала мы смотрим на числитель и находим в старшей степени:Старшая степень в числителе равна двум.

Теперь смотрим на знаменатель и тоже находим в старшей степени:Старшая степень знаменателя равна двум.

Затем мы выбираем самую старшую степень числителя и знаменателя: в данном примере они совпадают и равны двойке.

Итак, метод решения следующий: для того, чтобы раскрыть неопределенность  необходимо разделить числитель и знаменатель на  в старшей степени.

Разделим числитель и знаменатель на

Вот оно как, ответ , а вовсе не бесконечность.

Что принципиально важно в оформлении решения?

Во-первых, указываем неопределенность, если она есть.

Во-вторых, желательно прервать решение для промежуточных объяснений. Я обычно использую знак , он не несет никакого математического смысла, а обозначает, что решение прервано для промежуточного объяснения.

В-третьих, в пределе желательно помечать, что и куда стремится. Когда работа оформляется от руки, удобнее это сделать так: Для пометок лучше использовать простой карандаш.

Конечно, можно ничего этого не делать, но тогда, возможно, преподаватель отметит недочеты в решении либо начнет задавать дополнительные вопросы по заданию. А оно Вам надо?

Пример 5

Найти предел Снова в числителе и знаменателе находимв старшей степени:Максимальная степень в числителе: 3 Максимальная степень в знаменателе: 4 Выбираемнаибольшеезначение, в данном случае четверку. Согласно нашему алгоритму, для раскрытия неопределенностиделим числитель и знаменатель на. Полное оформление задания может выглядеть так:

Разделим числитель и знаменатель на

Пример 6

Найти предел Максимальная степень «икса» в числителе: 2 Максимальная степень «икса» в знаменателе: 1 (можно записать как) Для раскрытия неопределенностинеобходимо разделить числитель и знаменатель на. Чистовой вариант решения может выглядеть так:

 

Разделим числитель и знаменатель на

Под записью подразумевается не деление на ноль (делить на ноль нельзя), а деление на бесконечно малое число.

Таким образом, при раскрытии неопределенности вида у нас может получитьсяконечное число, ноль или бесконечность.

 

ПРАКТИКУМ 20

ЗАДАНИЕ N 1Тема: Раскрытие неопределенности вида «ноль на ноль»

Решение:Если вместо переменнойпоставить значение 7, к которому она стремится, то получим неопределенность видатогда

 ЗАДАНИЕ N 2Тема: Раскрытие неопределенности вида «ноль на ноль»

Решение:Если вместо переменнойпоставить значение 0, к которому она стремится, то получим неопределенность видатогда

ЗАДАНИЕ N 3Тема: Раскрытие неопределенности вида «ноль на ноль»

Решение:Если вместо переменнойпоставить значение 6, к которому она стремится, то получим неопределенность видатогда

ЗАДАНИЕ N 4Тема: Раскрытие неопределенности вида «бесконечность на бесконечность»

Решение:Так какито имеет место неопределенность видаДля ее раскрытия нужно разделить каждое слагаемое числителя и знаменателя на. Тогда, зная, чтополучим:

ЗАДАНИЕ N 5Тема: Раскрытие неопределенности вида «бесконечность на бесконечность»

Решение:Так какито имеет место неопределенность видаДля ее раскрытия нужно разделить каждое слагаемое числителя и знаменателя на. Тогда, зная, чтополучим:

САМОСТОЯТЕЛЬНАЯ РАБОТА 20

ЗАДАНИЕ N 1Тема: Раскрытие неопределенности вида «ноль на ноль»

 ЗАДАНИЕ N 2Тема: Раскрытие неопределенности вида «ноль на ноль»

 ЗАДАНИЕ N 3Тема: Раскрытие неопределенности вида «ноль на ноль»

ЗАДАНИЕ N 4Тема: Раскрытие неопределенности вида «бесконечность на бесконечность»

ЗАДАНИЕ N 5Тема: Раскрытие неопределенности вида «бесконечность на бесконечность»Предел функцииравен …

ЗАДАНИЕ N 6Тема: Раскрытие неопределенности вида «бесконечность на бесконечность»

studfiles.net

No related posts.