Линейная интерполяция онлайн калькулятор – —

Линейная интерполяция Онлайн

можно использовать:

дроби

1/2, -3/4, 5/7

дробные числа

1.52 или 0,19 можно иcпользовать как «.» так и «,»

квадратный корень

sqrt(4), sqrt(4/3)

тригонометрия

sin(1), cos(1), tan(1), atan(1)

возведение в степень

pow(3, 2) = 3*3 !при pow(3,2, 4,3) — система поймет что вы хотите 3.2 возвести в степень 4.3

арифметические операции

(3/4 + sqrt(5/7)) * pow(2, 4)

Сервис интерполяции и экстраполяции онлайн (линейная интерполяция/экстраполяция) поможет вам вычислить значение линейной функции, имея в распоряжении f(x) в двух различных точках, а также рассчитает уравнение прямой. Данный сервис автоматически определит нужный способ расчета — вам лишь надо ввести значения в двух произвольных точках, и указать необходимую точку, в которой нужно рассчитать значение. Если установить «галку» внутри кнопки «Рассчитать», калькулятор будет рассчитывать значение автоматически при любом изменении входных данных. Пример расчета интерполяции

Интерполяция — (от латинского interpolatio изменение, переделка), в математике и статике это способ вычислить промежуточное значение функции по нескольким уже известным ее значениям. Например.: Имеется функция f(x), известны результаты значения f(x) в точке x₀ и точке x₂, интерполяця помогает найти значение f(x₁) при условии что x₁ принадлежит интервалу от x₀ до x₂. Если x₁ лежит вне интервала (x₀, x₂), интерполяция не поможет, для этого нужно использовать «экстраполяцию». Этот метод часто называют «линейная интерполяция«, он дает 100% верный результат для уравнения прямой. Для вычесления резултата функций с двумя переменными существует «Билинейная интерполяция (Двойная интерполяция)». Также для рассчета интерполяции можно воспользоваться сервисом Интерполяция — полином Ньютона и Интерполяция — полином Лагранжа

Экстраполяция — в математике и статике это способ вычислить значение функции по нескольким уже известным ее значениям. Например.: Имеется функция f(x), известны результаты значения f(x) в точке x₁ и точке x₂, экстраполяция помогает найти значение f(x₀) либо f(x₃) при условии что x₀ либо x₃ меньше либо больше интервала x₁ до x₂. Если x_n лежит в интервале (x₁, x₂), экстраполяция не поможет, для того вам нужно использовать «интерполяцию» — для функций с одной переменной, и «двойная интерполяция» — для функций с двумя переменными.

Этот метод часто называют «линейная экстраполяция«, он дает 100% верный результат для уравнения прямой.

Как для интерполяции так и для экстраполяции в основе их рассчета лежит пропорция (y1 — y0)/(y2 — y0) = (x1 — x0)/(x2 — x0), прирощение значения в первой точке к прирощению значения во второй точке относится также как прирощение переменной в первой точке к прирощению переменной во второй точке (все относительно нулевой точки отсчета), из этой пропорции легко получить формулу рассчета любого значения

www.bl2.ru

Линейная интерполяция: онлайн калькулятор — формула и пример расчета

Интерполяция — метод нахождения промежуточных переменных функции по нескольким уже известным значениям. Впервые формулировка «интерполирование» была введена Джоном Валлисом в научном сочинении «Арифметика бесконечных».

Линейная интерполяция

Простейшим случаем интерполяции является «линейная», то есть нахождение величины по двум заданным точкам. Данный процесс вычисления можно рассмотреть как линейную функцию, тем самым делая расчёт более наглядным. Нанесение функции на систему координат называют аппроксимацией. Для этого на оси координат необходимо провести прямую через известные точки. Логично, что искомое значение, находящееся между первыми двумя точками, можно найти графически, зная абсциссу X. Если координата X искомой величины лежит за пределами известных значений (X

1, X₂), то процесс вычисления называется экстраполяция.

Калькулятор позволяет определить значение ординаты Y искомого значения, зная координаты X и Y двух других функций, а также её абсциссу. Для вычисления необходимо ввести значения заданных двух точек Х₁, Y₁ и X₂,Y₂, а также указать координату X искомой точки, а сервис автоматически определит метод расчёта и произведёт его.

Формула линейной интерполяции

Для вычисления используется следующая формула:

Пример расчёта

Дано: координаты двух точек А(3;1.5) и B(6;5).
Найти: ординату точки С с абсциссой 4.5.

Для удобства рекомендуется построить график: нанести точки на систему координат и провести прямую.

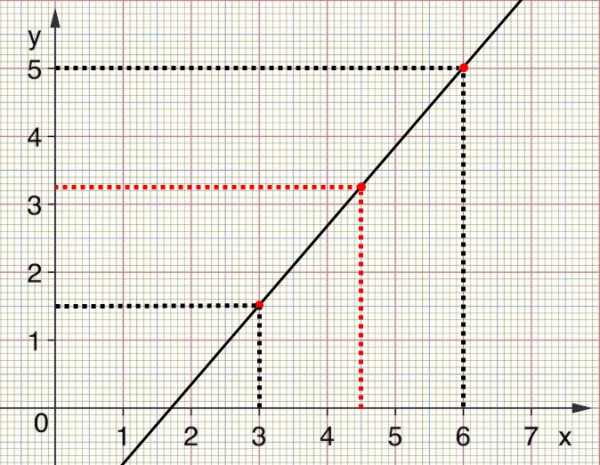
После этого подставляем значения в указанную формулу:

Y = 5 + (1.5 — 5) / (3 — 6) · (4.5 — 6) = 5 + (-3.5) / (-3) · (-1.5) = 3.25.

calcsoft.ru

Онлайн калькулятор: Аппроксимация функции одной переменной

Данный калькулятор по введенным данным строит несколько моделей регрессии: линейную, квадратичную, кубическую, степенную, логарифмическую, гиперболическую, показательную, экспоненциальную. Результаты можно сравнить между собой по корреляции, средней ошибке аппроксимации и наглядно на графике. Теория и формулы регрессий под калькулятором.

83 71 64 69 69 64 68 59 81 91 57 65 58 62Значения x, через пробел183 168 171 178 176 172 165 158 183 182 163 175 164 175Значения y, через пробел Линейная аппроксимация Квадратичная аппроксимация Кубическая аппроксимация Аппроксимация степенной функцией Показательная аппроксимация Логарифмическая аппроксимация Гиперболическая аппроксимация Экспоненциальная аппроксимацияТочность вычисления

Знаков после запятой: 4

Линейная регрессия

 

Коэффициент линейной парной корреляции

 

Коэффициент детерминации

 

Средняя ошибка аппроксимации, %

 

Квадратичная регрессия

 

Коэффициент корреляции

 

Коэффициент детерминации

 

Средняя ошибка аппроксимации, %

 

Кубическая регрессия

 

Коэффициент корреляции

 

Коэффициент детерминации

 

Средняя ошибка аппроксимации, %

 

Степенная регрессия

 

Коэффициент корреляции

 

Коэффициент детерминации

 

Средняя ошибка аппроксимации, %

 

Показательная регрессия

 

Коэффициент корреляции

 

Коэффициент детерминации

 

Средняя ошибка аппроксимации, %

 

Логарифмическая регрессия

 

Коэффициент корреляции

 

Коэффициент детерминации

 

Средняя ошибка аппроксимации, %

 

Гиперболическая регрессия

 

Коэффициент корреляции

 

Коэффициент детерминации

 

Средняя ошибка аппроксимации, %

 

Экспоненциальная регрессия

 

Коэффициент корреляции

 

Коэффициент детерминации

 

Средняя ошибка аппроксимации, %

 

Сохранить share extension

Линейная регрессия

Уравнение регрессии:

Коэффициент a:

Коэффициент b:

Коэффициент линейной парной корреляции:

Коэффициент детерминации:

Средняя ошибка аппроксимации:

Квадратичная регрессия

Уравнение регрессии:

Система уравнений для нахождения коэффициентов a, b и c:

Коэффициент корреляции:
,
где

Коэффициент детерминации:

Средняя ошибка аппроксимации:

Кубическая регрессия

Уравнение регрессии:

Система уравнений для нахождения коэффициентов a, b, c и d:

Коэффициент корреляции, коэффициент детерминации, средняя ошибка аппроксимации — используются те же формулы, что и для квадратичной регрессии.

Степенная регрессия

Уравнение регрессии:

Коэффициент b:

Коэффициент a:

Коэффициент корреляции, коэффициент детерминации, средняя ошибка аппроксимации — используются те же формулы, что и для квадратичной регрессии.

Показательная регрессия

Уравнение регрессии:

Коэффициент b:

Коэффициент a:

Коэффициент корреляции, коэффициент детерминации, средняя ошибка аппроксимации — используются те же формулы, что и для квадратичной регрессии.

Гиперболическая регрессия

Уравнение регрессии:

Коэффициент b:

Коэффициент a:

Коэффициент корреляции, коэффициент детерминации, средняя ошибка аппроксимации — используются те же формулы, что и для квадратичной регрессии.

Логарифмическая регрессия

Уравнение регрессии:

Коэффициент b:

Коэффициент a:

Коэффициент корреляции, коэффициент детерминации, средняя ошибка аппроксимации — используются те же формулы, что и для квадратичной регрессии.

Экспоненциальная регрессия

Уравнение регрессии:

Коэффициент b:

Коэффициент a:

Коэффициент корреляции, коэффициент детерминации, средняя ошибка аппроксимации — используются те же формулы, что и для квадратичной регрессии.

Вывод формул

Сначала сформулируем задачу:
Пусть у нас есть неизвестная функция y=f(x), заданная табличными значениями (например, полученными в результате опытных измерений).
Нам необходимо найти функцию заданного вида (линейную, квадратичную и т. п.) y=F(x), которая в соответствующих точках принимает значения, как можно более близкие к табличным.
На практике вид функции чаще всего определяют путем сравнения расположения точек с графиками известных функций.

Полученная формула y=F(x), которую называют эмпирической формулой, или уравнением регрессии y на x, или приближающей (аппроксимирующей) функцией, позволяет находить значения f(x) для нетабличных значений x, сглаживая результаты измерений величины y.

Для того, чтобы получить параметры функции F, используется метод наименьших квадратов. В этом методе в качестве критерия близости приближающей функции к совокупности точек используется суммы квадратов разностей значений табличных значений y и теоретических, рассчитанных по уравнению регрессии.

Таким образом, нам требуется найти функцию F, такую, чтобы сумма квадратов S была наименьшей:

Рассмотрим решение этой задачи на примере получения линейной регрессии F=ax+b.
S является функцией двух переменных, a и b. Чтобы найти ее минимум, используем условие экстремума, а именно, равенства нулю частных производных.

Используя формулу производной сложной функции, получим следующую систему уравнений:

Для функции вида частные производные равны:
,

Подставив производные, получим:

Далее:

Откуда, выразив a и b, можно получить формулы для коэффициентов линейной регрессии, приведенные выше.
Аналогичным образом выводятся формулы для остальных видов регрессий.

planetcalc.ru

Линейная интерполяция

линейная интерполяция онлайн, линейная интерполяция
Лине́йная интерполя́ция — интерполяция алгебраическим двучленом P1x = ax + b функции f, заданной в двух точках x0 и x1 отрезка a, b В случае, если заданы значения в нескольких точках, функция заменяется кусочно-линейной функцией

Содержание

• 1 Геометрическая интерпретация
• 2 Матричная форма
• 3 Применение
• 4 См также

Геометрическая интерпретацияправить

Геометрически это означает замену графика функции f прямой, проходящей через точки x 0 , f x 0 ,fx_ и x 1 , f x 1 ,fx_

График: пример линейной интерполяции

Уравнение такой прямой имеет вид:

y − f x 0 f x 1 − f x 0 = x − x 0 x 1 − x 0 -fx_=-x_

отсюда для x ∈ x 0 , x 1 ,x_

f x ≈ y = P 1 x = f x 0 + f x 1 − f x 0 x 1 − x 0 x − x 0 x=fx_+-fx_-x_x-x_

Это и есть формула линейной интерполяции, при этом

f x = P 1 x + R 1 x x+R_x\quad

где R 1 x x  — погрешность формулы:

R 1 x = f ″ ψ 2 x − x 0 x − x 1 , ψ ∈ x 0 , x 1 x=x-x_x-x_,\quad \psi \in x_,x_

Справедлива оценка

| R 1 x | ⩽ M 2 2 max | x − x 0 x − x 1 | = M 2 h 2 8 , M 2 = max x 0 , x 1 | f ″ x | , h = x 1 − x 0 x|\leqslant \max |x-x_x-x_|=h^,\quad M_=\max _,x_|f»x|,\quad h=x_-x_

Матричная формаправить

можно записать Px = ax + b следующим образом P x = a b x 1 a&b\endx\\1\\\end

условия будут записаны так: a b x 0 x 1 1 1 = P 0 P 1 a&b\endx_&x_\\1&1\\\end=P_&P_\\\end

отсюда можно найти: a b = P 0 P 1 x 0 x 1 1 1 − 1 a&b\end=P_&P_\\\endx_&x_\\1&1\\\end^
Получаем:
P x = P 0 P 1 x 0 x 1 1 1 − 1 x 1 P_&P_\\\endx_&x_\\1&1\\\end^x\\1\\\end
Распространяя на:

• двухмерный случай треугольник:
  

P x , y = P 0 P 1 P 2 x 0 x 1 x 2 y 0 y 1 y 2 1 1 1 − 1 x y 1 P_&P_&P_\\\endx_&x_&x_\\y_&y_&y_\\1&1&1\\\end^x\\y\\1\\\end

• трёхмерный случай тетраэдр:
  

P x , y , z = P 0 P 1 P 2 P 3 x 0 x 1 x 2 x 3 y 0 y 1 y 2 y 3 z 0 z 1 z 2 z 3 1 1 1 1 − 1 x y z 1 P_&P_&P_&P_\\\endx_&x_&x_&x_\\y_&y_&y_&y_\\z_&z_&z_&z_\\1&1&1&1\\\end^x\\y\\z\\1\\\end

Применениеправить

Линейная интерполяция применяется для уплотнения таблиц

Формула линейной интерполяции является частным случаем интерполяционной формулы Лагранжа и интерполяционной формулы Ньютона

См такжеправить

• Билинейная интерполяция
• Интерполяция алгебраическими многочленами
• Обратная матрица

линейная интерполяция, линейная интерполяция и, линейная интерполяция лагранжа, линейная интерполяция онлайн, линейная интерполяция это

---

Линейная интерполяция Информацию О

---

---

Линейная интерполяция Комментарии

Линейная интерполяция
Линейная интерполяция
Линейная интерполяция Вы просматриваете субъект

Линейная интерполяция что, Линейная интерполяция кто, Линейная интерполяция описание

There are excerpts from wikipedia on this article and video

www.turkaramamotoru.com