Уравнение сторон треугольника | Треугольники
Как составить уравнение сторон треугольника по координатам его вершин?
Зная координаты вершин треугольника, можно составить уравнение прямой, проходящей через 2 точки.
Пример.
Дано: ΔABC, A(-5;1), B(7;-4), C(3;7)
Составить уравнения сторон треугольника.
Решение:
1) Составим уравнение прямой AB, проходящей через 2 точки A и B.
Для этого в уравнение прямой y=kx+b подставляем координаты точек A(-5;1), B(7;-4) и из полученной системы уравнений находим k и b:
Таким образом, уравнение стороны AB
2) Прямая BC проходит через точки B(7;-4) и C(3;7):
Отсюда уравнение стороны BC —
3) Прямая AC проходит через точки A(-5;1) и C(3;7):
Уравнение стороны AC —
Уравнение прямой
www.treugolniki.ru
Уравнение треугольника : Геометрия — Страница 2
Выглядит уравнение интуитивно понятно, но как это строго доказать?
Вообще говоря, это морока. Надо нарисовать три прямых, на каждой из которых один из модулей обращается в ноль и которые делят плоскость на семь частей, и раскрывать модули в каждой из этих частей отдельно.
Но если уж мы знаем, что ответом должен быть треугольник, притом сплошной треугольник, а не только его контур, то всё очень сильно упрощается. Функция линейна на любом из участков разбиения плоскости теми линиями. Поэтому чтобы доказать, что эта функция тождественно равна нулю внутри треугольника (и на его границе), достаточно проверить, что она равна нулю в вершинах треугольника, т.е. в точках , и . Ну это очевидно.
А снаружи эта функция положительна (т.е. там исходное равенство для и не выполняется), поскольку поверхность в пространстве, задаваемая уравнением , представляет собой выпуклый многогранник.
Или если не нравится выпуклость, то можно так. На любом из участков плоскости, смежным с одной из сторон треугольника, тождество нарушается просто потому, что при переходе через эту сторону один из модулей раскрывается по-другому, чем внутри треугольника, а два других — так же, как и раньше. При этом нарушается оно в положительную сторону — ведь на любом из шести лучей тех трёх прямых, уходящих из вершины треугольника в сторону бесконечности, функция может уходить только на плюс бесконечность, но никак не на минус (модули-то всё-таки неотрицательны). А тогда и внутри каждого из трёх углов, ограниченного одной из пар этих лучей, функция тоже положительна, раз она положительна на границе этого угла. Итого — она положительна всюду, кроме треугольника.
dxdy.ru
Уравнение высоты треугольника | Треугольники
Как составить уравнение высоты треугольника по координатам его вершин?
Высота треугольника — это перпендикуляр, опущенный из вершины треугольника к прямой, содержащей противолежащую сторону.
Следовательно, для составления уравнения высоты треугольника нужно:
- Найти уравнение стороны треугольника.
- Составить уравнение прямой, перпендикулярной этой стороне и проходящей через противолежащую вершину треугольника.
Пример.
Дано: ΔABC, A(-7;2), B(5;-3), C(1;8).
Написать уравнения высот треугольника.
Решение:
1) Составим уравнение стороны BC треугольника ABC.
Прямая y=kx+b проходит через точки B(5;-3), C(1;8), значит, координаты этих точек удовлетворяют уравнению прямой. Подставив координаты B и C в уравнение прямой, составляем систему уравнений и решаем её:
Таким образом, уравнение прямой BC —
Угловой коэффициент прямой, перпендикулярной BC,
Значит, уравнение высоты, проведённой к стороне BC, имеет вид
Поскольку эта прямая проходит через точку A(-7;2), подставляем координаты точки в уравнение и находим b:
Итак, уравнение высоты, проведённой к стороне BC:
2) Составим уравнение стороны AB треугольника ABC. A(-7;2), B(5;-3):
Уравнение прямой AB:
Угловой коэффициент перпендикулярной ей прямой
Значит уравнение перпендикулярной AB прямой имеет вид y=2,5x+b. Подставляем в это уравнение координаты точки C(1;8): 8=2,5·1+b, откуда b=5,5.
Получили уравнение высоты, проведённой из точки C к стороне BC: y=2,5x+5,5.
3) Составим уравнение стороны AC треугольника ABC. A(-7;2), C(1;8):
Угловой коэффициент прямой, перпендикулярной AC,
Таким образом, уравнение перпендикулярной AC прямой имеет вид
Подставив в него координаты точки B(5;-3), найдём b:
Итак, уравнение высоты треугольника ABC, опущенной из вершины B:

www.treugolniki.ru
Все формулы для треугольника
1. Найти по формулам длину биссектрисы из прямого угла на гипотенузу:
L — биссектриса, отрезок ME , исходящий из прямого угла (90 град)
a, b — катеты прямоугольного треугольника
с — гипотенуза
α — угол прилежащий к гипотенузе
Формула длины биссектрисы через катеты, ( L):
Формула длины биссектрисы через гипотенузу и угол, ( L):
2. Найти по формулам длину биссектрисы из острого угла на катет:
L — биссектриса, отрезок ME , исходящий из острого угла
a, b — катеты прямоугольного треугольника
с — гипотенуза
α, β — углы прилежащие к гипотенузе
Формулы длины биссектрисы через катет и угол, (L):
Формула длины биссектрисы через катет и гипотенузу, (L):
www-formula.ru
Уравнение треугольника : Геометрия — Страница 2
Выглядит уравнение интуитивно понятно, но как это строго доказать?
Вообще говоря, это морока. Надо нарисовать три прямых, на каждой из которых один из модулей обращается в ноль и которые делят плоскость на семь частей, и раскрывать модули в каждой из этих частей отдельно.
Но если уж мы знаем, что ответом должен быть треугольник, притом сплошной треугольник, а не только его контур, то всё очень сильно упрощается. Функция линейна на любом из участков разбиения плоскости теми линиями. Поэтому чтобы доказать, что эта функция тождественно равна нулю внутри треугольника (и на его границе), достаточно проверить, что она равна нулю в вершинах треугольника, т.е. в точках , и . Ну это очевидно.
А снаружи эта функция положительна (т.е. там исходное равенство для и не выполняется), поскольку поверхность в пространстве, задаваемая уравнением , представляет собой выпуклый многогранник.
Или если не нравится выпуклость, то можно так. На любом из участков плоскости, смежным с одной из сторон треугольника, тождество нарушается просто потому, что при переходе через эту сторону один из модулей раскрывается по-другому, чем внутри треугольника, а два других — так же, как и раньше. При этом нарушается оно в положительную сторону — ведь на любом из шести лучей тех трёх прямых, уходящих из вершины треугольника в сторону бесконечности, функция может уходить только на плюс бесконечность, но никак не на минус (модули-то всё-таки неотрицательны). А тогда и внутри каждого из трёх углов, ограниченного одной из пар этих лучей, функция тоже положительна, раз она положительна на границе этого угла. Итого — она положительна всюду, кроме треугольника.
dxdy.ru
Уравнение биссектрисы треугольника | Треугольники
Как составить уравнение биссектрисы треугольника по координатам его вершин?
1 способ
Используя уравнение биссектрисы угла:
Пример.
Даны вершины треугольника A(-5;4), B(7;-1) и C(3;10).
1) Составить уравнение биссектрисы треугольника ABC, выходящей из вершины A.
2) Найти длину этой биссектрисы.
Решение:
1) Угол A образован прямыми AB и AC. Составим уравнения этих прямых.
Уравнение прямой, проходящей через две точки, можно найти, например, по формуле
Уравнение прямой AB:
Уравнение прямой AC:
Подставляем уравнения прямых AB и AC в формулы уравнения биссектрис угла:
и
то есть
и
Из этих уравнений является уравнением биссектрисы внутреннего угла BAC треугольника, другое — биссектрисой внешнего угла при вершине A. Как отличить уравнение биссектрисы внутреннего угла?
Точки B и C лежат по одну сторону от биссектрисы внешнего угла, поэтому при подстановке координат B и C в уравнение мы получим числа одинакового знака. От биссектрисы внутреннего угла B и C лежат по разные стороны, поэтому подстановка их координат в уравнение биссектрисы внутреннего угла даёт нам числа разных знаков.
Подставляем в уравнение x-8y+37=0 координаты B и C.
B(7;-1): 7-8·(-1)+37>0
C(3;10): 3-8·10+37<0.
Таким образом, уравнение x-8y+37=0 является уравнением биссектрисы AF треугольника ABC.
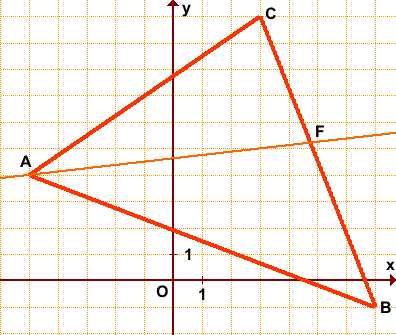
2) Чтобы найти длину биссектрисы, найдём точку пересечения прямых AF и BF.
Уравнение прямой BC:
Координаты точки пересечения прямых AF и BC находим из системы уравнений
Решение системы —
Длину биссектрисы AF находим по формуле расстояния между точками A и F:
2 способ
Используя свойство биссектрисы треугольника:
По формулам деления отрезка в данном отношении
разделим отрезок BC в отношении 13 к 10, то есть
Составим уравнение биссектрисы AF треугольника ABC как уравнение прямой, проходящей через точки
www.treugolniki.ru
Уравнение медианы | Треугольники
Как составить уравнение медианы треугольника по координатам его вершин?
Медиана соединяет вершину треугольника с серединой противолежащей стороны. Следовательно, при решении задачи составления уравнения медианы нужно:
- Найти координаты середины отрезка по координатам его концов.
- Составить уравнение прямой, проходящей через две точки: найденную середину отрезка и противолежащую вершину.
Пример.
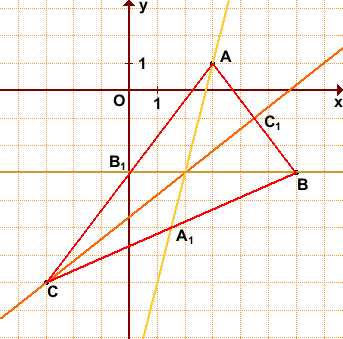
Дано: ΔABC, A(3;1), B(6;-3), C(-3;-7).
Найти уравнения медиан треугольника.
Решение:
Обозначим середины сторон BC, AC, AB через A1, B1, C1.
1) По формулам координат середины отрезка
Уравнение медианы AA1 будем искать в виде y=kx+b.
Найдём уравнение прямой, проходящей через точки A(3;1) и A1(1,5;-5). Составляем и решаем систему уравнений:
Отсюда k= 4; b= -11.
Уравнение медианы AA1: y=4x-11.
2) Аналогично, координаты точки B1 — середины отрезка AC
Можно в уравнение y=kx+b подставить координаты точек B(6;-3) и B1(0;-3) и найти k и b. Но так как ординаты обеих точек равны, уравнение медианы BB1 можно найти ещё быстрее: y= -3.
3) Координаты точки C1 — середины отрезка BC:
C(-3;-7), C(4,5;-1), y=kx+b:
Отсюда уравнение медианы CC1 : y=0,8x-4,6.