Маткад решение уравнений – . Mathcad

2 Решение уравнений средствами MathCAD

Ермоленко М.В. Введение в систему MathCAD

©Кафедра технической физики, 2008

Как известно, многие уравнения и системы уравнений не имеют аналитических решений. В первую очередь это относится к большинству трансцендентных уравнений. Доказано также, что нельзя построить формулу, по которой можно было бы решить произвольное алгебраическое уравнение степени выше четвертой1. Однако такие уравнения могут решаться численными методами с заданной точностью(не более значения заданного системной переменнойTOL).

2.1 Численное решение нелинейного уравнения

Для простейших уравнений вида f(x) = 0 решение в MathCAD находится с помощью функцииroot (Рисунок 5).

root( f(х1, x2, …), х1, a, b)

Возвращает значение х1, принадлежащее отрезку[a, b], при котором выражение или функцияf(х) обращается в 0. Оба аргумента этой функции должны быть скалярами. Функция возвращает скаляр.

Аргументы: f(х1, x2, …) — функция, определеннаягде-либов рабочем документе, или выражение. Выражение должно возвращать скалярные значения.

х1 — — имя переменной, которая используется в выражении. Этой переменной перед использованием функцииroot необходимо присвоить числовое значение. Mathcad использует его как начальное приближение при поиске корня.

a, b – необязательны, если используются, то должны быть вещественными числами, причемa < b.

Приближенные значения корней (начальные приближения) могут быть:

-Известны из физического смысла задачи.

-Известны из решения аналогичной задачи при других исходных дан-

ных.

— Найдены графическим способом.

Наиболее распространен графический способ определения начальных приближений. Принимая во внимание, что действительные корни уравненияf(x) = 0 — это точки пересечения графика функцииf(x) с осью абсцисс, достаточно построить график функцииf(x) и отметить точки пересеченияf(x) с осьюОх, или отметить на осиОх отрезки, содержащие по одному корню. Построение графиков часто удается сильно упростить, заменив уравнениеf(x) = 0равносильным ему уравнением:

f1( x )= f2( x )

где функции f1(x) иf2(x) — более простые, чем функцияf(x).

Тогда, построив графики функций у =f1(x) иу =f2(x), искомые корни получим как абсциссы точек пересечения этих графиков

1 Доказательство этого факта связано с именами замечательных математиков Абеля(1802-1829)и Галуа(1811-1832).

studfiles.net

Урок 22. Линейные уравнения в Mathcad

В этом уроке мы рассмотрим применение векторов и матриц, а именно решение систем линейных уравнений.

Пример

Есть система трех линейных уравнений с тремя неизвестными:

Традиционный метод решения таких систем – последовательное исключение переменных. Например, мы можем сложить (1) и (3), затем (2) и (3):

Из уравнения (5):

Затем, используя (4):

Наконец, из (1):

Итак, получили:

Линейные уравнения можно решить с помощью векторов и матриц. Запишем левую часть уравнений (1), (2) и (3) как произведение матрицы коэффициентов A на вектор решений X:

Убедитесь, что элементы матрицы A совпадают с коэффициентами системы уравнений. Правую часть запишем как вектор решений:

Краткая запись системы уравнений:

Тогда решение можно найти:

Такую запись можно применять к сколь угодно большим системам, будь там три, сорок или десять тысяч уравнений. Запомните, что решение есть произведение обратной матрицы коэффициентов и вектора результатов, при этом важна их последовательность. Такой метод решения не самый эффективный, но он хорош для решения многих задач.

Расчет цепи постоянного тока

Цепь состоит из резисторов и источников ЭДС. Необходимо определить токи во всех ветвях цепи:

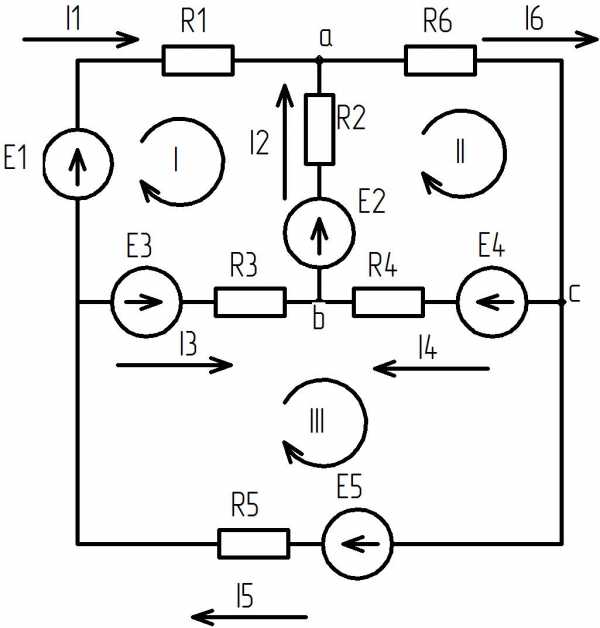
Примем значения сопротивлений и ЭДС:

Запишем уравнения для контуров I, II и III, исходя из второго правила Кирхгофа:

Для узлов a, b и c запишем уравнения по первому правилу Кирхгофа:

Запишем матрицу A, содержащую коэффициенты при токах, а в вектор b – правые части уравнений:

Решение системы уравнений:

Решение X можно найти по-другому – с помощью функции lsolve(A,B):

Линейные уравнения

С линейными уравнениями обычно не возникает проблем, но есть несколько вещей, о которых следует знать. Продемонстрируем их на системе двух уравнений:

Можно записать как:

Решение – точка (0,1), и здесь проблем не возникло:

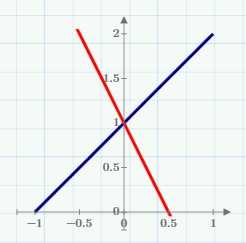
Это обычный случай. Интересно вычислить определитель матрицы коэффициентов:

Он не равен нулю. Теперь поменяем второе уравнение системы и попробуем найти решение:

Система имеет бесконечное множество решений:

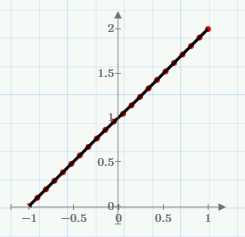
Определитель матрицы коэффициентов:

Он равен нулю. При попытке решить систему Mathcad скажет, что матрица является сингулярной. Здесь два уравнения идентичны, но результат будет тот же, если одно из уравнений кратно другому. Такие уравнения называются линейно зависимыми.

В третьем варианте изменим константу во втором уравнении:

Здесь нет решений: две прямые параллельны:

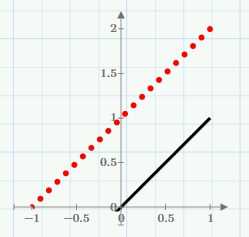
Как Вы догадывались, определитель снова равен нулю:

Поведение большего числа уравнений аналогично.

Таким образом, если определитель равен нулю, возникает проблема, которую часто сложно распознать. При записи большой системы уравнений легко ошибиться и, например, дважды записать одно уравнение.

Если в коэффициентах присутствует погрешность округления, Mathcad может принять эти два уравнения за разные. Ответ будет получен, но результат будет неверным.

Резюме

1. Система линейных уравнений обычно имеет своим решением столько переменных, сколько самих уравнений.
2. Небольшие системы линейных уравнений могут быть решены последовательным исключением переменных.
3. Для больших систем уравнений нужна краткая запись. Мы использовали векторы и матрицы. Левая часть уравнений является произведением матрицы коэффициентов A на вектор решений x, правая часть – это вектор решений b. Решение: .
4. С помощью матриц и векторов мы решили задачу цепи постоянного тока.
5. Решение не будет найдено, если матрица коэффициентов сингулярна.

Другие интересные материалы

sapr-journal.ru

5. Решение дифференциальных уравнений с помощью встроенных функций MathCad

72

Обыкновенное дифференциальное уравнение первого порядка, по определению, содержит, помимо самой искомой функции у(t), только ее первую производную y'(t). В подавляющем большинстве случаев дифференциальное уравнение можно записать в стандартной форме (форме Коши), разрешенное относительно старшей производной:

у'(t)=f(y(t),t)

Только с такой формой умеет работать вычислительный процессор Mathcad. Правильная с математической точки зрения постановка соответствующей задачи Коши для ОДУ первого порядка должна, помимо самого уравнения, содержать одно начальное условие — значение функции y(t0) в некоторой точке t0. Требуется явно определить функцию y(t) на интервале от t0 до tx. По характеру постановки задачи Коши называют еще задачами с начальными условиями (initial value problem), в отличие от краевых задач.

Для численного интегрирования одного ОДУ у пользователя Mathcad имеется выбор — либо использовать вычислительный блок Given – Odesolve( ), либо встроенные функции. Первый путь предпочтительнее из соображений наглядности представления задачи и результатов, а второй дает пользователю больше рычагов воздействия на параметры численного метода. Рассмотрим последовательно оба варианта решения.

Вычислительный блок Given – Odesolve( )

Вычислительный блок для решения одного ОДУ, реализующий численный метод Рунге-Кутта, состоит из трех частей:

— Given — ключевое слово;

— ОДУ и начальное условие, записанное с помощью Булевых операторов, причем начальное условие должно быть в форме у(t0) = b;

— Odesolve(t, t1) — встроенная функция для решения ОДУ относительно переменной t на интервале (t0,t1).

Допустимо, и даже часто предпочтительнее, задание функции Odesolve (t, t1, step) с тремя параметрами, где step – необязательный внутренний параметр численного метода, определяющий количество шагов, в которых по методу Рунге-Кутта будет получено решение дифференциального уравнения. Чем больше step, тем с лучшей точностью будет получен результат, но тем больше времени будет затрачено на его решение. Таким образом, подбором этого параметра можно заметно (в несколько раз) ускорить расчеты без существенного ухудшения их точности.

Пример решения задачи Коши для ОДУ первого порядка у’=у-у² посредством вычислительного блока Given – Odesolve( ) приведен на рис. 5.1. Вставлять логические операторы нужно при помощи панели инструментов Boolean (Булевы операторы). При вводе с клавиатуры логического знака равенства нужно использовать сочетание клавиш Ctrl =. Символ производной можно ввести как средствами панели Calculus (Вычисления), как это сделано на рис. 5.1, так и в виде штриха (‘), набрав его с помощью сочетания клавиш Ctrl +F7.

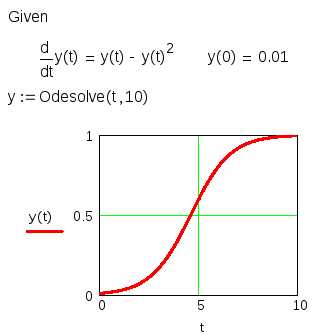
Рис.5.1. Решение задачи Коши для ОДУ первого порядка

Mathcad требует, чтобы конечная точка интегрирования ОДУ лежала правее начальной (t0<t1), иначе будет выдано сообщение об ошибке. Функция Odesolve( ) возвращает функцию y(t), определенную на интервале (t0,t1).

Пользователь имеет возможность выбирать между двумя модификациями численного метода Рунге-Кутта. Для смены метода необходимо нажать ПКМ на область функции Odesolve( ), вызвать контекстное меню и выбрать в нем один из двух пунктов: Fixed (Фиксированный шаг) или Adaptive (Адаптивный). По умолчанию применяется первый из них, т. е. метод Рунге — Кутта с фиксированным шагом.

studfiles.net

решение уравнений (различные способы). — КиберПедия

Символьное решение уравнений

 

Для введения знака равенства в уравнениях используется комбинация клавиш CTRL+=.Это очень важно, т.к. с точки зрения Mathcad такой знак равенства – совершенно другая операция, чем просто = (показать результат).

Решать уравнение символьно гораздо труднее, чем численно. Может оказаться, что в символьном виде решение не существует.

Чтобы символьно решить уравнение существует команда Решить относительно переменной из меню Символика.(Solve)

 

Для этого:

— напечатать уравнение.

— Убедитесь, что для введения знака равенства была использована комбинация клавиш CTRL+=

— Выделите переменную, относительно которой нужно решить уравнение, щелкнув на ней мышью.

— Выберите Решить относительно переменной из меню Символика.

 

MathCad решит уравнение относительно выделенной переменной и вставит результат в рабочий документ.

 

Пример:

Чтобы из приведенной формулы выразить r через А, выделите r и выберите команду Решить относительно переменной

 

Имеет решения

Для ввода знака равенства нажмите CTRL/=

 

Численное решение уравнений.

Решать уравнения численным методом можно следующими способами:

· С помощью функции root, polyroot, lsolve

· С помощью блока Given и функций Find и Minerr.

 

 

Решим уравнение x²=9.

Функция root ищет один из корней выражения. Поэтому, для первого способа решения уравнение надо представить в виде f(x)=0, т.е. в нашем случае x²-9=0.

Кроме того, в случае функции root надо задать начальное значение x для поиска. Чем ближе это значение к корню уравнения, тем меньше времени займет поиск. root находит только один из корней, обычно ближайший к начальному значению x для поиска.

 

Обратите внимание, что функция root находит только один из корней. Если вы хотите найти корень в определенном диапазоне, можно задать этот диапазон двумя последними параметрами, причем значения заданной функции в этих точках должны иметь разные знаки.

 

Корни полинома также можно найти функцией polyroots, в ней перечисляем коэффициенты полинома в виде вектора:

 

 

Второй вариант решения уравнений – использование блока Given:

 

Точно так же как и в случае с root надо задавать начальные значения. В блоке Given можно задать систему уравнений. Функция Find найдет только одно их возможных решений. Если решение не может быть найдено (численный метод не дает решения с точностью до TOL), то можно найти минимальное по ошибке решение, заменив Find() на MinErr().

Поскольку во всех этих способах используются численные методы, то на точность решения будут влиять значения переменных TOL и CTOL.

2. Операторы управления: оператор безусловного перехода, операторы продолжения и прерывания итерации цикла (с примерами), оператор switch.

Операторы ветвления.

cyberpedia.su

Работа с массивами и решение систем уравнений в Mathcad

Содержание

Введение

3. Решение систем линейных уравнений

4. Решение нелинейных уравнений

5. Решение систем нелинейных уравнений

Заключение

Библиографический список

Введение

Одна из задач ЭВМ — автоматизация труда, повышение эффективности научных исследований. Основная особенность ЭВМ — ориентация на применение пользователями, не владеющими языками программирования. Такой подход позволяет преодолевать языковой барьер, отделяющий человека от машины. С этой целью разрабатываются пакеты прикладных программ, рассчитанные на широкие круги специалистов. К подобным пакетам относится MATHCAD.

MATHCAD — универсальный математический пакет, предназначенный для выполнения инженерных и научных расчетов. Основное преимущество пакета — естественный математический язык, на котором формируются решаемые задачи.

Объединение текстового редактора с возможностью использования общепринятого математического языка позволяет пользователю получить готовый итоговый документ. Пакет обладает широкими графическими возможностями, расширяемыми от версии к версии. Практическое применение пакета существенно повышает эффективность интеллектуального труда.

Цель работы: изучение выполнения основных операций с массивами, решения систем линейных и нелинейных уравнений в Mathcad.

В математике часто возникает необходимость в задании некоторого ряда значений. Например, при вычислении

нужно сформировать ряд чисел от 1 до N с шагом 1 и перемножить их. Для создания таких рядов в Mathcad используются ранжированные переменные . В простом случае для создания ранжированной переменной используется выражение

Name:=Nbegin…Nend,

Где Name – имя переменной, Nbegin – начальное значение переменной, Nend – ее конечное значение. Символ «…» (он вводится с клавиатуры знаком точка с запятой «;») указывает на изменение переменной в заданных границах. Если Nbegin<Nend, то шаг изменения переменной будет равен +1, в противном случае –1. Например, выражение a:=1…10 описывает ранжированную переменную a со значениями от 1 до 10.

Для создания ранжированной переменной общего вида используется выражение

Name:=Nbegin, (Nbegin+Step)…Nend,

где Step — заданный шаг изменения переменной (он должен быть положительным, если Nbegin<Nend и отрицательным в противном случае).

Например, выражение a:=1, 1.5, …10 описывает ранжированную переменную a со значениями от 1 до 10 с шагом 0,5.

Ранжированные переменные широко применяются для представления функций в виде таблиц вывода , а также для построения их графиков.

Если после некоторого выражения с ранжированной переменной поставить знак равенства, то после щелчка мышью на экране будет выведена таблица значений этого выражения. Такие таблицы называются таблицами вывода .

Необходимо учитывать следующее свойство таблиц вывода: если количество значений ранжированной переменной и, соответственно, строк в таблице вывода больше 16, то выводятся первые 16 строк. Если указатель мыши находится в пределах таблицы, то щелчок левой кнопкой мыши приводит к появлению вертикальной полосы прокрутки, позволяющей просмотреть все строки таблицы.

Помните, что задание ранжированных переменных эквивалентно заданию конечных циклов.

Примеры использования ранжированных переменных приведены на рисунке 1.1.

Ранжированная переменная отличается от вектора (одномерного массива) тем, что невозможно использование ее отдельных значений. При необходимости иметь доступ к каждому значению переменной со многими компонентами она должна быть задана в виде одномерного (вектора) и двумерного (матрицы) массива.

Местоположение элемента массива задается одним индексом для вектора и двумя для матрицы. Индексы могут быть только положительными целыми числами . Для ввода индекса используется знак « [ » – прямая открывающая скобка.

Для задания массивов можно либо воспользоваться командой Matrices меню Math, либо нажать комбинацию клавиш Ctrl+V , либо щелкнуть на значке с изображением шаблона матрицы. Любое из этих действий вызывает появление диалогового окна, в котором надо указать количество строк m и столбцов n в массиве. При m=1 получим вектор-столбец, а при n=1 – вектор-строку.

В отношении массивов действуют те же правила присваивания и вывода, что и для обычных переменных. В частности, с помощью оператора присваивания можно создать массив заданного размера и заданного типа без ручного заполнения шаблона (рисунок 2.1.).

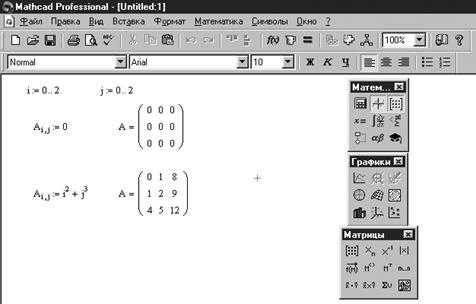
Рис. 2.1 Пример создания матриц без использования шаблонов матриц

Для работы с массивами Mathcad содержит ряд операторов и функций. Ниже представлены операторы для работы с векторами и матрицами. В таблице используются следующие обозначения: V – для векторов, M – для матриц, Z – для скалярных величин.

Существует ряд встроенных векторных и матричных функций . Они облегчают решение задач линейной алгебры и других сфер приложения векторов и матриц.

mirznanii.com