Сколько минут в одном градусе угла, как обозначаются минуты и секунды
Чтобы узнать, сколько градусов угловых минут, вам нужно использовать простой веб-калькулятор. Введите число градусов, которое вы хотите преобразовать в левое поле. В поле справа вы увидите результат расчета. Если вам нужно перевести градусы или углы минут в другие единицы измерения, просто нажмите соответствующую ссылку.
Что такое «ставка»,
Степени являются общепринятыми и наиболее часто используемыми единицами измерения прямых углов, равными 1/360 по периметру, 1/180 растянутым углом и 1/90 от прямого угла.
Название «степень» происходит от латинского gradus — деления, фрагмента, шага, а в тексте — символ (°), (1 ° — одна градус).
Причины выбора системы. Шестьдесят распределение угловых значений, которые генерируют размеры, единицы измерения неизвестны, но это версия, которая в древнем Вавилоне акадский математический круг делится на шесть равных частей с использованием равностороннего треугольника, который был основой для этого расчета.
Учитывая, что форма гексаэдра широко распространена в естественных природных структурах, таких как кристаллы (например, снежинки, например) или соты, этот выбор был явно оправдан.
Кроме того, в некоторых старых календарях, особенно в зороастрийском (древнем персидском) и древнем египтяне, продолжительность года составляет 360 дней и 5 дополнительных дней (эпигоменты) считаются священными днями с момента принятия «великого».
Также в течение пяти дополнительных дней ежедневные календари Maya и Aztec 360. Таким образом, вполне возможно, что культурные причины лежат в основе системы в шестидесятые годы.
Что такое «угловой момент»,
Угловая минута или минуты дуги представляет собой единицу измерения, равную 1/60 градуса. Одна минута состоит из 60 секунд. Единица используется в системе СИ, но она не принадлежит к единице этой системы, так как она является безграничной величиной.
Отдельная арка используется для измерения малых углов в астрономии, навигации или для определения точности записи. Стандартный символ минутного отверстия (бар) (‘), например, 1 минута, поскольку он записан как 1’.
Лист записи используется в документации, которая относится, в частности, к описанию точности стрельбы из огнестрельного оружия.
Сколько минут?
В метрических единицах 1 ‘на расстоянии 100 м = 2,908 см. В картографии 1 ‘на поверхности моря составляет приблизительно 1,86 км или 1 морскую милю. При определении остроты зрения таблицы Снеллена вид просматривается нормально, что позволяет читать шестую линию с расстояния 6 м, каждая буква имеет 5 ‘дугу.
Измерение углов
Измерить угол – значит найти его величину. Величина угла показывает, сколько раз угол, выбранный за единицу измерения, укладывается в данном углу.
Обычно за единицу измерения углов принимают градус. Градус – это угол, равный части развёрнутого угла. Для обозначения градусов в тексте, используется знак°, который ставится в правом верхнем углу числа, показывающего количество градусов (например, 60°).
Измерение углов транспортиром
Для измерения углов используют специальный прибор – транспортир:
У транспортира две шкалы – внутренняя и внешняя.
Начало отсчёта у внутренней и у внешней шкал располагается с разных сторон. Чтобы получить правильный результат измерения, отсчёт градусов должен начинаться с правильной стороны.
Измерение углов производится следующим образом: транспортир накладывают на угол так, чтобы вершина угла совпала с центром транспортира, а одна из сторон угла прошла через нулевое деление на шкале.
Тогда другая сторона угла укажет величину угла в градусах:
Говорят: и пишут: ∠BOC = 60°, ∠MON = 120°.
Для более точного измерения углов используют доли градуса: минуты и секунды. Минута – это угол, равный части градуса.
Секунда – это угол, равный части минуты.
Перевод градусов в угловые минуты
Минуты обозначают знаком ‘, a секунды – знаком ». Знак минут и секунд ставится в правом верхнем углу числа. Например, если угол имеет величину 50 градусов 34 минуты и 19 секунд, то пишут:
50°34’19»
Свойства измерения углов
Если луч делит данный угол на две части (на два угла), то величина данного угла равна сумме величин двух полученных углов.
Рассмотрим угол AOB:
Луч OD делит его на два угла: ∠AOD и ∠DOB.
Таким образом, ∠AOB= ∠AOD + ∠DOB.
Развёрнутый угол равен 180°.
Любой угол имеет определённую величину, большую нуля.
Как измеряется в разных единицах. Там могут быть тарифы, радианы. Наиболее распространенные углы измеряются в градусах. (Эта степень не должна смешиваться с температурным критерием, где также используется термин «шаг»).
1 градус — угол, который равен 1/180 угла отклонения. Другими словами, если взять под углом и разделить на 180 равных угловых частей, то каждая составляет 1 градус.
Размер всех других углов зависит от того, сколько таких маленьких углов можно поместить под измеренным углом.
Степень указывается знаком °. Это ничего, а не О. Это особый характер, который вводится для уровня класса, символа.
Таким образом, он разработан как 180 °, прямоугольный как 90 °, острые углы меньше 90 °, а углы больше 90 °.
В метрической системе измеритель используется для измерения расстояния.
Тем не менее, используются также большие и меньшие единицы. Например, сантиметр, миллиметр, километр, дециметр. По аналогии, в минутах градусов углов, мы также назначаем минуты и секунды.
Один уровень равен 1/60 градусов. Он отмечен одним знаком.
Минута (угол) на уровень
Второй — 1/60 минуты или 1/3600 градусов. Второй отмечен двумя символами, «то есть».
В школьной геометрии редко используются минуты и секунды, но, к примеру, они должны быть сопоставимы: 35 ° 21’45 «. Это означает, что это 35 градусов + 21 минута + 45 секунд.
С другой стороны, если угол не может быть точно измерен только в целых градусах, нет необходимости вводить минуты и секунды.
Достаточно использовать частичные ставки. Например, 96,5 °.
Понятно, что минуты и секунды могут быть переведены в градусы, выраженные в градусах градусов. Например, 30 ‘равно (30/60) ° или 0,5 °. 0,3 ° то же самое (0,3 * 60) ‘или 18’. Таким образом, использование минут и секунд — это только вопрос комфорта.
один градус широты (то есть в направлении север-юг) на любой параллели равен 111 км. А если не лень, посчитай: (2 х π х 6400км) / 360 Длина меридиана равна 40000 километров или 360 градусов. Следовательно, один градус широты (хоть северной, хоть южной) равен (40000 поделить на 360) 111,111…км. Если Вам надо точнее, то: 1 градус = 60 минут. Следовательно, 1 минута широты равна 1,851… км. Еще точнее? 1 минута = 60 секунд. Следовательно, 1 секунда широты равна 30,864…
м. Теперь про долготу: Перевод в километры зависит от широты данной местности. На экваторе один градус долготы равен все тем же 111,111…км, т. к. длина экватора, также как и длина меридиана, равна 40000 км. А севернее или южнее — уже меньше, а на полюсах вообще равна нулю километров. Связано это с тем, что все параллели имеют разную длину, равную длине экватора, умноженной на косинус угла, равного широте. Один градус долготы на широте 53,85° (53° 51′) равен (COS 53,85°) × 40000 / 360 = 0,59 × 111,111…
= 65,544… километров. Одна минута соответственно 65,544… / 60 = 1,092… километров. Одна секунда долготы уже равна 1092,41… / 60 = 18,207… метров.
Перевод в километры зависит от широты данной местности. На экваторе один градус долготы равен все тем же 111,111…км, т. к. длина экватора, также как и длина меридиана, равна 40000 км.
А севернее или южнее — уже меньше, а на полюсах вообще равна нулю километров.
Градус, минута, секунда
Связано это с тем, что все параллели имеют разную длину, равную длине экватора, умноженной на косинус угла, равного широте. Один градус долготы на широте 53,85° (53° 51′) равен (COS 53,85°) × 40000 / 360 = 0,59 × 111,111… = 65,544… километров. Одна минута соответственно 65,544…
/ 60 = 1,092… километров. Одна секунда долготы уже равна 1092,41… / 60 = 18,207… метров.
6371*tg1гр=111 км.
111,15
Степень (геометрия)
скорость в геометрии — это единица измерения прямых углов.
Если любой круг делится на 360 равных частей, а точки деления связаны с центром круга, круг делится на 360 фокусных углов. Каждый из них будет равен 1 °.
Рисунок 40 каждый 5 °, потому что круг мал: если вы рисуете линии в этом круге на 1 °, они будут сливаться.
Каждый круг должен содержать 360 °.
Размер уровня тот же в малых и больших кругах, но длина круга равна 1 °. Таким образом, окружность круга, равная 1 °, намного меньше миллиметра в пене, а экватор Земли составляет приблизительно 111 км (40 000 км / 360 = 111 км).
Фотографии (фото, картинки)
Рис.
40. Стоинье
Материал со страницы WikiWhat
На этом сайте вы можете найти следующие темы:
Резюме уровня
Она диплом в области геометрии
Отчет о происхождении словаря
Отчет о степенях
Какова степень определения в геометрии
vipstylelife.ru
Градус, минута, секунда — это… Что такое Градус, минута, секунда?
Градус, минута, секунда — общепринятые единицы измерения плоских углов и земного шара.
Градус
Градус (от лат. gradus — деление шкалы, шаг, ступень) обозначается °. Один оборот равен 360°. В прямом углу, таким образом, 90°, в развёрнутом — 180°.
Деление окружности на 360° придумали аккады (вавилоняне) — соответственно делению года в вавилонском календаре на 360 дней.
Минуты и секунды
В измерении углов традиционно используется шестидесятеричная система счисления. По аналогии с делением часа как интервала времени градус делят на 60 минут (′), а минуту — на 60 секунд (″).
- 1′ = ≈ 2,9088821×10-4 радиан.
- 1″ = ≈ 4,8481368×10-6 радиан.
Угловая секунда
Углова́я секу́нда (англ. arcsecond, arc second, as, second of arc; синонимы: дуговая секунда, секунда дуги[1]) — внесистемная астрономическая единица измерения малых углов, тождественная секунде плоского угла[2].
Использование
Угловая секунда (обозначается ″) используется в астрономии при измерении плоских углов в градусных мерах. При измерении углов в часовых мерах (в частности, для определения прямого восхождения) используется единица измерения «секунда» (обозначается с). Соотношение между этими величинами определяется формулой 1c = 15″.[3]
Иногда угловую секунду (и производные от неё дольные единицы) ошибочно называют арксекундой[1][4], что является простой транслитерацией с англ. arcsecond.
Дольные единицы
По аналогии с международной системой единиц (СИ), наряду с угловой секундой применяются и её дольные единицы измерения: миллисекунды (англ.
Дольные единицы могут использоваться для обозначения собственного движения звёзд и галактик, годичного параллакса и углового диаметра звёзд.[6]
Для наблюдения астрономических объектов под такими сверхмалыми углами астрономы прибегают к методу интерферометрии, при котором сигналы, принимаемые несколькими разнесёнными радиотелескопами, комбинируются в процессе апертурного синтеза. Так, используя методику интерферометрии со сверхдлинной базой (VLBI), астрономы получили возможность измерить собственное движение галактики Треугольника.
В видимом свете существенно труднее достичь миллисекундного разрешения. Тем не менее, спутник Hipparcos справился с этой задачей в процессе астрометрических измерений, по результатам которых были составлены наиболее точные (по состоянию на 1997 год) каталоги звёзд Tycho (TYC) и Hipparcos (HIP).[7][8]
Примечания
Литература
- Гельфанд И. М., Львовский С. М., Тоом А. Л. Малые углы // Тригонометрия. — М.: МЦНМО, 2002. — 199 с. — ISBN 5-94057-050-X
См. также
Wikimedia Foundation. 2010.
dic.academic.ru
| ПОЛЕЗНЫЕ ССЫЛКИ: БОНУСЫ ИНЖЕНЕРАМ!: МЫ В СОЦ.СЕТЯХ: | Навигация по справочнику TehTab.ru: главная страница / / Техническая информация / / Математический справочник / / Таблицы численных значений. (Таблица квадратов, кубов, синусов ….) + Таблицы Брадиса / / Определение и численные соотношения между единицами измерения углов в РФ. Тысячные, угловые градусы, минуты, секунды, радианы, обороты.
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
tehtab.ru
Градус, минута, секунда Википедия
У этого термина существуют и другие значения, см. Градус.Гра́дус, мину́та, секу́нда — общепринятые единицы измерения плоских углов. Также эти величины используются в картографии для определения координат произвольной точки земной поверхности, а также для определения азимута.
Градус
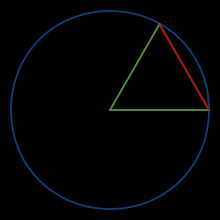Окружность с хордой, образованной стороной равностороннего треугольника (выделена красным). Одна шестидесятая этой дуги равна одному градусу. Шесть таких хорд охватывают полный круг.Градус (от лат. gradus — деление шкалы, шаг, ступень) обозначается °. Один полный оборот соответствует углу в 360°. В прямом угле, таким образом, 90°, в развёрнутом — 180°.
Причина выбора градуса как единицы измерения углов неизвестна. Одна из теорий предполагает, что это связано с тем, что 360 — приблизительное количество дней в году[1]. Некоторые древние календари, такие как древнеперсидский, использовали год в 360 дней.
Другая теория гласит, что аккадцы (вавилоняне) поделили окружность, используя угол равностороннего треугольника как базу и поделив результат на 60, следуя своей шестидесятеричной системе счисления[2][3].
Если построить окружность радиусом 57 см, то 1 градус будет примерно соответствовать 1 см длины дуги данной окружности.
Градус в альтернативных единицах измерения:
- 1∘=2π360{\displaystyle 1^{\circ }={\frac {2\pi }{\displaystyle {360}}}} радиан =π180=1p≈157,295779513∘{\displaystyle ={\frac {\pi }{\displaystyle {180}}}={\frac {1}{\displaystyle {p}}}\approx {\frac {1}{\displaystyle {57{,}295779513^{\circ }}}}}[4]≈0,0174532925{\displaystyle \approx 0{,}0174532925} (радиан в 1°)
- 1∘=1360{\displaystyle 1^{\circ }={\frac {1}{360}}} оборота=0,002(7) оборота=0,002777777777…
- 1∘=400360{\displaystyle 1^{\circ }={\frac {400}{360}}} градов=1,(1) градов=1,11111111111… градов
Минуты и секунды
По аналогии с делением часа как интервала времени градус делят на 60 минут (от лат. minutus — маленький, мелкий; обозначается штрихом x′), а минуту — на 60 секунд (от лат. secunda divisio — второе деление; обозначается двумя штрихами y″. Ранее употреблялась величина в 1/60 секунды — терция (третье деление), с обозначением тремя штрихами — z″′. Деление градуса на минуты и секунды ввёл Клавдий Птолемей[5]; корни же такого деления восходят к учёным Древнего Вавилона (где использовалась шестидесятеричная система счисления).
Минуты и секунды в других системах измерения:
- 1′=2π360∘⋅60′=1′p′≈1′3437,747′{\displaystyle 1’={\frac {2\pi }{\displaystyle {360^{\circ }}\cdot 60′}}={\frac {1′}{p’}}\approx {\frac {1′}{3437{,}747′}}}[4]≈2,90888208⋅10−4 rad{\displaystyle \approx 2{,}90888208\cdot 10^{-4}~{\text{rad}}} (1 минута в радианах)
- 1″=2π360∘⋅60′⋅60″=1″p″≈1″206264,8″{\displaystyle 1»={\frac {2\pi }{\displaystyle {360^{\circ }}\cdot 60’\cdot 60»}}={\frac {1»}{p»}}\approx {\frac {1»}{206264{,}8»}}}[4]≈4,848136811⋅10−6 rad{\displaystyle \approx 4{,}848136811\cdot 10^{-6}~{\text{rad}}} (1 секунда в радианах).
Минуты и секунды в радианной мере из-за своих чрезмерно малых величин представляют ограниченный интерес и практически очень мало используются.
Гораздо больший интерес представляет перевод десятичных (сотых, десятитысячных) долей градуса в минуты и секунды и обратно — см. Радиан#Связь радиана с другими единицами и Географические координаты.
Угловая секунда
Углова́я секу́нда (англ. arcsecond, arc second, as, second of arc; синонимы: дуговая секунда, секунда дуги[6]) — внесистемная астрономическая единица измерения малых углов, тождественная секунде плоского угла[7].
Использование
Угловая секунда (обозначается ″) используется в астрономии при измерении плоских углов в градусных мерах. При измерении углов в часовых мерах (в частности, для определения прямого восхождения) используется единица измерения «секунда» (обозначается s). Соотношение между этими величинами определяется формулой 1s=15″.[8]
Иногда угловую секунду (и производные от неё дольные единицы) ошибочно называют арксекундой[6][9], что является простой транслитерацией с англ. arcsecond.
Дольные единицы
По аналогии с международной системой единиц (СИ), наряду с угловой секундой применяются и её дольные единицы измерения: миллисекунды (англ. milliarcseconds, mas), микросекунды (англ. microarcseconds, µas) и пикосекунды (англ. picoarcseconds, pas). Они не входят в СИ (СИ рекомендует миллирадианы и микрорадианы), но допускаются к применению[7]. Однако согласно ГОСТ 8.417-2002, наименование и обозначения единиц плоского угла (градус, минута, секунда) не допускается применять с приставками[10], в связи с чем такие дольные величины должны приводиться либо к единицам СИ (миллирадианам и т. п.), либо к угловым секундам, либо обозначаться исходными единицами (mas, µas и pas соответственно).
| Единица | Величина | Обозначение | Аббревиатура | Радиан (прибл.) |
|---|---|---|---|---|
| градус | 1/360 окружности | ° | deg | 17,4532925 mrad |
| минута | 1/60 градуса | ′ | arcmin, amin, ′^{\displaystyle {\hat {‘}}}, MOA | 290,8882087 µrad |
| секунда | 1/60 минуты | ″ | arcsec | 4,8481368 µrad |
| миллисекунда | 1/1000 секунды | mas | 4,8481368 nrad | |
| микросекунда | 1 × 10−6 секунды | μas | 4,8481368 prad |
Дольные единицы могут использоваться для обозначения собственного движения звёзд и галактик, годичного параллакса и углового диаметра звёзд.
Для наблюдения астрономических объектов под такими сверхмалыми углами астрономы прибегают к методу интерферометрии, при котором сигналы, принимаемые несколькими разнесёнными радиотелескопами, комбинируются в процессе апертурного синтеза. Так, используя методику интерферометрии со сверхдлинной базой, астрономы получили возможность измерить собственное движение галактики Треугольника.[источник не указан 2529 дней]
В видимом свете существенно труднее достичь миллисекундного разрешения. Тем не менее, спутник Hipparcos справился с этой задачей в процессе астрометрических измерений, по результатам которых были составлены наиболее точные (по состоянию на 1997 год) каталоги звёзд Tycho (TYC) и Hipparcos (HIP)[11][12].
Примечания
- ↑ Weisstein, Eric W. Degree (англ.). Wolfram MathWorld. Дата обращения 26 ноября 2017.
- ↑ James Hopwood Jeans. The Growth of Physical Science. — 1947. — С. 7.
- ↑ Murnaghan, Francis D. Analytic geometry. — New York: Prentice-Hall, inc., 1946. — P. 2.
- ↑ 1 2 3 Переводные множители — <57,295779513>, <3437,747>, <206264,8> — см. Радиан#Связь радиана с другими единицами.
- ↑ Боголюбов, 1983, с. 393—394.
- ↑ 1 2 Англо-русско-английский астрономический словарь (неопр.). Astronet. Дата обращения 23 декабря 2007. Архивировано 23 августа 2011 года.
- ↑ 1 2 Non-SI units accepted for use with the International System of Units (англ.). SI brochure (8th ed.). Bureau International des Poids et Mesures. — Описание СИ на сайте Международного бюро мер и весов. Дата обращения 23 декабря 2007. Архивировано 23 августа 2011 года.
- ↑ Справочник. Некоторые внесистемные единицы (неопр.). ASTROLAB. Дата обращения 23 декабря 2007. Архивировано 23 августа 2011 года.
- ↑ Glossary entry for English term «arcsecond» (англ.). Справочник по услугам профессионального перевода, предоставляемым независимыми переводчиками и бюро перевода. ProZ.com. Дата обращения 23 декабря 2007. Архивировано 23 августа 2011 года.
- ↑ ГОСТ 8.417-2002. Единицы величин. Введён в действие с 1 сентября 2003 г. // Информационная система по оборудованию «Прибор.Инфо» : справочник. — 2003. Архивировано 5 августа 2013 года.
- ↑ Гурьянов С. Почему звезды называются именно так? (неопр.). проект «Астрогалактика» (29 октября 2005 года). Дата обращения 26 декабря 2007. Архивировано 23 августа 2011 года.
- ↑ Цветков А. С. Общие сведения о проекте Hipparcos // Руководство по практической работе с каталогом Hipparcos. — СПб.: АИ СПбГУ.
Литература
См. также
wikiredia.ru
Градус, минута, секунда Вики
У этого термина существуют и другие значения, см. Градус.Гра́дус, мину́та, секу́нда — общепринятые единицы измерения плоских углов. Также эти величины используются в картографии для определения координат произвольной точки земной поверхности, а также для определения азимута.
Градус[ | код]
Окружность с хордой, образованной стороной равностороннего треугольника (выделена красным). Одна шестидесятая этой дуги равна одному градусу. Шесть таких хорд охватывают полный круг.Градус (от лат. gradus — деление шкалы, шаг, ступень) обозначается °. Один полный оборот соответствует углу в 360°. В прямом угле, таким образом, 90°, в развёрнутом — 180°.
Причина выбора градуса как единицы измерения углов неизвестна. Одна из теорий предполагает, что это связано с тем, что 360 — приблизительное количество дней в году[1]. Некоторые древние календари, такие как древнеперсидский, использовали год в 360 дней.
Другая теория гласит, что аккадцы (вавилоняне) поделили окружность, используя угол равностороннего треугольника как базу и поделив результат на 60, следуя своей шестидесятеричной системе счисления[2][3].
Если построить окружность радиусом 57 см, то 1 градус будет примерно соответствовать 1 см длины дуги данной окружности.
Градус в альтернативных единицах измерения:
- 1∘=2π360{\displaystyle 1^{\circ }={\frac {2\pi }{\displaystyle {360}}}} радиан =π180=1p≈157,295779513∘{\displaystyle ={\frac {\pi }{\displaystyle {180}}}={\frac {1}{\displaystyle {p}}}\approx {\frac {1}{\displaystyle {57{,}295779513^{\circ }}}}}[4]≈0,0174532925{\displaystyle \approx 0{,}0174532925} (радиан в 1°)
- 1∘=1360{\displaystyle 1^{\circ }={\frac {1}{360}}} оборота=0,002(7) оборота=0,002777777777…
- 1∘=400360{\displaystyle 1^{\circ }={\frac {400}{360}}} градов=1,(1) градов=1,11111111111… градов
Минуты и секунды[ | код]
По аналогии с делением часа как интервала времени градус делят на 60 минут (от лат. minutus — маленький, мелкий; обозначается штрихом x′), а минуту — на 60 секунд (от лат. secunda divisio — второе деление; обозначается двумя штрихами y″. Ранее употреблялась величина в 1/60 секунды — терция (третье деление), с обозначением тремя штрихами — z″′. Деление градуса на минуты и секунды ввёл Клавдий Птолемей[5]; корни же такого деления восходят к учёным Древнего Вавилона (где использовалась шестидесятеричная система счисления).
Минуты и секунды в других системах измерения:
- 1′=2π360∘⋅60′=1′p′≈1′3437,747′{\displaystyle 1’={\frac {2\pi }{\displaystyle {360^{\circ }}\cdot 60′}}={\frac {1′}{p’}}\approx {\frac {1′}{3437{,}747′}}}[4]≈2,90888208⋅10−4 rad{\displaystyle \approx 2{,}90888208\cdot 10^{-4}~{\text{rad}}} (1 минута в радианах)
- 1″=2π360∘⋅60′⋅60″=1″p″≈1″206264,8″{\displaystyle 1»={\frac {2\pi }{\displaystyle {360^{\circ }}\cdot 60’\cdot 60»}}={\frac {1»}{p»}}\approx {\frac {1»}{206264{,}8»}}}[4]≈4,848136811⋅10−6 rad{\displaystyle \approx 4{,}848136811\cdot 10^{-6}~{\text{rad}}} (1 секунда в радианах).
Минуты и секунды в радианной мере из-за своих чрезмерно малых величин представляют ограниченный интерес и практически очень мало используются.
Гораздо больший интерес представляет перевод десятичных (сотых, десятитысячных) долей градуса в минуты и секунды и обратно — см. Радиан#Связь радиана с другими единицами и Географические координаты.
Угловая секунда[ | код]
Углова́я секу́нда (англ. arcsecond, arc second, as, second of arc; синонимы: дуговая секунда, секунда дуги[6]) — внесистемная астрономическая единица измерения малых углов, тождественная секунде плоского угла[7].
Использование[ | код]
Угловая секунда (обозначается ″) используется в астрономии при измерении плоских углов в градусных мерах. При измерении углов в часовых мерах (в частности, для определения прямого восхождения) используется единица измерения «секунда» (обозначается s). Соотношение между этими величинами определяется формулой 1s=15″.[8]
Иногда угловую секунду (и производные от неё дольные единицы) ошибочно называют арксекундой[6][9], что является простой транслитерацией с англ. arcsecond.
Дольные единицы[ | код]
По аналогии с международной системой единиц (СИ), наряду с угловой секундой применяются и её дольные единицы измерения: миллисекунды (англ. milliarcseconds, mas), микросекунды (англ. microarcseconds, µas) и пикосекунды (англ. picoarcseconds, pas). Они не входят в СИ (СИ рекомендует миллирадианы и микрорадианы), но допускаются к применению[7]. Однако согласно ГОСТ 8.417-2002, наименование и обозначения единиц плоского угла (градус, минута, секунда) не допускается применять с приставками[10], в связи с чем такие дольные величины должны приводиться либо к единицам СИ (миллирадианам и т. п.), либо к угловым секундам, либо обозначаться исходными единицами (mas, µas и pas соответственно).
| Единица | Величина | Обозначение | Аббревиатура | Радиан (прибл.) |
|---|---|---|---|---|
| градус | 1/360 окружности | ° | deg | 17,4532925 mrad |
| минута | 1/60 градуса | ′ | arcmin, amin, ′^{\displaystyle {\hat {‘}}}, MOA | 290,8882087 µrad |
| секунда | 1/60 минуты | ″ | arcsec | 4,8481368 µrad |
| миллисекунда | 1/1000 секунды | mas | 4,8481368 nrad | |
| микросекунда | 1 × 10−6 секунды | μas | 4,8481368 prad |
Дольные единицы могут использоваться для обозначения собственного движения звёзд и галактик, годичного параллакса и углового диаметра звёзд.
Для наблюдения астрономических объектов под такими сверхмалыми углами астрономы прибегают к методу интерферометрии, при котором сигналы, принимаемые несколькими разнесёнными радиотелескопами, комбинируются в процессе апертурного синтеза. Так, используя методику интерферометрии со сверхдлинной базой, астрономы получили возможность измерить собственное движение галактики Треугольника.[источник не указан 2529 дней]
В видимом свете существенно труднее достичь миллисекундного разрешения. Тем не менее, спутник Hipparcos справился с этой задачей в процессе астрометрических измерений, по результатам которых были составлены наиболее точные (по состоянию на 1997 год) каталоги звёзд Tycho (TYC) и Hipparcos (HIP)[11][12].
Примечания[ | код]
- ↑ Weisstein, Eric W. Degree (англ.). Wolfram MathWorld. Дата обращения 26 ноября 2017.
- ↑ James Hopwood Jeans. The Growth of Physical Science. — 1947. — С. 7.
- ↑ Murnaghan, Francis D. Analytic geometry. — New York: Prentice-Hall, inc., 1946. — P. 2.
- ↑ 1 2 3 Переводные множители — <57,295779513>, <3437,747>, <206264,8> — см. Радиан#Связь радиана с другими единицами.
- ↑ Боголюбов, 1983, с. 393—394.
- ↑ 1 2 Англо-русско-английский астрономический словарь (неопр.). Astronet. Дата обращения 23 декабря 2007. Архивировано 23 августа 2011 года.
- ↑ 1 2 Non-SI units accepted for use with the International System of Units (англ.). SI brochure (8th ed.). Bureau International des Poids et Mesures. — Описание СИ на сайте Международного бюро мер и весов. Дата обращения 23 декабря 2007. Архивировано 23 августа 2011 года.
- ↑ Справочник. Некоторые внесистемные единицы (неопр.). ASTROLAB. Дата обращения 23 декабря 2007. Архивировано 23 августа 2011 года.
- ↑ Glossary entry for English term «arcsecond» (англ.). Справочник по услугам профессионального перевода, предоставляемым независимыми переводчиками и бюро перевода. ProZ.com. Дата обращения 23 декабря 2007. Архивировано 23 августа 2011 года.
- ↑ ГОСТ 8.417-2002. Единицы величин. Введён в действие с 1 сентября 2003 г. // Информационная система по оборудованию «Прибор.Инфо» : справочник. — 2003. Архивировано 5 августа 2013 года.
- ↑ Гурьянов С. Почему звезды называются именно так? (неопр.). проект «Астрогалактика» (29 октября 2005 года). Дата обращения 26 декабря 2007. Архивировано 23 августа 2011 года.
- ↑ Цветков А. С. Общие сведения о проекте Hipparcos // Руководство по практической работе с каталогом Hipparcos. — СПб.: АИ СПбГУ.
Литература[ | код]
См. также[ | код]
ru.wikibedia.ru
Как градусы перевести в минуты, секунды и радианы?
Любые тела, форма которых является круглой, например сфера или окружность, нуждаются в специальных единицах измерения, отличающихся от таковых для линейных объектов. Этими единицами измерения стали градусы и радианы. При этом часто возникает вопрос о том, как градусы перевести в минуты, секунды и в радиальную систему измерения.
Единицы измерения: градусы
Приблизительно за тысячу лет до нашей эры древние вавилоняне применяли систему измерения небесных тел, по которой вся небесная сфера разделялась на 360 равных частей, что записывалось как 360 °. Одну трехсот шестидесятую часть они называли градусом.
Поскольку система исчисления древних вавилонян являлась шестидесятеричной, они разделяли каждый градус на 60 равных частей, и одна такая часть получила название минуты и обозначалась 1′. В свою очередь каждая минута делилась еще на 60 частей, 1/60 минуты называлась секундой и обозначалась 1».
Наша система исчисления, в отличие от системы древних вавилонян, является десятеричной, однако в области измерения круглых и сферических форм по-прежнему используются градусы, минуты и секунды в их первоначальном понимании. Например, прямым углом является угол в 90°, один градус содержит 60 минут, а одна минута — 60 секунд. Эту информацию рекомендуется запомнить, поскольку она помогает понять, как градусы перевести в минуты.
Единицы измерения: радианы
Наряду с градусами часто используются другие единицы измерения — радианы (от лат. radii — радиус). Радиан является более подходящей единицей измерения круглых тел, поскольку он непосредственно связан с их геометрией. Так, один радиан представляет собой угол, который опирается на длину дуги окружности, равную ее радиусу. Поскольку длина окружности вычисляется по формуле L = 2piR, где pi — число пи, равное 3,14, то полная окружность составляет 2pi радиан.
Измерение углов в радианах очень удобно в тригонометрии, где вычисления и преобразования тригонометрических функций выполняются именно в этой системе исчисления. Например, sin(pi/2) = 1.
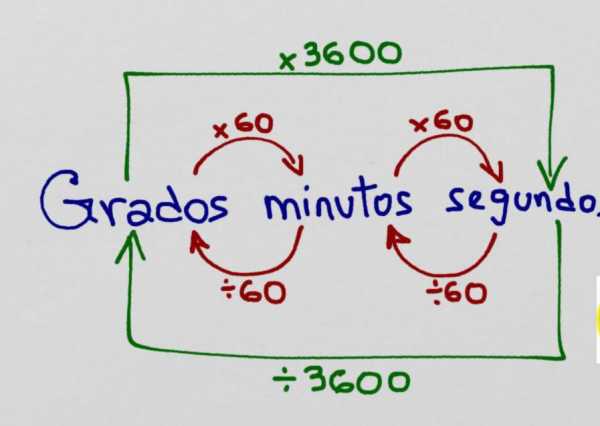
Как градусы перевести в минуты, секунды и радианы
Как сделать все правильно? Чтобы выполнить процедуру перевода градусов в минуты и секунды, нужно вспомнить, что в минутах он равен 60, а в секундах 60 x 60 = 3600 или 1° = 60′ и 1′ = 60».
Приведем пример: есть угол a = 12°. Как градусы перевести в минуты для него? Для этого составим пропорцию, из которой получим: a = 60′ x 12º/1º = 720′. Теперь рассмотрим более сложный случай: есть угол a = 32º 45′ 23». Для перевода этого угла в минуты необходимо прибегнуть к сложению в минутах каждого его разряда. В итоге получаем: a = 32 x 60 + 45 + 23/60 = 1965,383′. В секундах этот угол будет равен: a = 32 x 60 x 60 + 45 x 60 + 23 = 117923».
Чтобы перевести угол a из примера выше в радианы, нужно вспомнить, что 360° = 2pi. Теперь нужно указанный угол привести к градусам, получаем: a = 32 + 45/60 + 23/3600 = 32,75639°. Полученный в градусах угол через пропорцию переводим в радианы: a = 2pi x 32.75639°/360° = 0,5717 радиан.
fb.ru
Градус, минута, секунда Википедия
У этого термина существуют и другие значения, см. Градус.Гра́дус, мину́та, секу́нда — общепринятые единицы измерения плоских углов. Также эти величины используются в картографии для определения координат произвольной точки земной поверхности, а также для определения азимута.
Градус[ | ]
Окружность с хордой, образованной стороной равностороннего треугольника (выделена красным). Одна шестидесятая этой дуги равна одному градусу. Шесть таких хорд охватывают полный круг.Градус (от лат. gradus — деление шкалы, шаг, ступень) обозначается °. Один полный оборот соответствует углу в 360°. В прямом угле, таким образом, 90°, в развёрнутом — 180°.
Причина выбора градуса как единицы измерения углов неизвестна. Одна из теорий предполагает, что это связано с тем, что 360 — приблизительное количество дней в году[1]. Некоторые древние календари, такие как древнеперсидский, использовали год в 360 дней.
Другая теория гласит, что аккадцы (вавилоняне) поделили окружность, используя угол равностороннего треугольника как базу и поделив результат на 60, следуя своей шестидесятеричной системе счисления[2][3].
Если построить окружность радиусом 57 см, то 1 градус будет примерно соответствовать 1 см длины дуги данной окружности.
Градус в альтернативных единицах измерения:
- 1∘=2π360{\displaystyle 1^{\circ }={\frac {2\pi }{\displaystyle {360}}}} радиан =π180=1p≈157,295779513∘{\displaystyle ={\frac {\pi }{\displaystyle {180}}}={\frac {1}{\displaystyle {p}}}\approx {\frac {1}{\displaystyle {57{,}295779513^{\circ }}}}}[4]≈0,0174532925{\displaystyle \approx 0{,}0174532925} (радиан в 1°)
- 1∘=1360{\displaystyle 1^{\circ }={\frac {1}{360}}} оборота=0,002(7) оборота=0,002777777777…
- 1∘=
ru-wiki.ru