Множества и операции над ними
Понятие множества неопределимо. Пусть A, B, C –произвольные множества. a, b, c-их элементы. Основными не определяемыми отношениями в математике являются: a=b, a принадлежит множеству A. Введём следующее отношение:
A⊆B⇔∀a(a∈A→a∈B)
A=B⇔A⊆B&B⊆A
A⊂B⇔A⊆B&A≠B
A⊇B⇔B⊆A
A⊃B⇔A⊇B& A≠B
Введём обозначения: P(A)– множество всех подмножеств множества A. Перечеркнутый кружок — пустое множество и само множество А называются несобственными (тривиальными) подмножествами множества А.
Определим операции (функции) над множествами: A или B={x: x принадлежит A и x принадлежит B}
Декартово произведение A и B.
Замечание: Операции пересечения, объединения, разности множеств называются булевыми. Булевы операции и декартово произведение можно распространить на несколько сомножителей:
A1xA2x…xAk={(a1,a2,…,a
Пусть A, B, C есть произвольные подмножества некоторого универсального множества U (универсум).
Пусть не(A)=U-A (дополнение A до U). Иногда обозначают по другому.
Тогда справедливы следующие (булевы) свойства операций над множествами:
1. Идемпотентность (A и A) =A, (A или A)=A.
2. Коммутативность (A и B) = (B и A), (A или B) = (B или A).
3. Ассоциативность A и (B и C) = (A и B) и C, A или (B или C)=(A или B) или C.
4. Правило поглощения A и (A или B)=A, A или (A и B) = A.
5. Дистрибутивность A и (B или C)=(A и B) или (A и C), A или (B и C)=(A и B) или (A и C).
6. Инволюция не (не(A))=A.
7. Свойство констант (A и U) = A, (A или U) = U, (A и пустое множество) = пустое множество, (А или пустое множество) = A.
8. Закон исключённого третьего и закон противоречия (A или не(A)) = U, (A и не(A)) = пустое множество.
Перечисленные свойства доказываются непосредственно, как равенство двух множеств.
all4study.ru
Урок по математике на тему «Множества и операции над ними» (9 класс0
Открытый урок по математике в 9 классе.
( учитель математики Муниципального общеобразовательного учреждения «Средняя общеобразовательная школа № 3 г. Ершова Саратовской области» Уполовникова О.А.)
Тема урока: « Множества. Операции над множествами».
Цели урока:
Образовательная: ввести понятия множества и подмножества, способы задания множеств, виды множеств и операций над множествами.
Развивающая: развитие логического мышления, познавательного интереса; побуждать учеников к самоанализу своей учебной деятельности.
Воспитательная: воспитание интереса к предмету, умения работать самостоятельно.
Тип урока: изучение нового материала.
Оборудование: компьютер, мультимедийный проектор, презентация (Приложение 1)
Ход урока.
1. Организационный момент. Сообщение темы урока (презентация, слайд 1)
2. Объяснение новой темы.
1) Как вы думаете, что в русском языке означает слово множество? Давайте посмотрим как это слово трактуется в различных словарях (презентация, слайды 2, 3, 4 ).
2) Что же понимается под «множеством» в математике?
В конце 19 века Георг Кантор определил множество как « единое имя для совокупности всех объектов, обладающих данным свойством» (презентация слайд 5).
Понятие множества в современной математике ( презентация слайд 6).
3) Обозначение множеств и его элементов (презентация слайд 7).
4) Способы задания множеств (презентация слайды 8,9).
5) Предварительное закрепление знаний. Выполнить задание № 1 (устно) (слайд 10).
Задайте множество по его словесному описанию.
1. Целые положительные числа, которые меньше 4.
Выбери правильный вариант ответа:
а) {−4,−3,−2,−1};
б) {1,2,3};
в) {1,2,3,4};
г) {−1,−2,−3,−4,−5}.
2.Множество двузначных чисел, кратных 12.
6) Некоторые виды множеств (слайд 11).
Самостоятельно: запишите по два примера конечных и бесконечных множеств.
Например: конечное – множество двузначных чисел, являющихся квадратами натуральных чисел (16, 25, 36, 49, 64, 81).
7) Понятие подмножества (слайды 12, 13)
Выполнить задание № 2 устно (слайд 14).
Даны три множества А = {1, 2, 3,…, 37}, В = {2, 4, 6, 8, …}, С = {4, 8, 12, 16,…,36}.
Верно ли, что: а) А В; б) В С;
в) С А; г) С В?
9) Объединение множеств (слайд 16).
10) Разность множеств (слайд 17).
11) Выполнить задание № 3 (слайд 18).
1.Найди объединение, пересечение и разность множеств A и B, если A={0,1,2,3,4,5,6,7,8,9} и B={2,4,6,8,10}.
2.Даны три множества:
X={x,h,w,d},
Y={w,d,e,f},
Z={w,p,q}.
Найти (X∩Y) U Z .
У доски задание 1 выполняют трое учащихся (слабые), а задание 2 выполняет один более подготовленный ученик.
3. Закрепление изученного материала.
№ 3.2 (устно).
№ 3.12 (у доски).
Домашнее задание: № 3.1; № 3.8.
Источники:
1. Учебник «Алгебра 9 класс» под редакцией А.Г.Мордковича.
2. Множества и операции над множествами.
http://www.math5you.ru/theory/main-concept/set
3. http://referatbox.com/12698/ponyatie-mnozhestv-sposoby-zadaniya-mnozhestv/2/
4. http://www.yaklass.ru/p/algebra/9-klass/neravenstva-i-sistemy-neravenstv-9125/mnozhestva-i-operatcii-nad-nimi-12443
5. http://www.grandars.ru/student/vysshaya-matematika/mnozhestvo.html
infourok.ru
Множества и операции над ними

Множества, операции над ними преподаватель математики МИПК им. И.Федорова Епихина Е.В.

«Множество есть многое, мыслимое нами как единое».
Основоположник теории множеств немецкий математик
Георг Кантор
(1845-1918)

Понятие множества принадлежит к числу основных, неопределяемых понятий математики. Множество – набор, совокупность, собрание каких-либо объектов (элементов), обладающих общим для всех их характеристическим свойством. Примеры множеств: множество студентов в данной аудитории; множество людей, живущих на нашей планете в данный момент времени; множество точек данной геометрической фигуры; множество чётных чисел; множество корней уравнения 5х+6=0;

Объекты, составляющие данное множество, называют его элементами. Множество обычно обозначают большими латинскими буквами, а элементы множества − малыми латинскими буквам. Если элемент, а принадлежит множеству А, то пишут: а А Если а не принадлежит А, то пишут: а А.

В математике часто исследуются так называемые числовые множества, т.е. множества, элементами кото-рых являются числа. Для самых основных числовых множеств утвердились следующие обозначения: N — множество всех натуральных чисел; Z — множество всех целых чисел; Q — множество всех рациональных чисел; R — множество всех действительных чисел. Приняты также обозначения Z + , Q +, R + соответственно для множеств всех неотрицательных целых, рациональных и действительных чисел, и Z ¯, Q ¯, R ¯ -для множеств всех отрицательных целых, рациональных и действительных чисел.

Способы задания множества
- перечисление элементов множества;
А={ a ; b ; c ; …; d }
- указание характеристического свойства элементов множества, т.е. такого свойства, которым обладают все элементы данного множества и только они.
А={х | 5х+6=0}.

Поставьте вместо звездочки знак так, чтобы полу- чить правильное утверждение: 1) 5 * N ; 2) –5 * Q ; 3) 3,14 * Q ; 4) 2 * R ; 5) 0 * N ; 6) − 12 * Z ; 6) π * Q ; 8) 3 * ∅

Задайте перечислением элементов множество: 1) A = { x | x N , 2 x – 1 = 0}; 2) B = { x | x Z , | x | C = { x | x N , x ≤ 15, x = 7 k , k Z }.

Действия над множествами
- Включение и равенство множеств
Пусть Х и У – два множества. Если каждый элемент х множества Х является элементом множества У, то говорят, что множество Х содержится во множестве У и пишут: Х У или У Х. Говорят также, что Х включено в У или У включает Х, или что Х является подмножеством множества У.

Если для двух множеств Х и У одновременно имеют место два включения т.е. Х есть подмножество множества У и У есть подмножество множества Х, то множества Х и У состоят из одних и тех же элементов. Такие множества Х и У называют равными и пишут: Х=У.

Объединение множеств ( сложение)
Объединением А В множеств А и В называется множество, состоящее из всех элементов, принадлежащих хотя бы одному из множеств А или В.
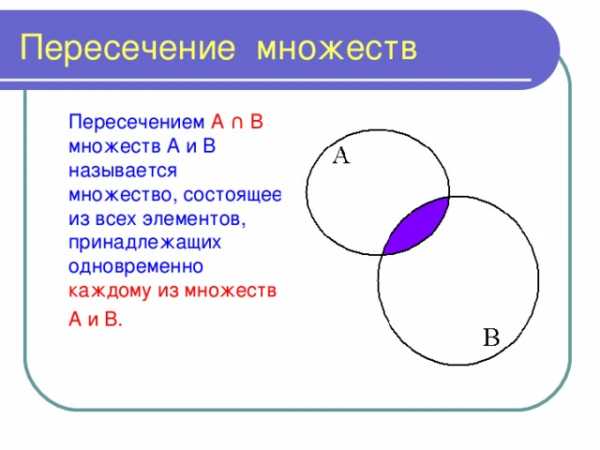
Пересечение множеств
Пересечением А ∩ В множеств А и В называется множество, состоящее из всех элементов, принадлежащих одновременно каждому из множеств
А и В.
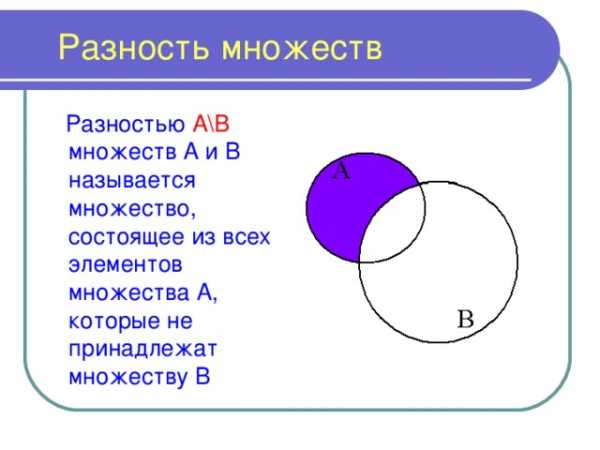
Разность множеств
Разностью А\В множеств А и В называется множество, состоящее из всех элементов множества А, которые не принадлежат множеству В
kopilkaurokov.ru
