На графике производная – График производной функции

Геометрический смысл производной. | Подготовка к ЕГЭ по математике

Категория: Справочные материалы

Елена Репина 2013-02-17 2014-01-12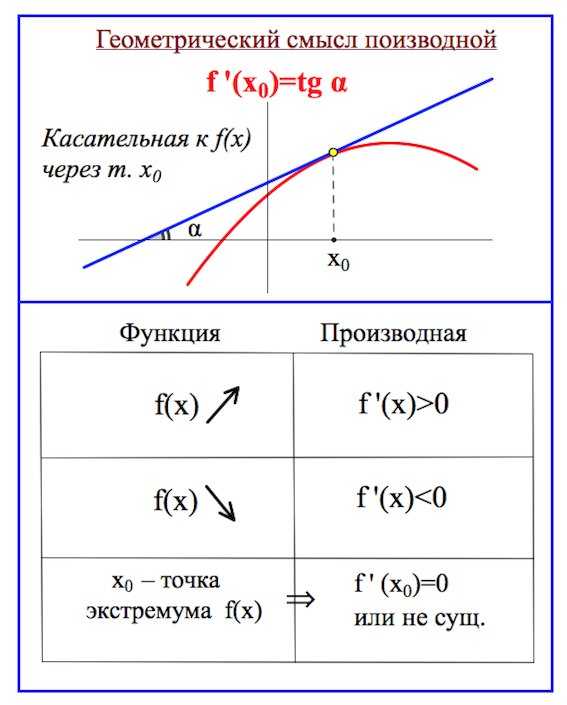

Прокомментируем таблицу.

Рассмотрим график функции, изображенный на рисунке.

Мы видим, что  функция возрастает в точке . Касательная, проведенная к графику функции в точке , имеет острый угол наклона к оси (ох), значит тангенс угла наклона касательной положителен, а значит, положительна и производная функции в точке .

Точка – точка минимума функции, касательная проведенная к графику функции через точку , параллельна оси (ох), значит тангенс угла наклона касательной равен нулю, значит и производная функции в точке равна нулю.

В точке функция убывает. Касательная, проведенная к графику функции в точке , имеет тупой угол наклона к оси (ох), значит тангенс угла наклона касательной отрицателен, а значит,

отрицательна  производная функции в точке .

Автор: egeMax | Нет комментариев | Метки: шпаргалки-таблицы

egemaximum.ru

Графики функций и их производных.

ИССЛЕДОВАНИЕ ФУНКЦИИ ПРИ ПОМОЩИ ПРОИЗВОДНОЙ

возрастание

убывание

функции.

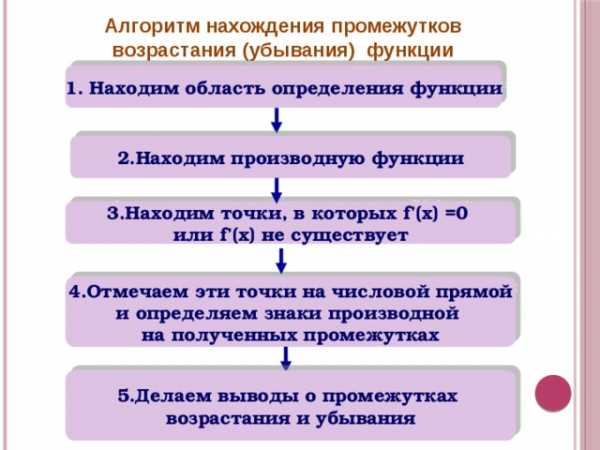
Алгоритм нахождения промежутков возрастания (убывания) функции

1. Находим область определения функции

2.Находим производную функции

3.Находим точки, в которых f’(x) =0

или f’(x) не существует

4.Отмечаем эти точки на числовой прямой

и определяем знаки производной

на полученных промежутках

5.Делаем выводы о промежутках

возрастания и убывания

Исследование

по формуле

по графику

0, значит, функция возрастает. Если f / (x) значит, функция убывает. «

Признаки:

Если f / (x) 0,

значит, функция возрастает.

Если f / (x)

значит, функция убывает.

По формуле функции

Практикум:

Найдите промежутки возрастания

(убывания) функции.

Задания:

1 вариант

D(f)

2 вариант

f ‘ (x)

f ‘ (x) = 0

(не существует)

Знаки

Промежутки возрастания

производной

Промежутки убывания

1 вариант

D(f)

2 вариант

f ‘ (x)

R

f ‘ (x) = 0

R

(не существует)

Знаки

-1; 1

1

Промежутки возрастания

производной

-1; 1

Промежутки убывания

—

—

—

-1

+

+

+

-1

1

Графики.

Графики

функций

Графики

производных

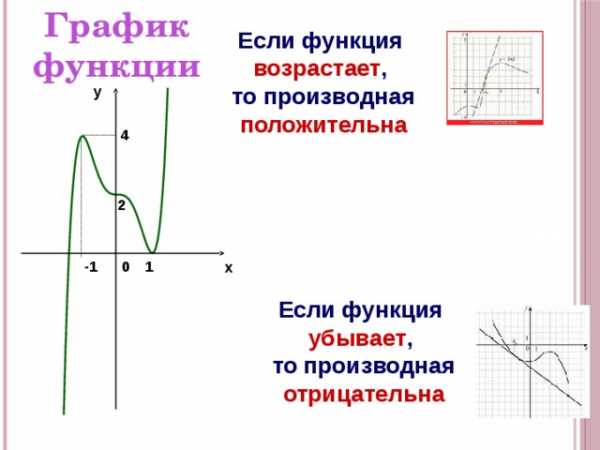
График

функции

Если функция возрастает ,

то производная

положительна

y

4

2

1

-1

0

x

Если функция убывает ,

то производная

отрицательна

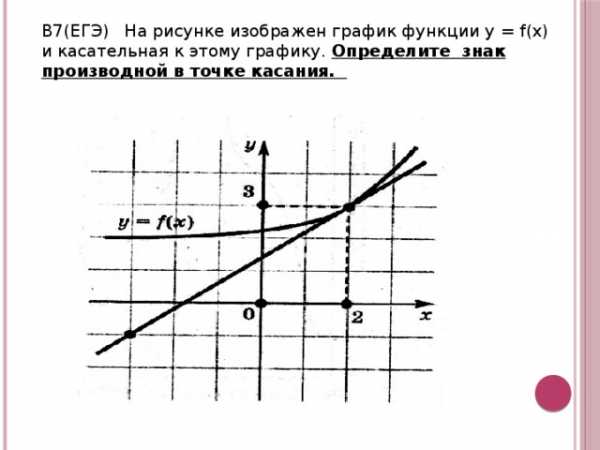
В7(ЕГЭ) На рисунке изображен график функции у = f(x) и касательная к этому графику. Определите знак производной в точке касания.

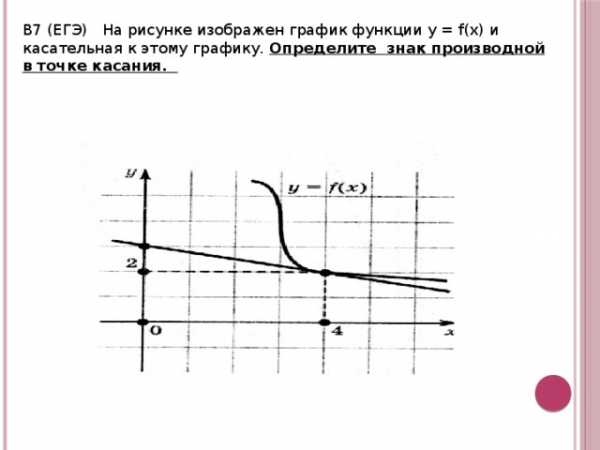
В7 (ЕГЭ) На рисунке изображен график функции у = f(x) и касательная к этому графику. Определите знак производной в точке касания.

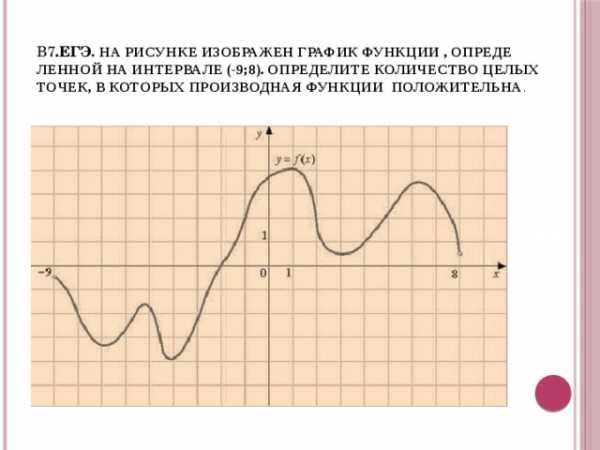
В7 .егэ .   На ри­сун­ке изоб­ра­жен гра­фик функ­ции , опре­де­лен­ной на ин­тер­ва­ле (-9;8). Опре­де­ли­те ко­ли­че­ство целых точек, в ко­то­рых про­из­вод­ная функ­ции  по­ло­жи­тель­на

.

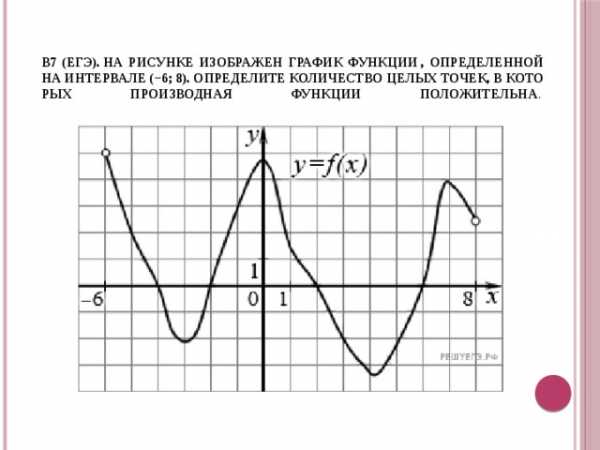
В7 (егэ). На ри­сун­ке изоб­ра­жен гра­фик функ­ции , опре­де­лен­ной на ин­тер­ва­ле (−6; 8). Опре­де­ли­те ко­ли­че­ство целых точек, в ко­то­рых про­из­вод­ная функ­ции по­ло­жи­тель­на . 

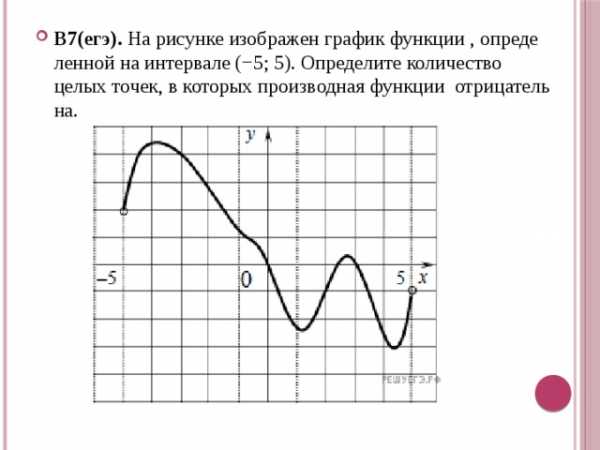
• В7(егэ).  На ри­сун­ке изоб­ра­жен гра­фик функ­ции , опре­де­лен­ной на ин­тер­ва­ле (−5; 5). Опре­де­ли­те ко­ли­че­ство целых точек, в ко­то­рых про­из­вод­ная функ­ции  от­ри­ца­тель­на.

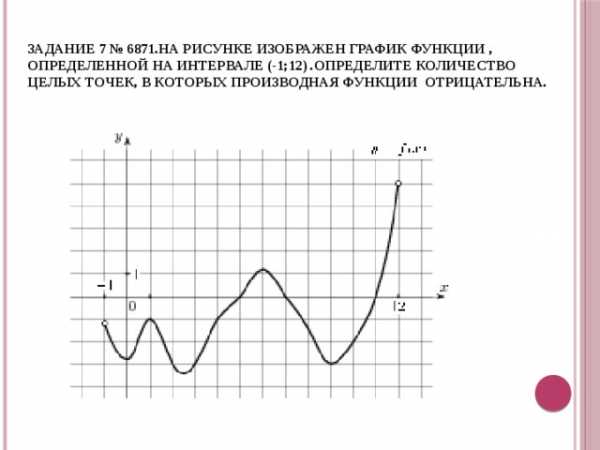
За­да­ние 7 № 6871.На ри­сун­ке изоб­ра­жен гра­фик функ­ции , опре­де­лен­ной на ин­тер­ва­ле (-1;12) .Опре­де­ли­те ко­ли­че­ство целых точек, в ко­то­рых про­из­вод­ная функ­ции от­ри­ца­тель­на.

0, значит, функция возрастает. Признаки: Если f / (x) значит, функция убывает. «

Графики производных

Задания В7 (ЕГЭ)

Если f / (x) 0,

значит, функция возрастает.

Признаки:

Если f / (x)

значит, функция убывает.

0, значит, функция возрастает. На рисунке изображен график y=f'(x)   — производной функции f(x) , определенной на интервале (-6;8) . Найдите количество промежутков возрастания функции f(x) . График производной «

Если f / (x) 0,

значит, функция возрастает.

На рисунке изображен график y=f'(x)   — производной функции f(x) , определенной на интервале (-6;8) . Найдите количество промежутков возрастания функции f(x)

.

График производной

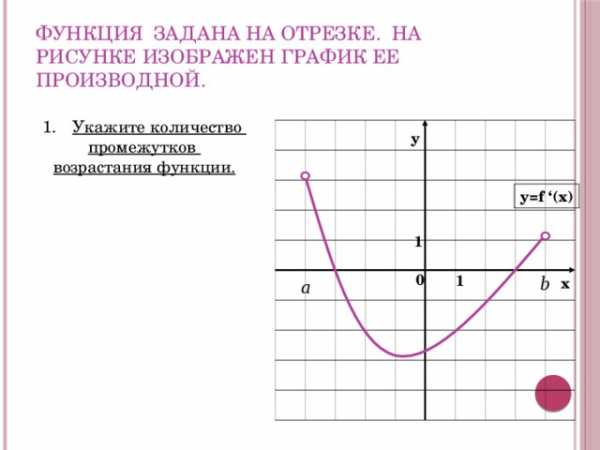
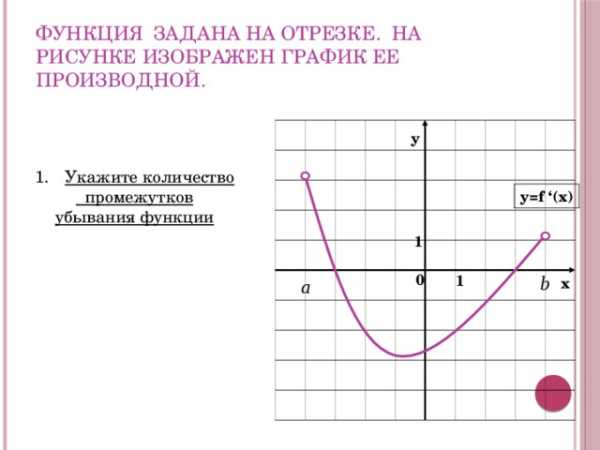
Функция задана на отрезке. На рисунке изображен график ее производной.

• Укажите количество

промежутков

возрастания функции.

у

y=f ‘(x)

1

0

b

1

х

а

На рисунке изображен график y=f'(x) — производной функции f(x) , определенной на интервале (-8;6) . Найдите количество промежутков убывания функции f(x).

Если f / (x)

значит, функция убывает.

Функция задана на отрезке. На рисунке изображен график ее производной.

у

• Укажите количество

промежутков

убывания функции

y=f ‘(x)

1

0

b

1

х

а

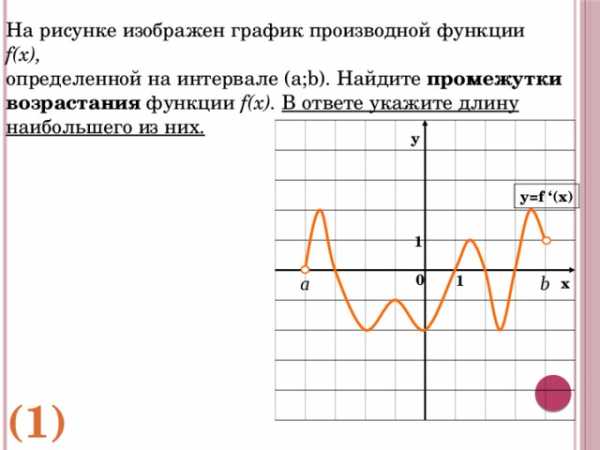
На рисунке изображен график производной функции f(x),

определенной на интервале (a;b). Найдите промежутки возрастания функции f(x). В ответе укажите длину наибольшего из них.

у

y=f ‘(x)

1

b

0

а

1

х

(1)

На рисунке изображен график производной функции f(x),

определенной на интервале (a;b). Найдите промежутки убывания функции f(x). В ответе укажите длину наибольшего из них.

у

y=f ‘(x)

1

b

0

а

1

х

(2)

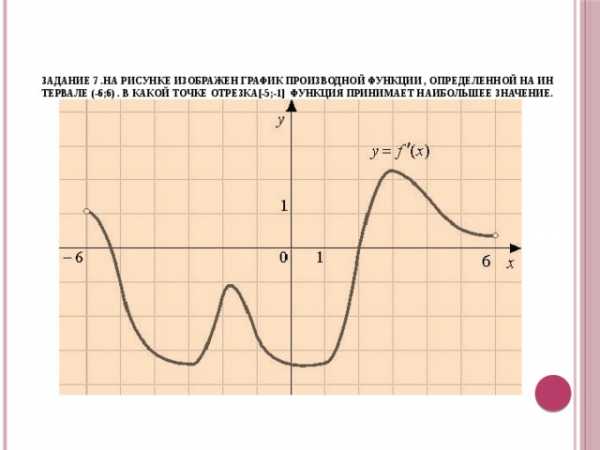
За­да­ние 7 .На ри­сун­ке изоб­ра­жен гра­фик про­из­вод­ной функ­ции , опре­де­лен­ной на ин­тер­ва­ле (-6;6) . В какой точке от­рез­ка[-5;-1]  функция при­ни­ма­ет наи­боль­шее зна­че­ние.  

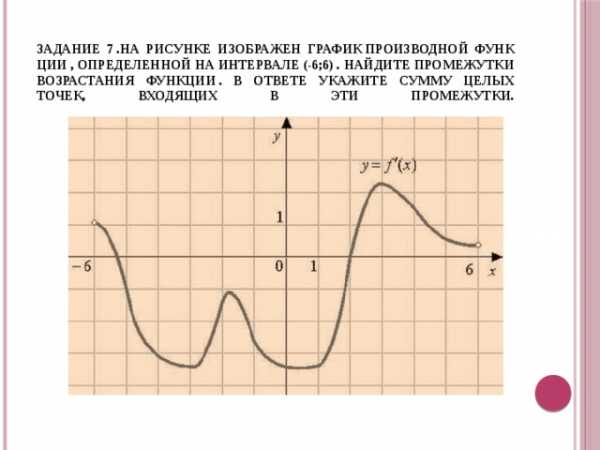
За­да­ние 7 .На ри­сун­ке изоб­ра­жен гра­фик про­из­вод­ной функ­ции , опре­де­лен­ной на ин­тер­ва­ле (-6;6) . Най­ди­те про­ме­жут­ки воз­рас­та­ния функ­ции . В от­ве­те ука­жи­те сумму целых точек, вхо­дя­щих в эти про­ме­жут­ки.  

За­да­ние 7.На ри­сун­ке изоб­ра­жен гра­фик про­из­вод­ной функ­ции, опре­де­лен­ной на ин­тер­ва­ле (-9;2). Най­ди­те про­ме­жут­ки убы­ва­ния функ­ции . В от­ве­те ука­жи­те сумму целых точек, вхо­дя­щих в эти про­ме­жут­ки.  

На ри­сун­ке изоб­ра­жен гра­фик про­из­вод­ной функ­ции , опре­де­лен­ной на ин­тер­ва­ле .Най­ди­те про­ме­жут­ки воз­рас­та­ния функ­ции . В от­ве­те ука­жи­те длину наи­боль­ше­го из них.  

Домашнее задание:

Составить подборку однотипных заданий В7 из сборника егэ, прорешать.

Спасибо

за урок!

23

multiurok.ru

Геометрический смысл производной

Геометрический смысл производной. Задачи на экзамене связанные данной темой у выпускников вызывают некоторые затруднения. Большинство же из них, на самом деле, очень просты. В этой статье разберём задания, в которых требуется найти производную при заданном графике функции  и касательной к графику в определённой точке

*При чём в этих задачах на эскизе явно отмечены как минимум две точки, через которые эта касательная проходит. Что нужно знать для решения?

Геометрический смысл производной

Построим произвольный график некой функции y = f (x)  на координатной плоскости, построим касательную в точке x_о, обозначим угол между прямой о осью ox как α (альфа)

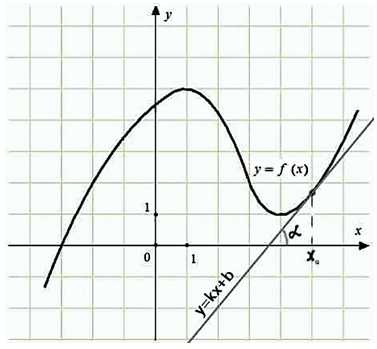
Из курса алгебры известно, что уравнение прямой имеет вид:

То есть производная функции  y = f(x) в точке x₀ равна угловому коэффициенту касательной:

А угловой  коэффициент в свою очередь равен тангенсу  угла α (альфа), то есть:

Угол α (альфа) может быть меньше, больше 90 градусов или равен нулю. 

Проиллюстрируем, два случая:

1.    Угол наклона касательной больше 90 градусов (тупой угол).

2.    Угол наклона касательной равен нулю градусов (касательная параллельна оси ох).

 

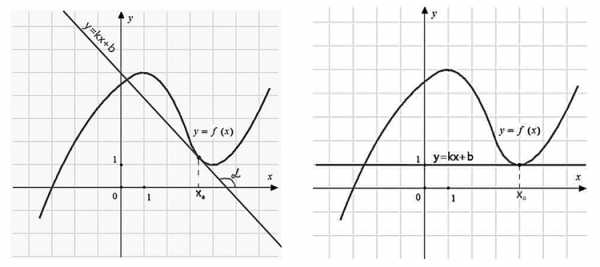
То есть задачи, в которых дан график функции, касательная к этому графику в определённой точке, и требуется найти производную в точке касания, сводятся к нахождению углового коэффициента касательной (либо тангенса угла наклона касательной, что одно и тоже).

Ниже рассмотрим  решение таких задач через нахождение тангенса угла между касательной и осью абсцисс (осью ох), ещё один способ решения (нахождение производной через угловой коэффициент) рассмотрим в недалёком будущем. Также будем рассматривать задачи, где требуется знание свойств производной для чтения графика функции. Не пропустите! 

Обратите внимание, что на координатной плоскости обозначены две точки через которые проходит касательная – это очень важный момент (можно сказать ключевой в этих задачах). 

Что ещё потребуется — это знание формулы приведения для тангенса тупого угла.

На рисунке изображены график функции y = f(x) и касательная к нему в точке с абсциссой x₀. Найдите значение производной функции y = f(x)  в точке  x₀.

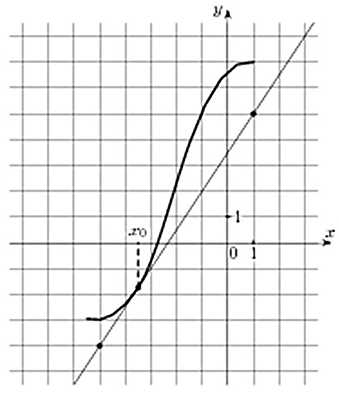
Значение производной в точке касания равно угловому коэффициенту касательной, который в свою очередь равен тангенсу угла наклона данной касательной к оси абсцисс. Для того, чтобы найти тангенс этого угла, построим прямоугольный треугольник, где отрезок ограниченный двумя точками на графике, будет являться гипотенузой, а катеты параллельны осям.  В данной задаче это точки  (–5; –4), (1; 5).

Напомню: тангенсом острого угла в прямоугольном треугольнике называется отношение противолежащего катета к прилежащему.

Катеты определяем по числу клеток.

Угол наклона касательной к оси абсцисс равен углу BAC, так как катет АС параллелен оси ох. Значит

Ответ: 1,5

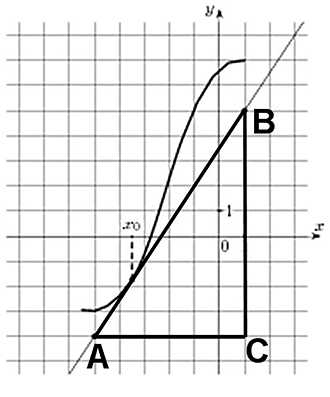
На рисунке изображены график функции y = f(x) и касательная к нему в точке с абсциссой x₀. Найдите значение производной функции y = f(x)  в точке  x₀.

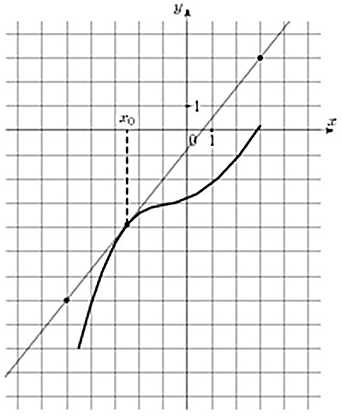
Задача аналогична предыдущей. Так же строим прямоугольный треугольник, где отрезок ограниченный двумя точками на графике, будет являться гипотенузой. В данной задаче это точки  (–5; –7), (3; 3).

Катеты также определяем по числу клеток.

Угол наклона касательной к оси абсцисс равен углу ВАС, так как катет АС параллелен оси ох. Значит

Ответ: 1,25

На рисунке изображены график функции y = f(x) и касательная к нему в точке с абсциссой x₀. Найдите значение производной функции y = f(x)  в точке  x₀.

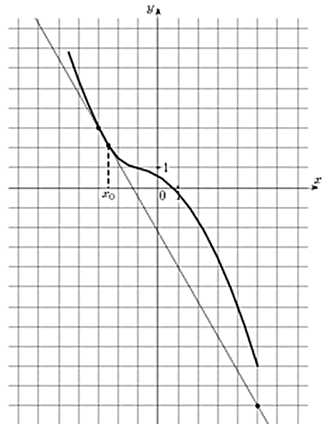
Строим прямоугольный треугольник, где отрезок ограниченный двумя точками на графике, будет являться гипотенузой. В данной задаче это точки  (–3; 3) и  (5; 11).  Из точки (5;11) построим продолжение катета так, чтобы  получился внешний угол.

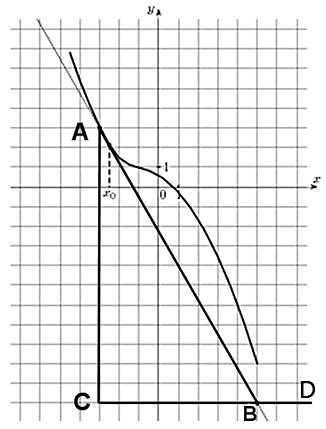
Так как CD параллельна оси ох, то угол ABD равен углу наклона касательной к оси ох.  Таким образом, мы будем вычислять тангенс угла ABD. Отметим, что он больше 90 градусов, поэтому здесь необходимо воспользоваться формулой приведения для тангенса:

Значит

*Длины катетов считаем по количеству клеток.

Ответ: -1,75

На рисунке изображены график функции y = f(x) и касательная к нему в точке с абсциссой x₀. Найдите значение производной функции y = f(x)  в точке  x₀.

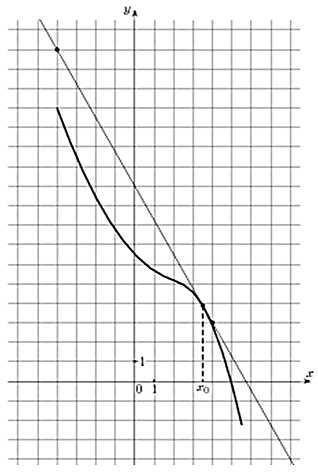
Решите задачу самостоятельно.

Ответ: -1,75

На рисунке изображен график функции y = f(x). Прямая, проходящая через начало координат, касается графика этой функции в точке с абсциссой 10. Найдите значение производной функции в точке х₀ = 10.

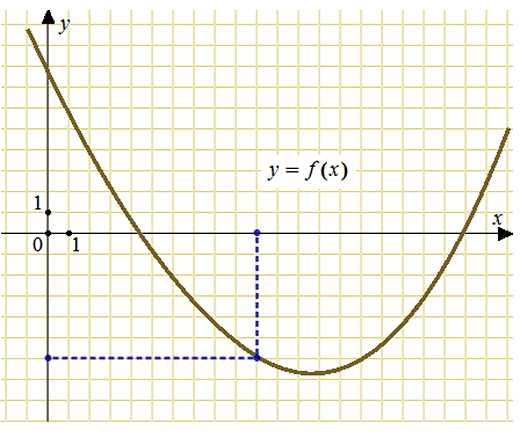
Построим касательную, проходящую через начало координат и точку графика с абсциссой равной 10. Обозначим угол наклона касательной как альфа, а смежный с ним угол как бета.

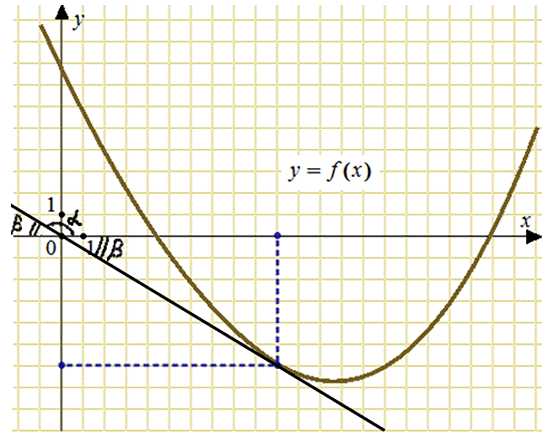
Значение производной в точке х₀ = 10 равно тангенсу угла наклона касательной к оси абсцисс. То есть, для нахождения производной достаточно вычислить тангенс  угла  альфа. Воспользуемся формулой приведения:

Тангенс угла бета можем найти из прямоугольного треугольника, катеты которого равны 6 и 10:

Ответ: — 0,6

На первый взгляд задачи, связанные с использованием производной входящие в ЕГЭ по математике, довольно разнообразны. Но на самом деле для их решения нужно изучить совсем небольшой «кусочек» теории. На этом всё. Второй способ решения представленных задач обязательно разберем. Надеюсь, статья была полезна.

На этом всё! Успеха вам!

С уважением, Александр Крутицких.

P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.

matematikalegko.ru

Исследование функции с помощью производной

Исследование функции с помощью производной. В этой статье мы с вами разберём некоторые задачи связанные с исследованием графика функции. В таких задачах, даётся график функции y = f (x) и ставятся вопросы, связанные с определением количества точек, в которых производная функции положительна (либо отрицательна), а также  другие. Их относят к заданиям на применение производной к исследованию функций.

Решение таких задач, и вообще задач связанных с исследованием, возможно только при полном понимании свойств производной для исследования графиков функций и геометрического смысла производной. Поэтому настоятельно рекомендую вам изучить соответствующую теорию. Можете изучить статью на блоге, а также посмотреть справочник (но в нём краткое изложение).

Задачи, где дан график производной мы будем также рассматривать в будущих статьях, не пропустите! Итак, задачи:

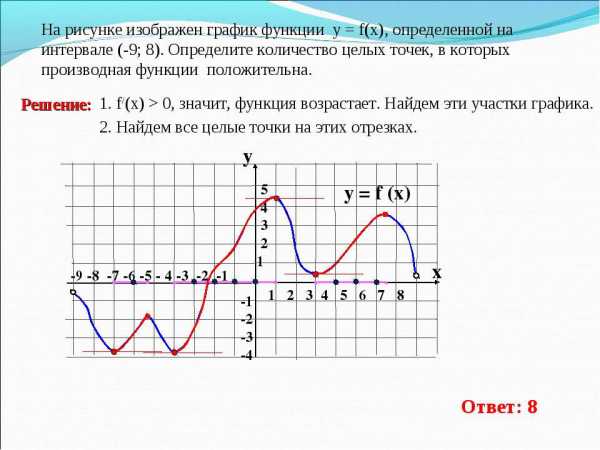
На рисунке изображен график функции у = f (х), определенной на интервале (−6; 8). Определите:

1. Количество целых точек, в которых производная функции отрицательна;

2. Количество точек, в которых касательная к графику функции параллельна прямой у = 2;

3. Количество точек, в которых производная равна нулю;

1. Производная функции отрицательна на интервалах, на которых функция убывает, то есть на интервалах (−6; –3), (0; 4,2), (6,9; 8). В них содержатся целые точки  −5,  −4,  1, 2, 3, 4,  и  7. Получили  7 точек.

2. Прямая  y = 2 параллельная оси ох.  Касательная будет параллельна прямой  y = 2 только в точках  экстремума (в точках, где график меняет своё поведение  с возрастания на убывание или наоборот). Таких точек четыре:  –3; 0; 4,2; 6,9

3. Производная равна нулю в четырёх точках (в точках экстремума), их мы уже указали.

Решите самостоятельно:

Определите количество целых точек, в которых производная функции положительна.

Посмотреть решение.

На рисунке изображен график функции у = f (х), определенной на интервале (−5; 5). Определите:

1. Количество целых точек, в которых производная функции положительна;

2. Количество целых точек, в которых касательная к графику функции параллельна прямой у = 3;

3. Количество точек, в которых производная равна нулю;

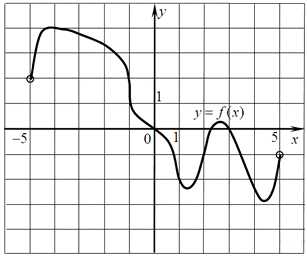
1. Из свойств производной функции известно, что она положительна на  интервалах, на которых функция возрастает, т. е. на интервалах (1,4; 2,5) и (4,4;5). В них содержится только  одна целая точка х = 2.

2. Прямая  y = 3 параллельная оси ох.  Касательная будет параллельна прямой  y = 3 только в точках  экстремума (в точках, где график меняет своё поведение  с возрастания на убывание или наоборот).

Таких точек четыре:  –4,3; 1,4; 2,5; 4,4

3. Производная равна нулю в четырёх точках (в точках экстремума), их мы уже указали.

Решите самостоятельно:

Определите количество целых точек, в которых производная функции  f (x) отрицательна.

Посмотреть решение.

На рисунке изображен график функции у = f (х), определенной на интервале  (−2; 12). Найдите:

1. Количество целых точек, в которых производная функции положительна;

2. Количество целых точек, в которых производная функции отрицательна;

3. Количество целых точек, в которых касательная к графику функции параллельна прямой у = 2;

4. Количество точек, в которых производная равна нулю.

1. Из свойств производной функции известно, что она положительна на  интервалах, на которых функция возрастает, т. е. на интервалах (–2; 1), (2;4), (7; 9) и (10;11). В них содержатся целые точки:   –1, 0, 3, 8. Всего их четыре.

2. Производная функции отрицательна на интервалах, на которых функция убывает, то есть на интервалах (1; 2), (4; 7), (9; 10), (11;12). В них содержатся целые точки  5  и  6. Получили  2 точки.

3. Прямая  y = 2 параллельная оси ох.  Касательная будет параллельна прямой  y = 2 только в точках  экстремума (в точках, где график меняет своё поведение  с возрастания на убывание или наоборот). Таких точек семь:  1; 2; 4; 7; 9; 10; 11.

4. Производная равна нулю в семи точках (в точках экстремума), их мы уже указали.

Решите самостоятельно:

Найдите сумму точек экстремумов функции f (x). Посмотреть решение.

Как видите, ничего сложного нет. Желаю вам успехов!

С уважением, Александр Крутицких

P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.

matematikalegko.ru

Связь графиков функции и производной — Студопедия.Нет

Производная характеризует скорость изменения функции Если функция возрастает – производная положительна (касательная наклонена вправо) Если функция убывает – производная отрицательна (касательная наклонена влево) Если функция имеет максимум или минимум, либо «точку перегиба» — производная равна нулю (касательная лежит горизонтально) Чем больше скорость возрастания (или убывания) функции, тем больше по модулю производная, и тем круче (ближе к вертикали) наклон касательной В точках А и D функция возрастает – производная положительна. В точке А наклон касательной круче, значит, и производная больше, чем в точке D. В точках В и С функция убывает – производная отрицательны. В точке В функция наклон касательной круче, значит, производная меньше, чем в точке C (ПО МОДУЛЮ – больше)

Геометрический смысл производной

Производная – это тангенс угла наклона касательной (или угловой коэффициент касательной)

Как найти угловой коэффициент касательной  (или производную)	Пример:   На рисунке изображены график функции и касательная к нему в точке с абсциссой . Найдите значение производной функции в точке .
1. Найти точки на линии касательной, которые точно попадают в пересечение клеточек (обычно на рисунке эти точки отмечены). 2. Через одну из точек провести горизонтальную линию, через другую – вертикальную. Получится треугольник. 3. Сосчитать (в клеточках) длины вертикальной и горизонтальной сторон треугольника. Разделить длину вертикалной стороны на длину горизонтальной 4. Если наклон касательной вправо («подъем») – ставим знак «плюс», если наклон влево («спуск») – ставим знак «минус»		Вертикаль: 2 клетки Горизонталь: 8 клеток Здесь «подъем», знак «плюс».
Ответ: Значение производной в точке х0 равно 0,25

 

Нахождение точек, где касательная параллельна прямой

 Если требуется определить точки, где касательная параллельна прямой , то надо искать точки, где производная равна k (числу перед иксом). А если касательная должна быть параллельна прямой  (или оси абсцисс), то производная должна быть равна 0)

Пример: Дан график производной функции f(x). Указать количество точек, в которых касательная к графику функции y=f(x) параллельна прямой y=x   Решение: для прямой y=x угловой коэффициент равен 1, значит, производная должна быть равна 1. Таких точек на графике две.

 

Физический смысл производной

• Если функцией является перемещение тела, то произвозная от этой функции – скорость
• Если функцией является скорость, то производная от этой функции – ускорение

Пример: Материальная точка движется по закону . Найти мгновенную скорость в момент

Скорость v – производная от перемещения s: . При t=5

Связь графиков функции и производной

Производная	Функция	Касательная к графику функции
Положительна	Возрастает	Наклонена вправо (острый угол с осью Х)
Отрицательна	Убывает	Наклонена влево (тупой угол с осью Х)
Равна нулю (с вариантами)	Стационарная точка	Горизонтальна (параллельна оси Х)
=0, меняет знак с мИнуса на плюс	Минимум (экстремум)
=0, меняет знак с плюСа на минус	МакСимум (экстремум)
=0, но знак не меняет	Точка перегиба

 

studopedia.net

Графики функций и их производных.

ИССЛЕДОВАНИЕ ФУНКЦИИ ПРИ ПОМОЩИ ПРОИЗВОДНОЙ

возрастание

убывание

функции.

Алгоритм нахождения промежутков возрастания (убывания) функции

1. Находим область определения функции

2.Находим производную функции

3.Находим точки, в которых f’(x) =0

или f’(x) не существует

4.Отмечаем эти точки на числовой прямой

и определяем знаки производной

на полученных промежутках

5.Делаем выводы о промежутках

возрастания и убывания

Исследование

по формуле

по графику

0, значит, функция возрастает. Если f / (x) значит, функция убывает. «

Признаки:

Если f / (x) 0,

значит, функция возрастает.

Если f / (x)

значит, функция убывает.

По формуле функции

Практикум:

Найдите промежутки возрастания

(убывания) функции.

Задания:

1 вариант

D(f)

2 вариант

f ‘ (x)

f ‘ (x) = 0

(не существует)

Знаки

Промежутки возрастания

производной

Промежутки убывания

1 вариант

D(f)

2 вариант

f ‘ (x)

R

f ‘ (x) = 0

R

(не существует)

Знаки

-1; 1

1

Промежутки возрастания

производной

-1; 1

Промежутки убывания

—

—

—

-1

+

+

+

-1

1

Графики.

Графики

функций

Графики

производных

График

функции

Если функция возрастает ,

то производная

положительна

y

4

2

1

-1

0

x

Если функция убывает ,

то производная

отрицательна

В7(ЕГЭ) На рисунке изображен график функции у = f(x) и касательная к этому графику. Определите знак производной в точке касания.

В7 (ЕГЭ) На рисунке изображен график функции у = f(x) и касательная к этому графику. Определите знак производной в точке касания.

В7 .егэ .   На ри­сун­ке изоб­ра­жен гра­фик функ­ции , опре­де­лен­ной на ин­тер­ва­ле (-9;8). Опре­де­ли­те ко­ли­че­ство целых точек, в ко­то­рых про­из­вод­ная функ­ции  по­ло­жи­тель­на .

В7 (егэ). На ри­сун­ке изоб­ра­жен гра­фик функ­ции , опре­де­лен­ной на ин­тер­ва­ле (−6; 8). Опре­де­ли­те ко­ли­че­ство целых точек, в ко­то­рых про­из­вод­ная функ­ции по­ло­жи­тель­на . 

• В7(егэ).  На ри­сун­ке изоб­ра­жен гра­фик функ­ции , опре­де­лен­ной на ин­тер­ва­ле (−5; 5). Опре­де­ли­те ко­ли­че­ство целых точек, в ко­то­рых про­из­вод­ная функ­ции  от­ри­ца­тель­на.

За­да­ние 7 № 6871.На ри­сун­ке изоб­ра­жен гра­фик функ­ции , опре­де­лен­ной на ин­тер­ва­ле (-1;12) .Опре­де­ли­те ко­ли­че­ство целых точек, в ко­то­рых про­из­вод­ная функ­ции от­ри­ца­тель­на.

0, значит, функция возрастает. Признаки: Если f / (x) значит, функция убывает. «

Графики производных

Задания В7 (ЕГЭ)

Если f / (x) 0,

значит, функция возрастает.

Признаки:

Если f / (x)

значит, функция убывает.

0, значит, функция возрастает. На рисунке изображен график y=f'(x)   — производной функции f(x) , определенной на интервале (-6;8) . Найдите количество промежутков возрастания функции f(x) . График производной «

Если f / (x) 0,

значит, функция возрастает.

На рисунке изображен график y=f'(x)   — производной функции f(x) , определенной на интервале (-6;8) . Найдите количество промежутков возрастания функции f(x) .

График производной

Функция задана на отрезке. На рисунке изображен график ее производной.

• Укажите количество

промежутков

возрастания функции.

у

y=f ‘(x)

1

0

b

1

х

а

На рисунке изображен график y=f'(x) — производной функции f(x) , определенной на интервале (-8;6) . Найдите количество промежутков убывания функции f(x).

Если f / (x)

значит, функция убывает.

Функция задана на отрезке. На рисунке изображен график ее производной.

у

• Укажите количество

промежутков

убывания функции

y=f ‘(x)

1

0

b

1

х

а

На рисунке изображен график производной функции f(x),

определенной на интервале (a;b). Найдите промежутки возрастания функции f(x). В ответе укажите длину наибольшего из них.

у

y=f ‘(x)

1

b

0

а

1

х

(1)

На рисунке изображен график производной функции f(x),

определенной на интервале (a;b). Найдите промежутки убывания функции f(x). В ответе укажите длину наибольшего из них.

у

y=f ‘(x)

1

b

0

а

1

х

(2)

За­да­ние 7 .На ри­сун­ке изоб­ра­жен гра­фик про­из­вод­ной функ­ции , опре­де­лен­ной на ин­тер­ва­ле (-6;6) . В какой точке от­рез­ка[-5;-1]  функция при­ни­ма­ет наи­боль­шее зна­че­ние.  

За­да­ние 7 .На ри­сун­ке изоб­ра­жен гра­фик про­из­вод­ной функ­ции , опре­де­лен­ной на ин­тер­ва­ле (-6;6) . Най­ди­те про­ме­жут­ки воз­рас­та­ния функ­ции . В от­ве­те ука­жи­те сумму целых точек, вхо­дя­щих в эти про­ме­жут­ки.  

За­да­ние 7.На ри­сун­ке изоб­ра­жен гра­фик про­из­вод­ной функ­ции, опре­де­лен­ной на ин­тер­ва­ле (-9;2). Най­ди­те про­ме­жут­ки убы­ва­ния функ­ции . В от­ве­те ука­жи­те сумму целых точек, вхо­дя­щих в эти про­ме­жут­ки.  

На ри­сун­ке изоб­ра­жен гра­фик про­из­вод­ной функ­ции , опре­де­лен­ной на ин­тер­ва­ле .Най­ди­те про­ме­жут­ки воз­рас­та­ния функ­ции . В от­ве­те ука­жи­те длину наи­боль­ше­го из них.  

Домашнее задание:

Составить подборку однотипных заданий В7 из сборника егэ, прорешать.

Спасибо

за урок!

23

multiurok.ru

КОГДА ПРОИЗВОДНАЯ ПОЛОЖИТЕЛЬНА НА ГРАФИКЕ — Производная функции. Геометрический смысл производной

На заданном интервале функция имеет 2 максимума и 2 минимума, итого 4 экстремума. Задание На рисунке изображен график производной функции, определенной на интервале. Решение На заданном отрезке производная функции положительна, поэтому функция на этом отрезке возрастает. Решение Если производная в некоторой точке равна нулю, а в ее окрестности меняет знак, то это точка экстремума.

Вычисление значения производной. Метод двух точек

1. По графику производной исследовать функцию. Функция y=f(x) убывает на промежутках (x1;x2) и (x3;x4). С помощью графика производной y=f ‘(x)также можно сравнивать значения функции y=f(x).

Обозначим эти точки A (x1; y1) и B (x2; y2). Правильно выписывайте координаты — это ключевой момент решения, и любая ошибка здесь приводит к неправильному ответу.

В физическом смысле производная — это скорость изменения любого процесса. Материальная точка движется прямолинейно по закону x(t) = t²-13t+23, где x — расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения.

Касательная к окружности, эллипсу, гиперболе, параболе.

Напомню, что звучит оно так: функция называется возрастающей/убывающей на промежутке, если большему аргументу функции соответствует большее/меньшее значение функции. Но посмотрите, пожалуйста, ваше решение к задаче 7089. Там при указании промежутков возрастания границы не включаются. Учтите, что задан график производной. Как обычно: выколотая точка не лежит на графике, значения в ней не существуют и не рассматриваются. Хорошо подготовленные дети различают понятия «производная» и «вторая производная». Вы путаете: если бы производная обращалась в 0, то в точке функция могла бы иметь минимум или максимум. Отрицательным значениям производной соответствуют интервалы, на которых функция f(x) убывает.

До этого момента мы занимались нахождением уравнений касательных к графикам однозначных функций вида y = f(x) в различных точках.

На рисунке ниже приведены три фактически разных секущих (точки А и В различны), но они совпадают и задаются одним уравнением. Но все же, если отталкиваться от определения, то прямая и ее секущая прямая совпадают. Приступим к нахождению координат точек касания. Просим обратить на него внимание, так как позже мы его используем при вычислении ординат точек касания. Гипербола с центром в точке и вершинами и задается равенством (рисунок ниже слева), а с вершинами и — равенством (рисунок ниже справа). Возникает логичный вопрос, как определить какой из функций принадлежит точка. Для ответа на него подставляем координаты в каждое уравнение и смотрим, какое из равенств обращается в тождество.

Иногда учащиеся спрашивают, что такое касательная к графику функции. Это прямая, имеющая на данном участке единственную общую точку с графиком, причем так, как показано на нашем рисунке. Похоже на касательную к окружности. Найдем . Мы помним, что тангенс острого угла в прямоугольном треугольнике равен отношению противолежащего катета к прилежащему. На графике это соответствует резкому излому, когда касательную в данной точке провести невозможно. А как найти производную, если функция задана не графиком, а формулой?

Отметить знаки производной на интервалах между нулями. Если в задаче установлены ограничения на переменную x, дополнительно отмечаем их на новом графике.

В тренде:

• Образ Коробочка Настасья Петровна «Мертвые души»Образ Плюшкина, описанный Николаем Васильевичем Гоголем – один из самых ярких и удачных в произведении «Мёртвые души». Это был образованный и неглупый человек, хороший хозяин. Плюшкин стал […]
• Как изменить размер значковЕсли вас не устраивает только размер значков на десктопе, а величину остальных элементов вы менять не хотите, то примените специальную функцию в контекстном меню, чтобы настроить […]
• Как перевести деньги через интернет?Здесь мы выбираем категорию «На другой телефон», нажимаем и переходим в оно оформления платежа. Здесь в принципе все понятно, заносим все данные: сумму необходимого перевода, телефон […]

estortenok.ru