Частные производные первого порядка, теория и примеры
Пусть функция определена в некоторой окрестности точки Придадим переменной приращение оставляя при этом значение переменной без изменения так, чтобы точка принадлежала этой окрестности.
Если существует предел
то он называется частной производной функции в точке по переменной и обозначается одним из следующих символов:
Аналогично частная производная функции по переменной определяется как предел
Она обозначается как
Согласно с определением, при нахождении частной производной находят обыкновенную производную функции одной переменной считая переменную постоянной, а при нахождении производной постоянной считается переменная
Следовательно, частные производные находятся по формулам и правилам дифференцирования функции одной переменной.
Частная производная характеризует скорость изменения функции в направлении оси – в направлении оси
Выясним геометрический смысл частных производных функции двух переменных. Геометрическим образом (графиком) функции есть некоторая поверхность. Графиком функции является линия пересечения этой поверхности с плоскостью Исходя из геометрического смысла производной функции одной переменной, получаем, что,
где – угол между осью и касательной, проведенной к пространственной кривой в точке Аналогично, где – угол между осью и касательной, проведенной к пространственной кривой (линии пересечения поверхности с плоскостью ) в точке
Для функции переменных можно найти частных производных первого порядка:
Чтобы найти частную производную необходимо взять обычную производную функции по переменной считая остальные переменные константами.
Примеры вычисления частных производных первого порядка
ru.solverbook.com
Частные производные. Примеры решений — Мегаобучалка
На данном уроке мы познакомимся с понятием функции двух переменных, а также подробно рассмотрим наиболее распространенное задание – нахождение частных производныхпервого и второго порядка, полного дифференциала функции.
Для эффективного изучения нижеизложенного материала Вам необходимо уметь более или менее уверенно находить «обычные» производные функции одной переменной. Научиться правильно обращаться с производными можно на уроках Как найти производную? и Производная сложной функции. Также нам потребуется таблица производных элементарных функций и правил дифференцирования, удобнее всего, если она будет под рукой в распечатанном виде.
Начнем с самого понятия функции двух переменных, постараемся ограничиться минимумом теории, так как сайт имеет практическую направленность. Функция двух переменных обычно записывается как , при этом переменные , называются независимыми переменными или аргументами.
Пример: — функция двух переменных.
Иногда используют запись . Также встречаются задания, где вместо буквы используется буква .
Полезно знать геометрический смысл функций. Функции одной переменной соответствует определенная линия на плоскости, например, – всем знакомая школьная парабола. Любая функция двух переменных с геометрической точки зрения представляет собой поверхность в трехмерном пространстве (плоскости, цилиндры, шары, параболоиды и т.д.). Но, собственно, это уже аналитическая геометрия, а у нас на повестке дня математический анализ.
Переходим к вопросу нахождения частных производных первого и второго порядков. Должен сообщить хорошую новость для тех, кто выпил несколько чашек кофе и настроился на невообразимо трудный материал: частные производные – это почти то же самое, что и «обычные» производные функции одной переменной.
Для частных производных справедливы все правила дифференцирования и таблица производных элементарных функций.
Есть только пара небольших отличий, с которыми мы познакомимся прямо сейчас.
Пример 1
Найти частные производные первого и второго порядка функции
Сначала найдем частные производные первого порядка. Их две.
Обозначения:
или – частная производная по «икс»
или – частная производная по «игрек»
Начнем с .
Важно! Когда мы находим частную производную по «икс», то переменнаясчитается константой (постоянным числом).
Решаем. На данном уроке будем сразу приводить полное решение, а комментарии давать ниже.
Комментарии к выполненным действиям:
(1) Первое, что мы делаем при нахождении частной производной – заключаем всюфункцию в скобки под штрих с подстрочным индексом.
Внимание, важно!Подстрочные индексы НЕ ТЕРЯЕМ по ходу решения. В данном случае, если Вы где-нибудь нарисуете «штрих» без , то преподаватель, как минимум, может поставить рядом с заданием (сразу откусить часть балла за невнимательность).
Далее данный шаг комментироваться не будет, все сделанные замечания справедливы для любого примера по рассматриваемой теме.
(2) Используем правила дифференцирования ; . Для простого примера, как этот, оба правила вполне можно применить на одном шаге. Обратите внимание на первое слагаемое: так как считается константой, а любую константу можно вынести за знак производной, то мы выносим за скобки. То есть в данной ситуации ничем не лучше обычного числа. Теперь посмотрим на третье слагаемое : здесь, наоборот, выносить нечего. Так как константа, то – тоже константа, и в этом смысле она ничем не лучше последнего слагаемого – «семерки».
(3) Используем табличные производные и .
(4) Упрощаем ответ.
Теперь определим . Когда мы находим частную производную по «игрек», то переменная считается константой (постоянным числом).
(1) Используем те же правила дифференцирования ; . В первом слагаемом выносим константу за знак производной, во втором слагаемом ничего вынести нельзя поскольку – уже константа.
(2) Используем таблицу производных элементарных функций. Мысленно поменяем в таблице все «иксы» на «игреки». То есть данная таблица рАвно справедлива для(и вообще для любой буквы).В данном случае, используемые нами формулы имеют вид: и .
Итак, частные производные первого порядка найдены
megaobuchalka.ru
1) Найти частные производные данных функций по каждой из независимых переменных (х, у – переменные)
Решение
Найдем частную производную функции по переменной х, а переменную у в этом случае будем считать постоянной:
.
Найдем частную производную функции по переменной у, а переменную х в этом случае будем считать постоянной:
.
2) Вычислить приближённо, заменяя приращение функции дифференциалом
Решение
Полагая, что есть частное значение функции в точке и что вспомогательная точка будет , получим
;
,
,
; .
Подставляя в формулу , найдем
.
Ответ:
3) Исследовать на максимум и минимум следующую функцию ,
Решение
Найдем частные производные и :
,
.
Решим систему уравнений Которая в данном случае примет вид:
Решения и не удовлетворяют условию
Получили точку возможного экстремума:
Определим частные производные второго порядка:
, , .
Найдем значение в точке :
, , .
Тогда . и функция в точке имеет экстремум.
Так как , то в точке функция имеет минимум и .
Ответ: т. — точка минимума,
4) Найти наибольшее и наименьшее значение функции в области ,
Решение
Функция непрерывна в замкнутом квадрате . Поэтому, согласно теореме Вейерштрасса, она на этом множестве достигает своих наибольшего и наименьшего, значений функции.
Найдём все решения системы уравнений:
Имеем
Все решения находятся в области
Найдём значения функции в найдённых стационарных точках:
На границе области
А) . Отсюда
Б) . Отсюда ,
С) . Отсюда
D) . Отсюда ,
Найдем значения функции в точках пересечения линий, ограничивающих область .
Выберем наибольшее и наименьшее значения:
,
5) Найти условные экстремумы функции при
Решение
Составим функцию Лагранжа
Имеем
Система имеет единственное решение
Далее
Найдём дифференциал второго порядка в точке :
Тогда
Из уравнения ограничения
При поэтому функция в точке имеет условный минимум,
Ответ: в точке имеет условный минимум,
| < Предыдущая | Следующая > |
|---|
matica.org.ua
Частные производные и дифференциалы /qualihelpy
Частные производные первого порядка и полный дифференциал функции
1. Рассмотрим функцию двух переменных .
Частные производные первого порядка функции в точке находят по формулам:
. (6.21)
Записывают: или и или .
Полный дифференциал
этой функции находят по формуле:. (6.22)
2. Рассмотрим функцию трех переменных .
Полный дифференциал этой функции находят по формуле:
. (6.23)
3. Рассмотрим функцию n переменных .
Аналогично записывают ее частные производные:
, , …, .
Полный дифференциал этой функции находят по формуле:
. (6.24)
4. Рассмотрим неявную функцию .
Частные производные этой функции находят по формулам:
, (6.25) . (6.25.1)
Частные производные и дифференциалы второго порядка
Рассмотрим функцию двух переменных .
Частные производные второго порядка этой функции записывают:
или ; (6.27)
или . (6.28)
. (6.29)
Дифференциал второго порядка функции находят по формуле:
helpy.quali.me
ЧАСТНЫЕ ПРОИЗВОДНЫЕ ФУНКЦИЙ ДВУХ ПЕРЕМЕННЫХ.
Рассмотрим функцию двух переменных z = f(x, y).
Частной производной функции двух переменных z = f(x, y) по х в точке (х, у) называется предел , если он существует. Частная производная есть обычная производная от функции f(x,y), рассматриваемой как функция только от переменной х при фиксированному.
Аналогично определяется частная производная по ув точке (х,у):
.
Если у функции существует частная производная снова по переменной х, то ее называют частной производной второго порядка от функции f(x,y) по переменной х и обозначают . Таким образом, .
Аналогично для переменной у: .
Если существует частная производная от функции по переменной у, то эту производную называют смешанной частной производной второго порядка от функции z = f(x, y) и обозначают .
В курсе высшей математики доказывается теорема о том, что если функция двух переменных определена вместе со своими частными производными в окрестности некоторой точки, причем смешанные частные производные непрерывны в этой точке, то в этом случае результат дифференцирования не зависит от порядка дифференцирования, т. е. .
ПРОИЗВОДНАЯ ПО НАПРАВЛЕНИЮ
Рассмотрим функцию двух переменных z = f(x, y). Если эта функция дифференцируема в точке (х,у), то для нее существует производная по направлению любого единичного вектора `n0 = (Cosa, Cosb), выражаемая формулой ,
где a и b — углы, которые вектор `n0составляет с осями хи у.
Если же необходимо найти производную по направлению произвольного вектора `n= a`i + в`j , то его необходимо сначала пронормировать и найти направляющие косинусы по формулам а потом воспользоваться приведенной выше формулой.
ГРАДИЕНТ ФУНКЦИИ
Градиентом функции z = f(x, y) в точке М(х0, у0) называется вектор grad z, координаты которого равны частным производным функции z = f(x, y), вычисленным в точке М(х0, у0)
.
ЗАДАЧА № 9
Найти частные производные функции z = f(x,y):
ЗАДАЧА № 10
Найти градиент и производную по направлению
ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ
ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ
НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
При изучении дифференцированного исчисления решалась следующая задача: дана функция F(x), найти ее производную F¢(x) (в дальнейшем производную F¢(x) будем обозначать f(x)). Интегральное исчисление решает задачу обратную: для непрерывной функции f(x) найти такую функцию F(x), производная которой была бы тождественно равна функции f(x). Функция F(x) называется первообразной, f(x) — подынтегральной. Ясно, что если F¢(x) = f(x), то и [F¢(x) + C]¢ = f(x). Здесь С — произвольная постоянная величина.
Определение:
Неопределенным интегралом называется функция F(x) + C, производная которой равна подынтегральной функции f(x), т.е.
= F(x) + C, если [F(x) + C]¢ = f(x).
Подынтегральное выражение f(x)dx есть дифференциал для всех первообразных, т.е. d[F(x) + C] = f(x)dx.
Из определения следует, что процесс нахождения неопределенного интеграла сводится к нахождению первообразной данной функции.
Вообще, используя таблицу производных, можно составить таблицу основных интегралов:
ОСНОВНЫЕ СВОЙСТВА НЕОПРЕДЕЛЕННОГО ИНТЕГРАЛА
1. , т.е. знаки d и ò, стоящие перед некоторой функцией, друг друга уничтожают. Так .
2. , т.е. постоянный множитель можно выносить за знаки интеграла.
3. , т.е. неопределенный интеграл от суммы некоторых функций равен сумме интегралов от этих функций.
ЗАДАЧА № 11
Найти неопределенный интеграл .
=
МЕТОД ПОДСТАНОВКИ
Метод заключается в том, что вместо переменной x вводят новую переменную, например t. Так, если положить х = j(t), то
Получаемый интеграл должен быть значительно проще данного. В противном случае следует искать другую форму введения новой переменной. Часто переменную t вводят так: t = j(x), а dt = j¢(x)dx. Это удобно, если данное подынтегральное выражение содержит дифференциал j¢(x)dx.
ЗАДАЧА № 12
Найти неопределенный интеграл .
=
ЗАДАЧА № 13
Найти неопределенный интеграл .
.
ЗАДАЧА № 14
Найти неопределенный интеграл .
=
ИНТЕГРИРОВАНИЕ ПО ЧАСТЯМ
Идея метода состоит в том, что подынтегральное выражение f(x)dx нужно представить в виде произведения U*dV , где U(x) и V(x) — дифференцируемые функции и воспользоваться формулой .
При этом вновь полученный интеграл должен быть проще данного.
ЗАДАЧА № 15
Найти неопределенный интеграл .
=
ЗАДАЧА № 16
Найти неопределенный интеграл .
=
infopedia.su
1.3. Частные производные функции двух переменных
Дадим независимой
переменной х приращение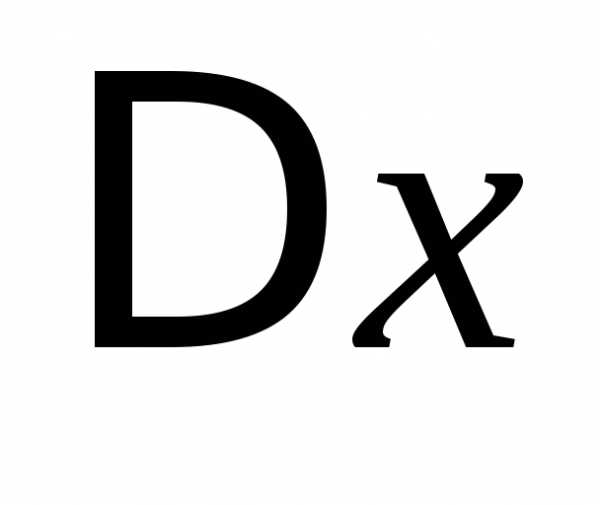 
,
тогда функцияполучит приращение, которое называетсячастным
приращением z по х и обозначается
.
Аналогично определяется частное приращение z по у:
.
Если же приращение получают одновременно х и у, то приращение
называется полным.
Определение 8. Частной производной от функции пох называется предел
,
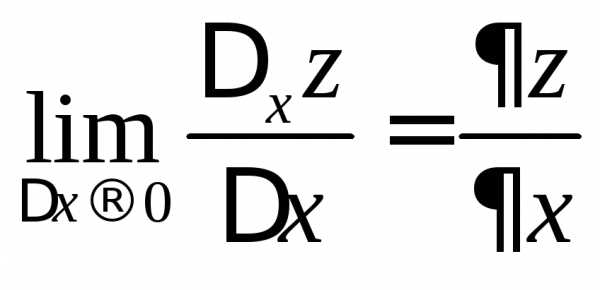или другие обозначения: .
Аналогично,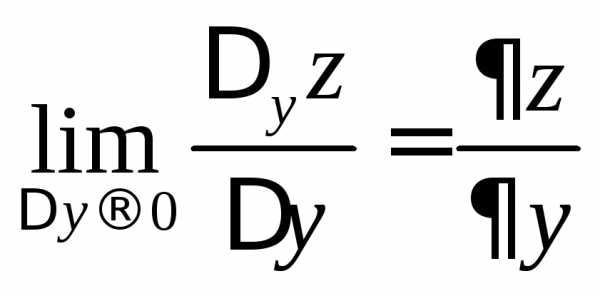 
,
или .
Из этих определений
следует, что правила вычисления частных
производных совпадают с правилами для
функции одного переменного. При этом,
например, если мы вычисляем производную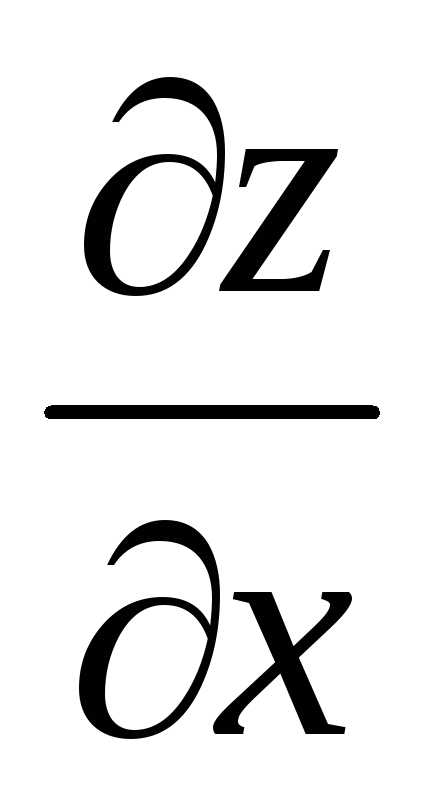 
,
то в процессе дифференцирования считаем,
что
Пример 5.
Найти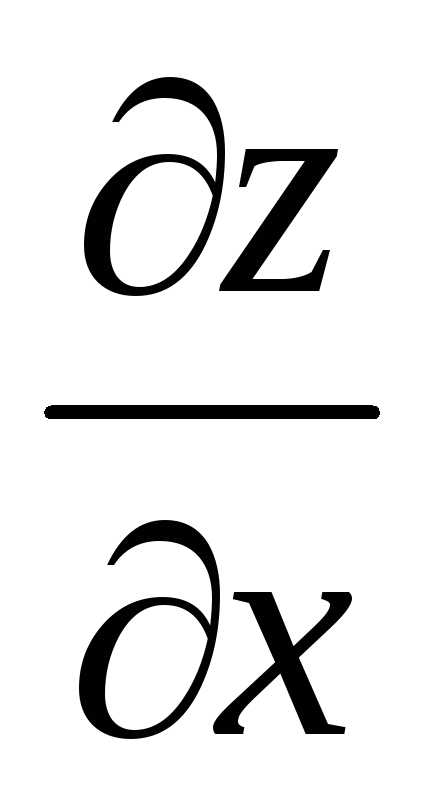 
и
,
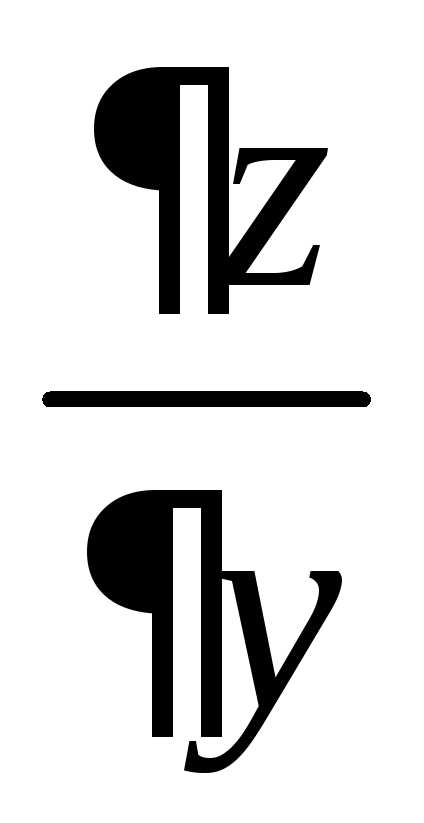если
1.4. Полный дифференциал функции двух переменных
Как известно, полное приращение функции определяется по формуле . Пустьимеет непрерывные частные производные, т.е. является дифференцируемой. Полное приращение представим в виде
.
К каждой разности применим теорему Лагранжа
,
где .
Так как в силу непрерывности существуют пределы:
; ,
то по теореме о пределе функции получим
где .
Это означает, что подчеркнутое слагаемое является б.м.в. при и тогда
,
где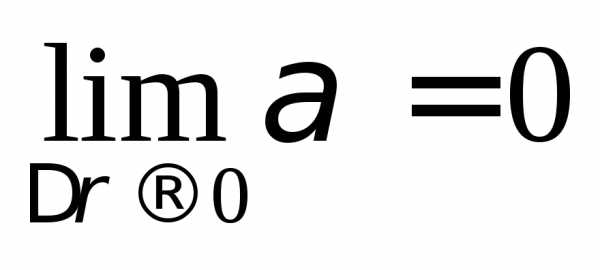 
.
Таким образом, получаем еще одно эквивалентное определение дифференцируемой функции двух переменных.
Определение 8. Функция
называется дифференцируемой в точке,
если её приращение можно представить
в виде суммы двух слагаемых, линейных
относительно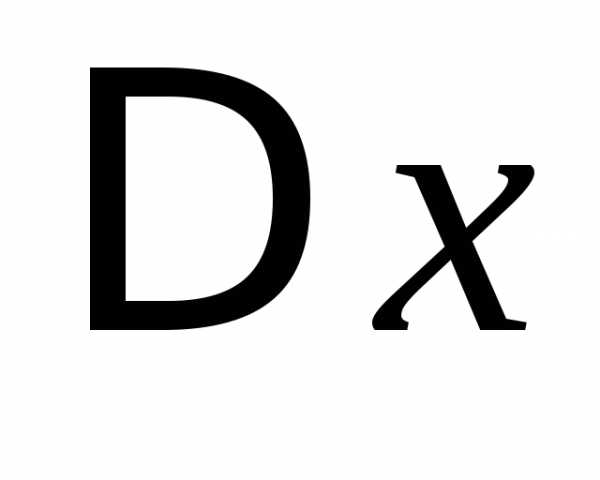
и
и величины бесконечно малой. высшего
порядка относительно
,
т.е.
При этом линейная
часть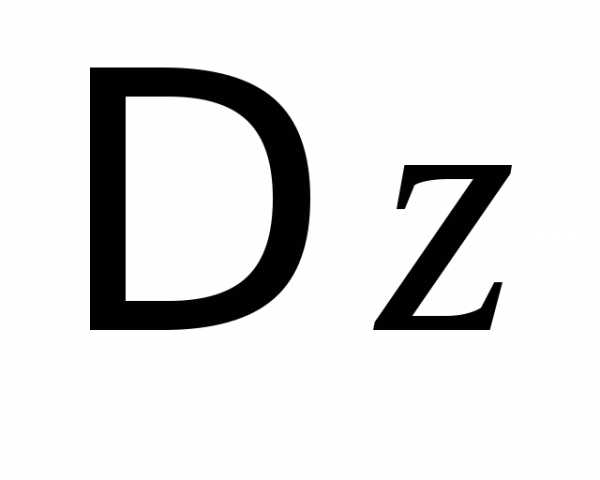 
называетсяполным
дифференциалом и обозначается
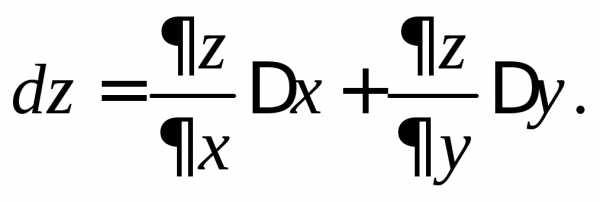
Так как приращения независимых переменных называются их дифференциалами, то окончательно
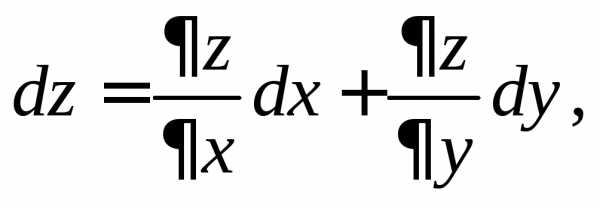
а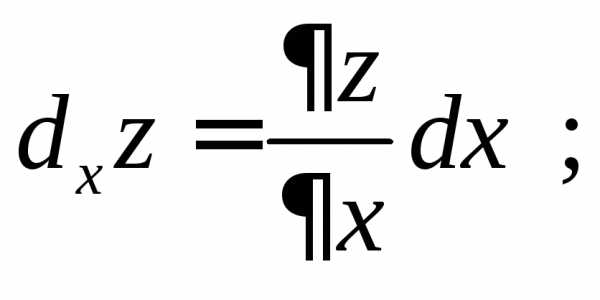 
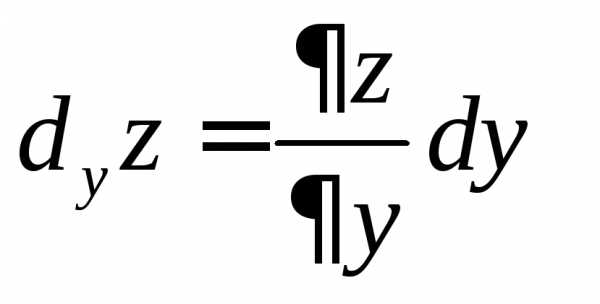частные
дифференциалы.
1.5. Производная сложной функции
Пусть задана функция , где. В этом случаеz является сложной функцией аргументов х иу. Пусть все эти функции имеют непрерывные частные производные.
Дадим переменной х приращение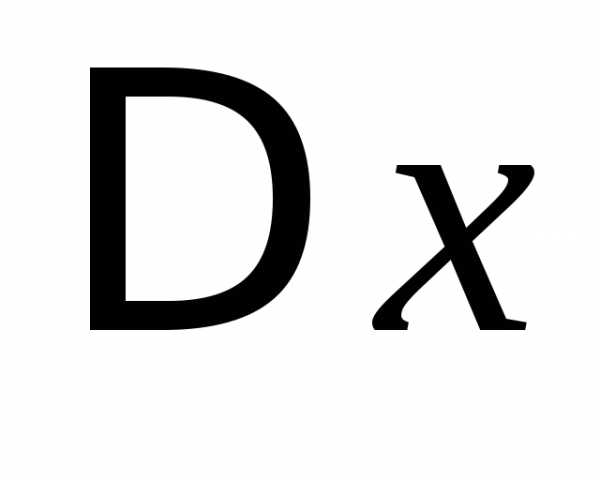 
,
тогда
где .
Разделим данное
равенство на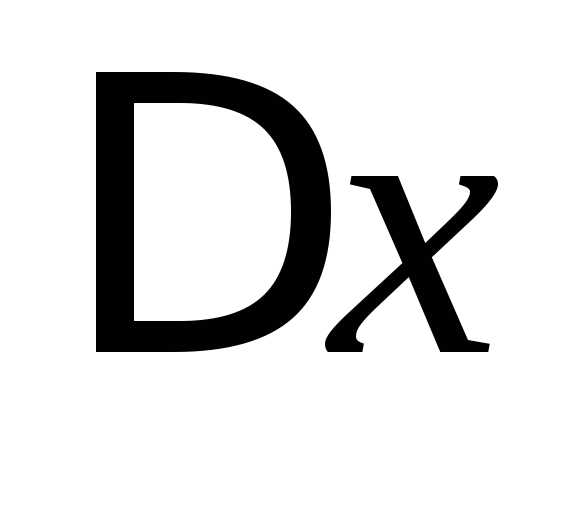 
и перейдём к пределу при
Отсюда следует .
Аналогично получим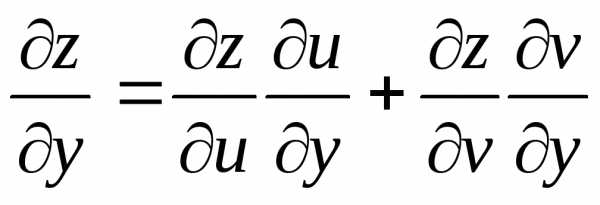 
.
Пример 6.
Найти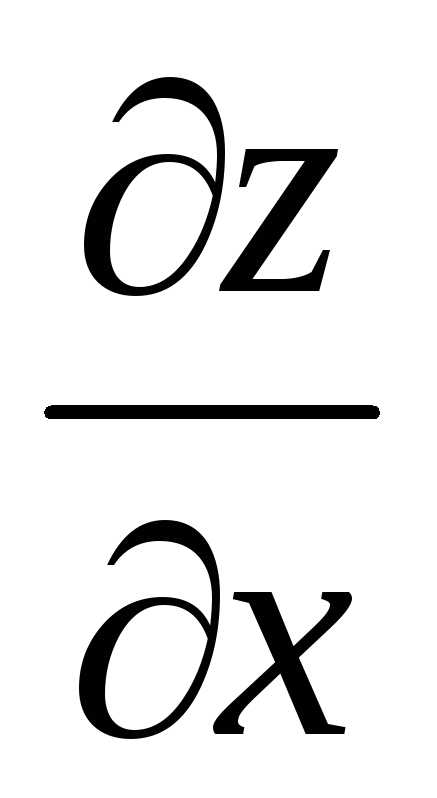 
и
,
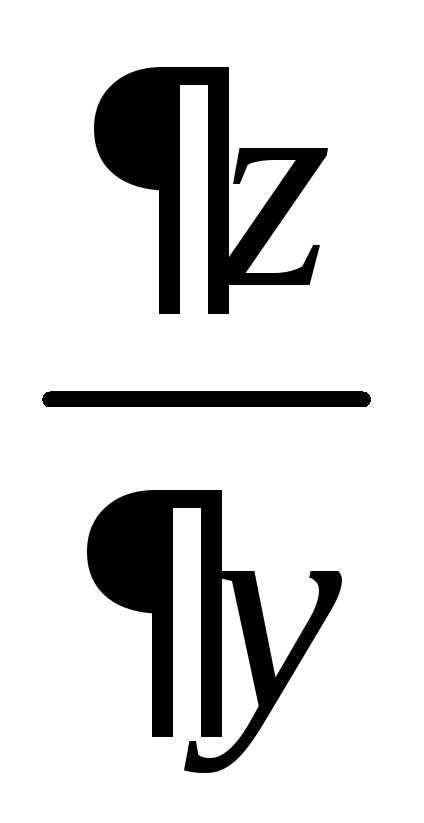если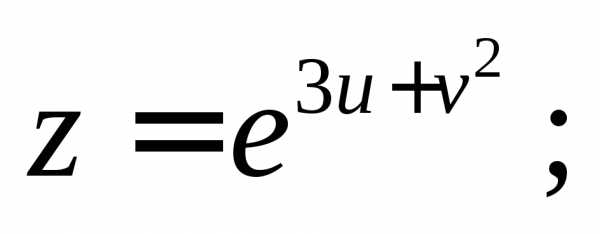
Лекция № 33. Тема 2 : Частные производные.
Производная по направлению. Градиент
2.1. Полная производная
Пусть дана функция , где. Тогда, обобщая формулу для случая производной функции двух переменных, получаем
. (1)
Формула (1) называется формулой полной производной.
Пример 1. Найти полную производную функции
,
если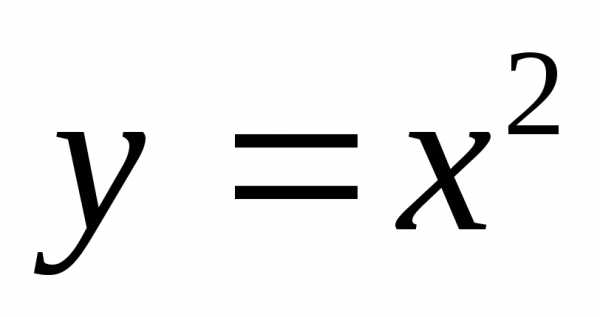
.
.
2 .2 . Частные производные функции, заданной неявно
Требуется найти
частные производные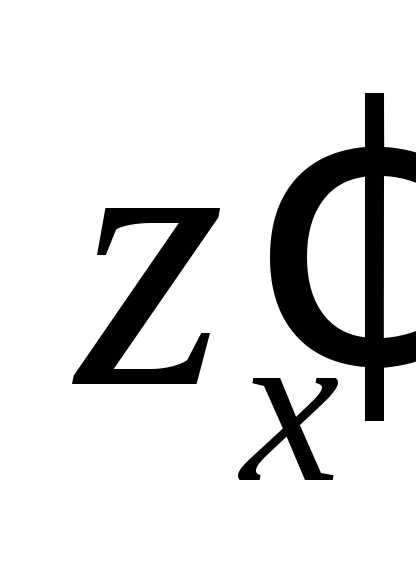 
и
,
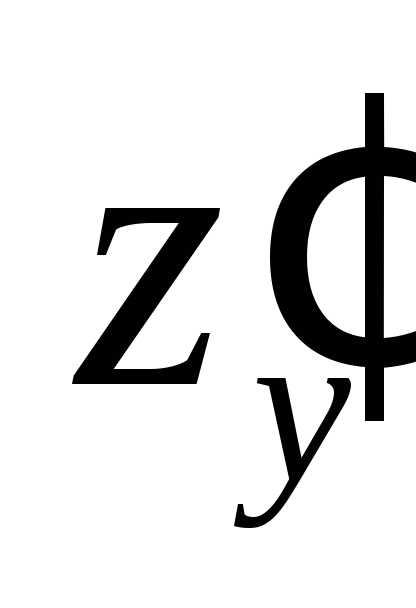если,
где.
Воспользуемся правилом дифференцирования
сложной функции для случая трёх
переменных
.
Аналогично находим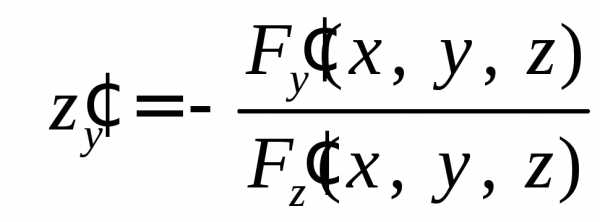 
.
Замечание 1. Отсюда следует ранее рассмотренный случай для функции одной переменной: Если , где.
Пример 2. Найти частные производные функции, заданной неявно
.
2.3. Частные производные высших порядков
Рассмотрим функцию
.
Если частные производные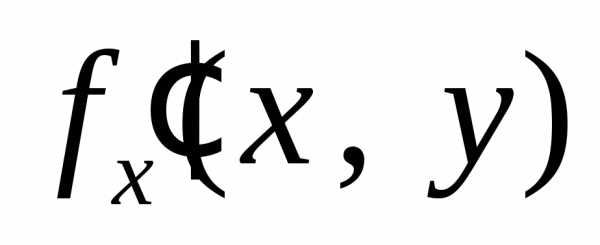
и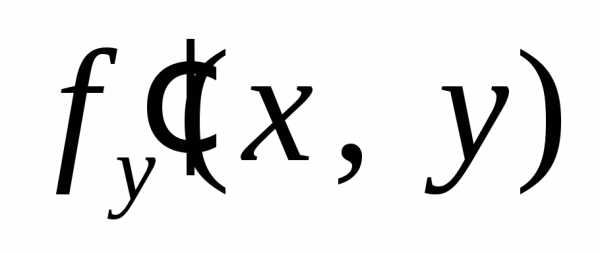
являются дифференцируемыми функциями,
то от них можно снова находить частные
производные. Частные производные второго
порядка определяются следующим
образом
Последние две производные называются смешанными производными второго порядка.
Аналогично определяются производные высших порядков. Например,
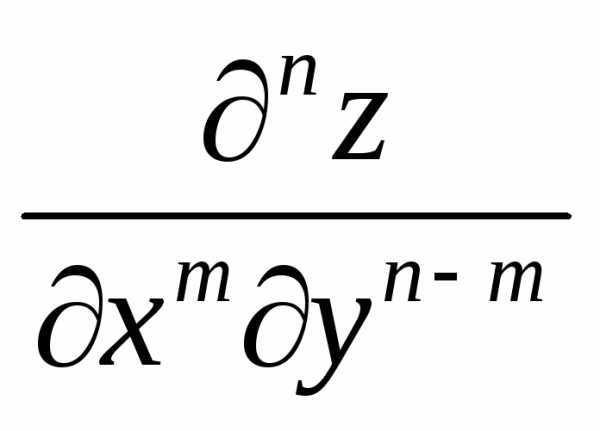означает, что
функция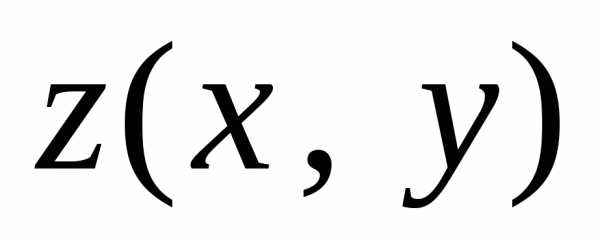 
сначала дифференцируетсят раз по х,
а затем п т раз по у.
Пример 3. Найти смешанные производные второго порядка функции .
Получено равенство двух смешанных производных второго порядка. Зависит ли в общем случае результат дифференцирования от порядка дифференцирования?
Теорема. Если функция
и ее частные производные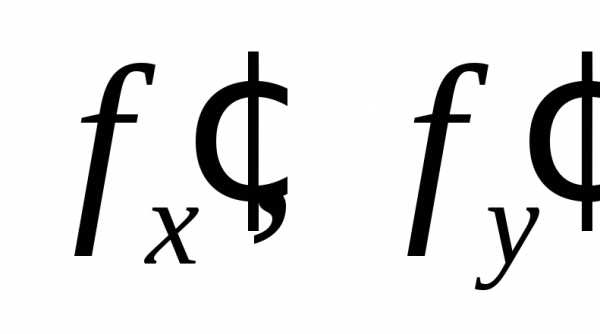
определены в некоторой окрестности
точкиМ и 
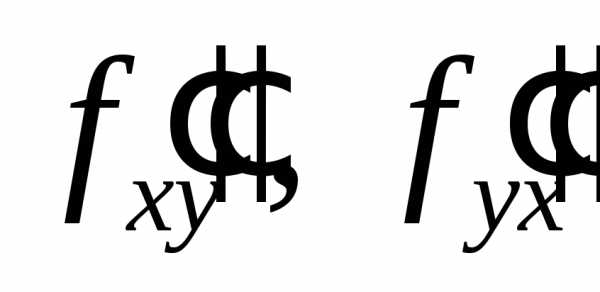непрерывны, то в этой окрестности
смешанные производные равны
.
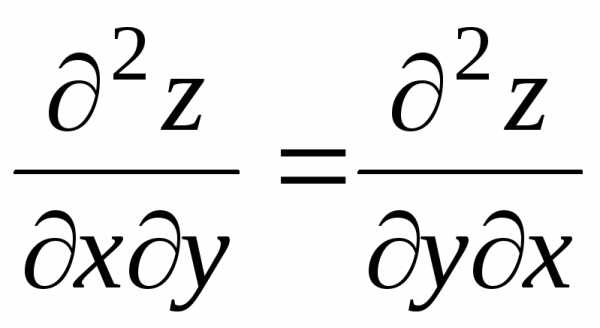studfiles.net