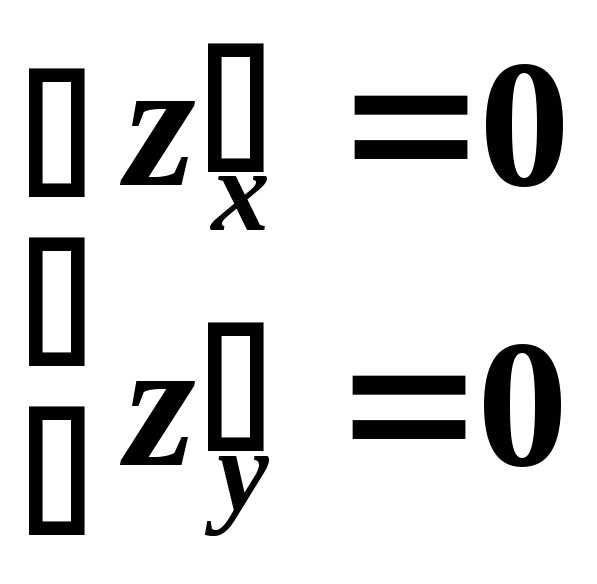Найти и изобразить область определения функции двух переменных онлайн – Область определения функции двух переменных

Содержание

Область определения функции двух переменных

Разделы: Математика

Цели работы:

повторить и систематизировать нахождение области определения функции, закрепить это понятие и наглядно представить в координатной плоскости и в пространстве;
рассмотреть аналитические и геометрические методы не изолированно друг от друга, а в тесной взаимосвязи. Это позволит облегчить переход от стандартных решений конкретных математических задач к нестандартным;
воспитание интереса к математике и мультимедиа, активности, мобильности; восприятие компьютера, как инструмента обучения;
использование компьютера для нахождения области определения и построения графиков с помощью графического редактора 3D Grapher 1.2, Copyright © 2000-2002 RomanLab Software и формирование информационной компетентности учащихся.

Определение функции двух переменных

Если каждой паре ( x;y) значений двух независимых друг от друга переменных величин х и у из некоторого множества D соответствует единственное значение величины, то говорят, что z есть функция двух независимых переменных x и y, определенная на множестве D.

Обозначается: z=f(x;y) или z=z(x;y).

Например, S=ab, S=S(a;b)- функции двух переменных; V=abc, V=V(a,b.c) – функция трех переменных;

A= – функция трех переменных.

Способы задания функций нескольких переменных

Чтобы задать функцию двух (трех) переменных, нужно указать способ, с помощью которого для каждой пары (тройки) значений аргументов можно найти соответствующее значение функции. Наиболее часто функция задается аналитически — это явное задание функции или неявное задание

Например, — это явно заданная функция двух переменных; уравнение задает неявно две функции двух переменных.

Область определения функции

Непрерывное множество пар значений независимых переменных , при которых функцияопределена, называется областью определения функции.

Область определения называется замкнутой областью, если она включает в себя свою границу; открытой областью, если она не включает в себя свою границу; ограниченной областью, если может быть помещена в круг конечного радиуса.

Геометрически изобразить область определения функции можно только для функций:

одной переменной – на прямой ,
двух переменных – на плоскости ,
трех переменных– в пространстве .

Геометрическое изображение самой функции возможно только для функции двух переменных.

Графиком функции двух переменных является поверхность, проектирующаяся на плоскость в область D, которая является областью определения функции.

На рис. изображена поверхность графика функции и ее область определения.

В курсе учебного материала 9-го класса мы рассматриваем следующие задания на нахождение и построение области определения функции.

ПРИМЕРЫ

Найти область определения функции

Решение. Областью определения данной функции является вся плоскость, т.к. нет ограничений на переменные

x и y.

2. Найти область определения функции .

Решение. Данная функция определена, когда xy > 0, т.е. в тех точках координатной плоскости, в которых знаки координат x и y - одинаковы. Это будут точки, лежащие в I и III координатных четвертях, т.е. множество точек, удовлетворяющих условиям:

3. Найти область определения функции .

Решение. Данная функция определена при условии, когда

т.е. . Это множество точек, лежащих внутри круга с центром в начале координат, радиус которого равен 2.

Изобразить на координатной плоскости Оху область определения функции .

Решение. Подкоренное выражение должно быть неотрицательно, т.е. следовательно, . Геометрическим решением неравенства служит полуплоскость, расположенная выше прямой и сама прямая.

5. Найти область определения функции и изобразить её графически.

Решение. Областью определения функции является множество точек плоскости, координаты которых удовлетворяют системе неравенств:

6. Изобразить на координатной плоскости Оху область определения функции

Решение. Эта функция определена, когда подкоренное выражение неотрицательно, т.е. Данным соотношениям удовлетворяют координаты всех точек, находящихся внутри кольца, образованного двумя окружностями с центрами в начале координат и радиусами R=3, R=4.

7. Изобразить на координатной плоскости Оху область определения функции

Решение. Учащиеся не могут найти область определения данной функции аналитически, но с помощью графического редактора 3D Grapher 1.2 это выполняется легко.

В Приложении приведено ещё несколько примеров, с решениями, для учащихся девятых классов.

Для учащихся 10-11 классов мы предлагаем систему упражнений по нахождению и построению области определения функции двух переменных. При этом отрабатываются свойства логарифмических, тригонометрических и обратных тригонометрических функций. Данные упражнения можно использовать при изучении нового материала, при повторении, при решении уравнений и неравенств.

Найти и изобразить на плоскости область определения функции

Решение. Область определения функции есть пересечение областей определения слагаемых функции. Для первой функции подкоренное выражение должно быть неотрицательным, т.е. Если значение логарифмической функции неотрицательно, то выражение, стоящее под знаком логарифма, должно быть больше или равно единице, т.е. отсюда . Это неравенство задает нам множество точек плоскости, лежащих вне окружности с центром в начале координат, радиуса 2, включая и точки данной окружности. Вторая функция определена при Следовательно, Имеем две параболы с вершиной в начале координат . Поэтому полученное неравенство задает нам часть плоскости, заключенную между этими параболами, включая границы без начала координат. Третья функция определена при

Областью определения данной функции является общая часть найденных областей определения слагаемых.

Покажите на координатной плоскости xOy область определения функции

Решение. Ограничения для функции имеют вид:

3. Изобразить область определения функции

Решение. Эта функция определена при , т.е.

Областью определения является часть плоскости, расположенная между двумя прямыми.

4. Найти область определения функции .

Решение. Областью определения функции является решение неравенства. Поэтому нужно решить неравенство

Решая данное неравенство, получим Это область, заключенная между двумя параболами и .

5. Построить область определения функции

Решение. Область определения данной функции определяется системой неравенств:

Первое неравенство определяет круг с центром в точке (-2;0) и радиусом равным 2 за исключением его границы:

Второе неравенство определяет I и III координатные четверти, за исключением осей.

В Приложении приведено ещё несколько примеров, с решениями, для учащихся десятых и одиннадцатых классов.

Рассмотрим задание С5, используя функцию двух переменных.

Найдите все значения параметра а, при которых система , имеет ровно два решения.

Решение. Из второго уравнения находим y =. Первое уравнение принимает вид .

Пусть . В этом случае уравнение имеет единственное решение .

Запишем второе уравнение в виде = 0. Его дискриминант равен 4 , и он положителен, поскольку . Уравнение имеет два различных корня и Значит, в этом случае система имеет ровно два решения и .

Пусть теперь 1. В этом случае уравнение если и имеет корни, то только больше единицы Но тогда дискриминант уравнения = 0 отрицателен. Решений нет.

Ответ: .

С помощью графического редактора задаем функцию двух переменных , Находим значения а, при которых функция обращается в ноль.

На рисунке видно, что решением является интервал от 0 до 1.

При подготовке учащихся к итоговой аттестации мы сталкиваемся с тем, что задания уровня С5 решаются тяжело и не сразу. А ведь это функция двух переменных! Оперирование геометрическими образами упрощает решение задач с параметрами, а в некоторых случаях геометрический подход часто является единственно возможным методом решения. В сборнике ЕГЭ-2011 предложено задание.

Найдите все значения а, такие, что для любого х выполняется неравенство.

Решение. Рассмотрим функцию

Если то убывает.

Если то возрастает.

Значит, наименьшее значение функции равно или , или . Поэтому решение задачи получаем из решения системы

Решений нет.

Ответ: .

C помощью графического редактора мы построили график функции и определили значение параметра а при . График функции в системе координат выглядит следующим образом.

Приложение 1

Приложение 2

Приложение 3

Список источников и литературы.

Математика (математический анализ): учебно-методическое пособие для студентов нематематических специальностей / О.Ю. Ватюкова, Е.Е.Зайцева, Ю.В.Зайцева и др.; ВолГУ.-4-е изд., Волгоград: Волгоградское научное издательство, 2009. – 238с.
Дифференциальное исчисление функций нескольких переменных: типовой расчет по высшей математике / Сост.: А. В. Анкилов, Н. Я. Горячева, Т. Б. Распутько.- Ульяновск: УлГТУ, 2004.-32 с.
ЕГЭ 2011. Математика. Типовые тестовые задания / И.Р. Высоцкий, Д.Д. Гущин, П.И.Захаров, В.С. Панферов, и др.; под ред. А.Л. Семенова, И.В. Ященко. -М.: Издательство “Экзамен”, 2011.-63с.
Самое полное издание типовых вариантов реальных заданий ЕГЭ: 2010: Математика/авт.- сост. И.Р.Высоцкий, Д.Д. Гущин, П.И. Захаров и др.; под ред. А.Л. Семенова, И.В. Ященко. -М.: АСТ: Астрель, 2010.-93с.
Мордкович А.Г. Алгебра . 9 класс. В 2 ч. Ч.1. Учебник для учащихся общеобразовательных учреждений / А.Г.Мордкович, П.В.Семенов .—11-е изд., стер. -М.: Мнемозина, 2009.-224 с.
Смирнова И.М. Геометрия. 10-11 кл.: Учеб. для общеобразоват. учреждений (гуманитарный профиль).- М.: Мнемозина,2004. -223с.

29.07.2013

urok.1sept.ru

Область определения функций нескольких переменных

Определенный интеграл

Министерство образования и науки Российской Федерации Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования «Сибирский государственный индустриальный университет»

Подробнее Вычисление и приложения тройного интеграла
Министерство образования и науки Российской Федерации Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования «Сибирский государственный индустриальный университет»
Подробнее Функции одной переменной
Министерство образования и науки Российской Федерации Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования «Сибирский государственный индустриальный университет»
Подробнее Несобственные интегралы
Министерство образования и науки Российской Федерации Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования «Сибирский государственный индустриальный университет»
Подробнее Тригонометрические ряды Фурье
Министерство образования и науки Российской Федерации Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования «Сибирский государственный индустриальный университет»
Подробнее Обыкновенные дифференциальные уравнения
Министерство образования и науки Российской Федерации Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования «Сибирский государственный индустриальный университет»
Подробнее Вычисление и приложения двойного интеграла
Министерство образования и науки Российской Федерации Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования «Сибирский государственный индустриальный университет»
Подробнее Поверхности второго порядка
Министерство образования и науки Российской Федерации Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования «Сибирский государственный индустриальный университет»
Подробнее Кривые второго порядка
Министерство образования и науки Российской Федерации Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования «Сибирский государственный индустриальный университет»
Подробнее Выпуклость, точки перегиба. Асимптоты
Министерство образования и науки Российской Федерации Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования «Сибирский государственный индустриальный университет»
Подробнее lim ПРЕДЕЛ ФУНКЦИИ Методические указания
Федеральное агентство по образованию Государственное образовательное учреждение высшего профессионального образования Ухтинский государственный технический университет (УГТУ) ПРЕДЕЛ ФУНКЦИИ Методические
Подробнее ФУНКЦИИ МНОГИХ ПЕРЕМЕННЫХ
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ федеральное государственное бюджетное образовательное учреждение высшего образования «Курганский государственный университет» Кафедра «Прикладная математика
Подробнее Электронная библиотека
ГОСУДАРСТВЕННОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ «БЕЛОРУССКО-РОССИЙСКИЙ УНИВЕРСИТЕТ» Кафедра «Высшая математика» ВЫСШАЯ МАТЕМАТИКА МАТЕМАТИКА МАТЕМАТИЧЕСКИЙ АНАЛИЗ Методические рекомендации
Подробнее Выборки и их характеристики
Министерство образования и науки Российской Федерации Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования «Сибирский государственный индустриальный университет»
Подробнее Контрольные работы по математике
МИНОБРНАУКИ РОССИИ Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования «Ухтинский государственный технический университет» (УГТУ) Контрольные работы по
Подробнее ФУНКЦИИ МНОГИХ ПЕРЕМЕННЫХ
Министерство образования и науки Российской Федерации Федеральное государственное бюджетное образовательное учреждение высшего образования «Московский авиационный институт (национальный исследовательский
Подробнее ПОДГОТОВКА К ТЕСТИРОВАНИЮ ПО МАТЕМАТИКЕ
РОСЖЕЛДОР Федеральное государственное бюджетное образовательное учреждение высшего образования «Ростовский государственный университет путей сообщения» ФГБОУ ВО РГУПС ЕВ Пиневич, ВА Липович, ИС Стасюк
Подробнее ИССЛЕДОВАНИЕ ФУНКЦИЙ С ПОМОЩЬЮ ПРОИЗВОДНЫХ
МИНИСТЕРСТВО ТРАНСПОРТА РОССИЙСКОЙ ФЕДЕРАЦИИ ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ УЛЬЯНОВСКОЕ ВЫСШЕЕ АВИАЦИОННОЕ УЧИЛИЩЕ ГРАЖДАНСКОЙ АВИАЦИИ (ИНСТИТУТ)
Подробнее Дифференциальные уравнения
Министерство образования Российской Федерации МАТИ — РОССИЙСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНОЛОГИЧЕСКИЙ УНИВЕРСИТЕТ им К Э ЦИОЛКОВСКОГО Кафедра Высшая математика Дифференциальные уравнения Методические указания
Подробнее Н. В. Деменева КОМПЛЕКСНЫЕ ЧИСЛА
Министерство сельского хозяйства Российской Федерации Федеральное государственное бюджетное образовательное учреждение высшего образования «Пермская государственная сельскохозяйственная академия имени
Подробнее КРАТНЫЕ ИНТЕГРАЛЫ (задачи и упражнения)
ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ «САМАРСКИЙ ГОСУДАРСТВЕННЫЙ АЭРОКОСМИЧЕСКИЙ УНИВЕРСИТЕТ имени академика СП КОРОЛЕВА»
Подробнее Вариационное исчисление
ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ «САМАРСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ» Кафедра прикладной математики и
Подробнее ДОПОЛНИТЕЛЬНЫЕ ГЛАВЫ ВЫСШЕЙ МАТЕМАТИКИ
СЫКТЫВКАРСКИЙ ЛЕСНОЙ ИНСТИТУТ Кафедра высшей математики ДОПОЛНИТЕЛЬНЫЕ ГЛАВЫ ВЫСШЕЙ МАТЕМАТИКИ САМОСТОЯТЕЛЬНАЯ РАБОТА СТУДЕНТОВ Методические указания для подготовки дипломированных специалистов по направлению
Подробнее 7 Координаты центра тяжести
7 Координаты центра тяжести Используя математический пакет Mm, найти координаты центра тяжести плоской фигуры Результат представить графически Найти координаты центра тяжести фигуры, ограниченной линиями
Подробнее СЫКТЫВКАРСКИЙ ЛЕСНОЙ ИНСТИТУТ
СЫКТЫВКАРСКИЙ ЛЕСНОЙ ИНСТИТУТ КАФЕДРА ВЫСШЕЙ МАТЕМАТИКИ АЛГЕБРА И ГЕОМЕТРИЯ САМОСТОЯТЕЛЬНАЯ РАБОТА СТУДЕНТОВ Методические указания для подготовки дипломированных специалистов по направлению 654700 «Информационные
Подробнее Электронная библиотека
ГОСУДАРСТВЕННОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ «БЕЛОРУССКО-РОССИЙСКИЙ УНИВЕРСИТЕТ» Кафедра «Высшая математика» ВЫСШАЯ МАТЕМАТИКА МАТЕМАТИКА Задания в тестовой форме для самостоятельной
Подробнее МАТЕМАТИКА ЧАСТЬ 3 ОМСК 2016
МАТЕМАТИКА ЧАСТЬ ОМСК 6 Министерство транспорта Российской Федерации Федеральное агентство железнодорожного транспорта Омский государственный университет путей сообщения Ю. Г. Галич МАТЕМАТИКА Часть Утверждено
Подробнее ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
Министерство образования и науки Российской Федерации Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования «Новгородский государственный университет имени
Подробнее МЕТОДИЧЕСКИЕ УКАЗАНИЯ
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ УКРАИНЫ НАЦИОНАЛЬНАЯ МЕТАЛЛУРГИЧЕСКАЯ АКАДЕМИЯ УКРАИНЫ МЕТОДИЧЕСКИЕ УКАЗАНИЯ к решению задач по дисциплине Высшая математика и варианты контрольных заданий практические
Подробнее Математический анализ.
Основная форма учебных занятий студентов-заочников самостоятельная работа над учебным материалом, слагающаяся из следующих составных элементов: изучение материала по учебникам, решение задач, самопроверка
Подробнее docplayer.ru
Область определения функции двух переменных в Wolfram|Alpha
Как найти область определения функции двух переменных?
В Wolfram|Alpha для нахождения области определения функции служит запрос domain. Применяя этот запрос к функции двух переменных, получим следующее:

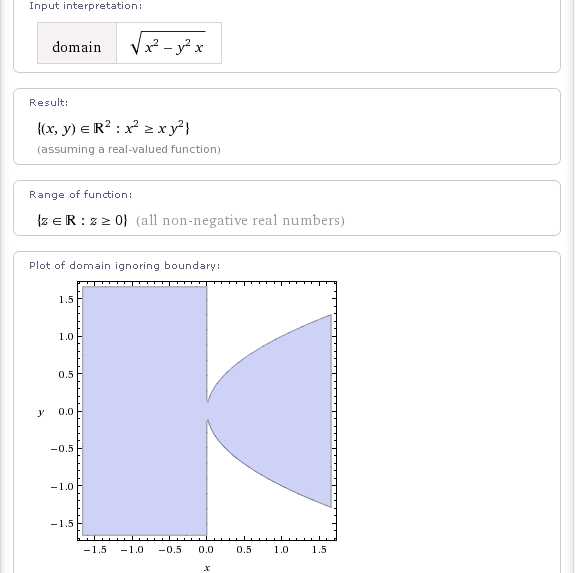
В общем-то, на этом вопрос про область определения функции двух переменных в Wolfram|Alpha исчерпан. Далее мне просто захотелось посмотреть, как будет изменяться область определения данной функции, если менять коэффициенты при аргументах, и в других случаях. И вот, что из этого получилось…
Например, чтобы развернуть область определения функции 2-х переменных на 90 градусов, нужно поменять местами обозначения аргументов:
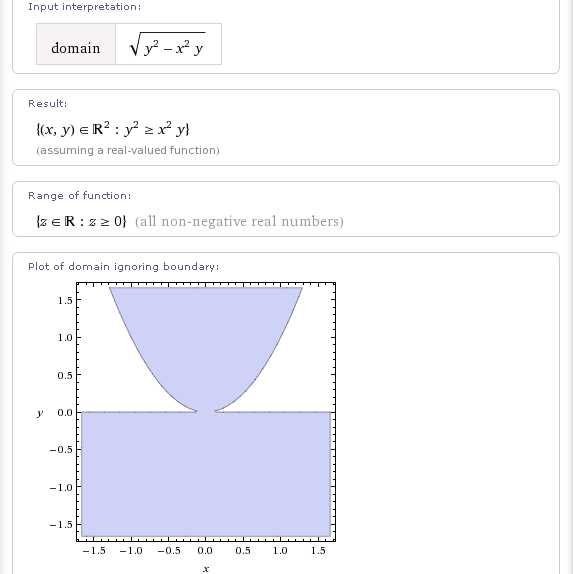
Параллельный перенос области определения на +1 вдоль оси абсцисс:
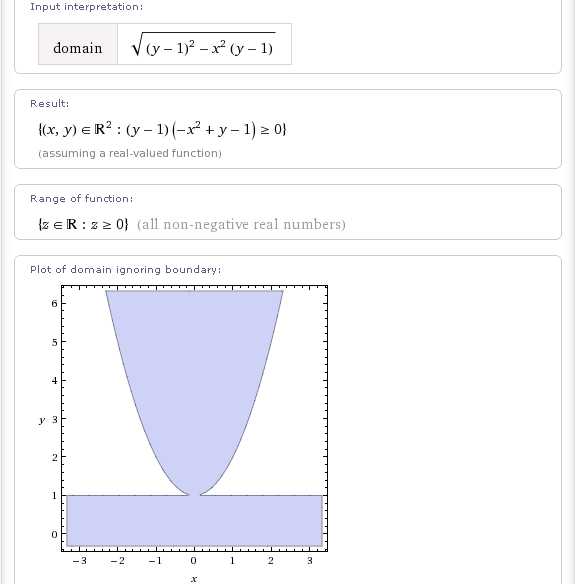
Если в данной функции поменять знаки перед слагаемыми на противоположные, то область определения инвертируется:
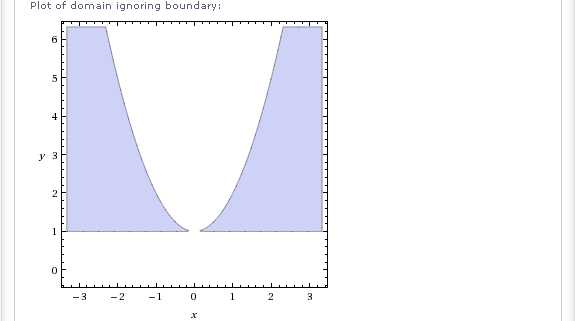
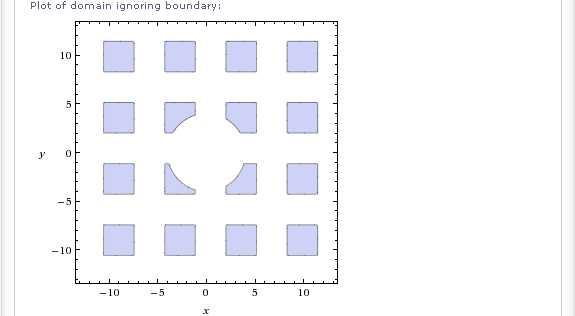
Интересный результат получаем в следующем случае:
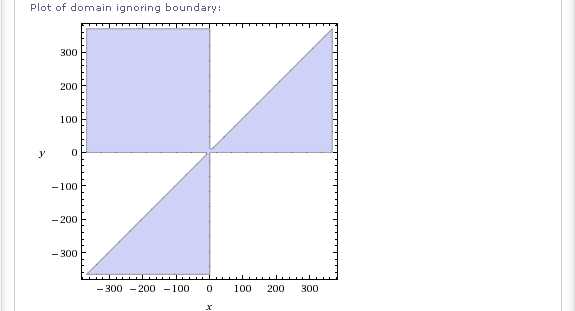
На предыдущей картинке, внимание привлекает область вблизи начала координат. Сначала кажется, что границы области определения пересекаются в центре картинки под острыми углами. Однако, присмотревшись, вы увидите, что это не так. Истинный характер этих линий хорошо виден лишь при большом увеличении на графическом изображении инвертированной области определения далее:
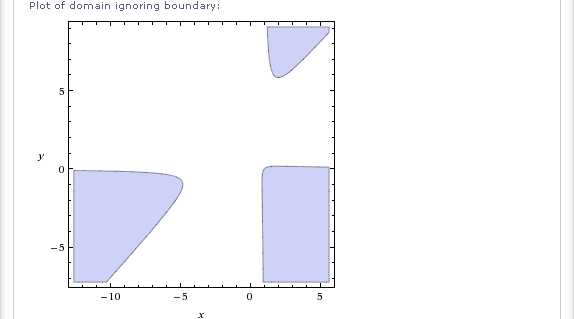
Наконец, вот такой симпатичный пример:
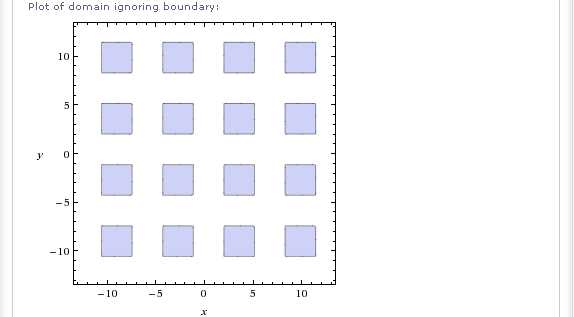
Конечно, есть еще много других интересных примеров. Думаю, вы рассмотрите их самостоятельно.
А я, напоследок, попробую что-нибудь такое:

www.wolframalpha-ru.com
1)Определение функции двух переменных
Если каждой паре ( x;y) значений двух независимых друг от друга переменных величин х и у из некоторого множества D соответствует единственное значение величины, то говорят, что z есть функция двух независимых переменных x и y, определенная на множестве D.
Обозначается: z=f(x;y) или z=z(x;y).
Например, S=ab, S=S(a;b)- функции двух переменных; V=abc, V=V(a,b.c) – функция трех переменных;
2)Область определения ф-ии двух переменных
Область определения функции z=f(x,y) называется совокупность пар чисел (x,y), которым соответствуют действительные значения функции. D={(x,y)}
Множество Z={f(x,y)} – множество значений функции.
3)График функции двух переменных. Линии уровня. Поверхности уровня.
Графиком функции z= f(x,y) называется поверхность, представляющая собой геометрическое место точек функции, когда точка (x,y) принимает все значения из области определения.
Линией уровня функции z= f(x,y) называется геометрическое место точек (x,y) плоскости, в которой функция принимает одно и то же значение С. Линию уровня можно построить, спроектировав на плоскость XOY множество точек пространства. Уравнение линии уровня имеет вид f(x,y)=С.
Поверхностью уровня u=с функции u= f(x,y,z) называется поверхность f(x,y,z)=с, в точках которой функция u= f(x,y,z) сохраняет значение, равное с.
4)Предел и непрерывность ф-ии нескольких переменных.
Введем понятие D-окрестности точки М0 (Х0 , у0) на плоскости ОХу как круга радиуса D с центром в данной точке. Аналогично можно определить D-окрестность в трехмерном пространстве как шар радиуса D с центром в точке М0 (Х0 , у0 , Z0). Для N-мерного пространства будем называть D-окрестностью точки М0 множество точек М С координатами , удовлетворяющими условию
Координаты точки М0. Иногда это множество называют «шаром» в N-мерном пространстве.
Число А называется Пределом функции нескольких переменных
В точке М0, если
Такое, что | F(M) – A| < ε для любой точки М из δ-окрестности М0.
Обозначения:
Необходимо учитывать, что при этом точка М может приближаться к М0, условно говоря, по любой траектории внутри D-окрестности точки М0. Поэтому следует отличать предел функции нескольких переменных в общем смысле от так называемых Повторных пределов, получаемых последовательными предельными переходами по каждому аргу
Функция
Называется Непрерывной в точке
М0
Если
Если ввести обозначения
То это условие можно переписать в форме
Внутренняя точка М0 Области определения функции Z = F (M) называется Точкой разрыва функции, если в этой точке не выполняется условие
Замечание. Множество точек разрыва может образовывать на плоскости или в пространстве Линии Или Поверхности разрыва.
5)Определение частных производных
Частные производные функции y=f(M)в том случае, если они существуют не в одной точке, а на некотором множестве A’, являются функциями, определенными на этом множестве. Поэтому удобно ввести следующие обозначения:
F’x1=g1(M), f’x2=g2(M)….
Полученные функции g1, g2….gn, определенные в A’, могут быть непрерывными и иметь частные производные в различных точках A’.Назовем частные производные от функций g1,g2…gn. частными производными высшего порядка от функции f(M) и примем для каждого j (j=1,2,3…n)
(fx1)’xj=f’’x1xj , (f’x2)’xj=f’’x2xj,…, (f’xn)’xj=f’’xnxj или (f’xi)’xj=f’’xixj, где I и j= 1,2,3…n.
Эти производные разбиваются на две группы: вторые частные производные от f по переменным xi
f’’x²i= (f’xi)’xj, i=1,2,…n, j=1,2,…n.
и смешанные частные производные от f по переменным xi и xj (i≠j)
f’’xixj=(f’xi)’xj, i=1,2…n, j=1,2…n.
Число вторых частных производных функции f(M)равно n, а число смешанных частных производных – разности n²-n=n(n-1). При этом величина n² определяет общее число всех старших производных и совпадает с числом элементов квадратной матрицы порядка n. Элементы такой матрицы имеют индексы I и j, которые находятся во взаимно однозначном соответствии с координатными индексами xi, xj, определяющими порядок частной производной.
studfiles.net
Тема: функция двух переменных.
Функция двух переменных
При изучении многих зависимостей используют понятие функции нескольких переменных.
Например: температура Т, измеряемая в различных точках некоторого тела или пространства, зависит от координат точки (х, у, z) (от места, где устанавливается термометр) и от момента времени t. В этом случае пишут T=f(x, у, z, t).
Мы будем рассматривать только случай функций двух переменных. Выводы, полученные при этом, можно легко распространить на функции от большего числа переменных.
Примером функции двух переменных может служить зависимость площади прямоугольника от длины a и от ширины b. формула имеет вид S=a*b Опр. Функция двух переменных – это правило, по которому каждой паре х и у ставится в соответствие единственное значение Z.
Обозначают z=f(x,y), f-закон соответствие по которому паре х и у ставится в соответствие значение Z.
Значение функции двух переменных находится так же как и для функции одной переменной
Например: Вычислить значение функции двух переменных Z=x²–2xy, в точке М(1,2)
Z(1,2)= f(x,y)=1²–2*1*2=1–4= –3
Опр. Область определения функции двух переменных z=f(x,y) называется множество пар переменных х и у для которых функция z=f(x,y) определена.
Область определения может иметь вид прямоугольника, круга, полуплоскости.
Пример 1:
Найти область определения для функции Z=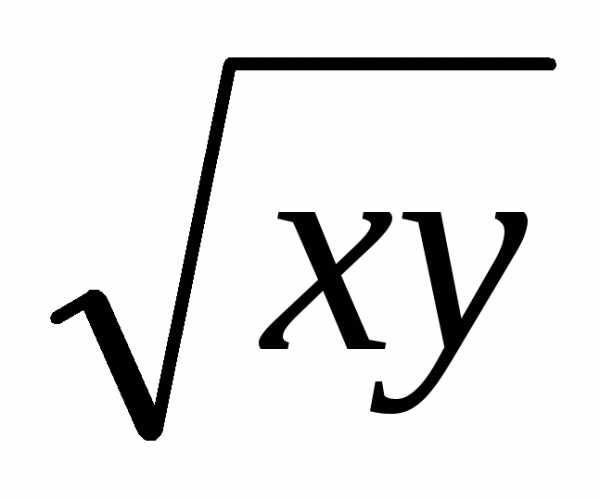
Корень существует, если ху0, это возможно когда
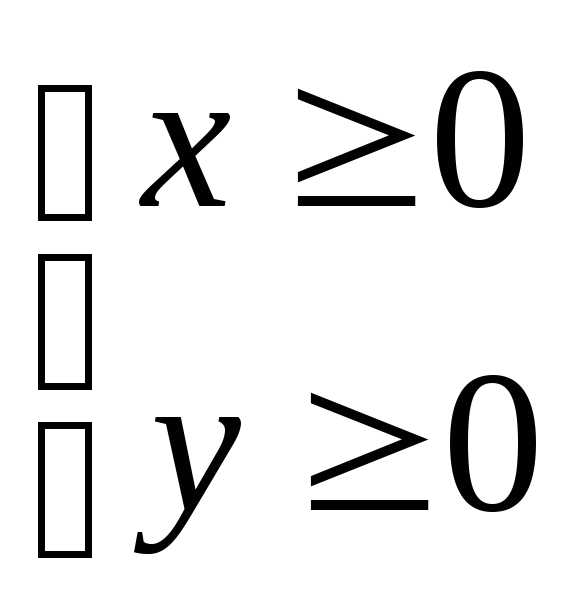или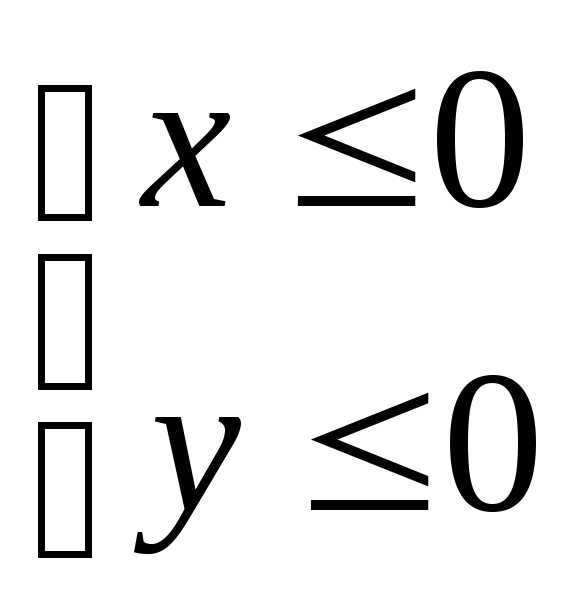
область определения функции двух переменных обычно изображается штриховкой в системе ПДСК координат на плоскости.
Пример 2:
Найти область определения для функции Z=,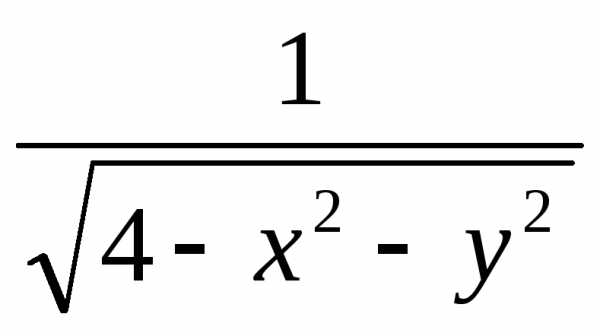
Выражение будет существовать когда корень 0, знаменатель 0
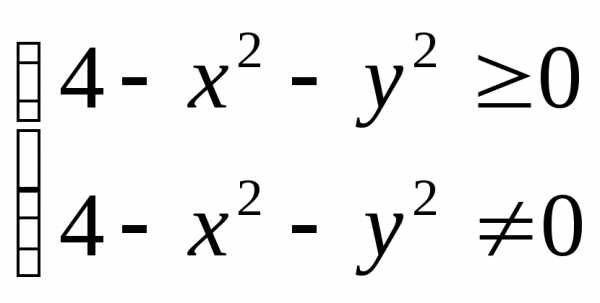, т.е. 4–х²–у²>0
4–х²–у²=0
х²+у²=4 окружность с центром в точке (0,0) и радиусом 2.
Возьмем точку из окружности (0,0) и подставим ее в неравенство, получим верное равенство, следовательно областью определений будет все множество точек лежащее внутри окружности.
Геометрический смысл функции двух переменных.
Дана функция двух переменных z=f(x,y). Каждой точке из области определения с координатами (х,у) соответствует одно значение переменной z=f(x,y). Таким образом определяется упорядоченная тройка чисел (х,у,f(x,y)), таких точек можно получить сколь угодно много, если переменные пробегают всевозможные значения из области определения, то в пространстве получится поверхность – график функции двух переменных.
Например: поверхность определяемая уравнением Z=x²+y² называется параболоид вращения.
Предел функции двух переменных.
Опр. Пределом функции двух переменных называется число к которому стремится сама функция при стремлении аргументов каждый к своему значению. z=f(x,y) , М(х₀,у₀) обозначается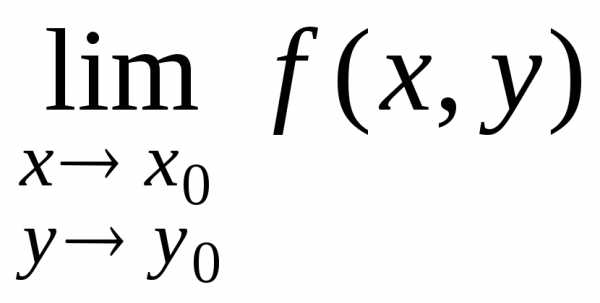
Например: z= x³–4xy² M(-1,0)
Непрерывность функции двух переменных.
Опр Функция f(х,у) называется непрерывной в точке (х₀;у₀), если бесконечно малым изменениям значений аргументов х и у соответствует бесконечно малое изменение функции f(х,у).
График непрерывной функции представляет собой поверхность без разрывов, «проколов» и других особенностей.
Опр Функция двух переменных называется непрерывной в своей области определения, если она непрерывна в каждой точке этой области.
Частные производные первого и второго порядка.
Рассмотрим функцию Z=f(x,y), зафиксируем переменную у=у₀, тогда из функции двух переменных получим функцию одной независимой переменной Z=f(x,y₀).
Опр. Разность между конечным и начальным значениями функции называется частным приращением функции от данной переменной.
Для х задаем приращение х
f(x+х,y₀)– f(x,y₀)= _хZ– частное приращение по переменной х
Опр. Частной производной функции двух переменных Z=f(x,y) по переменной х называется предел отношения приращения функции по переменной х к приращению аргумента х, при условии что х0.
Обозначают ,Z’_x, f’_x(x,y),
Z’_x=
Аналогично определяем другую частную производную Z’_у
Аналогично фиксируем переменную х=х₀, у-переменная
f(x₀,y+у)– f(x₀,y)= _уZ – частное приращение по переменной у,
Опр. Частной производной функции двух переменных Z=f(x,y) по переменной у называется предел отношения приращения функции по переменной у к приращению аргумента у, при условии что у0.
Z’_у=
Производные от функции двух переменных находится по тем же самым правилам и формулам, как и производная функции одной переменной. Только необходимо помнить, какая из данных переменных зафиксирована, а какая продолжает изменяться.
Пример:
Z= x²–3y²–6xy–2x–y+9 Z’_x =? Z’_у–?
Z’_x = (x²)’_x –(3y²)’_x–(6xy)’_x–(2x)’_x–(y)’_x+(9)’_x =2x–0–6у–2–0+0=2x–6у–2
У=const
Z’_у= (x²)’_у –(3y²)’_у–(6xy)’_у–(2x)’_у–(y)’_у+(9)’_у=0–6у–6х–0–1+0= –6у–6х–1
Частные производные по переменным Х и У, станут новыми функциями двух переменных и при необходимости от них можно найти частные производные как по переменной Х так и по У– они называются частными производными второго порядка.
Z”_x_х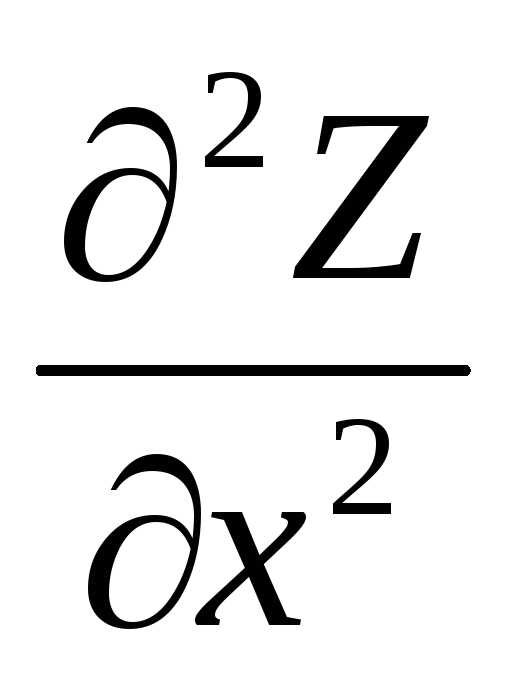– частная производная второго порядка дважды дифференцирован по переменной Х
Z”_уу ,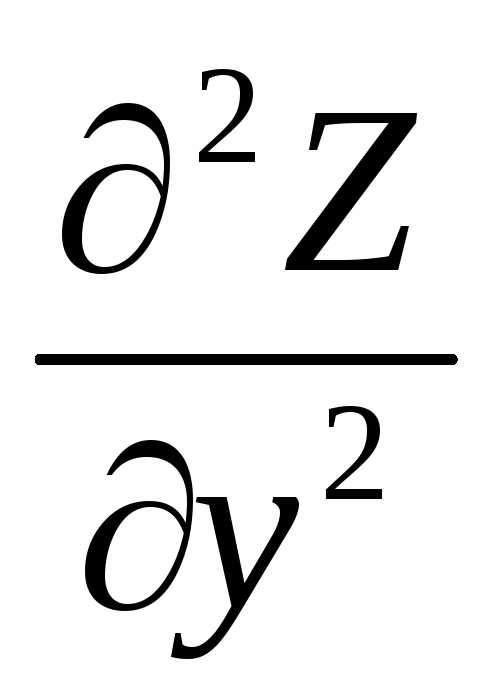– част пр-я 2-го порядка дважды дифференцирован по переменной У
Z”_ху ,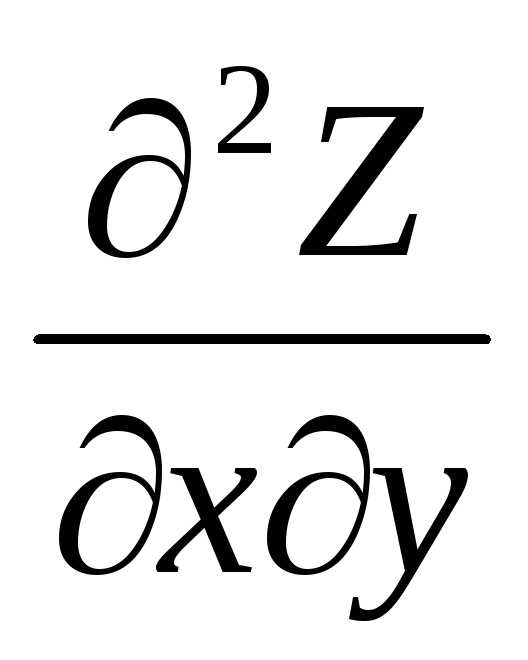– част пр-я 2-го порядка сначала найденная по перем Х, потом по У
Z”_ух ,– част пр-я 2-го порядка сначала найденная по перем У, потом по Х
Пример: Найти частные производные второго порядка от функции
Z=x²–3y²–6xy–2x–y+9
Z’_x = 2x–6у–2
Z’_у= –6у–6х–1
Z”_x_х = (Z’_x)’_х= (2x–6у–2)’_x=2-0-0=2
Z”_yy = (Z’_y)’_y= (–6у–6х–1)’_y=-6-0-0= –6
Z”_xy = (Z’_x)’_y= (2x–6у–2)’_y=0-5-0= –6
Z”_yx = (Z’_y)’_x= (–6у–6х–1)’_x=-0–5–0= –6
Заметим что частные производные второго порядка Z’_xy Z’_yx равны между собой, и следовательно не зависят от порядка дифференцирования.
Экстремум функции двух переменных.
Опр. Функция Z=f(x,y), в точке (х₀;у₀) будет иметь минимум, если для всех других точек с координатами (х;у) будет выполнено следующее условие: f(х₀;у₀)<f(x,y)
Опр. Функция Z=f(x,y), в точке (х₀;у₀) будет иметь максимум, если для всех других точек с координатами (х;у) будет выполнено следующее условие: f(х₀;у₀)>f(x,y)
Максимум и минимум функции как и в случае функции одной переменной будем называть экстремумами функции.
Теорема1: (необходимое условие существования экстремума)
Если функция Z=f(x,y) имеет экстремум в точке (х₀;у₀), то ее частные производные, первого порядка, в этой точке равны нулю.
Т.е. если для Z=f(x,y) (х₀;у₀)–экстремум 
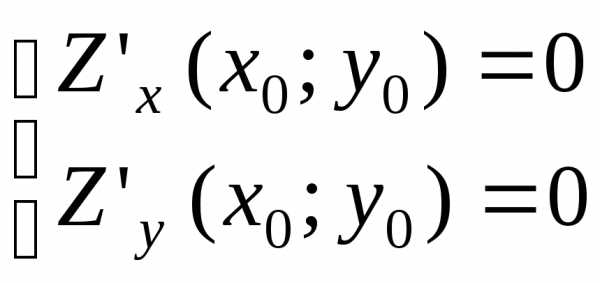
Точки в которых производная равна нулю называют критическими точками.
Теорема2: (достаточное условие существования экстремума)
Пусть функция Z=f(x,y)-непрерывная в области определения вместе со своими производными и точка М₀(х₀;у₀)–критическая точка, обозначим
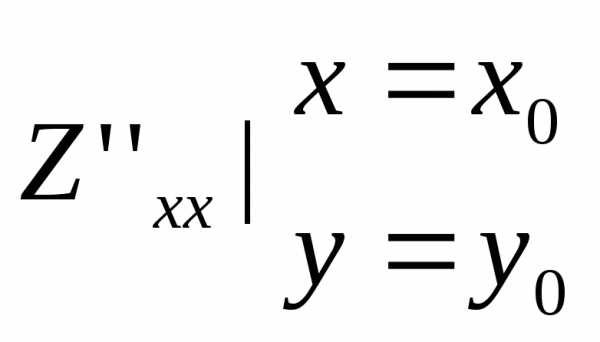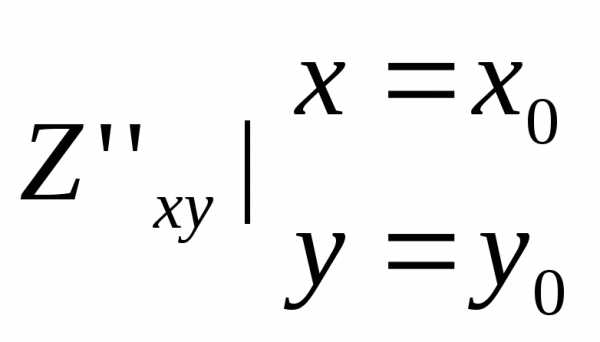А=B=C=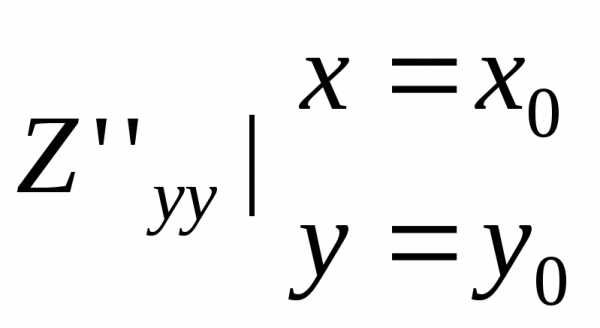
если АС–В²>0, то функция имеет экстремум в точке М₀, причем
минимум, если А>0
максимум, если А<0
если АС–В²<0, то точка Мо(х₀;у₀)– не является точкой экстремума
если АС–В²=0, то нужны дополнительные исследования на определение точек экстремума (сомнительный случай)
Алгоритм исследования функции двух переменных на экстремум.
Найти частные производные первого порядка.
Найти критические точки, т.е. решить систему
Найти частные производные второго порядка, т.е. найти А,В,С.
Сделать выводы на основании Т2 о точках экстремума.
Пример: Исследовать на экстремум функцию Z=3x²+3xy+у²–6х–2y+7
1. Z’_x = 6x+3у–6 Z’_у= 2у+3х–2
2. Решим систему:
у=2–2х
3х+2(2–2х)–2=0 х=2
у=2-2(2)=–2 (2;–2)– критическая точка
3. Z”_xx=6=A Z”_xy=3=B Z”_yy=2=C
4. АС–В²=3 >0 – экстремум есть и т.к. А=6>0 следовательно (2;–2) – точка минимума.
5.
(2;–2;3) – точка минимума.
Касательная плоскость и нормаль к поверхности
Пусть фиксированная точка на поверхности, заданной функцией
Касательной плоскостью к поверхности в точке называется плоскостьt проходящая через эту точку и такая, что угол между этой плоскостью и секущей проходящей через эту точку и любую точку поверхности стремится к нулю.
Уравнение t:
Нормалью называется прямая n, проходящая через точку 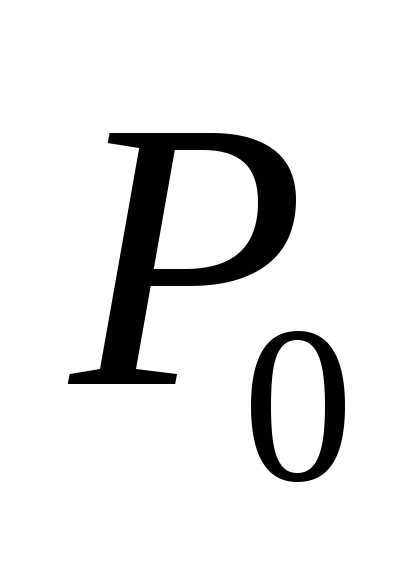и перпендикулярно касательной плоскости.
Уравнение n:
studfiles.net
Tиповой расчет 5
Типовой расчёт
Производная и дифференциал функции двух переменных.
Исследование функции двух переменных.
Образец решения типового расчёта.
Задание 1. Найти и изобразить на плоскости область определения функции двух переменных: .
Решение. Очевидно, аналитическое выражение, задающее данную функцию, имеет смысл тогда и только тогда, когда знаменатель дроби не равен нулю: . Уравнениезадаёт на координатной плоскостипараболу, вершина которой находится в точке, ветви направлены влево, а осью симметрии является ось абсцисс. Таким образом, областью определения данной функции являются все точки координатной плоскости, кроме тех, что лежат на параболе.
Задание 2. Найти частные производные первого порядка функций двух переменных:
2.1. .
Решение. .
2.2. .
Решение. .
2.3. .
Решение. .
Задание 3. Найти все частные производные второго порядка функции двух переменных: .
Решение. Сначала найдём частные производные первого порядка:
.
Теперь находим производные второго порядка по переменным и:
.
Находим смешанные производные:
.
Задание 4. Найти производную функции в точкепо направлению вектора.
Решение. Производная функции по направлению вектораравна:
, где направляющие косинусы вектора.
Находим частные производные данной функции:
.
Находим значения частных производных в точке :
.
Находим направляющие косинусы вектора :
.
Окончательно получим:
.
Задание 5. Найти градиент функции в точке.
Решение. Градиент функции двух переменных равен.
Найдём частные производные:
.
Найдём значения частных производных в точке :
.
Тогда градиент равен .
Задание 6. Исследовать функцию на экстремумы.
Решение. Областью определения данной функции является вся числовая плоскость . Найдём частные производные данной функции:
.
Производные первого порядка непрерывны на всей области определения функции. Для того, чтобы найти критические (стационарные) точки функции, решим систему уравнений:
Получили одну стационарную критическую точку . Для того, чтобы выяснить, является ли она точкой экстремума, найдём производные второго порядка.
.
Найдём дискриминант: где.
В данном случае, . В данной точке экстремума нет.
Задание 7. Найти экстремум функции при условии.
Решение. Областью определения данной функции является вся числовая плоскость . Выразим из уравнения связипеременную:. Далее рассмотрим оба возможных случая.
1) . Подставляя это выражение в исходную функцию, получим функцию одной переменной. Исследуем эту функцию на наибольшее и наименьшее значение при.
. Очевидно, при любых значениях переменной, и поэтому наибольшее и наименьшее значение достигается в концах отрезка.
.
2) . Подставляя это выражение в исходную функцию, получим функцию одной переменной. Исследуем эту функцию на наибольшее и наименьшее значение при.
. Получили две стационарные критические точки. Найдём значения функции в этих точках и на концах отрезка.
.
Таким образом, .
Задание 8. Найти наибольшее и наименьшее значение функции в области.
Решение. Прежде всего, заметим, что данная функция непрерывна в рассматриваемой области. Найдём критические (стационарные) точки функции, принадлежащие указанной области. Частные производные первого порядка непрерывны в данной области. Составим систему уравнений:
Получили одну стационарную критическую точку . Найдём значение функции в этой точке:. Далее, последовательно найдём значения функции на всех границах области.
1) . Функция принимает вид. Тогда.
2) . Функция принимает вид. Тогда.
3) . Функция принимает вид. Тогда.
4) . Функция принимает вид. Тогда.
Получили:
Задание 9. Найти с помощью полного дифференциала приближённое значение выражения
Решение. Воспользуемся приближённым равенством .
Отсюда .
Рассмотрим функцию . Найдём полный дифференциал этой функции:
.
Примем . Тогда получим:
. (Вычисление с помощью микрокалькулятора даёт результат 7,916).
Вариант № 1.
Задание 1. Найти и изобразить на плоскости область определения функции двух переменных: .
Задание 2. Найти частные производные первого порядка функций двух переменных:
2.1. ; 2.2.; 2.3..
Задание 3. Найти все частные производные второго порядка функции двух переменных: .
Задание 4. Найти производную функции в точкепо направлению вектора.
Задание 5. Найти градиент функции в точке.
Задание 6. Исследовать функцию на экстремумы.
Задание 7. Найти экстремум функции при условии.
Задание 8. Найти наибольшее и наименьшее значение функции в области.
Задание 9. Найти с помощью полного дифференциала приближённое значение выражения .
Вариант № 2.
Задание 1. Найти и изобразить на плоскости область определения функции двух переменных: .
Задание 2. Найти частные производные первого порядка функций двух переменных:
2.1. ; 2.2.; 2.3..
Задание 3. Найти все частные производные второго порядка функции двух переменных: .
Задание 4. Найти производную функции в точкепо направлению вектора.
Задание 5. Найти градиент функции в точке.
Задание 6. Исследовать функцию на экстремумы.
Задание 7. Найти экстремум функции при условии.
Задание 8. Найти наибольшее и наименьшее значение функции в области.
Задание 9. Найти с помощью полного дифференциала приближённое значение выражения .
Вариант № 3.
Задание 1. Найти и изобразить на плоскости область определения функции двух переменных: .
Задание 2. Найти частные производные первого порядка функций двух переменных:
2.1. ; 2.2.; 2.3..
Задание 3. Найти все частные производные второго порядка функции двух переменных: .
Задание 4. Найти производную функции в точкепо направлению вектора.
Задание 5. Найти градиент функции в точке.
Задание 6. Исследовать функцию на экстремумы.
Задание 7. Найти экстремум функции при условии.
Задание 8. Найти наибольшее и наименьшее значение функции в области.
Задание 9. Найти с помощью полного дифференциала приближённое значение выражения .
Вариант № 4.
Задание 1. Найти и изобразить на плоскости область определения функции двух переменных: .
Задание 2. Найти частные производные первого порядка функций двух переменных:
2.1. ; 2.2.; 2.3..
Задание 3. Найти все частные производные второго порядка функции двух переменных: .
Задание 4. Найти производную функции в точкепо направлению вектора.
Задание 5. Найти градиент функции в точке.
Задание 6. Исследовать функцию на экстремумы.
Задание 7. Найти экстремум функции при условии.
Задание 8. Найти наибольшее и наименьшее значение функции в области.
Задание 9. Найти с помощью полного дифференциала приближённое значение выражения .
Вариант № 5.
Задание 1. Найти и изобразить на плоскости область определения функции двух переменных: .
Задание 2. Найти частные производные первого порядка функций двух переменных:
2.1. ; 2.2.; 2.3..
Задание 3. Найти все частные производные второго порядка функции двух переменных: .
Задание 4. Найти производную функции в точкепо направлению вектора.
Задание 5. Найти градиент функции в точке.
Задание 6. Исследовать функцию на экстремумы.
Задание 7. Найти экстремум функции при условии.
Задание 8. Найти наибольшее и наименьшее значение функции в области.
Задание 9. Найти с помощью полного дифференциала приближённое значение выражения .
Вариант № 6.
Задание 1. Найти и изобразить на плоскости область определения функции двух переменных: .
Задание 2. Найти частные производные первого порядка функций двух переменных:
2.1. ; 2.2.; 2.3..
Задание 3. Найти все частные производные второго порядка функции двух переменных: .
Задание 4. Найти производную функции в точкев направлении, составляющем с осью абсцисс угол.
Задание 5. Найти градиент функции в точке.
Задание 6. Исследовать функцию на экстремумы.
Задание 7. Найти экстремум функции при условии.
Задание 8. Найти наибольшее и наименьшее значение функции в области.
Задание 9. Найти с помощью полного дифференциала приближённое значение выражения .
Вариант № 7.
Задание 1. Найти и изобразить на плоскости область определения функции двух переменных: .
Задание 2. Найти частные производные первого порядка функций двух переменных:
2.1. ; 2.2.; 2.3..
Задание 3. Найти все частные производные второго порядка функции двух переменных: .
Задание 4. Найти производную функции в точкев направлении, составляющем с осью абсцисс угол.
Задание 5. Найти градиент функции в точке.
Задание 6. Исследовать функцию на экстремумы.
Задание 7. Найти экстремум функции при условии.
Задание 8. Найти наибольшее и наименьшее значение функции в области.
Задание 9. Найти с помощью полного дифференциала приближённое значение выражения .
Вариант № 8.
Задание 1. Найти и изобразить на плоскости область определения функции двух переменных: .
Задание 2. Найти частные производные первого порядка функций двух переменных:
2.1. ; 2.2.; 2.3..
Задание 3. Найти все частные производные второго порядка функции двух переменных: .
Задание 4. Найти производную функции в точкев направлении, составляющем с осью абсцисс угол.
Задание 5. Найти градиент функции в точке.
Задание 6. Исследовать функцию на экстремумы.
Задание 7. Найти экстремум функции при условии.
Задание 8. Найти наибольшее и наименьшее значение функции в области.
Задание 9. Найти с помощью полного дифференциала приближённое значение выражения .
Вариант № 9.
Задание 1. Найти и изобразить на плоскости область определения функции двух переменных: .
Задание 2. Найти частные производные первого порядка функций двух переменных:
2.1. ; 2.2.; 2.3..
Задание 3. Найти все частные производные второго порядка функции двух переменных: .
Задание 4. Найти производную функции в точкев направлении, составляющем с осью абсцисс угол.
Задание 5. Найти градиент функции в точке.
Задание 6. Исследовать функцию на экстремумы.
Задание 7. Найти экстремум функции при условии.
Задание 8. Найти наибольшее и наименьшее значение функции в области.
Задание 9. Найти с помощью полного дифференциала приближённое значение выражения .
Вариант № 10.
Задание 1. Найти и изобразить на плоскости область определения функции двух переменных: .
Задание 2. Найти частные производные первого порядка функций двух переменных:
2.1. ; 2.2.; 2.3..
Задание 3. Найти все частные производные второго порядка функции двух переменных: .
Задание 4. Найти производную функции в точкев направлении, составляющем с осью абсцисс угол.
Задание 5. Найти градиент функции в точке.
Задание 6. Исследовать функцию на экстремумы.
Задание 7. Найти экстремум функции при условии.
Задание 8. Найти наибольшее и наименьшее значение функции в области.
Задание 9. Найти с помощью полного дифференциала приближённое значение выражения .
Вариант № 11.
Задание 1. Найти и изобразить на плоскости область определения функции двух переменных: .
Задание 2. Найти частные производные первого порядка функций двух переменных:
2.1. ; 2.2.; 2.3..
Задание 3. Найти все частные производные второго порядка функции двух переменных: .
Задание 4. Найти производную функции в точкев направлении, составляющем с осью абсцисс угол.
Задание 5. Найти градиент функции в точке.
Задание 6. Исследовать функцию на экстремумы.
Задание 7. Найти экстремум функции при условии.
Задание 8. Найти наибольшее и наименьшее значение функции в области.
Задание 9. Найти с помощью полного дифференциала приближённое значение выражения .
Вариант № 12.
Задание 1. Найти и изобразить на плоскости область определения функции двух переменных: .
Задание 2. Найти частные производные первого порядка функций двух переменных:
2.1. ; 2.2.; 2.3..
Задание 3. Найти все частные производные второго порядка функции двух переменных: .
Задание 4. Найти производную функции в точкев направлении, составляющем с осью абсцисс угол.
Задание 5. Найти градиент функции в точке.
Задание 6. Исследовать функцию на экстремумы.
Задание 7. Найти экстремум функции при условии.
Задание 8. Найти наибольшее и наименьшее значение функции в области.
Задание 9. Найти с помощью полного дифференциала приближённое значение выражения .
Вариант № 13.
Задание 1. Найти и изобразить на плоскости область определения функции двух переменных: .
Задание 2. Найти частные производные первого порядка функций двух переменных:
2.1. ; 2.2.; 2.3..
Задание 3. Найти все частные производные второго порядка функции двух переменных: .
Задание 4. Найти производную функции в точкев направлении, составляющем с осью абсцисс угол.
Задание 5. Найти градиент функции в точке.
Задание 6. Исследовать функцию на экстремумы.
Задание 7. Найти экстремум функции при условии.
Задание 8. Найти наибольшее и наименьшее значение функции в области.
Задание 9. Найти с помощью полного дифференциала приближённое значение выражения .
Вариант № 14.
Задание 1. Найти и изобразить на плоскости область определения функции двух переменных: .
Задание 2. Найти частные производные первого порядка функций двух переменных:
2.1. ; 2.2.; 2.3..
Задание 3. Найти все частные производные второго порядка функции двух переменных: .
Задание 4. Найти производную функции в точкев направлении, составляющем с осью абсцисс угол.
Задание 5. Найти градиент функции в точке.
Задание 6. Исследовать функцию на экстремумы.
Задание 7. Найти экстремум функции при условии.
Задание 8. Найти наибольшее и наименьшее значение функции в области.
Задание 9. Найти с помощью полного дифференциала приближённое значение выражения .
Вариант № 15.
Задание 1. Найти и изобразить на плоскости область определения функции двух переменных: .
Задание 2. Найти частные производные первого порядка функций двух переменных:
2.1. ; 2.2.; 2.3..
Задание 3. Найти все частные производные второго порядка функции двух переменных: .
studfiles.net
17.1. Определение функции многих переменных. Область определения функции многих переменных
Если множество рассматривать как множество точек на плоскости и каждой точкепоставить в соответствие определенное числото, тем самым, на множествеопределяется функциякоторую называют функцией двух переменных.
Геометрической интерпретацией функции двух переменных служит поверхность
которую называют графиком этой функции.
Подобным образом можно определить функцию трех переменных.
Для определения функций большого числа переменных потребуется рассматривать пространства размерности
Определение мерного арифметического пространства: множество всех упорядоченных совокупностей по действительных чисел
Элементы этого множества называют точками а числа — их координатами.
Если каждой точке из множестваточек пространствапоставлено в соответствие по некоторому закону числото на множествеопределена функцияпеременных
Рассмотрим примеры функций двух переменных.
Например, функция
Область определения этой функции – множество всех пар чисел т.е. вся плоскостьа множество значений – промежуток
Функция
Областью определения данной функции является множество всех точек, для которых выражение определено, т.е. множество точек, для которых
Множество всех таких точек образует круг с центром в начале координат и радиусом, равным единице. Множество значений функции представляет собой отрезок
Из рассмотренных примеров следует, что областью определения двух переменных может быть вся плоскость или ее часть.
Число называетсяпределом функции в точке если для любогосуществуеттакое, что при всехудовлетворяющих условиям
справедливо неравенство
Если предел функциив точкето
Функция называется непрерывной в точкеесли справедливо равенство
Например, функция
непрерывна в любой точке плоскости, за исключением точки в которой функция терпит бесконечный разрыв.
Функция, непрерывная во всех точках некоторой области называетсянепрерывной в данной области.
Если переменной дать некоторое приращениеаоставить постоянной, то функцияполучит приращениеназываемоечастным приращением функции по переменной
Аналогично, если переменная получает приращениеаостается постоянной, то частное приращение функциипо переменной
17.2. Частные производные и дифференциалы первого и высших порядков
Если существуют пределы
они называются частными производными функции по переменным исоответственно.
Аналогично определяются частные производные функций любого числа переменных.
Так как частная производная по любой переменной является производной по этой переменной, найденной при условии, что остальные переменные – постоянны, то все правила и формулы дифференцирования функции одной переменной применимы для нахождения частных производных функций любого числа переменных.
Рассмотрим примеры.
1)Найти частные производные функции
Частная производная по переменной :
Частная производная по переменной :
2)Найти частные производные функции
Частная производная по переменной :
Частная производная по переменной :
Дифференциал функции найденный при условии, что одна из независимых переменных изменяется, а вторая остается постоянной, называетсячастным дифференциалом, т.е. по определению
где произвольные приращения независимых переменных, называемые их дифференциалами. Это справедливо и для функции трех переменных
Вычислить значения частных производных функции
в точке
Находим частные производные
В полученные выражения подставляем координаты данной точки
Полным приращением функции называется разность
Главная часть полного приращения функции , линейно зависящая от приращений независимых переменныхназываетсяполным дифференциалом функции и обозначается
Если функция имеет непрерывные частные производные, то полный дифференциал существует и равен
где произвольные приращения независимых переменных, называемые их дифференциалами.
Рассмотрим пример.
Найти полный дифференциал функции
Найдем частные производные
Полный дифференциал
Полный дифференциал часто используется для приближенных вычислений значений функции, так как
т.е.
Рассмотрим пример.
Вычислить приближенно
Рассмотрим функцию При имеем
Найдем полный дифференциал функции в любой точке
Вычислим его значение в точке при данных приращениях
Тогда
Функция гденазываетсясложной функцией переменных Для нахождения частных производных сложных функций используются формулы
В случае, когда формула преобразуется к виду
Если же то формула имеет вид
Рассмотрим пример.
Найти частные производные функции
Если уравнение задает некоторую функциювнеявном виде и то
Если уравнение задает функцию двух переменныхв неявном виде и то справедливы формулы
Рассмотрим пример. Найти производную функции заданной неявно уравнением
Согласно формуле
получим
Частными производными второго порядка называют частные производные, взятые от частных производных первого порядка
studfiles.net
No related posts.