Координаты точки и координаты вектора. Как найти координаты вектора
Прямоугольная система координат
Чтобы определить понятие координат точек, нам необходимо ввести систему координат, в которой мы и будем определять ее координаты. Одна и та же точка в разных системах координат может иметь различные координаты. Здесь мы будем рассматривать прямоугольную систему координат в пространстве.
Возьмем в пространстве точку $O$ и введем для нее координаты $(0,0,0)$. Назовем ее началом системы координат. Проведем через нее три взаимно перпендикулярные оси $Ox$, $Oy$ и $Oz$, как на рисунке 1. Эти оси будут называться осями абсцисс, ординат и аппликат, соответственно. Осталось только ввести масштаб на осях (единичный отрезок) – прямоугольная система координат в пространстве готова (рис. 1)
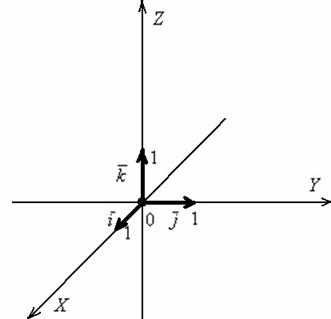
Рисунок 1. Прямоугольная система координат в пространстве. Автор24 — интернет-биржа студенческих работ
Координаты точки
Теперь разберем, как определяют в такой системе координаты любой точки. Возьмем произвольную точку $M$ (рис. 2).
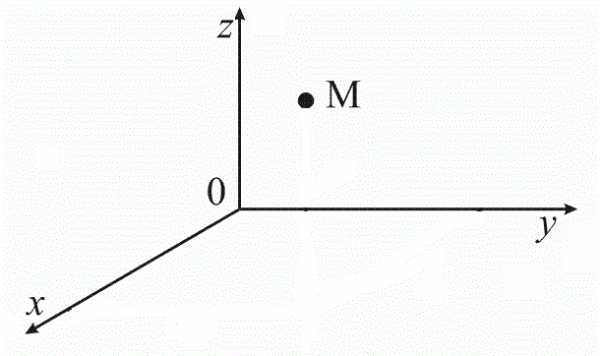
Рисунок 2. Произвольная точка. Автор24 — интернет-биржа студенческих работ
Построим на координатных осях прямоугольный параллелепипед, так, что точки $O$ и $M$ противоположные его вершины (рис. 3).
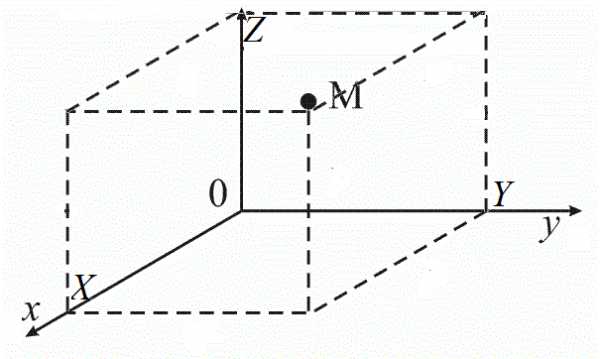
Рисунок 3. Построение прямоугольного параллелепипеда. Автор24 — интернет-биржа студенческих работ
Тогда точка $M$ будет иметь координаты $(X,Y,Z)$, где $X$ – значение на числовой оси $Ox$, $Y$ – значение на числовой оси $Oy$, а $Z$ – значение на числовой оси $Oz$.
Пример 1
Необходимо найти решение следующей задачи: написать координаты вершин параллелепипеда, изображенного на рисунке 4.
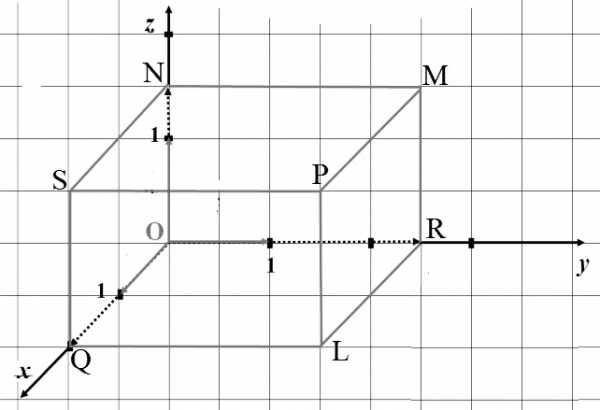
Рисунок 4. Параллелепипед. Автор24 — интернет-биржа студенческих работ
Решение.
Точка $O$ начало координат, следовательно, $O=(0,0,0)$.
Точки $Q$, $N$ и $R$ лежат на осях $Ox$, $Oz$ и $Oy$, соответственно, значит
$Q=(2,0,0)$, $N=(0,0,1.5)$, $R=(0,2.5,0)$
Точки $S$, $L$ и $M$ лежат в плоскостях $Oxz$, $Oxy$ и $Oyz$, соответственно, значит
$S=(2,0,1.5)$, $L=(2,2.5,0)$, $R=(0,2.5,1.5)$
Точка $P$ имеет координаты $P=(2,2.5,1.5)$
Координаты вектора по двум точкам и формула нахождения
Чтобы узнать, как найти вектор по координатам двух точек, необходимо рассмотреть введенную нами ранее систему координат. В ней от точки $O$ по направлению оси $Ox$ отложим единичный вектор $\overline{i}$, по направлению оси $Oy$ — единичный вектор $\overline{j}$, а единичный вектор $\overline{k}$ нужно направлять по оси $Oz$.
Для того чтобы ввести понятие координат вектора, введем следующую теорему (здесь ее доказательство мы рассматривать не будем).
Теорема 1
Произвольный вектор в пространстве может быть разложен по трем любым векторам, которые не лежат в одной плоскости, причем коэффициенты в таком разложении будут единственным образом определены.
Математически это выглядит следующим образом:
$\overline{δ}=m\overline{α}+n\overline{β}+l\overline{γ}$
Так как векторы $\overline{i}$, $\overline{j}$ и $\overline{k}$ построены на координатных осях прямоугольной системы координат, то они, очевидно, не будут принадлежать одной плоскости. Значит любой вектор $\overline{δ}$ в этой системе координат, по теореме 1, может принимать следующий вид
$\overline{δ}=m\overline{i}+n\overline{j}+l\overline{k}$ (1)
где $n,m,l∈R$.
Определение 1
Три вектора $\overline{i}$, $\overline{j}$ и $\overline{k}$ будут называться координатными векторами.
Определение 2
Коэффициенты перед векторами $\overline{i}$, $\overline{j}$ и $\overline{k}$ в разложении (1) будут называться координатами этого вектора в заданной нами системе координат, то есть
$\overline{δ}=(m,n,l)$
Линейные операции над векторами
Теорема 2
Теорема о сумме: Координаты суммы любого числа векторов определяются суммой их соответствующих координат.
Доказательство.
Будем доказывать эту теорему для 2-х векторов. Для 3-х и более векторов доказательство строится аналогичным образом. Пусть $\overline{α}=(α_1,α_2,α_3)$, $\overline{β}=(β_1,β_2 ,β_3)$.
Эти вектора можно записать следующим образом
$\overline{α}=α_1\overline{i}+ α_2\overline{j}+α_3\overline{k}$, $\overline{β}=β_1\overline{i}+ β_2\overline{j}+β_3\overline{k}$
$\overline{α}+\overline{β}=α_1\overline{i}+α_2\overline{j}+α_3\overline{k}+β_1\overline{i}+ β_2\overline{j}+β_3\overline{k}=(α_1+β_1 )\overline{i}+(α_2+β_2 )\overline{j}+(α_3+β_3)\overline{k}$
Следовательно
$\overline{α}+\overline{β}=(α_1+β_1,α_2+β_2,α_3+β_3)$
Теорема доказана.
Замечание 1
Замечание: Аналогично, находится решение разности нескольких векторов.
Теорема 3
Теорема о произведении на число: Координаты произведения произвольного вектора на действительное число определяется произведением координат на это число.
Доказательство.
Возьмем $\overline{α}=(α_1,α_2,α_3)$, тогда $\overline{α}=α_1\overline{i}+α_2\overline{j}+α_3\overline{k}$, а
$l\overline{α}=l(α_1\overline{i}+ α_2\overline{j}+α_3\overline{k})=lα_1\overline{i}+ lα_2\overline{j}+lα_3\overline{k}$
Значит
$k\overline{α}=(lα_1,lα_2,lα_3)$
Теорема доказана.
Пример 2
Пусть $\overline{α}=(3,0,4)$, $\overline{β}=(2,-1,1)$. Найти $\overline{α}+\overline{β}$, $\overline{α}-\overline{β}$ и $3\overline{α}$.
Решение.
$\overline{α}+\overline{β}=(3+2,0+(-1),4+1)=(5,-1,5)$
$\overline{α}-\overline{β}=(3-2,0-(-1),4-1)=(1,1,3)$
$3\overline{α}=(3\cdot 3,3\cdot 0,3\cdot 4)=(9,0,12)$
spravochnick.ru
Координаты вектора
Предварительные сведения
Здесь мы ограничимся двумерным случаем. Введение понятия для трехмерного случая проводится аналогично. Для того, чтобы ввести понятие координат вектора сначала введем и докажем следующие лемму и теорему.
Лемма 1: Если векторы $\overrightarrow{a}$ и $\overrightarrow{b}$ коллинеарны, и вектор $\overrightarrow{a}$ не является нулевым, то существует действительное число $k$, такое что выполняется равенство$\overrightarrow{b}=k\overrightarrow{a}$
Доказательство.
Возможны два случая:
$\overrightarrow{a}\uparrow \uparrow \overrightarrow{b}$
Обозначим число $k$ следующим образом: $k=\frac{|\overrightarrow{b}|}{|\overrightarrow{a}|}$. Так как векторы $\overrightarrow{a}$ и $\overrightarrow{b}$ сонаправлены, а $k\ge 0$, то векторы $k\overrightarrow{a}$ и $\overrightarrow{b}$ сонаправлены. Далее, имеем, что
\[\left|k\overrightarrow{a}\right|=\left|k\right|\left|\overrightarrow{a}\right|=\frac{|\overrightarrow{b}|}{|\overrightarrow{a}|}\left|\overrightarrow{a}\right|=|\overrightarrow{b}|\]Из этого всего следует, что $\overrightarrow{b}=k\overrightarrow{a}$.
$\overrightarrow{a}\uparrow \downarrow \overrightarrow{b}$
Обозначим число $k$ следующим образом: $k=-\frac{|\overrightarrow{b}|}{|\overrightarrow{a}|}$. Так как векторы $\overrightarrow{a}$ и $\overrightarrow{b}$ противоположно направленные, а $k \[\left|k\overrightarrow{a}\right|=\left|k\right|\left|\overrightarrow{a}\right|=\frac{|\overrightarrow{b}|}{|\overrightarrow{a}|}\left|\overrightarrow{a}\right|=|\overrightarrow{b}|\]
Из этого всего следует, что $\overrightarrow{b}=k\overrightarrow{a}$.
Лемма доказана.
Теорема 1
Любой вектор можно разложить по двум неколлинеарным векторам, причем коэффициенты разложения определяются единственным образом:
\[\overrightarrow{c}=m\overrightarrow{a}+n\overrightarrow{b}\]Доказательство.
Существование: Докажем, что такое разложение имеет место. Здесь возможны два случая:
Вектор $\overrightarrow{c}$ коллинеарен (к примеру) вектору $\overrightarrow{b}$.
По лемме 1, будем иметь
\[\overrightarrow{c}=n\overrightarrow{b}\]Значит, если число $m=0$, то получим
\[\overrightarrow{c}=m\overrightarrow{a}+n\overrightarrow{b}\]Вектор $\overrightarrow{c}$ не коллинеарен векторам $\overrightarrow{a}$ и $\overrightarrow{b}$.
Возьмем произвольную точку $O$ и отложим от нее векторы $\overrightarrow{OB}=\overrightarrow{b},\ \overrightarrow{OA}=\overrightarrow{a}$ и $\overrightarrow{OC}=\overrightarrow{c}$. Пусть Проведем прямую $CD||OB$ (рис. 1)

Рисунок 1. Иллюстрация теоремы 1
По правилу треугольника для сложения векторов, получим
\[\overrightarrow{c}=\overrightarrow{OD}+\overrightarrow{DC}\]По построению, получаем что векторы $\overrightarrow{OD}||\overrightarrow{a}$ и $\overrightarrow{DC}||\overrightarrow{b}$, следовательно, по лемме 1, имеем
\[\overrightarrow{OD}=m\overrightarrow{a},\ \overrightarrow{DC}=n\overrightarrow{b}\]Значит
\[\overrightarrow{c}=m\overrightarrow{a}+n\overrightarrow{b}\]
Единственность: Предположим противное, что помимо разложения$\overrightarrow{c}=m\overrightarrow{a}+n\overrightarrow{b}$ существует разложение $\overrightarrow{c}=m’\overrightarrow{a}+n’\overrightarrow{b}$. Вычтем эти два равенства из друг друга:
Получаем систему:
Рисунок 2.
Следовательно, разложение единственно.
Теорема доказана.
Координаты вектора
Рассмотрим далее систему координат. От начала координат $O$ в направлении оси $Ox$ отложим вектор $\overrightarrow{i}$, а в направлении оси $Oy$ отложим вектор $\overrightarrow{j}$, длины которых равны единице.
Определение 1
Векторы $\overrightarrow{i}$ и $\overrightarrow{j}$ называются координатными векторами.
Так как векторы $\overrightarrow{i}$ и $\overrightarrow{j}$ не коллинеарны то, по теореме 1, любой вектор можно разложить в виде $\overrightarrow{c}=m\overrightarrow{i}+n\overrightarrow{j}$.
Определение 2
Коэффициенты разложения вектора $\overrightarrow{c}=m\overrightarrow{i}+n\overrightarrow{j}$ называются координатами данного вектора в данной системе координат, то есть
\[\overrightarrow{c}=\{m,\ n\}\]Линейные операции над векторами
Теорема 2
Теорема о сумме векторов: Координаты суммы векторов равны сумме соответствующих координат этих векторов.
Доказательство.
Докажем теорему для двух векторов. Теорема для большего количества векторов доказывается аналогично. Пусть $\overrightarrow{a}=\left\{x_1,\ y_1\right\}$, $\overrightarrow{b}=\{x_2,\ y_2\}$, тогда
Следовательно
Теорема доказана.
Теорема 3
Теорема о разности векторов: Координаты разности векторов равны разности соответствующих координат этих векторов.
Доказательство.
Докажем теорему для двух векторов. Теорема для большего количества векторов доказывается аналогично. Пусть $\overrightarrow{a}=\left\{x_1,\ y_1\right\}$, $\overrightarrow{b}=\{x_2,\ y_2\}$, тогда
Следовательно
Теорема доказана.
Теорема 4
Теорема о произведении вектора на число: Координаты произведения вектора на число равны произведению соответствующих координат это число.
Пусть $\overrightarrow{a}=\left\{x,\ y\right\}$, тогда $\overrightarrow{a}=x\overrightarrow{i}+\ y\overrightarrow{j}.$
Следовательно
Теорема доказана.
Пример задачи на нахождение координат вектора
Пример 1
Пусть $\overrightarrow{a}=\left\{3,\ 4\right\}$, $\overrightarrow{b}=\{2,\ -1\}$. Найти $\overrightarrow{a}+\overrightarrow{b}$, $\overrightarrow{a}-\overrightarrow{b}$ и $3\overrightarrow{a}$.
Решение.
\[\overrightarrow{a}+\overrightarrow{b}=\left\{3+2,\ 4-1\right\}=\{5,\ 3\}\] \[\overrightarrow{a}-\overrightarrow{b}=\left\{3-2,\ 4+1\right\}=\{1,\ 5\}\] \[3\overrightarrow{a}=\left\{3\cdot 3,3\cdot 4\right\}=\{9,12\}\]spravochnick.ru
Найти координаты векторов. — МегаЛекции
Понятие вектора. Свободный вектор.
Сначала повторим школьное определение вектора. Вектором называется направленный отрезок, для которого указано его начало и конец:
В данном случае началом отрезка является точка А, концом отрезка – точка В. Сам вектор обозначен через . Направление имеет существенное значение, если переставить стрелку в другой конец отрезка, то получится вектор , и это уже совершенно другой вектор.
Отдельные точки плоскости, пространства удобно считать так называемым нулевым вектором . У такого вектора конец и начало совпадают.
!!! Примечание:Здесь и далее можете считать, что векторы лежат в одной плоскости или можете считать, что они расположены в пространстве – суть излагаемого материала справедлива и для плоскости и для пространства.
1) Векторы можно записать двумя большими латинскими буквами: , , ,… и так далее. При этом первая буква обязательно обозначает точку-начало вектора, а вторая буква – точку-конец вектора.
2) Векторы также записывают маленькими латинскими буквами: , , ,… Длиной или модулем ненулевого вектора называется длина отрезка АВ. Длина нулевого вектора равна нулю. Длина вектора обозначается знаком модуля:
Вектор можно отложить от любой точки:
И так, свободный вектор – это множество одинаковых направленных отрезков; подразумевает конкретный направленный отрезок, взятый из данного множества, который привязан к определённой точке плоскости или пространства.
Действия с векторами. Коллинеарность векторов.
Правило сложения векторов по правилу треугольников.
Рассмотрим два произвольных ненулевых вектора и :
Требуется найти сумму данных векторов. В силу того, что все векторы считаются свободными, отложим вектор от конца вектора :
Кстати, если вектор отложить от начала вектора , то получится эквивалентное правило параллелограмма сложения векторов.
Умножение вектора на число.
Два вектора называются коллинеарными, если они лежат на одной прямой или на параллельных прямых.
Если стрелки данных векторов направлены в одинаковом направлении, то такие векторы называются сонаправленнымии и обозначаются .
Если стрелки смотрят в разные стороны, то векторы будут противоположно направлены и обозначаются
Произведением ненулевого вектора на число является такой вектор , длина которого равна , причём векторы и сонаправлены при и противоположно направлены при .
Правило умножения вектора на число легче понять с помощью рисунка:
Равенство векторов.
Два вектора равны, если они сонаправлены и имеют одинаковую длину.
Координаты вектора на плоскости и в пространстве.
Первым пунктом рассмотрим векторы на плоскости. Изобразим декартову прямоугольную систему координат и от начала координат отложим единичные векторы и :
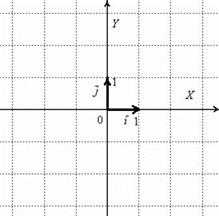
Единичные векторы и ортогональны (перпендикулярны). Обозначение: ортогональность векторов записывают значком перпендикулярности .
Рассматриваемые векторы называют координатными векторами или ортами. Данные векторы образуют базис на плоскости.
Разложение вектора по базису :
Координаты вектора:
Найти координаты векторов.
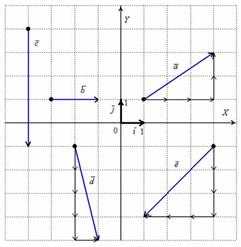
1. , 2. , 3. , 4. , 5. ,
Векторы в пространстве.
Рассмотрим векторы в трехмерном пространстве, здесь практически всё так же! Только добавится ещё одна координата.
Единичные векторы , и ортогональны (перпендикулярны). Обозначение: ортогональность векторов записывают значком перпендикулярности , ,
Рассматриваемые векторы называют координатными векторами или ортами. Данные векторы образуют базис в пространстве.
Базисные векторы записываются следующим образом: , ,
Разложение вектора по базису : радиус-вектор ,
Координаты вектора: ,
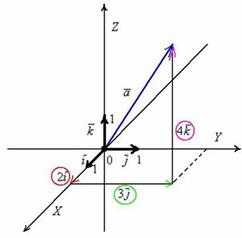
Длина вектора (модуль): ,
расстояние между двумя точками:
Действия над векторами.
Даны два вектора: и
1. Сумма векторов:
2. Разность векторов:
3. Умножение вектора на число
4. Скалярное произведение векторов:
5. Условие коллинеарности векторов: соответствующие координаты пропорциональны
6. Угол между векторами и , точнее его косинус:
7. Условие перпендикулярности векторов:скалярное произведение векторов равно нулю.
8. Векторное произведение векторов:
9. где S — площадь параллелограмма, построенного на векторах и :
10. Смешанное произведение векторов , и
11. Условие компланарности трех векторов (принадлежат плоскости или параллельны ей), если смешанное произведение равно нулю.
.Смешанное произведение трех векторов равно объему параллелепипеда, построенного на этих векторах, взятому со знаком плюс, если эти векторы образуют правую тройку, и со знаком минус, если они образуют левую тройку, т.е.
Если в разложении отсутствует один (или два) координатных вектора, то вместо них ставятся нули. Примеры:
вектор – запишем ;
вектор – запишем ;
вектор – запишем .
Простейшие задачи аналитической геометрии.
Действия с векторами в координатах.
Пример 1.Даны две точки плоскости и . Найти координаты вектора
Решение: по соответствующей формуле:
Ответ:
Пример 2. Это примеры для самостоятельного решения.
а) Даны точки и . Найти векторы и .
б) Даны точки и . Найти векторы и .
в) Даны точки и . Найти векторы и .
г) Даны точки . Найти векторы .
Пример 3. Даны точки и . Найти длину отрезка АВ.
Решение: по соответствующей формуле:
Ответ:
Задание для самостоятельного решения с отрезком в пространстве:
Пример 4
Даны точки и . Найти длину отрезка .
Пример 5.
а) Даны точки и . Найти длину вектора .
б) Даны векторы , , и . Найти их длины.
Пример 6.
Даны векторы и . Найти и
Решение:Для действий с векторами справедлив обычный алгебраический приоритет: сначала умножаем, потом складываем:
Ответ:
Пример 7. Найти косинус угла между векторами a = (4; 3; 0) и b = (0; 12; 5).
Решение. Поскольку координаты векторов даны, подставляем их в формулу Ответ: 36/65.
Пример 8.
Вычислить площадь треугольника с вершинами А(1;-1;2), В (5;-6;2), С(1;3;-1).
Решение.
,
тогда площадь треугольника АВС будет вычисляться следующим образом:
(кв. ед.)
Ответ: 12,5.
Пример 9. Вычислить смешанное произведение векторов Ответ: 95.
Рекомендуемые страницы:
Воспользуйтесь поиском по сайту:
megalektsii.ru
Определение координат вектора заданного координатами его начальной и конечной точки.
Навигация по странице:
Основное соотношение.Чтобы найти координаты вектора AB, зная координаты его начальной точек А и конечной точки В, необходимо из координат конечной точки вычесть соответствующие координаты начальной точки.
Формулы определения координат вектора заданного координатами его начальной и конечной точки
Формула определения координат вектора для плоских задач
В случае плоской задачи вектор AB заданный координатами точек A(Ax ; Ay) и B(Bx ; By) можно найти воспользовавшись следующей формулой
AB = {Bx — Ax ; By — Ay}
Формула определения координат вектора для пространственных задач
В случае пространственной задачи вектор AB заданный координатами точек A(Ax ; Ay ; Az) и B(Bx ; By ; Bz) можно найти воспользовавшись следующей формулой
AB = {Bx — Ax ; By — Ay ; Bz — Az}
Формула определения координат вектора для n -мерного пространства
В случае n-мерного пространства вектор AB заданный координатами точек A(A1 ; A2 ; … ; An) и B(B1 ; B2 ; … ; Bn) можно найти воспользовавшись следующей формулой
AB = {B1 — A1 ; B2 — A2 ; … ; Bn — An}
Примеры задач связанных с определением координат вектора по двум точкам
Примеры для плоских задач
Пример 1. Найти координаты вектора AB, если A(1; 4), B(3; 1).Решение: AB = {3 — 1; 1 — 4} = {2; -3}.
Пример 2. Найти координаты точки B вектора AB = {5; 1}, если координаты точки A(3; -4).Решение:
ABx = Bx — Ax => Bx = ABx + Ax => Bx = 5 + 3 = 8ABy = By — Ay => By = ABy + Ay => By = 1 + (-4) = -3
Ответ: B(8; -3).
Пример 3. Найти координаты точки A вектора AB = {5; 1}, если координаты точки B(3; -4).Решение:
ABx = Bx — Ax => Ax = Bx — ABx => Ax = 3 — 5 = -2ABy = By — Ay => Ay = By — ABy => Ay = -4 — 1 = -5
Ответ: A(-2; -5).
Примеры для пространственных задач
Пример 4. Найти координаты вектора AB, если A(1; 4; 5), B(3; 1; 1).Решение: AB = {3 — 1; 1 — 4; 1 — 5} = {2; -3; -4}.
Пример 5. Найти координаты точки B вектора AB = {5; 1; 2}, если координаты точки A(3; -4; 3).Решение:
ABx = Bx — Ax => Bx = ABx + Ax => Bx = 5 + 3 = 8ABy = By — Ay => By = ABy + Ay => By = 1 + (-4) = -3
ABz = Bz — Az => Bz = ABz + Az => Bz = 2 + 3 = 5
Ответ: B(8; -3; 5).
Пример 6. Найти координаты точки A вектора AB = {5; 1; 4}, если координаты точки B(3; -4; 1).Решение:
ABx = Bx — Ax => Ax = Bx — ABx => Ax = 3 — 5 = -2ABy = By — Ay => Ay = By — ABy => Ay = -4 — 1 = -5
ABz = Bz — Az => Az = Bz — ABz => Az = 1 — 4 = -3
Ответ: A(-2; -5; -3).
Примеры для n -мерного пространства
Пример 7. Найти координаты вектора AB, если A(1; 4; 5; 5; -3), B(3; 0; 1; -2; 5).Решение: AB = {3 — 1; 0 — 4; 1 — 5; -2 — 5; 5 — (-3)} = {2; -4; -4; -7; 8}.
Пример 8. Найти координаты точки B вектора AB = {5; 1; 2; 1}, если координаты точки A(3; -4; 3; 2).Решение:
AB1 = B1 — A1 => B1 = AB1 + A1 => B1 = 5 + 3 = 8AB2 = B2 — A2 => B2 = AB2 + A2 => B2 = 1 + (-4) = -3
AB3 = B3 — A3 => B3 = AB3 + A3 => B3 = 2 + 3 = 5
AB4 = B4 — A4 => B4 = AB4 + A4 => B4 = 1 + 2 = 3
Ответ: B(8; -3; 5; 3).
Пример 9. Найти координаты точки A вектора AB = {5; 1; 4; 5}, если координаты точки B(3; -4; 1; 8).Решение:
AB1 = B1 — A1 => A1 = B1 — AB1 => A1 = 3 — 5 = -2AB2 = B2 — A2 => A2 = B2 — AB2 => A2 = -4 — 1 = -5
AB3 = B3 — A3 => A3 = B3 — AB3 => A3 = 1 — 4 = -3
AB4 = B4 — A4 => A4 = B4 — AB4 => A4 = 8 — 5 = 3
Ответ: A(-2; -5; -3; 3).
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
0oq.ru
Как найти вектор по двум точкам?
Если даны две точки плоскости и , то вектор имеет следующие координаты:
Если даны две точки пространства и , то вектор имеет следующие координаты:
То есть, из координат конца вектора нужно вычесть соответствующие координаты начала вектора.
Задание: Для тех же точек запишите формулы нахождения координат вектора . Формулы в конце урока.
Пример 1
Даны две точки плоскости и . Найти координаты вектора
Решение: по соответствующей формуле:
Как вариант, можно было использовать следующую запись:
Эстеты решат и так:
Лично я привык к первой версии записи.
Ответ:
По условию не требовалось строить чертежа (что характерно для задач аналитической геометрии), но в целях пояснения некоторых моментов чайникам, не поленюсь:
Обязательно нужно понимать различие между координатами точек и координатами векторов:
Координаты точек – это обычные координаты в прямоугольной системе координат. Откладывать точки на координатной плоскости, думаю, все умеют ещё с 5-6 класса. Каждая точка обладает строгим местом на плоскости, и перемещать их куда-либо нельзя.
Координаты же вектора – это его разложение по базису , в данном случае . Любой вектор является свободным, поэтому при необходимости мы легко можем отложить его от какой-нибудь другой точки плоскости. Интересно, что для векторов можно вообще не строить оси, прямоугольную систему координат, нужен лишь базис, в данном случае ортонормированный базис плоскости .
Записи координат точек и координат векторов вроде бы схожи: , асмысл координат абсолютно разный, и вам следует хорошо понимать эту разницу. Данное отличие, разумеется, справедливо и для пространства.
Дамы и господа, набиваем руку:
Пример 2
а) Даны точки и . Найти векторы и .
б) Даны точки и . Найти векторы и .
в) Даны точки и . Найти векторы и .
г) Даны точки . Найти векторы .
Пожалуй, достаточно. Это примеры для самостоятельного решения, постарайтесь ими не пренебрегать, окупится ;-). Чертежи делать не нужно. Решения и ответы в конце урока.
Что важно при решении задач аналитической геометрии? Важно быть ПРЕДЕЛЬНО ВНИМАТЕЛЬНЫМ, чтобы не допустить мастерскую ошибку «два плюс два равно нулю». Сразу извиняюсь, если где ошибся =)
Как найти длину отрезка?
Длина, как уже отмечалось, обозначается знаком модуля.
Если даны две точки плоскости и , то длину отрезка можно вычислить по формуле
Если даны две точки пространства и , то длину отрезка можно вычислить по формуле
Примечание:Формулы останутся корректными, если переставить местами соответствующие координаты: и , но более стандартен первый вариант
Пример 3
Даны точки и . Найти длину отрезка .
Решение: по соответствующей формуле:
Ответ:
Для наглядности выполню чертёж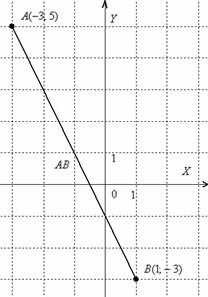
Отрезок – это не вектор, и перемещать его куда-либо, конечно, нельзя. Кроме того, если вы выполните чертеж в масштабе: 1 ед. = 1 см (две тетрадные клетки), то полученный ответ можно проверить обычной линейкой, непосредственно измерив длину отрезка.
Да, решение короткое, но в нём есть ещё пара важных моментов, которые хотелось бы пояснить:
Во-первых, в ответе ставим размерность: «единицы». В условии не сказано, ЧТО это, миллиметры, сантиметры, метры или километры. Поэтому математически грамотным решением будет общая формулировка: «единицы» – сокращенно «ед.».
Во-вторых, повторим школьный материал, который полезен не только для рассмотренной задачи:
Читаем!!!
Обратите внимание на важный технический приём – вынесение множителя из-под корня. В результате вычислений у нас получился результат и хороший математический стиль предполагает вынесение множителя из-под корня (если это возможно). Подробнее процесс выглядит так: . Конечно, оставить ответ в виде не будет ошибкой – но недочетом-то уж точно и весомым аргументом для придирки со стороны преподавателя.
Вот другие распространенные случаи:
Нередко под корнем получается достаточно большое число, например . Как быть в таких случаях? На калькуляторе проверяем, делится ли число на 4: . Да, разделилось нацело, таким образом: . А может быть, число ещё раз удастся разделить на 4? . Таким образом: . У числа последняя цифра нечетная, поэтому разделить в третий раз на 4 явно не удастся. Пробуем поделить на девять: . В результате:
Готово.
Вывод: если под корнем получается неизвлекаемое нацело число, то пытаемся вынести множитель из-под корня – на калькуляторе проверяем, делится ли число на: 4, 9, 16, 25, 36, 49 и т.д.
В ходе решения различных задач корни встречаются часто, всегда пытайтесь извлекать множители из-под корня во избежание более низкой оценки да ненужных заморочек с доработкой ваших решений по замечанию преподавателя.
Давайте заодно повторим возведение корней в квадрат и другие степени:
Правила действий со степенями в общем виде можно найти в школьном учебнике по алгебре, но, думаю, из приведённых примеров всё или почти всё уже ясно.
Задание для самостоятельного решения с отрезком в пространстве:
Пример 4
Даны точки и . Найти длину отрезка .
Решение и ответ в конце урока.
Как найти длину вектора?
Если дан вектор плоскости , то его длина вычисляется по формуле .
Если дан вектор пространства , то его длина вычисляется по формуле .
Данные формулы (как и формулы длины отрезка) легко выводятся с помощью небезызвестной теоремы Пифагора.
Пример 5
Даны точки и . Найти длину вектора .
Я взял те же точки, что и в Примере 3.
Решение: Сначала найдём вектор :
По формуле вычислим длину вектора:
Ответ:
Не забываем указывать размерность – «единицы»! Всегда ли, кстати, нужно рассчитывать приближенное значение (в данном примере 8,94), если этого не требуется в условии? С моей точки зрения, лишним не будет, отсутствие приближенного значения тянет на придирку. Округление целесообразно проводить до 2-3-х знаков после запятой.
Выполним чертеж к задаче: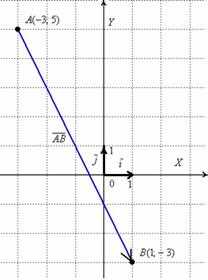
В чём принципиальное отличие от Примера 3? Отличие состоит в том, что здесь речь идёт о векторе, а не об отрезке. Вектор можно переместить в любую точку плоскости.
А в чём сходство Примера 3 и Примера 5? Геометрически очевидно, что длина отрезка равна длине вектора . Так же очевидно, что длина вектора будет такой же. По итогу:
Задачу 3 можно было решить и вторым способом, повторю условие: Даны точки и . Найти длину отрезка .
Вместо применения формулы , поступаем так:
1) Находим вектор .
2) А теперь ссылаемся на то, что длина отрезка равна длине вектора :
Этот способ широко практикуется в ходе решений задач аналитической геометрии.
Вышесказанное справедливо и для пространственного случая
Для тренировки:
Пример 6
а) Даны точки и . Найти длину вектора .
б) Даны векторы , , и . Найти их длины.
Решения и ответы в конце урока.
infopedia.su
Метод координат. Координаты вектора
Вопросы занятия:
· вспомнить, как определяют координаты векторов;
· рассмотреть три вспомогательные задачи: определение координат середины отрезка, вычисление длины вектора по его координатам и определение расстояния между точками.
Материал урока
Итак, построим прямоугольную систему координат. От точки О начала координат отложим единичные векторы и . Т.е. векторы длины, которых равны единице.
Причём, направление вектора совпадает с направлением оси , а направление вектора совпадает с направлением оси .
Векторы называются координатными векторами.
Понятно, что любой вектор можно разложить по векторам . Причём коэффициенты разложения, числа , определяются единственным образом.
Коэффициенты разложения вектора по координатным векторам называют координатами вектора в данной системе координат.
Напомним, что координаты вектора записывают в фигурных скобках через точку с запятой. При этом первым указывают коэффициент разложения , а вторым — .
Задание.
Записать координаты векторов, указанных на экране.
Решение.
Обратите внимание, что такие координаты данные векторы будут иметь только в конкретной системе координат и при конкретных координатных векторах .
Коэффициенты разложения нулевого вектора по векторам и равны нулю.
Тогда получаем, что нулевой вектор имеет координаты , причём в любой системе координат и при любых координатных векторах.
Если векторы равны, то их разложения по векторам и также будут равны, а значит, равны будут и коэффициенты разложения.
Таким образом, получаем, что координаты равных векторов соответственно равны.
Вспомним ещё один особенный случай — противоположные векторы. Их разложения противоположны.
Значит, противоположны будут и соответственные координаты.
Задание.
Разложить векторы по координатным векторам и и указать их координаты.
Решение.
Задание.
Построить векторы по их координатам.
Координатами вектора являются числа 8 и –1. Значит, чтобы переместиться из точки О на вектор , сначала нужно переместиться на вектор , а затем на вектор . Соединив точку О с конечной точкой, получим вектор .
Далее изобразим вектор . Для этого из точки О переместимся на вектор . Тем самым получим искомый вектор .
Чтобы из точки О переместиться на вектор , сначала переместимся на вектор , а затем на вектор . Проведём вектор из точки О в конечную точку. Так мы получили вектор .
Теперь давайте вспомним правила, позволяющие по координатам векторов находить координаты их суммы, разности и произведения вектора на число.
Сначала рассмотрим сумму двух векторов и , координаты которых равны:
Пользуясь их координатами, можем записать разложения данных векторов по координатным векторам и .
Сложим полученные равенства. Пользуясь свойствами сложения векторов и произведения вектора на число, получаем, что координаты вектора суммы векторов и равны:
Сформулируем правило.
Каждая координата суммы двух и более векторов равна сумме соответствующих координат этих векторов.
Задание.
Найти координаты векторов суммы, если , , , .
Координаты вектора суммы равны:
Координаты вектора суммы равны:
Перейдём к разности векторов и .
Из разложения вектора вычтем разложение вектора .
Получаем, что координаты вектора разности равны:
Сформулируем правило.
Каждая координата разности двух векторов равна разности соответствующих координат данных векторов.
Задание.
Найти координаты векторов разности, если , , , .
Разность векторов имеет координаты:
Разность векторов имеет координаты:
Далее получим координаты произведения вектора на число .
Получаем, что координаты произведения равны:
Сформулируем правило.
Каждая координата произведения вектора на число равна произведению соответствующей координаты вектора на это число.
Задание.
Найти координаты произведения вектора на число.
Координаты вектора . Они равны:
Координаты вектора равны:
Вектор имеет координаты:
Ну, а вектор имеет координаты:
Рассмотрим прямоугольную систему координат и какую-нибудь точку .
Проведём вектор из точки О к точке М. Такой вектор называют радиус-вектором точки М.
Давайте докажем, что координаты точки М равны соответствующим координатам её радиус-вектора .
Понятно, что вектор по правилу параллелограмма. Теперь необходимо доказать, что вектор , а вектор . Тем самым мы докажем, что вектор .
Если , то длина отрезка . А так как векторы и сонаправлены, то вектор , а длина .
Если же , то длина отрезка . Так как векторы и противоположно направлены, можно записать, что вектор . А .
Ну, и если , то точка М лежит на оси и вектор . Тогда его можно выразить как . А это значит, что справедливо равенство .
Абсолютно аналогично проводят доказательство того, что вектор .
Итак, мы доказали, что вектор . То есть координаты вектора , так же как и у точки М.
Что и требовалось доказать.
Задание.
Назвать координаты вектора.
Решение.
Итак, мы доказали, что координаты точки М равны соответствующим координатам её радиус-вектора.
Радиус-вектором точки называют вектор, начало которого совпадает с точкой начала координат, а конец — с данной точкой.
Пользуясь этим утверждением, выразим координаты вектора через координаты его начала и конца. Пусть точка А имеет координаты , а точка В имеет координаты .
Вектор . А они в свою очередь являются радиус-векторами точек В и А соответственно. А это значит, что координаты вектора , а координаты вектора . Можем найти координаты вектора разности: . Понятно, что эти значения и будут координатами вектора .
Так мы доказали, что каждая координата вектора равна разности соответствующих координат его конца и начала.
Задание.
По координатам точек и найти координаты вектора
.
Решение.
Теперь давайте рассмотрим три вспомогательных задачи, которые используют при решении геометрических задач методом координат.
Первой решим задачу на определение координат середины отрезка.
Пусть точка и точка — некоторые точки координатной плоскости. Точка — середина отрезка . И нам необходимо определить её координаты.
Воспользуемся ранее доказанным утверждением и на основании того, что — середина отрезка , запишем, что вектор .
Векторы и являются радиус-векторами точек А и В соответственно. Значит, координаты вектора , а координаты вектора .
Вектор их суммы будет иметь координаты .
Координаты вектора их полусуммы равны .
Эти значения и будут координатами вектора , который в свою очередь является радиус-вектором точки С. А это значит, что координаты точки равны соответствующим координатам её радиус-вектора.
Таким образом, мы получили, что каждая координата середины отрезка равна полусумме соответствующих координат его концов.
Далее рассмотрим вторую вспомогательную задачу — задачу на вычисление длины вектора по его координатам.
От начала координат отложим вектор . Проведём перпендикуляры и к осям.
Если точка , то и её радиус-вектор . При этом координаты вектора , ведь векторы .
Итак, можно сказать, что длина отрезка , а длина отрезка . Длину отрезка можем выразить из прямоугольного треугольника по теореме Пифагора, как
Но ведь векторы , а значит, . Получаем, что длина вектора равна корню квадратному из суммы квадратов его координат, причём от какой бы точки он не был отложен.
Далее решим последнюю вспомогательную задачу — задачу на определение расстояния между двумя точками.
Пусть точка , а точка . Выразим расстояние между этими точками через их координаты.
Для начала рассмотрим вектор . Его координаты равны разностям соответствующих координат конца М2 и начала М1.
Тогда длина этого вектора равна корню квадратному из суммы квадратов его координат.
Но с другой стороны, длина вектора . Отсюда получаем, что расстояние между двумя точками находят, как корень квадратный из суммы квадратов разностей соответствующих координат данных точек.
Итоги урока
На этом уроке мы поговорили о «методе координат». Вспомнили, как определяют координаты векторов. Рассмотрели три вспомогательные задачи: определение координат середины отрезка, вычисление длины вектора по его координатам и определение расстояния между точками.
videouroki.net
Нахождение вектора заданного декартовыми координатами его начальной и конечной точки
Чтобы найти координаты вектора AB, зная координаты его начальной точек А и конечной точки В, необходимо из координат конечной точки вычесть соответствующие координаты начальной точки.
Так в случае плоской задачи с точками A(
x1, y1
) и B(
x2, y2
) вектор
AB =
{x2 — x1; y2 — y1}
Пример нахождение вектора заданного декартовыми координатами его начальной и конечной точки:
Найти координаты вектора AB если A(1; 4), B(3; 1).
Решение: AB = {3 — 1; 1 — 4} = {2; -3}.
Так в случае пространственной задачи с точками A(
x1, y1, z1
) и B(
x2, y2, z2
) вектор
AB =
{x2 — x1; y2 — y1; z2 — z1}
Пример нахождение вектора заданного декартовыми координатами его начальной и конечной точки:
Найти координаты вектора AB если A(1; 4; 5), B(3; 4; 2).
Решение: AB = {3 — 1; 4 — 4; 2-5} = {2; 0; -3}.
Так как координаты а в декартовой прямоугольной системе координат равны проекциям вектора на координатные оси, то
а1 = |a|cos(альфа), a2 = |a|cos(бета), a3 = |a|cos(гамма). Отсюда:
cos (альфа)=a1||a|, cos(бета) =a2||a|, cos(гамма)= a3/|a|.
При этом |a|=sqrt(a1^2+ a2^2+ a3^2). Значит
cos (альфа)=a1|sqrt(a1^2+ a2^2+ a3^2), cos(бета) =a2|sqrt(a1^2+ a2^2+ a3^2),
cos(гамма)= a3/sqrt(a1^2+ a2^2+ a3^2).
Следует отметить основное свойство направляющих косинусов. Сумма квадратов направляющих косинусов вектора равна единице.
Действительно, cos^2(альфа)+cos^2(бета)+cos^2(гамма)=
= a1^2|(a1^2+ a2^2+ a3^2)+ a2^2|(a1^2+ a2^2+ a3^2)+ a3^2/(a1^2+ a2^2+ a3^2) =
=(a1^2+ a2^2+ a3^2)|(a1^2+ a2^2+ a3^2) = 1.
Первый способ
Пример: дано: вектор а={1, 3, 5). Найти его направляющие косинусы.
Решение. В соответствии с найденным выпишем:
|а|= sqrt(ax^2+ ay^2+ az^2)=sqrt(1+9 +25)=sqrt(35)=5,91.
Таким образом, ответ можно записать в следующей форме:
{cos(альфа), cos(бета), cos(гамма)}={1/sqrt(35), 3/sqrt (35), 5/(35)}={0,16;0,5;0,84}.
Второй способ
При нахождении направляющих косинусов вектора а, можно использовать методику определения косинусов углов с помощью скалярного произведения. В данном случае в виду имеются углы между а и направляющими единичными векторами прямоугольных декартовых координат i, j и k. Их координаты {1, 0, 0}, {0, 1, 0}, {0, 0, 1}, соответственно.
Следует напомнить, что скалярное произведение векторов определяется так.
Если угол между векторами ф, то скалярное произведение двух ветров (по определению) – это число, равное произведению модулей векторов на cosф. (a, b) = |a||b|cos ф. Тогда, если b=i, то (a, i) = |a||i|cos(альфа),
или a1 = |a|cos(альфа). Далее все действия выполняются аналогично способу 1, с учетом координат j и k.
20)
Скалярное произведение векторов
Скалярным произведением двух векторов называется число, равное произведению модулей этих векторов на косинус угла между ними.
Скалярное произведение векторов , обозначается символом (порядок записи сомножителей безразличен, то есть ).
Если угол между векторами , обозначить через , то их скалярное произведение можно выразить формулой
(1)
Скалярное произведение называется скалярным квадратом вектора и обозначается символом . Из формулы (1) следует, что скалярный квадрат вектора равен квадрату его модуля:
.
Если векторы и заданы своими координатами:
, ,
то их скалярное произведение может быть вычислено по формуле
.
Отсюда следует необходимое и достаточное условие перпендикулярности двух векторов
.
Угол между векторами
, ,
Свойства
· теорема косинусов легко выводится с использованием скалярного произведения:
· Угол между векторами:
· Оценка угла между векторами:
в формуле знак определяется только косинусом угла (нормы векторов всегда положительны). Поэтому скалярное произведение > 0, если угол между векторами острый, и < 0, если угол между векторами тупой.
· Проекция вектора на направление, определяемое единичным вектором :
,
· условие ортогональности (перпендикулярности) векторов и :
· Площадь параллелограмма, натянутого на два вектора и , равна
Неравенство Коши — Буняковского
Для любых элементов и линейного пространства со скалярным произведением выполняется неравенство [1]
Скалярное произведение в координатной форме
Воспользовавшись свойством скалярного произведения, получим
Скалярное произведение двух векторов в координатной форме равно сумме произведений одноимённых координат: .
Используя формулу для скалярного квадрата вектора, получим формулу для нахождения модуля вектора
.
Косинус угла между двумя векторами
Из определения скалярного произведения следует
.
В координатной форме эта формула примет вид
.
infopedia.su