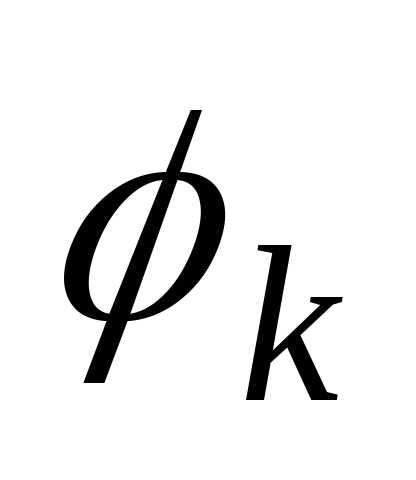Вычисление объема тела, образованного вращением плоской фигуры вокруг оси
Второй параграф будет еще интереснее, чем первый. Задание на вычисление объема тела вращения вокруг оси ординат – тоже достаточно частый гость в контрольных работах. Попутно будет рассмотрена задача о нахождении площади фигуры вторым способом – интегрированием по оси , это позволит вам не только улучшить свои навыки, но и научит находить наиболее выгодный путь решения. В этом есть и практический жизненный смысл! Как с улыбкой вспоминала мой преподаватель по методике преподавания математики, многие выпускники благодарили её словами: «Нам очень помог Ваш предмет, теперь мы эффективные менеджеры и оптимально руководим персоналом». Пользуясь случаем, я тоже выражаю ей свою большую благодарность, тем более, что использую полученные знания по прямому назначению =).
Рекомендую
для прочтения всем, даже полным
чайникам.
Пример 5
Дана плоская фигура, ограниченная линиями ,,.
1) Найти площадь плоской фигуры, ограниченной данными линиями. 2) Найти объем тела, полученного вращением плоской фигуры, ограниченной данными линиями, вокруг оси .
Внимание! Даже если вы хотите ознакомиться только со вторым пунктом, сначалаобязательно прочитайте первый!
Решение: Задача состоит из двух частей. Начнем с площади.
1) Выполним чертёж:
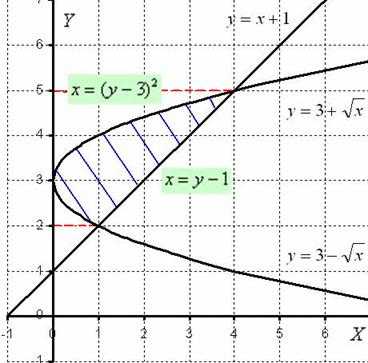
Легко заметить, что функция задает верхнюю ветку параболы, а функция– нижнюю ветку параболы. Перед нами тривиальная парабола, которая «лежит на боку».
Нужная фигура, площадь которой предстоит найти, заштрихована синим цветом.
Как найти площадь фигуры? Её можно найти «обычным» способом, который рассматривался на уроке Определенный интеграл. Как вычислить площадь фигуры. Причем, площадь фигуры находится как сумма площадей: – на отрезке ; – на отрезке.
Поэтому:
Чем в данном случае плох обычный путь решения? Во-первых, получилось два интеграла. Во-вторых, под интегралами корни, а корни в интегралах – не подарок, к тому же можно запутаться в подстановке пределов интегрирования. На самом деле, интегралы, конечно, не убийственные, но на практике всё бывает значительно печальнее, просто я подобрал для задачи функции «получше».
Есть более рациональный путь решения: он состоит в переходе к обратным функциям и интегрированию по оси .
Как перейти к обратным функциям? Грубо говоря, нужно выразить «икс» через «игрек». Сначала разберемся с параболой:
Этого достаточно, но убедимся, что такую же функцию можно вывести из нижней ветки:
Для самопроверки рекомендую устно или на черновике подставить координаты 2-3-х точек параболы в уравнение , они обязательно должны удовлетворять данному уравнению.
С прямой всё проще:
Теперь смотрим на ось : пожалуйста, периодически наклоняйте голову вправо на 90 градусов по ходу объяснений (это не прикол!). Нужная нам фигура лежит на отрезке, который обозначен красным пунктиром. При этом на отрезкепрямаярасположена выше параболы, а значит, площадь фигуры следует найти по уже знакомой вам формуле:. Что поменялось в формуле? Только буква, и не более того.
! Примечание: Пределы интегрирования по оси следует расставлятьстрого снизу вверх!
Находим площадь:
На отрезке , поэтому:
Обратите внимание, как я осуществил интегрирование, это самый рациональный способ, и в следующем пункте задания будет понятно – почему.
Для читателей, сомневающихся в корректности интегрирования, найду производные:
Получена исходная подынтегральная функция, значит интегрирование выполнено правильно.
Ответ:
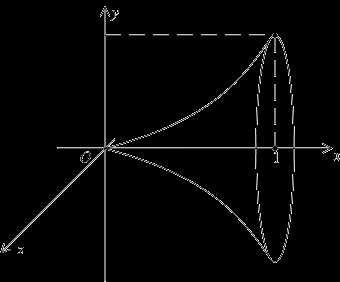
2) Вычислим объем тела, образованного вращением данной фигуры, вокруг оси .
Перерисую чертеж немного в другом оформлении:
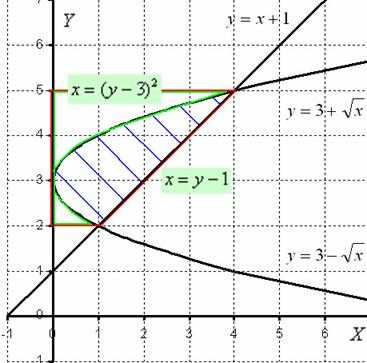
Итак, фигура, заштрихованная синим цветом, вращается вокруг оси . В результате получается «зависшая бабочка», которая вертится вокруг своей оси.
Для нахождения объема тела вращения будем интегрировать по оси . Сначала нужно перейти к обратным функциям. Это уже сделано и подробно расписано в предыдущем пункте.
Теперь снова наклоняем голову вправо и изучаем нашу фигуру. Очевидно, что объем тела вращения, следует найти как разность объемов.
Вращаем фигуру, обведенную красным цветом, вокруг оси , в результате получается усеченный конус. Обозначим этот объем через.
Вращаем фигуру, обведенную зеленым цветом, вокруг оси и обозначаем черезобъем полученного тела вращения.
Объем нашей бабочки равен разности объемов .
Используем формулу для нахождения объема тела вращения:
В чем отличие от формулы предыдущего параграфа? Только в букве.
А вот и преимущество интегрирования, о котором я недавно говорил, гораздо легче найти , чем предварительно возводить подынтегральную функцию в 4-ую степень.
Ответ:
Однако нехилая бабочка.
Заметьте, что если эту же плоскую фигуру вращать вокруг оси , то получится совершенно другое тело вращения, другого, естественно, объема.
Пример 6
Дана плоская фигура, ограниченная линиями ,и осью.
1) Перейти к обратным функциям и найти площадь плоской фигуры, ограниченной данными линиями, интегрированием по переменной . 2) Вычислить объем тела, полученного вращением плоской фигуры, ограниченной данными линиями, вокруг оси.
Это пример для самостоятельного решения. Желающие также могут найти площадь фигуры «обычным» способом, выполнив тем самым проверку пункта 1). А вот если, повторюсь, будете вращать плоскую фигуру вокруг оси , то получится совершенно другое тело вращения с другим объемом, кстати, правильный ответ(тоже для любителей порешать).
Полное же решение двух предложенных пунктов задания в конце урока.
Да, и не забывайте наклонять голову направо, чтобы разобраться в телах вращения и в пределах интегрирования!
Хотел, было уже, закончить статью, но сегодня принесли интересный пример как раз на нахождение объема тела вращения вокруг оси ординат. Свежачок:
Пример 7
Вычислить объем тела, образованного вращением вокруг оси фигуры, ограниченной кривымии.
Решение: Выполним чертеж:
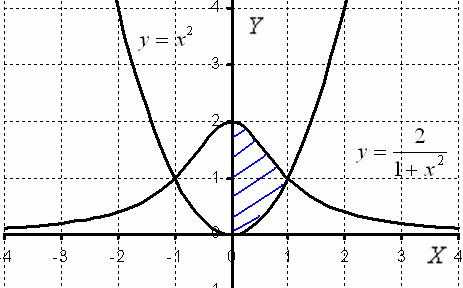
Попутно знакомимся с графиками некоторых других функций. Такой вот интересный график чётной функции ….
Для цели нахождения объема тела вращения достаточно использовать правую половину фигуры, которую я заштриховал синим цветом. Обе функции являются четными, их графики симметричны относительно оси , симметрична и наша фигура. Таким образом, заштрихованная правая часть, вращаясь вокруг оси, непременно совпадёт с левой нештрихованной частью.
Перейдем к обратным функциям, то есть, выразим «иксы» через «игреки»: Обратите внимание, что правой ветке параболысоответствует обратная функция. Левой неиспользуемой ветке параболы соответствует обратная функция. В таких случаях нередко возникают сомнения, какую же функцию выбрать? Сомнения легко, развеиваются, возьмите любую точку правой ветки и подставьте ее координаты в функцию. Координаты подошли, значит, функциязадает именно правую ветку, а не левую.
К слову, та же история и с функций . Чайнику, не всегда бывает сразу понятно, какую обратную функцию выбрать:или. В действительности я и сам всегда страхуюсь, подставляя в найденную обратную функцию пару точек графика.
Теперь наклоняем голову вправо и замечаем следующую вещь:
– на отрезке над осьюрасположен график функции; – на отрезкенад осьюрасположен график функции;
Логично предположить, что объем тела вращения нужно искать уже как сумму объемов тел вращений!
Используем формулу:
В данном случае:
Ответ:
В задаче нахождения площади фигуры суммирование площадей используется часто, а суммирование объемов тел вращения, видимо, редкость, раз такая разновидность чуть было не выпала из моего поля зрения. Все-таки хорошо, что своевременно подвернулся рассмотренный пример – удалось вытащить немало полезного.
Кроме всего перечисленного, иногда линии могут быть заданы параметрически, и такие задачи тоже рассмотрены на сайте!
Успешной раскрутки фигур!
И на посошок: как найти объём тела, если оно не является телом вращения? Используемобщий принцип интегрирования.
Решения и ответы:
Пример
2: Решение:
Выполним чертеж:  Объем
тела вращения: Ответ:
Объем
тела вращения: Ответ:
Пример 4: Решение: Выполним чертеж:
studfiles.net
Нахождение объёма тела по площадям поперечных сечений
П усть
в пространстве задано тело. Пусть
построены его сечения плоскостями,
перпендикулярными осии проходящими через точкиx
усть
в пространстве задано тело. Пусть
построены его сечения плоскостями,
перпендикулярными осии проходящими через точкиx на ней. Площадь фигуры, образующейся в
сечении, зависит от точки х,
определяющей плоскость сечения. Пусть
эта зависимость известна и задана
непрерывной на
на ней. Площадь фигуры, образующейся в
сечении, зависит от точки х,
определяющей плоскость сечения. Пусть
эта зависимость известна и задана
непрерывной на 
 функцией.
Тогда объем части тела, находящейся
между плоскостямих=а и х=в вычисляется по формуле
функцией.
Тогда объем части тела, находящейся
между плоскостямих=а и х=в вычисляется по формуле 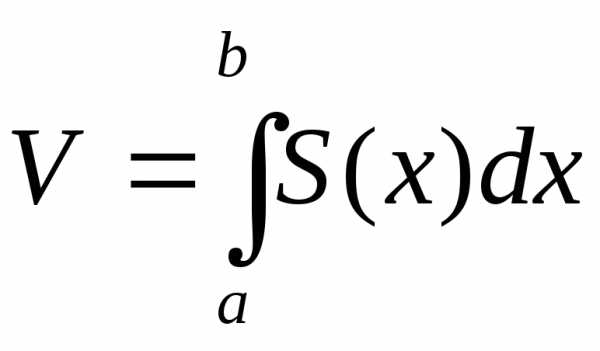
Пример. Найдём объём ограниченного тела, заключённого между поверхностью цилиндра радиуса :, горизонтальной плоскостьюи наклонной плоскостьюz=2y и лежащего выше горизонтальной плоскости .
Очевидно, что
рассматриваемое тело
проектируется
на осьв
отрезок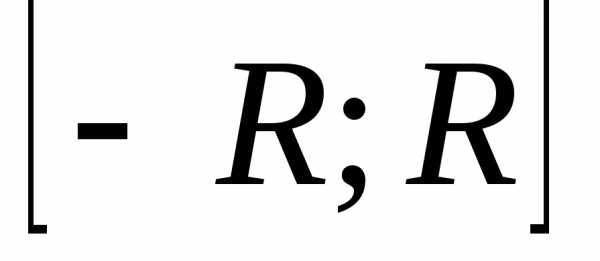 ,
а приx
,
а приx
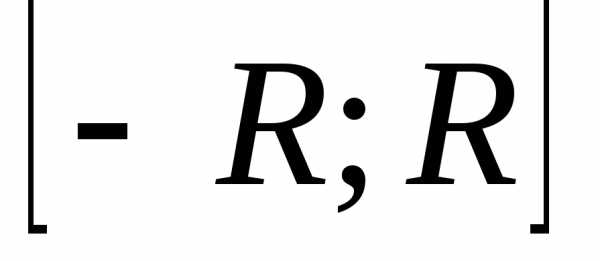 поперечное сечение тела представляет
собою прямоугольный треугольник с
катетамиy
и z=2y,
где y
можно выразить через x
из уравнения цилиндра:
поперечное сечение тела представляет
собою прямоугольный треугольник с
катетамиy
и z=2y,
где y
можно выразить через x
из уравнения цилиндра:
Поэтому площадь S(x) поперечного сечения такова:
Применяя формулу, находим объём тела :
Вычисление объемов тел вращения
Пусть
на отрезке [a, b]
задана непрерывная знакопостоянная
функция y=f(x). Объемы тела вращения, образованного
вращением вокруг оси Ох (или оси Оу)
криволинейной трапеции, ограниченной
кривой y=f(x) (f(x)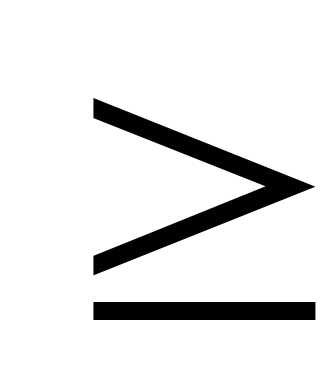 0)
и прямыми у=0,
х=а, х=b,
вычисляются соответственно по формулам:
0)
и прямыми у=0,
х=а, х=b,
вычисляются соответственно по формулам:
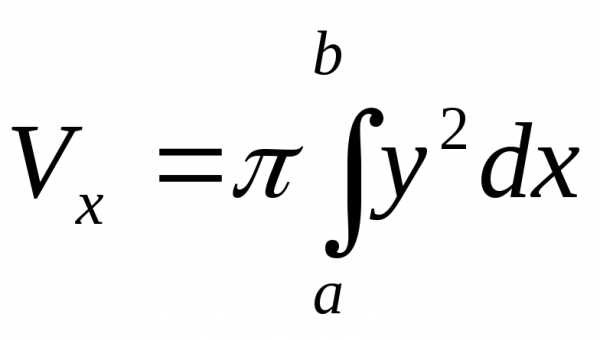 , (19)
, (19)
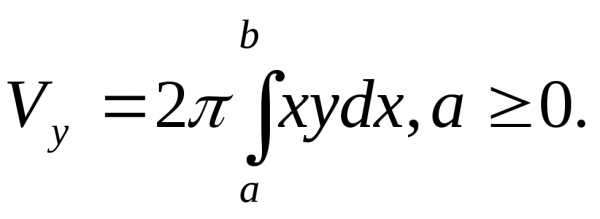 (20)
(20)
Если тело образуется при вращении вокруг оси Оу криволинейной трапеции, ограниченной кривойи прямымиx=0, y=c, y=d, то объем тела вращения равен
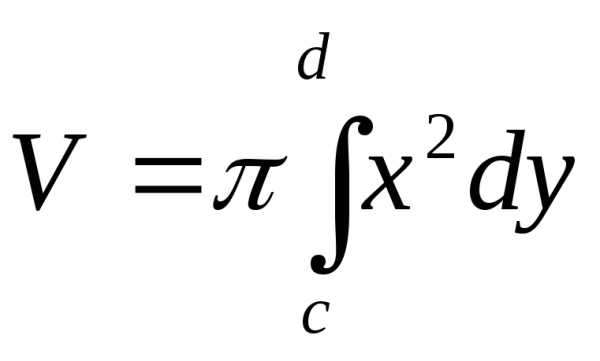 .
(21)
.
(21)
Пример. Вычислить объем тела, полученного вращением фигуры, ограниченной линиями вокруг осиОх.
По формуле (19) искомый объем
(ед.2)
Пример. Пусть в плоскости xOy
рассматривается линия y=cosx
на отрезке 
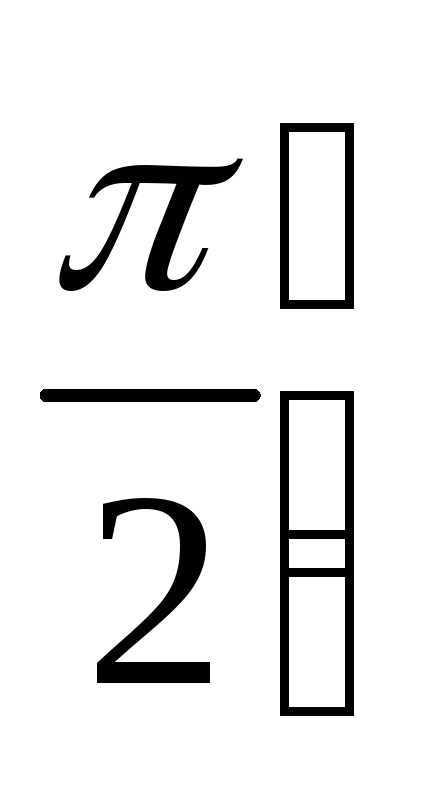 .
.
Э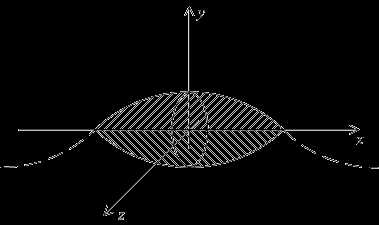 та
линия вращается в пространстве вокруг
оси,
и полученная поверхность вращения
ограничивает некоторое тело вращения
(см. рис.). Найдём объёмэтого
тела вращения.
та
линия вращается в пространстве вокруг
оси,
и полученная поверхность вращения
ограничивает некоторое тело вращения
(см. рис.). Найдём объёмэтого
тела вращения.
Согласно формуле, получаем:
Площадь поверхности вращения
Если дуга кривой,
заданная неотрицательной функцией 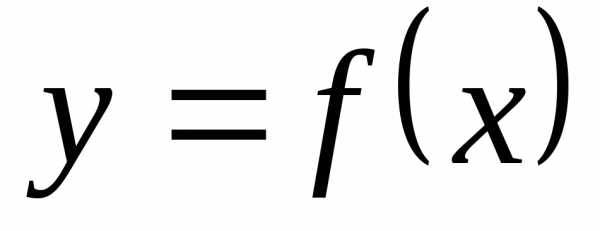 ,,
вращается вокруг осиOx,
то площадь поверхности вращения
вычисляется по формуле
,
гдеa и b — абсциссы начала и конца дуги.
,,
вращается вокруг осиOx,
то площадь поверхности вращения
вычисляется по формуле
,
гдеa и b — абсциссы начала и конца дуги.
Если дуга кривой,
заданная неотрицательной функцией 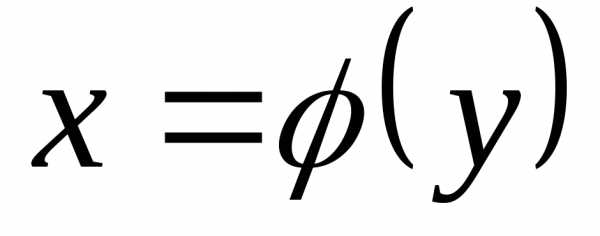 ,
,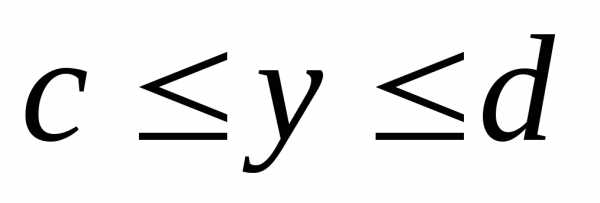 ,
вращается вокруг осиOy,
то площадь поверхности вращения
вычисляется по формуле
,
вращается вокруг осиOy,
то площадь поверхности вращения
вычисляется по формуле
,
где с и d — абсциссы начала и конца дуги.
Если дуга кривой
задана параметрическими
уравнениями 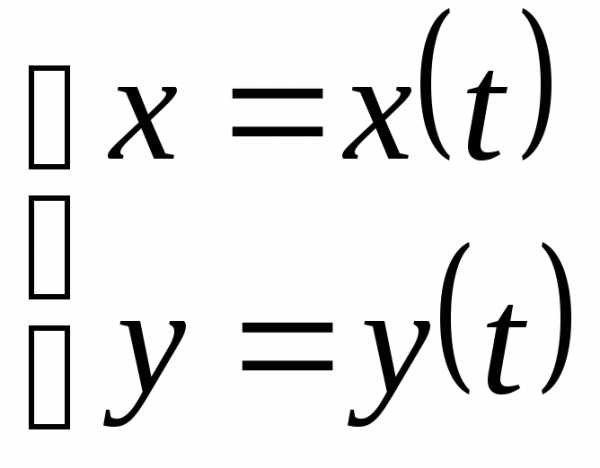 ,
,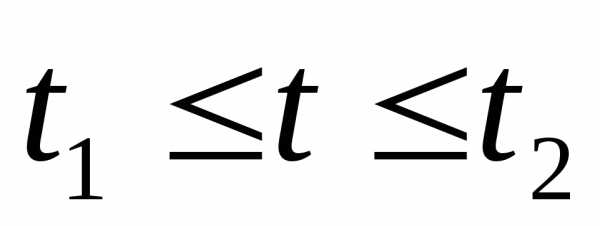 ,
причем
,
причем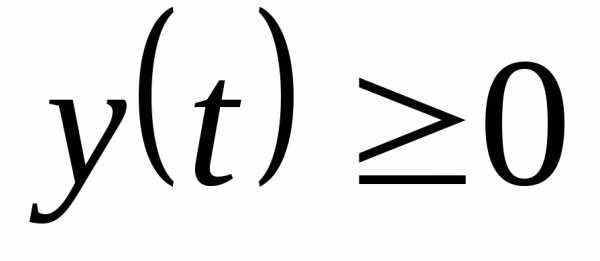 ,
то
,
то
Если дуга задана в полярных координатах , то
.
Пример. Вычислим площадь поверхности, образованной
вращением в пространстве вокруг оси
части линииy=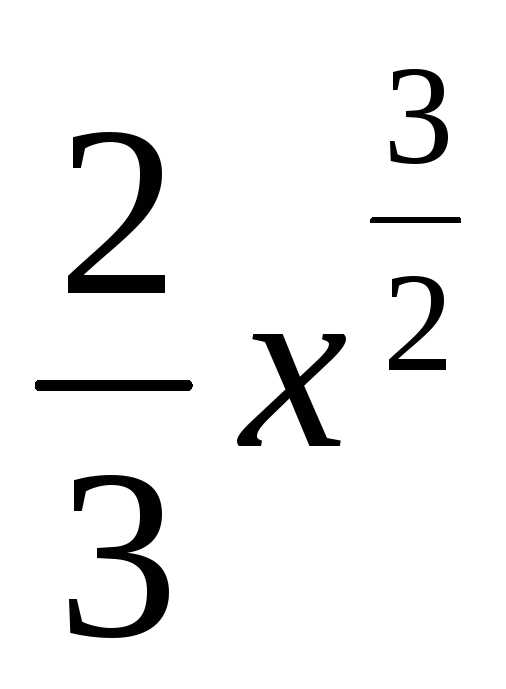 ,
расположенной над отрезкомоси.
,
расположенной над отрезкомоси.
Так как 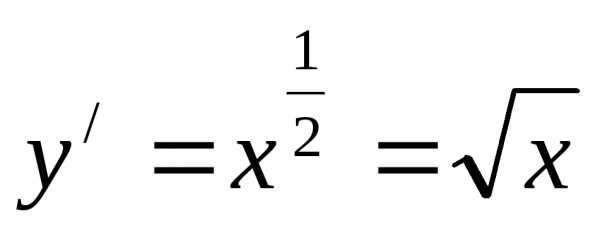 ,
то формула даёт нам интеграл
,
то формула даёт нам интеграл
Сделаем в последнем интеграле замену t=x+(1/2) и получим:
В первом из
интегралов правой части сделаем замену
z=t2—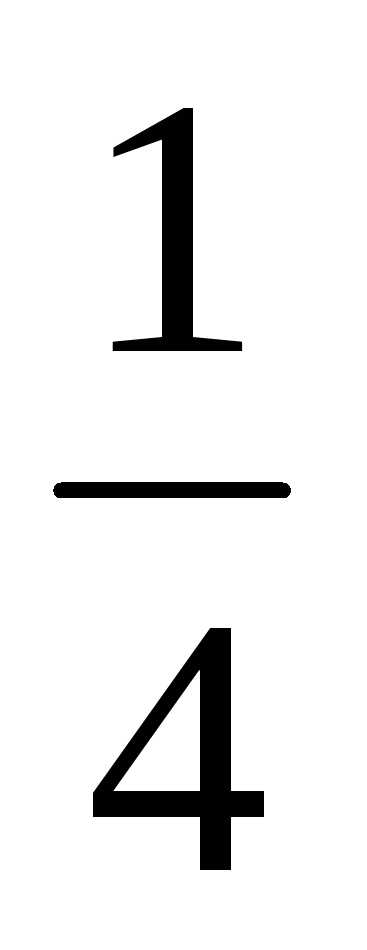 :
:
Для вычисления второго из интегралов в правой части обозначим его и проинтегрируем по частям, получив уравнение для:
Перенося в левую часть и деля на 2, получаем
откуда, наконец,
Приложения определенного интеграла к решению некоторых задач механики и физики
Работа переменной силы. Рассмотрим движение материальной точки вдоль оси OX под действием переменной силы f , зависящей от положения точки x на оси, т.e. силы, являющейся функцией x. Тогда работа A, необходимая для перемещения материальной точки из позиции x = a в позицию x = b вычисляется по формуле:
Для вычисления силы давления жидкости используют закон Паскаля, согласно которому давление жидкости на площадку равно ее площади S, умноженной на глубину погружения h, на плотность ρ и ускорение силы тяжести g, т.е.
.
1. Моменты
и центры масс плоских кривых.
Если дуга кривой задана уравнением
y=f(x), a≤x≤b, и имеет плотность 
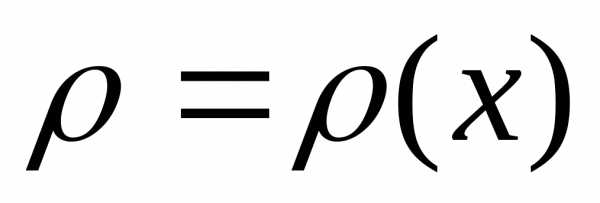 ,
тостатические
моменты этой дуги Mx и My относительно координатных осей Ox и Oy
равны
,
тостатические
моменты этой дуги Mx и My относительно координатных осей Ox и Oy
равны
;
моменты инерции IХ и Iу относительно тех же осей Ох и Оу вычисляются по формулам
а координаты
центра масс 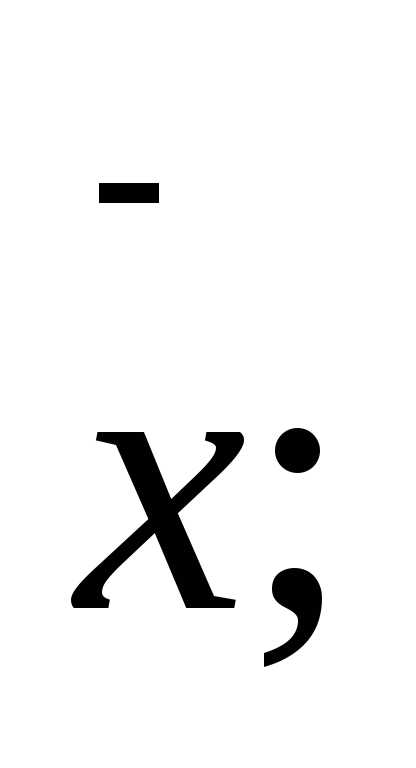 и
и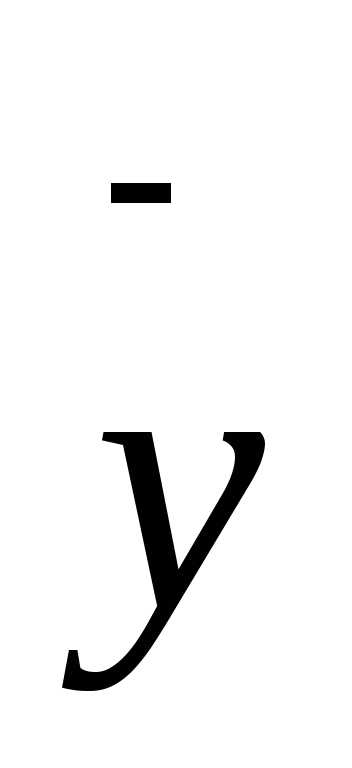 — по формулам
— по формулам
где l— масса дуги, т. е.
Пример 1. Найти статические моменты и моменты инерции относительно осей Ох и Оу дуги цепной линии y=chx при 0≤x≤1.
Если
плотность не указана, предполагается,
что кривая однородна и 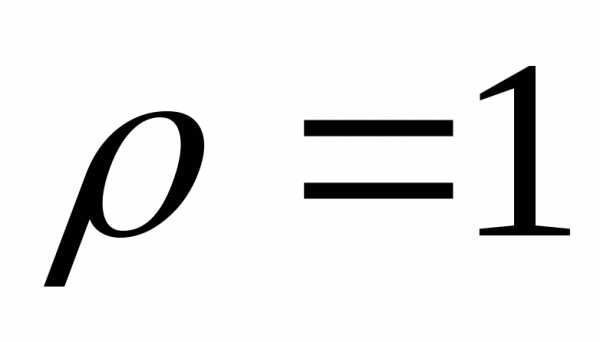 .
Имеем:Следовательно,
.
Имеем:Следовательно,

Пример 2. Найти координаты центра масс дуги окружности x=acost, y=asint, расположенной в первой четверти. Имеем:
Отсюда получаем:
В приложениях часто оказывается полезной следующая Теорема Гульдена. Площадь поверхности, образованной вращением дуги плоской кривой вокруг оси, лежащей в плоскости дуги и ее не пересекающей, равна произведению длины дуги на длину окружности, описываемой ее центром масс.
Пример 3. Найти координаты центра масс полуокружности
Вследствие
симметрии 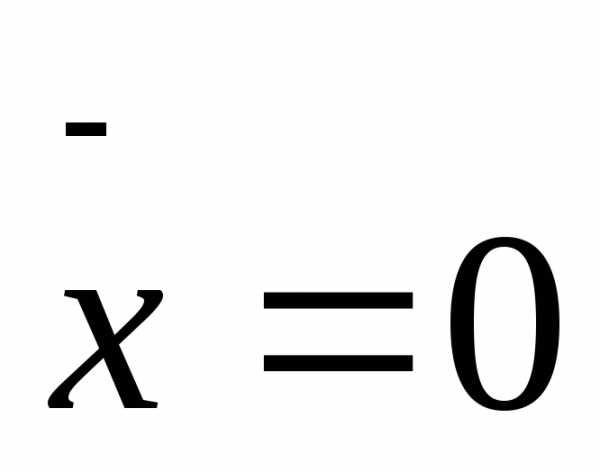 .
При вращении полуокружности вокруг оси
Ох получается сфера, площадь поверхности
которой равна,
а длина полуокружности равна па. По
теореме Гульдена имеем 4
.
При вращении полуокружности вокруг оси
Ох получается сфера, площадь поверхности
которой равна,
а длина полуокружности равна па. По
теореме Гульдена имеем 4
Отсюда 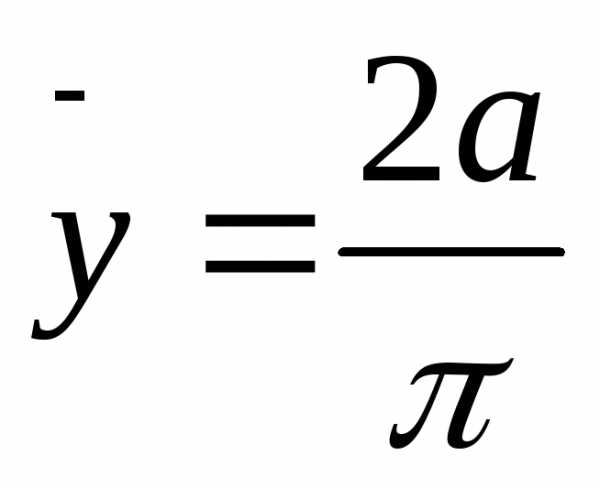 ,
т.е. центр масс C имеет координаты C
,
т.е. центр масс C имеет координаты C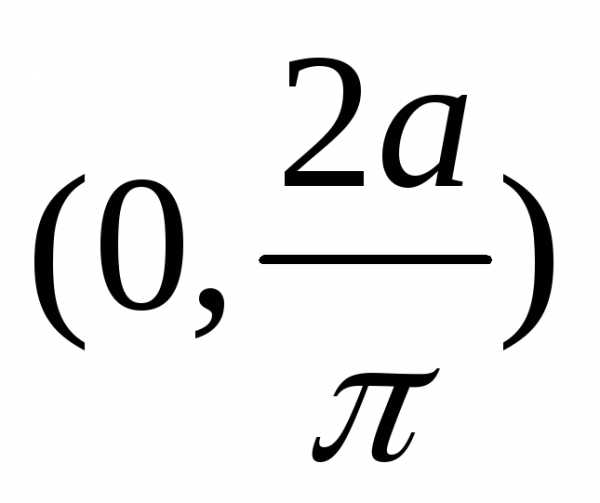 .
.
2. Физические задачи. Некоторые применения определенного интеграла при решении физических задач иллюстрируются ниже в примерах .
Пример 4. Скорость прямолинейного движения тела выражается формулой (м/с). Найти путь, пройденный телом за 5 секунд от начала движения.
Так как путь, пройденный телом со скоростью v(t) за отрезок времени [t1,t2], выражается интегралом
то имеем:
П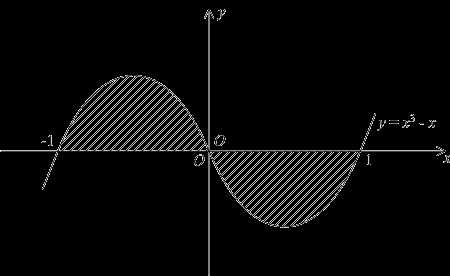 ример.
Найдём площадь
ограниченной
области, лежащей между осьюи
линиейy=x3-x.
Поскольку
ример.
Найдём площадь
ограниченной
области, лежащей между осьюи
линиейy=x3-x.
Поскольку
линия пересекает ось в трёх точка:x1=-1, x2=0, x3=1.
Ограниченная
область между линией и осью
проектируется
на отрезок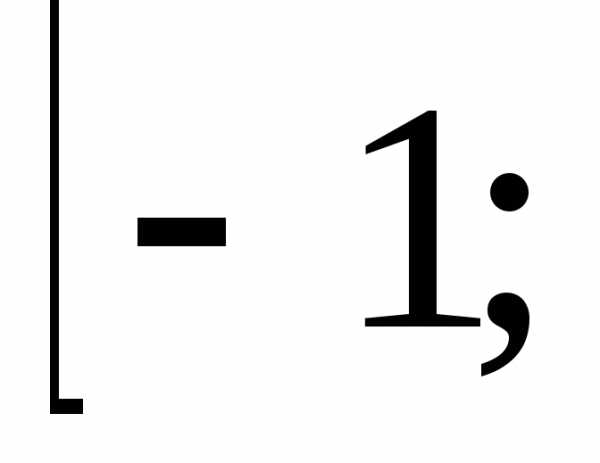 ,
,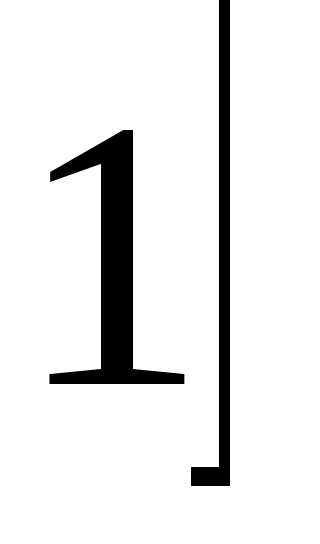 причём на отрезке
причём на отрезке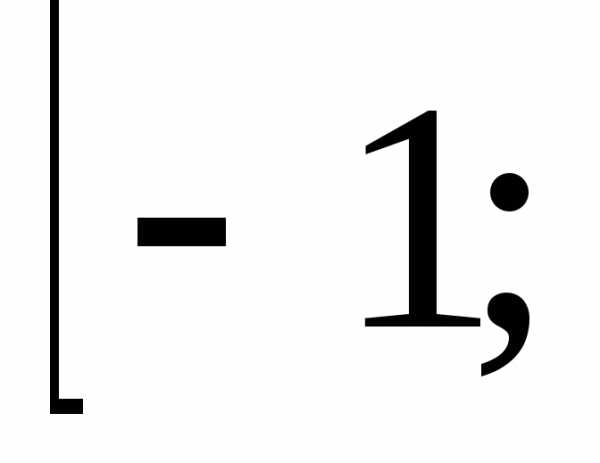 ,
,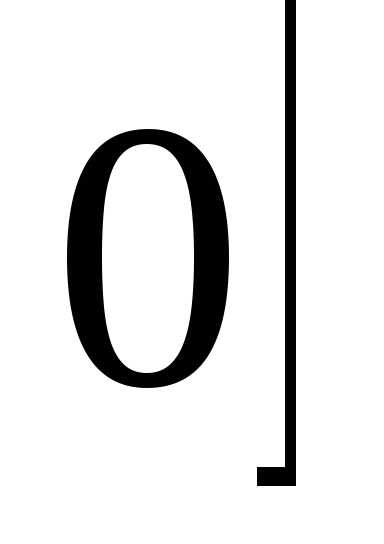 линияy=x3-x
идёт выше оси
(то
есть линииy=0,
а на
линияy=x3-x
идёт выше оси
(то
есть линииy=0,
а на 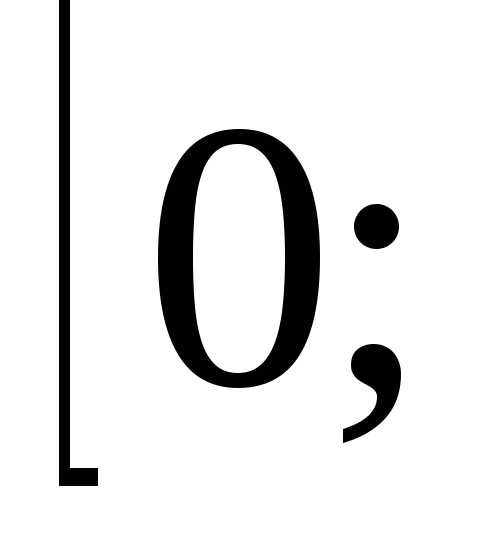
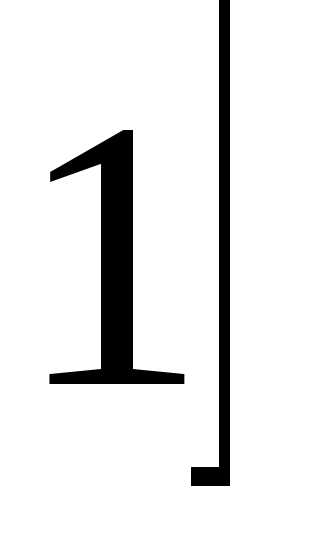 — ниже. Поэтому площадь области можно
подсчитать так:
— ниже. Поэтому площадь области можно
подсчитать так:
П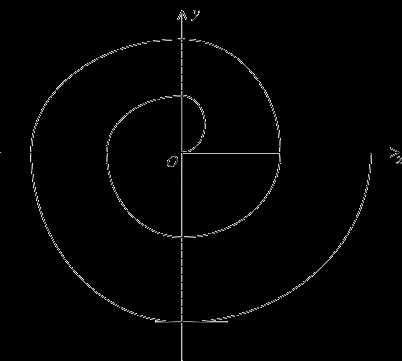 ример. Найдём площадь
области,
заключённой между первым и вторым витком
спирали Архимедаr=a
ример. Найдём площадь
области,
заключённой между первым и вторым витком
спирали Архимедаr=a (a>0)
и отрезком горизонтальной оси
(a>0)
и отрезком горизонтальной оси 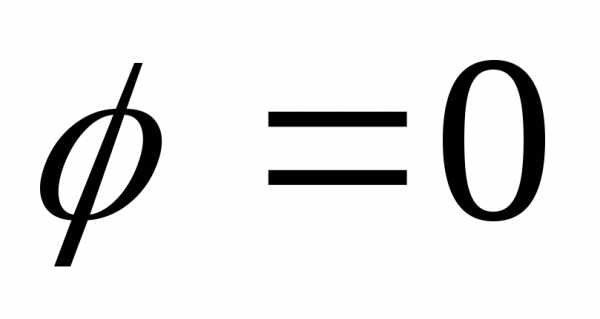
 .
.
Первый виток
спирали соответствует изменению угла
в
пределах от 0 до,
а второй — отдо.
Чтобы привести изменение аргумента к одному промежутку, запишем уравнение
второго витка спирали в виде,
к одному промежутку, запишем уравнение
второго витка спирали в виде, 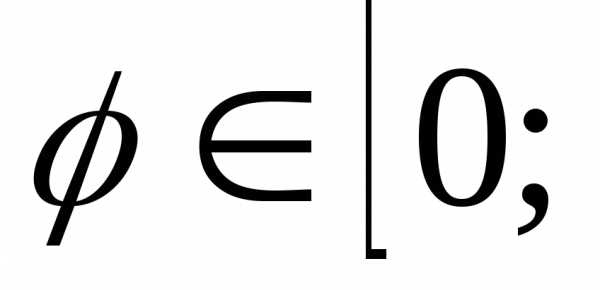
 .
Тогда площадь
можно
будет найти по формуле, положиви
:
.
Тогда площадь
можно
будет найти по формуле, положиви
:
П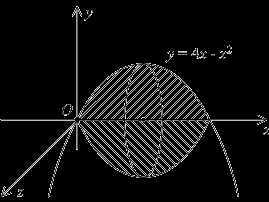 ример. Найдём объём
тела,
ограниченного поверхностью вращения
линииy=4x-x2 вокруг оси
(при).
ример. Найдём объём
тела,
ограниченного поверхностью вращения
линииy=4x-x2 вокруг оси
(при).
Для вычисления объёма тела вращения применим формулу
Имеем:
П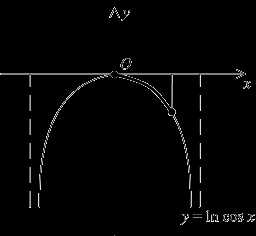 ример. Вычислим длину
дуги
линииy=lncosx,
расположенной между прямыми
и
ример. Вычислим длину
дуги
линииy=lncosx,
расположенной между прямыми
и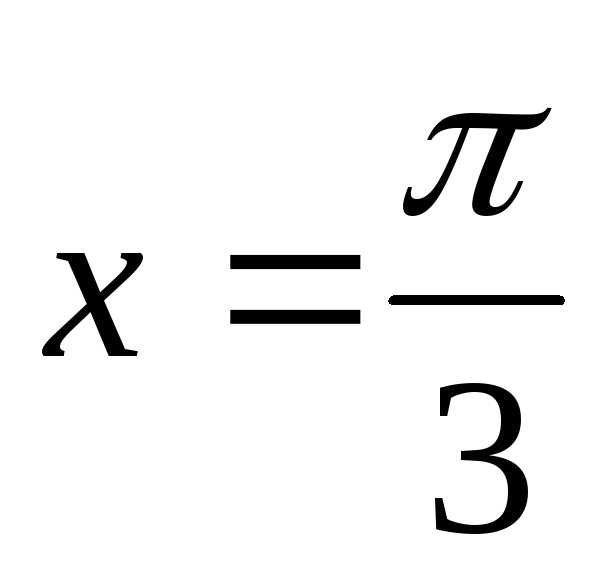 .
.
Так как
и
(мы взяли в качестве
значения корня
,
а не -cosx,
поскольку cosx
>0 при 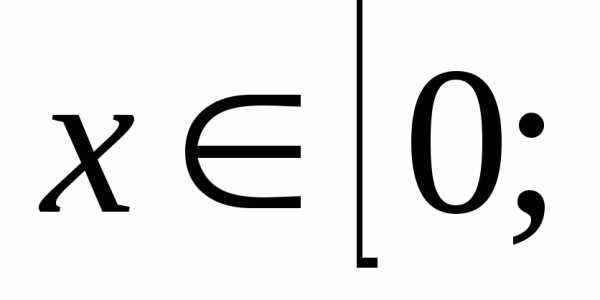
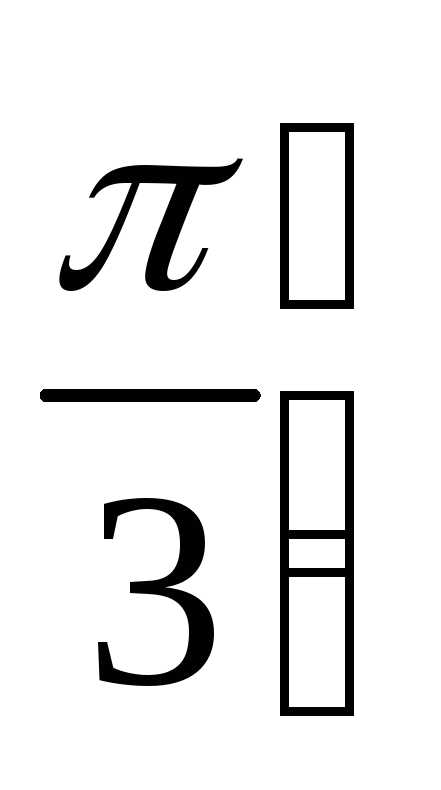 ,
длина дуги равна
,
длина дуги равна
Ответ: .
Пример. Вычислим площадь Q
поверхности вращения, полученной при
вращении дуги циклоиды x=t-sint
; y=1-cost,
при 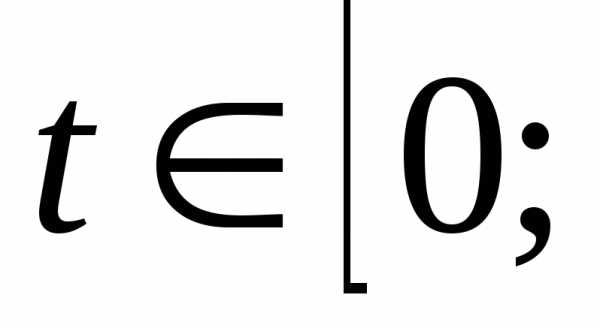
 ,
вокруг оси.
,
вокруг оси.
Д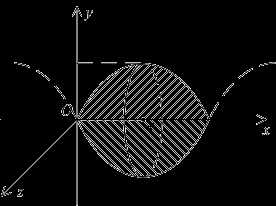 ля
вычисления применим формулу:
ля
вычисления применим формулу:
Имеем: 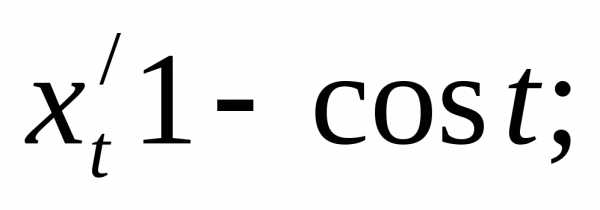
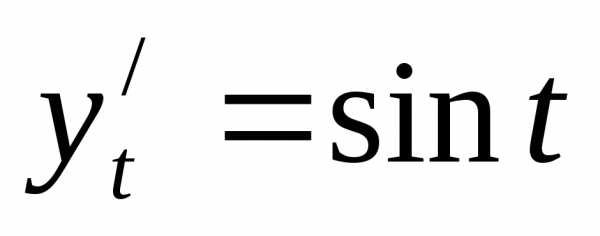 , так что
, так что
Для перехода под
знаком интеграла к переменной
заметим,
что при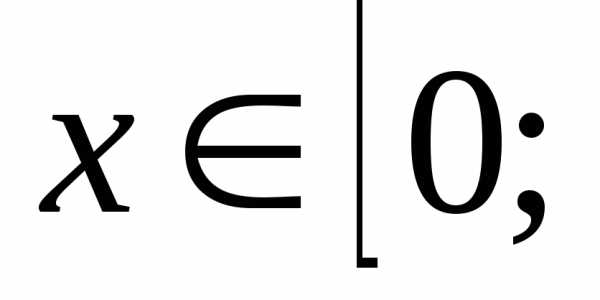
 получаем
получаем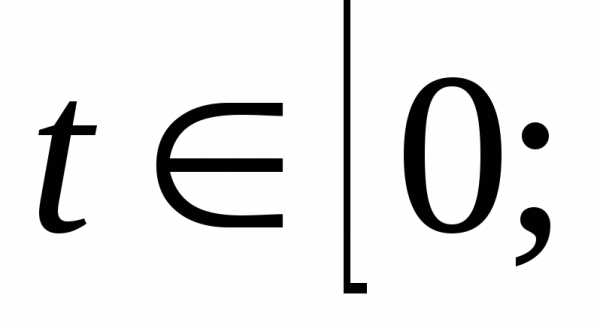
 ,
а также
,
а также
Кроме того, предварительно вычислим
(так что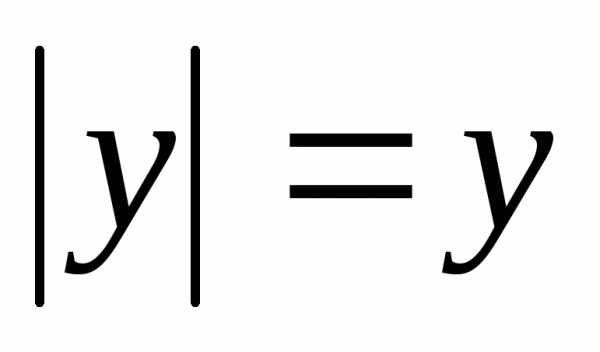 )
и
)
и
Получаем:
Делая замену , приходим к интегралу
studfiles.net
Вычисление объёмов тел вращения с помощью определённого интеграла
Объём тела, полученного от вращения вокруг оси Ох криволинейной трапеции, ограниченной непрерывной кривой, определяемой уравнением y=f(x)0, осью Ох и прямымиx=aиx=b, вычисляется по формуле
b
V=y2 dx (1)
a
Объём тела, полученного от вращения вокруг оси Оу криволинейной трапеции, ограниченной непрерывной кривой, определяемой уравнением х=(у)0, осью Оу и прямыми у=с иx=d, вычисляется по формуле
d
V=x2 dy (2)
c
Пример Вычислить объём тела, образованного вращением фигуры, ограниченной линиямиy2= 4x,x=3, вокруг оси Ох.
Решение:Построим параболу у2=4х и прямую х=3.
УПределы интегрирования а=0,b=3.
A Объём тела, полученного при вращении фигуры
ОАВ вокруг оси Ох найдём по формуле (1):
X=33 3
0Х V=4xdx=4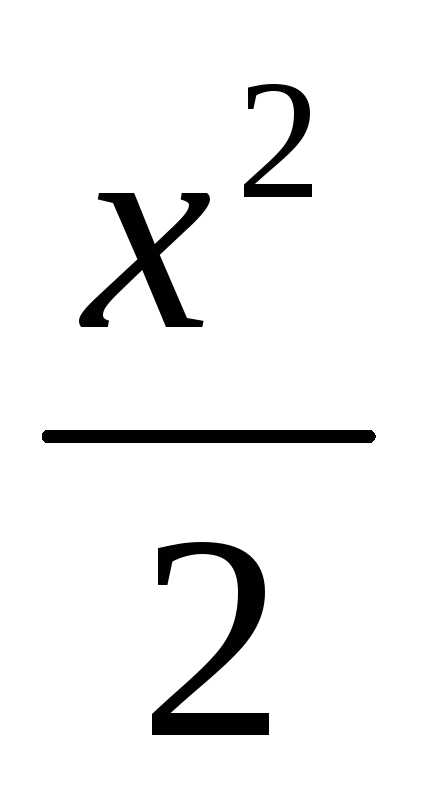 =18(куб.ед.)
=18(куб.ед.)
0 0
By2= 4x
НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ
Несобственными интеграламипервого рода называют интегралы от ограниченных функций с одним или двумя бесконечными пределами. Несобственный интеграл от функцииf(x) в пределах отaдо +определяется равенством
b
f(x) dx = lim f(x) dx
a b a
b b
f(x) dx = lim f(x) dx
a a
b
и f(x) dx = lim f(x) dx
a a
b
Если предел в правой части равенства существует и конечен, то несобственный интеграл называется сходящимся, если же предел не существует или бесконечен— расходящимся.
Несобственные интегралы второго родаэто интегралы на конечном отрезке от функций, котрые терпят бесконечный разрыв.
Если функция f(x) имеет бесконечный разрыв в точкесотрезка [a,b] и непрерывна приaxcиcxb, то по определению полагают
b c- b
f(x) dx = lim f(x) dx + lim f(x) dx
a a c+
Использование несобственных интегралов позволяет придать смысл такому понятию, как площадь полубесконечной (бесконечной) фигуры.
1. Вычислить 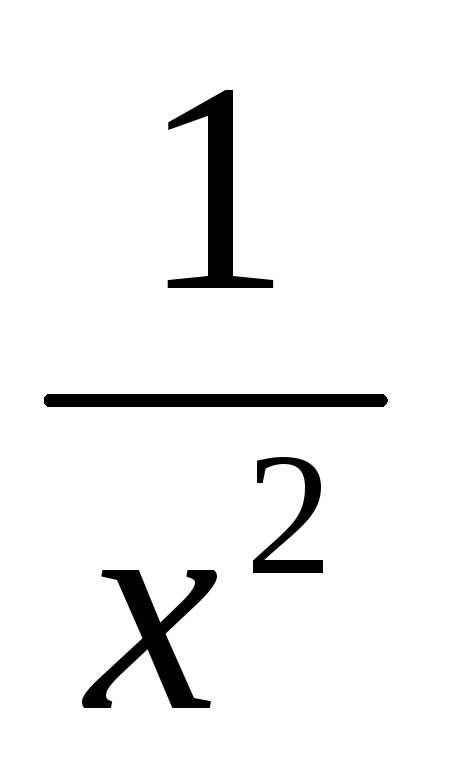 dx
dx
1bb
По определению 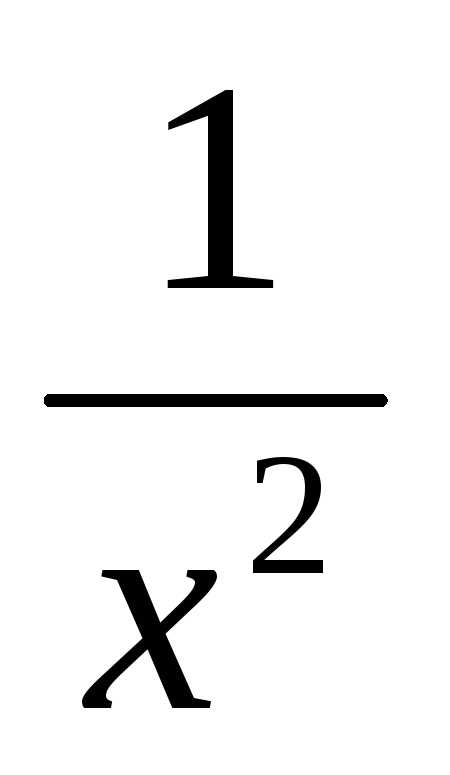 dx=lim
dx=lim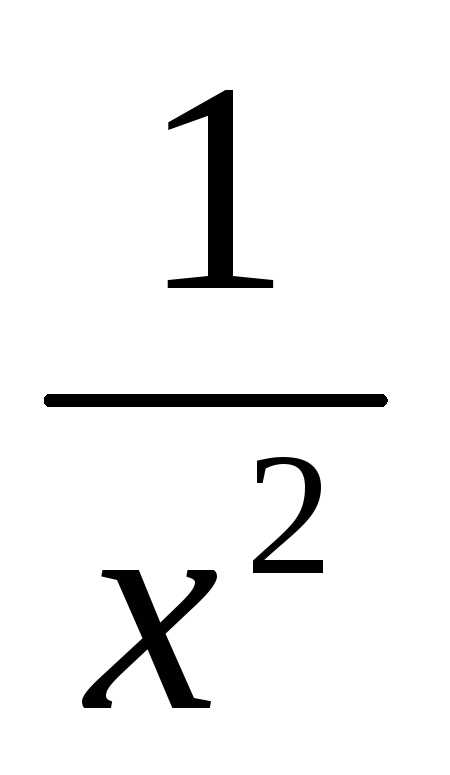 dx=lim(-
dx=lim(-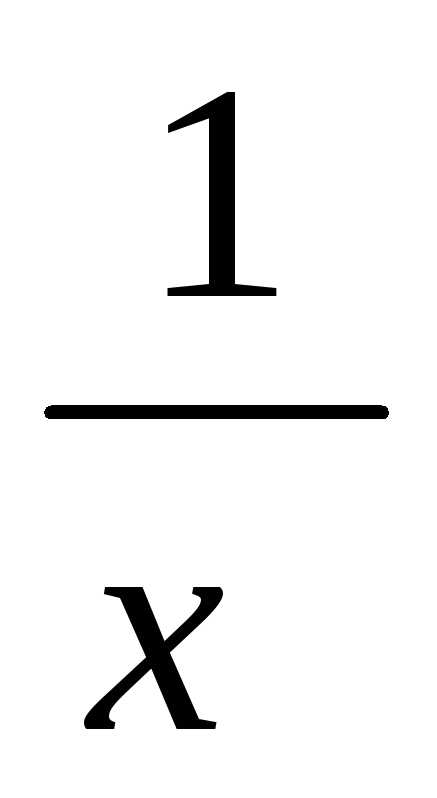 )
=lim(-
)
=lim(- +1)=1,
+1)=1,
1 b 1 b 1 b
т.е. искомый несобственный интеграл равен 1.
Используя формулу Ньютона-Лейбница, можно убедиться, что
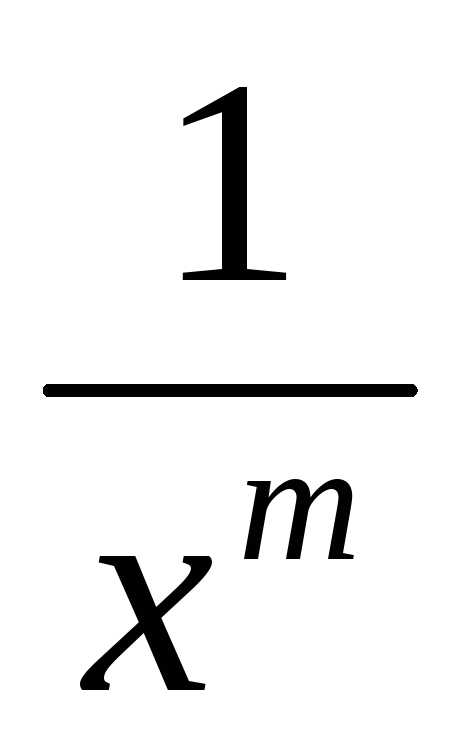 dx
dx
1
является
сходящимся к 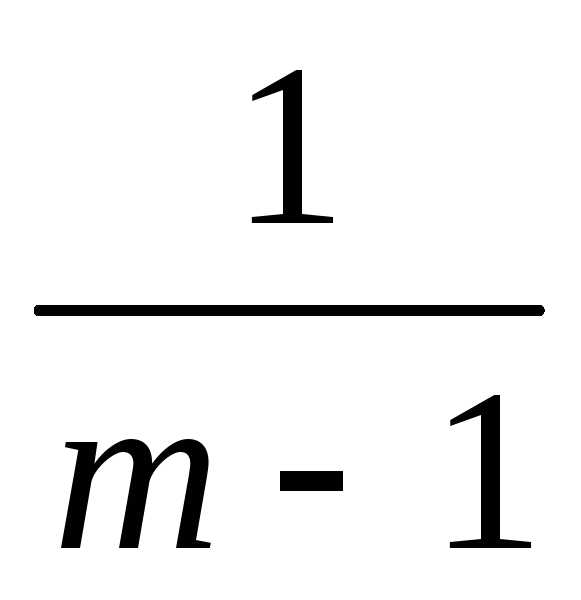 еслиm>1 и расходящимся,
еслиm1.
еслиm>1 и расходящимся,
еслиm1.
Геометрический смысл этого результата
состоит в том, что среди всех кривых
вида y=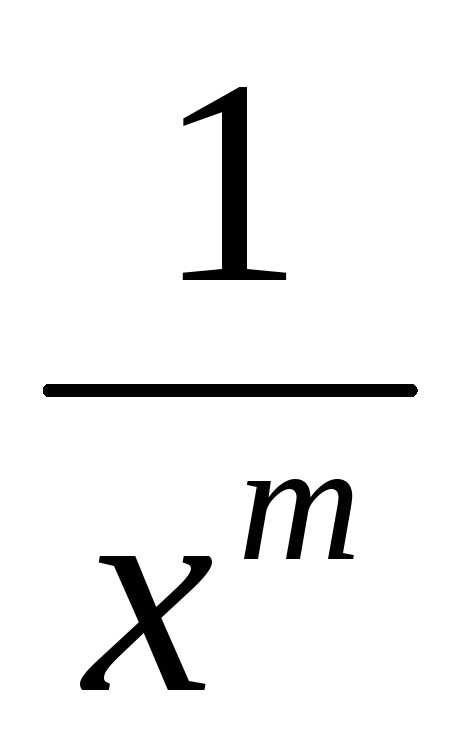 гиперболаy=
гиперболаy= 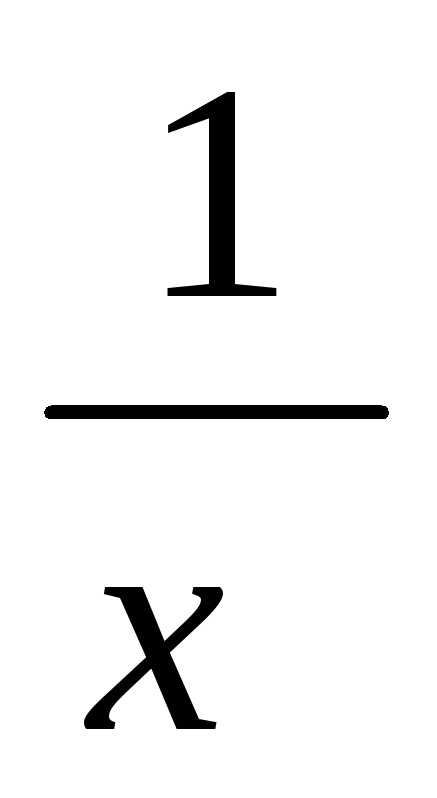 является своеобразным “порогом”.
является своеобразным “порогом”.
y
y=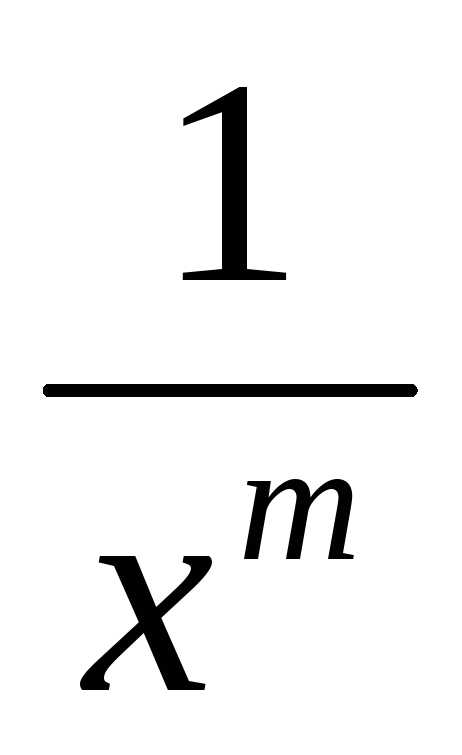 (m1)
(m1)
1
y=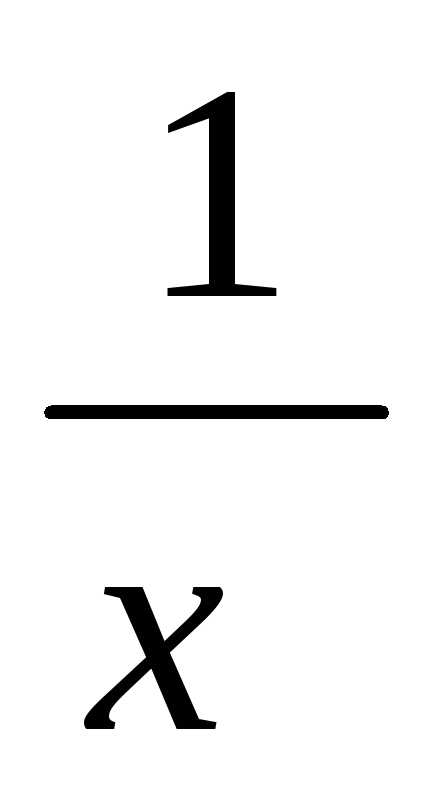
1 x
2. Вычислить (или установить расходимость)cosxdx
0
По определению имеем
bb
cosx dx = lim cosx dx = lim (sinx)= lim (sinb-sin0)=lim sinb,
0 b 0 b 0 b b
Последний предел не существует. Следовательно, несобственный интеграл расходится.
3. Найти 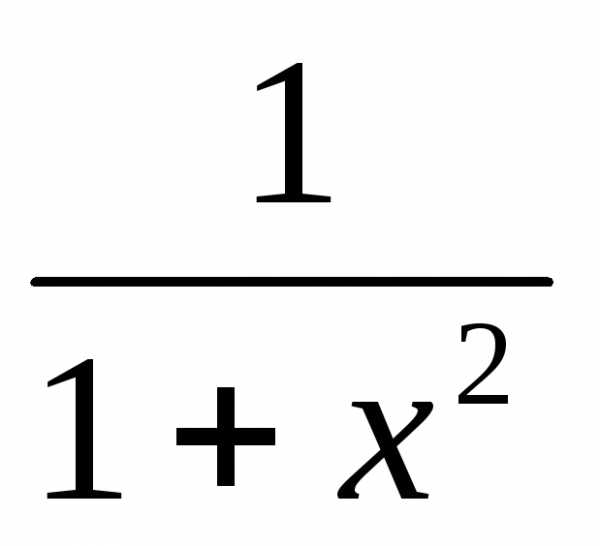 dx
dx
Подынтегральная функция четная, поэтому 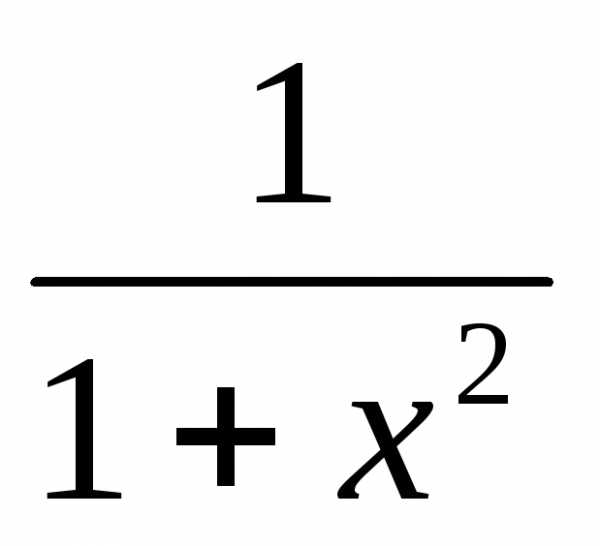 dx=2
dx=2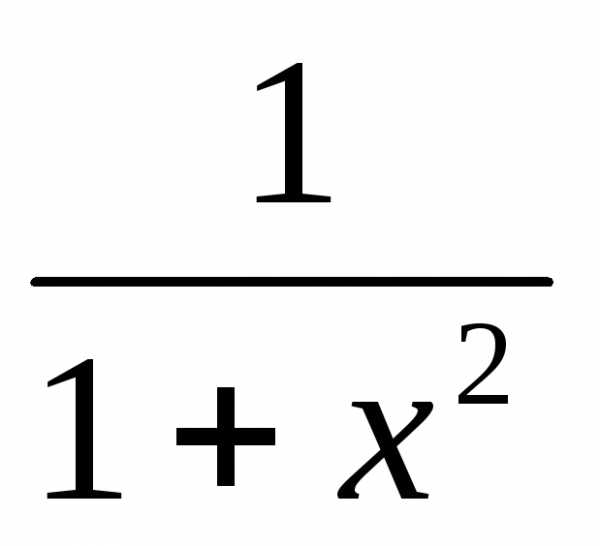 dx
dx
+bb 0
Тогда 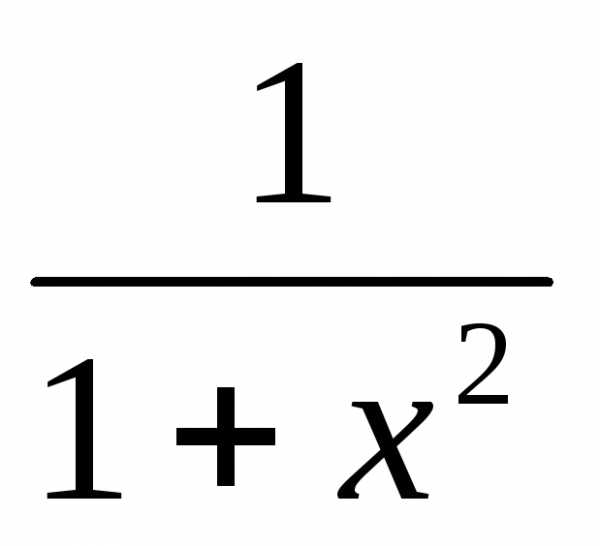 dx=
lim 1/(1+x2)
dx= lim arctg x
= lim arctg b=
dx=
lim 1/(1+x2)
dx= lim arctg x
= lim arctg b=
0 b 0 b 0 b
Т.о., 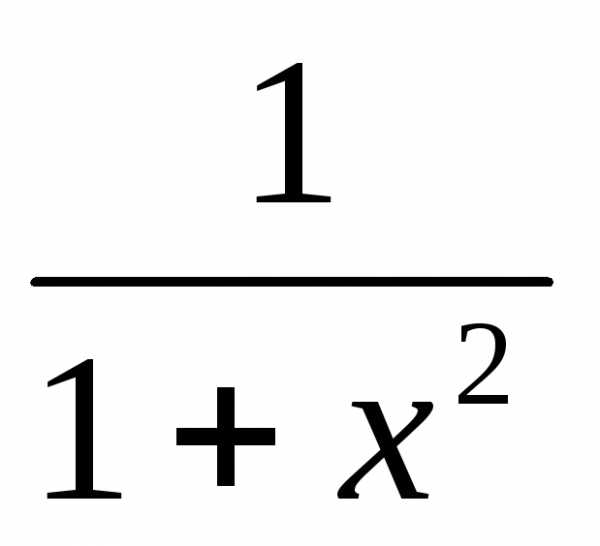 dx=
сходится.
dx=
сходится.
4. Найти xexdx.
0 b b
Имеем
xexdx=lim[- exd(-x2)]=lim[
exd(-x2)]=lim[ e-x]=
lim[-
e-x]=
lim[-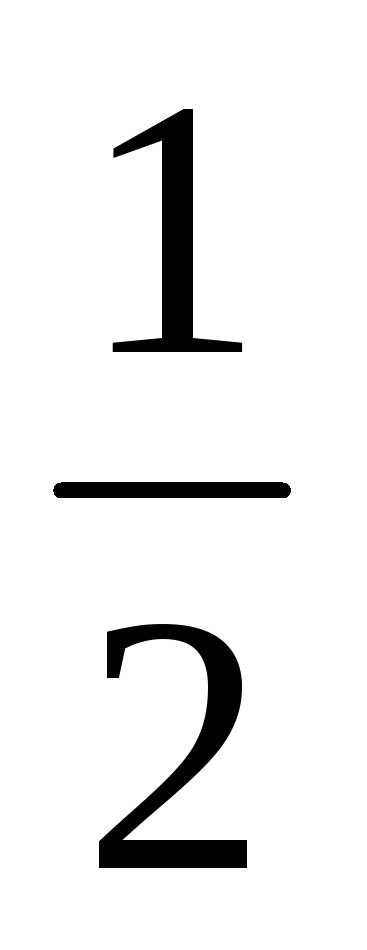 e-b+
e-b+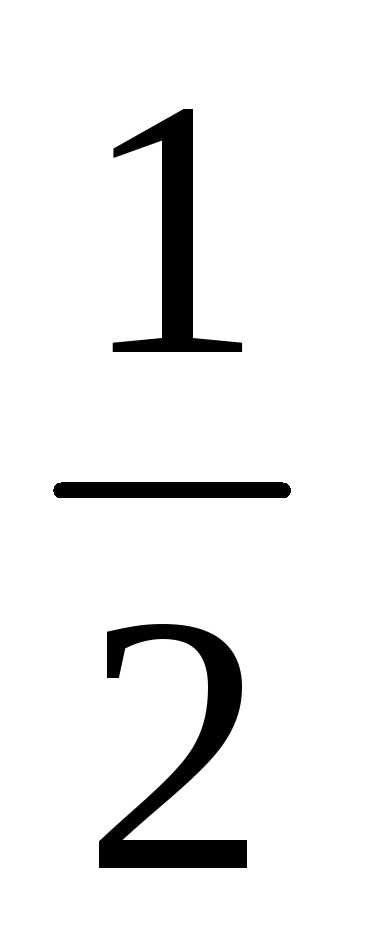 ]=
]=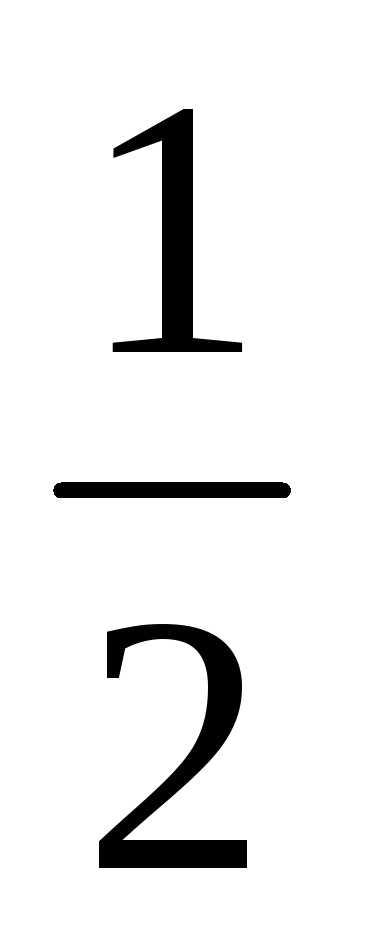 ,
,
0 b 0 0 b
1
5. Найти 1/x dx.
0
Подынтегральная функция f(x)=1/x в точкеx=0 неограничена. Поэтому:
1 1 1
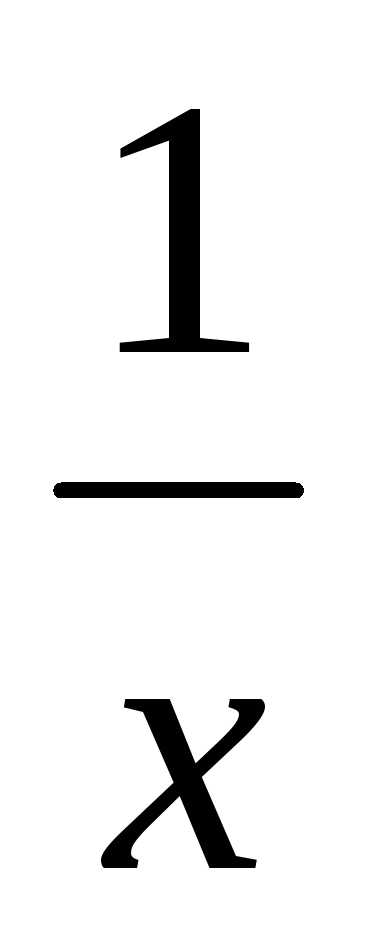 dx= lim
dx= lim 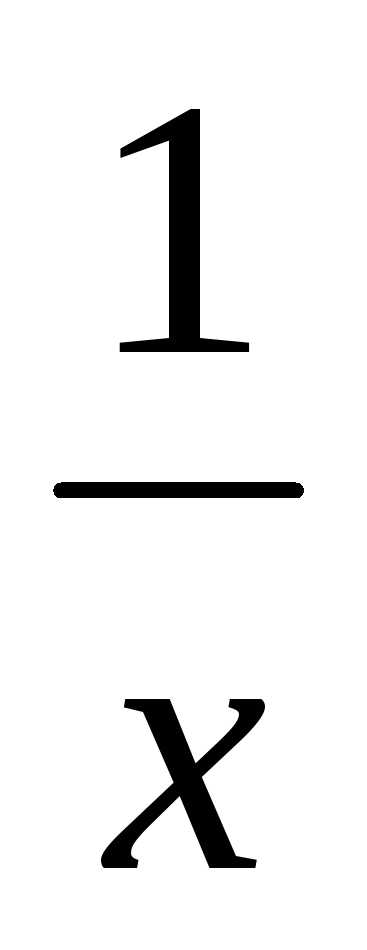 dx= lim(lnx)=lim(ln(1)-ln(a))=+
dx= lim(lnx)=lim(ln(1)-ln(a))=+
0 a0 a a0 a
Несобственный интеграл расходится.
studfiles.net
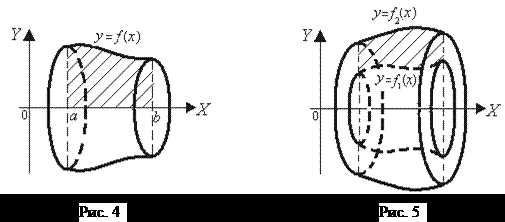
10. Вычисление объема тела вращения
Пусть криволинейная трапеция, ограниченная прямыми x = a, x= b,
y = 0 и непрерывной кривой y = f(x),
где 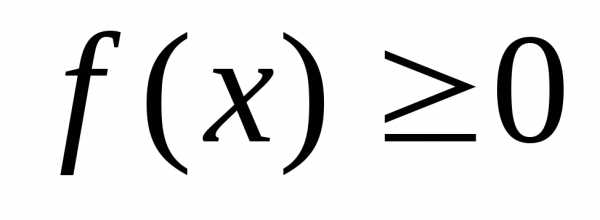 для
для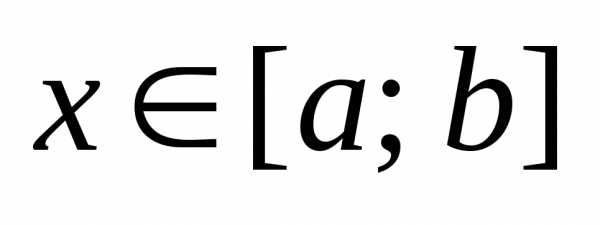 ,
вращается вокруг осиОX.
Объем полученного при этом тела вращения
(рис. 4) вычисляется по формуле:
,
вращается вокруг осиОX.
Объем полученного при этом тела вращения
(рис. 4) вычисляется по формуле:
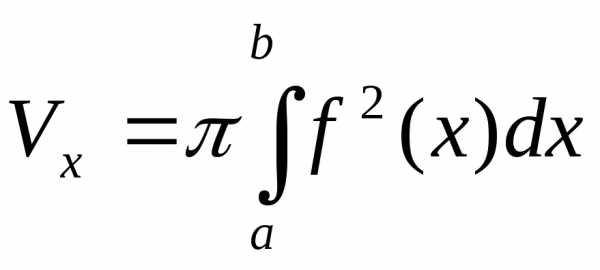 . (14)
. (14)
Если криволинейная трапеция ограничена линиями x = a, x= b,
y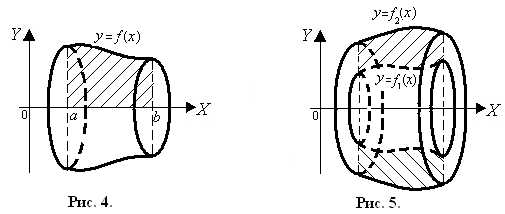 1 = f1(x)
и y2 = f2(x)
где
для
1 = f1(x)
и y2 = f2(x)
где
для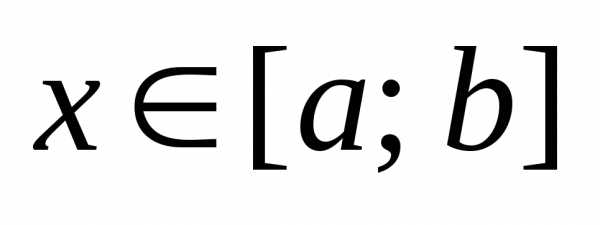 ,
то объем полученного при ее вращении
вокругОX тела (рис. 5) можно вычислить по формуле:
,
то объем полученного при ее вращении
вокругОX тела (рис. 5) можно вычислить по формуле:
. (15)
11. Вычисление длины дуги плоской кривой
Пусть
плоская кривая АВ задана уравнением y = f(x),
где 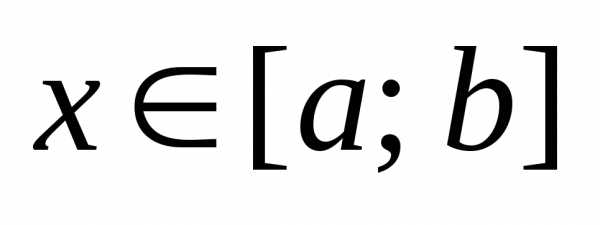 .
Если функцияf′(x)
и ее производная f·′(x)
непрерывны на промежутке [a; b],
то длина кривой АВ вычисляется по формуле:
.
Если функцияf′(x)
и ее производная f·′(x)
непрерывны на промежутке [a; b],
то длина кривой АВ вычисляется по формуле:
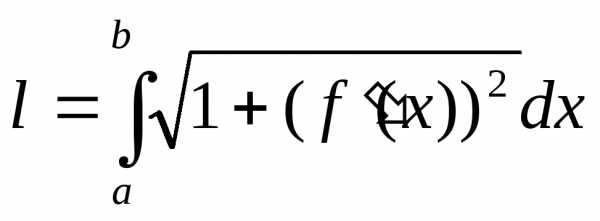 . (16)
. (16)
Примерный вариант и образец выполнения контрольной работы по теме «Интегральное исчисление функции одной переменной»
Задача 1. Найти неопределенные интегралы:
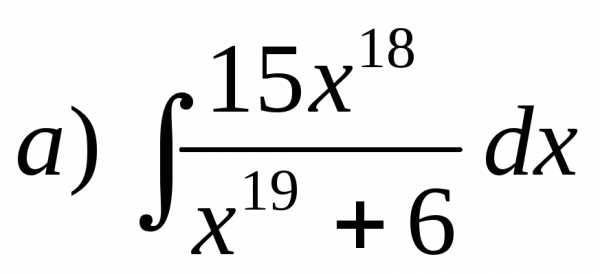 ,
,
,
,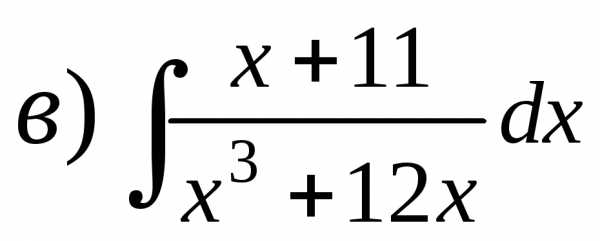 ,.
,.
В
примерах 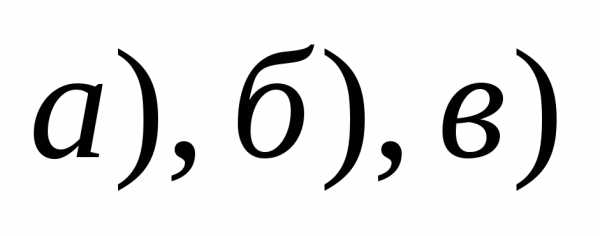 правильность полученных результатов
проверить дифференцированием.
правильность полученных результатов
проверить дифференцированием.
Задача 2. Вычислить несобственные интегралы или доказать их расходимость:
а)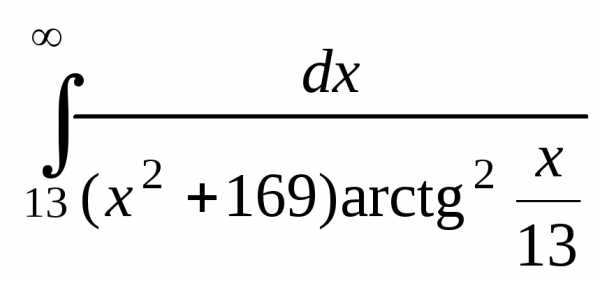 , б)
, б) 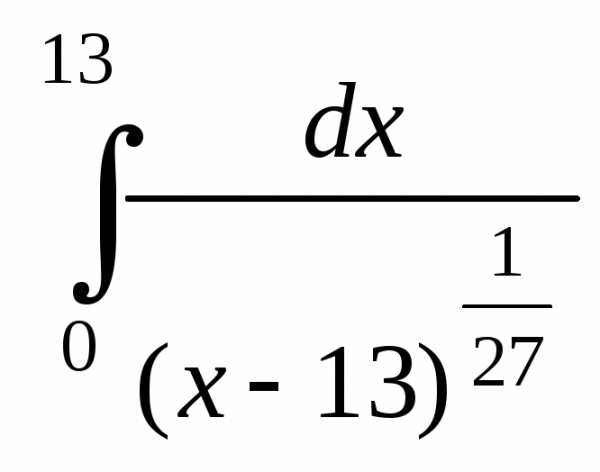 .
.
Задача 3.
а) Вычислить
с помощью определенного интеграла
площадь фигуры, ограниченной в ДСК
линиями l1: 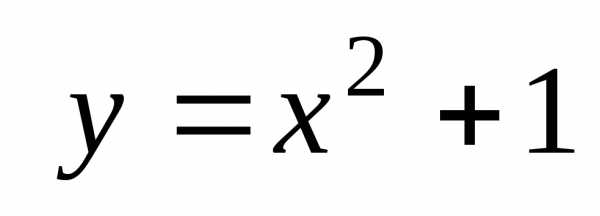 и l2: .
Сделать чертеж.
и l2: .
Сделать чертеж.
б) Вычислить с помощью определенного интеграла площадь фигуры, ограниченной в ПСК линией l: . Сделать чертеж.
Задача 4. Вычислить с помощью определенного интеграла объем тела, полученного вращением вокруг оси OX фигуры, ограниченной линиями
l1: 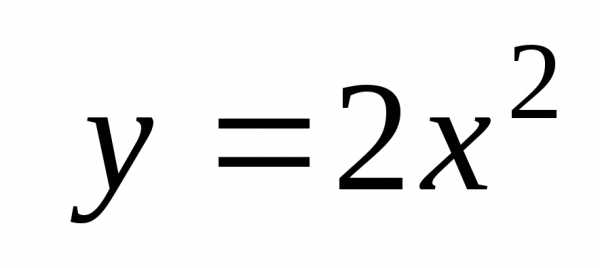 и l2: y
= 6x.
Сделать чертеж.
и l2: y
= 6x.
Сделать чертеж.
Задача 5. Вычислить с помощью определенного интеграла длину дуги кривой, заданной в ДСК уравнением , где . Сделать чертеж.
Решение задачи 1.
а)
Так как 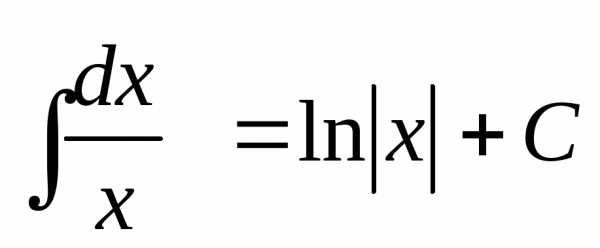 ,
то используя формулу (3), получим:
,
то используя формулу (3), получим:
.
Проверим результат дифференцированием:
следовательно, выполнено условие (1).
Ответ: 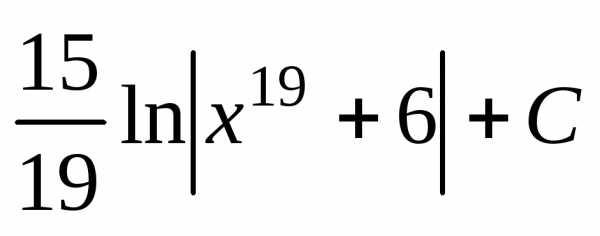 .
.
б) Интеграл относится к типу интегралов, берущихся по частям; это интеграл так называемого второго типа. Используя формулу (4), получим:
.
Проверим результат дифференцированием:
.
Ответ: .
в) Подинтегральная функция является правильной рациональной дробью, поэтому ее можно представить в виде суммы простейших дробей:
, отсюда
, или .
Неопределенные коэффициенты А, В, С найдем, приравнивая коэффициенты при одинаковых степенях х в левой и правой частях тождества:
Коэффициенты А, В, С можно найти другим способом – подставляя в тождество «удобные» значения х (метод отдельных значений):
Из первого уравнения получим: . Почленно вычитая два последних равенства, получим:, и из последнего уравнения
.
Таким образом,
Переходим к интегрированию:
.
Здесь использовано: ,
.
Проверим результат дифференцированием:
.
Ответ: .
г) Применим универсальную тригонометрическую подстановку:
.
Возвращаясь к переменной х, получаем:
.
Ответ: 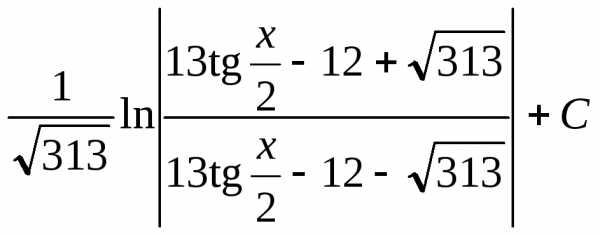 .
.
Решение задачи 2.
а) Данный интеграл является несобственным интегралом первого рода, поэтому
,
следовательно,
интеграл сходится и равен 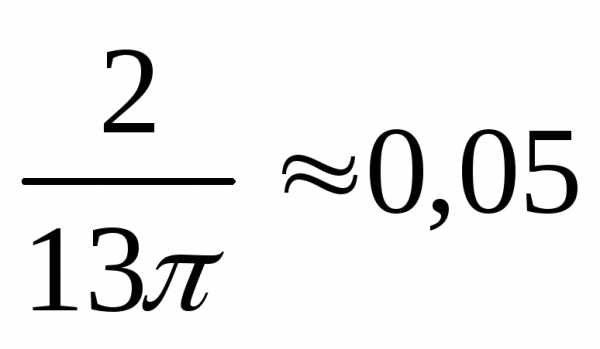 .
.
Здесь использовано:.
Ответ: 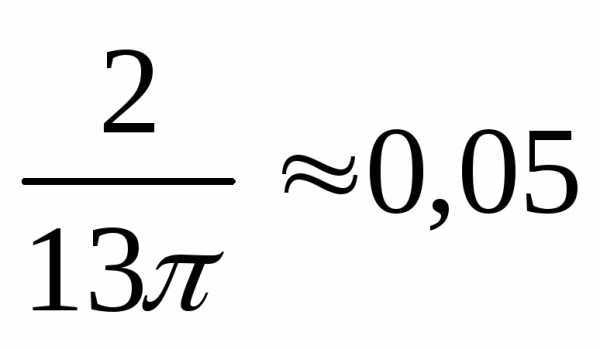 .
.
б) Данный интеграл является несобственным интегралом второго рода, поэтому
,
следовательно,
интеграл сходится и равен 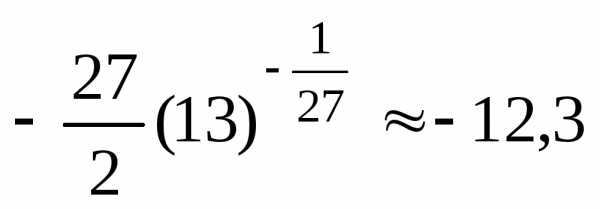 .
.
Ответ: 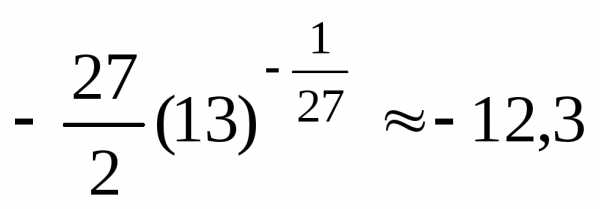 .
.
Решение задачи 3.
а)
Найдем точки пересечения кривых, для
чего составим и решим систему 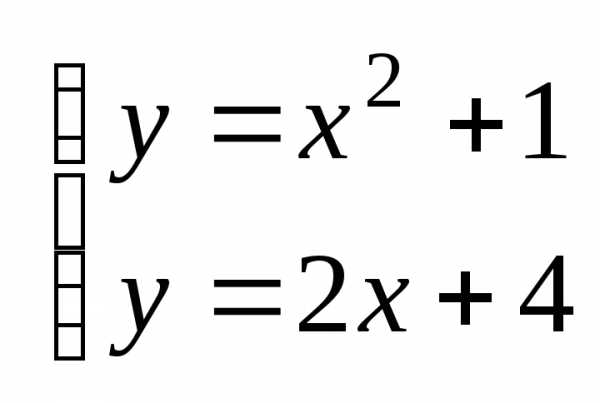 .
Приравнивая правые части, получаем
уравнение
,
решив которое, найдем абсциссы точек
пересечения: x = –1, x = 3.
.
Приравнивая правые части, получаем
уравнение
,
решив которое, найдем абсциссы точек
пересечения: x = –1, x = 3.
Построим чертеж (рис. 6). На рисунке видно, чтона промежутке [–1; 3].
Таким образом, используя формулу (12), вычислим площадь фигуры, ограниченной заданными линиями:
.
Ответ: 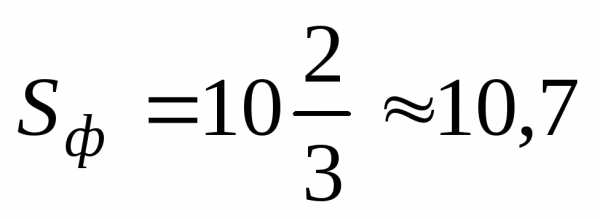 единиц площади.
единиц площади.
б)
Для построения кривой в ПСК составим таблицу значений функции
на промежутке 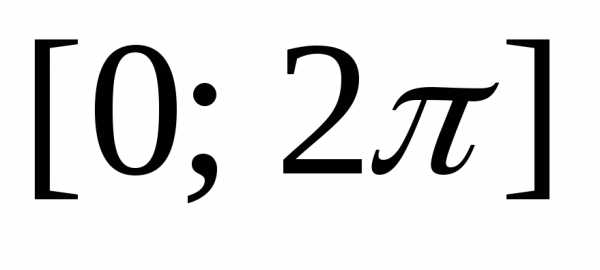 .
.
| 0 | π/4 | 2π/4 | 3π/4 | π | 5π/4 | 6π/4 | 7π/4 | 2π |
13 | 12,7 | 12 | 11,3 | 11 | 11,3 | 12 | 12,7 | 13 |
П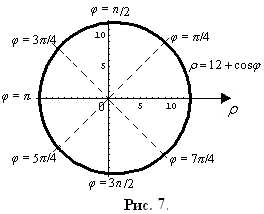 остроим
чертеж в ПСК (рис. 7).
остроим
чертеж в ПСК (рис. 7).
Так как фигура ограничена кривой,
заданной в полярной системе координат, то
площадь фигуры, ограниченной заданной линией, вычислим по формуле (13):
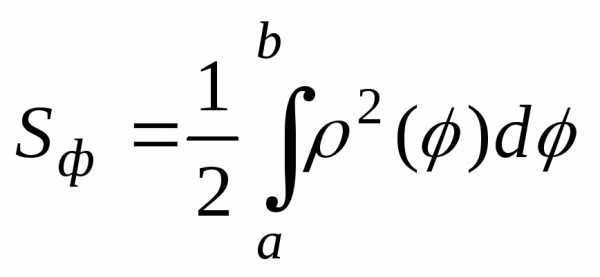 .
.
Для получаем:
.
Ответ: единицы площади.
Решение задачи 4.
Для
построения фигуры Ф,
ограниченной кривыми l1 и l2 нужно найти точки их пересечения, т.е.
решить систему: 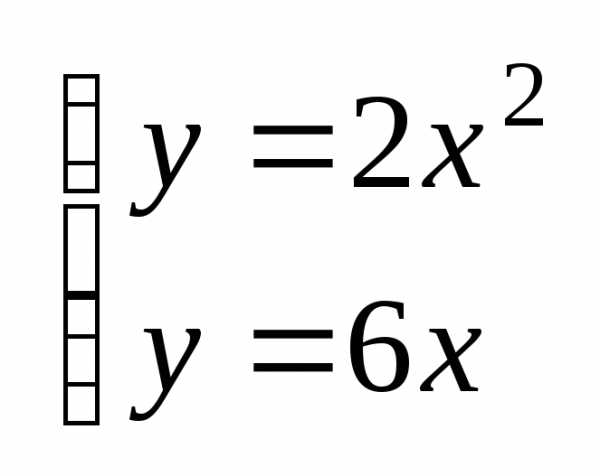 .
Приравнивая правые части равенств,
получаем уравнение
,
решив которое, найдем абсциссы точек
пересечения кривых:
.
.
Приравнивая правые части равенств,
получаем уравнение
,
решив которое, найдем абсциссы точек
пересечения кривых:
.
Объем тела вращения, полученного вращением фигуры Ф вокруг оси OX (рис. 8) можно найти как разность объемов двух тел по формуле (15):
.
Ответ: единиц объема.
Решение задачи 5.
Кривая
задана уравнением 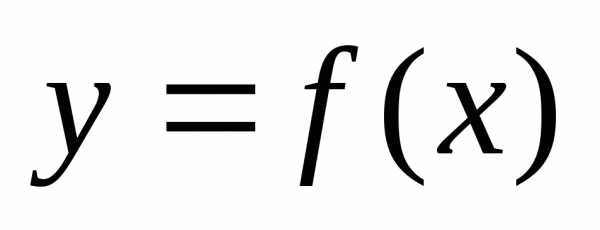 где
,
поэтому ее длина вычисляется по формуле
(16):
где
,
поэтому ее длина вычисляется по формуле
(16): 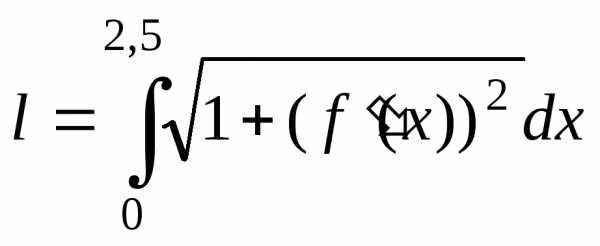 .
.
Для получаем: ,
тогда длина дуги кривой
.
Ответ: 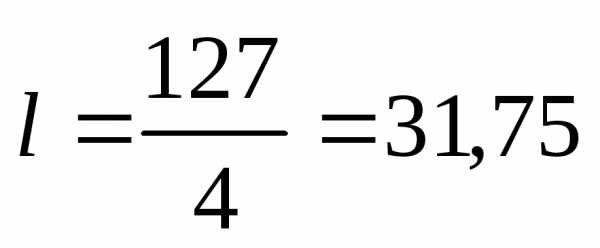 единиц длины.
единиц длины.
studfiles.net
Нахождение объемов тел вращения с помощью интегралов
– вокруг оси абсцисс ; – вокруг оси ординат .
В данной статье будут разобраны оба случая. Особенно интересен второй способ вращения, он вызывает наибольшие затруднения, но на самом деле решение практически такое же, как и в более распространенном вращении вокруг оси абсцисс. В качестве бонуса я вернусь кзадаче нахождения площади фигуры, и расскажу вам, как находить площадь вторым способом – по оси . Даже не столько бонус, сколько материал удачно вписывается в тему.
Начнем с наиболее популярной разновидности вращения.
Вычисление объема тела, образованного вращением плоской фигуры вокруг оси
Пример 1
Вычислить объем тела, полученного вращением фигуры, ограниченной линиями , вокруг оси
Решение: Как и в задаче на нахождение площади, решение начинается с чертежа плоской фигуры. То есть, на плоскости необходимо построить фигуру, ограниченную линиями , , при этом не забываем, что уравнение задаёт ось . Как рациональнее и быстрее выполнить чертёж, можно узнать на страницах Графики и свойства Элементарных функций и Определенный интеграл. Как вычислить площадь фигуры. Это китайское напоминание, и на данном моменте я больше не останавливаюсь.
Чертёж здесь довольно прост:
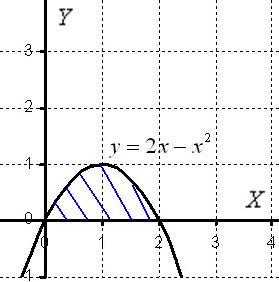
Искомая плоская фигура заштрихована синим цветом, именно она и вращается вокруг оси В результате вращения получается такая немного яйцевидная летающая тарелка, которая симметрична относительно оси . На самом деле у тела есть математическое название, но по справочнику что-то лень уточнять, поэтому едем дальше.
Как вычислить объем тела вращения?
Объем тела вращения можно вычислить по формуле:
В формуле перед интегралом обязательно присутствует число . Так повелось – всё, что в жизни крутится, связано с этой константой.
Как расставить пределы интегрирования «а» и «бэ», думаю, легко догадаться из выполненного чертежа.
Функция … что это за функция? Давайте посмотрим на чертеж. Плоская фигура ограничена графиком параболы сверху. Это и есть та функция, которая подразумевается в формуле.
В практических заданиях плоская фигура иногда может располагаться и ниже оси . Это ничего не меняет – подынтегральная функция в формуле возводится в квадрат: , таким образом интеграл всегда неотрицателен, что весьма логично.
25. Д.У. С разделяющимися переменными и метод его решения.
Дифференциальное уравнение называется уравнение с разделяющимися переменными, если его можно записать в виде: y’=, т.е. если его правая часть есть произведение 2 функций, одна из которых зависит от н, а другая от х
q(y)
Уравнение вида
называется уравнением с разделяющимися переменными.
Это уравнение может быть приведено к уравнению с разделенными переменными путем деления обеих его частей на выражение
или .
Общий интеграл полученного уравнения имеет вид:
.
Пример
Дано уравнение или . Разделим переменные и интегрируем .
В результате вычисления получим:
. Это выражение можно записать в иной форме: т.к. всякое число можно представить в виде логарифма другого.
28.Основные понятия комбинаторики: перестановка, размещение и сочетание….
Для вычисления благоприятствующих рассматриваемому событию исходов или общего числа элементарных исходов широко используются формулы комбинаторики.
Если составляются такие комбинации из n элементов по m, которые отличаются друг от друга только составом элементов, то они называются сочетаниями. Общее число сочетаний из n элементов по m определяется по формуле . Если комбинации отличаются не только составом элементов, но и порядком их следования, то она называются размещениями. Их число находится по формуле . Если комбинации берутся из всехn элементов и отличаются только порядком следования элементов, то они называются перестановками. Их число равно
studfiles.net
Вычисление площадей плоских фигур и объемов тел вращения с помощью определенного интеграла.
2. Если на отрезке [a; b] функция , то площадь криволинейной трапеции, ограниченной сверху кривой , снизу осью 0X, справа и слева прямыми и (рисунок 1), вычисляется по формуле:
(4.1)
2. Если на отрезке [a; b], то площадь фигуры (рисунок 2) вычисляется по формуле:
(4.2)
3. Если функция меняет знак на отрезке [a; b], то площадь фигуры (рисунок 3) вычисляется по формуле:
, (4.3)
где интегралы по отрезкам, на которых функция отрицательна, берутся по абсолютной величине.
4. Если на одном и том же отрезке [a; b] заданы две функции: и , причем для любых то площадь фигуры (рисунок 4) вычисляется по формуле:
(4.4)
5. Если фигура ограничена сверху разными линиями, заданными на разных отрезках (рисунок 5), имеющих один общий конец: при и при , то площадь такой фигуры определяется по формуле:
(4.5)
Задание 6. Вычислить площадь фигуры ограниченной графиками функций и
Решение
Изобразим фигуру, площадь которой надо найти, на координатной плоскости. Графиком функции g(x) является парабола, ветви которой направлены вверх. Найдем производную функции . Находим координаты вершины параболы С:
Точки пересечения параболы с осями координат:
С осью ох:
;
;
C осью оу: х=0;
Графиком функции является прямая, которую можно построить по двум точкам с координатами
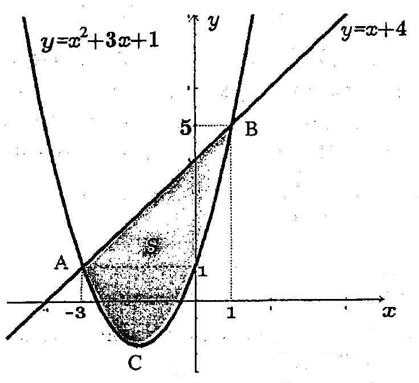
Рисунок 2 к задаче №6
Найдем точки пересечения графиков функций
;
Площадь S фигуры ABC, ограниченной графиками функций, находим по формуле .
Где для всех
Так как при , то
Ответ
6. Объем тела, образованного вращением вокруг оси ox криволинейной трапеции, ограниченной непрерывной кривой и прямыми (рисунок 6), равен
(4.6)
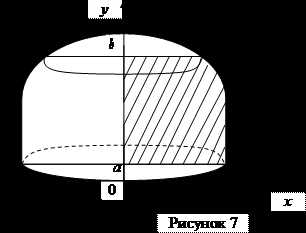
7. Объем тела, образованного вращением вокруг оси oy криволинейной трапеции, ограниченной непрерывной кривой и прямыми (рисунок 7), равен
(4.7)
Несобственные интегралы.
Если функция f(x) непрерывна при , то несобственным интегралам называется . Если этот предел существует и конечен, то интеграл называется сходящимся. В противном случае интеграл называется расходящимся.
Аналогично определяются интегралы
Если функция f(x) непрерывна при и имеет разрыв II рода в точке c, то несобственным интегралом называется
Так же, как и выше, несобственный интеграл называется сходящимся, если оба предела существуют и конечны. В противном случае несобственный интеграл называется расходящимся.
Если же точка разрыва находится в конце промежутка, то:
в) при c=a
г) при c=b
Если при и сходится, то сходится. Такая сходимость называется абсолютной.
Если при и расходится, то расходится.
Если при предел конечен и не равен нулю, то оба интеграла одновременно либо сходятся, либо расходятся.
Аналогичные признаки сходимости можно указать и для несобственных интегралов от разрывных функций.
Р Я Д Ы
ВВЕДЕНИЕ
Настоящее пособие является кратким изложением свойств бесконечных рядов, а также представление функций в виде бесконечных рядов более простых функций. Последнее делает бесконечные ряды одним из важнейших численных методов в математике и находит широкое практическое применение.
Рядом в математике называется бесконечная сумма чисел или функций, составленная по определенному закону:
u1 + u2 + u3 + … + un+……… (1),
где un — члены ряда; многоточие указывает на то, что выражение (1) не имеет последнего слагаемого, т.е. ряд – бесконечная сумма. Поэтому вместо (1), пользуясь знаком суммы, часто пишут так
Числовые ряды
Ряд называется числовым, если члены этого ряда – числа un, которые задаются только функциями номера n, т.е. un = f(n). Последовательно складывая члены ряда, составим (в бесконечном количестве) суммы:
S1 = u1 , S2 = u1+ u2 , …, Sn = u1+ u2+ u3+…+ un
Их называют частичными суммами ряда.
Конечный или бесконечный предел S частичной суммы Sn ряда (1) при
(2)
называют суммой ряда и записывают
S = u1+ u2+ u3+…+ un+… =
Если ряд имеет конечную сумму, то его называют сходящимся; в противном случае (т.е. если сумма равна ±¥, либо же суммы вовсе нет) – расходящимся.
Поясним понятие суммы ряда на конкретном примере. Пусть задан числовой ряд
(3)
каждый последующий член которого равен половине предыдущего.
Подсчитаем суммы одного, двух, трех, четырех, пяти его членов:
S1 = ,
S2 = ,
S3 = ,
S4 = ,
S5 = .
Значения этих сумм отличаются от 1 на т.е. при увеличении числа слагаемых получаем для их сумм значения все меньше отличающиеся от 1. Поясним сказанное на рис. 1.
Рис. 1
Прямоугольник площадью в одну квадратную единицу разобьем на два прямоугольника. Один из них вновь разобьем на два прямоугольника одинаковой площади. Продолжая этот процесс деления, получим прямоугольники, площади которых равны квадратных единиц. Объединение этих прямоугольников приближает нас к исходному. Следовательно, и сумма их площадей приближается к площади исходного прямоугольника, т.е. к 1. Число 1 называют суммой ряда (3).
Пример 1.
un= 1, Sn = 1 + 1 + 1 + ¼ + 1 = n,
Пример 2.
un= (-1)n, Sn = — 1 + 1 — 1 + 1 – 1 + ¼ + (-1)n.
Такой ряд предела не имеет, т.к. его верхний предел равен 0, а нижний предел равен –1.
Пример 3.
un= u1 qn-1, Sn = u1 + u1 q + u1 q2 + ¼ + u1 qn-1.
Этот ряд – геометрическая прогрессия со знаменателем q – называется геометрическим рядом. Умножим Sn на q и вычтем полученное выражение почленно из Sn
Sn q = u1 q + u1 q2 + u1 q3 + ¼ + u1 qn,
Sn — Sn q = u1 — u1 qn, Sn (1-q) = u1 (1-qn).
Для частичной суммы Snгеометрического ряда получаем
Sn = u1
предел которого и представляет сумму геометрического ряда
При |q| < 1, и , ряд сходится;
при |q| > 1 ряд геометрической прогрессии расходится;
при q = 1 см. пример 1;
при q = -1 см. пример 2.
Пример 4.
Запишем
Представим сумму п членов исследуемого ряда в виде:
тогда и Следовательно, ряд сходится.
Рекомендуемые страницы:
Воспользуйтесь поиском по сайту:
megalektsii.ru
Вычисление объема тела вращения — КиберПедия
Пусть криволинейная трапеция, ограниченная прямыми x = a, x= b,
y = 0 и непрерывной кривой y = f(x), где для , вращается вокруг оси ОX. Объем полученного при этом тела вращения (рис. 4) вычисляется по формуле:
. (14)
Если плоская фигура ограничена линиями x = a, x= b, y1 = f1(x) и
y2 = f2(x), где для , то объем полученного при ее вращении вокруг ОX тела (рис. 5) можно вычислить по формуле:
. (15)
11. Вычисление длины дуги плоской кривой
Пусть плоская кривая АВ задана уравнением y = f(x), где . Если функция f′(x) и ее производная f′(x) непрерывны на промежутке [a; b], то длина кривой АВ вычисляется по формуле:
. (16)
Примерный вариант и образец выполнения
контрольной работы 5
Задача 1. Найти неопределенные интегралы:
, , в) , .
В примерах правильность полученных результатов проверить дифференцированием.
Задача 2. Вычислить несобственные интегралы или доказать их расходимость:
а) , б) .
Задача 3. Вычислить с помощью определенного интеграла площадь плоской фигуры:
а) ограниченной в ДСК линиями l1: и l2: ;
б) ограниченной в ПСК линией l: .
Сделать чертежи.
Задача 4. Вычислить с помощью определенного интеграла объем тела, полученного вращением вокруг оси OX фигуры, ограниченной линиями
l1: y = 2x2 и l2: y = 6x. Сделать чертеж.
Задача 5. Вычислить с помощью определенного интеграла длину дуги кривой, заданной в ДСК уравнением , где .
Решение задачи 1
а) Так как , то используя формулу (3), получим:
.
Проверим результат дифференцированием:
следовательно, выполнено условие (1).
Ответ: = .
б) Интеграл относится к типу интегралов, берущихся по частям; это интеграл так называемого второго типа. Используя формулу (4), получим:
.
Проверим результат дифференцированием:
.
Ответ: = .
в) Подинтегральная функция является правильной рациональной дробью, поэтому ее можно представить в виде суммы простейших дробей:
, отсюда
или .
Неопределенные коэффициенты А, В, С найдем, приравнивая коэффициенты при одинаковых степенях х в левой и правой частях тождества:
Коэффициенты А, В, С можно найти другим способом – подставляя
в тождество «удобные» значения х (метод частных значений):
Из первого уравнения получим: А = 11/12. Почленно вычитая два последних равенства, получим: , и из последнего уравнения
.
Таким образом,
Переходим к интегрированию:
.
Здесь использовано:
,
.
Проверим результат дифференцированием:
.
Ответ: = .
г) Применим универсальную тригонометрическую подстановку:
.
Возвращаясь к переменной х, получаем:
Ответ: = .
Решение задачи 2
а) Данный интеграл является несобственным интегралом первого рода, поэтому
следовательно, интеграл сходится и равен .
Здесь использовано:
Ответ: интеграл сходится и равен .
б) Данный интеграл является несобственным интегралом второго рода, так как х = 13– точка бесконечного разрыва подинтегральной функции. Поэтому
,
следовательно, интеграл сходится и равен .
Ответ: интеграл сходится и равен .
Решение задачи 3
а) Найдем точки пересечения кривых, для чего составим и решим систему . Приравнивая правые части, получаем уравнение , решив которое, найдем абсциссы точек пересечения: x = –1, x = 3.
Построим чертеж (рис. 6). На рисунке видно, что на промежутке [–1; 3].
Используя формулу (12), вычислим площадь фигуры, ограниченной заданными линиями:
Ответ: единиц площади.
б) Для построения кривой в ПСК составим таблицу значений функции на промежутке .
| π/4 | 2π/4 | 3π/4 | π | 5π/4 | 6π/4 | 7π/4 | 2π | ||
| 12,7 | 11,3 | 11,3 | 12,7 |
Построим чертеж в ПСК (рис. 7). Так как фигура ограничена кривой, заданной в полярной системе координат, то площадь фигуры, ограниченной заданной линией,вычислим по формуле (13):
.
Для получаем:
.
Ответ: единицы площади.
Решение задачи 4
Для построения фигуры Ф, ограниченной кривыми l1 и l2, нужно найти точки их пересечения, т. е. решить систему: . Приравнивая правые части равенств, получаем уравнение 2x2 – 6x = 0, решив которое, найдем абсциссы точек пересечения кривых: x = 0, x = 3.
Объем тела вращения, полученного вращением фигуры Ф вокруг оси OX (рис. 8), можно найти как разность объемов двух тел по формуле (15):
.
Ответ: единиц объема.
Решение задачи 5
Кривая задана уравнением где , поэтому ее длина вычисляется по формуле (16): .
Для получаем: , тогдадлина дуги кривой
Ответ: единиц длины.
Справочный материал по теме
«Дифференциальные уравнения»
cyberpedia.su