Ни четная ни нечетная функция как определить – Ни четная ни нечетная функция

Нечётные и чётные функции Википедия

Нечётными и чётными называются функции, обладающие симметрией относительно изменения знака аргумента. Это понятие важно во многих областях математического анализа, таких как теория степенных рядов и рядов Фурье. Название связано со свойствами степенных функций: функция f(x)=xn{\displaystyle f(x)=x^{n}} чётна, когда n{\displaystyle n} чётно, и нечётна, когда n{\displaystyle n} нечётно.

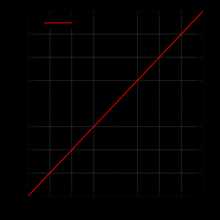f(x)=x{\displaystyle f(x)=x} — пример нечётной функции f(x)=x2{\displaystyle f(x)=x^{2}} — пример чётной функции f(x)=x3,{\displaystyle f(x)=x^{3},} нечётная f(x)=x3+1{\displaystyle f(x)=x^{3}+1} ни чётная, ни нечётная

• Нечётная функция — функция, меняющая значение на противоположное при изменении знака независимой переменной (график её симметричен относительно центра координат).
• Чётная функция — функция, не изменяющая своего значения при изменении знака независимой переменной (график её симметричен относительно оси ординат).
• Ни чётная, ни нечётная функция (функция общего вида). В эту категорию относят функции, не подпадающие под предыдущие 2 категории.

Строгое определение[ | ]

Определения вводятся для любой симметричной относительно нуля

ru-wiki.ru

Нечётная функция Википедия

Нечётными и чётными называются функции, обладающие симметрией относительно изменения знака аргумента. Это понятие важно во многих областях математического анализа, таких как теория степенных рядов и рядов Фурье. Название связано со свойствами степенных функций: функция f(x)=xn{\displaystyle f(x)=x^{n}} чётна, когда n{\displaystyle n} чётно, и нечётна, когда n{\displaystyle n} нечётно.

f(x)=x{\displaystyle f(x)=x} — пример нечётной функции f(x)=x2{\displaystyle f(x)=x^{2}} — пример чётной функции f(x)=x3,{\displaystyle f(x)=x^{3},} нечётная f(x)=x3+1{\displaystyle f(x)=x^{3}+1} ни чётная, ни нечётная

• Нечётная функция — функция, меняющая значение на противоположное при изменении знака независимой переменной (график её симметричен относительно центра координат).
• Чётная функция — функция, не изменяющая своего значения при изменении знака независимой переменной (график её симметричен относительно оси ординат).
• Ни чётная, ни нечётная функция (функция общего вида). В эту категорию относят функции, не подпадающие под предыдущие 2 категории.

Строгое определение[ | ]

Определения вводятся для любой симметричной относительно нуля

ru-wiki.ru

Ответы@Mail.Ru: определить четность/нечетность функций

1-я функция ни чётная, ни нечётная: sin(-x)-cos(-x)=-sin x-cos x=/= -(sin x-cos x) Во 2-й функции надо написать скобки? Тогда 2-я функция нечётная: (a^(-x)-a^(x))/2 = -(a^(x)-a^(-x))/2.

Первая ни та, ни другая. Говорят, функция общего вида. Вторая нечетная.

если f(x) = f(-x) функция четна если f(x) = -f(-x) функция нечетна в других случаяъ функция ни четна ни нечетна подставляй, проверяй

они обе общего вида

touch.otvet.mail.ru

3 функция ни четная, ни нечетная

с. 1
Приложение
Пример 8. Найти все a, для каждого из которых существует единственное b, такое, что .

Решение:

Выразим a через b:

Введем функцию: пусть .

Преобразуем функцию с выделением целой части:

1) наклонная асимптота

2)

вертикальная асимптота

3) функция ни четная, ни нечетная.

4) точки пересечения графика с осями координат:

с осью ординат график функции не пересекается, т.к. эта ось есть асимптота;

при , точка .

5) ; ;

6)

7) Построим график .

Ответ:

Пример 9. При каких значениях параметра a уравнение имеет единственное решение?

Решение: Т.к. не является корнем уравнения , то

Введем функцию :

1)

вертикальная асимптота

2) при

горизонтальная асимптота.

при

горизонтальная асимптота.

при , точка

при , точка

3) Построим график .

Ответ:

Пример 10. При каких значениях параметра a уравнение имеет единственное решение?

Решение:

Выразим a через x:

Рассмотрим функцию .

1)

2) точки пересечения графика с осями координат:

при , точка .

3) ; ;

4)

5) Построим график .

Ответ:

Пример 11. При каких значениях параметра a уравнение не имеет корней?

Решение:

Введем функцию и

1)

вертикальная асимптота

2) наклонная асимптота

3) нечетная, график симметричен относительно точки

4) точек пересечения с осями координат нет, т.к. они есть асимптоты.

5) ; ;

4)

5) Построим график .

Ответ: при

Пример 12. Найти множество значений функции , где

Решение.

Преобразуем функцию :

наклонная асимптота

2)

вертикальная асимптота

3) Точки пересечения с осями координат:

при , точка .

4) ; ;

5)

6) Построим график

Ответ:

с. 1

kz3.fatwords.org

Чётность функции — WiKi

Нечётными и чётными называются функции, обладающие симметрией относительно изменения знака аргумента. Это понятие важно во многих областях математического анализа, таких как теория степенных рядов и рядов Фурье. Название связано со свойствами степенных функций: функция f(x)=xn{\displaystyle f(x)=x^{n}} чётна, когда n{\displaystyle n} чётно, и нечётна, когда n{\displaystyle n} нечётно.

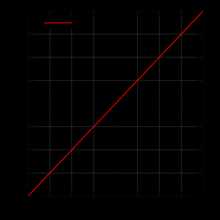f(x)=x{\displaystyle f(x)=x} — пример нечётной функции f(x)=x2{\displaystyle f(x)=x^{2}} — пример чётной функции f(x)=x3,{\displaystyle f(x)=x^{3},} нечётная f(x)=x3+1{\displaystyle f(x)=x^{3}+1} ни чётная, ни нечётная

• Нечётная функция — функция, меняющая значение на противоположное при изменении знака независимой переменной (график её симметричен относительно центра координат).
• Чётная функция — функция, не изменяющая своего значения при изменении знака независимой переменной (график её симметричен относительно оси ординат).
• Ни чётная, ни нечётная функция (функция общего вида). В эту категорию относят функции, не подпадающие под предыдущие 2 категории.

Определения вводятся для любой симметричной относительно нуля области определения X⊂R{\displaystyle X\subset \mathbb {R} } , например, отрезка или интервала.

• Функция f:X→R{\displaystyle f:X\to \mathbb {R} }  называется чётной, если справедливо равенство

f(−x)=f(x),∀x∈X.{\displaystyle f(-x)=f(x),\quad \forall x\in X.} 

• Функция называется нечётной, если справедливо равенство

f(−x)=−f(x),∀x∈X.{\displaystyle f(-x)=-f(x),\quad \forall x\in X.} 

• Функции, не принадлежащие ни одной из категорий выше, называются ни чётными, ни нечётными (или функциями общего вида).

ru-wiki.org

Чётность функции Википедия

Нечётными и чётными называются функции, обладающие симметрией относительно изменения знака аргумента. Это понятие важно во многих областях математического анализа, таких как теория степенных рядов и рядов Фурье. Название связано со свойствами степенных функций: функция f(x)=xn{\displaystyle f(x)=x^{n}} чётна, когда n{\displaystyle n} чётно, и нечётна, когда n{\displaystyle n} нечётно.

f(x)=x{\displaystyle f(x)=x} — пример нечётной функции f(x)=x2{\displaystyle f(x)=x^{2}} — пример чётной функции f(x)=x3,{\displaystyle f(x)=x^{3},} нечётная f(x)=x3+1{\displaystyle f(x)=x^{3}+1} ни чётная, ни нечётная

• Нечётная функция — функция, меняющая значение на противоположное при изменении знака независимой переменной (график её симметричен относительно центра координат).
• Чётная функция — функция, не изменяющая своего значения при изменении знака независимой переменной (график её симметричен относительно оси ординат).
• Ни чётная, ни нечётная функция (функция общего вида). В эту категорию относят функции, не подпадающие под предыдущие 2 категории.

ruwikiorg.ru

Как по графику определить является функция чётной или нечётной?

чётная — симметрична относительно оси оу, а нечетная относительно начала координат. Если не выпонимо, то ф=ия не обладает чётностью.

Если она симметрична относительно оси Y, то четна. Если «зеркальное перевернутое» отражение, то нечетна. Иначе не четна и не нечетна. (Если мне память не изменяет) . Например, косинус это четная функция, а синус нечетная.

В каких четвертях проходит

симметрия относительно оси Y (парабола например) означает чётность симметрия относительно начала координат (гипербола например) означает нечётность также могут попасться ни чётнаые ни нечётные функции (нессиметричные или симметричные относительно оси X)

touch.otvet.mail.ru