Примеры обратных функций | Математика
Обратная функция — функция y=g(x), которая получается из данной функции y=f(x), если из отношения x=f(y) выразить y через x.
Чтобы для данной функции y=f(x) найти обратную, надо:
1.В соотношении y=f(x) заменить x на y, а y — на x: x=f(y) .
2.В полученном выражении x=f(y) выразить y через x.
Функции f(x) и g(x) — взаимно обратны.
Примеры нахождения обратных функций:
1) y=3x-8
1. x=3y-8
2. 3y=x+8
y=(x+8)/3.
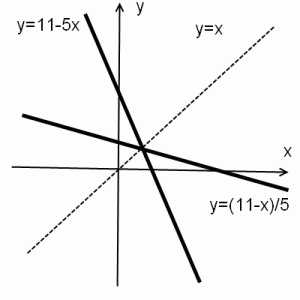
2) y=11-5x
1. x=11-5y
2. 5y=11-x
y=(11-x)/5.
Область определения и область значений функций f и g меняются местами: область определения f является областью значений g, а область значений f — областью определения g.
Не для всякой функции можно указать обратную. Условие обратимости функции — ее монотонность, то есть функция должна только возрастать или только убывать. Если функция не монотонна на всей области определения, но монотонная на некотором промежутке, тогда можно задать обратную ей функцию только на этом промежутке.
Пример обратных функций, заданных на промежутке.
y=x².
Это — квадратичная функция. Она убывает на промежутке (-∞;0), и
возрастает на промежутке (0;∞). Возьмем промежуток [0;∞). На этом промежутке функция монотонна, поэтому обратима. Ищем обратную функцию.
1. x=y²
2. y=√x.
y=x² и y=√x на [0;∞) — взаимно обратные функции.
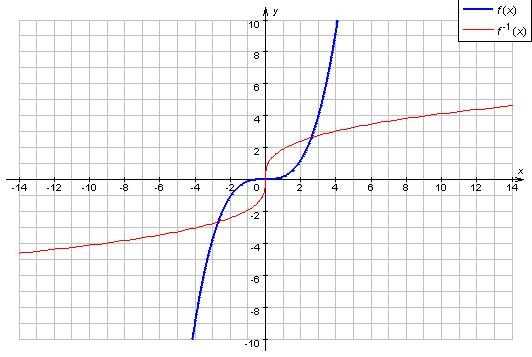
Графики взаимно-обратных функций симметричны относительно прямой y=x.
www.matematika.uznateshe.ru
3.1.4 Обратная функция. График обратной функции
Видеоурок 1: Обратные функции. Введение
Видеоурок 2: Обратные функции (Пример 1)
Видеоурок 3: Обратные функции (Пример 2)
Лекция: Обратная функция. График обратной функции
Рассмотрим некоторую функцию у = f(x), которая возрастает или же убывает, то есть является монотонной. Для нее будет иметься некоторая функция х = g(y), которая будет называться обратной функцией.
Что такое обратная функция?Давайте рассмотрим некое уравнение: соs(х) = 1/2.
Решением данного уравнения будет: x = ±arccos(1/2) + 2πk, k ϵ Z.
Косинус и арккосинус — это наглядный пример обратных функций.
Давайте рассмотрим обратные функции на примере.
Например, мы имеем функцию у = 3х + 2.
Для данной функции и область определения, и область значения может принимать все множество действительных чисел. Более того, данная функция является монотонно возрастающей на всем участке.
А теперь давайте из данной зависимости выразим «х». В результате этого получим:
х = у/3 — 2/3.
Полученная зависимость будет называться обратной функцией для той, что давалась изначально, только теперь мы получили зависимость «х» от «у».
Если записать второе уравнение в привычном нам виде, то есть заменить «х» на «у» и наоборот, получим:
у = х/3 — 2/3.
На графике изобразим первоначальную функцию, обратную ей, и функцию у = х.
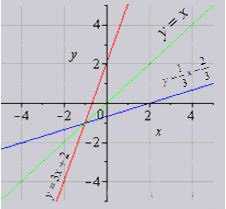
Можно заметить, что обратные функции симметричны относительно прямой у = х.
Свойства взаимообратных функций1.
2. Первое свойство дает понять, что область определения второй функции такая же, как и область значения первой.
3. Графики любых взаимообратных функций всегда будут симметричны относительно биссектрисы первой и третьей четверти.
4. Обратные функции имеют одинаковую монотонность.
Графики основных обратных функций
1. Степенная функция
Ниже представлены графики, полученные для положительного показателя степени и для отрицательного показателя степени:
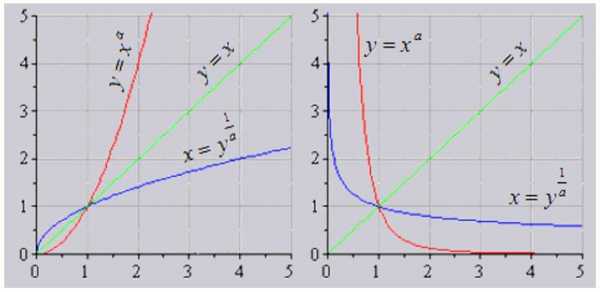
2. Обратные логарифмические функции и их графики:
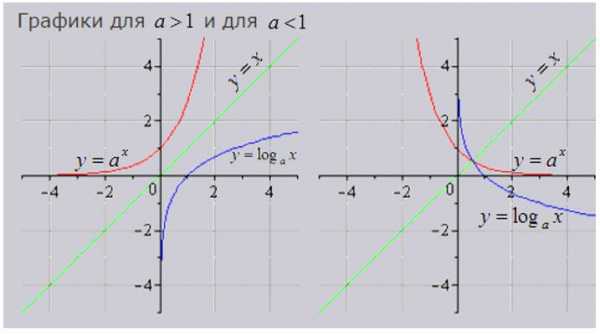
cknow.ru
Как найти обратную функцию для данной
Автор КакПросто!
Обратной функцией называют функцию, обращающую исходную зависимость у = f(x) таким образом, что аргумент х и функция у меняются ролями. То есть х становится функцией от y (х = f(у)). При этом графики взаимно обратных функций у = f (x) и х = f (у) симметричны по отношению к оси ординат в первой и третьей координатных четвертях декартовой системы. Областью определения обратной функции является область значений исходной, а областью значений в свою очередь – область определения заданной функции.
Статьи по теме:
Инструкция
В общем случае при нахождении обратной функции для заданной у = f(x) выразите аргумент х через функцию у. Для этого воспользуйтесь правилами умножения обеих частей равенства на одно и то же значение, переносом многочленов выражений, при этом учитывайте смену знака. В простом случае рассмотрения показательных функций вида: y = (7/x) + 11, обращение аргумента х производится элементарно: 7/x = у-11, х = 7*(у-11). Искомая обратная функция имеет вид х = 7*(у-11). Однако зачастую в функциях используются сложные степенные и логарифмические выражения, а также тригонометрические функции. В этом случае при нахождении обратной функции нужно учитывать известные свойства данных математических выражений. Если в исходной функции аргумент х стоит под степенью, для получения обратной функции возьмите от данного выражения корень с тем же показателем. Например, для заданной функции у = 7+ х² обратная будет иметь вид: f(у) = √у -7.При рассмотрении функции, где аргумент х представляет собой степень постоянного числа, примените определение логарифма. Из него следует, что для функции f(х) = ах обратной будет являться f(у) = logаy, причем основание логарифма а – в обоих случаях число, отличное от нуля. Так же и наоборот, рассматривая исходную логарифмическую функцию f(х) = logах, ее обратная функция представляет собой степенное выражение: f(у) = ау.
В частном случае исследования функции, содержащей натуральный логарифм ln х или десятичный lg х, т.е. логарифмы по основанию числа е и 10 соответственно, получение обратной функции проводится аналогично, только вместо основания а подставляется экспоненциальное число либо число 10. Например, f(х) = lg х -> f(у) = 10у и f(х) = ln х -> f(у) = еу.
Для тригонометрических функций обратными друг к другу являются следующие пары:
— y = cos x -> x = аrccos y;
— y = sin x -> x = аrcsin y;
— y = tan x -> x = аrctan y.
Обратите внимание
Следует помнить, что непрерывную функцию можно обратить лишь на тех промежутках ее значений, где она монотонна.
Совет полезен?
Статьи по теме:
Не получили ответ на свой вопрос?
Спросите нашего эксперта:
www.kakprosto.ru
