Обратная матрица существует когда – ?

11) Обратная матрица. Существование.

Определение 1. Квадратная матрица называется вырожденной, если ее определитель равен нулю, и невырожденной — в противном случае.

Определение 2. Матрица А^-1 называется обратной к квадратной матрице А n-го порядка, если А·А^-1= А^-1·А=Е.

Теорема 1. Для любой невырожденной квадратной матрицы существует единственная обратная матрица.

2 часть (существование). Дана матрица

А = , .

Построим обратную матрицу. Для этого совершим ряд действий:

1) заменим все элементы матрицы их алгебраическими дополнениями:

А* — матрица, присоединенная к матрице А;

2) транспонируем полученную матрицу:

(А*)

Т=;

3) разделим все элементы на число А

.

Проверим, будет ли полученная матрица обратной к исходной. Для этого умножим матрицу А на А^-1. Элемент, стоящий в i-й строке и j-м столбце матрицы произведения, будет равен

Элементы матрицы-результата совпадают с элементами единичной матрицы Е. Следовательно, А · А^-1=Е, т.е. А^-1 — обратная матрица к А.

12) Элементарные преобразования над матрицей. Второй способ нахождения обратной матрицы.

Определение 1. Элементарными преобразованиями над матрицей называются:

1)            умножение любой строки на число, отличное от нуля;

2)            прибавление к элементам одной строки соответствующих элементов другой, умноженных на одно и то же число;

3)            перестановка строк;

4)             отбрасывание строки из нулей.

Определение 2. Две матрицы называются эквивалентными (

АВ), если от одной можно перейти к другой с помощью конечного числа элементарных преобразований.

Теорема. Любую невырожденную квадратную матрицу с помощью элементарных преобразований можно привести к единичной матрице того же порядка. Применяя ту же последовательность элементарных преобразований к единичной матрице, можно получить обратную матрицу к данной.

Обычно элементарные преобразования производят над данной матрицей и единичной одновременно. Для этого составляют расширенную матрицу, в левой части которой стоит исходная матрица, а в правой — единичная матрица того же порядка. С помощью элементарных преобразований в левой части создают единичную матрицу, параллельно в правой части автоматически создается обратная матрица.

.

13. Ранг матрицы.

Пусть дана произвольная матрица размером . Возьмем произвольные k строк и k столбцов, . Минором порядка k называют определитель порядка

 k, составленный из элементов, расположенных на пересечении выбранных k строк и k столбцов, и обозначают M_k.

Для данной матрицы можно составить m · n миноров первого порядка,  миноров второго порядка и т.д.,  миноров k-го порядка.

Определение 1. Рангом матрицы называется максимальный порядок минора, отличного от нуля, и обозначаетсяr(A).

Очевидно, что .

Определение 2. Отличный от нуля минор порядка r=r(A) называется базисным минором матрицы А, а строки (столбцы), в которых он расположен, называют базисными строками (столбцами).

Теорема 1 (теорема о базисном миноре). Любой столбец (строка) матрицы А является линейной комбинацией ее базисных столбцов (строк).

Теорема 2

. Ранг матрицы равен максимальному числу линейно независимых строк (столбцов) матрицы.

При элементарных преобразованиях ранг матрицы не меняется. Ранг треугольной матрицы равен числу ненулевых строк этой матрицы.

Для того чтобы найти ранг матрицы, необходимо с помощью элементарных преобразований привести ее к треугольному виду и найти ранг полученной матрицы. Рассмотрим схему таких преобразований подробно. Пусть дана матрица

А=.

Предположим, что а₁₁ отличен от нуля (если а₁₁=0, то, переставив строки, этого можно добиться). Разделим первую строку на а₁₁, после чего на первом месте в первой строке будет стоять 1. Умножая последовательно первую строку на а₂₁, а_31, …, а_m1 и вычитая, соответственно, из второй, третьей, …, n-й, образуем в первом столбце все нулевые элементы.

А.

Преобразуем второй столбец, начиная с элемента а’₂₂. Если этот элемент отличен от нуля, то аналогично вышеизложенному получим на его месте единицу, а ниже расположенные элементы превратим в нули. Если а’₂₂=0, но ниже его в том же столбце есть элемент, отличный от нуля, то, поменяв местами строки, переставим его на место а’₂₂. Если в столбце не окажется ненулевых элементов, то можно поменять местами столбцы, пока на месте а’₂₂ не окажется ненулевой элемент.

После второго цикла получим новую эквивалентную матрицу.

А.

Выполняя последовательно несколько циклов подобных эквивалентных преобразований и отбросив нулевые строки, придем окончательно к матрице

А.

Буквой «а» условно обозначены элементы матрицы, которые могут принимать любые числовые значения.

Очевидно, что r(A)=m1, так как минор, расположенный в первых 

m1 строках и первых m1 столбцах, равен единице.

Вычисление ранга системы векторов можно свести к вычислению ранга матрицы. Из теоремы 2 следует, что ранг системы векторов равен рангу матрицы, столбцами (строками) которой являются векторы этой системы.

studfiles.net

Обратная матрица

Матрицу А^-1называютобратнойпо отношению к квадратной матрице А, если при умножении этой матрицы на матрицу А как справа, так и слева получается единичная матрица: А^-1* А = А * А^-1= Е.

Из определения следует, что обратная матрица является квадратной матрицей того же порядка, что и матрица А.

Можно отметить, что понятие обратной матрицы аналогично понятию обратного числа (это число, которое при умножении на данное число дает единицу: а*а

-1= а*(1/а) = 1).

Все числа, кроме нуля, имеют обратные числа.

Чтобы решить вопрос о том, имеет ли квадратная матрица обратную, необходимо найти ее определитель. Если определитель матрицы равен нулю, то такая матрица называется вырожденной, илиособенной.

Необходимое и достаточное условие существования обратной матрицы: обратная матрица существует и единственна тогда и только тогда, когда исходная матрица невырожденная.

Докажем необходимость. Пусть матрица А имеет обратную матрицу А^-1, т.е. А^-1* А = Е. Тогда |А^-1* А| = |А^-1| * |А| = |Е| = 1. Следовательно, |А|0.

Докажем достаточность. Чтобы его доказать, необходимо просто описать способ вычисления обратной матрицы, который мы всегда сможем применить для невырожденной матрицы.

Итак, пусть |А| 0. Транспонируем матрицу А. Для каждого элемента А^Т найдем алгебраическое дополнение и составим из них матрицу

, которую называютприсоединенной (взаимной, союзной):.

Найдем произведение присоединенной матрицы и исходной . Получим. Таким образом матрица В – диагональная. На ее главной диагонали стоят определители исходной матрицы, а все остальные элементы – нули:

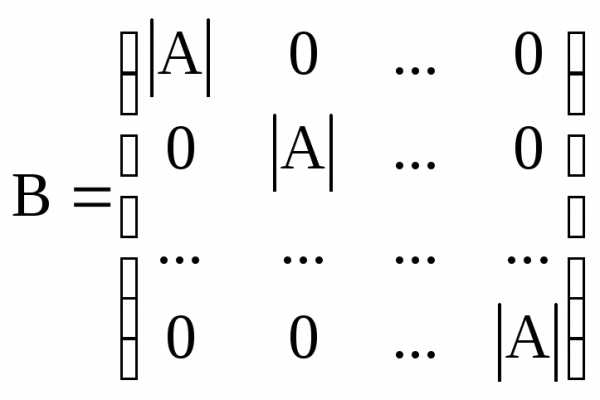
Аналогично можно показать, что .

Если разделить все элементы матрицы на |А|, то будет получена единичная матрица Е.

Таким образом , т.е..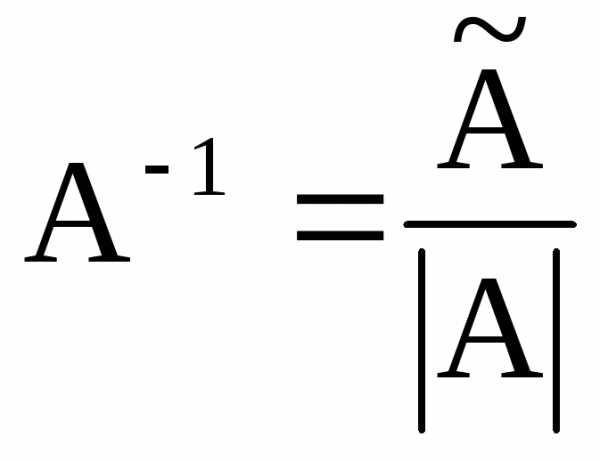

Докажем единственность обратной матрицы. Предположим, что существует другая обратная матрица для А, отличная от А^-1. Обозначим ее X. Тогда А * Х = Е. Умножим слева обе части равенства на А^-1.

А^-1* А * Х = А^-1* Е

Е * Х = А

-1

Х = А^-1

Единственность доказана.

Итак, алгоритм вычисления обратной матрицы состоит из следующих шагов:

1. Найти определитель матрицы |А| . Если |А| = 0, то матрица А — вырожденная, и обратную матрицу найти нельзя. Если |А| 0, то переходят к следующему шагу.

2. Построить транспонированную матрицу А^Т.

3. Найти алгебраические дополнения элементов транспонированной матрицы и построить присоединенную матрицу .

4. Вычислить обратную матрицу, разделив присоединенную матрицу на |А|.

5. Можно проверить правильность вычисления обратной матрицы в соответствии с определением: А^-1* А = А * А^-1= Е.

1. Найдем определитель этой матрицы по правилу треугольников:

 0.

Проверку опустим.

Можно доказать следующие свойства обращения матриц:

1) |А^-1

| = 1/|А|

2) (А^-1)^-1= А

3) (А^m)^-1= (А^-1)^m

4) (АB)^-1=B^-1* А^-1

5) (А^-1)^T= (А^T)^-1

Ранг матрицы

Минором k-го порядкаматрицы А размера m х n называют определитель квадратной матрицыk-го порядка, которая получена из матрицы А вычеркиванием каких-либо строк и столбцов.

Из определения следует, что порядок минора не превосходит меньшего из ее размеров, т.е. kmin{m;n}. Например, из матрицы А_5х3можно получить квадратные подматрицы первого, второго и третьего порядков (соответственно, рассчитать миноры этих порядков).

Рангомматрицы называют наивысший порядок отличных от нуля миноров этой матрицы (обозначают rang А, илиr(А)).

Из определения следует, что

1) ранг матрицы не превосходит меньшего из ее размеров, т.е. r(А)min{m;n};

2) r(А) = 0 тогда и только тогда, когда матрица нулевая (все элементы матрицы равны нулю), т.е.r(А) = 0А = 0;

3) для квадратной матрицы n-го порядка r(А) = n тогда и только тогда, когда эта матрица А невырожденная, т.е.r(А) = n|А|0.

На самом деле, для этого достаточно вычислить только один такой минор (тот, который получен вычеркиванием третьего столбца (потому что в остальных будет присутствовать нулевой третий столбец, и поэтому они равны нулю).

По правилу треугольника = 1*2*(-3) + 3*1*2 + 3*(-1)*4 – 4*2*2 – 1*(-1)*1 – 3*3*(-3) = -6 +6 – 12 – 16 + 1 +27 = 0.

Поскольку все миноры третьего порядка нулевые, r(А)2. Так как существует ненулевой минор второго порядка, например,

Очевидно, что использованные нами приемы (рассмотрение всевозможных миноров) не подходят для определения ранга в более сложных случаях ввиду большой трудоемкости. Обычно для нахождения ранга матрицы используют некоторые преобразования, которые называют элементарными:

1). Отбрасывание нулевых строк (столбцов).

2). Умножение всех элементов строки или столбца матрицы на число, отличное от нуля.

3). Изменение порядка строк (столбцов) матрицы.

4). Прибавление к каждому элементу одной строки (столбца) соответствующих элементов другой строки (столбца), умноженных на любое число.

5). Транспонирование.

Если матрица А получена из матрицы Bэлементарными преобразованиями, то эти матрицы называютэквивалентнымии обозначают АВ.

Теорема. Элементарные преобразования матрицы не изменяют ее ранг.

Доказательство теоремы следует из свойств определителя матрицы. В самом деле, при этих преобразованиях определители квадратных матриц либо сохраняются, либо умножаются на число, не равное нулю. В результате наивысший порядок отличных от нуля миноров исходной матрицы остается прежним, т.е. ее ранг не меняются.

С помощью элементарных преобразований матрицу приводят к так называемому ступенчатому виду (преобразуют в ступенчатую матрицу), т.е. добиваются, чтобы в эквивалентной матрице под главной диагональю стояли только нулевые элементы, а на главной диагонали – ненулевые:

Ранг ступенчатой матрицы равен r, так как вычеркиванием из нее столбцов, начиная с (r + 1)-го и дальше можно получить треугольную матрицу r-го порядка, определитель которой будет отличен от нуля, так как будет представлять собой произведение ненулевых элементов (следовательно, имеется минор r-го порядка, не равный нулю):

Пример. Найти ранг матрицы

1). Если а₁₁= 0 (как в нашем случае), то перестановкой строк или столбцов добьемся того, чтобы а₁₁0. Здесь поменяем местами 1-ю и 2-ю строки матрицы:

2). Теперь а₁₁0. Элементарными преобразованиями добьемся того, чтобы все остальные элементы в первом столбце равнялись нулю. Во второй строкеa₂₁= 0. В третьей строкеa₃₁= -4. Чтобы вместо (-4) стоял 0, прибавим к третьей строке первую строку, умноженную на 2 (т.е. на (-а₃₁/а₁₁) = -(-4)/2 = = 2). Аналогично к четвертой строке прибавим первую строку (умноженную на единицу, т.е. на (-а₄₁/а₁₁) = -(-2)/2 = 1).

3). В полученной матрице а₂₂0 (если бы было а₂₂= 0, то можно было бы снова переставить строки). Добьемся, чтобы ниже диагонали во втором столбце тоже стояли нули. Для этого к 3-й и 4-й строкам прибавим вторую строку, умноженную на -3 ((-а₃₂/а₂₂) = (-а₄₂/а₂₂) = -(-3)/(-1) = -3):

4). В полученной матрице две последние строки – нулевые, и их можно отбросить:

Получена ступенчатая матрица, состоящая из двух строк. Следовательно, r(A) = 2.

studfiles.net

4) Обратная матрица, вычисление, приложение.

Обра́тная ма́трица — такая матрица A⁻¹, при умножении на которую, исходная матрица A даёт в результате единичную матрицу E:

Квадратная матрица обратима тогда и только тогда, когда она невырожденная, то есть её определитель не равен нулю. Для неквадратных матриц и вырожденных матриц обратных матриц не существует.

Свойства обратной матрицы

, гдеобозначает определитель.

для любых двух обратимых матрици.

гдеобозначает транспонированную матрицу.

для любого коэффициента.

Если необходимо решить систему линейных уравнений , (b — ненулевой вектор) где— искомый вектор, и еслисуществует, то. В противном случае либо размерность пространства решений больше нуля, либо их нет вовсе.

Нахождение с помощью матрицы алгебраических дополнений

— транспонированная матрица алгебраических дополнений;

Полученная матрица A⁻¹и будет обратной. Сложность алгоритма зависит от сложности алгоритма расчета определителя Odet и равна O(n²)·Odet.

Иначе говоря, обратная матрица равна единице, делённой на определитель исходной матрицы и умноженной на транспонированную матрицу алгебраических дополнений элементов исходной матрицы.

5)Теорема о существовании и единственности обратной матрицы.

Теорема (единственности существования обратной матрицы): Если у матрицы существует обратная матрица, то она единственна.

Доказательство.

Пусть существует матрица , для которойи матрица, для которой.

Тогда , то есть. Умножим обе части равенства на матрицу, получим, гдеи.

Значит, , что и требовалось доказать.

6) Теорема Кронекера – Капели

Система линейных алгебраических уравнений совместна тогда и только тогда, когда ранг её основной матрицы равен рангу её расширенной матрицы, причём система имеет единственное решение, если ранг равен числу неизвестных, и бесконечное множество решений, если ранг меньше числа неизвестных.

Необходимость

Пусть система совместна. Тогда существуют числа такие, что. Следовательно, столбецявляется линейной комбинацией столбцовматрицы. Из того, что ранг матрицы не изменится, если из системы его строк (столбцов) вычеркнуть или приписать строку (столбец), которая является линейной комбинацией других строк (столбцов) следует, что.

Достаточность

Пусть . Возьмем в матрицекакой-нибудь базисный минор. Так как, то он же и будет базисным минором и матрицы. Тогда согласно теореме о базисном миноре последний столбец матрицыбудет линейной комбинацией базисных столбцов, то есть столбцов матрицы. Следовательно, столбец свободных членов системы является линейной комбинацией столбцов матрицы.

7) Метод крамера (вывод) решения систем линейных уравнений.

Метод (Крамера).

Если матрица квадратной системы невырожденная, то система определенная.

В этом случае решение системы может быть найдено по формулам ,

где — определитель системы;— определитель матрицы, получаемой из основной матрицы системы заменой её-го столбца столбцом свободных членов.

Теорема. (Правило Крамера):

Теорема. Система из n уравнений с n неизвестными

в случае, если определитель матрицы системы не равен нулю, имеет единственное решение и это решение находится по формулам:

x_i= D_i/D, где

D = det A, а D_i– определитель матрицы, получаемой из матрицы системы заменой столбца i столбцом свободных членов b_i.

D_i=

studfiles.net

Обратная матрица — Википедия. Что такое Обратная матрица

Обра́тная ма́трица — такая матрица A⁻¹, при умножении на которую исходная матрица A даёт в результате единичную матрицу E:

AA−1=A−1A=E{\displaystyle AA^{-1}=A^{-1}A=E}

Квадратная матрица обратима тогда и только тогда, когда она невырожденная, то есть её определитель не равен нулю. Для неквадратных матриц и вырожденных матриц обратных матриц не существует. Однако возможно обобщить это понятие и ввести псевдообратные матрицы, похожие на обратные по многим свойствам.

Свойства обратной матрицы

Способы нахождения обратной матрицы

Если матрица обратима, то для нахождения обратной матрицы можно воспользоваться одним из следующих способов:

Точные (прямые) методы

Метод Жордана—Гаусса

Возьмём две матрицы: саму A и единичную E. Приведём матрицу A к единичной матрице методом Гаусса—Жордана применяя преобразования по строкам (можно также применять преобразования и по столбцам). После применения каждой операции к первой матрице применим ту же операцию ко второй. Когда приведение первой матрицы к единичному виду будет завершено, вторая матрица окажется равной A⁻¹.

При использовании метода Гаусса первая матрица будет умножаться слева на одну из элементарных матриц Λi{\displaystyle \Lambda _{i}} (трансвекцию или диагональную матрицу с единицами на главной диагонали, кроме одной позиции):

Λ1⋅⋯⋅Λn⋅A=ΛA=E⇒Λ=A−1{\displaystyle \Lambda _{1}\cdot \dots \cdot \Lambda _{n}\cdot A=\Lambda A=E\Rightarrow \Lambda =A^{-1}}.

Λm=[1…0−a1m/amm0…0…0…1−am−1m/amm0…00…01/amm0…00…0−am+1m/amm1…0…0…0−anm/amm0…1]{\displaystyle \Lambda _{m}={\begin{bmatrix}1&\dots &0&-a_{1m}/a_{mm}&0&\dots &0\\&&&\dots &&&\\0&\dots &1&-a_{m-1m}/a_{mm}&0&\dots &0\\0&\dots &0&1/a_{mm}&0&\dots &0\\0&\dots &0&-a_{m+1m}/a_{mm}&1&\dots &0\\&&&\dots &&&\\0&\dots &0&-a_{nm}/a_{mm}&0&\dots &1\end{bmatrix}}}.

Вторая матрица после применения всех операций станет равна Λ{\displaystyle \Lambda }, то есть будет искомой. Сложность алгоритма — O(n3){\displaystyle O(n^{3})}.

С помощью матрицы алгебраических дополнений

Матрица, обратная матрице A{\displaystyle A}, представима в виде

A−1=adj(A)det(A){\displaystyle {A}^{-1}={{{\mbox{adj}}(A)} \over {\det(A)}}}

где adj(A){\displaystyle {\mbox{adj}}(A)} — присоединенная матрица (матрица, составленная из алгебраических дополнений для соответствующих элементов транспонированной матрицы).

Сложность алгоритма зависит от сложности алгоритма расчета определителя O_det и равна O(n²)·O_det.

Использование LU/LUP-разложения

Матричное уравнение AX=In{\displaystyle AX=I_{n}} для обратной матрицы X{\displaystyle X} можно рассматривать как совокупность n{\displaystyle n} систем вида Ax=b{\displaystyle Ax=b}. Обозначим i{\displaystyle i}-ый столбец матрицы X{\displaystyle X} через Xi{\displaystyle X_{i}}; тогда AXi=ei{\displaystyle AX_{i}=e_{i}}, i=1,…,n{\displaystyle i=1,\ldots ,n} ,поскольку i{\displaystyle i}-м столбцом матрицы In{\displaystyle I_{n}} является единичный вектор ei{\displaystyle e_{i}}. другими словами, нахождение обратной матрицы сводится к решению n уравнений с одной матрицей и разными правыми частями. После выполнения LUP-разложения (время O(n³)) на решение каждого из n уравнений нужно время O(n²), так что и эта часть работы требует времени O(n³)^[1].

Если матрица A невырождена, то для неё можно рассчитать LUP-разложение PA=LU{\displaystyle PA=LU}. Пусть PA=B{\displaystyle PA=B}, B−1=D{\displaystyle B^{-1}=D}. Тогда из свойств обратной матрицы можно записать: D=U−1L−1{\displaystyle D=U^{-1}L^{-1}}. Если умножить это равенство на U и L то можно получить два равенства вида UD=L−1{\displaystyle UD=L^{-1}} и DL=U−1{\displaystyle DL=U^{-1}}. Первое из этих равенств представляет собой систему из n² линейных уравнений для n(n+1)2{\displaystyle {\frac {n(n+1)}{2}}} из которых известны правые части (из свойств треугольных матриц). Второе представляет также систему из n² линейных уравнений для n(n−1)2{\displaystyle {\frac {n(n-1)}{2}}} из которых известны правые части (также из свойств треугольных матриц). Вместе они представляют собой систему из n² равенств. С помощью этих равенств можно реккурентно определить все n² элементов матрицы D. Тогда из равенства (PA)⁻¹ = A⁻¹P⁻¹ = B⁻¹ = D. получаем равенство A−1=DP{\displaystyle A^{-1}=DP}.

В случае использования LU-разложения не требуется перестановки столбцов матрицы D но решение может разойтись даже если матрица A невырождена.

Сложность алгоритма — O(n³).

Итерационные методы

Методы Шульца

{Ψk=E−AUk,Uk+1=Uk∑i=0nΨki{\displaystyle {\begin{cases}\Psi _{k}=E-AU_{k},\\U_{k+1}=U_{k}\sum _{i=0}^{n}\Psi _{k}^{i}\end{cases}}}

Оценка погрешности

Выбор начального приближения

Проблема выбора начального приближения U0{\displaystyle U_{0}} в рассматриваемых здесь процессах итерационного обращения матриц не позволяет относиться к ним как к самостоятельным универсальным методам, конкурирующими с прямыми методами обращения, основанными, например, на LU-разложении матриц. Имеются некоторые рекомендации по выбору U0{\displaystyle U_{0}}, обеспечивающие выполнение условия ρ(Ψ0)<1{\displaystyle \rho (\Psi _{0})<1} (спектральный радиус матрицы меньше единицы), являющегося необходимым и достаточным для сходимости процесса. Однако при этом, во-первых, требуется знать сверху оценку спектра обращаемой матрицы A либо матрицы AAT{\displaystyle AA^{T}} (а именно, если A — симметричная положительно определённая матрица и ρ(A)≤β{\displaystyle \rho (A)\leq \beta }, то можно взять U0=αE{\displaystyle U_{0}={\alpha }E}, где α∈(0,2β){\displaystyle \alpha \in \left(0,{\frac {2}{\beta }}\right)}; если же A — произвольная невырожденная матрица и ρ(AAT)≤β{\displaystyle \rho (AA^{T})\leq \beta }, то полагают U0=αAT{\displaystyle U_{0}={\alpha }A^{T}}, где также α∈(0,2β){\displaystyle \alpha \in \left(0,{\frac {2}{\beta }}\right)}; можно конечно упростить ситуацию и, воспользовавшись тем, что ρ(AAT)≤kAATk{\displaystyle \rho (AA^{T})\leq {\mathcal {k}}AA^{T}{\mathcal {k}}}, положить U0=AT‖AAT‖{\displaystyle U_{0}={\frac {A^{T}}{\|AA^{T}\|}}}). Во-вторых, при таком задании начальной матрицы нет гарантии, что ‖Ψ0‖{\displaystyle \|\Psi _{0}\|} будет малой (возможно, даже окажется ‖Ψ0‖>1{\displaystyle \|\Psi _{0}\|>1}), и высокий порядок скорости сходимости обнаружится далеко не сразу.

Примеры

Матрица 2 × 2

A−1=[abcd]−1=1detA[d−b−ca]=1ad−bc[d−b−ca]{\displaystyle \mathbf {A} ^{-1}={\begin{bmatrix}a&b\\c&d\\\end{bmatrix}}^{-1}={\frac {1}{\det \mathbf {A} }}{\begin{bmatrix}d&-b\\-c&a\\\end{bmatrix}}={\frac {1}{ad-bc}}{\begin{bmatrix}d&-b\\-c&a\\\end{bmatrix}}}^[2]

Обращение матрицы 2 × 2 возможно только при условии, что ad−bc=detA≠0{\displaystyle ad-bc=\det A\neq 0}.

Примечания

Ссылки

wiki.sc

Обратная матрица — это… Что такое Обратная матрица?

Обра́тная ма́трица — такая матрица A⁻¹, при умножении на которую, исходная матрица A даёт в результате единичную матрицу E:

Квадратная матрица обратима тогда и только тогда, когда она невырожденная, то есть её определитель не равен нулю. Для неквадратных матриц и вырожденных матриц обратных матриц не существует. Однако возможно обобщить это понятие и ввести псевдообратные матрицы, похожие на обратные по многим свойствам.

Свойства обратной матрицы

Способы нахождения обратной матрицы

Если матрица обратима, то для нахождения обратной матрицы можно воспользоваться одним из следующих способов:

Точные (прямые) методы

Метод Гаусса—Жордана

Возьмём две матрицы: саму A и единичную E. Приведём матрицу A к единичной матрице методом Гаусса—Жордана. После применения каждой операции к первой матрице применим ту же операцию ко второй. Когда приведение первой матрицы к единичному виду будет завершено, вторая матрица окажется равной A⁻¹.

При использовании метода Гаусса первая матрица будет умножаться слева на одну из элементарных матриц (трансвекцию или диагональную матрицу с единицами на главной диагонали, кроме одной позиции):

.

.

Вторая матрица после применения всех операций станет равна , то есть будет искомой. Сложность алгоритма — .

С помощью матрицы алгебраических дополнений

 — транспонированная матрица алгебраических дополнений;

Полученная матрица A⁻¹ и будет обратной. Сложность алгоритма зависит от сложности алгоритма расчета определителя O_det и равна O(n²)·O_det.

Иначе говоря, обратная матрица равна единице, делённой на определитель исходной матрицы и умноженной на транспонированную матрицу алгебраических дополнений элементов исходной матрицы.

Использование LU/LUP-разложения

Матричное уравнение для обратной матрицы можно рассматривать как совокупность систем вида . Обозначим -ый столбец матрицы через ; тогда , ,поскольку -м столбцом матрицы является единичный вектор . другими словами, нахождение обратной матрицы сводится к решению n уравнений с одной матрицей и разными правыми частями. После выполнения LUP-разложения (время O(n³)) на решение каждого из n уравнений нужно время O(n²), так что и эта часть работы требует времени O(n³)^[1].

Если матрица A невырождена, то для неё можно рассчитать LUP-разложение . Пусть , . Тогда из свойств обратной матрицы можно записать: . Если умножить это равенство на U и L то можно получить два равенства вида и . Первое из этих равенств представляет собой систему из n² линейных уравнений для из которых известны правые части (из свойств треугольных матриц). Второе представляет также систему из n² линейных уравнений для из которых известны правые части (также из свойств треугольных матриц). Вместе они представляют собой систему из n² равенств. С помощью этих равенств можно реккурентно определить все n² элементов матрицы D. Тогда из равенства (PA)⁻¹ = A⁻¹P⁻¹ = B⁻¹ = D. получаем равенство .

В случае использования LU-разложения не требуется перестановки столбцов матрицы D но решение может разойтись даже если матрица A невырождена.

Сложность алгоритма — O(n³).

Итерационные методы

Методы Шульца

Оценка погрешности

Выбор начального приближения

Проблема выбора начального приближения в рассматриваемых здесь процессах итерационного обращения матриц не позволяет относиться к ним как к самостоятельным универсальным методам, конкурирующими с прямыми методами обращения, основанными, например, на LU-разложении матриц. Имеются некоторые рекомендации по выбору , обеспечивающие выполнение условия (спектральный радиус матрицы меньше единицы), являющегося необходимым и достаточным для сходимости процесса. Однако при этом, во-первых, требуется знать сверху оценку спектра обращаемой матрицы A либо матрицы (а именно, если A — симметричная положительно определённая матрица и , то можно взять , где ; если же A — произвольная невырожденная матрица и , то полагают , где также ; можно конечно упростить ситуацию и, воспользовавшись тем, что , положить ). Во-вторых, при таком задании начальной матрицы нет гарантии, что будет малой (возможно, даже окажется ), и высокий порядок скорости сходимости обнаружится далеко не сразу.

Примеры

Матрица 2х2

Обращение матрицы 2х2 возможно только при условии, что .

Примечания

1. ↑ Кормен Т., Лейзерсон Ч., Ривест Р., Штайн К. Алгоритмы: построение и анализ, — М.: Вильямс, 2006 (стр. 700)

Ссылки

В этой статье не хватает ссылок на источники информации. Информация должна быть проверяема, иначе она может быть поставлена под сомнение и удалена. Вы можете отредактировать эту статью, добавив ссылки на авторитетные источники. Эта отметка установлена 14 мая 2011.

dic.academic.ru

Лекция 5. Обратная матрица

Обратные матрицы. Лекция 5.

Обратная матрица.

Квадратная матрица называетсяневырожденной, если её определитель не равен 0. В противном случае матрица называется вырожденной.

Матрица называетсяобратной к матрице , если выполняется следующее условие:. В этом случае обозначают.

Теорема 1. Всякая невырожденная матрица имеет свою обратную матрицу. Доказательство. Пусть дана матрица , причем. Составим матрицуследующим образом

,

где – алгебраические дополнения соответствующих элементовматрицы. Найдем произведение

На диагонали полученной матрицы стоят суммы произведений элементов строк на их алгебраические дополнения. По свойству 8 они равны определителю матрицы . На остальных местах стоят суммы произведений элементов строк на соответствующие алгебраические дополнения элементов других строк. По свойству 9 все они равны нулю. Поэтому

. Таким образом, . Аналогично можно получить равенство. Отсюда

По определению обратной матрицы

Так как , то матрицасуществует. Следовательно, матрицаимеет обратную матрицу. Теорема доказана.

Следствие: Для произвольной матрицы обратная матрица имеет вид .

Есть другой способ вычисления обратной матрицы методом элементарных преобразований. Для матрицы и единичной матрицысоставляется расширенная матрица, которая с помощью элементарных преобразований приводится к виду. Можно показать, что в этом случае.

Пример 25. Для матриц ивычислитьи.

Решение. Так как , то обратная матрица существует. Найдем алгебраические дополнения:

, ,,.

В соответствии с следствием из теоремы о существовании обратной матрицы . Сделаем проверку

.

Так как , то обратная матрица существует. Найдем алгебраические дополнения:

.

В соответствии с следствием из теоремы о существовании обратной матрицы . Сделаем проверку

Ответ:

Свойства обратной матрицы.

1. ;

2. ;

3. .

Ранг матрицы.

Пусть дана матрица размерности

.

Выделим в ней строк истолбцов.. Из элементов, стоящих на пересечениистрок истолбцов составим определитель– го порядка. Все такие определители называютминорами матрицы.

Пример 26. Для матрицы минорами второго порядка будут, например, определители

, ,,,,,,,.

Минорами третьего порядка — ,,,.

Всего для матрицы можно составитьминоров порядка, где. Так для матрицысуществует всего

миноров второго порядка.

Наибольший из порядков минора данной матрицы, отличных от нуля называется рангом матрицы. Обозначаются как .

Минор, порядок которого равен рангу матрицы, называют базисным минором. У каждой матрицы может быть несколько базисных миноров.

Свойства ранга матрицы.

1. При транспонировании матрицы её ранг не меняется.

2. Если из матрицы убрать нулевую строку (нулевой столбец), то ранг матрицы не изменится.

3. Ранг матрицы не меняется при её элементарных преобразованиях.

4. Ранг матрицы равен числу не нулевых строк в её ступенчатом виде.

27

studfiles.net

Обратная матрица

Обратная матрица

        Определение 14.8Матрицаназывается обратной матрицей для квадратной матрицы, если.

Из определения следует, что обратная матрица будет квадратной матрицей того же порядка, что и матрица(иначе одно из произведенийилибыло бы не определено).

Обратная матрица для матрицы обозначается. Таким образом, еслисуществует, то.

Из определения обратной матрицы следует, что матрица является обратной для матрицы, то есть. Про матрицыиможно говорить, что они обратны друг другу или взаимно обратны.

Предложение 14.20Если матрица имеет обратную, тои.

        Доказательство.     Так как определитель произведения матриц равен произведению определителей (предложение 14.7), то. Последствию 14.1, поэтому, что невозможно при. Из предыдущего равенства следует также.

Последнее предложение можно сформулировать в следующем виде.

Если определитель матрицы равен нулю, то обратная к ней не существует.

Так как для нахождения обратной матрицы важно, равен ли определитель марицы нулю или нет, то введем следующие определения.

        Определение 14.9Квадратную матрицуназовем вырожденной или особенной матрицей, если, и невырожденной или неособенной матрицей, если.

Предложение 14.21Если обратная матрица существует, то она единственна.

        Доказательство.     Пусть две матрицыиявляются обратными для матрицы. Тогда

и

Следовательно, .

Предложение 14.22Если квадратная матрица является невырожденной, то обратная для нее существует и

(14.14)

где — алгебраические дополнения к элементам.

        Доказательство.     Так как для невырожденной матрицыправая часть равенства (14.14) всегда существует, то достаточно показать, что эта правая часть является обратной матрицей для матрицы. Обозначим правую часть равенства (14.14) буквой. Тогда нужно проверить, чтои что. Докажем первое из этих равенств, второе доказывается аналогично.

Пусть . Найдем элементы матрицы, учитывая, что:

Если , то попредложению 14.17сумма справа равна нулю, то естьпри.

Если , то

Сумма справа представляет собой разложение определителя матрицы по-ой строке (предложение 14.16). Таким образом,

Итак, в матрице диагональные элементы равны 1, а остальные равны нулю, то есть.

Результаты предложений 14.20,14.21,14.22соберем в одну теорему.

Теорема 14.1Обратная матрица для квадратной матрицы существует тогда и только тогда, когда матрица— невырожденная, обратная матрица единственна, и справедлива формула (14.14).     

        Замечание 14.12Следует обратить особое внимание на места, занимаемые алгебраическими дополнениями в формуле обратной матрицы: первый индекс показывает номерстолбца, а второй — номерстроки, в которые нужно записать вычисленное алгебраическое дополнение.

        Пример 14.7Найдите обратную матрицу для матрицы.

Решение.Находим определитель

Так как , то матрица— невырожденная, и обратная для нее существует.

Находим алгебраические дополнения:

Составляем обратную матрицу, размещая найденные алгебраические дополнения так, чтобы первый индекс соответствовал столбцу, а второй — строке:

(14.15)

Полученная матрица и служит ответом к задаче.         

        Замечание 14.13В предыдущем примере было бы точнее ответ записать так:

(14.16)

Однако запись (14.15) более компактна и с ней удобнее проводить дальнейшие вычисления, если таковые потребуются. Поэтому запись ответа в виде (14.15) предпочтительнее, если элементы матриц — целые числа. И наоборот, если элементы матрицы— десятичные дроби, то обратную матрицу лучше записать без множителявпереди.

        Замечание 14.14При нахождении обратной матрицы приходится выполнять довольно много вычислений и необычно правило расстановки алгебраических дополнений в итоговой матрице. Поэтому велика вероятность ошибки. Чтобы избежать ошибок следует делать проверку: вычислить произведение исходной матрицы на итоговую в том или ином порядке. Если в результате получится единичная матрица, то обратная матрица найдена правильно. В противном случае нужно искать ошибку.

        Пример 14.8Найдите обратную матрицу для матрицы.

Решение.

— существует.

Ответ:.

Нахождение обратной матрицы по формуле (14.14) требует слишком много вычислений. Для матриц четвертого порядка и выше это неприемлемо. Реальный алгоритм нахождения обратной матрицы будет приведен позже.

Ремонт: дизайн магазина— дизайн интерьера Пиротехника,продажа пиротехникиБатареи салютов
Ядерное оружие | Инженерная графика | Высшая математика |Физика |Информатика | ТКМ| Электротехника | Атомная энергетика |Лекции
Начертательная геометрия и инженерная графика, перспектива Высшая математика примеры решения задач Физика для студентов технических университетов Электротехника, теоретические основы электротехники

studfiles.net