Онлайн графики в полярных координатах – Построение графика функции в полярных координатах · Калькулятор Онлайн

alexxlab / / Школьная жизнь

Построение графика функции в полярных координатах · Калькулятор Онлайн

Введите график функции

Важно  phi должно лежать в правильном промежутке, иначе график не сможет построиться

Построим график функции в полярных координатах r=r(φ),
где 0 <= φ <= 2π,
но вы можете задать свои границы φ.
Задайте также полярную функцию r(φ).

Правила ввода выражений и функций

Выражения могут состоять из функций (обозначения даны в алфавитном порядке):

absolute(x)
Абсолютное значение x
(модуль x или |x|)
arccos(x)
Функция — арккосинус от x
arccosh(x)
Арккосинус гиперболический от x
arcsin(x)
Арксинус от x
arcsinh(x)
Арксинус гиперболический от x
arctg(x)
Функция — арктангенс от
x
arctgh(x)
Арктангенс гиперболический от x
e
e число, которое примерно равно 2.7
exp(x)
Функция — экспонента от x (что и e^x)
log(x) or ln(x)
Натуральный логарифм от x
(Чтобы получить log7(x), надо ввести log(x)/log(7) (или, например для log10(x)=log(x)/log(10))
pi
Число — «Пи», которое примерно равно 3.14
sin(x)
Функция — Синус от x
cos(x)
Функция — Косинус от x
sinh(x)
Функция — Синус гиперболический от x
cosh(x)
Функция — Косинус гиперболический от x
sqrt(x)
Функция — квадратный корень из x
sqr(x) или x^2
Функция — Квадрат x
tg(x)
Функция — Тангенс от x
tgh(x)
Функция — Тангенс гиперболический от x
cbrt(x)
Функция — кубический корень из x
floor(x)
Функция — округление x в меньшую сторону (пример floor(4.5)==4.0)
sign(x)
Функция — Знак x
erf(x)
Функция ошибок (Лапласа или интеграл вероятности)

В выражениях можно применять следующие операции:

Действительные числа
вводить в виде 7.5, не 7,5
2*x
— умножение
3/x
— деление
x^3
— возведение в степень
x + 7
— сложение
x — 6
— вычитание

www.kontrolnaya-rabota.ru

Примеры графиков функций в полярных координатах

Поделиться в соцсетях:

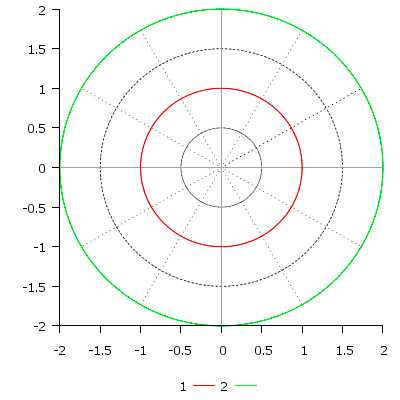
\[ r(t) = 1, \quad t \in [0; 2\pi] \\ r(t) = 2, \quad t \in [0; 2\pi] \]

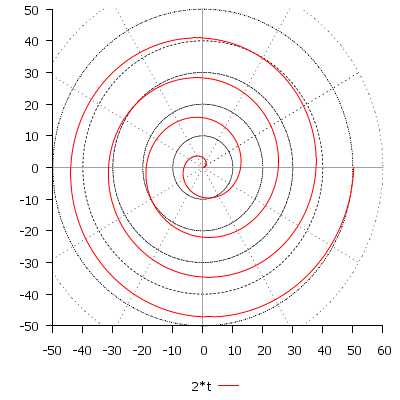
\[ r(t) = 2t, \quad t \in [0; 8\pi] \]

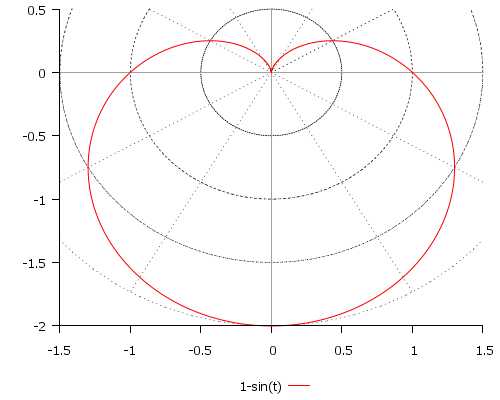
\[ r(t) = 1 — \sin(t), \quad t \in [0; 2\pi] \]

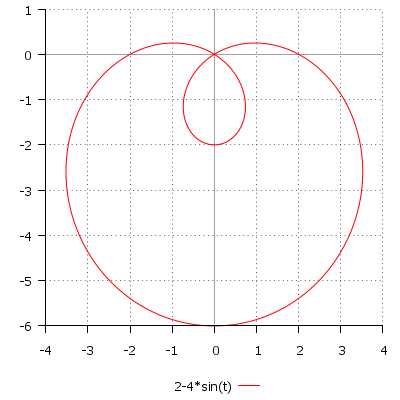
\[ r(t) = 2 — 4\sin(t), \quad t \in [0; 2\pi] \]

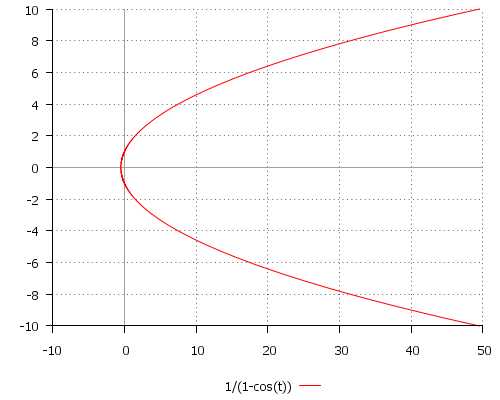
\[ r(t) = \frac{1}{1 — \cos(t)}, \quad t \in [0; 2\pi] \]

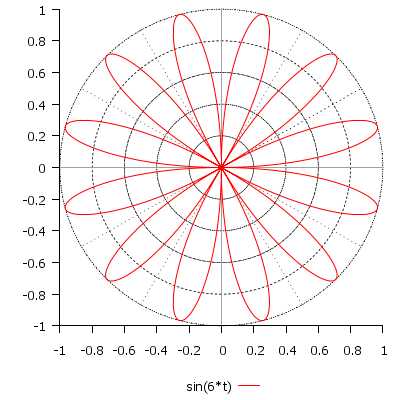
\[ r(t) = \sin(6t), \quad t \in [0; 2\pi] \]

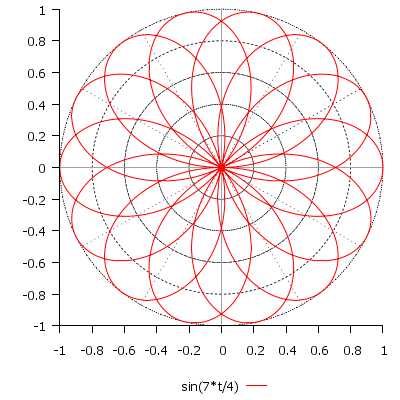
\[ r(t) = \sin\Big(\frac{7}{4}t\Big), \quad t \in [0; 8\pi] \]

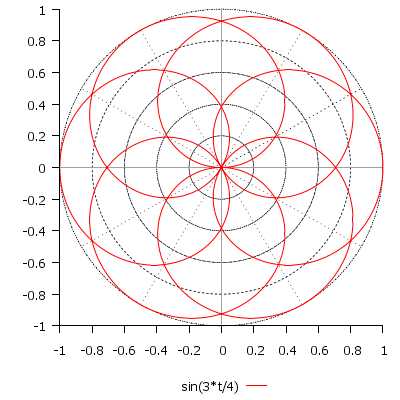
\[ r(t) = \sin\Big(\frac{3}{4}t\Big), \quad t \in [0; 8\pi] \]

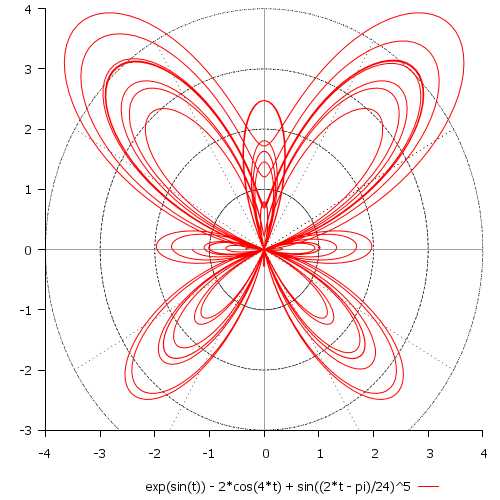
\[ r(t) = \mathrm{e}^{\sin(t)} — 2\cos(4t) + \sin^5\Big(\frac{2t — \pi}{24}\Big) \\ t \in [{-8\pi}; 8\pi] \]

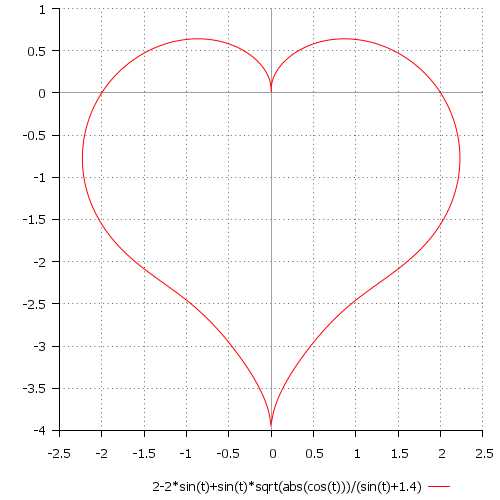
\[ r(t) = 2 — 2\sin(t) + \sin(t)\frac{\sqrt{|\cos(t)|}}{\sin(t) + 1,4} \\ t \in [0; 2\pi] \]

© OddLabs, 2011-2019 | Правильность результатов не гарантируется

grafikus.ru

Построить график функции онлайн

  • 2D в декартовых координатах
  • 2D график функции, которая задана параметрически
  • 2D график функции, в полярных координатах
  • 3D график поверхности, заданной уравнением
  • Построение графика по точкам
  • График неявно заданной функции

Это онлайн сервис в один шаг:

  • Ввести функцию, которую необходимо построить

Помимо построения графика функции, Вы получите результат исследования функции

Перейти: Онлайн сервис «Построение графика функции в декартовых координатах 2D» →

Это он-лайн сервис в три шага:

  • Ввести верхнюю и нижнюю границу для параметра
  • Ввести функцию x = x(t)
  • Ввести функцию y = y(t)

Перейти: Онлайн сервис «Построение графика функции параметрически» →

Это он-лайн сервис в два шага:

  • Указать границы полярного угла
  • Ввести функцию r=r(phi)

Перейти: Онлайн сервис «Построение графика функции в полярных координатах» →

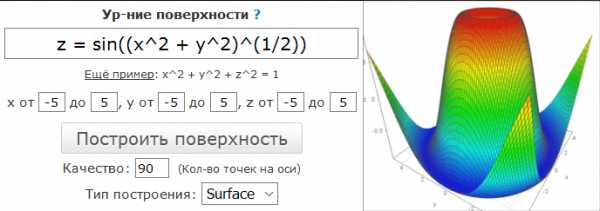
Это онлайн сервис в два шага:

  • Ввести верхние и нижние границы для графика поверхности
  • Ввести уравнение, для которого необходимо построить поверхность

Перейти: Онлайн сервис «Построение поверхности в декартовых координатах 3D» →

Это он-лайн сервис в один шаг:

  • Введите точки

Перейти: Онлайн сервис «Построение графика по точкам» →

www.kontrolnaya-rabota.ru

Построение графика в полярных координатах. Контрольные онлайн

Построение графика в полярных координатах

Дано уравнение кривой в полярной системе координат .
Требуется:
   а) построить кривую по точкам, придавая j значения из промежутка  с шагом ;
   б) записать уравнение этой кривой в декартовой прямоугольной системе координат, согласованной с полярной, и определить тип этой кривой. Решение
   а) Составим таблицу значений функции.

j

0

p/8

p/4

3p/8

p/2

5p/8

3p/4

7p/8

p

9p/8

5p/8

11p/8

3p/2

13p/8

7p/4

15p/8

r

3

2,8

2,32

1,72

1,5

1,26

1,11

1,02

1

1,02

1,11

1,26

1,5

1,72

2,32

2,8

   По этим данным отметим точки на плоскости и, плавно соединяя соседние точки, построим линию.

б) Перейдём к декартовой прямоугольной системе координат, пользуясь формулами , .
Заданное уравнение примет вид .
Преобразуем это уравнение: ,

, , , .
Выделив полные квадраты переменных  и , получим  или  .

   Это уравнение эллипса с центром в точке  и полуосями  и .

www.matem96.ru

Построение графика функции, заданной параметрически

Введите график функции

Важно  a должно быть меньше b, иначе график не сможет построиться

Видео пример:

Построим график параметрической функции x=x(t) и y=y(t),
где параметр t лежит в промежутке [a, b],
и вы можете задать свои границы.
Задайте также функции x и y, зависящих от параметра.

Правила ввода выражений и функций

Выражения могут состоять из функций (обозначения даны в алфавитном порядке):

absolute(x)
Абсолютное значение x
(модуль x или |x|)
arccos(x)
Функция — арккосинус от x
arccosh(x)
Арккосинус гиперболический от x
arcsin(x)
Арксинус от x
arcsinh(x)
Арксинус гиперболический от x
arctg(x)
Функция — арктангенс от x
arctgh(x)
Арктангенс гиперболический от x
e
e число, которое примерно равно 2.7
exp(x)
Функция — экспонента от x (что и e^x)
log(x) or ln(x)
Натуральный логарифм от x
(Чтобы получить log7(x), надо ввести log(x)/log(7) (или, например для log10(x)=log(x)/log(10))
pi
Число — «Пи», которое примерно равно 3.14
sin(x)
Функция — Синус от x
cos(x)
Функция — Косинус от x
sinh(x)
Функция — Синус гиперболический от x
cosh(x)
Функция — Косинус гиперболический от x
sqrt(x)
Функция — квадратный корень из x
sqr(x) или x^2
Функция — Квадрат x
tg(x)
Функция — Тангенс от x
tgh(x)
Функция — Тангенс гиперболический от x
cbrt(x)
Функция — кубический корень из x
floor(x)
Функция — округление x в меньшую сторону (пример floor(4.5)==4.0)
sign(x)
Функция — Знак x
erf(x)
Функция ошибок (Лапласа или интеграл вероятности)

В выражениях можно применять следующие операции:

Действительные числа
вводить в виде 7.5, не 7,5
2*x
— умножение
3/x
— деление
x^3
— возведение в степень
x + 7
— сложение
x — 6
— вычитание

www.kontrolnaya-rabota.ru

Построение графиков функций | Cubens

Как пользоваться программой

С помощью данной программы на Cubens можно построить график функции онлайн.

  • Десятичные дроби нужно разделять точкой
  • В некоторых случаях можно не писать знаки умножения
  • Можно строить множество графиков функций одновременно
  • Можно настроить названия осей и их интервалы
  • График можно скачать как PNG изображение
  • График можно распечатать
  • Можно получить ссылку на график чтобы поделиться им с другими
  • При наведении курсора на график его можно двигать, а также увеличивать или уменьшать масштаб

Предложения и замечания по работе программы можно оставить в комментариях ниже.

Режимы

На текущий момент в программе доступны четыре режима:

  • Обычный — в этом режиме можно строить графики функций, заданных уравнением
  • Параметрический — позволяет строить графики кривых, заданных параметрически, то есть, в виде и
  • Полярные координаты — позволяет строить графики кривых, заданных в полярной системе координат, то есть уравнением , где — радиальная координата, а — полярная координата
  • По точкам — этот режим предназначен для построения графиков функций указывая координаты их точек

График функции

Зависимость переменной от переменной называется функцией, если каждому значению соответствует единственное значение .

Функция обозначается или одной буквой или или равенством .

Область определения функции — это все значения, которые может принимать аргумент (переменная ).

Область значений функции — это все значения, которые может принимать функция (переменная ) при всех из области определения функции.

Функцию можно задать с помощью таблицы, графика или формулы. Формула задает правило, по которому каждому значению аргумента ставится в соответствие значение функции .

Графиком функции называется множество всех точек координатной плоскости с координатами , где первая координата пробегает всю область определения функции , а вторая координата — это соответствующее значение функции в точке .

cubens.com

площадь фигуры в полярных координатах — 22 Марта 2015 — Примеры решений задач

Площадь фигуры, заданной в полярных координатах

Рассмотрим примеры вычисления площади фигуры, заданной в полярных координатах кривой  ρ= ρ(φ), с помощью определенного интеграла по формуле

Пример 1. Вычислить площадь, ограниченную одним лепестком розы 

Решение.

Шаг 1. Выполним рисунок графика функции  с помощью калькулятора построения графиков функций в полярных координатах.

 

Шаг 2. Из рисунка видно, что угол φ в первой четверти изменяется от 0 до π/2, следовательно границы интегрирования φ1=0, φ2=π/2

Шаг 3.  Уравнение кривой , и границы φ1=0, φ2=π/2, подставляем в формулу

получаем площадь фигуры:

 

Замечание. Вычислить  площадь фигуры в полярных координатах можно с помощью калькулятора

 

www.reshim.su

No related posts.

Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *