Параллелограмм определение свойства признаки
Параллелограмм. Определение, свойства и признаки
Определение
Параллелограммом называют четырехугольник, который имеет параллельные противоположные стороны.
Отдельными видами параллелограмма являются прямоугольник, ромб и квадрат.
Свойства
- У параллелограмма пары противоположных сторон равны.
- У параллелограмма пары противоположных углов равны.
- У параллелограмма смежные (соседние) углы в сумме равны 180 градусов.
- Сумма всех углов параллелограмма равна 360 градусов.
- У параллелограмма диагонали пересекаются и при пересечении делятся пополам.
- Центр симметрии параллелограмма находится в точке пересечения его диагоналей.
- В параллелограмме диагонали и стороны связаны таким соотношением:
- Биссектриса угла параллелограмма отсекает от него равнобедренный треугольник.
Признаки
Существует несколько признаков, согласно которым четырехугольник является параллелограммом. Для этого достаточно выполнения одного из этих условий.
- Пары противоположных сторон четырехугольника равны.
- Пары противоположных углов равны.
- Диагонали четырехугольника пересекаются и при пересечении делятся пополам.
- Противоположные стороны четырехугольника равны и параллельны.
ru.solverbook.com
Конспект «Параллелограмм: свойства и признаки»
«Параллелограмм: свойства и признаки»

Параллелограмм — четырехугольник, у которого противолежащие стороны попарно параллельны. AB ∥ CD, BC ∥ AD.
Высота параллелограмма — перпендикуляр, проведенный из любой точки одной стороны на противолежащую сторону (расстояние между противолежащими сторонами).

Свойства параллелограмма:
1. Противолежащие стороны равны.
2. Противолежащие стороны параллельны.
3. Противолежащие углы равны.
4. Сумма соседних углов равна 180.
5. Диагонали параллелограмма пересекаются и точкой пересечения делятся пополам.
6. Диагональ делит параллелограмм на два равных треугольника.
7. Сумма квадратов диагоналей равна сумме квадратов его четырех сторон.
8. Диагонали параллелограмма делят его на четыре равновеликих треугольника.
Признаки параллелограмма:
— две противолежащие стороны равны и параллельны,
— противолежащие стороны попарно равны,
— диагонали пересекаются и точкой пересечения делятся пополам,
— каждая диагональ делит четырехугольник на два равных треугольника.
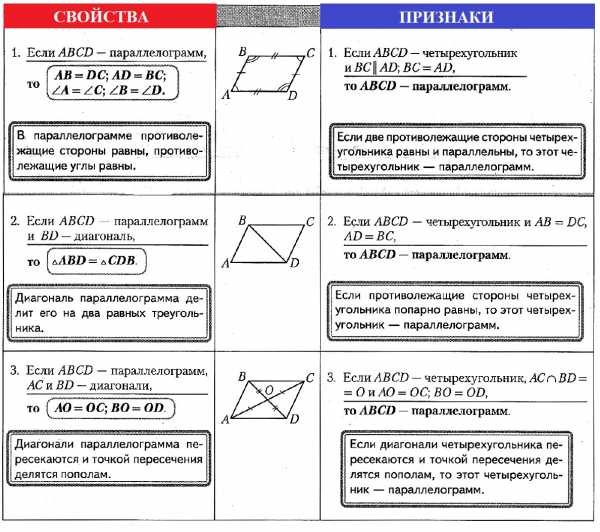
Это конспект по теме «Свойства и признаки параллелограмма». Выберите дальнейшие действия:
Параллелограмм: свойства и признаки
5 (100%) 4 vote[s]uchitel.pro
Определение параллелограмма и его свойства — ПАРАЛЛЕЛОГРАММ, ЕГО СВОЙСТВА. ПРИЗНАКИ ПАРАЛЛЕЛОГРАММА — ПЛАНИМЕТРИЯ — ГЕОМЕТРИЯ
ГЕОМЕТРИЯ
Раздел И. ПЛАНИМЕТРИЯ
§18. ПАРАЛЛЕЛОГРАММ, ЕГО СВОЙСТВА. ПРИЗНАКИ ПАРАЛЛЕЛОГРАММА.
1. Определение параллелограмма и его свойства.
Параллелограммом называют четырехугольник, у которого противоположные стороны попарно параллельны.
На рисунке изображен 236 параллелограмм АВСD: АВ || СD, АD || ВС.
Рассмотрим свойства параллелограмма:
1) Сумма любых двух соседних углов параллелограмма равна 180°.
2) Параллелограмм является выпуклым четырехугольником.
3) В паралелограмі противоположные стороны равны, противоположные углы равны.
На рисунке 236: АВ = СD, АD = ВС, A = C, B = D.
4) Периметр параллелограмма РАBCD = 2(АВ + ВС).
5) Диагонали параллелограмма пересекаются и точкой пересечения делятся пополам.
На рисунке 237: точка О — точка пересечения диагоналей параллелограмма; АО = ОС; ВО = ВD.
6) Сумма квадратов диагоналей параллелограмма равна сумме квадратов всех его сторон.
На рисунке 234:
Пример 1. Найдите все углы параллелограмма, если сумма двух из них равна 140°.
Решения. Поскольку сумма двух углов параллелограмма равен 140°, то это — противоположные углы, например A и C на рисунке 236. Поскольку A = C, то
Пример 2. В паралелограмі АВСВ биссектриса угла А делит сторону ВС на отрезки ВК = 3 см и КС = 2 см (рис. 238). Найдите периметр параллелограмма.
Решения.
1) ВС = ВК + КС = 3 + 2 = 5 (см).
2) KAD = ВКА (как внутренние разносторонние углы при пересечении параллельных прямых АВ и ВС секущей АК).
3) КАД = КАВ (по условию), поэтому ВКА = КАВ. Следовательно, по признаку равнобедренного треугольника: ∆АВК — равнобедренный, АВ = ВК = 3 см.
4) PABCD = 2(AB + ВС) = 2(3 + 5) = 16 (см).
Пример 3. Диагонали параллелограмма равны 7 см и 12 см, а одна из сторон на 1 см меньше второй. Найдите стороны параллелограмма.
Решение (рис. 237). 1) По условию АС = 11 см; D = 7 см. Пусть АD = х см, тогда ВС = (х — 1) см.
2) По свойству диагоналей параллелограмма имеем:
Учитывая х > 0, имеем х = 7. Итак, АD = 7 см, ВС = 6 см.
Высотой параллелограмма называют перпендикуляр, проведенный из любой точки стороны параллелограмма к прямой, содержит противоположную сторону.
На рисунке 239 MN — высота параллелограмма; МN АD, ММ ВС.
Из каждой вершины параллелограмма можно провести две высоты. Например, на рисунке 240 ВF и ВТ — висти параллелограмма, проведенные в соответствии с сторон АD и СD.
Пример 4. В паралелограмі ABCD из вершины тупого угла В проведена высоты BF и ВТ (рис. 240), FBT = 65°. Найдите угол А параллелограмма.
Решения. 1) В четырехугольнике FBTD: D = 360° — (65° + 2 ∙ 90°) = 115°.
2) Тогда A = 180° — D = 180° — 115° = 65°.
schooled.ru
Параллелограмм: свойства и признаки
Урок 5–6
Тема: Параллелограмм. Свойства и признаки параллелограмма.
Цель:
Опрос (фронтально).
Перечислите свойства равнобедренного треугольника.
Перечислите свойства прямоугольного треугольника.
Назовите признаки равенства треугольников.
Назовите признаки равенства прямоугольных треугольников.
Назовите признаки параллельности двух прямых.
1
Дайте определение многоугольника.
Начертите выпуклый и невыпуклый многоугольники. Назовите элементы многоугольника.
Дайте определение выпуклого многоугольника.
Напишите формулу для вычисления суммы углов выпуклого n-угольника.
Начертите 4-х-угольник. Покажите противоположные стороны и вершины. Чему равна сумма углов выпуклого 4-х-угольника.
ученик у доски
Карточка (слабым ученикам)

Новый материал.



Параллелограмм (греч. parallelógrammon, от parállelos—параллельный
и grámma — линия),
С
Доказательство
Д.п. АС-диагональ
АВС = АDС (по стороне и прилежащим к ней углам)
AC- общая
BAC=ACD –накрест лежащие углы при параллельных прямых АВ и CD и секущей AC
CAD=BCA –накрест лежащие углы при параллельных прямых ВC и AD и секущей AC
АВС = АDСAB=CD, BC=AD, B=D
A=BAC +CAD=BCA+ACD=C
войства параллелограмма 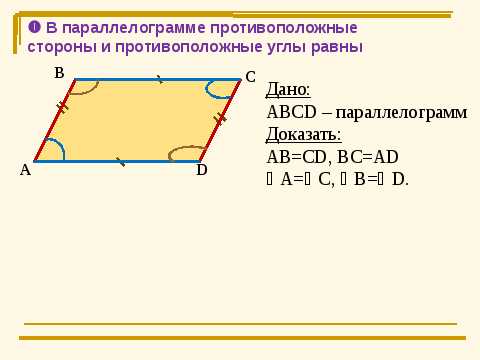
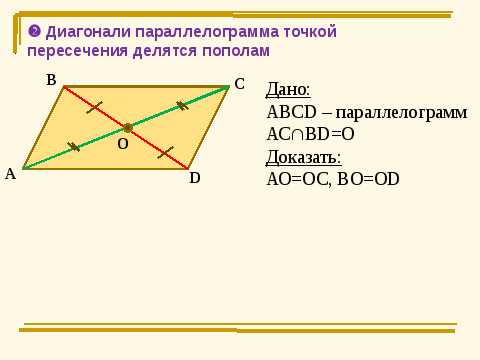
Доказательство
АОВ = СОD (по стороне и прилежащим к ней углам)
AВ=СD (свойство парал-ма)
ABО=CDО –накрест лежащие углы при параллельных прямых АВ и CD и секущей BD
ВAО=DCО –накрест лежащие углы при параллельных прямых АВ и CD и секущей AC
АОВ = СОDAО=ОC, BО=ОD.


Закрепление: № 376(а) (у), 376(б), 372(а), 374.

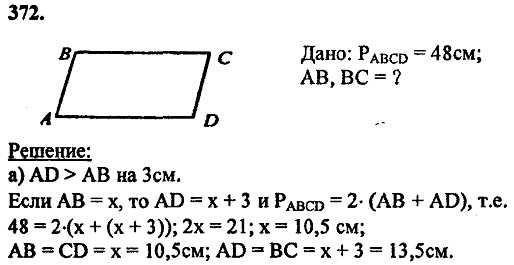

Признаки параллелограмма.
Теоремой, обратной данной, называется теорема, в которой условием является заключение данной теоремы, а заключением – условие данной теоремы.
Признаки – самостоятельно изучают по рядам, затем один ученик с ряда доказывает свой признак, с последующей записью в тетради.
Если в четырехугольнике две стороны равны и параллельны, то этот четырех угольник – параллелограмм
Дано: АВСD – четырехугольник, АВ=СD, АВСD
Доказать: АВСD – параллелограмм
Доказательство
Д.п. АС-диагональ
АВС = СDА (по 2-м сторонам и углу между ними)
AC- общая
АВ=CD (по условию)
ВAС=DCA – накрест лежащие углы при параллельных прямых АВ и СD и секущей AC
АВС = СDА BСА=DАС, BСА и DАС накрест лежащие углы при прямых ВС и АD и секущей AC ВС АD (признак параллельности прямых)
ВС АD (п.3), АВСD ( по условию) АВСD – параллелограмм (по определению)
Если в четырехугольнике противоположные стороны попарно равны, то этот четырех угольник – параллелограмм.
Дано: АВСD – четырехугольник, АВ=СD, ВС= АD
Доказать: АВСD – параллелограмм
Доказательство
Д.п. АС-диагональ
АВС = СDА (по 3-м сторонам)
АВС = СDА BАС=DСА, BСА и DАС накрест лежащие углы при прямых АВ и СD и секущей AC АВ СD (признак параллельности прямых)
АВСD (п.3), АВ=СD (по условию) АВСD – параллелограмм (1 признак параллелограмма)
Если в четырехугольнике диагонали пересекаются и точкой пересечения делятся пополам, то этот четырех угольник – параллелограмм
Дано: АВСD – четырехугольник, АСВD=О, АО=ОС, BО=ОD
Доказать: АВСD – параллелограмм
Доказательство
АОВ = СОD (по 2-м сторонам и углу между ними)
AОВ=СОD (св-во вертикальных углов)
АО=ОC (по условию)
ВО= ОD (по условию)
АОВ = СОD BАС=DСА, BСА и DАС накрест лежащие углы при прямых АВ и СD и секущей AC АВ СD (признак параллельности прямых)
АОВ = СОD АВ= СD
АВСD (п.2), АВ=СD (п.3) АВСD – параллелограмм (1 признак параллелограмма
Домашнее задание п.39-43, вопросы 1-9 стр.114, 372 (в), 375, 376(в,д), 377, 380.
Карточка (слабым ученикам)


Карточка (слабым ученикам)


infourok.ru
help. параллелограмм, определения, свойства, признаки (кратко)
Определение . Параллелограммом называется четырехугольник, у которго противоположные стороны параллельны, т. е. лежат на параллельных прямых Свойства Противоположные стороны параллелограмма равны | AB | = | CD | , | AD | = | BC | . Противоположные углы параллелограмма равны Диагонали параллелограмма пересекаются и точкой пересечения делятся пополам | AO | = | OC | , | BA | = | OD | . Сумма углов, прилежащих к одной стороне, равна 180 . Сумма всех углов равна 360° Сумма квадратов диагоналей параллелограмма равна удвоенной сумме квадратов его сторон: пусть а — длина стороны AB, b — длина стороны BC, d1 и d2 — длины диагоналей; тогда d1^2+d2^2=2(a^2+b^2) Признаки параллелограмма Четырёхугольник ABCD является параллелограммом, если выполняется одно из следующих условий: 1Противоположные стороны попарно равны: AB = CD, AD = BC. 2Противоположные углы попарно равны: ∠A = ∠C, ∠B = ∠D. 3Диагонали делятся в точке их пересечения пополам: AO = OC, BO = OD. 4Сумма соседних углов равна 180 градусов: ∠A + ∠B = 180, ∠B + ∠C = 180, ∠C + ∠D = 180, ∠D + ∠A = 180. 5Противоположные стороны попарно равны и параллельны: AB = CD, AB || CD. 6Сумма расстояний между серединами противоположных сторон выпуклого четырехугольника равна его полупериметру. 7 Противоположные стороны попарно параллельны: AB || CD, AD || BC.
Параллелограмм – четырёхугольник, у которого противолежащие стороны попарно параллельны, т. е. лежат на параллельных прямых. Противоположные стороны параллелограмма попарно равны. Частными случаями параллелограмма являются прямоугольник, квадрат и ромб.
спасибо большое !!!
докажите свойства медиан треугольника
пределение . Параллелограммом называется четырехугольник, у которго противоположные стороны параллельны, т. е. лежат на параллельных прямых Свойства Противоположные стороны параллелограмма равны | AB | = | CD | , | AD | = | BC | . Противоположные углы параллелограмма равны Диагонали параллелограмма пересекаются и точкой пересечения делятся пополам | AO | = | OC | , | BA | = | OD | . Сумма углов, прилежащих к одной стороне, равна 180 . Сумма всех углов равна 360° Сумма квадратов диагоналей параллелограмма равна удвоенной сумме квадратов его сторон: пусть а — длина стороны AB, b — длина стороны BC, d1 и d2 — длины диагоналей; тогда d1^2+d2^2=2(a^2+b^2) Признаки параллелограмма Четырёхугольник ABCD является параллелограммом, если выполняется одно из следующих условий: 1Противоположные стороны попарно равны: AB = CD, AD = BC. 2Противоположные углы попарно равны: ∠A = ∠C, ∠B = ∠D. 3Диагонали делятся в точке их пересечения пополам: AO = OC, BO = OD. 4Сумма соседних углов равна 180 градусов: ∠A + ∠B = 180, ∠B + ∠C = 180, ∠C + ∠D = 180, ∠D + ∠A = 180. 5Противоположные стороны попарно равны и параллельны: AB = CD, AB || CD. 6Сумма расстояний между серединами противоположных сторон выпуклого четырехугольника равна его полупериметру. 7 Противоположные стороны попарно параллельны: AB || CD, AD || BC.
touch.otvet.mail.ru
определение и свойства параллелограмма — КиберПедия
Напомним, что параллелограмм – это четырёхугольник, у которого противоположные стороны попарно параллельны. То есть, если – параллелограмм, то (см. Рис. 1).
Рис. 1
Параллелограмм обладает целым рядом свойств: противоположные углы равны ( ), противоположные стороны равны ( ). Кроме того, диагонали параллелограмма в точке пересечения делятся пополам, сумма углов, прилежащих к любой стороне параллелограмма, равна и т.д.
Но для того, чтобы пользоваться всеми этими свойствами, необходимо быть абсолютно уверенными в том, что рассматриваемый четырёхугольник – параллелограмм. Для этого и существуют признаки параллелограмма: то есть те факты, из которых можно сделать однозначный вывод, что четырёхугольник является параллелограммом. На предыдущем уроке мы уже рассмотрели два признака. Сейчас рассмотрим третий.
Третий признак параллелограмма и его доказательство
Если в четырёхугольнике диагонали в точке пересечения делятся пополам, то данный четырёхугольник является параллелограммом.
Дано:
– четырёхугольник; ; .
Доказать:
– параллелограмм.
Доказательство:
Для того чтобы доказать данный факт, необходимо доказать параллельность сторон параллелограмма. А параллельность прямых чаще всего доказывается через равенство внутренних накрест лежащих углов при этих прямых. Таким образом, напрашивается следующий способ доказательства третьего признака параллелограмма: через равенство треугольников .
Докажем равенство этих треугольников. Действительно, из условия следует: . Кроме того, поскольку углы – вертикальные, то они равны. То есть:
(первый признак равенства треугольников – по двум сторонам и углу между ними).
Из равенства треугольников: (так как равны внутренние накрест лежащие углы при этих прямых и секущей ). Кроме того, из равенства треугольников следует, что . Значит, мы получили, что в четырёхугольнике две стороны равны и параллельны. По первому признаку параллелограмма: – параллелограмм.
Доказано.
Пример задачи на третий признак параллелограмма и обобщение
Рассмотрим пример на применение третьего признака параллелограмма.
Пример 1
Дано:
–параллелограмм; . – середина , – середина , – середина , – середина (см. Рис. 2).
Рис. 2
Доказать: – параллелограмм.
Доказательство:
Значит, в четырёхугольнике диагонали в точке пересечения делятся пополам. По третьему признаку параллелограмма из этого следует, что – параллелограмм.
Доказано.
Если провести анализ третьего признака параллелограмма, то можно заметить, что этот признак соответствует свойству параллелограмма. То есть, то, что диагонали делятся пополам, является не просто свойством параллелограмма, а его отличительным, характеристическим свойством, по которому его можно выделить из множества четырёхугольников.
На следующем уроке мы рассмотрим решение различных задач про параллелограмм.
Домашнее задание
1. Диагонали четырёхугольника пересекаются в точке . Является ли данный четырёхугольник параллелограммом, если , , , . Ответ обоснуйте.
2. Диагонали четырёхугольника пересекаются в точке . Известно, что . Докажите, что данный четырёхугольник – параллелограмм.
Урок 9: Задачи на параллелограмм.
На уроке мы, прежде всего, повторим уже изученные ранее свойства и признаки параллелограмма и все основные понятия, которые связаны с этой геометрической фигурой. Главной целью занятия будет рассмотрение нескольких примеров на применение знаний о параллелограмме. В процессе решения примеров познакомимся с важнейшей теоремой, связанной с параллельностью прямых, – теоремой Фалеса.
1. Повторение определения, свойств и признака параллелограмма
Сегодня мы основное внимание уделим задачам на параллелограмм. Для этого нам необходимо владеть определением параллелограмма, его свойствами и признаками. Повторим эти факты, обобщим и структурируем их.
Определение. Параллелограмм– четырехугольник, у которого каждые две противоположные стороны параллельны (см. Рис. 1).
Рис. 1. Параллелограмм
Основные свойства параллелограмма:
Теорема.Первый признак параллелограмма.Если в четырехугольнике две противоположные стороны равны и параллельны (см. Рис. 2), то этот четырехугольник – параллелограмм. параллелограмм.
Рис. 2. Первый признак параллелограмма
Рис. 3. Второй признак параллелограмма
Теорема. Второй признак параллелограмма.Если в четырехугольнике каждые две противоположные стороны равны (см. Рис. 3), то этот четырехугольник –параллелограмм. параллелограмм.
Теорема. Третий признак параллелограмма.Если в четырехугольнике диагонали точкой пересечения делятся пополам (см. Рис. 4), то этот четырехугольник – параллелограмм. параллелограмм.
Рис. 4. Третий признак параллелограмма
Задачи на параллелограммы
Теперь рассмотрим решение задач с использованием определения, свойств и признаков параллелограмма.
Пример 1. В параллелограмме проведены биссектрисы и , которые пересекаются в точке . Найти .
Решение. Изобразим Рис. 5.
Рис. 5
Обозначим для удобства: . Следовательно, поскольку и биссектрисы.
По теореме о сумме внутренних углов треугольника .
Вспомним свойство параллелограмма о сумме углов, прилежащих к одной стороне: . Тогда:
.
Ответ. .
Пример 2. Прямая , проведенная через середину стороны параллельно стороне треугольника пересекает третью его сторону в середине. Доказать, что – это середина .
Доказательство. Изобразим Рис. 6 с дополнительными построениями: проведем .
Рис. 6
Рассмотрим четырехугольник :
параллелограмм по определению. Тогда по свойству равенства противоположных сторон , но по условию еще известно, что , следовательно, .
Рассмотрим треугольники и :
по второму признаку равенства треугольников (по стороне и прилежащим углам).
Из равенства указанных треугольников следует равенство их соответствующих сторон, т.е., например, что . Это означает, что точка является серединой стороны . Что и требовалось доказать.
Доказано.
Методы, которые мы рассмотрели сегодня на примерах, демонстрирующих свойства и признаки параллелограмма, помогут нам в дальнейшем при работе с параллелограммами в более сложных случаях.
Домашнее задание
1. В параллелограмме см, см, биссектрисы углов и пересекают сторону в точках и . Найдите длину отрезка .
2. Угол между высотами параллелограмма, проведенными из вершины тупого угла, равен . Найдите периметр параллелограмма, если его высоты равны 4 см и 6 см.
3. * Через середину диагонали параллелограмма проведена прямая, которая пересекает стороны и в точках и соответственно. Докажите, что четырехугольник параллелограмм.
Урок 10: Прямоугольник
На данном уроке мы будем рассматривать частный случай параллелограмма – прямоугольник. Мы введем его основные свойства, докажем теорему о равенстве диагоналей прямоугольника и сформулируем признак прямоугольника. Затем решим достаточно много задач, которые связаны с этой фигурой.
cyberpedia.su
Параллелограмм и его свойства
Муниципальное бюджетное общеобразовательное учреждение
Савинская средняя общеобразовательная школа
Исследовательская работа
Параллелограмм и его новые свойства
Выполнила: ученица 8Б класса
МБОУ Савинская СОШ
Кузнецова Светлана,14 лет
Руководитель: учитель математики
Тульчевская Н.А.
п. Савино
Ивановская область, Россия
2016г.
Содержание
I. Введение __________________________________________________ стр 3
II. Из истории параллелограмма ___________________________________стр 4
III Дополнительные свойства параллелограмма ______________________стр 4
IV. Доказательство свойств _____________________________________ стр 5
V. Решение задач с использованием дополнительных свойств __________стр 8
VI. Применение свойств параллелограмма в жизни ___________________стр 11
VII. Заключение _________________________________________________стр 12
VIII. Литература _________________________________________________стр 13
Введение
«Среди равных умов
при одинаковости прочих условий
превосходит тот, кто знает геометрию»
(Блез Паскаль).
Во время изучения темы «Параллелограмм» на уроках геометрии мы рассмотрели два свойства параллелограмма и три признака, но когда мы начали решать задачи, то оказалось, что этого недостаточно.
У меня возник вопрос, а есть ли у параллелограмма еще свойства, и как они помогут при решении задач.
И я решила изучить дополнительные свойства параллелограмма и показать, как их можно применить для решения задач.
Предмет исследования: параллелограмм
Объект исследования: свойства параллелограмма
Цель работы:
формулировка и доказательство дополнительных свойств параллелограмма, которые не изучаются в школе;
применение этих свойств для решения задач.
Задачи:
Найти дополнительную литературу по исследуемому вопросу;
Изучить дополнительные свойства параллелограмма и доказать их;
Показать применение этих свойств для решения задач;
Рассмотреть применение свойств параллелограмма в жизни.
Методы исследования:
Работа с учебной и научно – популярной литературой, ресурсами сети Интернет;
Изучение теоретического материала;
Выделение круга задач, которые можно решать с использованием дополнительных свойств параллелограмма;
Наблюдение, сравнение, анализ, аналогия.
Продолжительность исследования: 3 месяца: январь-март 2016г
Из истории параллелограмма
В учебнике геометрии мы читаем следующее определение параллелограмма: параллелограмм – это такой четырехугольник, у которого противоположные стороны попарно параллельны
Слово «параллелограмм» переводится как «параллельные линии» (от греческих слов Parallelos — параллельный и gramme — линия), этот термин был введен Евклидом. В своей книге «Начала» Евклид доказал следующие свойства параллелограмма: противоположные стороны и углы параллелограмма равны, а диагональ делит его пополам. О точке пересечения параллелограмма Евклид не упоминает. Только к концу средних веков была разработана полная теория параллелограммов И лишь в XVII веке в учебниках появились теоремы о параллелограммах, которые доказываются с помощью теоремы Евклида о свойствах параллелограмма.
III Дополнительные свойства параллелограмма
В учебнике по геометрии даны только 2 свойства параллелограмма:
Противоположные углы и стороны равны
Диагонали параллелограмма пересекаются и точкой пересечения делятся пополам
В различных источниках по геометрии можно встретить следующие дополнительные свойства:
Сумма соседних углов параллелограмма равна 1800
Биссектриса угла параллелограмма отсекает от него равнобедренный треугольник;
Биссектрисы противоположных углов параллелограмма лежат на параллельных прямых;
Биссектрисы соседних углов параллелограмма пересекаются под прямым углом;
Биссектрисы всех углов параллелограмма при пересечении образуют прямоугольник;
Расстояния от противоположных углов параллелограмма до одной и той же его диагонали равны.
Если в параллелограмме соединить противоположные вершины с серединами противоположных сторон, то получится еще один параллелограмм.
Сумма квадратов диагоналей параллелограмма равна удвоенной сумме квадратов его смежных сторон.
Если в параллелограмме из двух противоположных углов провести высоты, то получится прямоугольник.
IV Доказательство свойств параллелограмма
Сумма соседних углов параллелограмма равна 1800
Дано:
ABCD – параллелограмм
Доказать:
 A +
A + B =
B = 
Доказательство:
 А и
А и  B –внутренние односторонние углы при параллельных прямых ВС
B –внутренние односторонние углы при параллельных прямых ВС  АD и секущей АВ, значит,
АD и секущей АВ, значит,  A +
A + B =
B = 
2
Дано: АBCD — параллелограмм,
АК -биссектриса  А.
А.
Доказать:  АВК – равнобедренный
АВК – равнобедренный
Доказательство:
1)  1=
1= 3 (накрест лежащие при ВС
3 (накрест лежащие при ВС AD и секущей AK),
AD и секущей AK),
2)  2=
2= 3 т. к. АК – биссектриса,
3 т. к. АК – биссектриса,
значит  1=
1= 2.
2.
3)  АВК – равнобедренный т. к. 2 угла треугольника равны
АВК – равнобедренный т. к. 2 угла треугольника равны
3
Дано: АВСD – параллелограмм,
АК – биссектриса  A,
A,
СР — биссектриса  C.
C.
Доказать: АК ║ СР
Доказательство:
1)  1=
1= 2 т. к. АК-биссектриса
2 т. к. АК-биссектриса
2)  4=
4= 5 т.к. СР – биссектриса
5 т.к. СР – биссектриса
3)  3=
3= 1 (накрест лежащие углы при
1 (накрест лежащие углы при
ВС ║ АD и АК-секущей),
4)  A=
A= C (по свойству параллелограмма), значит
C (по свойству параллелограмма), значит 2=
2= 3=
3= 4=
4= 5.
5.
4) Из п. 3 и 4 следует, что  1=
1= 4, а эти углы соответственные при прямых АК и СР и секущей ВС,
4, а эти углы соответственные при прямых АК и СР и секущей ВС,
значит, АК ║ СР ( по признаку параллельности прямых)
. Биссектрисы противоположных углов параллелограмма лежат на параллельных прямыхБиссектрисы соседних углов параллелограмма пересекаются под прямым углом
Дано: АВСD — параллелограмм,
АК-биссектриса  A,
A,
DР-биссектриса  D
D
Доказать: DР  АК.
АК.
Доказательство:
1)  1=
1= 2, т.к. АК — биссектриса
2, т.к. АК — биссектриса
Пусть,  1=
1= 2=x, тогда
2=x, тогда  А=2x,
А=2x,
2)  3=
3= 4, т.к. DР – биссектриса
4, т.к. DР – биссектриса
Пусть,  3=
3= 4= у, тогда
4= у, тогда  D=2y
D=2y
3)  A+
A+ D=1800, т.к. сумма соседних углов параллелограмма равна 180
D=1800, т.к. сумма соседних углов параллелограмма равна 180
2x+2y=1800
x+y=900
2) Рассмотрим  AОD
AОD
 1+
1+ 3=900, тогда
3=900, тогда  <5=900 (сумма углов треугольников равна 1800)
<5=900 (сумма углов треугольников равна 1800)
5. Биссектрисы всех углов параллелограмма при пересечении образуют прямоугольник
Дано: АВСD — параллелограмм, АК-биссектриса  A,
A,
DР-биссектриса  D,
D,
CM -биссектриса  C,
C,
BF -биссектриса  B.
B.
Доказать: KRNS-прямоугольник
Доказательство:
Исходя из предыдущего свойства  8=
8= 7=
7= 6=
6= 5=900,
5=900,
значит KRNS-прямоугольник.
Расстояния от противоположных углов параллелограмма до одной и той же его диагонали равны.
Дано: ABCD-параллелограмм, АС-диагональ.
ВК  АС, DP
АС, DP AC
AC
Доказать: BК=DР
Доказательство: 1) DCР=
DCР= КAB, как внутренние накрест лежащие при АВ ║ СD и секущей АС.
КAB, как внутренние накрест лежащие при АВ ║ СD и секущей АС.
2)  AКB=
AКB= CDР (по стороне и двум прилежащим к ней углам АВ=СD
CDР (по стороне и двум прилежащим к ней углам АВ=СD  CDР=
CDР= ABК).
ABК).
А в равных треугольниках соответственные стороны равны, значит DР=BК.
Если в параллелограмме соединить противоположные вершины с серединами противоположных сторон, то получится еще один параллелограмм.
Дано: ABCD-параллелограмм.
Доказать: ВКDР – параллелограмм.
Доказательство:
1) BР=КD (AD=BC, точки К и Р
делят эти стороны пополам)
2) ВР ║ КD (лежат на АD  BC)
BC)
Если в четырехугольнике противоположные стороны равны и параллельны, значит, этот четырехугольник — параллелограмм.
Р
Если в параллелограмме из двух противоположных углов провести высоты, то получится прямоугольник.
Сумма квадратов диагоналей параллелограмма равна удвоенной сумме квадратов его смежных сторон.
Дано: ABCD – параллелограмм. BD и AC — диагонали.
Доказать: АС2 +ВD2 =2(AB2+ AD2)
Доказательство: 1) АСК: AC²=
АСК: AC²=  +
+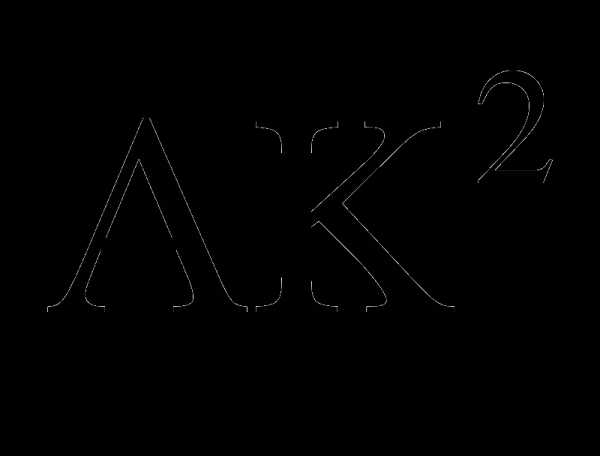
2) BРD: BD2 =BР2 + РD2 (по теореме Пифагора)
BРD: BD2 =BР2 + РD2 (по теореме Пифагора)
3) AC²+BD²=СК²+AК²+BР²+РD²
4) СК = ВР = Н (высота)
5) АС2+ВD2=H2+AК2+H2+РD2
6) Пусть DК=AР=х, тогда  CКD: H2=CD2 – х2 по теореме Пифагора)
CКD: H2=CD2 – х2 по теореме Пифагора)
7) АС²+ВD² = СD2— х²+ АК1²+CD2-х2+РD2,
АС²+ВD²=2СD2-2х2+AК2+РD2
8) AК=AD+х, РD=AD-х,
АС²+ВD² =2CD2-2х2+(AD+х)2+(AD-х)2,
АС²+ВD²=2СD²-2х² +AD2+2ADх+х2+AD2-2ADх+х2,
АС²+ВD²=2CD2+2AD2=2(CD2+AD2).
С
V. Решение задач с использованием этих свойств
Точка пересечения биссектрис двух углов параллелограмма, прилежащих к одной стороне, принадлежит противоположной стороне. Меньшая сторона параллелограмма равна 5. Найдите его большую сторону.
Р
Дано: ABCD – параллелограмм,
АК – биссектриса  А,
А,
DК – биссектриса  D, АВ=5
D, АВ=5
Найти: ВС
ешениеРешение
Т.к. АК — биссектриса  А, то
А, то  АВК – равнобедренный.
АВК – равнобедренный.
АВ=ВК= 5
Т.к. DК – биссектриса  D, то
D, то  DCK- равнобедренный
DCK- равнобедренный
DC=CК= 5
Тогда, ВС=ВК+СК=5+5 = 10
Ответ: 10
2. Найдите периметр параллелограмма, если биссектриса одного из его углов делит сторону параллелограмма на отрезки 7 см и 14 см.
1 случай
Дано: ABCD – параллелограмм, АК – биссектриса  А,
А,
ВК=14 см, КС=7 см
Найти: Р параллелограмма
Решение
ВС=ВК+КС=14+7=21 (см)
Т.к. АК – биссектриса  А, то
А, то  АВК – равнобедренный.
АВК – равнобедренный.
АВ=ВК= 14 см
Тогда Р=2 (14+21) =70 (см)
2
случайДано: ABCD – параллелограмм,
DК – биссектриса  D,
D,
ВК=14 см, КС=7 см
Найти: Р параллелограмма
Решение
ВС=ВК+КС=14+7=21 (см)
Т.к. DК – биссектриса  D, то
D, то  DCK- равнобедренный
DCK- равнобедренный
DC=CК= 7
Тогда, Р= 2 (21+7) = 56 (см)
Ответ: 70см или 56 см
3.Стороны параллелограмма равны 10 см и 3 см. Биссектрисы двух углов, прилежащих к большей стороне, делят противоположную сторону на три отрезка. Найдите эти отрезки.
1 случай: биссектрисы пересекаются вне параллелограмма
Дано: ABCD – параллелограмм, АК – биссектриса  А,
А,
DК – биссектриса  D, АВ=3 см, ВС=10 см
D, АВ=3 см, ВС=10 см
Найти: ВМ, МN, NC
Решение
Т.к. АМ — биссектриса  А, то
А, то  АВМ – равнобедренный.
АВМ – равнобедренный.
АВ=ВМ= 3
Т.к. DN – биссектриса  D, то
D, то  DCN- равнобедренный
DCN- равнобедренный
DC=CN= 3
Тогда, МN= 10 – (BM+NC) = 10 – (3+3)=4 см
2 случай: биссектрисы пересекаются внутри параллелограмма
Т.к. АN — биссектриса  А, то
А, то  АВN – равнобедренный.
АВN – равнобедренный.
АВ=ВN= 3
Т.к. DM – биссектриса  D, то
D, то  DCM- равнобедренный
DCM- равнобедренный
DC=CM= 3
Тогда, BN=3 см, СN=10 – 3 = 7 см,
CM= 3 см, ВМ=10 – 3 =7 см, чего быть не может, т.к. ВC=10 см
2 случай не возможен.
Ответ: 3см, 4 см, 3 см
4. (ЕГЭ-2010) В параллелограмме ABCD биссектрисы углов при стороне AD делят сторону ВС точками М и N так, что BM : MN = 1:5. Найдите ВС, если АВ =3
В этой задаче также возможны два случая:
биссектрисы пересекаются вне параллелограмма и внутри параллелограмма.
1 случай: биссектрисы пересекаются вне параллелограмма
C
Дано: ABCD – параллелограмм, АМ – биссектриса  А,
А,
DN – биссектриса  D, АВ=3 см, BM : MN = 1:5
D, АВ=3 см, BM : MN = 1:5
Найти: BC
Решение
Т.к. АМ — биссектриса  А, то
А, то  АВМ – равнобедренный.
АВМ – равнобедренный.
АВ=ВМ= 3 см
Т.к. DN – биссектриса  D, то
D, то  DCN— равнобедренный
DCN— равнобедренный
DC=CN= 3 см
Т.к. ВМ: МN=1:5, то на отрезок ВМ приходится 1 часть, а на отрезок MN – 5 частей,
Значит, MN=
Тогда, ВС= ВМ +МN+NC=3+15+3=21 см
2 случай: биссектрисы пересекаются внутри параллелограмма
Т.к. АN — биссектриса  А, то
А, то  АВN – равнобедренный.
АВN – равнобедренный.
АВ=ВN= 3
Т.к. DM – биссектриса  D, то
D, то  DCM- равнобедренный
DCM- равнобедренный
DC=CM= 3
Тогда, BN=3 см и BN = 6 частей, значит 1 часть = 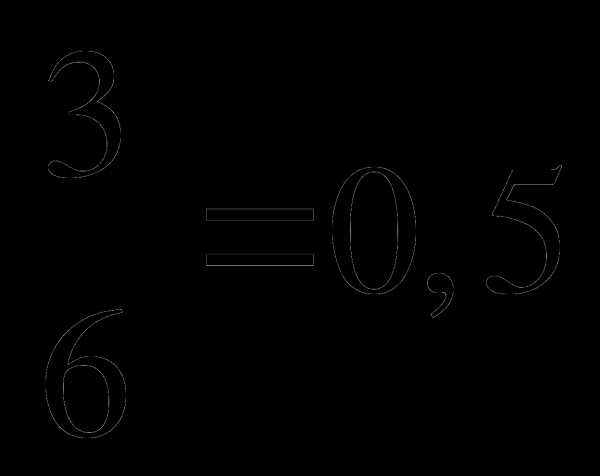 см
см
MN = 5 частей, значит, MN = см
CN= CM-MN=3-2,5=0,5
BC=BM+MN+NC=0,5+2,5+0,5=3,5 см
Ответ: 21 см или 3,5 см
VI. Применение свойств параллелограмма в жизни
Параллелограмм не является жесткой фигурой. Эта особенность параллелограмма позволила инженерам применить свойства параллелограмма в практической жизни.
Свойство «движимости» параллелограмма широко используется на практике.
Благодаря его движимости лампу можно устанавливать в удобное для работы положение
А раздвижную решетку – отодвигать на необходимое расстояние в дверном проеме
Параллелограммный механизм — четырёхзвенный механизм, звенья которого составляют параллелограмм. Применяется для реализации поступательного движения шарнирными механизмами.
Параллелограмм с неподвижным звеном — одно звено неподвижно, противоположное совершает качательное движение, оставаясь параллельным неподвижному. Два параллелограмма, соединённых друг за другом, дают конечному звену две степени свободы, оставляя его параллельным неподвижному.
Примеры: стеклоочистители автобусов, погрузчики, штативы, подвесы, автомобильные подвески.
Параллелограмм с неподвижным шарниром — используется свойство параллелограмма сохранять постоянное соотношение расстояний между тремя точками. Пример: чертёжный пантограф — прибор для масштабирования чертежей.
Ромб — все звенья одинаковой длины, приближение (стягивание) пары противоположных шарниров приводит к раздвиганию двух других шарниров. Все звенья работают на сжатие.
Примеры — автомобильный ромбовидный домкрат, трамвайный пантограф.
Ножничный или X-образный механизм, также известный как Нюрнбергские ножницы— вариант ромба — два звена, соединённые посередине шарниром. Достоинства механизма — компактность и простота, недостаток — наличие двух пар скольжения. Два (и более) таких механизма, соединённые последовательно, образуют в середине ромб(ы). Применяется в подъёмниках, детских игрушках.
VII Заключение
Кто с детских лет занимается математикой,
тот развивает внимание, тренирует свой мозг,
свою волю, воспитывает в себе настойчивость
и упорство в достижении цели
А. Маркушевич
В ходе работы я доказала дополнительные свойства параллелограмма.
Я убедилась, что применяя эти свойства, можно решать задачи быстрее.
Я показала, как применяются эти свойства на примерах решения конкретных задач.
Я узнала много нового о параллелограмме, чего нет в нашем учебнике геометрии
Я убедилась в том, что знания геометрии очень важны в жизни на примерах применения свойств параллелограмма.
Цель моей исследовательской работы выполнена.
О том, насколько важны математические знания, говорит тот факт, что была учреждена премия тому, кто издаст книгу о человеке, который всю жизнь прожил без помощи математики. Эту премию до сих пор не получил ни один человек.
VIII Литература
ПогореловА.В. Геометрия 7-9: учебник для общеобразоват. учреждений-М.: Просвещение, 2014г
Л.С.Атанасян и др. Геометрия. Доп. Главы к учебнику 8 кл.: учеб. пособие для учащихся школ и классов с углубл. изуч.математики. – М.: Вита-пресс, 2003
Ресурсы сети Интернет
материалы Википедии
http://repetitor—problem.net/svoystva—parallelogramma—v—zhizni
http://www.problems.ru/view_by_subject_new.php?parent=631&start=25
infourok.ru
