Как найти область определения функции?
Для того, чтобы понять, что такое область определения функции, необходимо знать области определения основных элементарных функций. Для этого нужно углубить знания данной статьей. Будут рассмотрены различные сложнейшие комбинации функций вида y=x+x-2 или y=5·x2+1·x3, y=xx-5 или y=x-15-3. Рассмотрим теорию и решим несколько примеров с подобными заданиями.
Yandex.RTB R-A-339285-1Что значит найти область определения
После того, как функция задается, указывается ее область определения. Иначе говоря, без области определения функция не рассматривается. При задании функции вида y=f(x) область определения не указывается, так как ее ОДЗ для переменной x будет любым. Таким образом, функция определена на всей области определения.
Ограничение области определения
Область определения рассматривается еще в школьной курсе. у действительных чисел она может быть (0, +∞) или такой [−3, 1)∪[5, 7). Еще по виду функции можно визуально определить ее ОДЗ. Рассмотрим, на что может указывать наличие области определения:
- при имеющемся знаменателе необходимо производить деление такого типа функции как y=x+2·xx4-1;
- при наличии переменной под знаком корня необходимо обращать внимание на корень четной степени типа y=x+1 или y=23·x+3x;
- при наличии переменной в основании степени с отрицательным или нецелым показателем такого типа, как y=5·(x+1)-3, y=-1+x113, y=(x3-x+1)2, которые определены не для всех чисел;
- при наличии переменной под знаком логарифма или в основании вида y=lnx2+x4 или y=1+logx-1(x+1) причем основание является числом положительным, как и число под знаком логарифма;
- при наличии переменной, находящейся под знаком тангенса и котангенса вида y=x3+tg2·x+5 или y=ctg(3·x3-1), так как они существуют не для любого числа;
- при наличии переменной, расположенной под знаком арксинуса или арккосинуса вида y=arcsin(x+2)+2·x2, y=arccosx-1+x, область определения которых определяется ни интервале от -1 до 1.
При отсутствии хотя бы одного признака, область определения приходится искать другим образом. Рассмотрим пример функц
zaochnik.com
Функции. Область определения и множество значений функции. Четные и нечетные функции (дидактический материал).
МИНИСТЕРСТВО ОБРАЗОВАНИЯ САХАЛИНСКОЙ ОБЛАСТИ
ГБПОУ «СТРОИТЕЛЬНЫЙ ТЕХНИКУМ»
Практические работы
По дисциплине «Математика»
Раздел: «Функции, их свойства и графики».
Тема: Функции. Область определения и множество значений функции. Четные и нечетные функции.
(дидактический материал)
Составила:
Преподаватель
Казанцева Н.А.
( )
Южно-сахалинск-2017
Практические работы по математике по разделу «Функции, их свойства и графики» и методические указания по их выполнению предназначены для студентов ГБПОУ «Сахалинский строительный техникум»
Составитель: Казанцева Н. А., преподаватель математики
Материал содержит практические работы по математике «Функции, их свойства и графики» и указания по их выполнению. Методические указания составлены в соответствии с рабочей программой по математике и предназначены для студентов Сахалинского строительного техникума, обучающихся по программам общего образования.
СОДЕРЖАНИЕ
1)Практическое занятие №1. Функции. Область определения и множество значений функции.………………………………………………………………4
2)Практическое занятие №2. Четные и нечетные функции……………….6
Практическое занятие №1
Функции. Область определения и множество значений функции.
Цели: закрепить умения и навыки решения задач по теме: «Область определения и множество значений функции.
Оборудование: тетрадь для практических работ, ручка, методические рекомендации по выполнению работы
Указание. Сначала следует повторить теоретический материал по теме: «Область определения и множество значений функции», после чего можно приступать к выполнению практической части.
Не забывайте о правильном оформлении решения.
Методические указания:
Определение: Область определения функции – это множество всех значений аргумента х, на котором задается функция (или множество х при которых функция имеет смысл).
Обозначение: D(у), D(f )- область определения функции.
Определение: Область значения функции – это множество у, при которых функция имеет смысл.
Обозначение: Е(у), Е(f )- область значения функции.
Правило: Для нахождения области значения функции по графику необходимо график спроектировать на ОУ.
Задания для практической работы:
№ 1.Найдите значения функции:
a) f(x) = 4x + в точках 2;20 ;
б) f(x) = 2·cos(x) в точках ; 0;
в) f(x) = в точках 1;0; 2;
г) f(x) = 6 sin 4x в точках ; 0;
е) f(x) = 2 9x + 10 в точках 2; 0; 5.
№ 2.Найдите область определения функции:
a) f(x) = ; б) f(x) = ; в) f(x) = ;
г) f(x) = ; д) f(x) = ; е) f (x) = 6x +1;
ж) f(x) = ; з) f(x) = .
№3. Найдите область значений функции:
а) f(x) = 2+3x ; б) f(x) = 2 7x + 3.
№ 4.Найдите область определения и область значения функции, график которой изображен на рисунке:
Практическое занятие №2
Четные и нечетные функции.
Цели: закрепить умения и навыки решения задач по теме: «Четные и нечетные функции».
Оборудование: тетрадь для практических работ, ручка, методические рекомендации по выполнению работы
Указание. Сначала следует повторить теоретический материал по теме: «Четные и нечетные функции», после чего можно приступать к выполнению практической части.
Не забывайте о правильном оформлении решения.
Методические указания:
К важнейшим свойствам функций относится четность и нечетность.
Определение: Функция называется нечетной, если при изменении знака аргумента, она меняет свое значение на противоположное,
т.е. f(х)= f(х).
График нечетной функции симметричен относительно начала координат (0;0).
Примеры: нечетными функциями являются у=х, у=, у=sinх и др.
Например, график у= действительно обладает симметричностью относительно начала координат (см. рис.1):
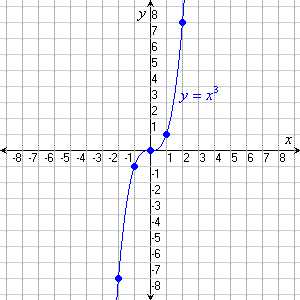
Рис.1. График у= (кубическая парабола)
Определение: Функция называется четной, если при изменении знака аргумента, она не меняет свое значение, т.е. f(х)= f(х).
График четной функции симметричен относительно оси ОУ.
Примеры
: четными функциями являются функции у=, у=,у=cos x и др.
Например, покажем симметричность графика у= относительно оси ОУ:
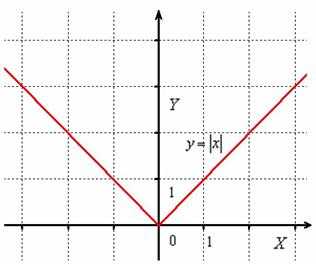
Рис.2. График у=
Задания для практической работы:
№1. Исследуйте функцию на четность или нечетность аналитическим путем:
1) f(х) = 2х3 – 3; 2) f(х) = 5х2 + 3;
3) g(х) = – + ; 4) g(х) = –2х3 + 3;
5) у(х)= 7хсtg x; 6) у(х)= +cos x;
7) t(х)= tg x3; 8) t(х)= +sin x.
№2. Исследуйте функцию на четность или нечетность аналитическим путем:
1) f(х) = ; 2) f(х) = 6 + · sin 2x·cos x;
3) f(х) = ; 4) f(х) = 2 + · cos 2x· sin x;
5) f(х) = ; 6) f(х) = 3 + · sin 4x·cos x;
7) f(х) = ; 8) f(х) = 3 + · cos 4x· sin x.
№3. Исследуйте функцию на четность или нечетность по графику:
№4. Проверьте, является ли четной или нечетной функция?
infourok.ru
Функция задана графиком. Укажите область определения этой функции.
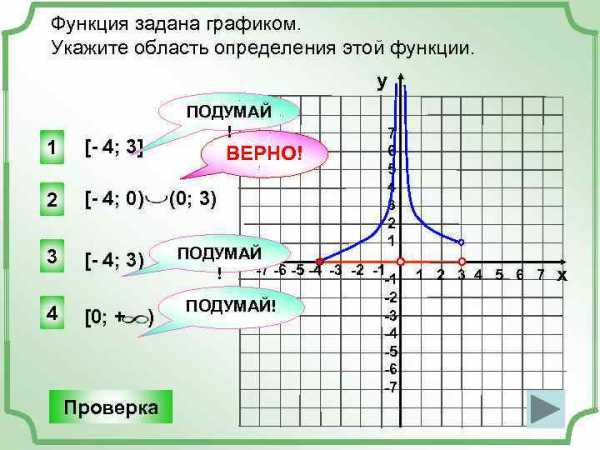Функция задана графиком. Укажите область определения этой функции. у 1 [- 4; 3] 2 [- 4; 0) 3 ПОДУМАЙ ! [- 4; 3) 4 [0; + ВЕРНО! (0; 3) 7 6 5 4 3 2 1 ПОДУМАЙ -7 -6 -5 -4 -3 -2 -1 ! -1 ) Проверка ПОДУМАЙ! -2 -3 -4 -5 -6 -7 1 2 3 4 5 6 7 х
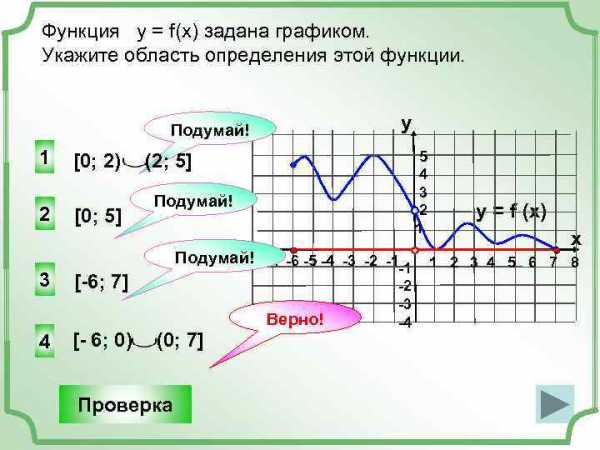Функция у = f(x) задана графиком. Укажите область определения этой функции. y Подумай! 1 2 3 [0; 2) [0; 5] 5 4 3 2 1 (2; 5] Подумай! -7 -6 -5 -4 -3 -2 -1 -1 [-6; 7] Верно! 4 [- 6; 0) (0; 7] Проверка -2 -3 -4 y = f (x) x 1 2 3 4 5 6 7 8
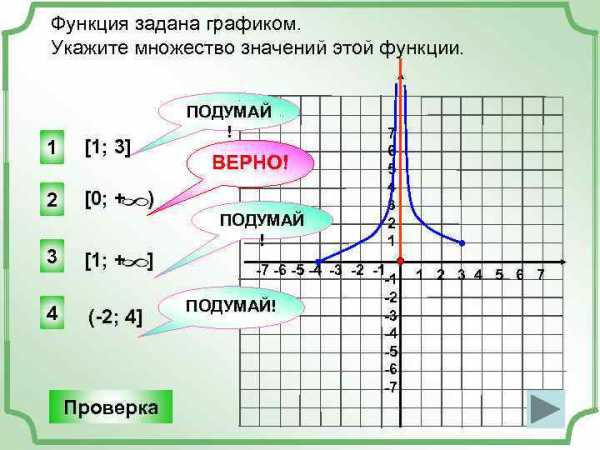
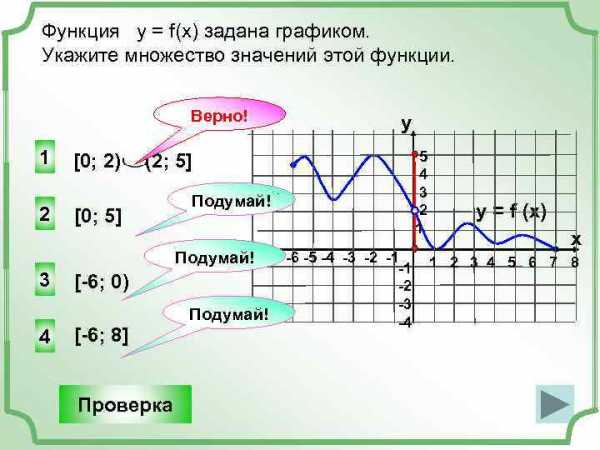Функция у = f(x) задана графиком. Укажите множество значений этой функции. Верно! 1 2 [0; 2) y 5 4 3 2 1 (2; 5] [0; 5] Подумай! -7 -6 -5 -4 -3 -2 -1 3 [-6; 0) Подумай! 4 [-6; 8] Проверка -1 -2 -3 -4 y = f (x) x 1 2 3 4 5 6 7 8
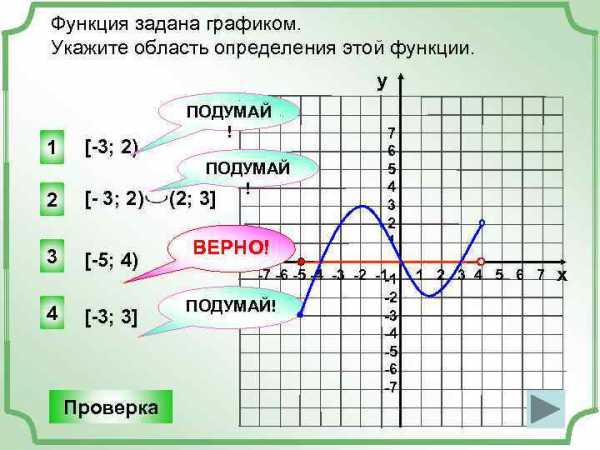Функция задана графиком. Укажите область определения этой функции. у 1 [-3; 2) 2 [- 3; 2) 3 [-5; 4) 4 [-3; 3] Проверка ПОДУМАЙ ! (2; 3] ВЕРНО! 7 6 5 4 3 2 1 -7 -6 -5 -4 -3 -2 -1 -1 -2 ПОДУМАЙ! -3 -4 -5 -6 -7 1 2 3 4 5 6 7 х
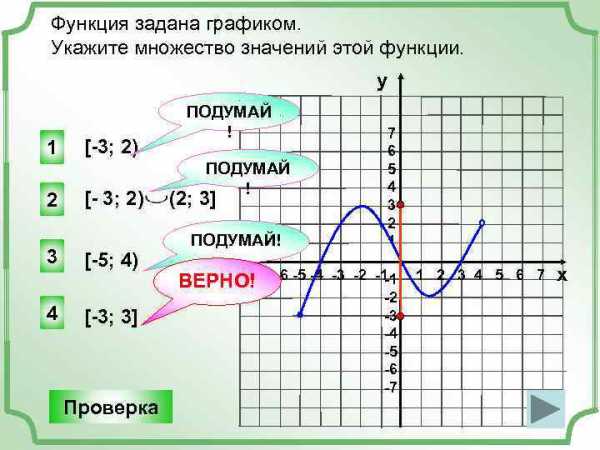Функция задана графиком. Укажите множество значений этой функции. у 1 2 [-3; 2) [- 3; 2) 3 [-5; 4) 4 [-3; 3] Проверка ПОДУМАЙ ! (2; 3] ПОДУМАЙ! ВЕРНО! -7 -6 -5 -4 7 6 5 4 3 2 1 -3 -2 -1 -1 -2 -3 -4 -5 -6 -7 1 2 3 4 5 6 7 х
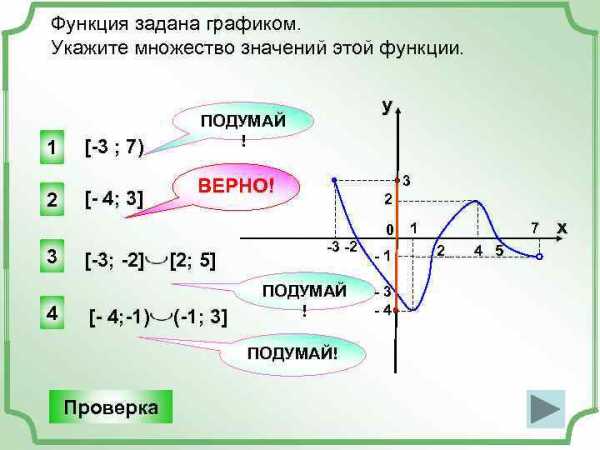Функция задана графиком. Укажите множество значений этой функции. 1 2 3 4 [-3 ; 7) [- 4; 3] [-3; -2] [- 4; -1) y ПОДУМАЙ ! 3 ВЕРНО! [2; 5] (-1; 3] 2 -3 -2 ПОДУМАЙ ! ПОДУМАЙ! Проверка 0 -1 -3 -4 1 7 2 4 5 x
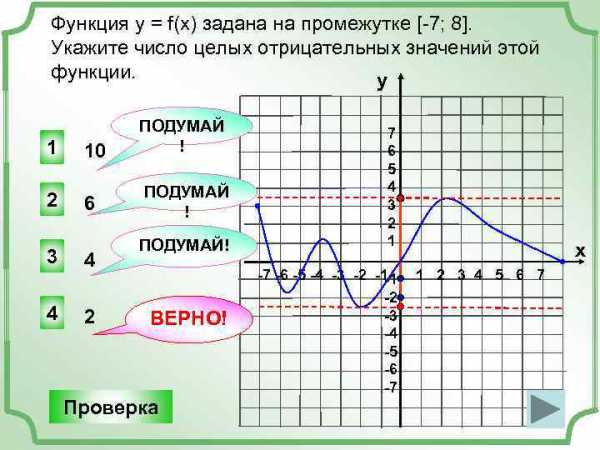Функция y = f(x) задана на промежутке [-7; 8]. Укажите число целых отрицательных значений этой функции. у 1 10 ПОДУМАЙ ! 2 6 ПОДУМАЙ ! 3 4 4 2 ПОДУМАЙ! ВЕРНО! Проверка 7 6 5 4 3 2 1 -7 -6 -5 -4 -3 -2 -1 -1 -2 -3 -4 -5 -6 -7 х 1 2 3 4 5 6 7
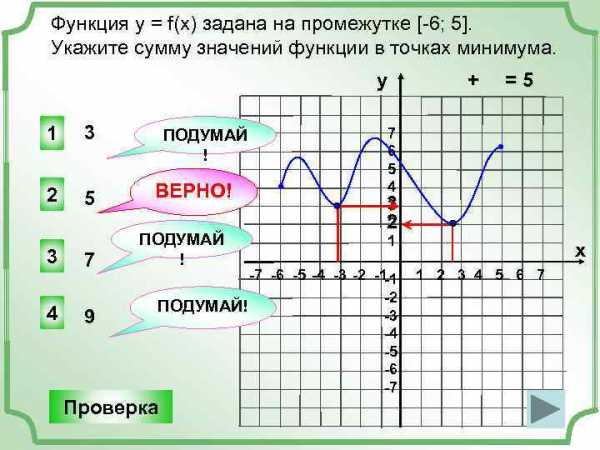Функция y = f(x) задана на промежутке [-6; 5]. Укажите сумму значений функции в точках минимума. у 1 3 2 5 3 7 4 9 ПОДУМАЙ ! ВЕРНО! ПОДУМАЙ ! =5 7 6 5 4 3 3 2 1 -7 -6 -5 -4 -3 -2 -1 -1 -2 ПОДУМАЙ! -3 -4 -5 -6 -7 Проверка + х 1 2 3 4 5 6 7
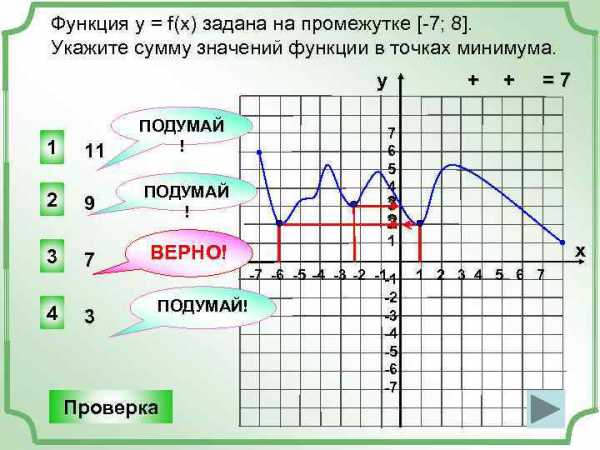Функция y = f(x) задана на промежутке [-7; 8]. Укажите сумму значений функции в точках минимума. у 1 11 ПОДУМАЙ ! 2 9 ПОДУМАЙ ! 3 7 ВЕРНО! 4 3 + =7 7 6 5 4 3 3 2 1 -7 -6 -5 -4 -3 -2 -1 -1 -2 ПОДУМАЙ! -3 -4 -5 -6 -7 Проверка + х 1 2 3 4 5 6 7
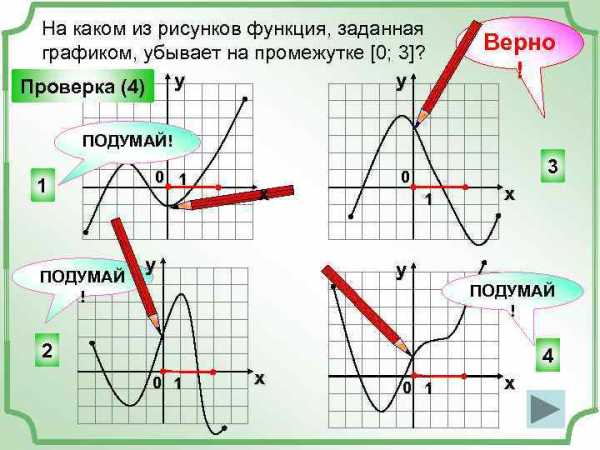На каком из рисунков функция, заданная графиком, убывает на промежутке [0; 3]? y Проверка (4) y Верно ! ПОДУМАЙ! 1 ПОДУМАЙ ! 0 1 x y 3 0 1 x y ПОДУМАЙ ! 2 0 1 x 4 0 1 x
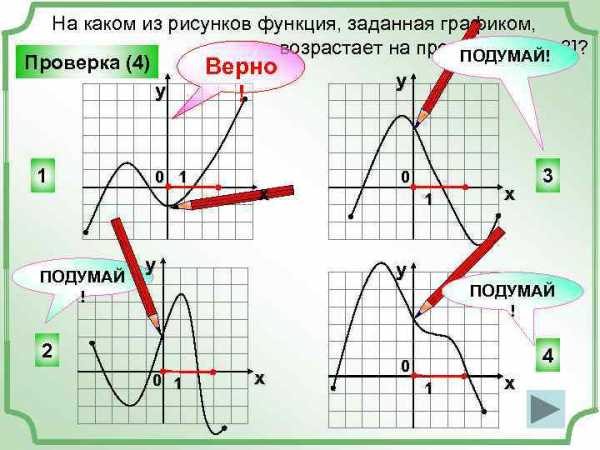На каком из рисунков функция, заданная графиком, возрастает на промежутке [0; 3]? ПОДУМАЙ! Проверка (4) Верно y y ! 1 ПОДУМАЙ ! 0 1 x y 0 1 x 3 y ПОДУМАЙ ! 2 0 1 x 4 0 1 x
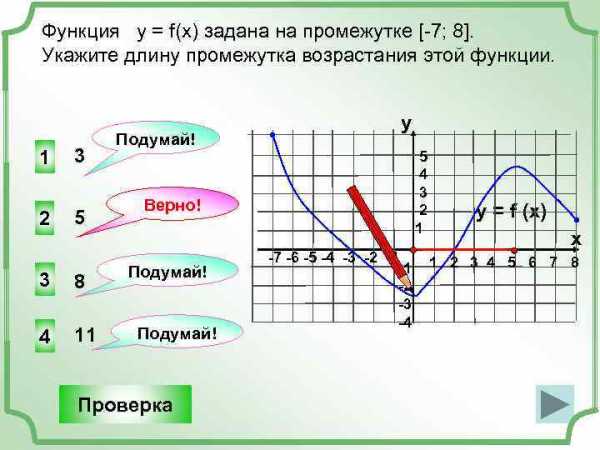Функция у = f(x) задана на промежутке [-7; 8]. Укажите длину промежутка возрастания этой функции. 1 2 3 5 3 8 4 11 Подумай! y 5 4 3 2 1 Верно! Подумай! Проверка -7 -6 -5 -4 -3 -2 -1 -1 -2 -3 -4 y = f (x) x 1 2 3 4 5 6 7 8
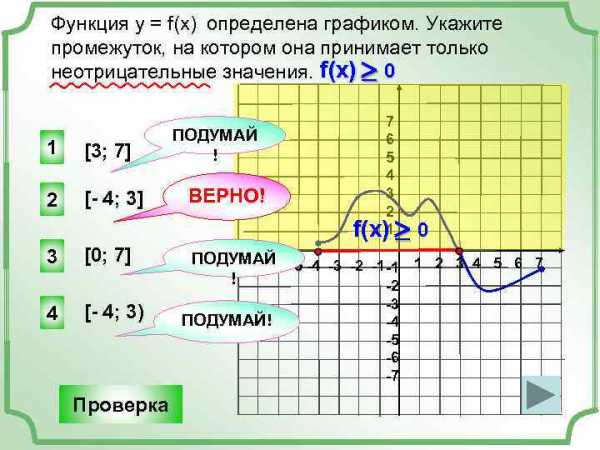Функция у = f(x) определена графиком. Укажите промежуток, на котором она принимает только неотрицательные значения. f(x) ³ 0 1 [3; 7] 2 [- 4; 3] 3 [0; 7] 4 [- 4; 3) Проверка ПОДУМАЙ ! ВЕРНО! 7 6 5 4 3 2 f(x)1 ³ 0 ПОДУМАЙ -5 -4 -3 -2 -1 -7 -6 -1 1 2 3 4 5 6 7 ! -2 ПОДУМАЙ! -3 -4 -5 -6 -7
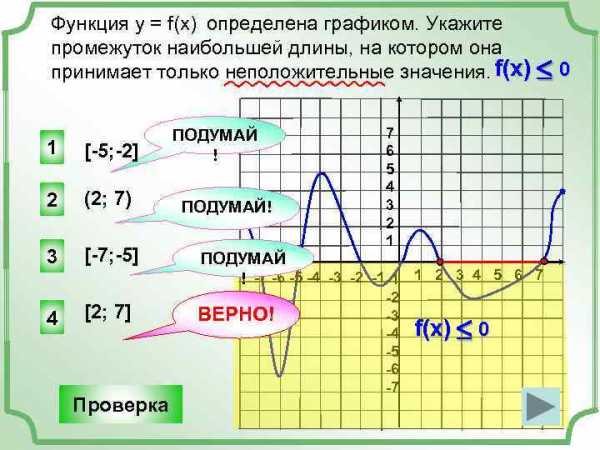Функция у = f(x) определена графиком. Укажите промежуток наибольшей длины, на котором она принимает только неположительные значения. f(x) £ 0 1 [-5; -2] 2 (2; 7) 3 [-7; -5] 4 [2; 7] Проверка ПОДУМАЙ ! ПОДУМАЙ! 7 6 5 4 3 2 1 ПОДУМАЙ ! -7 -6 -5 -4 -3 -2 -1 -1 1 2 3 4 5 6 7 ВЕРНО! -2 -3 -4 -5 -6 -7 f(x) £ 0
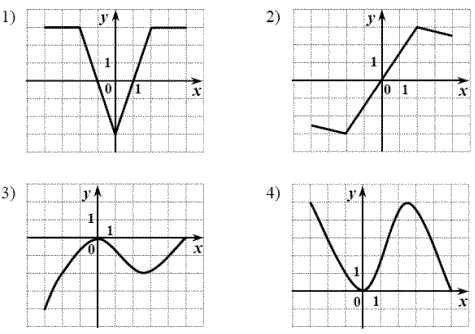
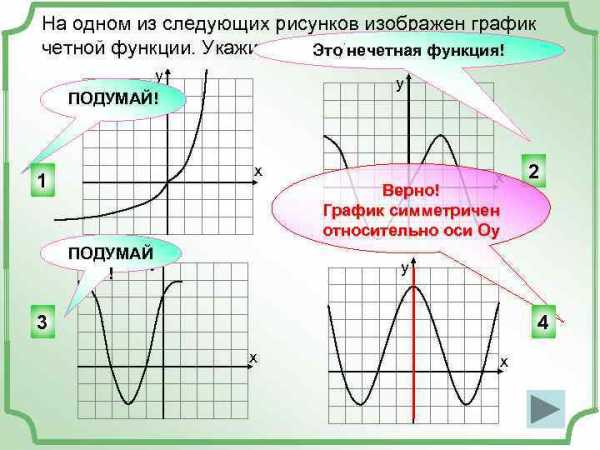На одном из следующих рисунков изображен график четной функции. Укажите этот график. функция! Это нечетная у ПОДУМАЙ! у х 1 х Верно! График симметричен относительно оси Оу ПОДУМАЙ у ! 2 у 3 4 х х
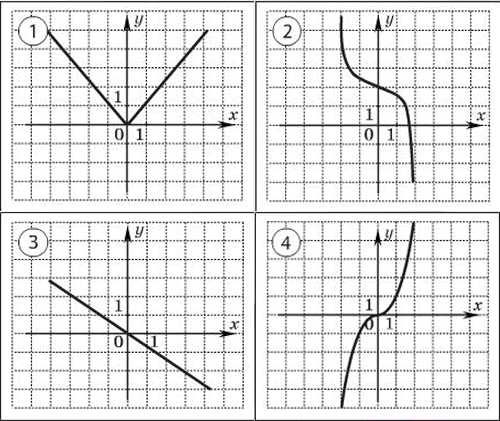
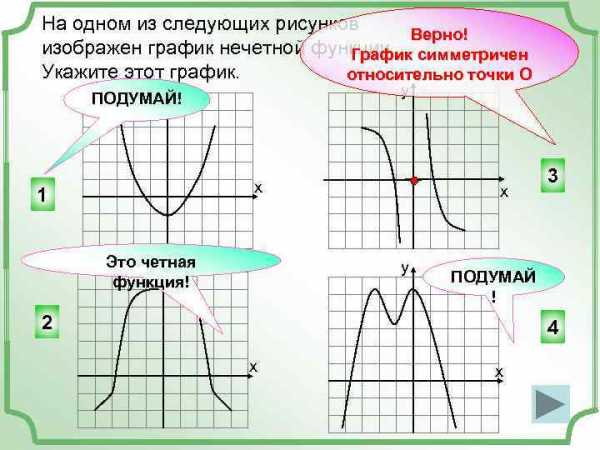На одном из следующих рисунков Верно! изображен график нечетной функции. симметричен График Укажите этот график. относительно точки О у ПОДУМАЙ! у х 1 Это четная у функция! х у 3 ПОДУМАЙ ! 2 4 х х
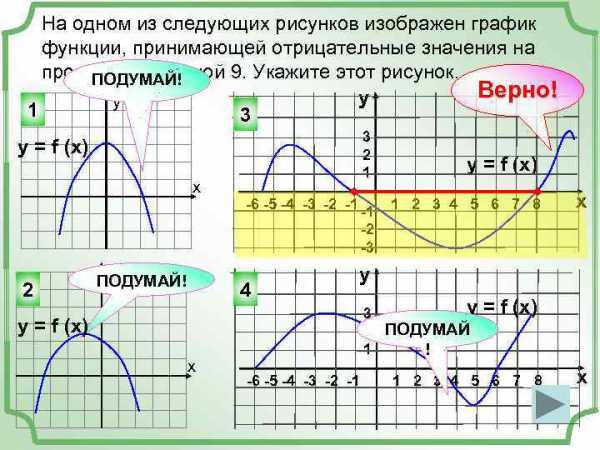На одном из следующих рисунков изображен график функции, принимающей отрицательные значения на промежутке длиной 9. Укажите этот рисунок. ПОДУМАЙ! Верно! y у 1 3 3 2 1 y = f (x) х -6 -5 -4 -3 -2 -1 -1 -2 -3 2 у ПОДУМАЙ! 4 1 2 3 4 5 6 7 8 x y y = f (x) х y = f (x) -6 -5 -4 -3 -2 -1 y 3 2 ПОДУМАЙ 1 ! = f (x) 1 2 3 4 5 6 7 8 x
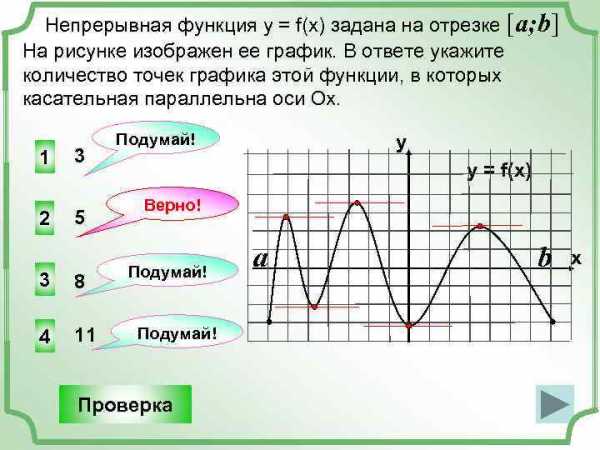Непрерывная функция у = f(x) задана на отрезке [a; b] На рисунке изображен ее график. В ответе укажите количество точек графика этой функции, в которых касательная параллельна оси Ох. 1 2 3 3 5 8 Подумай! y y = f(x) Верно! Подумай! b a 4 11 Подумай! Проверка x
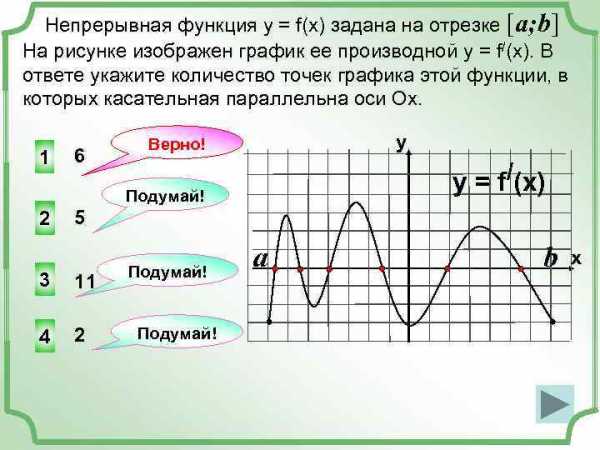Непрерывная функция у = f(x) задана на отрезке [a; b] На рисунке изображен график ее производной у = f/(x). В ответе укажите количество точек графика этой функции, в которых касательная параллельна оси Ох. 1 6 y Верно! /(x) y=f Подумай! 2 3 5 11 Подумай! b a 4 2 Подумай! x
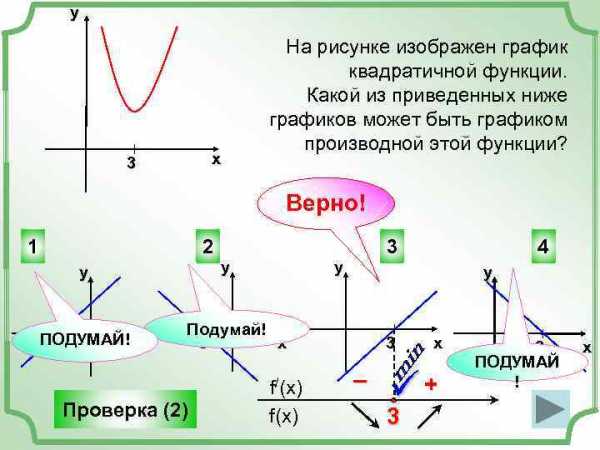у х 3 На рисунке изображен график квадратичной функции. Какой из приведенных ниже графиков может быть графиком производной этой функции? Верно! 1 2 у ПОДУМАЙ! х -3 у у Подумай! -3 х Проверка (2) f/(x) f(x) 4 3 – ü 3 х + 3 ПОДУМАЙ ! х
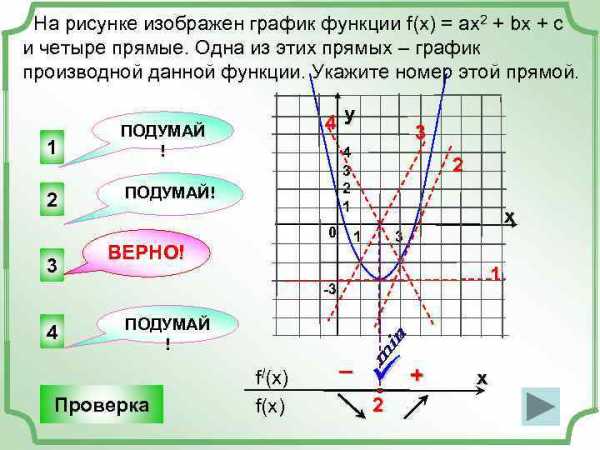На рисунке изображен график функции f(x) = ax 2 + bx + c и четыре прямые. Одна из этих прямых – график производной данной функции. Укажите номер этой прямой. 1 ПОДУМАЙ ! 2 4 у ПОДУМАЙ! 3 3 4 3 2 1 0 ВЕРНО! 2 х 1 3 1 -3 4 ПОДУМАЙ ! Проверка f/(x) f(x) – ü+ 2 х
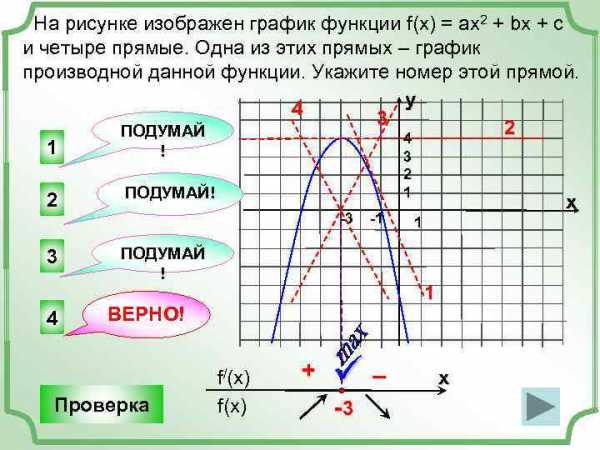На рисунке изображен график функции f(x) = ax 2 + bx + c и четыре прямые. Одна из этих прямых – график производной данной функции. Укажите номер этой прямой. у 4 3 2 ПОДУМАЙ 4 1 ! 3 2 3 4 2 1 ПОДУМАЙ! -3 -1 ПОДУМАЙ ! 1 1 ВЕРНО! Проверка х f/(x) f(x) + ü– -3 х
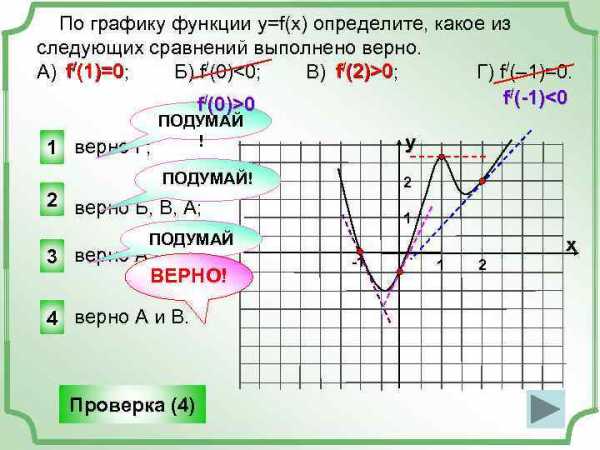По графику функции y=f(x) определите, какое из следующих сравнений выполнено верно. f (1)=0; Б) f/(0)0 f (2)>0; Г) f/(– 1)=0. А) f/(1)=0 f/(-1)0 f 1 ПОДУМАЙ ! верно Г; у ПОДУМАЙ! 2 2 верно Б, В, А; 3 ПОДУМАЙ верно А и Б; ! ВЕРНО! 4 верно А и В. Проверка (4) 1 -1 х 1 2
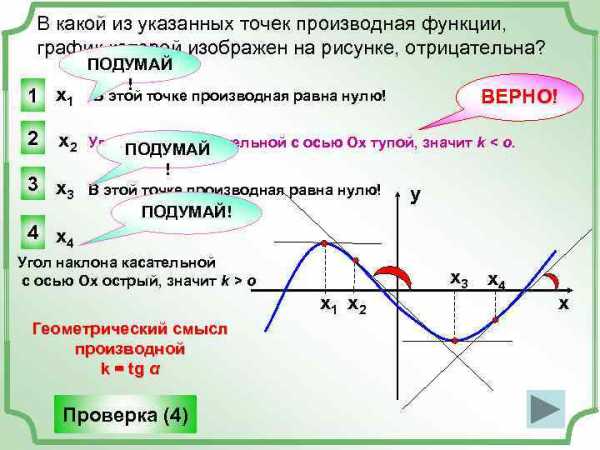В какой из указанных точек производная функции, график которой изображен на рисунке, отрицательна? 1 х1 ПОДУМАЙ ! ВЕРНО! В этой точке производная равна нулю! 2 х2 Угол наклона касательной с осью Ох тупой, значит k o х1 х2 Геометрический смысл производной k = tg α Проверка (4) х3 х4 х
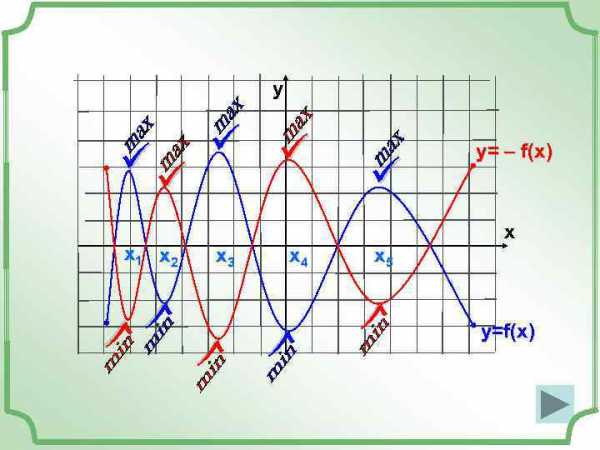y y = – f (x ) x x 3 x 4 ü ü x 1 x 2 ü x 5 ü ü ü y = f(x ) üü üü
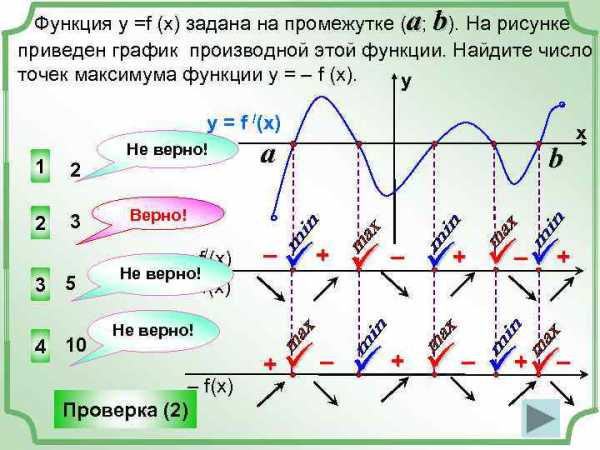Функция у =f (x) задана на промежутке (a; b). На рисунке приведен график производной этой функции. Найдите число точек максимума функции у = – f (x). y y = f /(x) 1 2 2 3 3 5 4 10 Не верно! a b Верно! f/(x) Не верно! f(x) – ü + ü – ü+ ü–ü+ + ü – ü+ü– Не верно! – f(x) Проверка (2) x
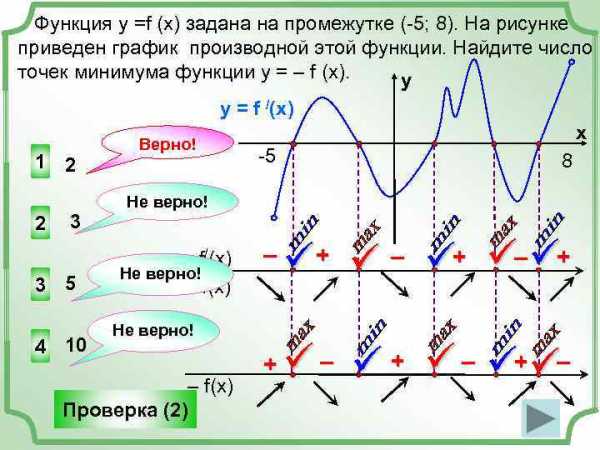Функция у =f (x) задана на промежутке (-5; 8). На рисунке приведен график производной этой функции. Найдите число точек минимума функции у = – f (x). y y = f /(x) 1 2 Верно! x -5 8 2 3 3 5 4 10 Не верно! f/(x) Не верно! f(x) – ü + ü – ü+ ü–ü+ + ü – ü+ü– Не верно! – f(x) Проверка (2)
present5.com