Основные соотношения комбинаторики
Литература
1) Бронштейн Е.М. Комбинаторика в задачах. Методические указания. Уфа: УГАТУ. 1988.
1. Основной принцип комбинаторики.
1.1. От Москвы до Уфы можно добраться поездом, самолетом, теплоходом, а от Уфы до райцентра поездом, самолетом, автобусом. Сколькими способами можно в совокупности добраться от Москвы до райцентра через Уфу?
1.2. Есть конверты без марок 5 видов и марки 4 видов. Сколькими способами можно выбрать конверт с маркой?
1.3. Из 12 слов мужского рода, 9 женского и 10 среднего нужно выбрать по одному слову каждого рода. Сколькими способами можно сделать этот выбор?
1.4. Сколькими способами можно выбрать на шахматной доске белую и черную клетки, не лежащие на одной горизонтали или вертикали?
1.5. (Обобщение). Если элемент а
a1n1,
a2n2,
………
amnm,
то сколькими способами можно выбрать вектор (a1, …,am)? Ответ:n1n2…nm.
Ответ задачи 1.5 называется основным принципом комбинаторики или принципом произведения.
2. Размещение с повторениями
2.1. Замок в автоматической камере хранения содержит 4 диска, на каждом из которых записаны цифры 0,1,…,9. Сколько различных кодов можно получить?
2.2. В группе из 25 человек разыгрывается три различных приза. Призы могут достаться одному человеку, двоим, троим. Сколькими способами призы могут распределиться?
2.3. В пачке 20 экзаменационных билетов. Каждый студент получает билет, отвечает на него, билет возвращается в пачку и после этого заходит следующий студент. Сколько различных вариантов раздачи билетов существует для 10 студентов?
2.4. На складе имеется 7 рулонов ткани различных цветов и 5 различных стульев. Каждого рулона достаточно для обивки всех стульев. Сколькими способами можно обить стулья?
2.5. (Обобщение). В пачке n карточек с
номерами. Исследователь достает карточку,
записывает номер и возвращает карточки
назад. После этого он снова достает
карточку и т.д. Сколько различных записей
может быть после того, как доставалось
k карточек? . (Комбинации 1-2-3, 1-3-2 и т.д.
считаются разными.) Ответ: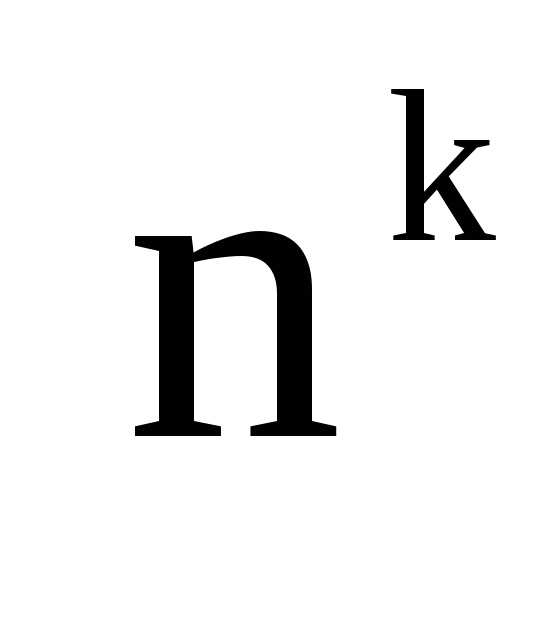 .
.
3. Размещение без повторений
3.1. Сколько словарей надо издать, чтобы можно было непосредственно выполнять переводы с любого из 5 языков на любой другой? А если языков 10?
3.2. Каков будет ответ в задаче 2.2, если каждый человек может получить лишь один приз?
3.3. Каков будет ответ в задаче 2.3, если экзаменатор не возвращает в пачку использованный билет?
3.4. Каков будет ответ в задаче 2.4, если каждого рулона ткани хватит только на один стул?
3.5. Пусть в коробке имеется nкарточек. Достается одна из них, причем в коробку не возвращается. Так повторяетсяkраз. Сколько существует различных комбинаций выбора карточек. (Комбинации 1-2-3, 1-3-2 и т.д. также считаются разными.
3.5. (Обобщение). Пусть дано множество А, содержащее n элементов. Сколько существует различных векторов в множестве Аk, все компоненты каждого из которых различны?
Ответ: — число размещений из n по .k.
4. Перестановки
4.1. Сколькими способами можно сформировать очередь из 5 человек?
4.2. Каков будет ответ в задаче 3.3, если студентов 20?
4.3. Каков будет ответ в задаче 3.4, если стульев 7?
(Обобщение). Сколькими способами элементы n- элементного множества А можно расположить в цепочку?
Ответ: Рn=n(n-1)…1=n! — число перестановок из n.
studfiles.net
Основные соотношения комбинаторики
Литература
1) Бронштейн Е.М. Комбинаторика в задачах. Методические указания. Уфа: УГАТУ. 1988.
1. Основной принцип комбинаторики.
1.1. От Москвы до Уфы можно добраться поездом, самолетом, теплоходом, а от Уфы до райцентра поездом, самолетом, автобусом. Сколькими способами можно в совокупности добраться от Москвы до райцентра через Уфу?
1.2. Есть конверты без марок 5 видов и марки 4 видов. Сколькими способами можно выбрать конверт с маркой?
1.3. Из 12 слов мужского рода, 9 женского и 10 среднего нужно выбрать по одному слову каждого рода. Сколькими способами можно сделать этот выбор?
1.4. Сколькими способами можно выбрать на шахматной доске белую и черную клетки, не лежащие на одной горизонтали или вертикали?
1.5. (Обобщение). Если элемент а1можно выбрать n1способами, после каждого выбора следующий за ним элемент а2 можно выбрать n2способами, …, после выбора элементов а1, …, аk-1 элемент аkвыбирается nkспособами, т.е.
a1n1,
a2n2,………
amnm,
то сколькими способами можно выбрать вектор (a1, …,am)? Ответ:n1n2…nm.
Ответ задачи 1.5 называется основным принципом комбинаторики или принципом произведения.
2. Размещение с повторениями
2.1. Замок в автоматической камере хранения содержит 4 диска, на каждом из которых записаны цифры 0,1,…,9. Сколько различных кодов можно получить?
2.2. В группе из 25 человек разыгрывается три различных приза. Призы могут достаться одному человеку, двоим, троим. Сколькими способами призы могут распределиться?
2.3. В пачке 20 экзаменационных билетов. Каждый студент получает билет, отвечает на него, билет возвращается в пачку и после этого заходит следующий студент. Сколько различных вариантов раздачи билетов существует для 10 студентов?
2.4. На складе имеется 7 рулонов ткани различных цветов и 5 различных стульев. Каждого рулона достаточно для обивки всех стульев. Сколькими способами можно обить стулья?
2.5. (Обобщение). В пачке n карточек с
номерами. Исследователь достает карточку,
записывает номер и возвращает карточки
назад. После этого он снова достает
карточку и т.д. Сколько различных записей
может быть после того, как доставалось
k карточек? . (Комбинации 1-2-3, 1-3-2 и т.д.
считаются разными.) Ответ: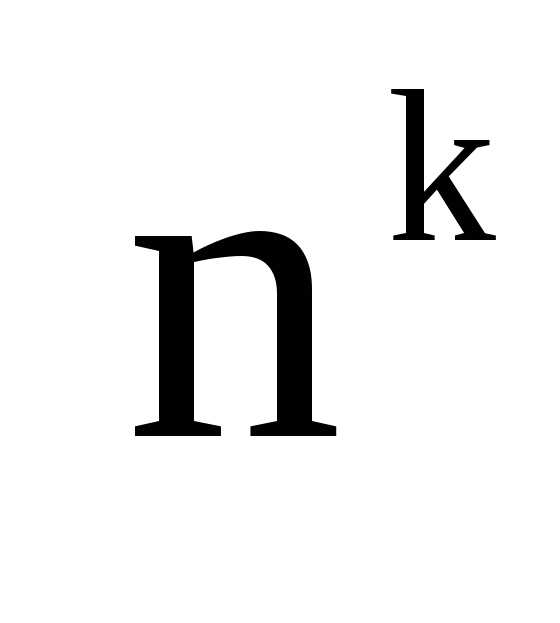 .
.
3. Размещение без повторений
3.1. Сколько словарей надо издать, чтобы можно было непосредственно выполнять переводы с любого из 5 языков на любой другой? А если языков 10?
3.2. Каков будет ответ в задаче 2.2, если каждый человек может получить лишь один приз?
3.3. Каков будет ответ в задаче 2.3, если экзаменатор не возвращает в пачку использованный билет?
3.4. Каков будет ответ в задаче 2.4, если каждого рулона ткани хватит только на один стул?
3.5. Пусть в коробке имеется nкарточек. Достается одна из них, причем в коробку не возвращается. Так повторяетсяkраз. Сколько существует различных комбинаций выбора карточек. (Комбинации 1-2-3, 1-3-2 и т.д. также считаются разными.
3.5. (Обобщение). Пусть дано множество А, содержащее n элементов. Сколько существует различных векторов в множестве Аk, все компоненты каждого из которых различны?
Ответ: — число размещений из n по .k.
4. Перестановки
4.1. Сколькими способами можно сформировать очередь из 5 человек?
4.2. Каков будет ответ в задаче 3.3, если студентов 20?
4.3. Каков будет ответ в задаче 3.4, если стульев 7?
(Обобщение). Сколькими способами элементы n- элементного множества А можно расположить в цепочку?
Ответ: Рn=n(n-1)…1=n! — число перестановок из n.
studfiles.net
Основные соотношения комбинаторики
Литература
1) Бронштейн Е.М. Комбинаторика в задачах. Методические указания. Уфа: УГАТУ. 1988.
1. Основной принцип комбинаторики.
1.1. От Москвы до Уфы можно добраться поездом, самолетом, теплоходом, а от Уфы до райцентра поездом, самолетом, автобусом. Сколькими способами можно в совокупности добраться от Москвы до райцентра через Уфу?
1.2. Есть конверты без марок 5 видов и марки 4 видов. Сколькими способами можно выбрать конверт с маркой?
1.3. Из 12 слов мужского рода, 9 женского и 10 среднего нужно выбрать по одному слову каждого рода. Сколькими способами можно сделать этот выбор?
1.4. Сколькими способами можно выбрать на шахматной доске белую и черную клетки, не лежащие на одной горизонтали или вертикали?
1.5. (Обобщение). Если элемент а1можно выбрать n1способами, после каждого выбора следующий за ним элемент а2 можно выбрать n2способами, …, после выбора элементов а1, …, аk-1 элемент аkвыбирается nkспособами, т.е.
a1n1,
a2n2,
………
amnm,
то сколькими способами можно выбрать вектор (a1, …,am)? Ответ:n1n2…nm.
Ответ задачи 1.5 называется основным принципом комбинаторики или принципом произведения.
2. Размещение с повторениями
2.1. Замок в автоматической камере хранения содержит 4 диска, на каждом из которых записаны цифры 0,1,…,9. Сколько различных кодов можно получить?
2.2. В группе из 25 человек разыгрывается три различных приза. Призы могут достаться одному человеку, двоим, троим. Сколькими способами призы могут распределиться?
2.3. В пачке 20 экзаменационных билетов. Каждый студент получает билет, отвечает на него, билет возвращается в пачку и после этого заходит следующий студент. Сколько различных вариантов раздачи билетов существует для 10 студентов?
2.4. На складе имеется 7 рулонов ткани различных цветов и 5 различных стульев. Каждого рулона достаточно для обивки всех стульев. Сколькими способами можно обить стулья?
2.5. (Обобщение). В пачке n карточек с
номерами. Исследователь достает карточку,
записывает номер и возвращает карточки
назад. После этого он снова достает
карточку и т.д. Сколько различных записей
может быть после того, как доставалось
k карточек? . (Комбинации 1-2-3, 1-3-2 и т.д.
считаются разными.) Ответ: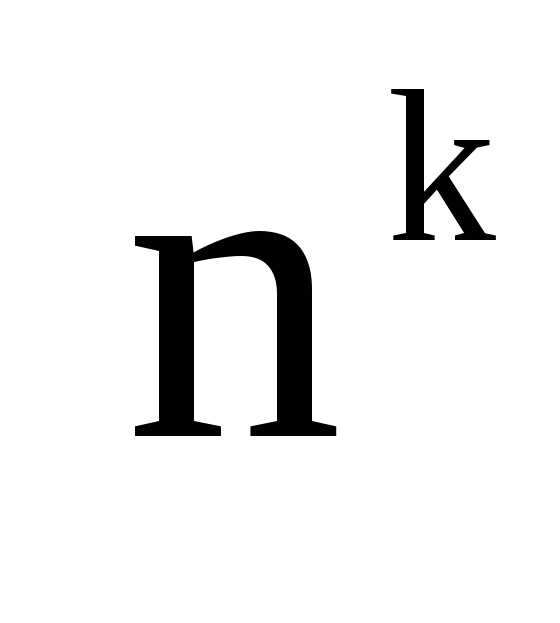 .
.
3. Размещение без повторений
3.1. Сколько словарей надо издать, чтобы можно было непосредственно выполнять переводы с любого из 5 языков на любой другой? А если языков 10?
3.2. Каков будет ответ в задаче 2.2, если каждый человек может получить лишь один приз?
3.3. Каков будет ответ в задаче 2.3, если экзаменатор не возвращает в пачку использованный билет?
3.4. Каков будет ответ в задаче 2.4, если каждого рулона ткани хватит только на один стул?
3.5. Пусть в коробке имеется nкарточек. Достается одна из них, причем в коробку не возвращается. Так повторяетсяkраз. Сколько существует различных комбинаций выбора карточек. (Комбинации 1-2-3, 1-3-2 и т.д. также считаются разными.
3.5. (Обобщение). Пусть дано множество А, содержащее n элементов. Сколько существует различных векторов в множестве Аk, все компоненты каждого из которых различны?
Ответ: — число размещений из n по .k.
4. Перестановки
4.1. Сколькими способами можно сформировать очередь из 5 человек?
4.2. Каков будет ответ в задаче 3.3, если студентов 20?
4.3. Каков будет ответ в задаче 3.4, если стульев 7?
(Обобщение). Сколькими способами элементы n- элементного множества А можно расположить в цепочку?
Ответ: Рn=n(n-1)…1=n! — число перестановок из n.
studfiles.net
2.7. Производящие функции числа основных комбинаторных объектов
Производящая функция является устройством, отчасти напоминающим мешок. Вместо того чтобы нести отдельно много предметов, что могло бы оказаться затруднительным, мы собираем их вместе, и тогда нам нужно нести лишь один предмет – мешок.
Д. Пойа
Биномиальная теорема указывает на то, что (1+z)n – это производящая функция для последовательности . Действительно,
Часто бывает удобно вместо ряда (5) рассматривать ряд вида
, (7)
который мы будем называть экспоненциальной производящей функцией последовательности (4).
Производящие функции числа основных комбинаторных объектов:
производящая функция для
Производящей функцией числа сочетаний из множества
E = {e1, e2, …, en}, заданных условиями, согласно которым кратность каждого элемента ei может быть одним из чисел является функция
+…),
а коэффициент при xk , полученный после раскрытия скобок, равен числу таких сочетаний.
3) Найти число сочетаний с повторениями из n элементов по k без всяких ограничений на кратность элементов в данном сочетании (т.е. кратность каждого элемента может быть любым целым неотрицательным числом), таким образом,
В данном случае производящая функция выглядит следующим образом:
.
4) Найти число сочетаний с повторениями из n элементов по k, в которых каждый элемент встречается не менее r раз (т.е. кратность каждого элемента может быть одним из чисел r, r+1, r+2, …). Производящей функцией для числа сочетаний такого вида является функция
.
5)
– экспоненциальная производящая функция числа размещений Ank.
6)
– экспоненциальная производящая функция числа nk (т.е. числа k-перестановок с повторением элементов в n-элементном множестве).
Пример 18. Какой вид имеет производящая функция для сочетаний из трех элементов, в которых каждый элемент встречается не менее одного раза?
Решение: n = 3, r = 1, тогда
Пример 19. Имеется множество M = {a, b, c}, из элементов которого строятся пятиместные размещения со следующими ограничениями на частоту повторения элементов:
элемент a может входить в размещение не более одного раза;
элемент b может входить в размещение один или два раза;
элемент c может входить в размещение неограниченное число раз.
Найти число размещений описанного типа.
Решение: Как известно, число k-размещений с повторением элементов в n-элементом множестве равняется nk.
Производящая функция для размещений с повторениями выглядит так:
коэффициент при равен .
Согласно условиям исходной задачи производящая функция выглядит следующим образом:
.
Теперь, перемножив скобки, ищем коэффициент перед , он и есть решение исходной задачи.
Получаем
=
=
.Число размещений равно 65.
Пример 20. Какой вид имеет производящая функция для размещений из трех разных элементов, в которых каждый элемент встречается не менее двух раз?
Решение: Известно, что .
2.8. Задания для самостоятельной работы
1.Найти сумму корней уравнения= 18 ·
2. Какой коэффициент имеет слагаемое в разложении выражения
( — )20, содержащее одночлен a7?
3. Сколько целых неотрицательных решений имеет уравнение
4. Найти количество способов выбора пяти делегатов на конференцию из восьми человек.
5. Найти количество перестановок букв в слове «цифра».
6. Найти число четырехзначных чисел, которые можно составить из четырех карточек с цифрами 1, 2, 5, 7.
7. Найти количество способов выбора четырех спортсменов из семи для участия в кроссе.
8. Сколько различных «слов» можно составить из слова «карта» (под словом понимается произвольное сочетание букв)?
9. На десяти одинаковых карточках написаны буквы м, а, т, е, м, а, т, и, к, а. Найти число способов получить слово «математика» при случайном выкладывании карточек в ряд.
10. Найдите количество слов длины 6 в алфавите {a, b, c, d}, в которых буква a встречается на один раз больше буквы b.
11. Найдите количество слов длины 7 в алфавите {a, b, c, d}, в которых буквы a и b встречаются одинаковое количество раз.
12. Найдите количество слов длины 6 в алфавите {a, b, c, d}, в которых буква a встречается столько же раз, сколько буквы b и c вместе взятые.
13. Найдите количество слов длины 8 в алфавите {a, b, c, d}, в которых буква a встречается дважды, а буква b – не менее трех раз.
14. Найдите количество слов длины 5 в алфавите {a, b, c, d}, в которые буква a входит не более двух раз.
15. Найдите количество слов длины 8 в алфавите {a, b, c, d}, в которые буква a входит не более двух раз.
16. Найдите количество слов длины 8 в алфавите {a, b, c, d}, в которые буква a входит не менее 3 раз и не более 5 раз.
17. Найдите количество слов длины 6 в алфавите {a, b, c, d}, в которые буква a входит не менее 3 раз.
18. Найдите количество слов длины 7 в алфавите {a, b, c, d}, в которые буква a входит не более 2 раз, а суммарное число вхождений букв b, c, d равно 3.
19. Найдите количество слов длины 7 в алфавите {a, b, c, d}, в которые буквы a,b,c входят одинаковое количество раз.
studfiles.net
Основные понятия комбинаторики.
n – факториал ‒ произведение первых n ‒ натуральных чисел (обозначается n!).
Основными понятиями комбинаторики являются ‒ размещения, перестановки и сочетания.
Определение 1. Пусть имеется множество, содержащее n ‒ элементов.
Размещением из n ‒ элементов по m ‒ элементов (m ≤ n) ‒ называются все подмножества, содержащие m ‒ элементов и отличающиеся друг от друга или составом своих элементов или порядком их следования.
‒ число размещений из n ‒ элементов по m ‒ элементов.
Определение 2. Перестановками из n ‒ элементов называются размещения из n ‒ элементов по n ‒ элементов.
–число перестановок из n ‒ элементов.
Определение 3. Сочетаниями из n ‒ элементов по m ‒ элементов (m≤n) называются все m‒ элементные подмножества n ‒ элементного множества, отличающиеся друг от друга только составом своих элементов.
‒ число сочетаний из n ‒ элементов по m ‒ элементов.
Свойства сочетаний:
1.
Доказательство:
Так как
Следовательно,
Примеры:
2.
Доказательство:
Примеры:
3.
Доказательство:
Примеры:
Бином Ньютона и его свойства.
Воспользуемся формулами:
=+2ab+=+
==
Используя принцип математической индукции (от частных примеров к общей формуле), получим формулу Ньютона:
=
Или кратко:
– формула Ньютона для степени бинома или бином Ньютона.
Свойства:
1. Формула содержит (n+1) ‒ слагаемое.
2. Показатель степени a ‒ убывает от n до 0; Показатель степени b – возрастает от 0 до n.
3. Любой член разложения можно найти по формуле:
.
4. Коэффициентыназываются – биноминальными. Биноминальные коэффициенты, равноудаленные от концов разложения, равны между собой.
5. Сумма всех биноминальных коэффициентов находятся по формуле:
Доказательство:
Пусть a = b = 1.
Тогда
Примеры на формулу Ньютона и ее свойства:
Пример 1.
Где
Следовательно,
Пример 2.
Найти: .
Решение:
В комбинаторных задачах удобно пользоваться следующей таблицей:
Выбор | Сочетания | Размещения | Перестановки |
Без повторения | |||
С повторением |
2.Понятие случайного события. Виды случайных событий.
Случайным событием, связанным с некоторым опытом (испытанием) называется всякое событие, которое при осуществлении опыта может произойти, а может и не произойти.
Случайные события обозначаются, заглавными буквами латинского алфавита A,B,C….
Виды случайных событий:
1. Событие, которое всегда происходит в результате опыта, называется достоверным. Обозначается .
2. Событие, которое никогда не происходит в результате опыта, называется – невозможным. Обозначается .
3. Событие, состоящее в том, чтобы событие A не произошло называется противоположным событию А. Обозначается .
4. События A и B называются несовместными, если они не могут произойти одновременно.
5. Событияназываютпопарно несовместными, если никакие два из них не могут произойти одновременно.
6. События образуютполную группу событий, если в результате опыта непременно произойдет, хотя бы одно из них.
7. События A и B называются равновероятными, если в результате опыта нет оснований считать одно из них более возможным, чем другое.
8. Событие, приводящее к наступлению события A, называется благоприятствующим событию А.
9. События , образующие полную группу попарно несовместных равновероятных событий, называютсяэлементарными событиями.
studfiles.net
Комбинаторика — основные понятия и формулы с примерами
Комбинаторика — раздел математики. Основные понятия и формулы комбинаторики как науки применяются во всех сферах жизни.
Неудивительно, что она включена в программу 11 класса, а также во вступительные испытания во многих ВУЗах РФ. Ее основы лежат в прикладном искусстве многих сфер деятельности человека.
Ее история насчитывает более 6 веков. Первые комбинаторные задачи появились в трудах философов и математиков Средневековья.
Представители того научного мира пытались найти методы решения таких задач, их базовые правила и понятия, утвердить уникальные формулы и уравнения для тех, кто ещё не встречался с ними. Такая информация в наше время называется информацией «для чайников».
Попытаемся разобраться в аспектах этой области науки: каковы элементы, свойства, правила, методы и основное ее применение в нашей жизни? Конечно, всю область в одной статье невозможно охватить. Поэтому ниже будет представлено всё самое основное.
Что такое комбинаторика в математике
Суть этого термина дают книги прошлых лет: это раздел математики, занимающийся операциями со множеством элементов.

В интернете есть учебники по информатике и математике для детей, школьников, сборники материалов и задач для начинающих, где в доступном виде объяснена «занимательная» комбинаторика. Нужно твердо выяснить, как решать подобные задачи.
В младших классах задачи на эту тему решают на дополнительных кружках, а в школах с углубленным изучением математики — на основных уроках. К тому же, задачи по комбинаторике включены в олимпиады всех уровней.
Основные понятия

Их несколько:
- Элемент – любой объект или явление, входящий в искомое множество.
- Сочетание – подмножества, находящиеся в произвольном порядке в исходном множестве.
- Перестановка – элементы во множестве находятся в строго определенном порядке.
- Размещение – упорядоченные подмножества в исходном множестве.
Правило произведения
Является одним из основных правил при решении таких задач и звучит так:
При выборе элемента А из n способов и выборе элемента В из m способов верно утверждение, что выбрать пару А и В одновременно можно n*m способами.

Рассмотрим на конкретных примерах.
Задача №1.
В коробке лежит 2 мяча и 6 скакалок. Сколько существует способов достать 1 мяч и 1 скакалку?
Ответ прост: 2 * 6 = 12.
Задача №2.
Есть 1 кубик, 2 шарика, 3 цветка и 4 конфеты. Сколькими способами можно вытянуть кубик, шарик, цветок и конфету?
Решение аналогично: 1 * 2 * 3 * 4 = 24.
Причем левую часть можно записать гораздо проще: 4!
! в данном случае является не знаком препинания, а факториалом. С помощью него можно вычислить более сложные варианты и решать трудные задачи (существуют разные формулы, но об этом позже).
Задача №3.
Сколько двузначных чисел можно составить из 2 цифр?
Ответ: 2! = 2.
Задача №4.
Сколько десятизначных чисел можно составить из 10 цифр?
10! = 3628800.
Правило суммы
Тоже является базовым правилом комбинаторики.
Если А можно выбрать n раз, а В — m раз, то А или В можно выбрать (n + m) раз.

Задача №5.
В коробке лежат 5 красных, 3 желтых, 7 зеленых, 9 черных карандашей. Сколько есть способов вытащить 1 любой карандаш?
Ответ: 5 + 3 + 7 + 9 = 24.
Сочетания с повторениями и без повторений
Под этим термином понимают комбинации в произвольном порядке из множества n по m элементов.

Число сочетаний равно количеству таких комбинаций.

Задача №6.
В коробке находится 4 разных фрукта. Сколькими способами можно достать одновременно 2 разных фрукта?
Решение простое:
Где 4! – комбинация из 4 элементов.
С повторениями чуть сложней, комбинации считаются по такой формуле:
Задача №7.
Возьмем тот же самый случай, но при условии, что один фрукт возвращается в коробку.
В этом случае:
Размещения с повторениями и без повторений

Под этим определением понимают набор m элементов из множества n элементов.

Задача №8.
Из 3 цифр надо выбрать 2, чтобы получались разные двузначные числа. Сколько вариантов?
Ответ прост:
А как же быть с повторениями? Здесь каждый элемент может размещаться несколько раз! В таком случае общая формула будет выглядеть следующим образом:
Задача №9.
Из 12 букв латинского алфавита и 10 цифр натурального ряда надо найти все варианты составления автомобильного кода региона.
Решение:
Перестановки с повторениями и без повторений

Под этим термином понимают все возможные комбинации из n элементного множества.

Задача №10.
Сколько возможных пятизначных чисел можно составить из 5цифр? А шестизначных из 6 цифр? Семизначных из 7 цифр?
Решения, согласно вышеприведенной формуле, следующие:
5! = 120;
6! = 720;
7! = 5040.
А как же быть с повторениями? Если в таком множестве есть одинаковые по своей значимости элементы, то перестановок будет меньше!
Задача №11.
В коробке есть 3 одинаковых карандаша и одна ручка. Сколько перестановок можно сделать?
Ответ прост: 4! / (3! * 1!) = 4.
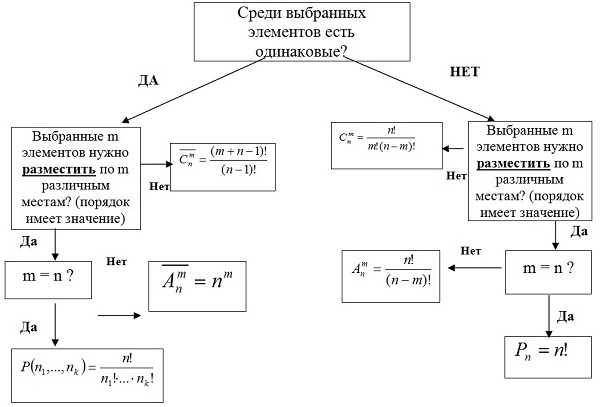
Комбинаторные задачи с решениями
Примеры всех возможных типов задач с решениями были даны выше. Здесь попробуем разобраться с более сложными случаями, встречающимися в нашей жизни.
| Типы задач | Что требуется найти | Методы решения |
| Магический квадрат | Фигура, в которой сумма чисел в рядах и столбцах должна быть одинакова (его разновидность – латинский квадрат). | Рекуррентные соотношения. Решается подобная же задача, но с гораздо меньшим множеством элементов по известным правилам и формулам. |
| Задача размещения | Стандартная производственная задача (например, в лоскутной технике) — найти возможные способы разложения количества продуктов в ячейки в определенном порядке. | Включения и исключения. Как правило, применяется при доказательстве различных выражений. |
| Задачи про торговцев | Суть — найти все возможные пути прохождения людей из пункта А в пункт В. | Траектории. Для этого вида задач характерно геометрическое построение возможных способов решения. |
Заключение
Стоит изучать эту науку, поскольку в век быстрой модернизации технологий потребуются специалисты, способные предоставить различные решения тех или иных практических задач.
1001student.ru
Элементы комбинаторного анализа
Теория
Общие определения комбинаторики
Понятие -выборки
Определение.Пусть заданоrмножеств:, при этом, тогдаr-выборкойназывается упорядоченная совокупность элементов вида:
(5.1)
Определение.Множество всех выборокназываетсятеоретико-множественным произведениемили произведением r множеств. Обозначается
!!! 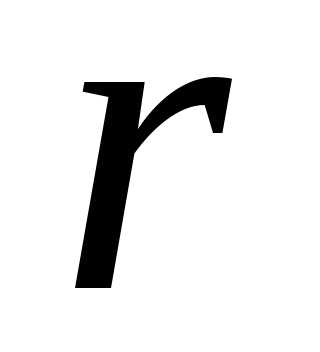 -выборка
не множество, а элемент теоретико-множественного
произведения.
-выборка
не множество, а элемент теоретико-множественного
произведения.
В 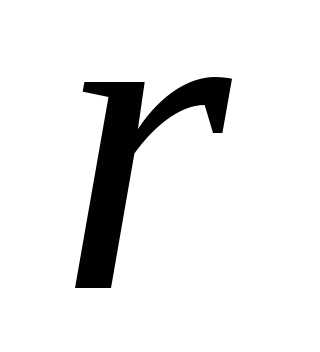 -выборке
каждый элемент(компонента) может
повторяться, но их порядок фиксирован.
-выборке
каждый элемент(компонента) может
повторяться, но их порядок фиксирован.
Определение.Две упорядоченные выборкиравныилиэквивалентнытогда и только тогда, когда соответствующие элементы равны
Определение.r-выборка с
произвольным порядком размещения
компонент называетсянеупорядоченной
r-выборкой. Обозначается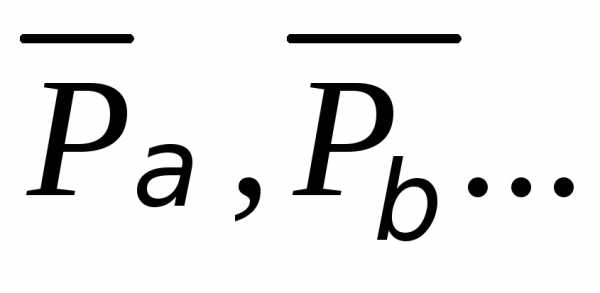
Модели комбинаторных конфигураций
Для формулировки и решения комбинаторных задач используют различные модели комбинаторных конфигураций. Примерами комбинаторных конфигураций являются:
Определение.Размещением 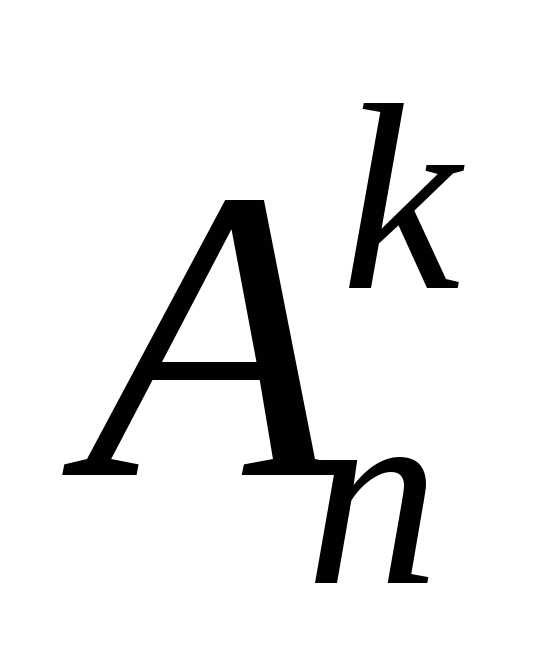 из
из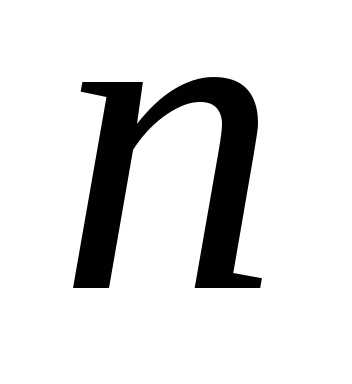 элементов по
элементов по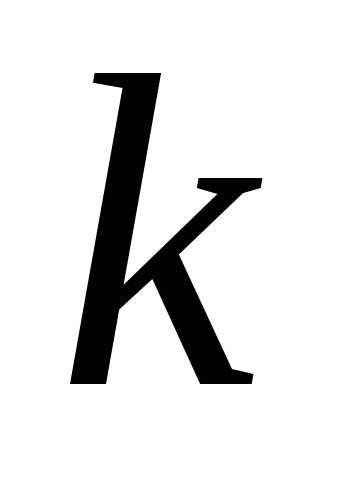 называетсяупорядоченный
набориз
называетсяупорядоченный
набориз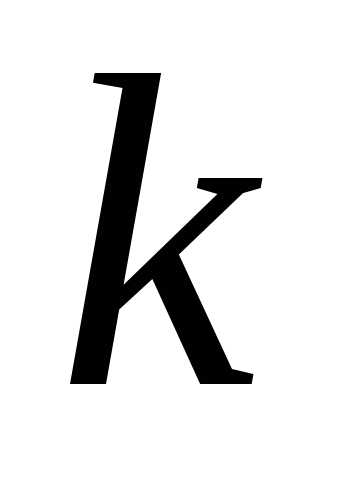 различных элементов некоторого
различных элементов некоторого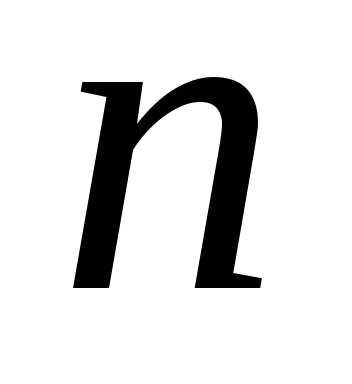 -элементного
множества.
-элементного
множества.
Определение.Перестановкой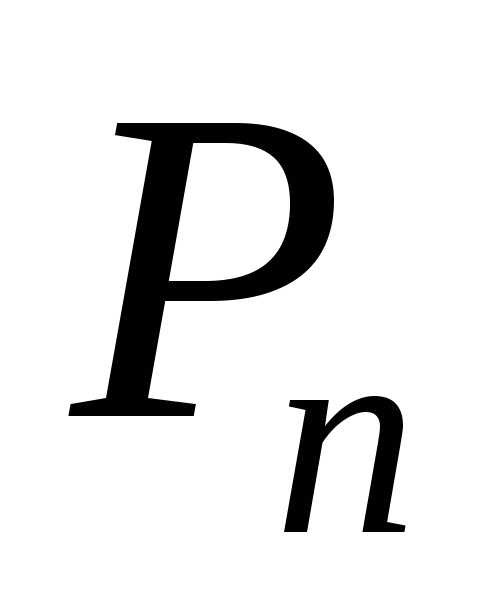 из
из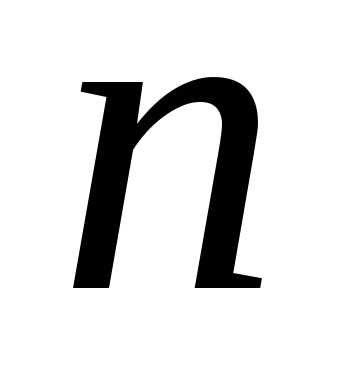 элементов (например, чисел
элементов (например, чисел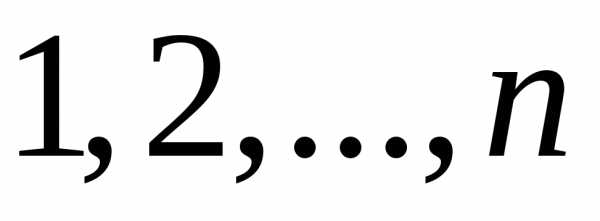 )
называется всякий упорядоченный набор
из этих элементов. Перестановка также
является размещением из
)
называется всякий упорядоченный набор
из этих элементов. Перестановка также
является размещением из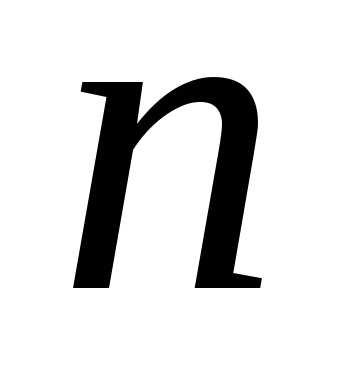 элементов
по
элементов
по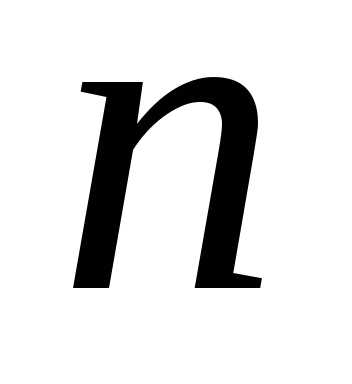 .
.
Определение.Сочетанием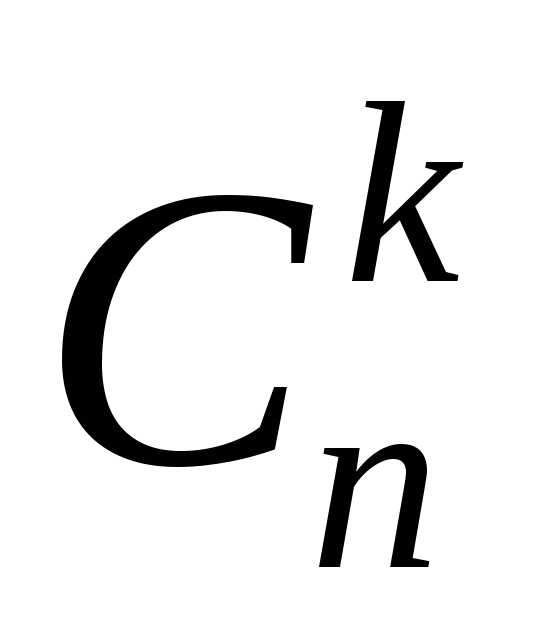 изпо
изпо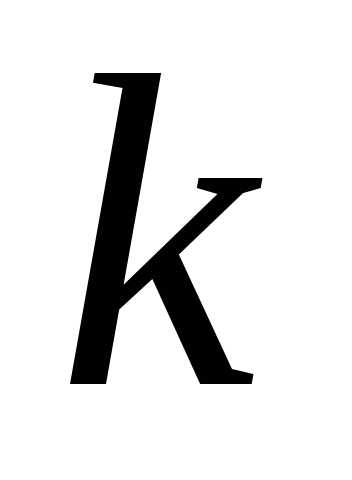 называется набор
называется набор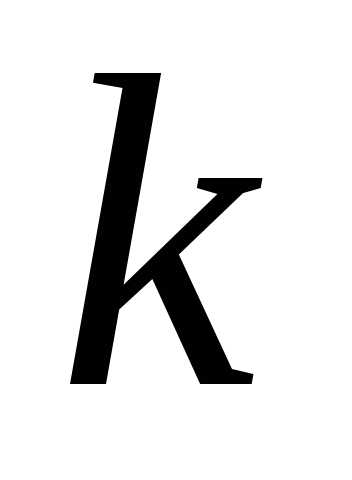 элементов, выбранных из данных
элементов, выбранных из данных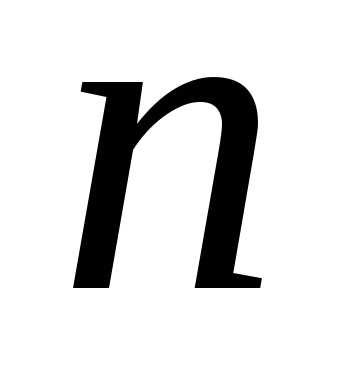 элементов. Наборы, отличающиеся только
порядком следования элементов (но не
составом), считаютсяодинаковыми,
этим сочетания отличаются от размещений.
элементов. Наборы, отличающиеся только
порядком следования элементов (но не
составом), считаютсяодинаковыми,
этим сочетания отличаются от размещений.
Определение.Композицией
числа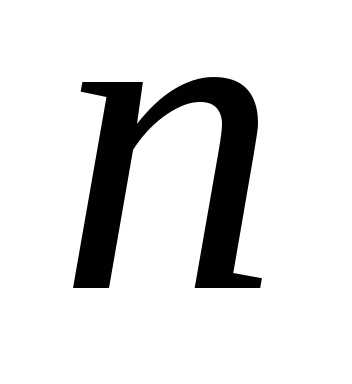 называется всякое представление
называется всякое представление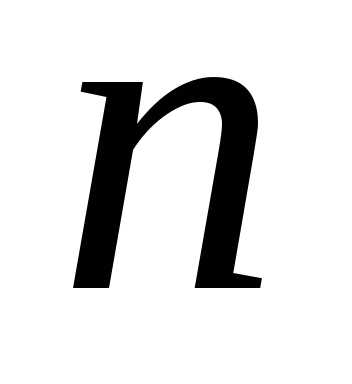 в виде упорядоченной суммы целых
положительных чисел.
в виде упорядоченной суммы целых
положительных чисел.
Определение.Разбиением
числа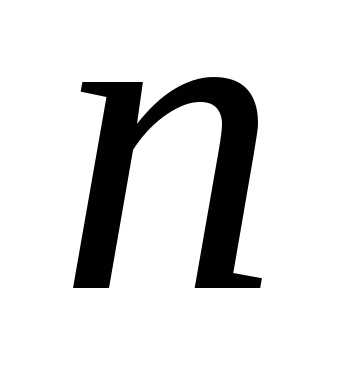 называется всякое представление
называется всякое представление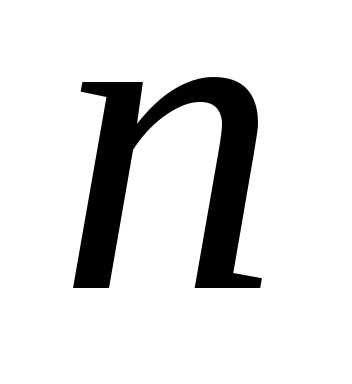 в виде неупорядоченной суммы целых
положительных чисел.
в виде неупорядоченной суммы целых
положительных чисел.
Общие правила и задачи комбинаторики
Основными и типичными операциями и связанными с ними задачамикомбинаторики являются:
1) образование упорядоченных множеств, состоящее в установлении определенного порядка следования элементов множества друг за другом, –
составление перестановок;
2) образование подмножеств, состоящее в выделении из данного множества некоторой части его элементов, – составление сочетаний;
3) образование упорядоченных подмножеств – составление размещений.
Большинство комбинаторных задач решается с помощью двух основных правил – правила суммы и правила произведения.
Основные правила комбинаторики
Правила суммы и произведения используются при вычислении количества различных комбинаций.
Правило
суммы. Если  и
и – несвязанные события, и существует
– несвязанные события, и существует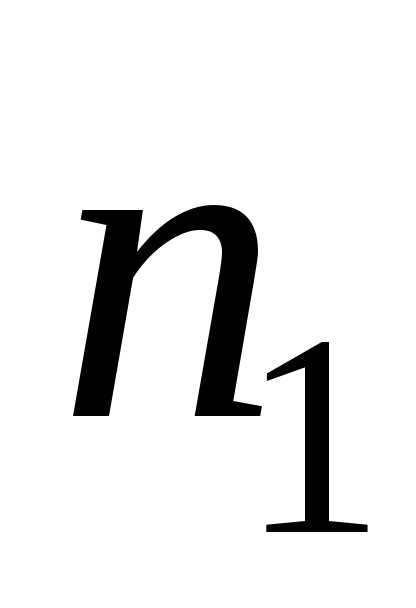 возможных исходов события
возможных исходов события ,
и
,
и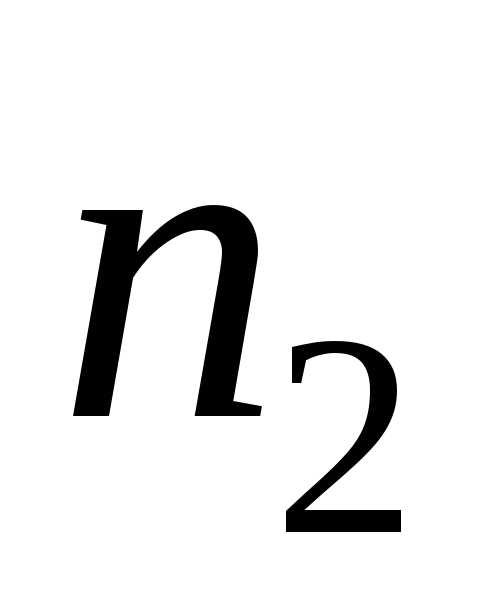 возможных исходов события
возможных исходов события ,
то возможное число исходов события «
,
то возможное число исходов события « или
или »
равно сумме
»
равно сумме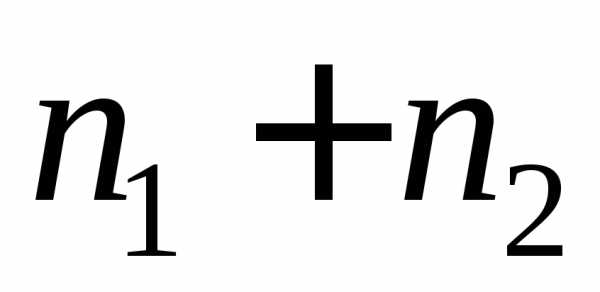 .
.
Интерпретация. Если элемент  можно выбрать
можно выбрать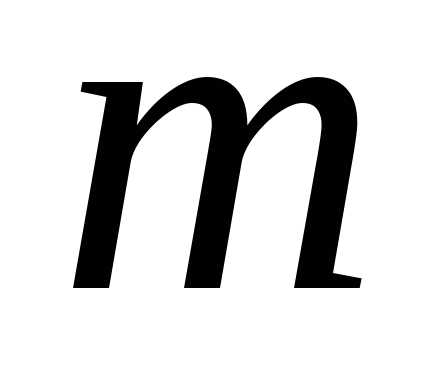 способами, а элемент
способами, а элемент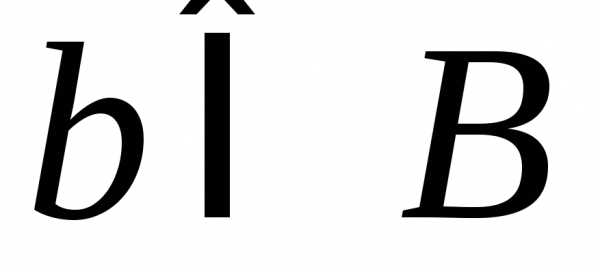 –
–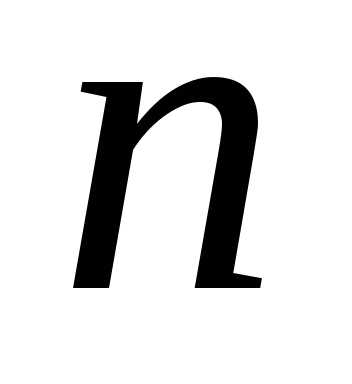 способами, то выбор элементаможно осуществить
способами, то выбор элементаможно осуществить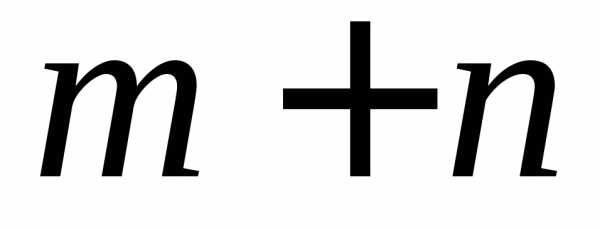 способами. Пусть
– попарно непересекающиеся
множества,
,
где
способами. Пусть
– попарно непересекающиеся
множества,
,
где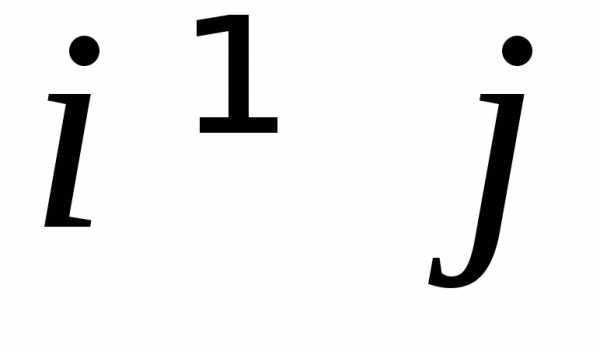 .
Тогда, очевидно, выполняется равенство
.
Тогда, очевидно, выполняется равенство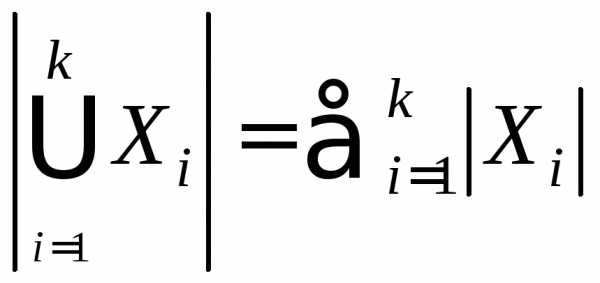 .
.
Правило произведения. Если дана последовательность 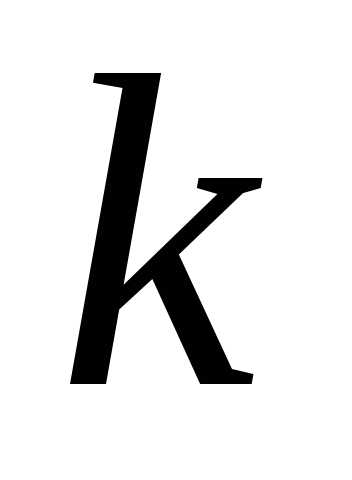 событий с
событий с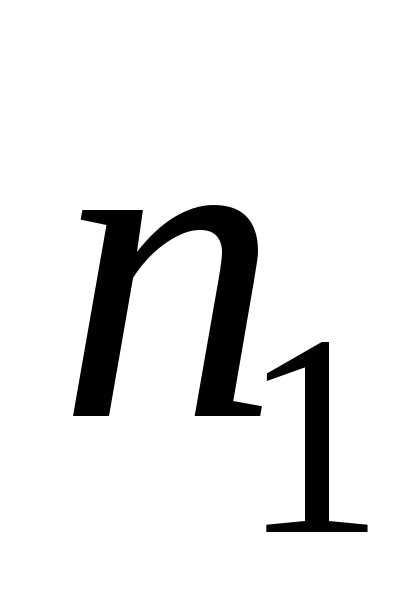 возможными исходами первого,
возможными исходами первого,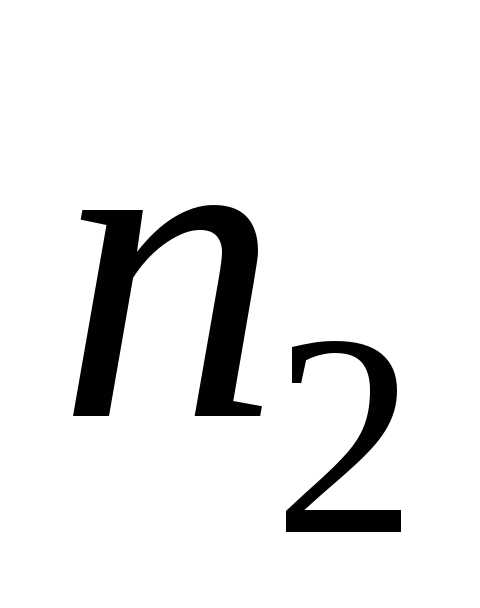 – второго, и т.д., вплоть до
– второго, и т.д., вплоть до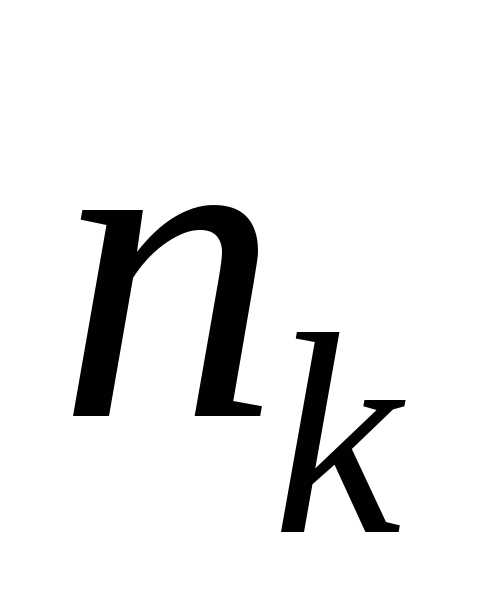 возможных исходов последнего, то общее
число исходов последовательности k
событий равно произведению.
возможных исходов последнего, то общее
число исходов последовательности k
событий равно произведению.
Правило произведения тоже
можно сформулировать на языке теории
множеств. Пусть  обозначает множество
обозначает множество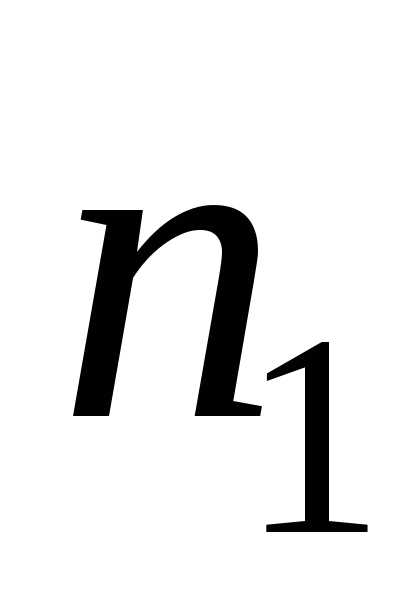 исходов первого события,
исходов первого события, – множество
– множество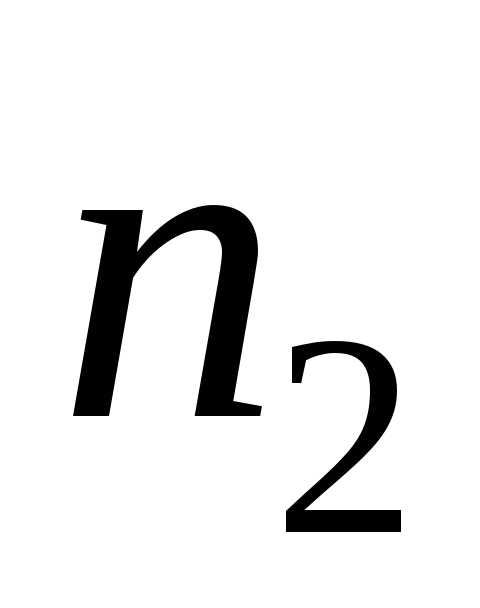 исходов второго, и т. д. Тогда любую
последовательность
исходов второго, и т. д. Тогда любую
последовательность событий можно рассматривать как элемент
декартова произведения,
чья мощность равна.
событий можно рассматривать как элемент
декартова произведения,
чья мощность равна.
Пример. Из 28 костей домино берутся 2 кости. В каком числе комбинаций вторая кость будет приложима к первой?
На первом шаге имеется два варианта: выбрать дубль (7 комбинаций) или не дубль (21 комбинация). В первом случае имеется 6 вариантов продолжения, во втором – 12.
Общее число благоприятных комбинаций равно: .
А всего вариантов выбора 2 костей из 28 равно 378; т. е. при большом числе экспериментов в 7 случаях из 9 (294/378 = 7/9) при выборе 2 костей одна кость окажется приложимой к другой.
studfiles.net
