Отличие арифметической прогрессии геометрической прогрессии – Чем отличается арифметическая прогрессия от геометрической прогрессии?

Прогрессия арифметическая и геометрическая — Чем арифметическая прогрессия отличается от геометрической? — 22 ответа



Арифметическая и геометрическая прогрессия

В разделе Школы на вопрос Чем арифметическая прогрессия отличается от геометрической? заданный автором Переброситься лучший ответ это Арифметическая прогрессия — это последовательность в разницу НА определенное число.
Например: 1,5,9,13,…
Здесь разница на 4
Геогметрическая прогрессия — это последовательность в разницу В определенное число
Например: 1,4,16,64,…
Здесь последующее число больше предыдущего в 4 раза

Ответ от 22 ответа[гуру]

Привет! Вот подборка тем с ответами на Ваш вопрос: Чем арифметическая прогрессия отличается от геометрической?

Ответ от Виктор боярский[новичек]
арифметическая — это прибавление. Например 1, 5, 9 и т. д, т. е. прибавляем к последнему числу 4.
геометрическая- это умножение. Например: : 1, 3,9,27

Ответ от Алексей Онорин[гуру]
Арифметическая — 1;2;4;8;16;32;64;128;256 и т д. Геомерическая — 1;2;4;16;256;65536 и т д. Чувствуешь разницу?

Ответ от Голосовать[гуру]
2+2=4+4=8+8=16+16=32….Это арифметическая
2*2=4*4=16*16=256….Это геометрическая

Ответ от Евровидение[новичек]
арифметическая это сумма каких либо членов, а геометрическая произведение

Ответ от Аноним[гуру]
Арифметическая увеличивается НА сколько то, геометрическая ВО сколько то

Ответ от Алексей Дурнев[гуру]
В арифметической каждый последующий член равен предыдущему плюс одно и тоже число
В геометрической каждый последующий член равен предыдущему умноженному на одно и тоже число

Ответ от 2 ответа[гуру]

Привет! Вот еще темы с нужными ответами:

Арифметическая прогрессия на Википедии
Посмотрите статью на википедии про Арифметическая прогрессия

Геометрическая прогрессия на Википедии

Посмотрите статью на википедии про Геометрическая прогрессия

 

Ответить на вопрос:

22oa.ru

Сравнение арифметической и геометрической прогрессий

Урок-лекция «Сравнение арифметической и геометрической прогрессий»

План урока дан для сильного, думающего, увлеченного математикой класса, обучающегося в обычной школе. Изучение арифметической и геометрической прогрессий проводится параллельно.

Алгебра 9 класс. Тема: «Прогрессии» (16 — 18 часов)
(По учебнику «Алгебра 9» под редакцией С.А. Теляковского)

Поурочное планирование:
1. Вводное занятие «Понятие последовательности», 1 час.
2. Лекция «Сравнение арифметической и геометрической прогрессий», 2 часа.
3. Обзор лекции, решение опорных задач, 2 часа.
4. Уроки практикума, 8 часов.

5. Урок-семинар, 2 часа.
6. Урок-зачет, 1 час.
7. Контрольная работа, 2 часа.

Вопросы к зачету:
1. Что такое числовая последовательность? Привести пример.
2. Определение арифметической, геометрической прогрессий.
3. Формула n-ого члена (вывод).
4. Свойства прогрессий.
5. Формула суммы n первых членов прогрессий (вывод).
6. Сумма бесконечно убывающей геометрической прогрессии.

Цели урока:
1. Образовательные – ввести определения арифметической, геометрической прогрессий; вывести формулы n-го члена, суммы n первых членов, суммы бесконечной геометрической прогрессии при |q| 2. Развивающие – продолжить дальнейшую работу по выработке умения сравнивать математические понятия, находить сходства и различия, умения наблюдать, подмечать закономерности, проводить рассуждения по аналогии; сформировать умение строить и интерпретировать математическую модель некоторой реальной ситуации.

3. Воспитательные – содействовать воспитанию интереса к математике и ее приложениям, активности, умению общаться, аргументировано отстаивать свои взгляды.

Оборудование: кодоскоп, рисунки к задачам, сравнительная таблица «Виды последовательности», портреты Гаусса, Л.Н. Толстого.

Тип урока: лекция по введению и самостоятельному приобретению новых знаний.

Метод обучения: учебно-познавательная работа учащихся по самостоятельному приобретению новых знаний; работа по обобщающей схеме, самопроверка, взаимопроверка.

Эпиграф к уроку: «Сравнение есть основа всякого понимания и всякого мышления, чтобы какой-нибудь предмет был понят ясно, отличайте его от самых сходных с ним предметов и находите сходство с самыми отдельными от него предметами, тогда только вы выясните себе все существенные признаки, а это значит – понять предмет». (К.Д. Ушинский)

Ход урока:

1. Подготовительная работа.

Формулирование определения умения сравнивать:
«Сравнение – сопоставление объектов с целью выявления черт сходства и черт различия между ними. Суждения, выражающие результат сравнения, служат цели раскрытия содержания понятий сравниваемых объектов». (Философский словарь)

1. Выделение объектов исследования.

Сравнить между собой последовательности:
1) 2, 7, 9, 12, …;
2) 3, 5, 7, 9, 11, …;
3) 4, 8, 16, 32, …;
4) –17, 25, 36, 2, 18, …;
5) –1, 2, –4, 8, –16, …;
6) 10, 9, 8, 7, 6, …;


9) 3, 3, 3, …;

11) 1, –3, 9, –27, 81, …;
12) –1, –1, –1, … .
а) Опишите закономерность, с помощью которой вы это сделали?
б) Объедините последовательности в группы.

Вывод: Сравнивая между собой эти последовательности, учащиеся обнаружат среди них такие, которые образованы при помощи одного и того же общего для всех свойства, а затем установят способ их конструирования.

2. Обнаружение свойств изучаемых объектов, которые являются основанием для определения.

На доску слева проецируется задача, приводящая к арифметической, а справа – к геометрической прогрессии.

Задача Рабочий выложил плитку следующим образом: в первом ряду — 3 плитки, во втором — 5 плиток и т.д., увеличивая каждый ряд на 2 плитки. Сколько плиток понадобиться для седьмого ряда? Рис. 1

Задача В благоприятных условиях бактерии размножаются так, что на протяжении одной минуты одна из них делится на две. Указать количество бактерий, рожденных одной бактерией за 7 минут. Рис. 2

Вопросы к задачам:
1. Записать последовательность в соответствии с условием задачи.
2. Указать последующий, предыдущий члены. Чем они отличаются?
3. Найти разность между предыдущим и последующими членами в первой задаче и частное от деления последующего члена на предыдущий во второй задаче.

4. Дать определение арифметической (геометрической) прогрессии.

2. Учебно-познавательная работа учащихся по самостоятельному приобретению новых знаний.

«Прогрессия» – латинское слово, означающее «движение вперед», было введено римским автором Боэцием (VI век) и понималось в более широком смысле, как бесконечная числовая последовательность. Предлагается разделить страницу тетради на две части и слева написать «Арифметическая прогрессия», а справа «Геометрическая прогрессия». Всю работу школьники проделывают на доске и в тетрадях одновременно для обеих прогрессий.

Арифметическая прогрессия	Геометрическая прогрессия
Определение
3, 5, 7, 9, 11, 13, 15, … 5 = 3 + 2; 7 = 5 + 2; … Арифметической прогрессией называется последовательность, каждый член которой, начиная со второго, равен предыдущему члену, сложенному с одним и тем же числом (). d – разность прогрессии, где	1, 2, 4, 8, 16, 32, 64, … 2 = 1·2; 4 = 2 · 2; 8 = 4 · 2; … Геометрической прогрессией называется последовательность отличных от нуля чисел, каждый член которой, начиная со второго, равен предыдущему члену, умноженному на одно и то же число (). q – знаменатель прогрессии, где
(В задании № 1 указать разность (знаменатель) прогрессии, дать понятие возрастающей или убывающей прогрессии)
Задание прогрессии
Формула n-ого члена
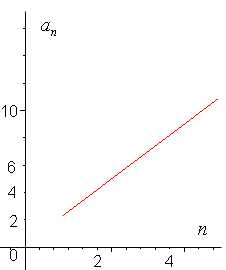
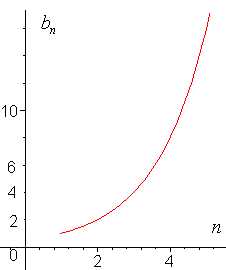
Работа по выводу формулы n – ого члена проводится самостоятельно по вариантам, затем делаем вывод и записываем формулы (). Далее предложить учащимся сравнить прогрессии, изобразив графически, зависимость n – ого члена от порядкового номера, используя данные приведенных выше задач.
Рис. 3 Разность двух рядом стоящих членов остается одно и та же, вследствие чего члены прогрессии возрастают (убывают) равномерно. Отсюда ясно, что любая арифметическая прогрессия может быть задана формулой вида Верно и обратное: учебник стр. 85.	Рис.4 Разность двух соседних членов увеличивается по мере удаления их от начала ряда; вследствие этого, члены такой прогрессии, по мере их удаления от начала ряда, возрастают все быстрее и быстрее, что наглядно изображено на рис. 4. Данная зависимость представляет собой показательную функцию, с которой учащиеся познакомятся в старших классах.
Характеристическое свойство Вопросы и задания к учащимся: 1) Найти среднее арифметическое (геометрическое) чисел 2 и 8. Записать найденное число с данными в порядке возрастания. Образуют ли эти числа арифметическую (геометрическую) прогрессию?
2) Справедлива ли эта зависимость для трех последовательных членов рассматриваемых последовательностей?
3) Доказать, что для членов прогрессий справедлива закономерность:
Доказательство провести по вариантам и обменяться мнениями:
Следствие
Из определения разности следует, что т.е. сумма членов, равноудаленных от концов прогрессии, есть величина постоянная.	Из определения знаменателя следует, что т.е. произведение членов, равноотстоящих от концов прогрессии, есть величина постоянная.
Формула суммы п первых членов
Вернемся задаче: Сколько потребуется рабочему плиток, чтобы выложить 5 рядов? Рассуждение поясним на рис. 5. Рис. 5 Сумму 3+5+7+9+11 можно изобразить так, как показано на рис. 5 и из двух таких фигурок составить прямоугольник , тогда рабочему потребуется (5 ·14) ÷ 2 плиток. Продолжим рассуждения: S = 3 + 5 + 7 + 9 + 11. Напишем в обратном порядке: S = 11 + 9 + 7 + 5 + 3. И сложим эти равенства: S = 3 + 5 + 7 + 9 + 11 + + 11 + 9 + 7 + 5 + 3. В каждом столбце стоят 2 числа, дающие в сумме 14. Поэтому: Вывод: в общем случае будет n столбцов с одинаковой суммой, равной сумме первого и последнего членов. Поэтому Задача: найти сумму первых ста натуральных чисел 1 + 2 + 3 + … + 98 + 99 + 100? Используя исторический материал, рассказать ребятам историю о знаменитом немецком математике К. Гауссе (1777-1855 г.г.), который обнаружил выдающиеся способности к математике. Учитель предложил сложить все натуральные числа от 1 до 100. Маленький Гаусс решил эту задачу за минуту. Сообразив, что 1 + 100, 2 + 99 и т.д. равны, он умножил 101 · 50 = 5050. Иначе говоря, он заметил закономерность, которая присуща арифметической прогрессии. Заметим, что если заданы первый член и разность, то удобно пользоваться формулой суммы, представленной в другом виде. Так как	Учащимся предлагается задача, при решении которой возникает необходимость в выводе новой формулы. «Индийский царь Шерам призвал к себе изобретателя шахмат, ученого Сету, и предложил, чтобы он сам выбрал себе награду за создание интересной и мудрой игры. Царя изумила скромность просьбы, услышанной им от изобретателя: тот попросил выдать ему за первую клетку шахматной доски одно пшеничное зерно, за вторую — два, за третью — еще в два раза больше и т.д. Сколько зерен должен получить изобретатель шахмат?» Возникает необходимость найти , где Имеем: Умножим обе части равенства на знаменатель q = 2; получим Вычтем почленно из второго равенства первое и проведем упрощения: Эта задача привлекла внимание Л.Н. Толстого. Приведем часть его расчета (кодоскоп): 1 кл. — 1 2 кл. — 2 3 кл. — 4 … 35 кл. — 17 179 869 184 … 64 кл. — 9 223 372 036 854 775 808 Общее число зерен: 18 446 744 073 709 551 615. Масса такого числа зерен больше триллиона тонн. Это заведомо превосходит количество пшеницы, собранной человечеством до настоящего времени. Воспользуемся тем же приемом, с помощью которого была вычислена сумма (Предложить учащимся самостоятельно получить формулу суммы n первых членов).

Сумма бесконечной геометрической прогрессии при |q|

Особого внимания заслуживает бесконечно убывающая геометрическая прогрессия, где |q| Это лучше всего объяснить на примерах. Один из «парадоксов Зенона» (древнегреческого философа) состоит в следующем (в изложении Льва Толстого в «Войне и мире», т. 3, ч. 3).
… Ахиллес никогда не догонит впереди идущую черепаху, несмотря на то, что Ахиллес идет в десять раз скорее черепахи: как только Ахиллес пройдет пространство, отделяющее его от черепахи, черепаха пройдет впереди его одну десятую этого пространства; Ахиллес пройдет эту десятую, черепаха пройдет одну сотую и т.д. до бесконечности. Задача представлялась древним неразрешимой.
Отрезки, последовательно пробегаемые Ахиллесом, составляют геометрическую прогрессию

со знаменателем 0,1. (за единицу принимаем начальное расстояние между Ахиллесом и черепахой). Общее расстояние, пройденное Ахиллесом до встречи с черепахой, есть «сумма бесконечного числа членов»:

Способ 1: Обозначим сумму через S:


Способ 2: Будем добавлять слагаемые по одному:

Способ 3: По формуле суммы геометрической прогрессии:


Получаем формулу:

(изменили знаки в числителе и знаменателе).

Способ 4: Здравый смысл подсказывает, что Ахиллес догонит черепаху, пробежав некоторое расстояние S. За это время черепаха, скорость которой в 10 раз меньше, проползает расстояние S/10 и расстояние между ними уменьшится на

В начале оно равнялось 1, а в момент встречи стало нулевым, так что

Затем предложить учащимся ознакомиться с выводом формулы суммы бесконечной геометрической прогрессии при |q|
и рассмотреть в учебнике задания на применение данной формулы.

3. Подведение итогов урока

Предложить учащимся ответить на вопросы:
1) по какому плану сравнивали изучаемые понятия «Арифметическая и геометрическая прогрессии»;
2) укажите их общие существенные признаки;
3) определите существенные различия между ними;
4) сделайте вывод, вытекающий из сравнения.

Результаты можно оформить в виде таблицы «Вид последовательности».

Арифметическая прогрессия	Геометрическая прогрессия
Определение
d – разность.	q – знаменатель.
Формула n-ого члена
Характеристическое свойство
Формула суммы п первых членов
	Сумма бесконечной геометрической прогрессии при |q|

 

4. Задание на дом

1. Учебник «Алгебра 9» (под редакцией С.А. Теляковского), изучать параграфы 7, 8.
2. Исторические сведения о прогрессиях (учащиеся по желанию готовят выступления, доклады).
3. Составить задачи на применение арифметической и геометрической прогрессий.
4. Найти сумму первых п четных чисел; нечетных чисел.

kopilkaurokov.ru

как определить геометрическая прогрессия или арифметическая

Подробно <a rel=»nofollow» href=»http://www.math.md/school/praktikum/progr/progr.html» target=»_blank»>http://www.math.md/school/praktikum/progr/progr.html</a>

В геометрической прогрессии идет умножение на предыдущее, а в арифметической сложение

Любой член геометрической прогрессии может быть вычислен по формуле: b_n=b_1q^{n-1} \quad Если b_1&gt;0 и q&gt;1, прогрессия является возрастающей последовательностью, если 0&lt;q&lt;1, — убывающей последовательностью, а при q&lt;0 — знакочередующейся [2]. Своё название прогрессия получила по своему характеристическому свойству: |b_{n}| = \sqrt{b_{n-1} b_{n+1}}, то есть каждый член равен среднему геометрическому его соседей.

Арифметическая прогрессия — это последовательность в разницу НА определенное число. Например: 1,5,9,13,… Здесь разница на 4 Геогметрическая прогрессия — это последовательность в разницу В определенное число Например: 1,4,16,64,… Здесь последующее число больше предыдущего в 4 раза

Арифметическая прогрессия (an) ,d-знаменатель. d=a2-a1,d=a3-a2,d=a4-a3 и тд. Например: 2,4,6,8,10..-арифмитическая прогрессия. а1=2,а2=4,а3=6,а4=8,а5=10. d=a2-a1=4-2=2. d=a3-a2=6-4=2. Геометрическая прогрессия (bn) q-знаменатель. q=b2:b1,q=b3:b2,q=b4:b3 и т. д. Везде q будет одинаковым если прогрессия правильная. например: 2,4,8,16… b1=2,b2=4,b3=8,b4=16. q=b2:b1=4:2=2. q=b3:b2=8:4=2. q=b4:b3=16:8=2. Вывод: В арифмитической прогрессий каждый последующий член больше на d.В геометрической прогрессии каждый последующий член больше в q раз.

touch.otvet.mail.ru

Арифметическая и геометрическая прогрессии

Арифметическая и геометрическая прогрессия не будет для Вас сложной темой после просмотра следующих примеров. Внимательно ознакомьтесь с ответами среднего уровня сложности и выберите для себя самое необходимое. Если приведенные примеры для Вас тяжелые, прочитайте для начала простые примеры на арифметическую и геометрическую прогрессию (1 уровень).

Группа Б (уровень 2)

Пример 1. В арифметической прогрессии а₈=12,4; a₂₃=4,7. Вычислить сумму а₁₄+a₁₇.
Решение: Представим 14 член прогрессии через 8 и 17 через 23. В виде формул они будут запись
a₁₄=а₈+6d;
a₁₇=a₂₃-6d.
Находим искомую сумму членов прогрессии
a₁₄+a₁₇=a₈+6d+a₂₃-6d=a₈+a₂₃;
a₁₄+a₁₇=12,4+4,7=17,1.
Ответ: сумма равна 17,1.

 

Пример 2. В геометрической профессии b₄=3; b₁₇=14,7. Вычислить произведение b₉*b₁₂.
Решение: Учитывая свойства геометрической прогрессии, запишем ее 9 член через 4, а 12 через 17.


Видим, что при умножении знаменатель геометрической прогрессии упрощается

b₉*b₁₄=3*14,7=44,1.
Ответ: произведение равно 44,1.

 

Пример 3. Сумма п первых членов арифметической прогрессии выражается формулой S_n=3n²+6n. Вычислить a₆.
Решение: Найдем первый член прогрессии и сумму первых двух
a₁=S₁=3+6=9;
a₁+a₂=2a₁+d=S₂=3*2^2+6*2=24.
Из второго уравнения, учитывая значение первого члена, находим шаг прогрессии
d=24-2a₁=24-2*9=6.
По общей формуле вычисляем 6 член арифметической прогрессии
a₆=a₁+5d=9+5*6=39.
Ответ: a₆=39.

 

Пример 4. Сумма п первых членов арифметической прогрессии выражается формулой S_n=n²+5n. Вычислить a₁₀.
Решение: Задача идентичное предыдущей, только на этот раз попробуем решить по другой методике. Используем сумму арифметической прогрессии в виде

Подставим в эту формулу заданную зависимость суммы и приравняем коэффициенты при одинаковых степенях n


Это и есть важная формула, из которой находим первый член прогрессии и разность (шаг)

d=2; a₁=5+d/2=6.
Вычисляем 10 член прогрессии
a₁₀=a₁+9d=6+9*2=24.
Ответ: a₁₀=24.

 

Пример 5. Вычислить сумму всех четных натуральных чисел до 100 включительно.
Решение: Первый элемент последовательности равен a₁=2, последний равен 100. От 1 до 10 имеем 5 четных чисел. В сотни всего 10 десятков то есть 10*5 четных чисел. Если рассуждать по-другому, то половина элементов до 100 четные, половина — нечетные.
100/2=50 – количество четных чисел.
Разница прогрессии равна 2.
Далее подставляем известные значения в формулу и вычисляем

Сумма четных чисел до 100 равна 2550.
Ответ: S₅₀=2550.

 

Пример 6. Вычислить сумму всех двузначных чисел.
Решение: Номер члена прогрессии будет равен его значению
a₁=1;… a₉₉=99.
Разница прогрессии равна единице d=1. Находим сумму арифметической прогрессии по формуле

Сумма равна 4950.
Ответ: S₉₉=4950.

 

Пример 7. В арифметической прогрессии а₂+a₁₁=10, а₅+a₆=13. Вычислить разницу прогрессии.
Решение: Аглоритм решения подобных примеров следующий: Выражаем члены прогрессии через один, имеющий наименьший порядковый номер
a₁₁=a₂+9d;
a₅=a₂+3d;
a₆=a₂+4d.
Подставляем ету запись в сумму членов прогрессии
a₂+a₂+9d=2*a₂+9d=10;
a₂+3d+a₂+4d=2*a₂+7d=13.
Есть два уравнения с двумя неизвестными. Для отыскания разницы прогрессии от первого уравнения вычитаем второе
9d-7d=2d=10-13;
2d=-3; d=-1,5.
Ответ: d=-1,5.

 

Пример 8. В арифметической прогрессии а₂+a₁₁=10, а₅+a₆=13. Вычислить a₁.
Решение: Задача аналогична предыдущей. Выражаем, для удобства, все члены суммы через 1 номер
a₂=a₁+d; a₁₁=a₁+10d;
a₅=a₁+4d; a₆=a₁+5d.
Подставляем в формулы и составляем уравнение
a₁+d+a₁+10d=2*a₁+11d=10;
a₁+4d+a₁+5d=2*a₁+9d=13.
От первого уравнения вычтем второе и найдем шаг прогрессии
11d-9d=2d=10-13=-3.
2d=-3; d=-1,5.
Зная шаг прогрессии, первый ее элемент находим из уравнения
2*a₁+9*(-1,5)=13; 2*a₁=13+13,5=26,5;
a₁=26,5/2=13,25.
Ответ: a₁=13,25.

 

Пример 9. Вычислить сумму всех двузначных натуральных чисел которые при делении на 3 дают в остатка 2.
Решение: Сначала запишем общую формулу члена прогрессии для данной задачи. Учитывая условие получим зависимость
a[n]=3*n+2.
Первое двузначное число, которое удовлетворяет условию это 11.
a[3]=3*3+2=11.
Последнее число равно 98 и оно соответствует 32 номеру прогрессии
a[32]=3*32+2=98.
Дальше есть выбор из двух вариантов — искать частичную сумму прогрессии или от полной суммы вычесть первых два элемента. Поступим по второй схеме
a₁=3+2=5; a₂=3*2+2=8;

От найденной суммы вычитаем первые два элемента прогрессии
S=1648-5-8=1635.
Ответ: S=1635.

 

Пример 10. Вычислить сумму всех двузначных натуральных чисел которые при делении на 4 дают в остатка 1.
Решение: Выпишем общую формулу члена прогрессии
a[n]=4*n+1.
Всегда поступайте таким образом для описания прогрессии.
Первое нужное число равно 13. Его легко получить взяв несколько членов прогрессии – 5; 9;13; …
С последним номером немного больше поисков, но можно установить, что это будет 97.
a[3]=13; a[24]=97.
Шаг прогрессии составляет d=4.
Находим сумму двузначных натуральных чисел

Получили в сумме 1210.
Ответ: S=1210.

 

Пример 11. Вычислить сумму всех нечетных натуральных чисел от 13до 81 включительно.
Решение: Запишем формулу нечетных чисел.
a[n]=2*n+1, n=0; 1; …
Сделаем замену в прогрессии так, чтобы элемент под первым номером был равен 13.
a[n]=2*n+1=13.
Отсюда n=6. Значит новая прогрессия выходит с предыдущей добавлением к индексу n+1=6; n=5.
b[n]=2(n+5)+1.
Найдем под каким номером в прогрессии идет число 81.
2*(n+5)+1=81;
n+5=(81-1)/2=40; n=35.
Итак b[35]=81.
Находим сумму первых 35 членов прогрессии

Следовательно, искомая сумма равна 1645.
Второй метод заключается в нахождении суммы прогрессии a[n] с определенного ее номера. Для этого нужно знать формулу, которую порой нет возможности на контрольных или тестах выводить из формулы суммы прогрессии

Если Вы ее знаете, то в этом случае нужную найти сумму от 6 до 40 члена прогрессии a[n]

И на «закуску» третий способ, который заключается в вычитании из полной суммы прогрессии суммы ее первых членов.

На этом вычисления примера завершены.
Ответ: S=1645.

 

Пример 12. В арифметической прогрессии а₁₈=12,3; a₃₂=2,8. Вычислить а₂₁+a₂₉.
Решение: Если Вы внимательно просмотрели ответы в предыдущих примерах то знаете как поступить в этом задании. Сначала выражаем 21 и 29 член прогрессии через 18 и 32.
a₂₁=a₁₈+(21-18)d=a₁₈+3d;
a₂₉=a₃₂+(29-32)d=a₃₂-3d.
Легко видеть, что при суммировании разница прогрессии пропадает
a₂₁+a₂₉=a₁₈+a₃₂=12,3+2,8=15,1.
Ответ: сумма равна 15,1.

 

Пример 13. Сумма п первых членов арифметической прогрессии выражается формулой S_n=13n²+5n. Вычислить разницу прогрессии.
Решение: Подобная задача рассматривали под номером 3, 4. Запишем общую формулу суммы прогрессии и приравняем к заданной

Приравняем коэффициенты при квадрате номера прогрессии

Разница прогрессии равна 26
Ответ: d=26.

 

Пример 14 Сумма п первых членов арифметической прогрессии выражается формулой S_n=3n²+8n. Вычислить разницу прогрессии.
Решение: Здесь не будем Вас утомлять и по аналогии с предыдущим примером запишем, что коэффициент при квадрате индекса равен половине разницы прогрессии
d/2=3; d=3*2=6.
Видим, наскоько просто найти разницу прогрессии.
Ответ: d=6.

 

Пример 15. В геометрической прогрессии b_m-n=7,2; b_m=9,6. Вычислить b_m+n
Решение: На вид задания на геометрическую прогрессию сложное. Однак простые формулы позволяют вычислить все.
Запишем b_m через предварительный известный член прогрессии b_m-n
b[m]=b[m-n]*q^n.
Такое же выполним для b_m+n
b[m+n]= b[m]*q^n.
Осталось из первого уравнения выразить знаменатель прогрессии
q^n= b[m]/b[m-n]
и подставить во второе

Подставим заданные значения в формулу

Искомый член геометрической прогрессии равен 12,8.
Ответ: b[m+n]=12,8.

 

Пример 16. В геометрической прогрессии b_m+n=6,3; b_m=4,2. Вычислить b_m-n
Решение: Этот пример построен по обратному принципом к предыдущему, однако ход вычислений подобный. Из анализа значений геометрической прогрессии следует, что b_m-n должен быть меньше b_m=4,2. А аналогии с предыдущим примером позволяют припустить, что ответом будет квадрат меньшего числа разделен на большее значение.
b_m-n= b_m* b_m/b_m+n
и сейчас Вы в этом убедитесь.
Запишем следующие члены геометрической прогрессии через предыдущие
b[m]=b[m-n]*q^n;
b[m+n]= b[m]*q^n.
С первой зависимости находим b_т-п, а з 2 – q^n.

Выполним соответствующие расчеты
b[m-n]=4,2*4,2/6,3=2,8.
Ответ: b[m-n]=2,8.

 

Пример 17. В арифметической прогрессии а_т+п=1,4; а_т-п=92,8. Вычислить а_т.
Решение: Неизвестный член арифметической прогрессии равен среднему арифметическому соседних элементов. Поскольку а_т+п и а_т-п есть равноудалены елементами прогрессии от а_т , то его находим по формуле

a[m]=(92,8+1,4)/2=47,1.
Ответ a[m]=47,1.

 

Пример 18. В арифметической прогрессии а_т =8,75; а_т+п=13,8. Вычислить a[m-n]

Решение: Выразим следующие члены прогрессии через предыдущие
a[m+n]=a[m]+n*d;
a[m]=a[m-n]+ n*d.
С первой формулы находим произведение n*d и подставляем во вторую
n*d= a[m+n]-a[m];
a[m-n]=a[m]-n*d=2*a[m]-a[m+n].
Подставим значение в формулу и найдем нужный элемент прогрессии
a[m-n]= 2*8,75-13,8=3,7.
Ответ: a[m-n]=3,7.

 

Пример 19. В геометрической прогрессии b₂1*b₇=62,7. Вычислить b₁₉ если b₉=5,5.
Решение: Задача одна из сложных среди всех которые рассмотренные здесь, однако на практике решить возможно. Запишем все старшие члены геометрической прогрессии через b₇

Запишем произведение 21 и 7 члена геометрической прогрессии и расписано b₉

Чтобы получить выражение для 19 члена прогрессии нужно произведение b₂₁*b₇ разделить на b₉

С опытом Вы увидите, что в подобных примерах остается делить одни значения на вторые или умножать, примеры где нужно тянуть корни или подносить к степени в геометрических прогрессиях встречаются крайне редко.
Вычисляем b₁₉
b[19]=62,7/5,5=11,4.
Ответ: b[19]=11,4.

 

Пример 20. Вычислить сумму первых двадцати членов арифметической прогрессии (а_n) если а₆ +а₉+а₁₂+ а₁₅ = 20 .
Решение: Выглядит на первый взгляд непонятно, как с такой записи получить сумму. Однако, если вспомнить формулу суммы арифметической прогрессии, то все что там фигурирует — это первый и последний член суммы, а также их количество. Таким образом следует представить сумму заданных членов прогрессии через первый и последний элемент. Уверяю Вас, что разница прогрессии в расчетах упростится и заданное условие не что иное, как удвоенная сумма первого и 20 члена прогрессии. В этом Вы сейчас наглядно убедитесь. Расписываем первые два слагаемые суммы через a [1], а остальные через a[20].
a[6]=a[1]+5d;
a[9]=a[1]+8d;
a[12]=a[20]-8[d];
a[15]=a[20]-5d.
Просуммировав их всех получим
a[6]+a[9]+a[12]+a[15]=2*a₁+2*a[20].
Формула суммы 20 членов арифметической прогрессии имеет вид

Числитель дроби и является заданной суммой, разделенной на 2 Поэтому сразу выполняем вычисления
S[20]=20/2/2*20=100.
Ответ: S[20]=100.

 

Пример 21. Сумма первого и пятого членов арифметической прогрессии равна 28,а произведение четвертого и третьего членов 280. Вычислить сумму первых десяти членов прогрессии.
Решение: В этом задании и подобных нужно составлять систему уравнений. Для этого запишем сначала условие задания в виде
a[1]+a[5]=28; a[3]*a[4]=28.
Поскольку 3 член прогрессии является равноудален от 1 и 5, то их среднее арифметическое и будет 3 членом прогрессии
a[3]=(a[1]+a[5])/2=28/2=14.
Произведение распишем через 3 член прогрессии
a[3]*a[4]=a[3]*(a[3]+d)=280;
14*(14+d)=280.
Отсюда находим разницу прогрессии
14+d=280/14=20;
d=20-14=6.
Вычислим 1 и 10 член арифметической прогрессии
a[1]=a[3]-2d=14-2*6=2;
a[10]=a[3]+7d=14+7*2=28.
Есть все необходимые елементы для вычисления суммы прогрессии
S[10]=(2+28)*10/2=150.
Ответ: S[10]=150.

 

Пример 22. Знайты четыре числа которые образуют геометрическую прогрессию в которой третий член больше первого на 9, а второй больше четвертого на 18. В ответе записать их сумму.
Решение: Запишем условие задачи в виде
b[3]-b[1]=9; b[2]-b[4]=18.
Распишем члены геометрической прогрессии через 1 элемент

Поделив второе уравнения на первое получим знаменатель прогрессии

Из первого уравнения находим 1 член геометрической прогрессии

Все остальные члены прогрессии получаем умножением предыдущего номера на знаменатель.
b[2]=b[1]*q=3*(-2)=-6;
b[3]=b[2]*q=-6*(-2)=12;
b[4]=12*(-2)=-24.
Осталось вычислить сумму членов геометрической прогрессии
S=3-6+12-24=-15.
Ответ: S=-15.

 

Пример 23. Знаменатель геометрической прогрессии 1/3, третий член геометрической прогрессии 1/9, а сумма всех членов геометрической прогрессии 13/9. Найти количество членов геометрической прогрессии.
Решение: Сумма членов геометрической прогрессии находим по формуле

Найдем первый член прогрессии через 3 и знаменатель.


Подставим значение в формулу суммы и найдем количество суммируемых членов


Итак, получили 3 члена геометрической прогрессии.
Ответ: n=3.

 

Пример 24. Дано две арифметические прогрессии. Первый и пятый члены первой прогрессии соответственно равны 7 и -5. Первый член второй прогрессии равна 0, а последний 7/2. Вычислить сумму членов второй прогрессии если известно,что третьи члены обеих прогрессий равны между собой.
Решение: Запишем условие примера
a[1]=7;a[5]=-5;
b[1]=0; b[n]=7/2;
a[3]=b[3]; S[n]-?
Найдем 3 член первой прогрессии через среднее арифметическое соседних
a[3]=(a[1]+a[5])/2=(7-5)/2=1.
Учитывая что
b[3]=a[3]=1,
найдем шаг второй прогрессии.
b[3]=b[1]+2*d;
1=0+2*d; d=1/2=0,5.
Найдем номер последнего члена второй прогрессии
b[n]=0+(n-1)d=7/2=3,5;
n-1=3,5/d=3,5/0,5=7;
n=7+1=8.
Вычислим сумму восьми членов прогрессии
S[8]=(0+3,5)*8/2=3,5*4=14.
Ответ: S[8]=14.

 

После такой практиктики я думаю Вы знаете как находить сумму арифметической и геометрической прогрессии. Если нет ознакомьтесь с примерами изначально (это была шутка).

Похожие материалы:

Если примеры были полезны Вам — посоветуйте их друзьям.

yukhym.com

Урок математики «Арифметическая и геометрическая прогрессия»

Тема: Арифметическая и геометрическая прогрессии

Тип урока: урок обобщения и систематизации знаний.

Цель: актуализация имеющиеся знания об арифметической и геометрической прогрессиях с использованием стратегий критического мышления; отработать умения: анализировать и систематизировать материал; участвовать в учебном диалоге; сотрудничать при выполнении учебных задач.

Задачи:

– обобщить и систематизировать знания об арифметической и геометрической прогрессиях;

– контроль усвоения знаний и умений;

– способствовать развитию умений анализировать, обобщать, сравнивать, самостоятельно применять знания, умения и навыки по теме, осуществлять их перенос в новые условия; развитию памяти, внимания, логического мышления, правильной математической речи, познавательного интереса;

– способствовать воспитанию ответственности, активности, умения работать в группах, общей культуры.

Ход урока

I. Вводно-мотивационная часть.

II. Стратегия вызова. Актуализация имеющихся знаний.

Использование приема критического мышления «Корзина идей»

1. Каждый ученик вспоминает и записывает в тетради все, что знает по теме «Арифметическая и геометрическая прогрессии» (индивидуальная работа продолжается 1-2 минуты).

2. Обмен информацией в парах.

3. Далее каждая группа называет какое-то одно сведение или факт, не повторяя ранее сказанного.

4. Все сведения кратко записываются в «корзине идей», даже если они ошибочны.

5. Все ошибки исправляются по ходу обсуждения.

III. Стадия осмысления содержания. 

Класс делится на три группы следующим способом. Имеются листки с различными последовательностями: арифметической, геометрической, ни арифметической, не геометрической. Учащиеся вытягивают листки, и по виду последовательности, определяют свою группу.

III а. Разминка.

Для того, чтобы учащиеся окончательно убедились в своих твердых знаниях теоретического материала и формул группам предлагаются задания.

Задание для первой группы.

Мама предложила сыну на выбор два варианта: давать ему ежедневно на карманные расходы в течении месяца по 200 тенге в день или дать в первый день 50 тенге, зато в следующий на 50 тенге больше, в следующий еще на 50 тенге больше и так далее в течении месяца. Какой вариант выгоднее для сына, если мама с сыном договаривается на апрель? На март?

Задание для второй группы.

Подготовку к экзамену начинают с 15 мин. В каждый следующий день ее время увеличивают на 10 мин. Сколько дней следует готовиться к экзамену в указанном режиме, чтобы достичь максимальной продолжительности подготовки, не влияющей на здоровье подростка, 1 час 45 минут?

Задание для третьей группы.

Является ли число 156 членом арифметической прогрессии в которой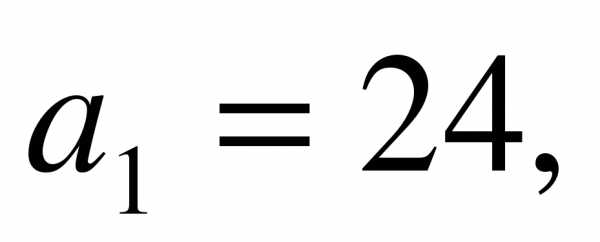

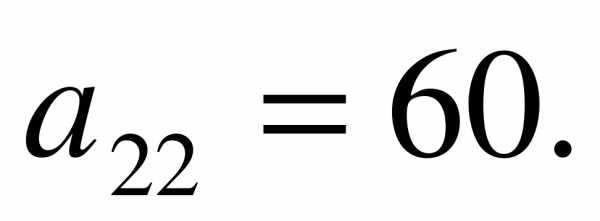
Проверка.

Группы меняются выполненными карточками и осуществляют взаимопроверку. Проверяют правильность выполненной работы по слайду с готовым решением 

III б. Работа со всем классом. Фронтальная работа. Тренировка смысловой памяти, наблюдательности, поиск закономерностей составления таблицы.

Учитель: Ну а мы с вами ребята, займемся тренировкой памяти.

Задание: Запомнить все числа, включенные в таблицу, а затем их воспроизвести. (Постарайся увидеть закономерность.) Задания представлены на слайде.

7	14	28
56	112	224
448	896	1792

Разгадка: это геометрическая прогрессия со знаменателем 2. Необходимо запомнить два числа 7 и 2.

Разгадка: это арифметическая прогрессия с разностью 3. Необходимо запомнить два числа -12 и 3.

III в. Задачи для работы в группе. Стратегия «Карусель». Группам раздается по одной задаче. Из предложенной задаче группа составляет еще 2 задачи. Составленные задачи по методу карусели предаются для решения соседней группе.

Задача для первой группы

При хранении бревен строевого леса их укладывают так, как показано на рисунке. Сколько бревен находится в одной кладке, если в ее основании положено 12 бревен?

Задача для второй группы

Для укрепления иммунитета больному следует принимать капли настойки прополиса. Начиная с 1 капли, больной должен увеличивать дозу каждый день на одну каплю. После того как больной примет 40 капель, ему следует уменьшать дозу каждый день на 2 капли в день. Сколько капель должен выпить больной и какова продолжительность курса лечения?

Задача для третьей группы

Рабочий выложил плитку следующим образом: в первом ряду – 3 плитки, во втором – 5 плиток и т.д., увеличивая каждый ряд на 2 плитки. Сколько плиток понадобится для 7 ряда?

IV. Стадия рефлексии. Подведение итогов работы, постановка домашнего задания.

Составить 3 комбинированных задачи по теме «Прогрессии» и их решения оформить на альбомном листе.

Рефлексия. 

Прием «Рюкзак». Суть – зафиксировать свои продвижения в учебе, а также, возможно, в отношениях с другими. Рюкзак перемещается от одного ученика к другому. Каждый не просто фиксирует успех, но и приводит конкретный пример. Если нужно собраться с мыслями, можно сказать «пропускаю ход».

Пример.

– я научился составлять решать задачи по теме «Прогрессии»;

– я запомнил формулу для нахождения суммы n-го члена геометрической прогрессии;

– я наконец-то запомнил, чем арифметическая прогрессия отличается от геометрической.

videouroki.net

Арифметическая и геометрическая прогрессии. Решения

На Ваше рассмотрение представлены решения примеров повышенной сложности на арифметическую и геометрическую прогрессии. Методика вычислений является полезной для практических занятий как в школе, так и ВУЗах и соответствует школьной программе. Если приведенные примеры для Вас трудны прочтите для начала простые задачи на арифметическую и геометрическую прогрессию.

Пример 1. В геометрической прогрессии b₁₀* b₁₄* b₂₁=-0,125. Вычислить b₁₅.
Решение. Приведем методику которая упростит решение подобных примеров. Для начала найдем сумму индексов членов прогрессии.
10+14+21=45.
Сумма 45 нацело делится на 15 и получаем 3. Заданное произведение членов прогресии можно представить в виде
b₁₀* b₁₄* b₂₁=(b₁₅)^3
Это следует и со свойств геометрической прогреси.
Отсюда вычисляем искомый член прогрессии

Итак, 15 член прогрессии равен -0,5.

 

Пример 2. Сумма трех чисел, представляющих возрастающую арифметическую прогрессию равна 21. Если к ним, соответственно, добавить 2, 3, и 9 то образованные числа составят геометрическую прогрессию. Найти наибольшее из искомых членов проргресии.
Решение. Таким заданием можно проверить знание формул арифметической и геометрической прогрессии.
Обозначим члены возрастающей прогрессии через a-d, a, a+d.
Тогда их сумма равна 3a=21, откуда a=21/3=7.
Такое быстрое решение получили за счет удачного выбора формул членов прогресии. Таким образом средний член арифметической прогрессии известен.
Далее найдем неизвестные члены геометрической прогрессии
Первый – a-d+2=7-d+2=9-d
второй a+3=7+3=10.
третий a+d+9=7+d+9=16+d.
По свойству геометрической прогрессии о среднем геометрическом значении получим что квадрат среднего ее члена равен произведению равноудаленных, т.е.

Подставим члены геометрической прогрессии в формулу
(9-d)(16+d)=10^2=100.
Думаю Ви знаете что делать с подобным уравнением.
Раскроем скобки и сведем к квадратному уравнению относительно разницы арифметической прогрессии.


Находим дискриминант

и шаг арифметической прогрессии

Отсюда находим нужный член арифметической прогрессии
a+d=7+4=11.
Вот такие сложные задачи на прогрессию Вам могут встретиться в обучении.

 

Пример 3. Три числа которые составляют возрастающую арифметическую прогрессию дают в сумме 15. Если к первому и второму из них добавить по единице, а к третьему числу прибавить 4, то новые числа составят геометрическую прогрессию. Найти старшый член заданной прогресии.
Решение. Задача аналогична предыдущей. Вводим те же обозначения что и в предыдущем примере, тогда средний член арифметической прогрессии равен 15/3=5, а соседние – 5-d и 5+d.
По условию запишем члены геометрической прогрессии
(5-d+1)=6-d; 5+1=6; 5+d+4=9+d
и составим из них уравнение
(6-d)(9+d)=6*6=36.
Раскрываем скобки и сводим к квадратному уравнению


Вычисляем дискриминант

и разницу арифметической прогрессии
d=(-3+9)/2=3.
Больший из членов прогресии равен 8
a+d=5+3=8.

 

Пример 4. Три числа b₁, b₂, b₃ образуют возрастающую геометрическую прогрессию. Вычислить b₃ если b₁*b₂*b₃=64, b₁+b₂+b₃=14.
Решение. Опять имеем задание на составление уравнения. Обозначим члены геометрической прогрессии в нужном для нас виде
b/q;b;b*q.
Подставив в условие можно найти средний член геометрической прогрессии
b/q*b*b*q=b^3=64.
Отсюда средний член геометрической прогрессии равен корню кубическому из 64

С учетом найденного значения, запишем второе условие задания

b₁+b₂+b₃=14;

Умножым на знаменатель прогресии

и сведем к квадратному уравнению

Вычислим дискриминант уравнения

и знаменатель геометрической прогрессии

Второе значение отбрасываем, так как при нем геометрическая прогрессия становится убывающей, а по условию мы ищем возрастающую прогрессию.
Теперь без труда находим старший член геометрической прогрессии
b*q=4*2=8.

 

Пример 5. Три числа b₁, b₂, b₃ образуют убивающую геометрическую прогрессию. Вычислить b₃ если b₁*b₂*b₃=27, b₁+b₂+b₃= 13.
Решение. По свойству геометрической прогрессии имеем
b₂/q*b₂*b₂*q=2^3=27.
Отсюда второй член геометрической прогресии равен b[2]=3.
Из второго условия получим уравнение


Найдем дискриминант квадратного уравнения

и определим знаменатель прогрессии

Первое значение q=3 не удовлетворяет начальное условие (убивающая прогресия).
При q=1/3 третий член геометрической прогрессии равен
b[3]=b[2]*q=3/3=1.
Рекомендуем используйте приведенный алгоритм вычислений в подобных задачах.

 

Пример 6. Определить седьмой член возрастающей арифметической прогрессии если а₃+а₉=24, а₃*а₉=108.
Решение. Задача не сложная, поскольку имеем два условия и две неизвестные. Так что решение найти можно. Выразим из первого уравнения a[9] и подставим во второе


Последнее уравнение решаем через дискриминант


С первого условия
а₃+а₉=24
видим, что при а₃=18 прогрессия не будет возрастающей. Итак, остается а₃=6. Отсюда
a[9]=24-a[3]=24-6=18.
С другой стороны
a[9]=a[3]+6d
имеем условие для нахождения разницы прогрессии
6+6d=18; 6d=12; d=12/6=2.
По формуле находим седьмой член арифметической прогрессии
a[7]=a[3]+4d=6+4*2=14.
Вот и весь алгоритм подобных вычислений.

 

Пример 7. Определить восьмой член возрастающей арифметической прогрессии если а₂+а₇=18, а₂*а₇=56.
Решение. Подобнаяе по схеме вычислений задача уже рассматривалась. Выразим из первого уравнения a[2] и подставим во второе
a[2]=18-a[7]; (18-a[7]) a[7]=56.
Раскроеем скобки и сведем к квадратному уравнению

С помощью дискриминанта

вычислим неизвестный член прогрессии

С первого условия делаем вывод что только при a[7]=14 арифметическая прогрессия будет возрастающей.
Соответственно второй член прогресии равен
a[2]=18-a[7]=18-14=4.
По формуле
a[7]=a[2]+5d
определяем шаг прогрессии
14=4+5d; 10=5d; d=2.
Находим 8 член арифметической прогрессии
a[8]=a[7]+d=14+2=16.
Для самопроверки можете подставить найдены члены прогрессии в условие задания.

 

Пример 8. Вычислить сумму первых восьми членов нисходящей арифметической прогрессии если а₂+а₆=24, а₂*а₆=128.
Решение. Чтобы найти сумму прогрессии нам нужно знать первый и восьмой член прогрессии, или 1 член прогрессии и разность (шаг).
Для начала определим из двух уравнений хотя бы один член прогрессии
a[2]=24-a[6];
(24-a[6])*a[6]=128.
При раскрытии скобок получим квадратное уравнение

Как решать квадратные уравнения Вы уже знаете. Дискриминант принимает значение

Далее считаем 6 член арифметической прогрессии

При a[6]=8 арифметическая прогрессия является убывающей. Находим разницу прогрессии
a[2]=24-a[6]=24-8=16.
a[6]=a[2]+4d=16+4d=8;
4d=-8;d=-2.
Легко заметить что значение второго члена прогрессии всегда совпадает с корнем уравнения который отвергаем по условию задачи. Это своего рода подсказка правильности вычислений.
Находим первый и восьмой член прогрессии
a[1]=a[2]-d=16-(-2)=18;
a[8]=a[6]+2d=8+2*(-2)=4.
Найденные значения подставляем в формулу суммы арифметической прогрессии
S=(a[1]+a[8])*8/2=(18+4)*8/2=88.
Сумма восьми членов прогрессии равна 88.

Конечно это не все примеры, которые можно встретить в интернете среди возможных, однако и на их базе можно взять для себя несколько удачных приемов которые можно использовать на практике при решении упражнений на арифметическую и геометрическую прогрессии. Навыки приходят с практикой, поэтому ищите подобные задачи и учитесь решать!

Похожие материалы:

yukhym.com

Арифметическая и геометрическая прогрессии. Формулы для вычисления разности арифметической прогрессии и знаменателя геометрической прогрессии.

Более 50 лет существовала система закрытых текстов письменных работ к экзаменам по математике за курс основной и средней школы. Затем был введен экзамен за курс основной школы по открытым текстам. За пять лет до введения ЕНТ и в 11 классе был также введен экзамен по открытым текстам.

Использование тестов в процессе обучения – это требование времени. Задача учителя – подготовить школьников к процессу тестирования, научить  рациональным  и кратким способам решения задач.

При широком применении тестовых заданий по математике, как и по другим предметам, возникла необходимость принятия быстрого решения того или иного примера.

Так, при изучении темы «Арифметическая прогрессия» учащиеся должны твердо усвоить определение арифметической прогрессии, формулы n-ого члена и суммы n первых членов арифметической прогрессии. Следует обратить внимание учащихся на формулы, которые используются при решении упражнений.

При вычислении суммы n первых членов прогрессии учащиеся могут использовать ту из двух формул, применение которой в каждом конкретном случае целесообразно. Упражнения, приведенные в учебниках, направлены, прежде всего, на формирование умений применять    рассмотренные формулы при решении задач.       

Изложение материала по теме «Геометрическая прогрессия» построено по аналогии с изложением арифметической прогрессии: определение, формула ого члена, формула суммы первых членов геометрической прогрессии. Прочитав подряд определения арифметической и геометрической прогрессии, можно обратить внимание на то, что они похожи. Надо лишь заменить сложение умножением или наоборот. А зная формулу ого члена арифметической прогрессии, можно получить формулу для геометрической прогрессии, если заменить сложение умножением, а умножение – возведением в степень.

Весь материал — смотрите документ.

videouroki.net