Графики функций. Прямая. Парабола. Функция корня. Тригонометрические функции
Факт 1.
\(\bullet\) Линейная функция – функция вида \(f(x)=kx+b\), где \(k,b\) – некоторые числа.
\(\bullet\) Графиком линейной функции является прямая.
\(\bullet\) Если \(b=0\), то прямая проходит через начало координат.
\(\bullet\) Графиком \(x=a\) является прямая, параллельная оси \(Oy\).
\(\bullet\) Графиком \(y=с\) является прямая, параллельная оси \(Ox\).
\(\bullet\) Для \(f(x)=kx+b\) коэффициент \(k\) равен тангенсу угла наклона прямой к положительному направлению оси \(Ox\).
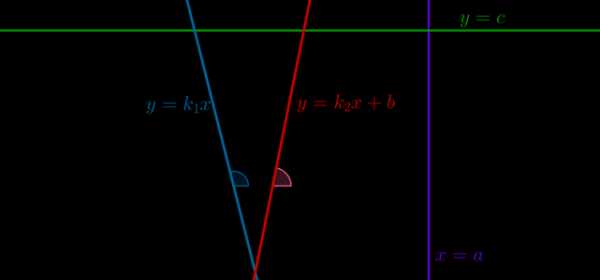
\(k_1=\mathrm{tg}\alpha\), \(k_2=\mathrm{tg}\beta\).
\(\bullet\) Если две прямые \(y=k_1x+b_1\) и \(y=k_2x+b_2\) параллельны, то \(k_1=k_2\).
\(\bullet\) Если эти прямые взаимно перпендикулярны, то \(k_1\cdot
k_2=-1\).
Факт 2.
\(\bullet\) Квадратичная функция – функция вида \(f(x)=ax^2+bx+c\), где \(a, b, c\) – некоторые числа, причем \(a\ne 0\).
\(\bullet\) Графиком квадратичной функции является парабола.
\(\bullet\) Если \(a>0\), то ветви параболы направлены вверх, если \(a<0\) – ветви направлены вниз.
\(\bullet\) Абсцисса вершины параболы \[x_0=-\dfrac b{2a}\] \(\bullet\) Всякая парабола симметрична относительно прямой \(x=x_0\).
\(\bullet\) Корни уравнения \(ax^2+bx+c=0\) – точки пересечения параболы с осью \(Ox\).

Факт 3.
\(\bullet\) Кубическая функция – функция вида \(f(x)=ax^3+bx^2+cx+d\), где \(a, b, c, d\) – некоторые числа, причем \(a\ne 0\).
\(\bullet\) Графиком кубической функции является кубическая парабола.
\(\bullet\) Если уравнение \(ax^3+bx^2+cx+d=0\) имеет 1 корень, то график \(y=ax^3+bx^2+cx+d\) выглядит, например, как \((1)\).
\(\bullet\) Если уравнение \(ax^3+bx^2+cx+d=0\) имеет 2 корня, то график \(y=ax^3+bx^2+cx+d\) выглядит, например, как \((2)\).
\(\bullet\) Если уравнение \(ax^3+bx^2+cx+d=0\) имеет 3 корня, то график \(y=ax^3+bx^2+cx+d\) выглядит, например, как \((3)\).

Факт 4.
\(\bullet\) Функция корня – функция \(f(x)=\sqrt x\).
\(\bullet\) График функции \(y=\sqrt x\):

\(\bullet\) Заметим, что \(y=\sqrt x\) определена при \(x\geqslant 0\) и принимает значения \(y\geqslant 0\).
Факт 5.
\(\bullet\) Графиком функции \(y=\sin x\) является синусоида
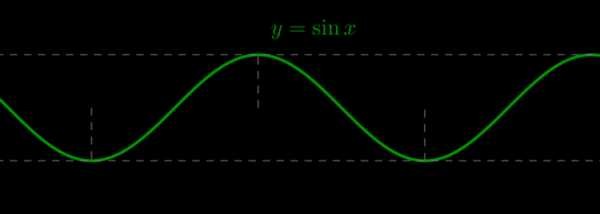
\(\bullet\) Графиком функции \(y=\cos x\) также является синусоида, но сдвинутая на \(\frac{\pi}2\) единиц влево по оси \(Ox\)
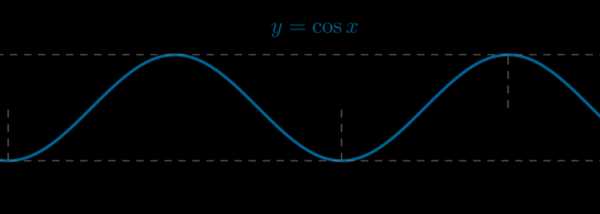
\(\bullet\) Обе функции \(y=\sin x\) и \(y=\cos x\) периодичны с периодом \(2\pi\). Обе функции могут принимать значения \(y\in [-1;1]\).
\(\bullet\) Функция \(y=\sin x\) – нечетная, функция \(y=\cos x\) – четная.
Факт 6.
\(\bullet\) График функции \(y=\mathrm{tg} \,x\)
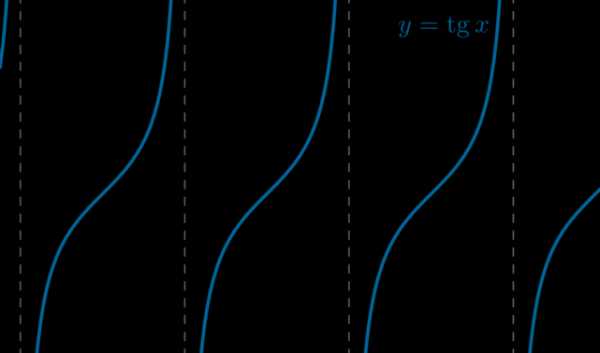
Прямые \(x=k\cdot \frac{\pi}2\), где \(k\) – нечетное число, являются асимптотами графика (то есть график их не пересекает).
\(\bullet\) График функции \(y=\mathrm{ctg} \,x\)
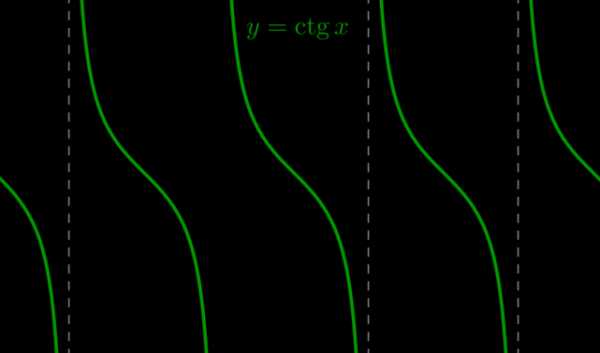
Прямые \(x=n\cdot \pi\), где \(n\) – целое число, являются асимптотами графика (то есть график их не пересекает).
\(\bullet\) Обе функции \(y=\mathrm{tg} \,x\) и \(y=\mathrm{ctg} \,x\) периодичны с периодом \(\pi\) и нечетны.
Факт 7.
\(\bullet\) Показательная функция \(f(x)=a^x\) при \(a>1\) является возрастающей при всех \(x\), область значений \(a^x\in (0;+\infty)\):
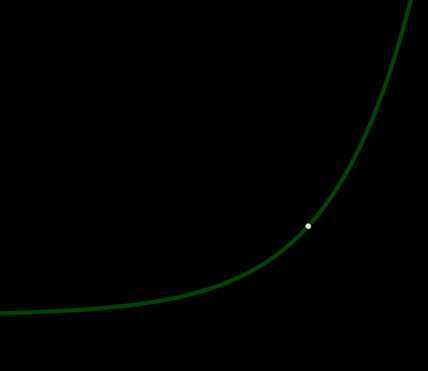
Ее график всегда проходит через точку \((0;1)\).
\(\bullet\) Показательная функция \(f(x)=a^x\) при \(0<a<1\) является убывающей при всех \(x\), область значений также \(a^x\in (0;+\infty)\):

Ее график всегда проходит через точку \((0;1)\).
Факт 8.
\(\bullet\) Логарифмическая функция \(y=\log_ax\) при \(a>1\) является возрастающей, ее область определения \(x>0\), ее область значений \((-\infty;+\infty)\):

Ее график всегда проходит через точку \((1;0)\).
\(\bullet\) Логарифмическая функция \(y=\log_ax\) при \(0<a<1\) является убывающей, ее область определения \(x>0\), ее область значений \((-\infty;+\infty)\):

Ее график всегда проходит через точку \((1;0)\).
shkolkovo.net
Как легко составить уравнение параболы по графику
Автор Сергей Валерьевич
Среда, Август 3, 2016
В данной статье репетитор по математике рассказывает о простом и эффективном способе составления уравнения параболы по её графику, которому вас не научат в школе. Дочитайте эту статью до конца или посмотрите видео с подробным объяснением, потому что эта информация может вам пригодиться на экзамене.
Задача состоит в том, чтобы по графику параболы (см. рисунок) определить коэффициенты a, b и c соответствующей квадратичной функции :
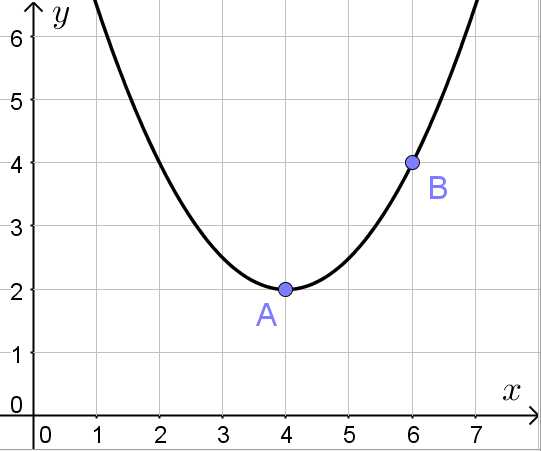
Существует стандартный и крайне неэффективный способ решения этой задачи. Он заключается в том, чтобы через координату вершины параболы связать коэффициенты a и b, используя формулу . Затем взять координаты двух точек, которые принадлежат параболе, составить систему уравнений и решить её относительно искомых коэффициентов. Считать придётся долго и муторно.
Мы не пойдём этим путём. Предлагаемый в данной статье способ намного более прост и изящен. Введём новую систему координат с центром в вершине параболы и осями, сонаправленными с исходной системой координат. В данной системе координат уравнение нашей параболы будет иметь вид: , где . Изобразим в новой системе координат график квадратичной функции (синяя пунктирная линия на рисунке):

Абсциссы точек C и B в новой системе координат равны. Ордината точки C в 2 раза больше ординаты точки B. Значит график исходной параболы в новой системе координат получен умножением на всех ординат точек графика функции . Откуда получаем, что . Значит исходная парабола может быть представлена в виде следующего выражения в новой системе координат: .
Осталось перейти в исходную систему координат. Поскольку новая система координат получена путём параллельного переноса исходной системы координат на 4 единичных отрезка вправо и 2 единичных отрезка вверх, то в исходной системе координат наша парабола может быть представлена в виде следующего выражения:
yourtutor.info
Смещение графика квадратичной функции y = (x
Разделы: Математика, Конкурс «Презентация к уроку»
Презентация к уроку
Загрузить презентацию (805,9 кБ)
Внимание! Предварительный просмотр слайдов используется исключительно в ознакомительных целях и может не давать представления о всех возможностях презентации. Если вас заинтересовала данная работа, пожалуйста, загрузите полную версию.
Цели урока:
Образовательная: исследовать смещение графика квадратичной функции, определить положение графика в зависимости от значений коэффициентов b, c.
Воспитательная: умение работать в группе, организованности.
Развивающая: навыки исследовательской работы, умение выдвигать гипотезы, анализировать полученные результаты, систематизировать полученные данные.
Структура урока
- Организационный момент – 3 минуты.
- Исследовательская работа – 20 минут.
- Закрепление изученного материала – 15 минут.
- Рефлексия – 2 минут.
- Итог урока – 3 минуты.
- Домашнее задание – 2 минуты.
Ход урока
1. Организационный момент.
Цель урока провести исследовательскую работу. Объектом исследования будут квадратичные функции разного вида. Вам предстоит определить, как влияют коэффициенты b, cна график функций вида y=x2+с, y=(x-b)2, y=(x-b)2+c.
Для выполнения задания необходимо разделиться на группы (4 группы по 5 человек, одна группа “эксперты” наиболее подготовленные ученики).
Каждая группа получает план исследования <Приложение>, лист формата А3 для оформления результатов.
2. Исследовательская работа
.Две группы (уровень А) исследуют функции вида y= x2+с, одна группа (уровень В) исследует функцию вида y=(x-b)2, одна группа (уровень С) исследует функцию y=(x-b)2+c. Группа “Экспертов” исследует все функции.
| Функция | Результат | ||
| 1 группа | у=x2+3; | <Рисунок 10> | |
| 2 группа | у=x2-5; | <Рисунок 11> | |
| 3 группа | у=(х-4)2; | <Рисунок 12> | |
| 4 группа | у=(х-2)2+3. | <Рисунок 13> |
План работы
- Для того чтобы выдвинуть гипотезу сделайте предположение, как может выглядеть ваша функция.
- Постройте график исследуемых функций (определите вершину параболы (х0, y0), задайте таблицей 4 точки).
- Сравните получившийся график с контрольным образцом y=x2.
- Сделайте вывод (как изменилось положение графика вашей функции относительно контрольного образца).
- Результаты оформите на листе формата А3 и представьте “экспертной” группе.
“Экспертная” группа сверяет результаты свои с результатами остальных групп, систематизирует и обобщает результаты, выступает с выводами. В случае неточностей или ошибок учитель вносит коррекционные замечания.
Сверка полученных результатов со слайдами №2-5.
Любую квадратичную функцию y=ax2+bx+c, можно записать в виде y=a(x-x0
)2+y0, где x0 и y0 выражаются через коэффициенты a, b, c. Таким образом, ваши коэффициенты b=x0, c=y0 являются координатами вершины параболы.3. Закрепление изученного материала.
Фронтальная работа с классом.
1. Найти ошибку в графиках функций (Слайды№6-9).
y=(х+6)2 |
у=х2-2 |
Коэффициент b |
Нет ошибки |
Рисунок 1 |
Рисунок 2 |
| у=(х+5)2 |
у=(х-2)2+2 |
| Коэффициент b и с | Коэффициент b |
| Рисунок 3 | Рисунок 4 |
Результаты
<Рисунок 7>
<Рисунок 2>
<Рисунок 8>
<Рисунок 9>
Какой коэффициент вам помог найти ошибку?
2. Соотнесите графики функций согласно цветам (слайд №10).
Рисунок 5
| y=(х-4)2-2 | синий |
| y=-x2+5 | красный |
| y=(x+1)2+3 | зеленый |
| y=(x-3)2 | фиолетовый |
4. Рефлексия.
Группа “Экспертов” отвечают на вопросы:
– Какие ошибки допустили группы?
– Достигнута ли цель занятия?
– Соответствуют ли полученные результаты исследования поставленной гипотезе?
5. Итог урока (слайд №11)
:На положение графика функции y=(x-b)2+c влияют коэффициенты b и c,
“+b” парабола сдвинута вправо по оси абсцисс на b единичных отрезков,
“–b” парабола сдвинута влево по оси абсцисс на b единичных отрезков,
“+с” парабола сдвинута вверх по оси ординат на с единичных отрезков,
“-с” парабола сдвинута вниз по оси ординат на с единичных отрезков.
6. Домашнее задание
- Построить график квадратичной функции, имеющую вершину в точке А(1;-2), коэффициент a=1.
- Подумайте, в какой области можно использовать знания по данной теме (практическое применение).
Приложение
7.01.2012
Поделиться страницей:xn--i1abbnckbmcl9fb.xn--p1ai
Квадратичная функция, график квадратичной функции
Определение: Квадратичной функцией называют функцию вида , где
Свойства квадратичной функций
- Область определения
- Множественное значение
- Четность, нечетность
- Непрерывность и дифференцируемость
- Возрастание и убывание, экстремумы
- Графиком квадратичной функции всегда является парабола, ветви которой направлены вверх при и вниз при
при
при
при — функция ни четная, ни нечетная
при — парная
Квадратичная функция непрерывна и диференційовна на всей числовой прямой
при убывает на и возрастает на , — точка минимума, — минимум
при возрастает на и убывает на , — точка максимума, — максимум
Координаты вершины параболы:
; , где
Ось симметрии параболы
Графики квадратичных функций
Симметрия относительно оси
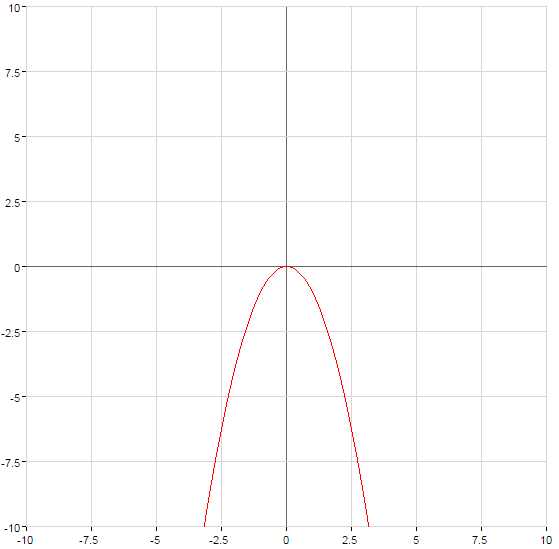
График функции сжимается при или растягивается при относительно оси на количество единиц, равное числу а
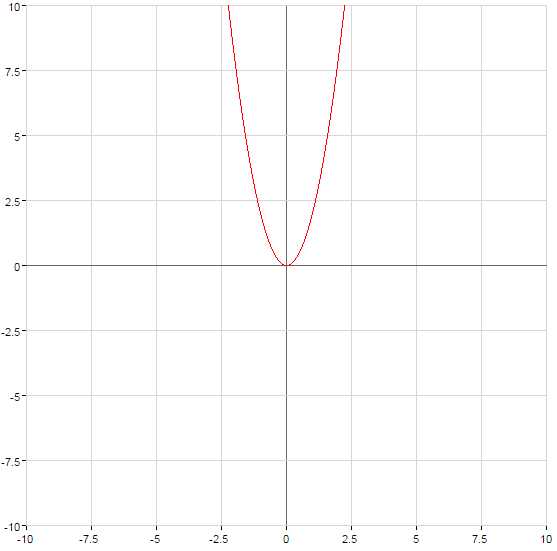
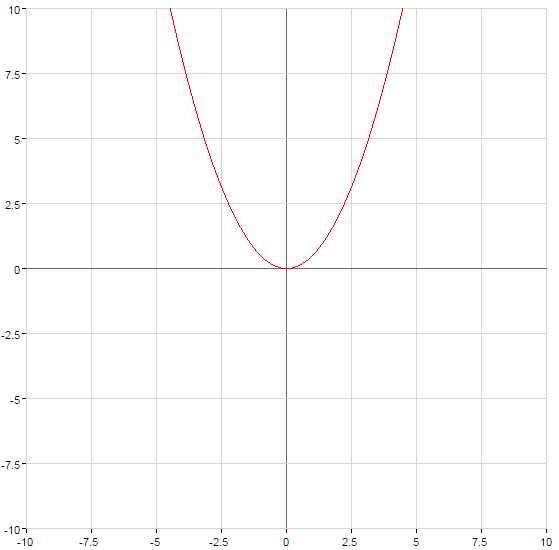
График функции поднимается при или опускается при на количество единиц, равное числу c
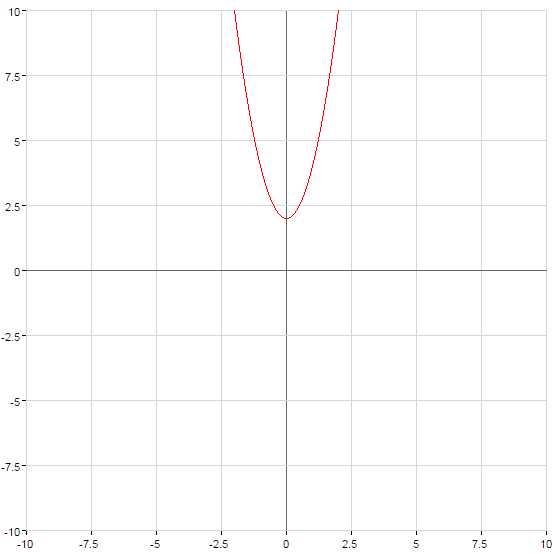
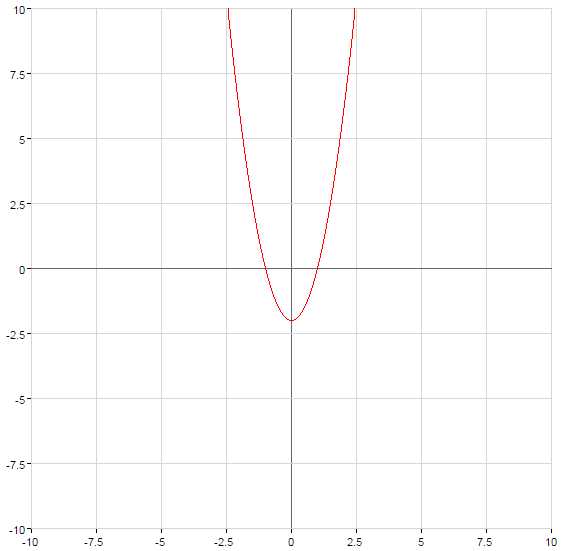
Парабола пересекает ось в точке с
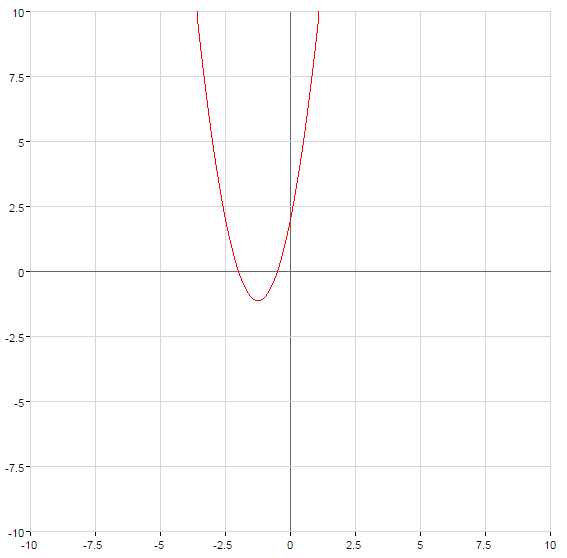
Как построить график квадратичной функции
И способ
- Вычислить абсцису вершины
- Подставить в уравнение и вычислить ординату вершины —
- Построить эскиз параболы (вида ) с вершиной в точке
при — ветви вверх, при — ветви вниз
II способ
- Розвязати квадратное уравнение
- Используя элементарные преобразования графиков, выполнить параллельный перенос параболы
(вдоль оси на , вдоль оси на )
cubens.com
от чего зависит вид графика функции
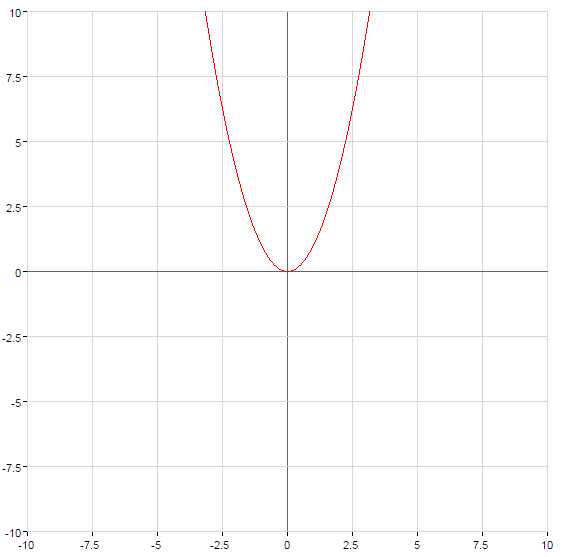
Функция вида y = a*x2 + b*x + c, где a, b, c – некоторые вещественные числа, причем а отлично от нуля, а x и y – переменные, называется квадратичной функцией. Графиком квадратичной функции y = a*x2 + b*x + c является линия, называемая в математике параболой. Общий вид параболы представлен на рисунке ниже.
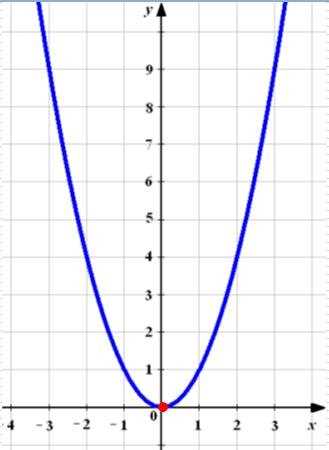
График квадратичной функции
Исследуем расположение графика квадратичной функции, в зависимости от формы и вида квадратного трехчлена. Первым критерием, влияющим на общий вид графика квадратичной функции, является знак при старшем коэффициенте.
Если при старшем коэффициенте в квадратном трехчлене стоит знак «плюс», то парабола будет иметь ветви направленные вверх. Если при старшем коэффициенте в квадратном трехчлене стоит знак «минус», то парабола будет иметь ветви направленные вниз.
Следующим критерием является значение дискриминанта квадратного уравнения.
Формула корней квадратного уравнения a*x2 + b*x+ c = 0.
x = (-b ± √D)/(2*a), где D = b2 — 4 *a*c.
В формуле корней квадратного уравнения выражение D (b2 — 4*a*c) называется дискриминантом квадратного уравнения a*x2 + b*x + c = 0. Такое название пришло из латинского языка, в переводе означает «различитель». В зависимости от того, какое значение имеет дискриминант, квадратное уравнение будет иметь два или один корень либо не иметь корней.
Если дискриминант больше нуля, то квадратное уравнение имеет два корня: (x = (-b ± √D)/(2*a)). Если дискриминант равен нулю, то квадратное уравнение имеет один корень: (x = (-b/(2*a)). Если дискриминант отрицателен, то квадратное уравнение не имеет корней.
Корнем квадратного уравнения a*x2 + b*x + c = 0 называют любое значение переменной х, такое, что квадратный трехчлен a*x2 + b*x + c обращается в нуль. Обращение в нуль значение функции равносильно тому, что график функции будет в этой точке пересекать ось Ох.
Следовательно, в зависимости от, того какое будет значение дискриминанта, вершина параболы будет расположена относительно оси координат одним из следующих трех способов: ниже оси Ох, на оси Ох, выше оси Ох. На следующем рисунке показаны основные расположения графика квадратичной функции, в зависимости от перечисленных выше двух критериев.
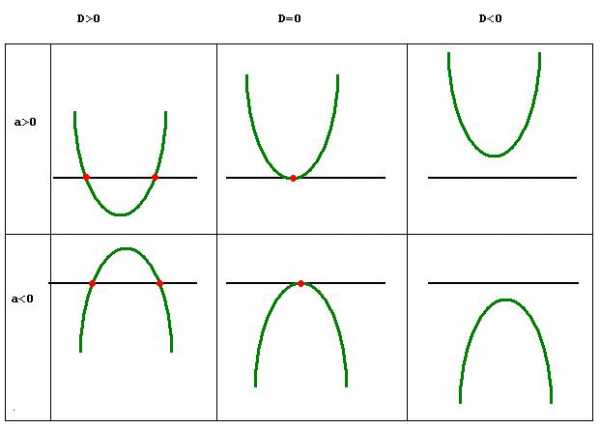
Нужна помощь в учебе?
Предыдущая тема: Квадратичная функция: ее график и свойства
Следующая тема:   Построение графика квадратичной функций: алгоритм и примеры
Все неприличные комментарии будут удаляться.
www.nado5.ru
Построение графика квадратичной функции | Алгебра
Построение графика квадратичной функции продолжим рассмотрением способа, базирующегося на преобразованиях координатной плоскости.
II способ.
1) Находим координаты вершины параболы y=ax²+bx+c — точку (xo; yo)
2) Осуществляем параллельный перенос начала отсчёта — точки O (0; 0) — в точку (xo; yo). При таком преобразовании новыми осями координат x’ и y’ становятся прямые y=yo и x=xo.
2) Строим параболу y=x² (если a>o)либо y= -x² (если a<0) с вершиной в новом начале отсчёта (достаточно отметить базовые точки).
3) От вершины строим график функции y=ax². При |a|>1 график может быть получен растяжением от оси y=y0 в |a| раз, при |a|<1 — сжатием в |a| раз.
(Вариант — график функции y=ax² можно построить с началом отсчёта в точке O (0; 0), а затем осуществить его параллельный перенос).
Примеры.
1) Построить график функции y=3x²-24x+43.
Решение:
y=3x²-24x+43 — квадратичная функция. Её график — парабола, ветви которой направлены вверх (так как a=3>0). Координаты вершины параболы
Точка (4; -5) — новое начало отсчёта. Построим параболу y=x² с вершиной в этой точке (достаточно отметить базовые точки — 1 единица вправо, 1 — вверх, 2 вправо. 4 — вверх, 1 — влево, 1 — вверх, 2 — влево, 4 — вверх.
График функции y=3x² может быть получен из графика y=x² растяжением от оси x’ (x= -5) в 3 раза:
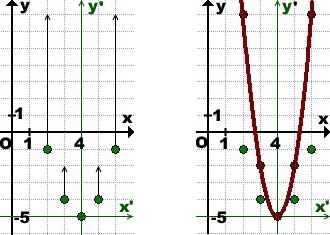
Построение графика квадратичной функции y=3x²-24x+43
2) Построить график функции y= -0,5x²-2x+1
Решение:
y= -0,5x²-2x+1 — квадратичная функция. График — парабола ветвями вниз (так как a= -0,5<0).
Координаты вершины параболы
Точка (-2; 3) — новое начало отсчёта. Построим параболу y= -x² с вершиной в этой точке. График функции
может быть получен из графика y= -x² сжатием к оси x’ (y=3) в 2 раза.
Построение графика функции y= -0,5x²-2x+1
Для построения графика квадратичной функции этим способом нужно хорошее владение навыками геометрических преобразований графиков.
Если координаты вершины параболы не являются целыми числами, этот способ менее удобен, чем построение по точкам.
Какой бы способ вы для себя ни выбрали, важно вовремя качественно усвоить данную тему, поскольку с построением графиков функций в алгебре придётся иметь дело ещё не раз.
www.algebraclass.ru
